近年来,无源定位算法由于其本身不辐射电磁信号,具有电磁隐蔽性[1]等优点受到了国内外学者的广泛关注,它已经被大量应用在无线传感器网络、雷达、麦克风阵列以及声呐系统[2-9]等领域中。无源定位技术可以归纳为依靠传感器网络获取不同类型的观测量进行求解,这些观测量主要包括到达时间(Time of Arrival, TOA)、到达时间差(Time Difference of Arrival, TDOA)、到达角(Angle of Arrival, AOA)、以及上述参数的相互结合。当运动目标或者传感器与目标之间存在相对运动关系时,还可以利用到达频率差(Fequency Difference of Arrival, FDOA)观测量对目标的位置以及速度进行估计。
本文主要针对运动目标无源定位算法进行研究。由于其相关的最大似然问题存在高度的非线性以及非凸性,因此寻找全局最优解变得十分困难。为此,国内外学者提出了大量的算法:线性化的最大似然估计(Maximum Likelihood Estimation, MLE)[10-11]是解决定位问题十分有效的算法,但是这种算法的性能以及收敛性依赖于一个好的初始位置值,一旦该值选取较差其性能也会变差。为了克服这个问题,Ho和Xu提出了著名的两步加权最小二乘(Two-Stage Weighted Least Squares, TSWLS)算法[12],TSWLS算法第1步引入额外变量并且建立了伪线性方程,随后给出了加权最小二乘(Weighted Least Squares, WLS)解,第2步利用额外变量与目标位置的关系建立了新的等式方程以提高定位精度。虽然TSWLS算法实时性较高,但是在定位精度方面还有待进一步提高;半定松弛(SeminDefine Relaxation, SDR)算法[13-14]首先将定位问题描述为具有二次约束条件的优化问题,随后利用合理的近似以及适当的松弛条件将其转化为了半定规划(SeminDefine Programming, SDP)问题,最后利用优化工具箱给出了具有高精度的估计值。但是这个问题的计算复杂度较高,需要在实时性以及精度两者之间进行较好的折中。文献[15]给出了一种基于定位误差修正的算法,第1步与传统的TSWLS相同,第2步对估计误差做了修正并给出了最终的定位估计值。文献[16]首先将定位问题描述为具有二次约束条件的二次规划(Quadratically Constrained Quadratic Programming, QCQP)问题,随后利用WLS的解,将二次约束转化为了线性约束,即将QCQP问题转化为了线性约束二次规划(Linearly Constrained Quadratic Programming, LCQP)问题;最后利用广义逆矩阵的性质对LCQP问题求解,并且形成一种迭代算法,这种算法具有闭式解的优点,同时在高斯噪声模型下,其定位性能优于现存的技术。
除上述提到的非凸性以及非线性问题,传感器参数存在误差时也会对无源算法的性能产生较大的影响,文献[17]详细阐述了不考虑传感器参数误差时产生的影响并且将TSWLS算法扩展到了存在传感器参数误差时的场景中;随后文献[18]中的TSWLS在其基础上进一步提高了算法精度,并且该算法适用非相交多源的定位解算。文献[13]中的SDR算法同样给出了一种考虑了传感器参数误差的情况,但是SDR算法计算复杂度远高于TSWLS算法。而近几年,文献[19-20]分别提出了存在传感器位置误差情况下改进的TSWLS算法以及多维标度(MultiDimensional Scaling, MDS)算法;但是,这些算法是基于TDOA观测量对目标定位解算,并不能应用到对运动目标参数估计的场景之中。因此针对存在传感器参数误差的情况下,研究一种运动目标无源定位的闭式算法十分有必要。
本文主要针对TDOA/FDOA运动目标定位场景,在考虑了传感器存在参数误差的情况下,提出了一种改进的两步加权最小二乘算法;该算法分为两步,其中第1步与文献[18]中经典的TSWLS算法第1步相同,首先引入了辅助向量,并且建立了伪线性方程,给出了辅助向量的WLS解;第2步中,与文献[18]有所区别,利用辅助向量中额外变量与目标参数之间的关系,构造了新的等式方程,并且利用WLS给出最终解。理论分析表明该算法在测量噪声较小时下可以实现克拉美罗下界(Cramér-Rao Lower Bound, CRLB)[21],并且该算法仍然是闭式解,计算复杂度与TSWLS算法相当,远小于SDR算法。此外,经过适当的维度调整,该算法同样适用于对多非相交源的定位场景。仿真实验验证了所提算法的有效性。
1 定位场景考虑在三维空间中使用M个传感器对一个运动目标的位置uo=[xo, yo, zo]T以及速度
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{s}}_i} = \mathit{\boldsymbol{s}}_i^{\rm{o}} + \Delta {\mathit{\boldsymbol{s}}_i} = {{\left[ {{x_i},{y_i},{z_i}} \right]}^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\dot s}}}_i} = \mathit{\boldsymbol{\dot s}}_i^{\rm{o}} + \Delta {{\mathit{\boldsymbol{\dot s}}}_i} = {{\left[ {{{\dot x}_i},{{\dot y}_i},{{\dot z}_i}} \right]}^{\rm{T}}}} \end{array} $ | (1) |
式中:si和
将所有可利用的传感器位置和速度值使用向量形式表示为
| $ \begin{array}{l} \mathit{\boldsymbol{s}} = {\left[ {\mathit{\boldsymbol{s}}_1^{\rm{T}},\mathit{\boldsymbol{s}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{s}}_M^{\rm{T}}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{s}}^{\rm{o}}} + \Delta \mathit{\boldsymbol{s}}\\ \mathit{\boldsymbol{\dot s}} = {\left[ {\mathit{\boldsymbol{\dot s}}_1^{\rm{T}},\mathit{\boldsymbol{\dot s}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\dot s}}_M^{\rm{T}}} \right]^{\rm{T}}} = {{\mathit{\boldsymbol{\dot s}}}^{\rm{o}}} + \Delta \mathit{\boldsymbol{\dot s}} \end{array} $ | (2) |
式中:
记
| $ \Delta \mathit{\boldsymbol{\beta }} = \mathit{\boldsymbol{\beta }} - {\mathit{\boldsymbol{\beta }}^{\rm{o}}} = {\left[ {\Delta {\mathit{\boldsymbol{s}}^{\rm{T}}},\Delta {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}} \right]^{\rm{T}}} $ | (3) |
式中:总的测量噪声向量Δβ服从零均值高斯分布,其协方差矩阵为E(ΔβTΔβ)=Qβ。
不失一般性地,选取第1个传感器为参考传感器。因此由M个传感器可以得到(M-1)个TDOA值,乘以信号传播速度之后,得到如下表达式:
| $ r_{i1}^{\rm{o}} = r_i^{\rm{o}} - r_1^{\rm{o}}\;\;\;i = 2,3, \cdots ,M $ | (4) |
式中:ri1o为TDOA乘以信号传播速度得到的距离差(Range Difference, RD)。rio为目标与第i个传感器之间的距离,其表达式为
| $ r_i^{\rm{o}} = \left\| {{\mathit{\boldsymbol{u}}^{\rm{o}}} - \mathit{\boldsymbol{s}}_i^{\rm{o}}} \right\|\;\;\;\;i = 2,3, \cdots ,M $ | (5) |
对式(4)两边关于时间求导有
| $ \dot r_{i1}^{\rm{o}} = \dot r_i^{\rm{o}} - \dot r_1^{\rm{o}}\;\;\;i = 2,3, \cdots ,M $ | (6) |
式中:
| $ \dot r_i^{\rm{o}} = {\left( {{\mathit{\boldsymbol{u}}^{\rm{o}}} - \mathit{\boldsymbol{s}}_i^{\rm{o}}} \right)^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} - \mathit{\boldsymbol{\dot s}}_i^{\rm{o}}} \right)/r_i^{\rm{o}} $ | (7) |
分别记RD以及RDR的测量向量为r和
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{r}} = {\left[ {{r_{21}},{r_{31}}, \cdots ,{r_{M1}}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{r}}^{\rm{o}}} + \Delta \mathit{\boldsymbol{r}}\\ \mathit{\boldsymbol{\dot r}} = {\left[ {{{\dot r}_{21}},{{\dot r}_{31}}, \cdots ,{{\dot r}_{M1}}} \right]^{\rm{T}}} = {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}} + \Delta \mathit{\boldsymbol{\dot r}} \end{array} \right. $ | (8) |
式中:ro=[r21o, r31o, …, rM1o]T和
同样,记α=[rT,
| $ \Delta \mathit{\boldsymbol{\alpha }} = \mathit{\boldsymbol{\alpha }} - {\mathit{\boldsymbol{\alpha }}^{\rm{o}}} = {\left[ {\Delta {\mathit{\boldsymbol{r}}^{\rm{T}}},\Delta {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}} \right]^{\rm{T}}} $ | (9) |
式中:
本节具体给出所提出算法的推导过程,由于所提出的算法第1步与文献[18]的第1步相同,因此第1步仅给出简单的总结;在新的第2步中,详细给出了推导过程。
2.1 算法第1步首先将额外变量r1o在s1处进行一阶泰勒级数展开有
| $ r_1^{\rm{o}} = \left\| {{\mathit{\boldsymbol{u}}^{\rm{o}}} - \mathit{\boldsymbol{s}}_1^{\rm{o}}} \right\| \approx d_1^{\rm{o}} + \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},{\mathit{\boldsymbol{s}}_1}}^{\rm{T}}\Delta {\mathit{\boldsymbol{s}}_1} $ | (10) |
式中:
对式(4)移项并且两边进行平方,将RD测量值ri1、可利用的传感器位置si以及式(10)代入,同时仅保留线性误差项可以得到一组TDOA等式为
| $ \begin{array}{l} {\varepsilon _i} = 2r_i^{\rm{o}}\Delta {n_{i1}} + 2{\left( {{\mathit{\boldsymbol{u}}^{\rm{o}}} - {\mathit{\boldsymbol{s}}_i}} \right)^{\rm{T}}}\Delta {\mathit{\boldsymbol{s}}_i} - 2\mathit{\boldsymbol{\eta }}_{1i}^{\rm{T}}\Delta {\mathit{\boldsymbol{s}}_1} = \\ \;\;\;r_{i1}^2 + {\left\| {{\mathit{\boldsymbol{s}}_1}} \right\|^2} - {\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^2} + 2{\left( {{\mathit{\boldsymbol{s}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}{\mathit{\boldsymbol{u}}^{\rm{o}}} + 2{r_{i1}}d_1^o\\ \;\;\;\left( {i = 2,3, \cdots ,M} \right) \end{array} $ | (11) |
式中:
对式(11)两边关于时间求导可以得到一组FDOA方程为
| $ \begin{array}{l} {{\dot \varepsilon }_i} = 2\dot r_i^{\rm{o}}\Delta {n_{i1}} + 2r_i^{\rm{o}}\Delta {{\dot n}_{i1}} + 2{\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} - {{\mathit{\boldsymbol{\dot s}}}_i}} \right)^{\rm{T}}}\Delta {\mathit{\boldsymbol{s}}_i} - \\ \;\;\;\;\;\;2\mathit{\boldsymbol{\eta }}_{2i}^{\rm{T}}\Delta {\mathit{\boldsymbol{s}}_1} + 2{\left( {{\mathit{\boldsymbol{u}}^o} - {\mathit{\boldsymbol{s}}_i}} \right)^{\rm{T}}}\Delta {{\mathit{\boldsymbol{\dot s}}}_i} - 2\mathit{\boldsymbol{\eta }}_{1i}^{\rm{T}}\Delta {{\mathit{\boldsymbol{\dot s}}}_1} = \\ \;\;\;\;\;\;2{\left( {{{\mathit{\boldsymbol{\dot s}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)^{\rm{T}}}{\mathit{\boldsymbol{u}}^{\rm{o}}} + 2{\left( {{\mathit{\boldsymbol{s}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} + \\ \;\;\;\;\;\;2{r_{i1}}d_1^{\rm{o}} + 2{r_{i1}}\dot d_1^{\rm{o}} + 2\left( {{{\dot r}_{i1}}{r_{i1}} + \mathit{\boldsymbol{\dot s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{\dot s}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_i}} \right)\\ \;\;\;\;\;\;\left( {i = 2,3, \cdots ,M} \right) \end{array} $ | (12) |
式中:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\eta }}_{2i}} = \left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} - {{\mathit{\boldsymbol{\dot s}}}_1} + \gamma {r_{i1}} + {{\dot r}_{i1}}{\mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},{\mathit{\boldsymbol{s}}_1}}}} \right)\\ \mathit{\boldsymbol{\gamma }} = \left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} - {{\mathit{\boldsymbol{\dot s}}}_1} + \dot d_1^{\rm{o}}{\mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},{\mathit{\boldsymbol{s}}_1}}}} \right)/d_1^{\rm{o}} \end{array} \right. $ | (13) |
定义
| $ {\mathit{\boldsymbol{\varepsilon }}_1} = {\mathit{\boldsymbol{B}}_1}\Delta \alpha + {\mathit{\boldsymbol{D}}_1}\Delta \beta = {\mathit{\boldsymbol{h}}_1} - {\mathit{\boldsymbol{G}}_1}\mathit{\boldsymbol{\varphi }}_1^o $ | (14) |
式中:h1=[htT, hfT]T为一个2(M-1)维的列向量;G1=[GtT, GfT]T为一个2(M-1)×8的矩阵;ε1为服从零均值高斯分布的等式误差向量;ht和hf的每个元素分别表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{h}}_{\rm{t}}}\left( {i - 1} \right) = r_{i1}^2 - \mathit{\boldsymbol{s}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_i} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1}\\ {\mathit{\boldsymbol{h}}_{\rm{f}}}\left( {i - 1} \right) = 2\left( {{r_{i1}}{{\dot r}_{i1}} - \mathit{\boldsymbol{\dot s}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_i} + \mathit{\boldsymbol{\dot s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1}} \right) \end{array} \right. $ | (15) |
同样,矩阵Gt和Gf的每一行元素分别为
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_{\rm{t}}}\left( {i - 1,:} \right) = - 2\left[ {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{s}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}}&{{r_{i1}}}&{{\bf{0}}_{3 \times 1}^{\rm{T}}}&0 \end{array}} \right]\\ {\mathit{\boldsymbol{G}}_{\rm{f}}}\left( {i - 1,:} \right) = - 2\left[ {{{\left( {{{\mathit{\boldsymbol{\dot s}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)}^{\rm{T}}}{{\dot r}_{i1}}\quad {{\left( {{\mathit{\boldsymbol{s}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}{r_{i1}}} \right] \end{array} $ | (16) |
另外,
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{D}}_{1{\rm{t}}}}\left( {i - 1,:} \right) = 2\left[ { - \mathit{\boldsymbol{\eta }}_{1i}^{\rm{T}},{\bf{0}}_{3(i - 2) \times 1}^{\rm{T}},{{\left( {{\mathit{\boldsymbol{u}}^o} - {\mathit{\boldsymbol{s}}_i}} \right)}^{\rm{T}}},} \right.\\ \;\;\;\;\;\;\left. {{\bf{0}}_{3\left( {M - i} \right) \times 1}^{\rm{T}}} \right]\\ {{\mathit{\boldsymbol{\dot D}}}_{1{\rm{f}}}}\left( {i - 1,:} \right) = 2\left[ { - \mathit{\boldsymbol{\eta }}_{2{\rm{i}}}^{\rm{T}},{\bf{0}}_{3(i - 2) \times 1}^{\rm{T}},{{\left( {{{\mathit{\boldsymbol{\dot u}}}^o} - {{\mathit{\boldsymbol{\dot s}}}_i}} \right)}^{\rm{T}}},} \right.\\ \;\;\;\;\;\;\left. {{\bf{0}}_{3\left( {M - i} \right) \times 1}^{\rm{T}}} \right] \end{array} \right. $ | (17) |
矩阵方程(14)的加权最小二乘解为
| $ {{\mathit{\boldsymbol{\hat \varphi }}}_1} = {\left( {\mathit{\boldsymbol{G}}_1^{\rm{T}}{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{G}}_1}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_1^{\rm{T}}{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{h}}_1} $ | (18) |
式中:u=φ1(1:3)和
记
| $ \Delta {\mathit{\boldsymbol{\varphi }}_1} = {\left( {\mathit{\boldsymbol{G}}_1^{\rm{T}}{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{G}}_1}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_1^{\rm{T}}{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{\varepsilon }}_1} $ | (19) |
由于式(19)中ε1均值为0,因此第1步的估计值在测量噪声较小时近似为无偏估计;经过简单的矩阵运算,式(18)估计值的协方差矩阵近似为
第1步中引入的辅助向量是假设目标参数与额外变量d1o以及
| $ \left\{ {\begin{array}{*{20}{l}} {d_1^{{\rm{o}}2} = {{\left( {{\mathit{\boldsymbol{u}}^{\rm{o}}} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}^{\rm{o}}} - {\mathit{\boldsymbol{s}}_1}} \right)}\\ {\dot d_1^{\rm{o}}d_1^{\rm{o}} = {{\left( {{\mathit{\boldsymbol{u}}^{\rm{o}}} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)} \end{array}} \right. $ | (20) |
文献[18]的第2步同样考虑了这种非线性关系,并且建立了等式方程,而本文第2步建立了一个不同于文献[18]的等式方程;另外,文献[18]中的TSWLS第2步得到结果之后还需要进行一些其他操作(如平方根运算等)才能得到最终结果,相比之下,算法第2步更简洁明了,可以直接得到最终的WLS估计结果;第2步的具体过程如下。
根据第1步的估计误差Δφ1,真实向量值φ1o中的各个元素可以表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}^{\rm{o}}} = \mathit{\boldsymbol{u}} - \Delta \mathit{\boldsymbol{u}},{\mathit{\boldsymbol{u}}^{\rm{o}}} = \mathit{\boldsymbol{u}} - \Delta \mathit{\boldsymbol{u}}}\\ {d_1^o = {d_1} - \Delta {d_1},\dot d_1^o = {{\dot d}_1} - \Delta {{\dot d}_1}} \end{array}} \right. $ | (21) |
将式(21)代入式(20),并且只保留线性误差项,则有如下等式:
| $ \begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}\Delta \mathit{\boldsymbol{u}} - {d_1}\Delta {d_1}} \right) = 0.5\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - d_1^2} \right) - }\\ {\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{u}}^{\rm{o}}}\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{T}}}\Delta \mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{u}}^{\rm{T}}}\Delta \mathit{\boldsymbol{\dot u}} - {{\dot d}_1}\Delta {d_1} - {d_1}\Delta {{\dot d}_1}} \right) = }\\ {\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{T}}}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\dot s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - {{\dot d}_1}{d_1}} \right) - \mathit{\boldsymbol{\dot s}}_1^{\rm{T}}{\mathit{\boldsymbol{u}}^{\rm{o}}} - \mathit{\boldsymbol{s}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}}} \end{array} $ | (22) |
另外,第1步得到的位置和速度估计误差可以进一步改写为
| $ \Delta \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}^{\rm{o}}},\Delta \mathit{\boldsymbol{\dot u}} = \mathit{\boldsymbol{\dot u}} - {{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}} $ | (23) |
联合式(22)和式(23),将它们用矩阵形式表示可以建立新的矩阵方程为
| $ {\mathit{\boldsymbol{B}}_2}\Delta {\mathit{\boldsymbol{\varphi }}_1} = {\mathit{\boldsymbol{h}}_2} - {\mathit{\boldsymbol{G}}_2}\mathit{\boldsymbol{\varphi }}_2^{\rm{o}} $ | (24) |
式中:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{h}}_2} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot u}}}\\ {0.5\left( {{{\mathit{\boldsymbol{\dot u}}}^{\rm{T}}}\mathit{\boldsymbol{\dot u}} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - \hat d_1^2} \right)}\\ {\mathit{\boldsymbol{\dot u}}}\\ {\left( {{{\mathit{\boldsymbol{\hat {\dot u}}}}^{\rm{T}}}\mathit{\boldsymbol{\dot u}} + \mathit{\boldsymbol{\dot s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - \hat {\dot d}_1^2{{\hat d}_1}} \right)} \end{array}} \right],{\mathit{\boldsymbol{G}}_2} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&\mathit{\boldsymbol{O}}\\ {\mathit{\boldsymbol{s}}_1^{\rm{T}}}&\mathit{\boldsymbol{O}}\\ \mathit{\boldsymbol{O}}&\mathit{\boldsymbol{I}}\\ {\mathit{\boldsymbol{\dot s}}_1^{\rm{T}}}&{\mathit{\boldsymbol{s}}_1^{\rm{T}}} \end{array}} \right]\\ {\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&{{{\bf{0}}_{3 \times 1}}}&\mathit{\boldsymbol{O}}&{{{\bf{0}}_{3 \times 1}}}\\ {{\mathit{\boldsymbol{u}}^{\rm{T}}}}&{ - {d_1}}&{{\bf{0}}_{3 \times 1}^{\rm{T}}}&0\\ \mathit{\boldsymbol{O}}&{{{\bf{0}}_{3 \times 1}}}&\mathit{\boldsymbol{I}}&{{{\bf{0}}_{3 \times 1}}}\\ {{{\mathit{\boldsymbol{\dot u}}}^{\rm{T}}}}&{ - {{\dot d}_1}}&{{\mathit{\boldsymbol{u}}^{\rm{T}}}}&{ - {d_1}} \end{array}} \right] \end{array} \right. $ | (25) |
式(24)的WLS解为
| $ {{\mathit{\boldsymbol{\hat \varphi }}}_2} = {\left( {\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{G}}_2}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{h}}_2} $ | (26) |
式中:加权矩阵
记
| $ \Delta {{\mathit{\boldsymbol{\hat \varphi }}}_2} = {\left( {\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{G}}_2}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{B}}_2}\Delta {\mathit{\boldsymbol{\varphi }}_1} $ | (27) |
同样,由于E(Δφ1)=0,因此当测量噪声较小时第2步的估计近似为无偏估计,其协方差矩阵近似为
| $ {\rm cov}{{\mathit{\boldsymbol{\hat \varphi }}}_2} = {\left( {\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{G}}_2}} \right)^{ - 1}} $ | (28) |
至此,本文算法通过式(26)给出了最终的目标位置和速度估计值分别为
此外,还需要注意:
1) 加权矩阵W1和W2的获取均需要真实位置和速度,我们首先对加权矩阵近似为W1=Qα-1,并利用式(18)得到初始的参数估计值;随后利用获得的参数值更新加权矩阵W1和W2,得到一个更精确的估计值。仿真实验表明了这种加权矩阵的近似带来的性能损失是可以忽略不计的。
2) 若使用该算法对多非相交源的参数进行估计时,只需要对相应的矩阵进行维度调整,对此本文不在赘述,仅给出大致思路:其中,第1步与文献[18]算法的第1步相同;第2步中φ2o扩展为全部目标的位置和速度向量,每个目标均能构造出矩阵G2以及B2,将这些矩阵联合为块对角矩阵即可建立新的矩阵G2和矩阵B2,进而类似的矩阵方程也随之建立;最后同样利用加权最小二乘方法给出估计解。
3 性能分析本节将对所提出算法的性能进行分析,给出本文定位场景下的CRLB,并且理论推导证明在测量噪声较小时,所提算法可以达到CRLB。
上面已经提到过,本文算法给出的目标位置以及速度估计在测量噪声较小时是无偏的,因此只需要证明协方差矩阵
| $ \begin{array}{l} {\left( {{\rm cov}{{\mathit{\boldsymbol{\hat \varphi }}}_2}} \right)^{ - 1}} = \mathit{\boldsymbol{G}}_3^{\rm{T}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}{\mathit{\boldsymbol{G}}_3} - \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{G}}_3^{\rm{T}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}{\mathit{\boldsymbol{G}}_4}{\left( {\mathit{\boldsymbol{Q}}_\beta ^{ - 1} + \mathit{\boldsymbol{G}}_4^{\rm{T}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}{\mathit{\boldsymbol{G}}_4}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_4^{\rm{T}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}{\mathit{\boldsymbol{G}}_3} \end{array} $ | (29) |
式中:
根据文献[17], CRLB(φ2o)的表达式为
| $ {\rm{CRL}}{{\rm{B}}^{ - 1}}\left( {\mathit{\boldsymbol{\varphi }}_2^{\rm{o}}} \right) = \mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{Z}}^{ - 1}}{\mathit{\boldsymbol{Y}}^{\rm{T}}} $ | (30) |
式中:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}} = {\left( {\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial \varphi _2^{\rm{o}}}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial \mathit{\boldsymbol{\varphi }}_2^{\rm{o}}}}\\ \mathit{\boldsymbol{Y}} = {\left( {\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial \mathit{\boldsymbol{\varphi }}_2^{\rm{o}}}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{\beta }}^{\rm{o}}}}}\\ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{Q}}_\beta ^{ - 1} + {\left( {\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{\beta }}^{\rm{o}}}}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}_\alpha ^{ - 1}\frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{\beta }}^{\rm{o}}}}} \end{array} \right. $ | (31) |
附录A中给出了
| $ {\rm cov}{{\mathit{\boldsymbol{\hat \varphi }}}_2} = {\rm{CRLB}}\left( {\mathit{\boldsymbol{\varphi }}_2^{\rm{o}}} \right) $ | (32) |
即本文提出的算法在测量噪声较小时能够实现CRLB。
4 仿真实验本节给出了仿真实验进一步验证本文所提出算法的定位性能。假设TDOA与FDOA测量误差之间相互独立,RD及RDD测量误差协方差矩阵设置为Qα=σ2blkdiag(R, 0.01R),这里,测量噪声的方差设置为σ2=10-4,R为对角线元素均为1,其他元素为0.5的矩阵。与文献[13, 17]相同,仿真实验选取了6个传感器,所有传感器位置和速度的真实值在表 1中给出。可利用的传感器位置和速度值由真实值添加高斯噪声得到,噪声协方差矩阵的设置与文献[13]相同,为Qβ=σs2blkdiag(J, 0.5J),其中σs2为噪声功率且J=[1, 1, 1, 2, 2, 2, 10, 10, 10, 40, 40, 40, 20, 20, 20, 3, 3, 3]。通过进行多次蒙特卡罗实验获取目标位置和速度估计的均方根误差(Root Mean Square Error, RMSE)和偏差(Bias)来评估算法的性能,蒙特卡罗仿真次数设置为l=10 000次,均方根误差以及偏差的指标定义为
| 观测站序号i | 位置/m | 速度/(m·s-1) | |||||
| xio | yio | zio | |
|
|
||
| 1 | 300 | 100 | 150 | 30 | -20 | 20 | |
| 2 | 400 | 150 | 100 | -30 | 10 | 20 | |
| 3 | 300 | 500 | 200 | 10 | -20 | 10 | |
| 4 | 350 | 200 | 100 | 10 | 20 | 30 | |
| 5 | -100 | -100 | -100 | -20 | 10 | 10 | |
| 6 | 200 | -300 | -200 | 20 | -10 | 10 | |
| $ \begin{array}{l} {\rm RMSE}\left( {{{\mathit{\boldsymbol{\hat \varphi }}}_2}} \right) = \sqrt {\sum\limits_{i = 1}^l {{{\left\| {\mathit{\boldsymbol{\hat \varphi }}_2^i - \mathit{\boldsymbol{\varphi }}_2^{\rm{o}}} \right\|}^2}} /l} \\ {\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat \varphi }}}_2}} \right) = \sum\limits_{i = 1}^l {{{\left\| {\mathit{\boldsymbol{\hat \varphi }}_2^i - \mathit{\boldsymbol{\varphi }}_2^{\rm{o}}} \right\|}^2}} /l \end{array} $ | (33) |
式中:
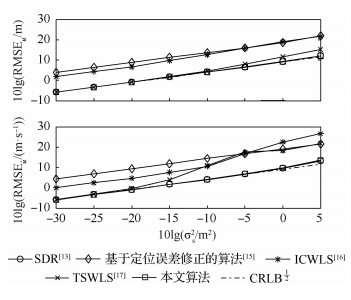
图 1和图 2给出的是不同算法对近场目标位置以及速度估计性能的比较,目标位置和速度分别选取为uo=[305, 500, 165]T m和
|
| 图 1 近场目标参数估计均方根误差对比 Fig. 1 Comparison of parameters estimation of RMSE for near-field source |
|
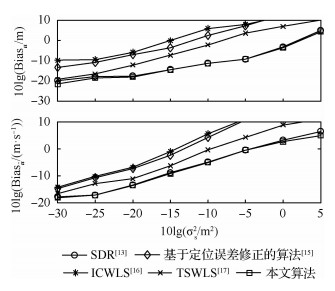
| 图 2 近场目标参数估计偏差对比 Fig. 2 Comparison of parameters estimation of bias for near-field source |
如图 2所示,对于近场目标估计偏差性能而言,没有考虑传感器误差的算法[15-16]具有较大的位置和速度估计偏差。当测量噪声较小时,TSWLS算法能够提供和SDR算法以及本文提出算法比较接近的估计偏差,但是当噪声继续增大时,TSWLS的偏差性能开始下降。当测量噪声达到5 dB时,TSWLS算法的目标位置估计偏差比本文提出的算法大约高出了6 dB,同样,目标速度估计偏差比本文提出的算法大约高出了6 dB。SDR算法与本文所提出的算法在整个噪声功率范围内对于目标参数估计的偏差比较接近,均能够实现较小的位置与速度估计偏差,这两种算法具有较好的定位性能。但是需要强调的是,SDR算法求解优化问题需要大量的计算复杂度,该算法实时性难以保证;本文算法是一种闭式解法,因此具有较高的实时性(见第5节表 2)。
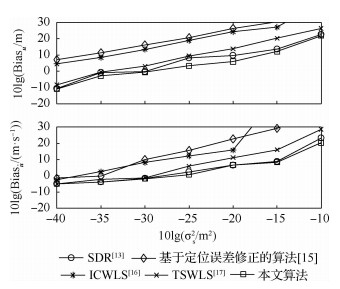
图 3和图 4给出的是不同算法对远场目标位置以及速度估计性能的比较,目标位置和速度选取为uo=[2 000, 2 500, 3 000]T m和

|
| 图 3 远场目标参数估计均方根误差对比 Fig. 3 Comparison of parameters estimation of RMSE for far-field source |
|
| 图 4 远场目标参数估计均方根误差对比 Fig. 4 Comparison of parameters estimation of bias for far-field source |
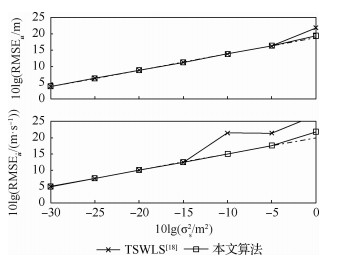
另外,本文算法还可以扩展到对非相交多目标定位解算的场景中;图 5和图 6给出了不同算法的估计性能。目标位置分别选取为u1o=[305, 500, 165]T m和u2o=[600, 650, 500]T m;速度为
|
| 图 5 两个不相交目标参数估计均方误差对比 Fig. 5 RMSE comparison of parameters estimation for two disjoint sources. |
|
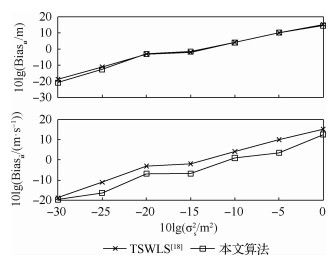
| 图 6 两个不相交目标参数估计偏差对比 Fig. 6 Comparison of parameters estimation of bias for two disjoint sources. |
如图 5所示,对于位置估计均方根误差,当噪声小于-5 dB时,2种算法均能够实现CRLB。但是当噪声继续增大时,2种算法定位性能开始下降,当噪声为0 dB时,本文算法得到的均方根误差比文献[18]的TSWLS得到的均方根误差大约降低了4 dB。对于速度估计均方根误差,当噪声大于-15 dB时,文献[18]TSWLS算法的估计性能出现了较大的下降,而本文算法在噪声大于-5 dB时才开始偏离CRLB,本文算法具有更好的鲁棒性。图 6给出了2种算法对于目标参数估计的偏差性能,对于位置估计偏差性能,文献[18]的算法与本文算法十分接近;但是对于速度估计偏差,本文算法显然比文献[18]的算法具有更小的偏差,当测量噪声等于-5 dB时,本文算法比文献[18]算法的估计偏差大约减少了7 dB。
5 计算量分析本节主要对所提出算法的计算复杂度进行分析,为了分析简便,主要以实数乘法进行分析。
首先分析本文算法第1步的计算量。
1) 计算W1:包括计算① B1QαB1T,② D1QβD1T,③求逆运算,以上每个步骤分别需要进行16(M-1)3、36(M-1)M2以及8(M-1)3次实数乘法。
2) 计算
接下来给出第2步计算量的分析过程,第2步中计算与观测站数目无关,因此能够得到准确的乘法次数。
1) 计算W2:包括计算① B2-T,② B2-Tcov-1
2) 计算
此外,由于TSWLS的第1步需要对加权矩阵初始化,并且更新加权矩阵W1一般需要重复计算两次,则第1步中1)需要计算2次,2)需要计算3次,因此本文提出的算法一共需要(120M3-120M2+688M+5 688)次的实数乘法运算。同样,文献[17-18]中的TSWLS算法第2步均与观测站数目无关,计算量主要都体现在了第1步中,因此本文算法与它们计算量相当,这从表 2中也可以看出,表 2中给出了考虑传感器参数误差存在情况下不同算法的平均CPU运行时间,显然TSWLS算法以及本文算法计算量相当。而SDR算法需要进行大量的运行时间。本文算法具有相当高的实时性,这一点在定位解算中具有重要意义。
6 结论1) 所提出算法在测量噪声较小时能够实现CRLB。另外,经过适当的维度调整,可以应用于多非相交源的定位场景中。
2) 所提算法计算复杂度与TSWLS算法相当,同时能提供不高于SDR算法的均方根误差和偏差估计性能。
附录A
这里给出了
条件①:
条件②:
| $ \frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial \mathit{\boldsymbol{\varphi }}_2^{\rm{o}}}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{u}}^{\rm{o}}}}}}&{\frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}}}}}\\ {\frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{u}}^{\rm{o}}}}}}&{\frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}}}}} \end{array}} \right] $ | (A1) |
式中:
| $ \frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{u}}^{\rm{o}}}}}\left( {i - 1,:} \right) = \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_i^{\rm{o}}}^{\rm{T}} - \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_1^{\rm{o}}}^{\rm{T}} $ | (A2) |
| $ \frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}}}}\left( {i - 1,:} \right) = \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_i^{\rm{o}}}^{\rm{T}} - \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_1^{\rm{o}}}^{\rm{T}} $ | (A3) |
| $ \frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}\left( \mathit{\boldsymbol{\theta }} \right)}}{{\partial {{\mathit{\boldsymbol{\dot u}}}^{\rm{o}}}}}\left( {i - 1,:} \right) = \mathit{\boldsymbol{\gamma }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_i^{\rm{o}}}^{\rm{T}} - \mathit{\boldsymbol{\gamma }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_1^{\rm{o}}}^{\rm{T}} $ | (A4) |
式中:
同样,
| $ \frac{{\partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{\beta }}^{\rm{o}}}}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{s}}^{\rm{o}}}}}}&{\frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot s}}}^{\rm{o}}}}}}\\ {\frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{s}}^{\rm{o}}}}}}&{\frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot s}}}^{\rm{o}}}}}} \end{array}} \right] $ | (A5) |
式中:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{s}}^{\rm{o}}}}}\left( {i - 1,:} \right) = \frac{{\partial {\mathit{\boldsymbol{r}}^{\rm{o}}}}}{{\partial {{\mathit{\boldsymbol{\dot s}}}^{\rm{o}}}}}\left( {i - 1,:} \right)\\ \;\;\;\;\;\; = \left[ {\mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_1^{\rm{o}}}^{\rm{T}},{\bf{0}}_{3\left( {i - 2} \right) \times 1}^{\rm{T}}, - \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_i^{\rm{o}}}^{\rm{T}},{\bf{0}}_{3\left( {M - i} \right) \times 1}^{\rm{T}}} \right] \end{array} $ | (A6) |
| $ \frac{{\partial {{\mathit{\boldsymbol{\dot r}}}^{\rm{o}}}}}{{\partial {\mathit{\boldsymbol{s}}^{\rm{o}}}}}\left( {i - 1,:} \right) = \left[ {\mathit{\boldsymbol{\gamma }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_1^{\rm{o}}}^{\rm{T}},{\bf{0}}_{3\left( {i - 2} \right) \times 1}^{\rm{T}}, - \mathit{\boldsymbol{\gamma }}_{{\mathit{\boldsymbol{u}}^{\rm{o}}},\mathit{\boldsymbol{s}}_i^{\rm{o}}}^{\rm{T}},{\bf{0}}_{3\left( {M - i} \right) \times 1}^{\rm{T}}} \right] $ | (A7) |
且i=2, 3, …, M-1。
将相关矩阵代入G3=B1-1G1B2-1G2以及G4=B1-1D1,经过一些简单的矩阵运算,同时利用条件①和条件②可以得到
| $ {\mathit{\boldsymbol{G}}_3} = \partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}/\partial \mathit{\boldsymbol{\varphi }}_2^{\rm{o}},{\mathit{\boldsymbol{G}}_4} = - \partial {\mathit{\boldsymbol{\alpha }}^{\rm{o}}}/\partial {\mathit{\boldsymbol{\beta }}^{\rm{o}}} $ | (A8) |
| [1] |
田中成, 刘聪锋. 无源定位技术[M]. 北京: 国防工业出版社, 2015: 8-12. TIAN Z C, LIU C F. Passive locating technology[M]. Beijing: National Defence Industry Press, 2015: 8-12. (in Chinese) |
| [2] | PATWARI N, ASH J, KYPEROUNTAS S, et al. Locating the nodes:Cooperative localization in wireless sensor networks[J]. IEEE Signal Process Magazine, 2005, 22(4): 54-69. |
| Click to display the text | |
| [3] |
朱国辉, 冯大政, 聂卫科. 传感器位置误差情况下基于多维标度分析的时差定位算法[J]. 电子学报, 2016, 44(1): 21-26. ZHU G H, FENG D Z, NIE W K. Multidimensional scaling based TDOA localization algorithm with sensor location errors[J]. Acta Electronica Sinica, 2016, 44(1): 21-26. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [4] | LE T K, HO K C. Uncovering source ranges from range differences observed by sensors at unknown positions:Fundamental theory[J]. IEEE Transactions on Signal Processing, 2019, 67(10): 2665-2678. |
| Click to display the text | |
| [5] | HAO B J, GU L M, LI Z, et al. Passive radar source localisation based on PSAAA using single small size aircraft[J]. IET Signal Processing, 2016, 10(7): 1191-1200. |
| Click to display the text | |
| [6] |
朱建丰, 陈玥, 郝本建, 等. 基于合成孔径阵列的雷达辐射源被动定位技术研究[J]. 电子学报, 2017, 45(10): 22-26. ZHU J F, CHEN Y, HAO B J. Passive radar source localization using synthetic aperture antenna array[J]. Acta Electronica Sinica, 2017, 45(10): 22-26. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [7] | NORTHARD T, NARDONE S C. Track-before-detect bearings-only localization performance in complex passive sonar scenarios:A case study[J]. IEEE Journal of Oceanic Engineering, 2019, 44(2): 482-491. |
| Click to display the text | |
| [8] | LIU H P, SUN F C, FANG B, et al. Robotic room-level localization using multiple sets of sonar measurements[J]. IEEE Transactions on Instrumentation and Measurements, 2017, 66(1): 2-13. |
| Click to display the text | |
| [9] | SALVATI D, DRIOLI C, FORESTI G L. Sound source and microphone localization from acoustic impulse responses[J]. IEEE Signal Processing Letters, 2016, 23(10): 1459-1463. |
| Click to display the text | |
| [10] | FOY W H. Position-location solutions by Taylor-series estimation[J]. IEEE Transactions on Aerospace & Electronic Systems, 1987, 12(2): 187-194. |
| Click to display the text | |
| [11] | TOORRIER D J. Statistical theory of passive location systems[J]. IEEE Transaction on Aerospace & Electronic System, 1984, 20(2): 183-198. |
| Click to display the text | |
| [12] | HO K C, XU W W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453-2463. |
| Click to display the text | |
| [13] | WANG G, LI Y, ANSARI N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Vehicular Technology, 2013, 62(2): 852-863. |
| Click to display the text | |
| [14] | WANG Y L, WU Y. An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements[J]. IEEE Communication Letters, 2017, 21(1): 80-83. |
| Click to display the text | |
| [15] |
刘洋, 杨乐, 郭福成, 等. 基于定位误差修正的运动目标TDOA/FDOA无源定位方法[J]. 航空学报, 2015, 36(5): 1617-1626. LIU Y, YANG L, GUO F C, et al. Moving targets TDOA/FDOA passive localization algorithm based on localization error refinement[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1617-1626. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [16] | QU X M, XIE L H, TAN W R. Iterative constrained weighted least squares source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(15): 3990-4003. |
| Click to display the text | |
| [17] | HO K C, LU X, KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors:Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684-696. |
| Click to display the text | |
| [18] | SUN M, HO K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3434-3440. |
| Click to display the text | |
| [19] | LIU Y, GUO F C, YANG L, et al. An improved algebraic solution for TDOA localization with sensor position errors[J]. IEEE Communication Letters, 2015, 19(12): 2218-2221. |
| Click to display the text | |
| [20] | CAO J M, WAN Q, OUYANG X X, et al. Multidimensional scaling-based passive emitter localisation from time difference of arrival measurements with sensor position uncertainties[J]. IET Signal Processing, 2017, 11(1): 43-50. |
| Click to display the text | |
| [21] | KAY S M. Fundamentals of statistical signal processing volume I:Estimation theory[M]. Upper Saddle River, NJ: Prentice Hall, 1998: 23-45. |



