合成孔径雷达(Synthetic Aperture Radar, SAR)[1-2]可以对区域进行全天时观测,且不受气候约束。在军事和民用领域得到了广泛应用。在某些特殊应用背景下,比如小型飞机[3-4]、无人机[5]和导弹[6-7],由于加速度的存在,使得SAR载体运动特性较为复杂,并呈现出曲线运动轨迹。此时,根据线性轨迹建立的传统处理方法失效。传统的双曲方程不能准确描述曲线运动轨迹SAR的斜距历程,必须建立新的斜距模型及成像方法。
在文献[8-11]中,用二阶或三阶Taylor级数来近似曲线SAR的斜距历程,但较大的近似误差影响了回波二维频谱的精确性。文献[12-13]分别提出了改进的斜距模型和改进的双曲斜距方程,这些斜距的数学表达式比较简单,但准确度不够。文献[14]提出改进的等效斜视距离模型,只考虑了两维加速度,不能用来表达具有三维加速度的曲线运动轨迹SAR的斜距历程。
文献[8-19]提出了各种相关的曲线运动轨迹SAR成像算法。后向投影算法[10, 15]可以处理各种运动轨迹的SAR数据,但计算复杂度较高。文献[16]中的Keystone Transform(KT)算法移除了二维交叉耦合项并对地形误差进行补偿,但二维方位向频域KT算法仅适应于低轨道。文献[17]提出了曲线拟合的方法来构造CS相位函数,但是距离徙动曲线与斜距不是线性关系,拟合误差对成像影响较大。文献[18]中,利用Taylor幂级数分解原始斜距和二维频域解耦合,但是幂级数展开的精确度和展开点的位置密切相关,因此不同点目标的展开精度不同。文献[19]中的波数域算法在考虑了SAR载体的二维速度和二维加速度的条件下成像质量良好,但不适用于具有三维速度和三维加速度的曲线运动轨迹SAR;而且改进的斜距方程缺少方位向时间的三次项,斜距表达式的精度不够。
在前述研究工作的基础上,提出了一种适用于曲线运动轨迹SAR的高效Chirp Scaling(CS)算法。在第1节中,讨论了具有三维速度和三维加速度的斜距方程,并进行Chebyshev近似,按方位时间的幂级数整理,得到斜距表达式,并推导其等效的双曲方程。在第2节中,提出了一种改进的CS算法,此算法消除了距离徙动(Range Cell Migration, RCM)的空间变化性,并在距离多普勒域中通过乘以相位补偿函数实现了方位聚焦,从而得到聚焦图像。在第3节,对改进的CS算法分别与文献[18-19]的算法进行仿真对比,仿真结果证明了所提出的斜距模型与成像算法的有效性与优越性。最后,进行了总结。
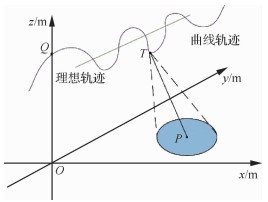
1 曲线运动轨迹SAR理论 1.1 Chebyshev近似的曲线运动轨迹SAR的等效斜距模型机载SAR平台由于加速度的存在而产生曲线运动,该模式下的系统几何模型如图 1所示,初始时刻位于点Q(0, 0, HQ)处的SAR载体以初始速度(vx, vy, vz)、加速度(ax, ay, az)沿y轴方向飞行,tv时刻到达T(xtv, ytv, ztv)点。假设观测场景内目标点P坐标为(XP, YP, 0)。
|
| 图 1 曲线运动轨迹SAR几何模型 Fig. 1 Geometric mode of curved trajectory SAR |
由物理运动学方程得到:xtv=vxtv+
| $ R({t_{\rm{v}}}) = \sqrt {{{\left( {{v_x}{t_{\rm{v}}} + \frac{1}{2}{a_x}t_{\rm{v}}^2 - {X_P}} \right)}^2} + {{\left( {{v_y}{t_{\rm{v}}} + \frac{1}{2}{a_y}t_{\rm{v}}^2 - {Y_P}} \right)}^2} + {{\left( {{v_z}{t_{\rm{v}}} + \frac{1}{2}{a_z}t_{\rm{v}}^2 + {H_Q}} \right)}^2}} $ | (1) |
整理得
| $ R({t_{\rm{v}}}) = \sqrt {R_P^2 + {A_1}{t_{\rm{v}}} + {A_2}t_{\rm{v}}^2 + {A_3}t_{\rm{v}}^3 + {A_4}t_{\rm{v}}^4} $ | (2) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_P} = \sqrt {X_P^2 + Y_P^2 + H_Q^2} }\\ {{A_1} = 2({v_z}{H_Q} - {v_x}{X_P} - {v_y}{Y_P})}\\ {{A_2} = v_x^2 + v_y^2 + v_z^2 + {a_z}{H_Q} - {a_x}{X_P} - {a_y}{Y_P}}\\ {{A_3} = {v_x}{a_x} + {v_y}{a_y} + {v_z}{a_z}}\\ {{A_4} = \frac{1}{4}(a_x^2 + a_y^2 + a_z^2)} \end{array}} \right. $ |
为了方便后续信号处理,需要把式(2)展开成tv的幂级数形式。由于切比雪夫多项式能提供连续函数的最佳一致逼近,因此为了提高斜距精度,不同于传统的采用泰勒分解的方法,将式(2)进行切比雪夫正交分解,得到
| $ R({t_{\rm{v}}}) = \frac{{{c_0}}}{2} + \sum\limits_{i = 1}^n {{c_i}} {T_i}({t_{\rm{v}}}) $ | (3) |
式中:n为展开的阶数,本文取4;Ti(tv)为切比雪夫多项式,且有Ti(tv)=2tvTi-1(tv)-Ti-2(tv),(T0(tv)=1,T1(tv)=tv);ci为切比雪夫系数,且有ci=
将式(3)按照tv的幂级数排序得到
| $ R({t_{\rm{v}}}) = {B_0} + {B_1}{t_{\rm{v}}} + {B_2}t_{\rm{v}}^2 + {B_3}t_{\rm{v}}^3 + {B_4}t_{\rm{v}}^4 $ | (4) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{B_0} = \frac{{{c_0}}}{2} - {c_2} + {c_4}}\\ {{B_1} = ({c_1} - 3{c_3})\frac{2}{{{T_{{\rm{syn}}}}}}}\\ {{B_2} = (2{c_2} - 8{c_4}){{\left( {\frac{2}{{{T_{{\rm{syn}}}}}}} \right)}^2}}\\ {{B_3} = 4{c_3}{{\left( {\frac{2}{{{T_{{\rm{syn}}}}}}} \right)}^3}}\\ {{B_4} = 8{c_4}{{\left( {\frac{2}{{{T_{{\rm{syn}}}}}}} \right)}^4}} \end{array}} \right. $ |
下面对斜距误差进行分析,分别把式(3)的2阶、3阶和4阶展开式与式(2)的误差进行仿真,仿真参数如表 1所示。
| 参数 | 数值 |
| 载波频率/GHz | 10 |
| 信号带宽/MHz | 100 |
| 采样频率/MHz | 260 |
| 发射信号时宽/μs | 5 |
| 脉冲重复频率/Hz | 1 400 |
| 三维速度/(m·s-1) | 100, 35, 2 |
| 三维加速度/(m·s-2) | 0.1, 0.1, -0.1 |
如图 2(a)所示,在0 s时刻处,各阶斜距的误差均接近为0 m。但是,当方位向时间远离0 s时刻时,2阶和3阶斜距的误差急剧增大,而4阶斜距的误差几乎保持不变,接近于0 m。图 2(b)是本文采用的基于Chebyshev正交分解的4阶斜距和传统的基于Taylor展开的4阶斜距的误差对比。由图可知,基于Chebyshev正交分解的4阶斜距误差更小,基本趋于0 m,而基于Taylor展开的斜距误差在合成孔径边缘急剧增大。

|
| 图 2 不同斜距模型的误差比较 Fig. 2 Error comparison of different slant range models |
由仿真可知,式(3)进行4阶Chebyshev近似,误差在10-6量级。而进行4阶Taylor近似,斜距误差在10-5量级。
1.3 曲线运动轨迹SAR的双曲等效斜距模型及回波为了用CS算法处理曲线SAR数据,需要将上述所获得的斜距模型用双曲方程等效,即将式(4)改写为
| $ R({t_{\rm{v}}}) = \sqrt {R_{{\rm{eq}}}^2 + \nu _{{\rm{eq}}}^2t_{\rm{v}}^2} + D{t_{\rm{v}}} + Et_{\rm{v}}^3 + Ft_{\rm{v}}^4 $ | (5) |
联立式(4)和式(5),得到Req=B0, D=B1,νeq=
依据斜距模型式(5),则雷达回波信号表达式为
| $ \begin{array}{l} s({t_{\rm{r}}},{t_{\rm{v}}}) = {u_{\rm{r}}}\left( {{t_{\rm{r}}} - \frac{{2R({t_{\rm{v}}})}}{c}} \right){u_{\rm{v}}}({t_{\rm{v}}}) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( { - {\rm{j}}\frac{{4\pi R({t_{\rm{v}}})}}{\lambda }} \right){\rm{exp}}\left( {{\rm{j}}\pi {K_{\rm{r}}}{{\left( {{t_{\rm{r}}} - \frac{{2R({t_{\rm{v}}})}}{c}} \right)}^2}} \right) \end{array} $ | (6) |
式中:tr、tv分别为距离向快时间和方位向慢时间; Kr为发射信号的调频斜率;λ为发射信号的波长;c为光速;ur(·)和uv(·)分别为距离向和方位向的时域包络。
2 改进的Chirp Scaling成像算法曲线运动轨迹SAR的合成孔径是曲线状,求解CS因子必须考虑RCM的空间变化性。为了方便计算相位,忽略包络变化形式。
根据驻留相位原理[13, 20-21],将式(6)进行距离向傅里叶变换(Fourier Transform, FT),得到距离频域的信号表达式为
| $ \begin{array}{l} S({f_{\rm{r}}},{t_{\rm{v}}}) = {U_{\rm{r}}}({f_{\rm{r}}}){u_{\rm{v}}}({t_{\rm{v}}}){\rm{exp}}\left( { - {\rm{j}}\pi \frac{{f_{\rm{r}}^2}}{{{K_{\rm{r}}}}}} \right) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( { - {\rm{j}}4\pi \frac{{{f_{\rm{r}}} + {f_{\rm{c}}}}}{c}R({t_{\rm{v}}})} \right) \end{array} $ | (7) |
式中:fr为距离向频率;Ur(·)为距离向频谱包络;fc为载波频率。
由式(5)知,斜距表达式存在一次项,即式(7)存在线性距离走动(Linear Range Walk, LRW)[22]。由于距离走动在时间域与目标位置有关,因此距离走动的校正应该相对于场景中心进行,于是构建线性距离走动校正(Linear Range Walk Correction, LRWC)函数为
| $ {H_{{\rm{1rwc}}}}({f_{\rm{r}}},{t_{\rm{v}}}) = {\rm{exp}}\left( {{\rm{j}}4\pi \frac{{{f_{\rm{r}}} + {f_{\rm{c}}}}}{c}{D_{\rm{o}}}{t_{\rm{v}}}} \right) $ | (8) |
式中:Do为相对场景中心位置(Xo, Yo, 0)的参数。
补偿后的信号为
| $ \begin{array}{*{20}{c}} {S({f_{\rm{r}}},{t_{\rm{v}}}) = {U_{\rm{r}}}({f_{\rm{r}}}){u_{\rm{v}}}({t_{\rm{v}}}){\rm{exp}}\left( { - {\rm{j}}\pi \frac{{f_{\rm{r}}^2}}{{{K_{\rm{r}}}}}} \right) \cdot }\\ {{\rm{exp}}\left( { - {\rm{j}}4\pi \frac{{{f_{\rm{r}}} + {f_{\rm{c}}}}}{c}(R({t_{\rm{v}}}) - {D_{\rm{o}}}{t_{\rm{v}}})} \right)} \end{array} $ | (9) |
距离走动校正近似解决了曲线SAR回波信号的距离向频率fr与方位向时间tv的线性耦合问题,简化了后面的处理过程。
由于CS算法是在距离-多普勒域进行,但直接对式(6)进行方位向傅里叶变换比较困难。因此先利用驻留相位原理[13, 20-21]对式(9)进行方位向傅里叶变换,将信号转换到二维频域,再进行距离向逆傅里叶变换(Inverse Fourier Transform, IFT),转换到距离-多普勒域。
因为高次相位是缓慢变化的,对驻相点不敏感,所以高次相位并不参与驻相点的计算,只需将驻相点求出直接代入高次项即可[1]。最后得到回波信号的二维频谱表达式为
| $ \begin{array}{l} \begin{array}{*{20}{c}} {S({f_{\rm{r}}},{f_{\rm{v}}}) = {U_{\rm{r}}}({f_{\rm{r}}}){U_{\rm{v}}}({f_{\rm{v}}}){\rm{exp}}\left( { - {\rm{j}}\pi \frac{{f_{\rm{r}}^2}}{{{K_{\rm{r}}}}}} \right) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( { - {\rm{j}}\frac{{4\pi {R_{{\rm{eq}}}}}}{\lambda }\sqrt {{{\left( {1 + \frac{{{f_{\rm{r}}}}}{{{f_{\rm{c}}}}}} \right)}^2} - {{\left( {\frac{{\lambda {f_{\rm{v}}}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} - } \right.} \end{array}\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}4\pi \frac{{{f_{\rm{r}}} + {f_{\rm{c}}}}}{c}(Et_{\rm{v}}^{*3} + Ft_{\rm{v}}^{*4})} \right) \end{array} $ | (10) |
式中:tv*=
再次利用驻留相位原理[13, 20-21]将式(10)进行距离向逆傅里叶变换,得到信号在距离-多普勒域的表达式为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {s({t_{\rm{r}}},{f_v}) = {u_{\rm{r}}}({t_{\rm{r}}}){U_{\rm{v}}}({f_{\rm{v}}}) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left\{ {{\rm{j}}\pi {K_{{\rm{eq}}}}{{[{t_{\rm{r}}} - 2{R_{{\rm{eq}}}}/(c\sqrt {1 - \frac{{\lambda f_{\rm{v}}^2}}{{2{\nu _{{\rm{eq}}}}}}} )]}^2} - } \right.} \end{array}\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{{4{R_{{\rm{eq}}}}}}{\lambda }\sqrt {1 - {{\left( {\frac{{\lambda {f_{\rm{v}}}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} - {\rm{j}}\pi \frac{4}{\lambda }(Et_{\rm{v}}^{\# 3} + Ft_{\rm{v}}^{\# 4})} \right\} \end{array} $ | (11) |
式中:tv#=
由式(11)可知,瞬时斜距表达式为r(tr, fv; Req)=R(tv#)-Dotv#=Req/
| $ \begin{array}{*{20}{l}} {{H_{{\rm{cs}}}}({t_{\rm{r}}},{f_{\rm{v}}}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( {{\rm{j}}\pi {K_{{\rm{eq}}}}{C_{\rm{s}}}{{\left( {{t_{\rm{r}}} - 2\frac{{r({t_{\rm{r}}},{f_{\rm{v}}};{R_{{\rm{ref}}}})}}{c}} \right)}^2}} \right)} \end{array} $ | (12) |
式中:Rref为参考点处的斜距,一般选择场景中心作为参考点。
将式(11)与式(12)相乘进行CS操作,再进行距离向傅里叶变换,得到回波信号的二维频谱函数
| $ \begin{array}{l} \begin{array}{*{20}{l}} {S({f_{\rm{r}}},{f_{\rm{v}}}) = {U_{\rm{r}}}({f_{\rm{r}}}){U_{\rm{v}}}({f_{\rm{v}}}) \cdot }\\ {\quad {\rm{exp}}\left( { - {\rm{j}}\frac{{4\pi }}{{{c^2}}}{K_{{\rm{eq}}}}{C_{\rm{s}}}(1 + {C_{\rm{s}}}){{({R_{{\rm{eq}}}} - {R_{\rm{ret}}})}^2} - } \right.} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{{4{R_{{\rm{eq}}}}}}{\lambda }\sqrt {1 - {{\left( {\frac{{\lambda {f_{\rm{v}}}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} - {\rm{j}}\pi \frac{4}{\lambda }(Et_{\rm{v}}^{\# 3} + Ft_{\rm{v}}^{\# 4}) - \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{{f_{\rm{r}}^2}}{{{K_{{\rm{eq}}}}(1 + {C_{\rm{s}}})}} - {\rm{j}}\frac{{4\pi }}{c}({R_{{\rm{eq}}}} + {R_{{\rm{ref}}}}{C_{\rm{s}}}){f_{\rm{r}}}} \right) \end{array} $ | (13) |
分析式(13)的相位结构可知,第1项是CS操作产生的残余相位;第2项是方位调制项用于方位压缩;第3项是方位调制的高阶项;第4项是距离调制项,对应距离压缩和二次距离压缩;第5项是距离徙动项,经过CS操作后,距离徙动为RrefCs,即不同距离处的距离徙动都校正为参考距离处的距离徙动。
由此构造距离压缩和二次距离压缩函数为
| $ {H_{{\rm{rc + src}}}}({f_{\rm{r}}},{f_{\rm{v}}}) = {\rm{exp}}\left( {{\rm{j}}\pi \frac{{f_{\rm{r}}^2}}{{{K_{{\rm{ref}}}}(1 + {C_{\rm{s}}})}}} \right) $ | (14) |
式中:Kref为参考点处的调频斜率。
CS处理解除了距离徙动曲线的空变性。因此,不同距离的距离徙动校正函数都为
| $ {H_{{\rm{rcmc}}}}({f_{\rm{r}}},{f_{\rm{v}}}) = {\rm{exp}}\left( {{\rm{j}}\frac{{4\pi }}{c}{R_{{\rm{ref}}}}{C_{\rm{s}}}{f_{\rm{r}}}} \right) $ | (15) |
完成距离压缩、二次距离压缩和距离徙动校正的信号为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {S({f_{\rm{r}}},{f_{\rm{v}}}) = {U_{\rm{r}}}({f_{\rm{r}}}){U_{\rm{v}}}({f_{\rm{v}}}) \cdot }\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left\{ { - {\rm{j}}\frac{{4\pi }}{{{c^2}}}{K_{{\rm{eq}}}}{C_{\rm{s}}}(1 + {C_{\rm{s}}}){{({R_{{\rm{eq}}}} - {R_{{\rm{ret}}}})}^2} - } \right.} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{{4{R_{{\rm{eq}}}}}}{\lambda }\sqrt {1 - {{\left( {\frac{{\lambda {f_{\rm{v}}}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} - \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{4}{\lambda }(Et_{\rm{v}}^{\# 3} + Ft_{\rm{v}}^{\# 4}) - {\rm{j}}\frac{{4\pi }}{c}{R_{{\rm{eq}}}}{f_{\rm{r}}}} \right\} \end{array} $ | (16) |
将式(16)进行距离向逆傅里叶变换,得到信号在距离-多普勒域的表达式为
| $ \begin{array}{l} s({t_{\rm{r}}},{f_{\rm{v}}}) = {\rm{sinc}} \left( {{t_{\rm{r}}} - \frac{{2{R_{{\rm{eq}}}}}}{c}} \right){U_{\rm{v}}}({f_{\rm{v}}}) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( { - {\rm{j}}\frac{{4\pi }}{{{c^2}}}{K_{{\rm{eq}}}}{C_{\rm{s}}}(1 + {C_{\rm{s}}}){{({R_{{\rm{eq}}}} - {R_{{\rm{ref}}}})}^2} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{j}}\pi \frac{{4{R_{{\rm{eq}}}}}}{\lambda }\sqrt {1 - {{\left( {\frac{{\lambda {f_{\rm{v}}}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} - {\rm{j}}\pi \frac{4}{\lambda }(Et_{\rm{v}}^{\# 3} + Ft_{\rm{v}}^{\# 4})} \right) \end{array} $ | (17) |
在距离-多普勒域,进行相位补偿和方位压缩,相应的处理函数为
| $ \begin{array}{l} {H_{\rm{a}}}({t_{\rm{r}}},{f_{\rm{v}}}) = {\rm{exp}}\left( {{\rm{j}}2\pi \left[ {\frac{2}{{{c^2}}}{K_{{\rm{eq}}}}{C_{\rm{s}}}(1 + {C_{\rm{s}}}) \cdot } \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {({R_{{\rm{eq}}}} - {R_{{\rm{ref}}}})^2} + \frac{{2{R_{{\rm{eq}}}}}}{\lambda }\sqrt {1 - {{\left( {\frac{{\rm{v}}}{{2{\nu _{{\rm{eq}}}}}}} \right)}^2}} + \\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{\lambda }(Et_{\rm{v}}^{\# 3} + Ft_{\rm{v}}^{\# 4})} \right]} \right) \end{array} $ | (18) |
式(17)乘以式(18),完成方位压缩后,将信号进行方位向逆傅里叶变换,得到聚焦图像。改进的CS算法流程见图 3。

|
| 图 3 改进的CS算法流程图 Fig. 3 Improved CS algorithm flow chart |
为了证明改进的CS算法对具有三维速度和加速度的机载曲线运动轨迹SAR数据处理的有效性,采用表 1所示参数对多点目标进行仿真。图 4表示场景区域下5×5点阵中等间距100 m的目标位置。

|
| 图 4 5×5点阵分布图 Fig. 4 Distribution map of 5×5 point targets |
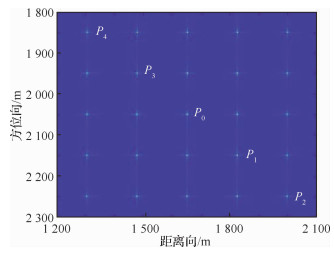
图 5显示了等间距为100 m的5×5点阵在改进CS算法下的聚焦效果,由仿真图可知,此算法能对多点目标进行有效成像,并且中心点和边缘点的成像效果几乎一致。
|
| 图 5 改进的CS算法对点阵的成像效果图 Fig. 5 Imaging results of improved CS algorithm on point targets |
为了更仔细地观察成像细节,把中心点P0和边缘点P2的成像结果进行放大,并分别和文献[18-19]的曲线SAR成像算法进行比较(为便于和文献[19]比较,令vy=0 m/s,ay=0 m/s2,即实验处于二维运动变量状态,其他参数如表 1所示)。
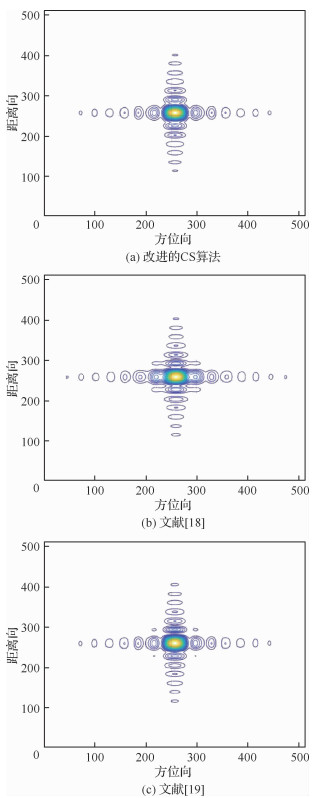
图 6是采用所提出的基于Chebyshev正交分解的CS算法、文献[18-19]所提算法分别对点P0成像得到的高线图。图 6(a)的聚焦效果图中,距离向和方位向的主旁瓣清晰,对称性很好,与理想点目标一致。图 6(b)的方位向出现模糊。图 6(c)出现微小的不对称。
|
| 图 6 场景中心点P0的等高线图 Fig. 6 Contour map of scene center point P0 |
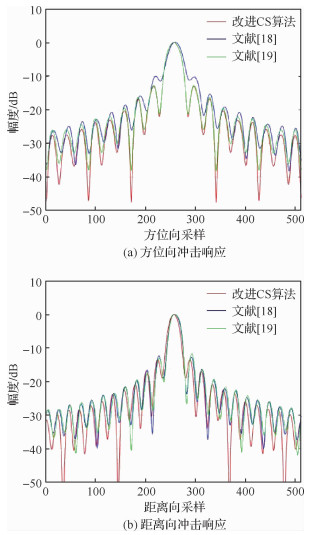
图 7是3种算法对P0点成像得到的方位冲激响应和距离向冲激响应的比较图。由图 7(a)可知,文献[18]的方位向脉冲冲激响应的旁瓣升高,聚焦性能下降,出现方位向的模糊。而改进的CS算法和文献[19]在方位向的聚焦性能是基本一样的。由图 7(b)可知,3种算法的距离向冲激响应略有差别,文献[18-19]的主瓣均稍有偏移,旁瓣均略有升高并出现不对称现象,而改进的CS算法的聚焦性能稍好。
|
| 图 7 场景中心点P0的冲激响应比较 Fig. 7 Comparison of impulse responses of scene center point P0 |
在只考虑两维速度和加速度的条件下,改进的CS算法和文献[19]的算法效果大体上近似,皆好于文献[18]所提出的算法。但是文献[19]的算法不能处理具有三维速度和三维加速度的曲线SAR数据。改进的CS算法和文献[18]所提出的算法都能处理具有三维速度和加速度的曲线SAR数据,但斜距采用Chebyshev多项式近似比文献[18]采用的Taylor级数逼近的精度高,因此成像效果显著。
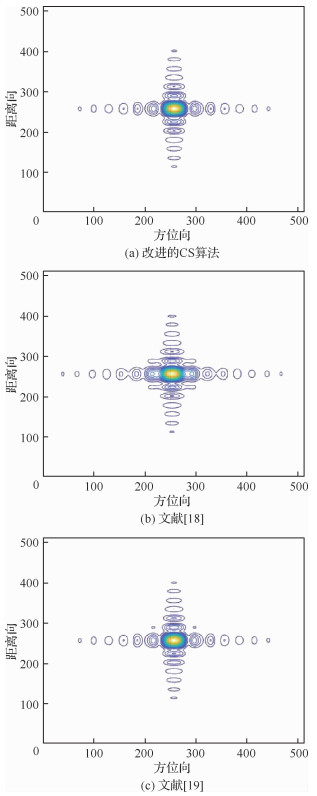
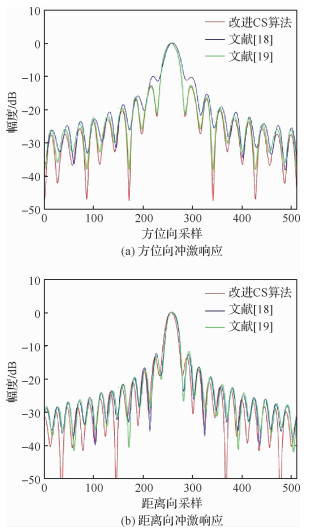
图 8和图 9分别显示了场景边缘点P2在3种算法下的轮廓图以及方位冲激响应和距离向冲激响应的比较。由图可知,3种算法对边缘点P2的成像效果与中心点P0比较只有微小的差别。在只考虑两维速度和加速度的情况下,改进的CS算法和文献[19]的聚焦性能大体上一致,而文献[18-19]的算法在距离向旁瓣约有升高,且在方位向的聚焦性能下降。再次证明了基于Chebyshev正交分解的斜距模型及CS成像算法的有效性。
|
| 图 8 场景边缘点P2的等高线图 Fig. 8 Contour map of scene edge point P2 |
|
| 图 9 场景边缘点P2的冲击响应比较 Fig. 9 Comparison of impulse responses of scene edge point P2 |
为了进一步比较3种算法的聚焦性能,表 2所示的距离向和方位向的积分旁瓣比(Integral Side Lobe Ratio, ISLR)、峰值旁瓣比(Peak Side Lobe Ratio, PSLR)和主瓣宽度(Impulse Response Width, IRW)也定量地证明了改进的CS算法的优越性。即无论是场景中心点P0还是场景边缘点P2,改进的CS算法在距离向和方位向的性能均优于文献[18-19]的算法(由于P4和P2位置对称,P3和P1位置对称,因此只给出P0、P1、P2的聚焦性能参数)。
| 点目标 | 算法 | 距离向 | 方位向 | |||||
| PSLR/dB | ISLR/dB | IRW/m | PSLR/dB | ISLR/dB | IRW/m | |||
| P0 | CS算法 | -13.473 1 | -10.623 8 | 1.427 6 | -13.037 2 | -10.568 1 | 1.796 6 | |
| 文献[18] | -12.580 2 | -10.531 2 | 1.418 9 | -10.191 4 | -8.466 8 | 1.893 6 | ||
| 文献[19] | -11.857 5 | -10.506 7 | 1.433 3 | -13.009 9 | -10.554 3 | 1.796 1 | ||
| P1 | CS算法 | -13.246 6 | -10.595 7 | 1.680 3 | -13.045 3 | -10.566 8 | 1.794 5 | |
| 文献[18] | -12.052 9 | -10.470 0 | 1.458 5 | -10.291 4 | -8.464 3 | 1.933 8 | ||
| 文献[19] | -11.644 8 | -10.449 4 | 1.433 0 | -13.007 9 | -10.554 3 | 1.795 9 | ||
| P2 | CS算法 | -13.146 2 | -10.691 6 | 1.423 1 | -13.072 1 | -10.583 9 | 1.795 0 | |
| 文献[18] | -12.754 3 | -10.608 9 | 1.423 8 | -10.301 8 | -8.469 9 | 1.935 8 | ||
| 文献[19] | -12.980 2 | -10.622 2 | 1.426 6 | -13.015 4 | -10.555 9 | 1.795 7 | ||
产生成像性能差异的一个原因是各算法的斜距模型不一样,从而产生不同的相位误差。在表 1所示参数下,对各算法的斜距误差进行仿真。改进的CS算法采用切比雪夫多项式来逼近斜距历程,文献[18]算法采用传统的泰勒级数来逼近斜距,文献[19]算法提出了考虑两维速度和加速度的斜视双曲斜距方程,3种斜距模型的误差比较如图 10(a)所示。文献[18-19]的斜距误差在合成孔径中心近似为0 m,但在合成孔径边缘,误差增大。而所提出的Chebyshev式斜距误差在整个孔径内都近似为0 m。图 10(b)是由斜距误差产生的多普勒相位误差,该误差也有相同的变化趋势。

|
| 图 10 不同模型的斜距及多普勒相位误差比较 Fig. 10 Comparison of slant range and doppler phase error of different models |
下面探讨本算法的适用范围。由式(2)推导出4阶近似斜距的误差为
| $ \begin{array}{*{20}{l}} {\Delta R \le }\\ {\quad \left( {\frac{{12{A_4}}}{{{R_p}}} - \frac{{3(A_2^2 + 2{A_1}{A_3})}}{{R_p^3}} + \frac{{9A_1^2{A_2}}}{{2R_p^5}} - \frac{{15A_1^4}}{{16R_p^7}}} \right)t_{\rm{v}}^4} \end{array} $ | (19) |
式中:
在合成孔径边缘,斜距误差产生的最大多普勒相位误差为
| $ \begin{array}{l} \Delta {\varPhi _{\rm{m}}} = \frac{{4\pi }}{\lambda }\Delta {R_{\rm{m}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{12{A_4}}}{{{R_p}}} - \frac{{3(A_2^2 + 2{A_1}{A_3})}}{{R_p^3}} + \frac{{9A_1^2{A_2}}}{{2R_p^5}} - \frac{{15A_1^4}}{{16R_p^7}}} \right) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\pi T_{{\rm{syn}}}^4}}{{4\lambda }} \end{array} $ | (20) |
SAR成像要求ΔΦm <
| $a_{x}^{2}+a_{y}^{2}+a_{z}^{2}<\frac{\lambda R_{P}}{3 T_{\mathrm{syn}}^{4}} $ | (21) |
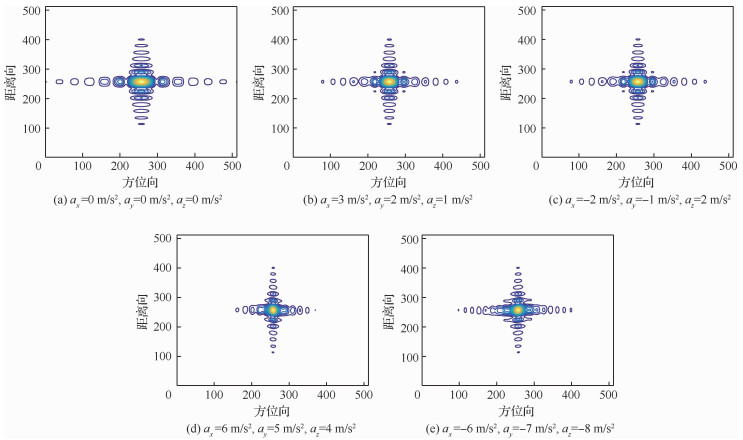
为了验证上述结论,取表 1所示参数对场景中心点P0在不同三维加速度下进行仿真,如图 11所示。合成孔径时间Tsyn=2 s。
|
| 图 11 不同三维加速度下中心点P0的等高线图 Fig. 11 Contour map of scene center point P0 under different three-dimensional acceleration |
由图 11的仿真结果可知,在满足式(21)的约束条件下,本文算法都能有效成像。式(20)的多普勒相位误差存在相加相减项,因此加速度的方向对多普勒相位误差也有影响,导致加速度的边界很复杂。在保证曲线运动的条件下,对应于表 1的机载曲线SAR系统参数,在Tsyn=2 s时,可得到本文算法适用的加速度的正向边界(10 m/s2,9 m/s2,8 m/s2)和负向边界(-10 m/s2,-9 m/s2,-8 m/s2)。
本算法的加速度适用范围与合成孔径时间相关。采用表 1所示参数,对不同合成孔径时间下的成像效果进行比较。
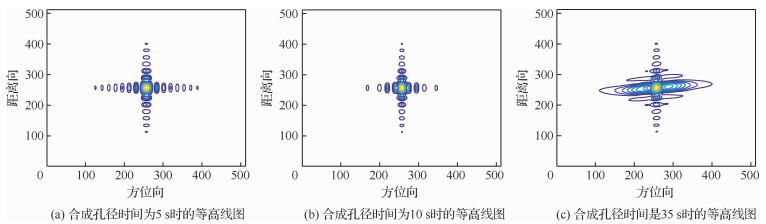
图 12显示不同合成孔径时间下的场景中心点P0的成像等高线图。随着合成孔径时间增加,点目标的高线图开始失真,合成孔径时间超过35 s时,方位向散焦,算法失效。
|
| 图 12 不同合成孔径时间下的等高线图 Fig. 12 Contour map of different synthetic aperture time |
随着日益复杂的外界环境和多样化的应用需求,曲线运动轨迹SAR成像的研究具有特殊的应用价值。曲线运动轨迹SAR克服了机载直线SAR系统因成像特性的限制而存在的前视盲区,能灵活地选择成像区域。但复杂的距离历程给成像处理带来了困难,针对三维加速度的影响,提出了一种基于Chebyshev多项式的等效双曲斜距模型及该斜距模型对应的CS成像算法,并给出了三维加速度的边界值和最大合成孔径时间。通过运动方程得到SAR载体和目标之间的斜距表达式,并进行Chebyshev近似,推导了与传统SAR类似的等效斜距模型。然后,在考虑载体三维运动参数的基础上,引入CS成像算法消除距离徙动的空间变化性。仿真实验表明,该算法提高了大合成孔径时间下场景点目标的成像质量。
| [1] | CUMMING I G, WONG F K. Digital processing of synthetic aperture radar data algorithms and implementation[M]. Norwood: Artech House, 2005: 625-670. |
| [2] | SUN Z C, WU J J, LI Z Y, et al. Highly squint SAR data focusing based on keystone transform and azimuth extended nonlinear chirp scaling[J]. IEEE Geoscience and Remote Sensing Letter, 2015, 12(1): 145-149. |
| Click to display the text | |
| [3] | LIANG Y, LI Z Y, ZENG L T, et al. A high-order phase correction approach for focusing HS-SAR small-aperture data of high-speed moving platforms[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(9): 4551-4561. |
| Click to display the text | |
| [4] | LIU Y, XING M D, SUN G C, et al. Echo model analyses and imaging algorithm for high-resolution SAR on highspeed platform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 933-950. |
| Click to display the text | |
| [5] | ZHANG L, QIAO Z J, XING M D, et al. A robust motion compensation approach for UAV SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3202-3218. |
| Click to display the text | |
| [6] | CHEN S, YUAN Y, ZHANG S N, et al. A new imaging algorithm for forward-looking missile-borne bistatic SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(4): 1543-1552. |
| Click to display the text | |
| [7] | TANG S Y, ZHANG L R, GUO P, et al. Processing of monostatic SAR data with general configurations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6529-6546. |
| Click to display the text | |
| [8] | HU C, LIU Z P, LONG T. An improved CS algorithm based on the curved trajectory in geosynchronous SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(3): 795-808. |
| Click to display the text | |
| [9] | TANG S Y, LIN C H, ZHOU Y, et al. Processing of long integration time spaceborne SAR data with curved orbit[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 888-904. |
| Click to display the text | |
| [10] | LIU J B, QIU X L, HUANG L J, et al. Curved path SAR geolocation error analysis based on BP algorithm[J]. IEEE Access, 2019, 7: 20337-20345. |
| Click to display the text | |
| [11] | AN H Y, WU J J, SUN Z C, et al. A two-step nonlinear chirp scaling method for multichannel GEO spaceborne airborne bistatic SAR spectrum reconstructing and focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3713-3728. |
| Click to display the text | |
| [12] | BAO M, XING M D, LI Y C, et al. Two-dimensional spectrum for MEO SAR processing using a modified advanced hyperbolic range equation[J]. Electronics Letters, 2011, 47(18): 1043-1045. |
| Click to display the text | |
| [13] | LI Z Y, LIANG Y, XING M D, et al. An improved range model and Omega-K-based imaging algorithm for high-squint SAR with curved trajectory and Constant acceleration[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(5): 656-660. |
| Click to display the text | |
| [14] | WANG P B, LIU W, CHRN J, et al. A high-order imaging algorithm for high-resolution spaceborne SAR based on a modified equivalent squint range model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1225-1235. |
| Click to display the text | |
| [15] | DONG Q, SUN G C, YANG Z M, et al. Cartesian factorized back projection algorithm for high-resolution spotlight SAR imaging[J]. IEEE Sensors Journal, 2018, 18(3): 1160-1168. |
| Click to display the text | |
| [16] | LIANG M, SU W M, GU H. Focusing high-resolution high forward-looking bistatic SAR with nonequal platform velocities based on keystone transform and modified nonlinear chirp scaling algorithm[J]. IEEE Sensors Journal, 2019, 19(3): 901-908. |
| Click to display the text | |
| [17] | HU B, JIANG Y C, ZHANG S S, et al. Focusing of geosynchronous SAR with nonlinear chirp scaling algorithm[J]. Electronics Letters, 2015, 51(15): 1195-1197. |
| Click to display the text | |
| [18] | WU J J, AN H Y, ZHANG Q H, et al. Two-dimensional frequency decoupling method for curved trajectory synthetic aperture radar imaging[J]. IET Radar, Sonar and Navigation, 2018, 12(7): 766-773. |
| Click to display the text | |
| [19] | LIAO Y, ZHOU S, YANG L. Focusing of SAR with curved trajectory based on improved hyperbolic range equation[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(3): 454-458. |
| Click to display the text | |
| [20] |
包敏, 周鹏, 保铮, 等. 地球同步轨道SAR曲线轨迹模型下的改进CS成像算法[J]. 电子与信息学报, 2011, 33(11): 2686-2693. BAO M, ZHOU P, BAO Z, et al. Improved CS imaging algorithm based on SAR curve trajectory model in geostationary orbit[J]. Journal of Electronic & Information Technology, 2011, 33(11): 2686-2693. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [21] | FAN W N, ZHANG M, LI J X, et al. Modified range doppler algorithm for high squint SAR echo processing[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 422-426. |
| Click to display the text | |
| [22] |
李相平, 陈麒, 祝明波, 等. 一种基于改进WLBF频谱的异构双基地前视SAR成像算法[J]. 航空学报, 2018, 39(8): 321886. LI X P, CHEN Q, ZHU M B, et al. An imaging algorithm for heterogeneous bistatic forward-looking SAR based on modified WLBF spectrum[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(8): 321886. (in Chinese) |
| Cited By in Cnki | Click to display the text |



