气动外形简洁的无尾布局由于其气动效率高、结构重量小、雷达隐身特性好等优点,成为未来作战飞机气动布局研究的热点方向[1-6]。但没有尾翼也使得无尾布局面临着较为严重的操稳控制问题,特别是寻找能够产生足够航向增稳和控制力矩的新型部件或舵面配置[7]。
国内外对于无尾布局航向操稳控制研究的重点,主要集中于新型航向控制舵面的探索以及基于新型舵面的布局航向操稳控制分析两方面。新型航向控制舵面主要有全动翼尖、差动前缘襟翼、嵌入式舵面、阻力方向舵和组合舵面等形式[8-13],尽管上述舵面具有一定的航向控制能力,但是在大迎角或超声速状态则面临舵面效率明显降低的问题[14-17]。李林等针对基于现有舵面的无尾布局,选取跨超声速巡航和低速起降等典型飞行状态,定量分析了构型参数、飞行状态与三轴稳定性以及典型模态之间的线化规律[18]。
对于航向稳定性不足的无尾布局,在受到横航向扰动时利用控制舵面主动偏转来提供恢复力矩是实现布局航向增稳的典型方法[19],但这会带来舵面可用偏度减小、飞机系统可靠性降低等问题[20]。为此,宋磊等提出了一种通过改变机翼上反角来提高横航向动稳定性的无尾布局设计方法[20]。对于同样存在航向稳定性不足问题的升力体布局,赵俊波和沈清结合流场特点,提出了一种基于当地侧向流动压缩/膨胀原理的航向气动增稳设计方法,通过后移侧向气动压心,较为明显地改善了布局的航向静稳定性[21]。
针对超声速状态舵面效率明显下降、舵面控制能力不足的问题,为了保证无尾布局具有足够的航向操稳控制能力,有必要针对布局本身开展超声速航向增稳设计研究。本文结合超声速流场所特有的压缩/膨胀流动,通过分析后体型面与后体流场的相互关系,开展无尾布局后体超声速航向增稳设计方法研究,并基于典型方案分析了该方法所适用的速度范围及其对于布局升阻特性的影响。
1 计算方法及验证 1.1 计算方法本文数值模拟所用方程为三维Navier-Stokes(N-S)方程。在直角坐标系中三维N-S方程守恒形式可表示为
| $ \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial \mathit{\boldsymbol{t}}}} + \frac{{\partial {\mathit{\boldsymbol{f}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_i}}} = \frac{{\partial {\mathit{\boldsymbol{f}}_{{\rm{v}}i}}}}{{\partial \mathit{\boldsymbol{x}}i}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1, 2, 3 $ | (1) |
式中:w为状态矢量;f为无黏(对流)通矢量;fv为黏性(耗散)通矢量。
采用Menter’s剪切应力输运(SST)湍流模型,利用有限体积法将控制方程离散,计算采用非结构网格,为了保证能够模拟边界层内的流动特征,在物面附近生成棱柱层网格,第1层网格高度为飞机参考长度的10-6,网格点数为400万左右。物面采用无滑移物面边界条件,对称面采用对称边界条件,远场由当地一维黎曼不变量确定。
无尾布局超声速航向静稳定性评估的典型计算状态为:马赫数Ma=2.0,飞行高度H=18 km,侧滑角β=4°,计算迎角α=-3°~6°。
1.2 计算验证选择小展弦比飞翼布局标模[13]来验证数值模拟方法的精度。采用非结构网格进行计算,网格点数为400万。计算来流马赫数Ma=0.95,计算飞行高度H=10 km。
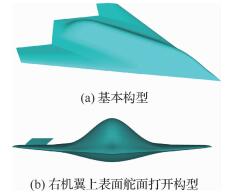
计算模型在机翼外侧上下表面带有用于航向控制的嵌入舵面,计算构型为无舵面偏转的基本构型和仅右机翼上表面舵面打开的舵面偏转构型,如图 1所示。典型状态表面及空间网格如图 2所示。
|
| 图 1 模型外形 Fig. 1 Shape of model |

|
| 图 2 计算网格 Fig. 2 Computational mesh |
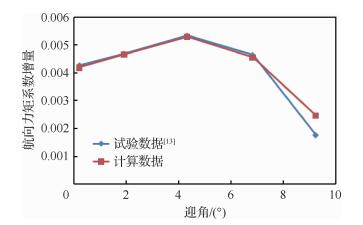
马赫数Ma=0.95、侧滑角β=5°时,右侧机翼上表面嵌入舵面偏转30°,相对无舵偏基本构型的航向力矩增量计算结果与试验数据[13]对比如图 3所示。数值模拟结果在小迎角范围内与试验数据基本吻合,在计算迎角范围内航向力矩增量变化规律一致。说明本文所采用的数值模拟方法具有较高的精度,可用于计算和分析无尾布局的航向力矩特性。
|
| 图 3 航向力矩系数增量的计算结果与试验数据对比 Fig. 3 Comparison of directional moment coefficient increment between calculation and test results |
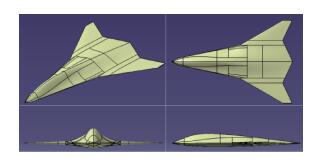
参考超声速飞机完成无尾布局基本方案气动外形设计(图 4)。该方案以双后掠前缘飞翼布局为基础,前机身在保证装载空间要求下与边条融合设计,后体扁平,暂未考虑进气道布置。布局主要参数见表 1。
|
| 图 4 无尾布局基本方案 Fig. 4 Base model of tailless configuration |
| 参数 | 数值 |
| 参考面积/m2 | 60 |
| 参考长度/m | 4 |
| 翼展/m | 11 |
| 机身长度/m | 16 |
| 参考重心轴向位置/m | 9 |
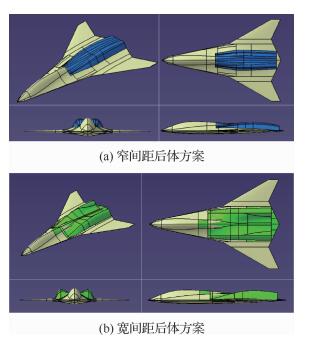
由于无尾布局基本方案后体空间有限,在工程实际中需要对后体外形进行适当修改以满足内部装载要求。从隐身角度考虑,选择发动机及排气系统背置形式。对于双发布局,根据尾喷管的间距,完成窄间距后体和宽间距后体两种方案外形设计,如图 5所示。
|
| 图 5 无尾布局常规后体方案 Fig. 5 Conventional after body models of tailless configuration |
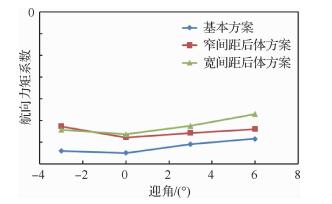
无尾布局基本方案和两种常规后体方案超声速航向力矩系数随迎角变化曲线如图 6所示。后体扁平的基本方案呈现明显的航向静不稳定性,两种常规后体方案的航向力矩系数曲线上移,航向静不稳定度降低。其中窄间距后体贡献的航向增稳力矩随着迎角的增加而减小,宽间距后体所提供的航向增稳力矩则基本不随迎角变化。上述航向增稳力矩随迎角变化规律的差异使得重心后侧向投影面积较大窄间距后体方案只在负迎角状态具有稍小的航向静不稳定度,而在较大迎角时,其航向静不稳定度要大于宽间距后体方案。
|
| 图 6 常规后体方案航向力矩系数曲线(Ma=2.0,H=18 km,β=4°) Fig. 6 Directional moment coefficient curves of conventional after body models (Ma=2.0, H=18 km, β=4°) |
无尾布局基本方案和两种常规后体方案在超声速、定侧滑时不同迎角下的表面压力系数Cp分布云图如图 7所示。

|
| 图 7 常规后体方案表面压力分布云图(Ma=2.0,H=18 km,β=4°) Fig. 7 Surface pressure distribution contour of conventional after body models (Ma=2.0, H=18 km, β=4°) |
上述3种方案的前体流场基本相同,主要表现为迎风侧机体表面为高压区,而背风侧机体表面为低压区的压力分布形态。
对于基本方案,其后体流场呈现为迎风侧机体表面低压、背风侧机体表面高压的压力分布形态,即前后体都产生航向不稳定力矩。
对于窄间距后体,突起的后体型面改变了后体流向,后体迎风侧与背风侧表面压差合力产生航向增稳力矩。但是随着迎角的增加,突起的后体型面对流场干扰能力减弱,迎风侧与背风侧的压力不对称程度降低,后体提供的航向增稳力矩也随之减小。
对于宽间距后体,沿流向逐渐变宽的后体型面对后体迎风外表面流场产生压缩作用,在后体背风外表面产生膨胀作用,进而形成航向增稳力矩。而后体型面曲率变化导致后体内凹区域产生了与之相反的航向不稳定力矩,使得宽间距后体所产生总的航向增稳力矩有所降低。随着迎角的增加,内凹区域的低压区总体向迎风侧移动,宽间距后体两侧内外表面都形成航向增稳力矩,尽管此时后体外表面压差所形成的航向增稳力矩略有降低,但是总的航向增稳力矩变化不大。
可以看出,增加后体侧向投影面积可以降低无尾布局超声速航向静不稳定度,但不同后体型面的降低程度相差较大。从窄间距后体方案与宽间距后体方案的超声速航向力矩系数曲线和表面流场对比来看,通过调整后体型面来有效利用超声速流场中的压缩和膨胀流动,能够在后体表面形成航向增稳的侧向压差,进而实现后体的超声速航向增稳设计。
为此,本文提出一种利用超声速流场压缩/膨胀流动的后体超声速航向气动增稳设计方法,即通过后体型面的针对性设计,在后体超声速流场中构建一系列压缩和膨胀流动(图 8),使得后体迎风面产生高压区,背风面产生低压区,结合具有侧向投影面积的后体型面,形成超声速航向增稳力矩,实现无尾布局后体的超声速航向增稳设计。

|
| 图 8 无尾布局后体超声速航向增稳设计原理 Fig. 8 Supersonic directional stability augmentation principle of after body for tailless configuration |
基于两种常规后体方案提炼能够影响后体超声速航向静稳定性的后体型面特征,确定后体型面关键参数,并以此为基础完成后体型面的参数化建模(图 9)。

|
| 图 9 后体参数化型面及其控制曲线 Fig. 9 Parametric surface and surface control curves of after body |
单侧后体型面主要控制曲线包括一条后体脊线曲线和两条后体控制截面曲线,通过修改上述曲线参数即可完成后体型面的调整。本文分析的后体型面参数主要包括后体侧向投影面积、后体脊线形状和后体控制截面形状三方面。
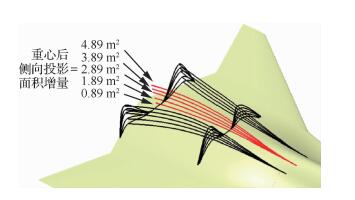
4.2 后体侧向投影面积影响后体侧向投影面积通常由脊线高度和型面后端截面曲线高度控制,而后端截面曲线高度受喷管形状约束。基于基本方案后体,通过对后体控制曲线在翼平面法向的仿射变化,获得一系列增加后体侧向投影面积的型面曲面,型面外形控制曲线对比如图 10所示,不同后体型面的无尾布局方案后体侧向投影面积增量ΔSaft、重心前后侧向投影面积比例Sfore/Saft对比见表 2,在不同迎角下不同后体型面超声速航向力矩系数随重心后侧向投影面积增量ΔSaft和重心前后侧向投影面积比Sfore/Saft变化的曲线如图 11所示。
|
| 图 10 后体侧向投影面积影响方案控制曲线对比 Fig. 10 Comparison of control curves of after body area impact cases |
| 序号 | 后体侧向投影面积增量/m2 | 重心前后侧向投影面积比例 |
| 1 | 0 | 2.42 |
| 2 | 0.89 | 2.03 |
| 3 | 1.89 | 1.72 |
| 4 | 2.89 | 1.49 |
| 5 | 3.89 | 1.32 |
| 6 | 4.89 | 1.18 |
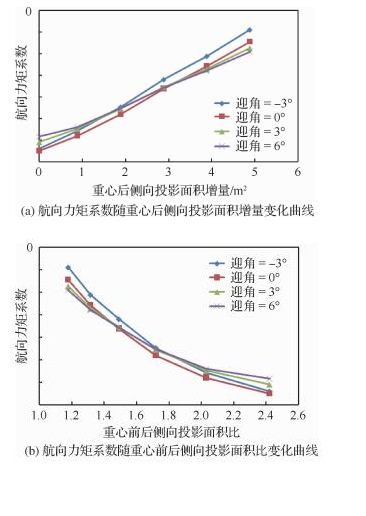
|
| 图 11 不同迎角下后体侧向投影面积影响方案航向力矩系数曲线(Ma=2.0,H=18 km,β=4°) Fig. 11 Directional moment coefficient curves of after body lateral projected area impact cases in different angles of attack (Ma=2.0, H=18 km, β=4°) |
可以看出,在无尾布局扁平后体的基础上增加后体能够降低布局的航向静不稳定性,且后体型面所提供的航向增稳力矩与后体侧向投影面积增量ΔSaft近似呈正比关系,即ΔSaft越大,后体型面所提供的航向增稳力矩越大,布局航向静不稳定度越小。与之相对应,在固定迎角下,布局航向力矩与重心前后侧向投影面积比例Sfore/Saft呈反比关系。迎角α=-3°时,后体侧向投影面积增加2.89 m2,布局航向静不稳定度减小50%;后体侧向投影面积增加4.89 m2,尽管仍然是航向静不稳定状态,但布局航向静不稳定度相对基本布局减小86%。迎角α=6°时,后体侧向投影面积增加2.89 m2,布局航向静不稳定度减小39%;后体侧向投影面积增加4.89 m2,布局航向静不稳定度减小67%。
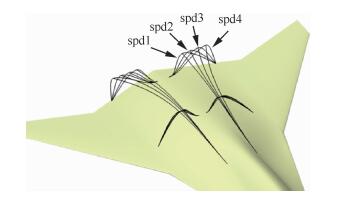
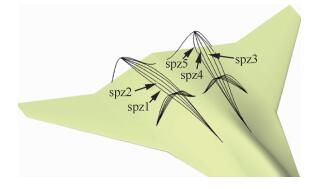
4.3 后体脊线形状影响后体脊线形状影响研究分为两个部分:一是脊线后端的展向位置影响(图 12),其中spd1~spd4方案后体脊线外形相似,脊线前端位置相同,各方案脊线后端端点间距相差0.3 m;二是脊线后端展向位置固定时的脊线形状影响(图 13, spz1~spz5)。需要说明的是,后体脊线形状变化时,后体控制截面形状也随着变化,因此后体脊线形状影响也部分包含了后体截面形状的影响。
|
| 图 12 后体脊线后端展向位移影响方案控制曲线对比 Fig. 12 Comparison of control curves of after body surface spine curve's span wise position impact cases |
|
| 图 13 后体脊线形状影响方案控制曲线对比 Fig. 13 Comparison of control curves of after body surface spine curve's shape impact cases |
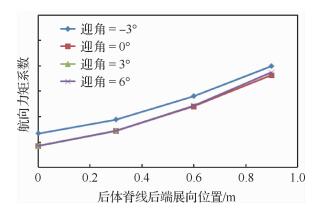
以spd1方案后体脊线为基准,在不同固定迎角下,布局航向力矩系数随后体脊线后端点展向外移距离变化规律如图 14所示。后体脊线后端端点越靠外,布局后体所产生的航向增稳力矩越大。迎角α=-3°时,后体脊线后端端点外移0.3 m,布局航向静不稳定度减小6.9%;后体脊线后端端点外移0.9 m,布局航向静不稳定度相对基本布局减小33.1%。迎角α=6°时,后体脊线后端端点外移0.3 m,布局航向静不稳定度减小7.2%;后体脊线后端端点外移0.9 m,布局航向静不稳定度相对基本布局减小34.8%。
|
| 图 14 不同迎角下后体脊线后端展向位置对布局航向力矩系数影响曲线(Ma=2.0,H=18 km,β=4°) Fig. 14 Directional moment coefficient curves of after body surface spine curve's span wise position impact cases in different angles of attack(Ma=2.0, H=18 km, β=4°) |
但是从图 12也应注意到,后体脊线后端端点的外移会减小后体截面与外翼之间的夹角(趋向于90°),增加布局的侧向雷达波的反射,导致布局侧向雷达隐身性能降低。因此后体脊线后端端点展向位置需综合考虑才能确定。
后体脊线后端端点展向位置固定时的后体脊线形状对布局航向力矩特性影响曲线如图 15所示。图中spz1~spz5方案后体型面控制曲线对比见图 13,其中spz1方案后体脊线靠外,在翼平面内投影呈S形,曲率变化拐点最靠前,而spz5方案后体脊线最靠内,在翼平面内投影为内凹曲线,spz2~spz4方案为介于spz1方案和spz5方案的中间方案。

|
| 图 15 后体脊线形状对布局航向力矩系数影响曲线(Ma=2.0,H=18 km,β=4°) Fig. 15 Directional moment coefficient curves of after body surface spine curve's shape impact cases(Ma=2.0, H=18 km, β=4°) |
可以看出,spz1方案和spz5方案的航向力矩系数随迎角变化呈现完全相反的规律:对于spz1方案,后体所提供的航向增稳力矩随着迎角的增加而增加,迎角α=6°时的布局航向静不稳定度相对迎角α=-3°减小23.2%;而对于spz5方案,后体所提供的航向增稳力矩随着迎角的增加而减小,迎角α=6°时的布局航向静不稳定度相对迎角α=-3°增加5.3%。
对于后体脊线在翼平面内曲率拐点接近中间的spz2方案,后体型面在小迎角范围内所提供的航向增稳力矩明显增加,与spz5方案相当,在整个迎角范围内具有最好的航向增稳能力。对于后体脊线在翼平面内曲率拐点靠后的spz3方案和完全内凹的spz4方案,后体型面在正迎角状态所提供的航向增稳力矩要明显小于spz2方案,可见后体脊线在翼平面内投影的曲率拐点位置是影响后体型面在宽迎角范围内航向增稳能力的关键参数。
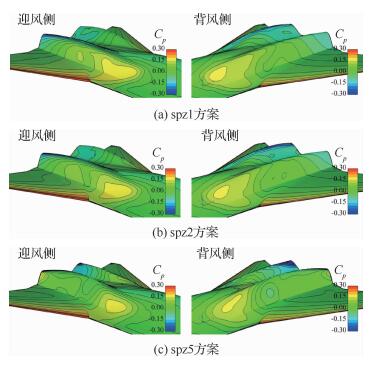
为明确不同脊线形状方案航向力矩系数随迎角变化规律存在差异的物理成因,选取spz1方案、spz2方案和spz5方案在典型迎角下的后体上表面压力分布(图 16和图 17)进行对比分析。上述3种方案的主要差异在于脊线在翼平面投影内的曲线形状,其中存在曲率拐点的spz1方案和spz2方案表面压力分布相似,不同于整体内凹的spz5方案。可以看出,后体增稳力矩主要来源于后体型面两侧的内外表面压差,且迎风外表面与背风内表面所形成的压差要明显大于迎风内表面与背风外表面所形成的压差。为了分析方便,对比的重点集中于迎风外表面和背风内表面的压力分布变化。
|
| 图 16 后体脊线形状影响方案表面压力分布云图(Ma=2.0,H=18 km,α=-3°,β=4°) Fig. 16 Surface pressure distribution contour of after body surface spine curve's shape impact cases(Ma=2.0, H=18 km, α=-3°, β=4°) |
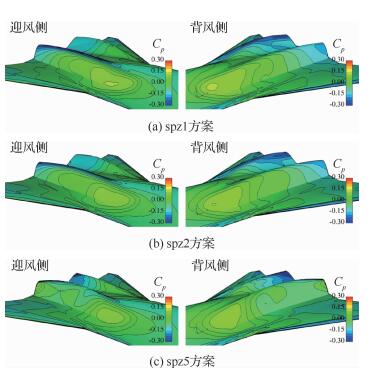
|
| 图 17 后体脊线形状影响方案表面压力分布云图(Ma=2.0,H=18 km,α=3°,β=4°) Fig. 17 Surface pressure distribution contour of after body surface spine curve's shape impact cases (Ma=2.0, H=18 km, α=3°, β=4°) |
在负迎角状态(图 16),后体型面整体处于迎风面,后体前端具有明显的压缩流动。对于spz5方案,气流在迎风侧后体外表面呈压缩流动,表面压力沿流向逐渐升高,而在背风侧内表面呈膨胀流动,表面压力沿流向逐渐降低,由此在后体形成了较大的航向增稳力矩。对于spz1方案,由于脊线在翼平面内的投影曲线曲率拐点靠前,气流在迎风侧后体外表面经过曲率拐点后由减速压缩流动较早地转为加速膨胀流动,使得后体后段的表面压力降低较多,与之相反,气流在背风侧内表面经曲率拐点后受到型面压缩,压力有所增加,后体内外型面的有利压差减小,导致航向增稳力矩损失较大。而对于spz2方案,由于其脊线的曲率拐点较为靠后,曲率变化所导致的气流在后体后段膨胀(迎风侧外表面)或压缩(背风侧内表面)程度减弱,内外型面仍然具有较大压差,后体依然能够产生较大的航向增稳力矩。
在正迎角状态(图 17),后体型面整体处于背风面,后体前端的压缩流动减弱,后体气流流动对脊线曲率拐点位置的敏感性降低,spz1方案和spz2方案的后体表面压力分布相似。此时气流在背风内表面的膨胀流动更强,表面压力下降较多,尽管迎风外表面压力因为压缩作用减小而有所降低,但内外表面压差仍然明显增加,两种方案的后体都产生了较大的航向增稳力矩。而对于spz5方案,气流在后体迎风外表面的压缩强度降低,表面压力减小,完全内凹的脊线形状限制了后体背风内表面低压区范围的扩展,气流膨胀对于后体背风内表面的影响有限,导致后体内外表面有利压差减小,后体所提供的航向增稳力矩也随之降低。
4.4 后体控制截面形状影响后体控制截面形状直接决定后体型面曲率的展向分布,为了明确其对后体型面航向增稳特性的影响,完成3种后体方案设计,如图 18所示。3种后体方案的主要差别在于脊线附近曲率变化,其中spc1方案后体控制截面曲线在脊线附近曲率最大,截面积也最小,而spc3方案后体控制截面曲线在脊线附近的曲率则接近0,截面积最大,后体型面在脊线附近也更为平坦。

|
| 图 18 后体截面形状影响方案控制曲线对比 Fig. 18 Control curves comparison of after body surface section curve's shape impact cases |
后体截面形状影响方案航向力矩系数随迎角变化曲线如图 19所示。可以看出,增加脊线附近的截面曲线曲率会明显降低后体型面所产生的航向增稳力矩,且航向增稳力矩变化量几乎不随迎角改变。相较于脊线附近截面曲线曲率较大的spc1方案,截面曲线曲率较小的spc2方案后体增稳能力减弱,布局航向静不稳定度增加。但是随着后体截面曲线在后体脊线附近的曲率进一步增大后,后体型面所提供航向增稳力矩的减小幅度降低。迎角α=6°时,spc2方案布局航向静不稳定度相对spc1方案增加10.3%,spc3方案布局航向静不稳定度相对spc1方案增加15.3%。

|
| 图 19 后体截面形状对布局航向力矩系数影响曲线(Ma=2.0,H=18 km,β=4°) Fig. 19 Directional moment coefficient curves of after body surface section shape (Ma=2.0, H=18 km, β=4°) |
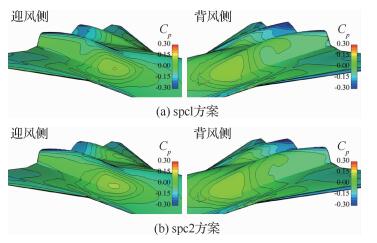
典型后体截面形状影响方案表面压力分布对比如图 20所示。可以看出,spc1方案和spc2方案后体型面表面压力分布相似,差别主要包括两个方面:一是脊线附近压力梯度差异;spc2方案在后体型面脊线附近型面曲率较小,气流在其后体迎风侧外表面脊线附近的压缩强度降低,迎风外表面低压区范围增加;二是后体型面内表面的压力变化,spc2方案脊线附近曲率增加使得后体型面前部的内表面凸起,对气流产生压缩作用,由此导致内型面压力增加,后体型面内外侧有利压差减小。上述两方面的综合作用导致spc2方案后体型面所提供的航向增稳力矩降低。
|
| 图 20 后体截面形状影响方案表面压力分布云图(Ma=2.0,H=18 km,α=3°,β=4°) Fig. 20 Surface pressure distribution contour of after body surface section shape's impact cases (Ma=2.0, H=18 km, α=3°, β=4°) |
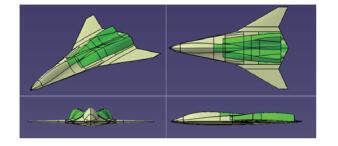
根据后体型面参数对布局航向力矩特性影响规律,结合布局后体几何约束,完成典型后体超声速航向增稳方案设计(图 21)。由于本文的研究重点在于后体型面对于布局航向特性的影响,因此对尾喷管进行了简化处理。
|
| 图 21 无尾布局超声速航向增稳后体方案 Fig. 21 Directional augmentation after body model of supersonic tailless configuration |
为了较为全面地分析超声速后体航向增稳方案的综合气动特性,选取无尾布局基本方案、窄间距后体方案、宽间距后体方案和后体增稳方案进行数值计算,计算状态见表 3。
| 序号 | 高度/km | 马赫数 | 迎角/(°) | 侧滑角/(°) |
| 1 | 11 | 0.9 | -3, 0, 3, 6 | 0, 4 |
| 2 | 18 | 1.2, 1.5, 2.0 | -3, 0, 3, 6 | 0, 4 |
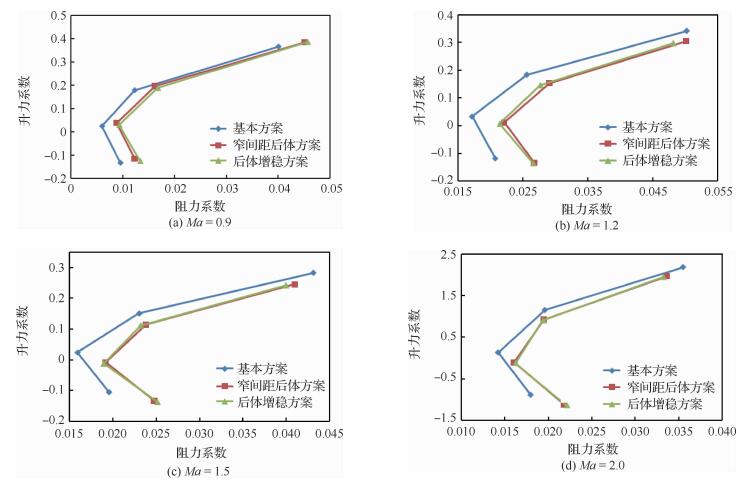
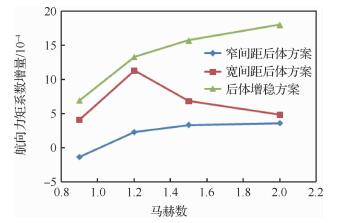
不同马赫数下极曲线对比如图 22所示,图中升阻力系数的计算未计及尾喷管端面部件。相对于常规窄间距后体方案,后体航向增稳方案的阻力只在跨声速时有所增加,而在超声速状态的阻力反而略有降低。由此可以看出,后体型面的航向增稳设计并不会明显影响布局的升阻特性。无尾布局不同后体方案相对基本方案在不同迎角下的航向力矩系数增量均值随Ma变化曲线如图 23所示。对于窄间距后体方案,尽管后体型面增加了重心后侧向投影面积,但由于后体型面对全机流场的不利影响,跨声速时布局的航向不稳定度反而有所增加。超声速状态,后体型面基本起到了航向增稳的作用。对于宽间距后体方案,其后体型面在跨声速和超声速状态都能提供较大的航向增稳力矩,但是后体航向增稳能力却随着Ma的增加而降低。对于后体增稳方案,其后体型面在跨声速和超声速范围都能提供较大的航向增稳力矩,且航向增稳力矩的量值随着Ma的增加而增加。
|
| 图 22 无尾布局多方案极曲线(Ma=2.0,H=18 km) Fig. 22 Polar curves of tailless configuration cases(Ma=2.0, H=18 km) |
|
| 图 23 无尾布局后体方案航向力矩系数增量曲线(Ma=2.0,H=18 km) Fig. 23 Directional moment coefficient increment curves of tailless configuration after body cases (Ma=2.0, H=18 km) |
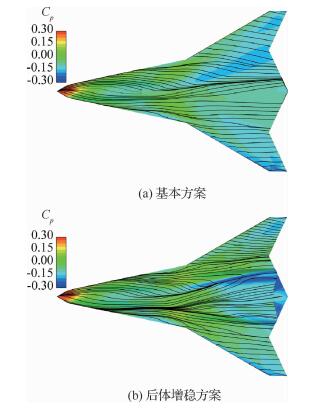
无尾布局基本方案和后体增稳方案表面压力分布和表面极线流线见图 24所示。对于无尾布局基本方案,尽管后体扁平光顺,但是因为前体流场影响,表面极限流线在中后机身中间位置汇聚成表面分离线;分离线右侧气流尽管处于压缩流动状态,因为靠近膨胀区,流速较高,布局表面压力较低;而分离线左侧气流为膨胀流动状态,但因靠近压缩流动区,流速较低,布局表面压力较高。对于后体增稳方案,由于后体型面脊线附近曲率较大,脊线附近气流流动变化剧烈,中后机身存在的分离线与后体型面迎风侧的脊线重合。由于脊线后段外移,限制了气流在迎风侧翼面的膨胀流动,加强了对后体流场的压缩作用,后体型面迎风外表面压力增加,而在后体型面背风内表面则形成明显的气流膨胀区,表面压力降低,进而形成有利于航向增稳的左右压差。对于后体型面的背风侧,受背风侧脊线曲率变化的影响,气流在后体型面背风外表面呈现加速流动,导致表面压力降低,而当气流绕过后体脊线后受到阻滞,呈减速流动,迎风内表面压力升高,由此也形成有利于航向增稳的左右压差。正是左右机身两侧后体型面对后体流场的共同作用,形成了较大的航向增稳力矩。
|
| 图 24 无尾布局表面流场(Ma=2.0,H=18 km,α=3°,β=4°) Fig. 24 Surface flow field of tailless configuration (Ma=2.0, H=18 km, α=3°, β=4°) |
1) 针对无尾布局超声速航向增稳设计,后体型面主要控制参数包括重心后侧向投影面积增量、后体型面脊线形状和后体型面截面形状3个部分。
2) 对于无尾布局后体超声速航向增稳型面设计,后体航向增稳力矩基本与重心后侧向投影面积增量呈正比关系,重心后侧向投影面积增量越大,后体型面所提供的航向增稳力矩越大。
3) 对于无尾布局后体超声速航向增稳型面设计,后体脊线后端点展向位置离对称面越远,后体型面所产生的航向增稳力矩越大。后体型面脊线在翼平面内投影呈S形,且曲率拐点居中可以降低后体型面航向增稳能力的迎角敏感性,提高宽迎角范围内的航向增稳能力。
4) 对于无尾布局后体超声速航向增稳型面设计,减小后体型面脊线位置的截面曲线曲率,会减弱后体型面脊线附近的压力梯度,降低后体型面的航向增稳能力。
5) 针对无尾布局,通过后体超声速航向增稳设计,可以在不明显增加布局阻力的情况下,大幅降低布局在跨声速和超声速时的航向静不稳定度。
| [1] |
车竞, 何开锋, 钱炜祺. 制空型无人机的关键技术、气动布局及特性[J]. 空气动力学学报, 2017, 35(1): 13-26. CHE J, HE K F, QIAN W Q. Key technique and aerodynamic configuration characteristic of UCAV with command of the air[J]. Acta Aerodynamica Sinica, 2017, 35(1): 13-26. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [2] |
孙隆和. 第六代战斗机的竞争[J]. 电光与控制, 2012, 19(10): 1-7. SUN L H. The competition of the sixth generation fighters[J]. Electronics Optics and Control, 2012, 19(10): 1-7. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [3] |
石怀林, 武卫兵, 张立, 等. 美军第六代战斗机典型技术特征[J]. 国防科技, 2010, 31(4): 10-13. SHI H L, WU W B, ZHANG L, et al. A review on the typical technic characters of fighters of the sixth generation in the U.S. air force[J]. National Defense Science and Technology, 2010, 31(4): 10-13. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [4] |
李金梁, 涂泽中, 刘振庭. 美第六代战斗机研究进展情况[J]. 电光与控制, 2014, 21(6): 3-8. LI J L, TU Z Z, LIU Z T. The research progress of the sixth generation fighter of USAF[J]. Electronics Optics and Control, 2014, 21(6): 3-8. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [5] | SATHE A, PANT R. Conceptual design studies of an unmanned combat aerial vehicle: AIAA-2010-9306[R]. Reston: AIAA, 2010. |
| Click to display the text | |
| [6] | ADDINGTON G A, MYATT J H. Control surface deflection effects on the innovative control effectors (ICE 101) design: AFRL-VA-WP-T R-2000-3027[R]. Reston: AFRL, 2010. |
| [7] | BOWLUS J A, MULTHOPP D, BANDA S S. Challenges and opportunities in tailless aircraft stability and control: AIAA-1997-3830[R]. Reston: AIAA, 1997. |
| Click to display the text | |
| [8] | DORSETT K M, MEHL D R. Innovative control effectors(ICE): WL-TR-96-3043[R]. Reston: AFRL, 1996. |
| [9] |
马松辉, 吴成富, 陈怀民. 飞翼飞机稳定性与操纵性研究[J]. 飞行力学, 2006, 24(3): 17-21. MA S H, WU C F, CHEN H M. Study on stability and maneuverability of flying wing aircraft[J]. Flight Dynamics, 2006, 24(3): 17-21. (in Chinese) |
| Cited By in Cnki (52) | Click to display the text | |
| [10] | GILLARD W J, DORSETT K M. Directional control for tailless aircraft using all moving tips: AIAA-1997-3487[R]. Reston: AIAA, 1997. |
| Click to display the text | |
| [11] |
李忠剑, 马东立. 飞翼布局阻力类偏航操纵装置操纵特性分析[J]. 北京航空航天大学学报, 2014, 40(5): 695-700. LI Z J, MA D L. Control characteristics analysis of drag yawing control devices of flying wing configuration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 695-700. (in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [12] |
张彬乾, 马怡, 褚胡冰, 等. 小展弦比飞翼布局航向控制的组合舵面研究[J]. 航空学报, 2013, 11(34): 2436-2443. ZHANG B Q, MA Y, CHU H B, et al. Investigation on combined control surfaces for the yaw control of low aspect ratio flying wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2013, 11(34): 2436-2443. (in Chinese) |
| Cited By in Cnki (9) | Click to display the text | |
| [13] |
单继祥, 黄勇, 苏继川, 等. 小展弦比飞翼布局新型嵌入面航向控制特性研究[J]. 空气动力学学报, 2015, 33(3): 296-301. SHAN J X, HUANG Y, SU J C, et al. Effect of the novel embedded control surfaces on direction control characteristic of low-aspect-ratio flying-wing configuration[J]. Acta Aerodynamica Sinica, 2015, 33(3): 296-301. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [14] | BOLSUNOVSKY A L, BUZOVERYA N P, GUREVICH B I, et al. Flying wing problems and decisions[J]. Aircraft Design, 2001, 4: 193-219. |
| Click to display the text | |
| [15] | DMITRIEV V G, DENISOV V E, GUREVICH B I, et al. The flying wing concept chances and risks: AIAA-2003-2887[R]. Reston: AIAA, 2003. |
| Click to display the text | |
| [16] | ESTENBAN S. Static and dynamic analysis of an unconventional plane flying wing: AIAA-2001-4010[R]. Reston: AIAA, 2001. |
| Click to display the text | |
| [17] |
冯立好, 王晋军, 于东升. 多操纵面无尾布局飞机横航向控制[J]. 北京航空航天大学学报, 2010, 36(9): 1038-1042. FENG L H, WANG J J, YU D S. Lateral-directional control of tailless aircraft with multiple control surfaces[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(9): 1038-1042. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [18] |
李林, 马超, 王立新. 小展弦比飞翼布局飞机稳定特性[J]. 航空学报, 2007, 28(6): 1312-1317. LI L, MA C, WANG L X. Stability features of low aspect-ratio flying wings[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(6): 1312-1317. (in Chinese) |
| Cited By in Cnki (33) | Click to display the text | |
| [19] | STENFELT G, RINGERTZ U. Yaw control of a tailless aircraft configuration[J]. Journal of Aircraft, 2010, 47(5): 1807-1810. |
| Click to display the text | |
| [20] |
宋磊, 杨华, 颜旭峰, 等. 飞翼无增稳条件下横航向动稳定设计方法[J]. 系统工程与电子技术, 2015, 37(11): 2561-2565. SONG L, YANG H, YAN X F, et al. Increasing the flying wing lateral-directional dynamic stability without relying on augmentation system[J]. Systems Engineering and Electronics, 2015, 37(11): 2561-2565. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [21] |
赵俊波, 沈清. 升力体布局飞行器偏航气动增稳方法研究[J]. 空气动力学学报, 2016, 34(3): 322-326. ZHAO J B, SHEN Q. Directional stability augmentation method for a lifting body configuration[J]. Acta Aerodynamica Sinica, 2016, 34(3): 322-326. (in Chinese) |
| Cited By in Cnki | Click to display the text |



