2. 中国运载火箭技术研究院, 北京 100076;
3. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083;
4. 北京航空航天大学 中法工程师学院, 北京 100083;
5. 北京航空航天大学 大数据科学与脑机智能高精尖创新中心, 北京 100083
2. China Academy of Launch Vehicle Technology, Beijing 100076, China;
3. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China;
4. School of Sino-French Engineer, Beihang University, Beijing 100083, China;
5. Beijing Advanced Innovation Center for Big Data and Brain Computing, Beihang University, Beijing 100083, China
高超声速滑翔飞行器具有高速、高机动、射程远等优点[1-3]。其作为进攻性武器,能够在大气层内保持长时滑翔的同时,实行无规律的变轨变射面飞行,大大增加现有反导防空系统的弹道预报与拦截难度,引起了各军事强国的关注。近些年许多学者在高超声速滑翔飞行器弹道规划、制导控制领域展开了广泛研究。
文献[3]针对高超声速滑翔飞行器大横程侧向机动的任务需求,设计了一种考虑机动系数的三维再入轨迹快速规划方法。Shen和Lu[4]基于准平衡滑翔条件,设计了一种在倾侧角边界内求取倾侧角幅值与倾侧角符号的再入轨迹规划方法。文献[5]针对单级入轨飞行器再入返回段,设计了一种考虑多种目标函数的轨迹规划方法。文献[6]设计了一种考虑圆形禁飞区约束的侧向再入制导方法。在此基础上,文献[7]研究了一种适用于规避多种不规则形状禁飞区的再入制导方法。文献[8]设计了一种考虑匹配点与禁飞区约束的再入制导方法。文献[9]运用高斯伪谱法提出了一套求取复杂约束条件下的再入轨迹规划方法。凸优化问题具有在多项式时间内求解收敛的特点,Lu等[10-11]基于二阶锥规划方法实现了再入段快速轨迹规划,为再入段实时轨迹规划的实现提供了一种可能的解决方案。
目前高超再入制导与轨迹规划领域的研究成果较多,但这些方法仅适用于单枚飞行器。随着防空反导技术的不断发展,单枚飞行器完成突防与攻击变得愈加困难。为有效突破日益完善的反导系统,可以采用饱和攻击的作战样式,即利用多枚飞行器同时攻击单个目标,提高对防御系统的突防概率与作战效能。能够实现这种作战方式的制导方法称为时间约束制导方法。目前时间约束制导方法主要有2种:基于独立导引的时间约束制导方法[12-16]和基于协同导引的时间约束制导方法[17-21]。文献[12-16]中各飞行器基于预设的期望飞行时间,采用时间约束制导律实现了对目标的同时命中。文献[17-21]中的协同制导方法则是以飞行器间的正常通信为前提,采用不同的协调变量与控制方法实现了对目标的协同攻击。
上述协同制导方法虽然对攻击时间的控制效果较好,但都是基于质点运动学模型,忽略了飞行器的动力学特性。对于高超声速滑翔飞行器,其再入动力学复杂,初终端约束条件多,飞行过程中速度、高度等状态量变化剧烈。且具有较大升阻比的滑翔飞行器多为面对称构型,基于倾斜转弯(Bank to Turn, BTT)的控制方式难以实现对航向角等状态量的精确控制。此外,上述协同制导方法多数是针对末段协同导引问题提出的。对于高超声速滑翔飞行器,其再入段飞行时间占据了整个返回段的绝大部分。若未在再入段进行时间协同,可能造成多飞行器飞抵终端交接班区域的时间偏差较大,而末制导段有限的时间调节能力难以对其实现修正。因此,研究适用于再入滑翔式飞行器的协同制导/规划方法具有重要的理论意义与工程价值。目前关于多飞行器协同再入问题的研究成果较少。文献[22]在高度-速度剖面上设计了分段多项式剖面,通过预测调整多项式参数在纵向平面上实现了对多弹再入飞行时间的控制。该方法求解高度-速度剖面时需要严格满足准平衡滑翔这一软约束,致使纵向轨迹机动平缓;预测剩余航程时基于大圆弧飞行轨迹假设,计算得到的真实轨迹在侧向平面的机动程度同样有限,这些都不利于进攻性武器的突防。文献[23]基于静态模型预测控制设计了协同再入方法。该方法通过事先获取各飞行器的再入时间,调整各飞行器的发射时刻以实现协同再入,严重影响了作战灵活性与任务适应性。文献[24]基于Radau伪谱法实现了多飞行器的时间协同再入轨迹规划。由于伪谱法的方法特性,再入轨迹的规划不仅严重依赖于初值,而且引入再入时间约束后会使得优化计算规模与复杂度明显增加,规划求解的可行性与快速性难以保证。
针对以上问题,本文提出了一种多飞行器再入段时间协同弹道规划方法。首先规划得到满足终端约束的纵向标称轨迹,采用以待飞航程为自变量的轨迹跟踪律跟踪纵向标称轨迹,用以满足航程、高度、速度等纵向状态变量的终端精度。提出了一种考虑初始横侧向状态的多边界航向偏差角走廊来控制飞行器的横侧向机动,以满足对到达时间和终端航向角偏差的控制。在此基础上分析计算到达时间分布并完成了多飞行器协同攻击时间决策。仿真结果验证了本文所设计的协同再入轨迹规划方法的可行性。
1 多飞行器协同攻击建模 1.1 动力学方程假设地球为均匀圆形球体,同时忽略因地球自转产生的牵连加速度与科式加速度,第i枚高超声速滑翔飞行器的三自由度动力学方程为
| $ {\frac{{{\rm{d}}{r_i}}}{{{\rm{d}}t}} = {v_i}{\rm{sin}}{\gamma _i}} $ | (1) |
| $ {\frac{{{\rm{d}}{v_i}}}{{{\rm{d}}t}} = - {D_i} - {g_i}{\rm{sin}}{\gamma _i}} $ | (2) |
| $ \frac{{{\rm{d}}{\gamma _i}}}{{{\rm{d}}t}} = \frac{1}{{{v_i}}}\left( {{L_i}{\rm{cos}}{\sigma _i} - {g_i}{\rm{cos}}{\gamma _i} + \frac{{v_i^2{\rm{cos}}{\gamma _i}}}{{{r_i}}}} \right) $ | (3) |
| $ {\frac{{{\rm{d}}{\theta _i}}}{{{\rm{d}}t}} = \frac{{{v_i}{\rm{cos}}{\gamma _i}{\rm{sin}}{\psi _i}}}{{{r_i}{\rm{cos}}{\phi _i}}}} $ | (4) |
| $ {\frac{{{\rm{d}}{\phi _i}}}{{{\rm{d}}t}} = \frac{{{v_i}{\rm{cos}}{\gamma _i}{\rm{cos}}{\psi _i}}}{{{r_i}}}} $ | (5) |
| $ \frac{{{\rm{d}}{\psi _i}}}{{{\rm{d}}t}} = \frac{1}{{{v_i}}}\left( {\frac{{{L_i}{\rm{sin}}{\sigma _i}}}{{{\rm{cos}}{\gamma _i}}} + \frac{{v_i^2{\rm{cos}}{\gamma _i}{\rm{sin}}{\psi _i}{\rm{tan}}{\phi _i}}}{{{r_i}}}} \right) $ | (6) |
式中:下标i表示第i枚高超声速飞行器;r为地心距;v为速度;γ为弹道倾角;θ与ϕ分别为经度和纬度;ψ为航向角;σ为倾侧角;L、D和g分别为飞行器受到的升力加速度、阻力加速度与重力加速度,表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {L = \frac{1}{{2m}}\rho {v^2}{S_{{\rm{ref}}}}{C_L}(\alpha ,Ma)}\\ {D = \frac{1}{{2m}}\rho {v^2}{S_{{\rm{ref}}}}{C_D}(\alpha ,Ma)}\\ {g = {g_0}\frac{{R_0^2}}{{{r^2}}}} \end{array}} \right. $ | (7) |
式中:ρ为大气密度,与飞行高度有关,计算公式为ρ=ρ0e-h/hs,其中ρ0=1.752 kg/m3,hs=6 700 m,h=r-R0,R0为地球半径;m为飞行器质量,Sref为参考面积;CL和CD分别为升力系数和阻力系数,是关于攻角α与马赫数Ma的函数。
1.2 飞行约束条件再入飞行过程中,为满足气动加热、结构强度等条件,飞行器要严格满足热流密度约束、动压约束和过载约束。同时为控制弹道倾角变化率,引入准平衡滑翔条件[4]。该约束不需要严格满足,仅作为轨迹设计时的参考。多飞行器需要满足过程约束:
| $ {{{\dot Q}_i} = {K_Q}\rho _i^{0.5}v_i^{3.15} \le {{\dot Q}_{{\rm{max}}}}} $ | (8) |
| $ {{q_i} = \frac{1}{2}{\rho _i}v_i^2 \le {q_{{\rm{max}}}}} $ | (9) |
| $ {{n_i} = \sqrt {L_i^2 + D_i^2} \le {n_{{\rm{max}}}}} $ | (10) |
| $ {{L_i}{\rm{cos}}\sigma - {g_i} + \frac{{v_i^2}}{{{r_i}}} \ge 0} $ | (11) |
式中:
为完成飞行任务,要求飞行器在进入终端区域时满足高度、速度和待飞航程约束。初始约束与终端约束可以表达为
| $ \left\{ {\begin{array}{*{20}{l}} {{h_i}({t_0}) = {h_{0,i}}}\\ {{v_i}({t_0}) = {v_{0,i}}}\\ {{\gamma _i}({t_0}) = {\gamma _{0,i}}}\\ {{s_i}({t_0}) = {s_{0,i}}} \end{array}} \right. $ | (12) |
| $ \left\{ {\begin{array}{*{20}{l}} {{h_i}({t_{f,i}}) = h_i^*}\\ {{v_i}({t_{f,i}}) = v_i^*}\\ {{s_i}({t_{f,i}}) = s_i^*} \end{array}} \right. $ | (13) |
式中:t0表示再入段初始时间;tf表示到达终端区域的时间。对于k枚飞行器时间协同再入需求,需要满足:
| $ {t_{f,1}} = {t_{f,2}} = \cdots = {t_{f,k}} = {t^*} $ | (14) |
式中:下标“0”与上标“*”分别表示初始条件与终端条件;s表示飞行器当前点(θ,ϕ)至终端目标点(θ*,ϕ*)的待飞航程,计算公式为
| $ s = {R_0}{\rm{co}}{{\rm{s}}^{ - 1}}[{\rm{cos}}\phi {\rm{cos}}{\phi ^*}{\rm{cos}}(\theta - {\theta ^*}) + {\rm{sin}}\phi {\rm{sin}}{\phi ^*}] $ | (15) |
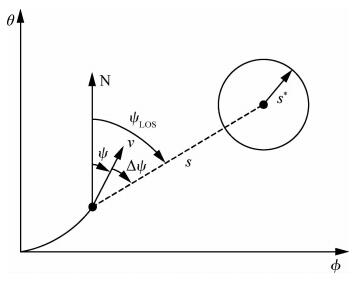
如图 1所示,终端区域通常表示为终端目标点(θ*,ϕ*)为圆心,终端待飞航程s*为半径的形式。ΨLOS为飞行器相对于目标的视线角,ΔΨ表示飞行器航向角与视线角之间的偏差。为了实现对目标的打击,需要飞行器进入终端区域时的航向角偏差小于一定范围:
|
| 图 1 航向角约束与终端区域 Fig. 1 Heading angle constraint and terminal area |
| $ |\psi ({s_f}) - {\psi _{{\rm{LOS}}}}({s_f})| \le \Delta {\varPsi ^*} $ | (16) |
式中:ΔΨ*表示允许的终端航向角最大偏差。
2 时间协同弹道规划方法 2.1 纵向轨迹规划纵向轨迹规划的目标是通过调整攻角与倾侧角剖面,来满足初始与终端约束。首先采用分段线性函数设计飞行器的攻角剖面,形式为
| $ \alpha = \left\{ {\begin{array}{*{20}{l}} {{\alpha _1}}&{v \ge {v_{\alpha ,1}}}\\ {{\alpha _2} + \frac{{{\alpha _1} - {\alpha _2}}}{{{v_{\alpha ,1}} - {v_{\alpha ,2}}}}(v - {v_{\alpha ,2}})}&{{v_{\alpha ,2}} < v < {v_{\alpha ,1}}}\\ {{\alpha _2}}&{v \le {v_{\alpha ,2}}} \end{array}} \right. $ | (17) |
式中:α1为一较大攻角;α2为满足射程需求的最大升阻比的攻角;vα, 1与vα, 2分别为给定值。
在给定攻角方案后,将热流密度约束、动压约束和过载约束代入到准平衡滑翔约束中,可以解出倾侧角边界为
| $ \left\{ {\begin{array}{*{20}{l}} {|{\sigma _Q}(v)| \le {\rm{co}}{{\rm{s}}^{ - 1}}\left[ {\left( {g - \frac{{{v^2}}}{r}} \right)\frac{{2m{v^{4.3}}}}{{{S_{{\rm{ref}}}}{C_L}}}{{\left( {\frac{{{K_Q}}}{{{{\dot Q}_{{\rm{max}}}}}}} \right)}^2}} \right]}\\ {|{\sigma _q}(v)| \le {\rm{co}}{{\rm{s}}^{ - 1}}\left[ {\left( {g - \frac{{{v^2}}}{r}} \right)\frac{m}{{{q_{{\rm{max}}}}{C_L}{S_{{\rm{ref}}}}}}} \right]}\\ {|{\sigma _n}(v)| \le {\rm{co}}{{\rm{s}}^{ - 1}}\left[ {\left( {g - \frac{{{v^2}}}{r}} \right)\frac{{\sqrt {{{({C_D}/{C_L})}^2} + 1} }}{{{n_{{\rm{max}}}}}}} \right]} \end{array}} \right. $ | (18) |
由式(18),可以得到倾侧角走廊的上边界:
| $ {\sigma _{{\rm{max}}}}(v) = {\rm{min}}\{ {\sigma _Q}(v),{\sigma _q}(v),{\sigma _n}(v)\} $ | (19) |
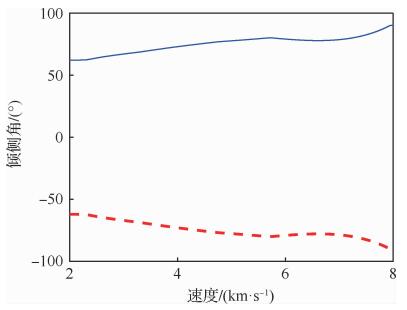
图 2为满足各项过程约束的倾侧角走廊,该走廊上下边界对称。
|
| 图 2 倾侧角走廊 Fig. 2 Bank angle corridor |
对于纵向轨迹规划问题,给定攻角剖面后,可以通过单独调整倾侧角剖面来满足各项约束。倾侧角的符号并不影响纵向飞行轨迹,故假设倾侧角为正值。设计如下分段线性倾侧角剖面:
| $ \begin{array}{l} \sigma = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{\sigma _1}}&{v \ge {v_{\sigma ,1}}}\\ {{\sigma _j} + \frac{{{\sigma _j} - {\sigma _{j + 1}}}}{{{v_{\sigma ,j}} - {v_{\sigma ,j + 1}}}}(v - {v_{\sigma ,j}})}&{{v_{\sigma ,j + 1}} < v < {v_{\sigma ,j}}}\\ {{\sigma _N}}&{v \le {v_{\sigma ,N}}} \end{array}} \right. \end{array} $ | (20) |
式中:vσ, 1与vσ, N分别为初始速度与终端速度;σ1和σN分别为初始倾侧角和终端倾侧角,其中σN可由准平衡滑翔约束求解。σj(j=1, 2, …, N-1)为在vσ, j节点处的倾侧角幅值,为纵向轨迹规划的待优化变量,N-1为待优化节点个数。由式(19)和式(20),可以得到倾侧指令角为
| $ {\sigma _{{\rm{ ref }}}}(v) = \left\{ {\begin{array}{*{20}{l}} {{\sigma _{{\rm{max}}}}(v)}&{\sigma (v) > {\sigma _{{\rm{max}}}}(v)}\\ {\sigma (v)}&{\sigma (v) \le {\sigma _{{\rm{max}}}}(v)} \end{array}} \right. $ | (21) |
基于给定的攻角与倾侧角剖面,通过积分飞行器纵向动力学方程即可得到纵向轨迹。取纵向轨迹规划的目标函数为
| $ J = {\left( {\frac{{h({s_f}) - {h^*}}}{{\Delta {h_{{\rm{max}}}}}}} \right)^2} + {\left( {\frac{{v({s_f}) - {v^*}}}{{\Delta {v_{{\rm{max}}}}}}} \right)^2} $ | (22) |
式中:Δhmax与Δvmax分别为可接受的终端高度与终端速度的最大偏差值。轨迹积分过程中,当满足s=s*条件时停止积分。h(sf)与v(sf)分别为纵向轨迹积分中止时的高度与速度。该纵向轨迹规划方法通过优化第j个节点下的倾侧角幅值来满足纵向约束条件。对于这一单变量多参数优化问题,本文采用序列二次规划(Sequential Quadratic Programming, SQP)方法进行求解。
2.2 到达时间约束下的三维再入轨迹规划得到满足纵向终端约束的最优飞行轨迹后,采用如下方法规划满足到达时间约束的三维再入轨迹:在纵向平面采用以待飞航程为自变量的轨迹跟踪律跟踪纵向标称轨迹,用以满足h、v等纵向状态变量的终端精度;在横侧向平面内采用考虑初始横侧向状态的多边界航向角偏差走廊来控制飞行器的横侧向机动,以满足对到达时间和终端航向角偏差的控制。
取待飞航程s为自变量,X=[r, v, γ]T为状态变量,u=[σ, α]T为控制变量。假设实际飞行轨迹位于标准参考轨迹的偏差走廊内,小扰动线性化后得到
| $ \delta \mathit{\boldsymbol{\dot X}} = {\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{X}}}\delta \mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{X}}}\delta \mathit{\boldsymbol{u}} $ | (23) |
式中:时变矩阵AX和BX的表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{X}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{1}{{{{({\rm{cos}}\gamma )}^2}}}}\\ { - \frac{{{D_r} + {\rm{sin}}\gamma {g_r}}}{{v{\rm{cos}}\gamma }}}&{ - \frac{{D - g{\rm{sin}}\gamma }}{{{v^2}{\rm{cos}}\gamma }}}&{ - \frac{{D{\rm{sin}}\gamma + g}}{{{v^2}{\rm{cos}}\gamma }}}\\ {\frac{{{\rm{cos}}\sigma {L_r}}}{{{v^2}{\rm{cos}}\gamma }} - \frac{{{g_r}}}{{{v^2}}} - \frac{1}{{{r^2}}}}&{\frac{{2g}}{{{v^3}}}}&{\frac{{L{\rm{cos}}\sigma {\rm{sin}}\gamma }}{{{v^2}{{({\rm{cos}}\gamma )}^2}}}} \end{array}} \right] \end{array} $ | (24) |
| $ {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{X}}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&{ - \frac{{{D_\alpha }}}{{v{\rm{cos}}\gamma }}}\\ { - \frac{{L{\rm{sin}}\sigma }}{{{v^2}{\rm{cos}}\gamma }}}&{\frac{{{L_a}{\rm{cos}}\sigma }}{{{v^2}{\rm{cos}}\gamma }}} \end{array}} \right] $ | (25) |
式中:Lr和Dr分别为升力加速度和阻力加速度对地心距r的导数;Lα和Dα分别为升力加速度和阻力加速度对攻角α的导数,可以根据升力、阻力系数与攻角的关系得到,表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{L_r} = \frac{1}{{2m}}{v^2}{C_L}{S_{{\rm{ref}}}}\frac{{\partial \rho }}{{\partial r}} = - \frac{L}{{hs}}}\\ {{D_r} = \frac{1}{{2m}}{v^2}{C_D}{S_{{\rm{ref}}}}\frac{{\partial \rho }}{{\partial r}} = - \frac{D}{{hs}}}\\ {{L_\alpha } = \frac{1}{{2m}}\rho {v^2}{S_{{\rm{ref}}}}C_L^\alpha }\\ {{D_\alpha } = \frac{1}{{2{m^\rho }}}{\rho ^2}{S_{{\rm{ref}}}}C_D^\alpha } \end{array}} \right. $ | (26) |
针对式(23)~式(26)所描述的系统,本文采用线性二次调节(Linear Quadratic Regulator, LQR)方法设计纵向轨迹跟踪律,取性能指标:
| $ J = \mathop \smallint \nolimits_s^{{s_f}} [\delta {\mathit{\boldsymbol{X}}^{\rm{T}}}(s){\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}}\delta \mathit{\boldsymbol{X}}(s) + \delta {\mathit{\boldsymbol{u}}^{\rm{T}}}(s){\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{X}}}\delta \mathit{\boldsymbol{u}}(s)]{\rm{d}}s $ | (27) |
其中:权重QX和RX取对角型,
| $ {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}} = \left[ {\begin{array}{*{20}{c}} {{Q_1}}&0&0\\ 0&{{Q_2}}&0\\ 0&0&{{Q_3}} \end{array}} \right],{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{X}}} = \left[ {\begin{array}{*{20}{c}} {{R_1}}&0\\ 0&{{R_2}} \end{array}} \right] $ | (28) |
根据Bryson原则[25],矩阵元素设计为
| $ {Q_1}\delta r_{\max }^2 = {Q_2}\delta v_{\max }^2 = {Q_3}\delta \gamma _{\max }^2 = {R_1}\delta \sigma _{\max }^2 = {R_2}\delta _{\max }^2 $ | (29) |
式中:δrmax、δvmax、δγmax分别为地心距、速度、弹道倾角的最大允许误差;δσmax和δαmax分别为倾侧角和攻角的最大调整值。根据庞特里亚金极大值原理,求解黎卡提方程后,即可得到最优时变反馈矩阵KX(s)。根据反馈矩阵,得到基于LQR的控制律为
| $ $ \left[ {\begin{array}{*{20}{c}} {\Delta \sigma }\\ {\Delta \alpha } \end{array}} \right] = {\mathit{\boldsymbol{K}}^{2 \times 3}}(s)\left[ {\begin{array}{*{20}{c}} {\Delta r}\\ {\Delta v}\\ {\Delta \gamma } \end{array}} \right] $ | (30) |
然后根据纵向参考轨迹中气流指令角可以得到攻角与倾侧角的实际值:
| $ \left\{ {\begin{array}{*{20}{l}} {|\sigma | = {\sigma _{{\rm{ref}}}}(v) + \Delta \sigma }\\ {\alpha = {\alpha _{{\rm{ref}}}}(v) + \Delta \alpha } \end{array}} \right. $ | (31) |
针对多弹协同再入的作战需求,侧向制导需要同时考虑航向角偏差控制与到达时间控制。由待飞航程的微分方程易得
| $ \frac{{{\rm{d}}t}}{{{\rm{d}}s}} = - \frac{1}{{v{\rm{cos}}\gamma {\rm{cos}}\Delta \psi }} $ | (32) |
对式(32)进行积分,可以得到飞行器抵达终端区域时的到达时间:
| $ {t_f} = {t_0} + \int_{{s_f}}^{{s_0}} {\frac{1}{{v{\rm{cos}}\gamma {\rm{cos}}\Delta \psi }}} {\rm{d}}s $ | (33) |
从式(33)可以看出,飞行器的到达时间会随着航向角偏差的增大而单调增大,因此可以通过改变航向角偏差走廊的上限值来增大或减小飞行过程中航向角偏差的绝对平均值,实现对飞行器到达时间的控制。
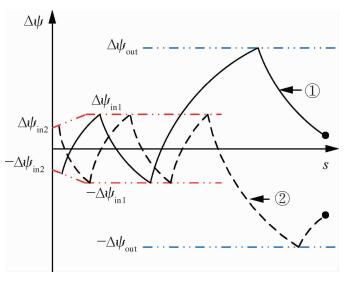
根据初始航向角偏差符号与初始倾侧角符号的不同,本文设计了一种考虑初始横侧向状态的多边界航向角偏差走廊来实现对飞行器的到达时间与终端航向角偏差的同时控制,如图 3与图 4所示。图 3中,Δψin1、-Δψin1、Δψin2和-Δψin2为航向角偏差走廊的内边界值,用于控制飞行器的终端航向角偏差;由于航向角偏差会在一定程度上影响航程,因此采用边界可调式走廊来保证待飞航程精度;Δψout和-Δψout为航向角偏差走廊的外边界值,用于控制飞行器的到达时间;情形①与情形②的初始航向角偏差符号与初始倾侧角符号相同,故倾侧角首先向与初始航向角偏差符号一致的方向偏转,在航向角偏差到达航向角偏差走廊外边界后,迅速转向航向角偏差走廊的内边界。
|
| 图 3 初始偏差与倾侧角同号情形下的多边界航向角偏差走廊 Fig. 3 Multi-layer bounded corridor for heading error (under the same sign of initial heading angle and bank angle) |
|
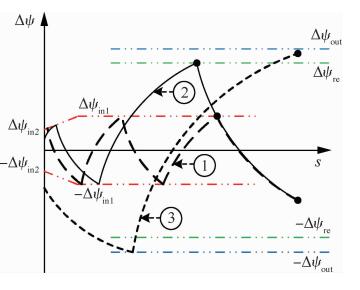
| 图 4 初始偏差与倾侧角异号情形下的多边界航向角偏差走廊 Fig. 4 Multi-layer bounded corridor for heading error (under the different sign of initial heading angle and bank angle) |
图 4给出了初始航向角偏差与初始倾侧角异号下的倾侧角翻转逻辑。图中情形①与情形②具有相同的初始条件,初始航向角偏差绝对值小于Δψre,而情形③中的初始航向角偏差绝对值≥Δψre且 < Δψout。其中,Δψre是为了满足初始航向角偏差与初始倾侧角异号情形下,由于初始航向角偏差较大引起的横侧向控制能力不足问题而设定的航向角偏差走廊修正外边界。情形①与情形②具有相同的初始条件,效果上情形①中倾侧角的翻转仅使用了航向角偏差走廊的内边界,而情形②中倾侧角的翻转用到的是航向角偏差走廊的内外两个边界。可以看出,情形②中的侧向机动能力与时间调节能力明显优于情形①。图 4中情形②与情形③的航向角偏差均在初始时刻偏向初始航向角偏差方向的反方向,相比于图 3中的情形,航向角偏差在倾侧角第1次变号之前的飞行过程更长。情形③中的初始航向角偏差与航向角偏差走廊外边界值较大,受限于飞行器的飞行能力,直至终端时刻也未能满足终端约束;情形②中的初始航向角偏差绝对值小于Δψre,且航向角偏差走廊外边界值经过重新修正选取,航向角偏差最终收敛在航向角偏差走廊内边界。
综上所述,倾侧角的翻转策略为
| $ \begin{array}{*{20}{l}} {{\rm{if }}\left\{ {\begin{array}{*{20}{l}} {\Delta \psi ({s_0}) \ge 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sign}} [\sigma ({s_0})] = 1}\\ {\Delta \psi ({s_0}) < 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sign}} [\sigma ({s_0})] = - 1} \end{array}} \right.}\\ {{\rm{then }}\Delta {\psi _{\max }} \ge \Delta {\psi _{{\rm{ out }}}} \ge \Delta {\psi _{{\rm{min}}}} = \Delta {\psi _f} > \Delta {\psi _{{\rm{ in1 }}}} > \Delta {\psi _{{\rm{ in2 }}}}} \end{array} $ | (34) |
| $ \begin{array}{*{20}{c}} {{\rm{if}}\left\{ {\begin{array}{*{20}{l}} {\Delta \psi ({s_0}) \ge 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sign}} [\sigma ({s_0})] = - 1}\\ {\Delta \psi ({s_0}) < 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sign}} [\sigma ({s_0})] = 1} \end{array}} \right.}\\ {{\rm{ then }}\Delta {\psi _{{\rm{max}}}} \ge \Delta {\psi _{{\rm{ out }}}} > \Delta {\psi _{{\rm{ re }}}} \ge \Delta {\psi _{{\rm{min}}}} = }\\ {\Delta {\psi _f} > \Delta {\psi _{{\rm{ in1 }}}} > \Delta {\psi _{{\rm{ in2 }}}}} \end{array} $ | (35) |
式中:Δψmin与Δψmax分别为航向角偏差走廊外边界值的最小最大限幅。
由式(34)、式(35)考虑初始横侧向状态的多边界航向角偏差走廊,可以将再入段时间协同弹道规划问题转化为航向角偏差走廊外边界值的优化求解过程,具体问题描述为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} J(\Delta {\psi _{{\rm{ out }}}}) = |{t_f} - {t^*}|}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{s_f} = {s^*}}\\ {\Delta {\psi _{{\rm{max}}}} \le \Delta {\psi _{{\rm{out}}}} \le \Delta {\psi _{{\rm{min}}}}} \end{array}} \right.} \end{array} $ | (36) |
| $ \begin{array}{l} {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J(\Delta {\psi _{{\rm{re}}}}) = \left| {{t_f} - {t^*}} \right|\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{s_f} = {s^*}}\\ {\Delta {\psi _{{\rm{max}}}} \le \Delta {\psi _{{\rm{out}}}} < \Delta {\psi _{{\rm{re}}}} \le \Delta {\psi _{{\rm{min}}}}} \end{array}} \right. \end{array} $ | (37) |
式中:t*为设定的期望到达时间;tf为在航向角偏差外边界。Δψout或Δψre确定后,基于所设计的纵向标称轨迹与轨迹跟踪律对三自由度动力学方程积分得到的终端到达时间。从式(36)与式(37)可以看出,再入段时间协同弹道规划问题是一个单参数优化问题,本文采用牛顿迭代法进行求解:
| $ \Delta \psi _{{\rm{out}}}^{(l + 1)} = \Delta \psi _{{\rm{out}}}^{(l)} - \frac{{\Delta \psi _{{\rm{out}}}^{(l)} - \Delta \psi _{{\rm{out}}}^{(l - 1)}}}{{t_f^{(l)} - t_f^{(l - 1)}}}(t_f^{(l)} - {t^*}) $ | (38) |
式中:l为迭代求解的次数。
3 飞行能力分析与攻击时间决策 3.1 飞行能力分析与到达时间分布在进行协同再入轨迹规划之前,需要先进行飞行能力分析与到达时间区间计算,具体方法为:对于某一飞行任务,根据初始航向角偏差符号与初始倾侧角符号的不同,选取相应的多边界航向角偏差走廊作为倾侧角翻转策略,在不同的航向角偏差外边界值下依次进行计算。
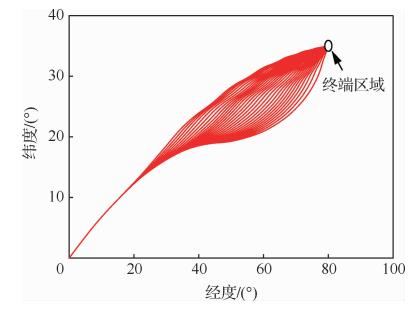
取以下任务条件:h0=65 km,v0=6 700 m/s,θ0=0°,ϕ0=0°,h*=30 km,v*=2 000 m/s,θ*=80°,ϕ*=35°,s*=100 km,Δψ*=5°,然后分别在Case 1(ψ0 = 54.6°,sign[σ(s0)]=1)和Case 2(ψ0=74.6°,sign[σ(s0)] = -1)情形下求取到达时间分布。图 5~图 7和图 8~图 10分别给出了Case 1与Case 2的仿真结果。
|
| 图 5 Case 1下的地面轨迹分布 Fig. 5 Distribution of ground tracks in Case 1 |
|
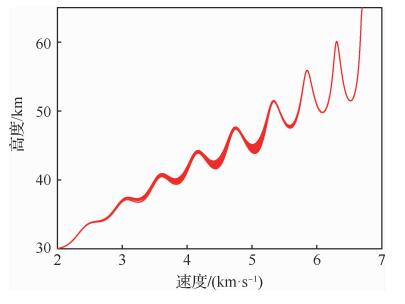
| 图 6 Case 1下的高度-速度剖面分布 Fig. 6 Distribution of altitude-velocity profiles in Case 1 |
|
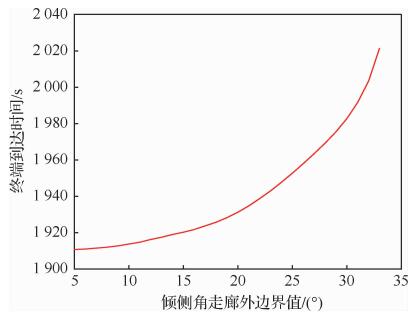
| 图 7 Case 1下的到达时间分布 Fig. 7 Distribution of arrival time in Case 1 |
|
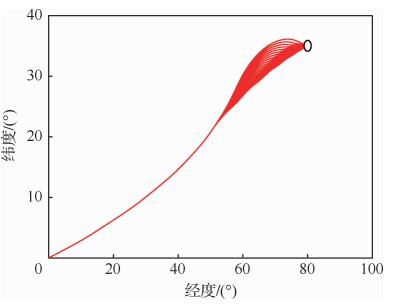
| 图 8 Case 2下的地面轨迹分布 Fig. 8 Distribution of ground tracks in Case 2 |
|
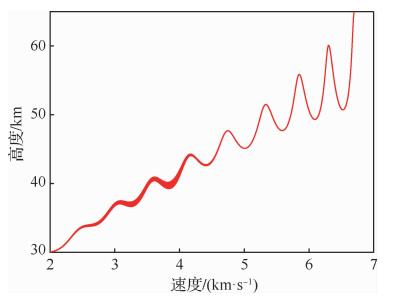
| 图 9 Case 2下的高度-速度剖面分布 Fig. 9 Distribution of altitude-velocity profiles in Case 2 |
|
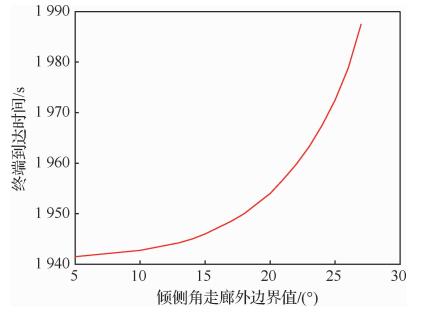
| 图 10 Case 2下的到达时间分布 Fig. 10 Distribution of arrival time in Case 2 |
图 5与图 8分别为Case 1与Case 2下,不同的航向角偏差外边界值下满足终端约束的横侧向飞行轨迹, 可以看出不同的偏差角外边界值下横侧向轨迹的变化范围较大,在横侧向通道内具备良好的侧向机动能力。图 6与图 9分别为2种情形下相应的纵向飞行轨迹, 可以看出纵向轨迹呈现出较强程度的跳跃。同时为了适应不同侧向机动需求,在纵向轨迹跟踪律的作用下,不同偏差角外边界值下的高度-速度飞行剖面相较于纵向标称剖面产生了一定程度的拉偏,在接近终端条件时实际的飞行高度与速度均以较高精度收敛至终端目标值。图 7与图 10分别为2种情形下的到达时间分布, 可以看出,2种情形下的到达时间均随着倾侧角偏差外边界走廊值的增大而增大,呈单调变化,与式(33)中分析一致。Case 1中的时间调节范围约为110 s,Case 2中的时间调节范围约为45 s。Case 2中的时间调节范围小于Case 1中的原因是:Case 2中的初始航向角偏差较大,约为20°,而初始倾侧角符号与初始航向角偏差符号异号,造成飞行前段的横侧向整体机动程度较小,导致到达时间调节的效果主要体现于后段的横侧向机动。基于本文所提出的方法,初始航向角偏差越小,横侧向的整体机动程度越大,到达时间的调节范围就越大。若要实现较大程度的到达时间调节,需要提高对再入段初始阶段航向角偏差的交接精度。
从以上结果可以看出,本文所提出的方法在保证了飞行器具备一定的到达时间调节能力外,在纵向与横侧向通道上实现了较强程度的机动。这些特点均有利于进攻性武器的突防。
3.2 多飞行器协同攻击时间决策进行多飞行器攻击时间决策时,需要分析多飞行器的到达时间调节能力。基于图 3与图 4所示的考虑初始横侧向状态的多边界航向角偏差走廊,结合式(32)可以得到2种情形下的飞行器到达时间表达式为
| $ \begin{array}{*{20}{l}} {{t_f} = {t_0} + \int_{{s_{{\rm{ out }}}}}^{{s_{\rm{0}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s_{{\rm{ in1 }}}}}^{{s_{{\rm{ out }}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \cdots + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{s_{{\rm{ in2 }}}}}^{{s_{{\rm{ in1 }}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s^ * }}^{{s_{{\rm{ in2 }}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s} \end{array} $ | (39) |
| $ \begin{array}{*{20}{l}} {{t_f} = {t_0} + \int_{{s_{{\rm{re}}}}}^{{s_0}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{re}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \cdots + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{s_{{\rm{in2}}}}}^{{s_{{\rm{in1}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s^*}}^{{s_{{\rm{in2}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} ds} \end{array} $ | (40) |
式中:sout、sre、sin1、sin2分别为航向角偏差首次到达航向角偏差走廊边界Δψout、Δψre、Δψin1、Δψin2时的待飞航程;K(s)为纵向通道待飞航程的负导数,
| $ K(s) = \frac{1}{{v(s){\rm{cos}}\gamma (s)}} $ | (41) |
为了满足终端航向角偏差精度,图 3与图 4中所示的航向角偏差内边界值Δψin1和Δψin2通常较小,为了简化计算,可取cosΔψ = 0。此时式(39)、式(40)可以改写为
| $ {t_f} = {t_0} + \int_{{s_{{\rm{out}}}}}^{{s_0}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{out}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s^*}}^{{s_{{\rm{in1}}}}} K (s){\rm{d}}s $ | (42) |
| $ {t_f} = {t_0} + \int_{{s_{{\rm{re}}}}}^{{s_0}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{re}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s + \int_{{s^*}}^{{s_{{\rm{in1}}}}} K (s){\rm{d}}s $ | (43) |
采用摄动理论进行分析:假设相比于没有引入航向角偏差外边界时的情况,Δψout引起了飞行过程中航向角偏差的微弱变化δψ,且δψ的变化量正比于Δψout的变化量。前后2种情形下的终端到达时间变化量可以近似表示为
| $ \begin{array}{l} \delta {t_f} \approx \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{out}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta {\psi _{new}}}}} {\rm{d}}s - \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{out}}}}} {\frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} {\rm{d}}s \approx \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{s_{{\rm{in1}}}}}^{{s_{{\rm{out}}}}} {\left[ {\frac{{K(s)}}{{\cos [\Delta \psi + \delta \psi {\rm{sign}} (\Delta {\psi _{{\rm{out}}}})]}} - \frac{{K(s)}}{{{\rm{cos}}\Delta \psi }}} \right]{\rm{d}}s} \end{array} $ | (44) |
从式(44)可以看出,飞行器的实际终端到达时间会随着航向角偏差外边界值的增大而增大。因此可以得出每枚飞行器到达时间的上下界:
| $ \begin{array}{l} {\rm{if}}\left\{ {\begin{array}{*{20}{l}} {\Delta {\psi _i}({s_{0,i}}) \ge 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sign [\sigma ({s_{0,i}})] = 1}\\ {\Delta {\psi _i}({s_{0,i}}) < 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sign [\sigma ({s_{0,i}})] = - 1} \end{array}} \right.\\ \begin{array}{*{20}{l}} {{\rm{then }}\left\{ {\begin{array}{*{20}{l}} {{t_{{\rm{min}},i}} = F(\Delta {\psi _{{\rm{ out }}}} = \Delta {\psi _{{\rm{min}}}})}\\ {{t_{{\rm{max}},i}} = F(\Delta {\psi _{{\rm{ out }}}} = \Delta {\psi _{{\rm{max}}}})} \end{array}} \right.}\\ {{\rm{where }}i = 1,2, \cdots ,k} \end{array} \end{array} $ | (45) |
| $ \begin{array}{l} {\rm{if}}\left\{ {\begin{array}{*{20}{l}} {\Delta {\psi _i}({s_{0,i}}) \ge 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sign [\sigma ({s_{0,i}})] = - 1}\\ {\Delta {\psi _i}({s_{0,i}}) < 0}&{{\rm{ and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sign [\sigma ({s_{0,i}})] = 1} \end{array}} \right.\\ \begin{array}{*{20}{l}} {{\rm{then }}\left\{ {\begin{array}{*{20}{l}} {{t_{{\rm{min}},i}} = F(\Delta {\psi _{{\rm{re}}}} = \Delta {\psi _{{\rm{min}}}})}\\ {{t_{{\rm{max}},i}} = F(\Delta {\psi _{{\rm{re}}}} = \Delta {\psi _{{\rm{max}}}} - \Delta {\psi _\xi })} \end{array}} \right.}\\ {{\rm{where }}i = 1,2, \cdots ,k} \end{array} \end{array} $ | (46) |
式中:F表示是以航向角偏差外边界值Δψout、Δψre为输入、终端飞行时间为输出的函数; Δψξ为由飞行任务决定的两个走廊外边界的偏差值。
为了满足k枚飞行器同时到达终端区域的作战需求,假设k枚飞行器均实现了良好的初制导交接班,且再入段初始时刻k枚飞行器的到达时间区间存在交集。基于以上假设,期望飞行时间需要在多枚飞行器到达时间区间的交集内选取:
| $ {t^*} \in [{t_{{\rm{min,1}}}},{t_{{\rm{max,1}}}}] \cap \cdots \cap [{t_{{\rm{min}},k}},{t_{{\rm{max}},k}}] $ | (47) |
再入过程中存在诸多干扰与不确定性。为增加对到达时间漂移的适应性,期望飞行时间的选取,需要相对于到达时间的边界留有一定冗余。因此本文采用如下方式给定期望飞行时间:
| $ {t^*} = \frac{{{\rm{max}}[{t_{{\rm{min,1}}}}, \cdots ,{t_{{\rm{min}},k}}] + {\rm{min}}[{t_{{\rm{max,1}}}}, \cdots ,{t_{{\rm{max}},k}}]}}{2} $ | (48) |
采用CAV-H[26]的气动参数进行仿真验证。该型飞行器的质量为907 kg,参考面积为0.484 m2。假设共有4枚飞行器(i = 1, 2, 3, 4),初始条件如表 1所示。4枚飞行器的终端约束条件相同,与3.1节一致。各飞行器的分段线性攻角剖面参数均取为α1=20°,α2=12°,vα, 1=5 700 m/s,vα, 1=2 300 m/s。倾侧角终值采用准平衡滑翔约束求取。取可接受的终端高度、终端速度、终端待飞航程和终端航向角的最大误差分别为0.5 km、5 m/s、3 km和5°。纵向剖面待优化的倾侧角节点数取2。取纵向轨迹跟踪律参数δrmax=500 m、δγmax=0.5°、δvmax=5 m/s、δσmax=30°和δαmax = 5°,然后令Q1 = 1,根据式(29),即可求出Q2、Q3、R1、R2。式(34)、式(35)中的航向角偏差走廊相关取值分别为Δψmax=33°,Δψmin=5°,Δψξ=5°,Δψin1=10°和Δψin2=3°。对于式(22)、式(36)与式(37)所描述的优化问题,终止条件均为对应的纵向或三维轨迹的待飞航程满足终端待飞航程精度。式(38)对应的退出条件为前后两次迭代的到达时间偏差小于2 s。
| 飞行器编号 | 1 | 2 | 3 | 4 |
| 高度/km | 65 | 65 | 65 | 65 |
| 速度/(m·s-1) | 6 700 | 6 700 | 6 700 | 6 700 |
| 经度/(°) | 0 | 10 | -24 | 15 |
| 纬度/(°) | 0 | -12 | 30 | -20 |
| 弹道倾角/(°) | 0 | 0 | 0 | 0 |
| 航向角/(°) | 54.5 | 45 | 70 | 40 |
| 初始倾侧角符号 | -1 | -1 | -1 | 1 |
本节针对多飞行器协同再入任务,采用表 1中4枚飞行器的再入初始条件与终端目标条件,对所设计的协同再入弹道规划方法进行仿真分析,结果见表 2、表 3和图 11~图 15。
飞行器 编号 |
初始航 向角/(°) |
初始倾侧 角符号 |
最小到达 时间/s |
最大到达 时间/s |
| 1 | -0.086 | -1 | 1 907.8 | 2 021.4 |
| 2 | -6.182 | -1 | 1 916 | 2 018 |
| 3 | 16.856 | -1 | 1 945.6 | 1 987.5 |
| 4 | -8.476 | 1 | 1 928 | 1 996.4 |
飞行器 编号 |
高度/m | 速度/ (m·s-1) |
待飞 航程/m |
到达时间 偏差/s |
航向 角/(°) |
| 1 | 20.48 | 0.876 | 2 790 | 0.10 | -2.551 |
| 2 | 156.11 | 0.043 | 2 951 | -0.05 | -2.205 |
| 3 | 75.61 | 1.674 | 2 882 | -0.10 | 2.224 |
| 4 | -20.09 | 0.867 | 2 969 | -0.15 | 1.711 |
|
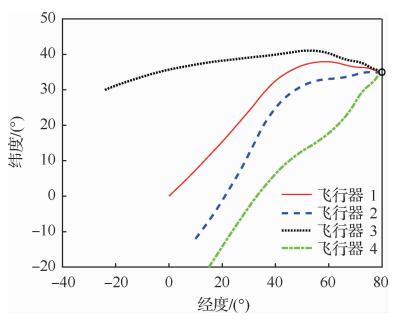
| 图 11 4枚飞行器的地面轨迹 Fig. 11 Ground tracks for 4 vehicles |
|
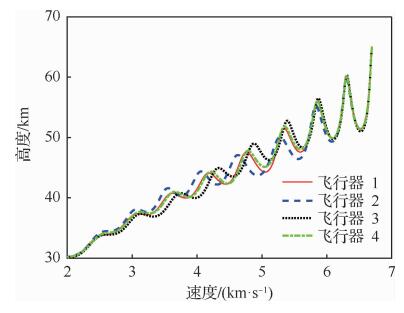
| 图 12 4枚飞行器的高度-速度剖面 Fig. 12 Altitude-velocity profiles for 4 vehicles |
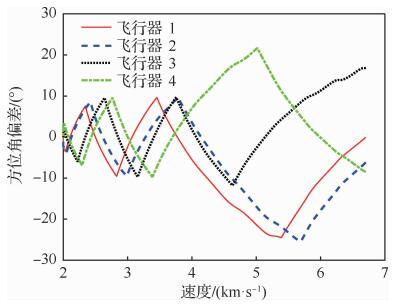
|
| 图 13 4枚飞行器的航向角偏差 Fig. 13 Heading errors for 4 vehicles |
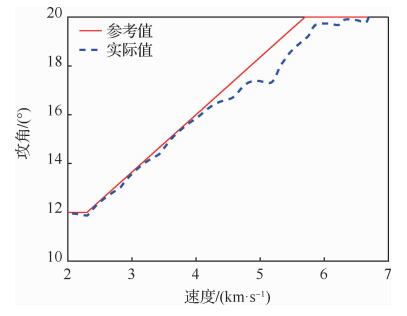
|
| 图 14 飞行器1的攻角 Fig. 14 Angle of attacks for Vehicle 1 |
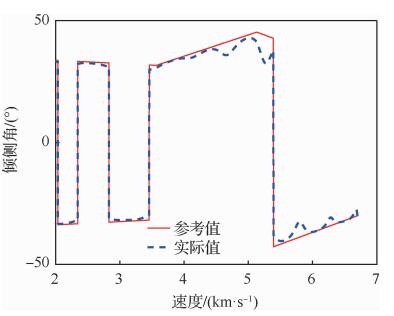
|
| 图 15 飞行器1的倾侧角 Fig. 15 Bank angles for Vehicle 1 |
表 2给出了4枚飞行器的初始航向角偏差与到达时间区间。可以看出,第3枚飞行器的初始航向角偏差最大且初始偏差与初始倾侧角符号异号,其到达时间区间宽度也最小,这一结果与3.1节中的分析一致。根据式(46)~式(48),可以计算得到t* =1 966.5 s。表 3为4枚飞行器的终端误差。可以看出,4枚飞行器的终端高度、速度、待飞航程与航向角偏差均小于设定的允许最大偏差,到达时间偏差仅为0.2 s。4枚飞行器实现了对目标的协同攻击,本文所设计的协同再入轨迹规划方法的可行性得到验证。
图 11给出了4枚飞行器的地面轨迹,可以看出4枚飞行器在不同的初始条件下,为满足期望的终端时间均进行了合理的侧向机动,最终实现了从不同方向同时飞抵终端目标区域。图 12给出了4枚飞行器的高度-速度剖面, 可以看出由于初始横侧向状态的不同,不同飞行器间的高度-速度数值存在较大偏差,但在接近终端速度的过程中实现了逐渐收敛。图 13为不同飞行器的航向角偏差曲线, 可以看出在不同的初始横侧向条件下各枚飞行器均按照2.2节中设计的多边界航向角偏差走廊进行了合理的横侧向机动,在实现到达时间一致的同时具备良好的航向角偏差精度。以第一枚飞行器为例,图 14和图 15分别给出了攻角、倾侧角的参考值与实际值, 从图中可以看出,在生成三维轨迹时为满足到达时间与终端条件约束,轨迹跟踪律对攻角与倾侧角参考值进行了一定程度的修正。
4.2 扰动条件下的时间约束仿真实际飞行过程中,飞行器会受到多种外界扰动和参数不确定性的影响,可能存在有多种初始参数偏差与过程参数偏差。为验证再入段时间协同弹道规划方法在复合扰动下的计算精度与鲁棒性,采用表 1中飞行器1的初始条件进行蒙特卡洛仿真计算,偏差限设定如表 4所示。此外,为进一步验证考虑初始横侧向状态的多边界航向角偏差走廊的到达时间控制效果,初始倾侧角符号随机选取正负。
| 偏差类型 | 偏差限3σ |
| 初始高度/km | 2 |
| 初始速度/(m·s-1) | 30 |
| 初始经度/(°) | 2 |
| 初始纬度/(°) | 2 |
| 初始弹道倾角/(°) | 0.2 |
| 初始航向角/(°) | 3 |
| 升力系数 | 0.1 |
| 阻力系数 | 0.1 |
| 大气密度/(kg·m-3) | 0.1 |
| 飞行器质量/kg | 0.03 |
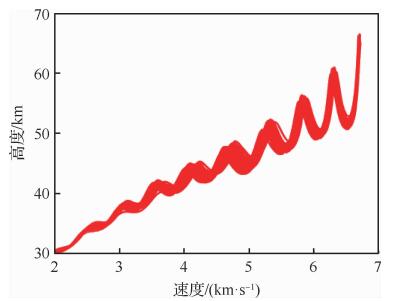
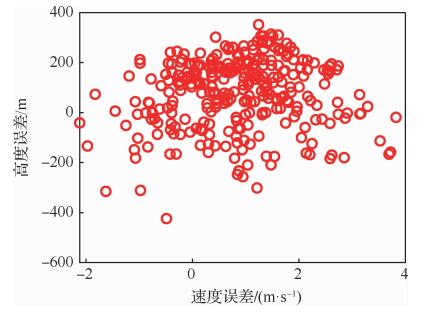
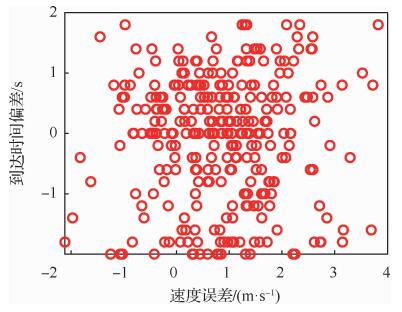
图 16和图 17分别给出了300次仿真后的地面飞行轨迹与高度-速度剖面。从图 16可以看出,在初始航向角偏差与初始倾侧角符号随机选取的情形下,为满足到达时间约束和终端约束,飞行器均进行了合理的侧向机动,最终均以较高的待飞航程精度到达终端区域。由于初始与过程扰动因素的影响,图 17中不同仿真情形下的高度-速度曲线分布较大,但在接近终端区域的过程中均逐渐收敛至目标值。图 18为终端高度-速度的误差分布,可以看出终端高度误差基本保持在400 m以内,终端速度误差在4 m以内,满足给定的终端精度需求。图 19为到达时间-终端速度误差分布,可以看出到达时间偏差基本处在2 s以内,说明该方法对再入时间的控制精度较高。仿真表明,本文所设计的时间协同再入弹道规划方法具备良好的求解精度与鲁棒性,可为后续的多飞行器末段协同突防提供良好的初始条件。
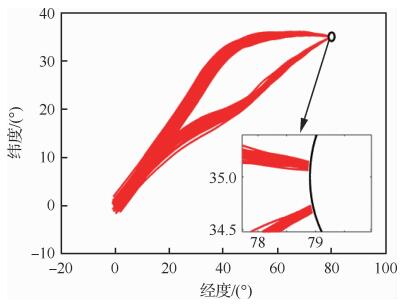
|
| 图 16 扰动条件下的地面轨迹 Fig. 16 Ground tracks under disturbances |
|
| 图 17 扰动条件下的高度-速度剖面 Fig. 17 Altitude-velocity profiles under disturbances |
|
| 图 18 扰动条件下的终端高度与终端速度误差 Fig. 18 Terminal altitude-velocity errors under disturbances |
|
| 图 19 扰动条件下的到达时间偏差与终端速度误差 Fig. 19 Terminal arrival time-velocity errors under disturbances |
1) 采用所设计的多边界航向角偏差走廊,能够在不同的初始横侧向状态下生成具有一定到达时间调节能力的再入轨迹。理论分析与仿真计算验证了该方法的可行性。
2) 分析计算多枚飞行器的到达时间调节能力与到达时间分布后,采用所设计的协同攻击时间决策方法保证了多飞行器协同再入的任务需求。
3) 协同再入与扰动情形下的仿真结果表明,该方法能够以较高精度满足到达时间与终端约束,具备一定的计算精度与鲁棒性。规划结果在保证一定的到达时间调节能力外,在纵向与横侧向实现了较强的机动,有利于进攻性武器的突防。
| [1] |
柳青, 朱坤, 赵欣. 高超声速精确打击武器制导控制关键技术[J]. 战术导弹技术, 2018(6): 63-69. LIU Q, ZHU K, ZHAO X. Key technologies of guidance and control for hypersonic precise strike weapon[J]. Tactical Missile Technology, 2018(6): 63-69. (in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [2] |
柴琨琦, 王健, 杨令飞. 高超声速快速精确打击技术发展分析[J]. 战术导弹技术, 2015(5): 13-17, 29. CHAI K Q, WANG J, YANG L F. Analysis of hypersonic prompt precision strike technique development[J]. Tactical Missile Technology, 2015(5): 13-17, 29. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [3] | LIANG Z X, REN Z, LI Q D, et al. Decoupled three-dimensional entry trajectory planning based on maneuver coefficient[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2017, 231(7): 1281-1292. |
| Click to display the text | |
| [4] | SHEN Z J, LU P. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111-121. |
| Click to display the text | |
| [5] | CHOU H C, ARDEMA M D, BOWLES J V. Near-optimal entry trajectories for reusable launch vehicles[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(6): 983-990. |
| Click to display the text | |
| [6] | LIANG Z X, LIU S Y, LI Q D, et al. Lateral entry guidance with no-fly zone constraint[J]. Aerospace Science and Technology, 2017, 60: 39-47. |
| Click to display the text | |
| [7] | LIANG Z X, REN Z. Tentacle-based guidance for entry flight with no-fly zone constraint[J]. Journal of Guidance, Control, and Dynamics, 2017, 41(4): 1-10. |
| Click to display the text | |
| [8] | JORRIS T R, COBB R G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 551-572. |
| Click to display the text | |
| [9] | ZHAO J, ZHOU R. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1544-1553. |
| Click to display the text | |
| [10] | LIU X F, SHEN Z J, LU P. Solving the maximum-crossrange problem via successive second-order cone programming with a line search[J]. Aerospace Science and Technology, 2015, 47: 10-20. |
| Click to display the text | |
| [11] | LIU X F, SHEN Z J, LU P. Entry Trajectory optimization by second-order cone programming[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(2): 227-241. |
| Click to display the text | |
| [12] | JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266. |
| Click to display the text | |
| [13] | KIM T H, LEE C H, JEON I S, et al. Augmented polynomial guidance with impact time and angle constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2806-2817. |
| Click to display the text | |
| [14] | JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280. |
| Click to display the text | |
| [15] | JUNG B, KIM Y. Guidance laws for anti-ship missiles using impact angle and impact time[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2006. |
| [16] | CHO D, KIM H J, TAHK M J. Nonsingular sliding mode guidance for impact time control[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 61-68. |
| Click to display the text | |
| [17] |
孙雪娇, 周锐, 吴江, 等. 多导弹分布式协同制导与控制方法[J]. 北京航空航天大学学报, 2014, 40(1): 120-124. SUN X J, ZHOU R, WU J, et al. Distributed cooperative guidance and control for multiple missiles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 120-124. (in Chinese) |
| Cited By in Cnki (19) | Click to display the text | |
| [18] |
赵启伦, 陈建, 董希旺, 等. 拦截高超声速目标的异类导弹协同制导律[J]. 航空学报, 2016, 37(3): 936-948. ZHAO Q L, CHEN J, DONG X W, et al. Cooperative guidance law for heterogeneous missiles intercepting hypersonic weapon[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 936-948. (in Chinese) |
| Cited By in Cnki (34) | Click to display the text | |
| [19] | ZHAO J, ZHOU R. Obstacle avoidance for multi-missile network via distributed coordination algorithm[J]. Chinese Journal of Aeronautics, 2016, 29(2): 441-447. |
| Click to display the text | |
| [20] | ZHAO J, ZHOU R, DONG Z. Three-dimensional cooperative Guidance laws against stationary and maneuvering targets[J]. Chinese Journal of Aeronautics, 2015, 28(4): 1104-1120. |
| Click to display the text | |
| [21] | ZHOU J, YANG J. Distributed guidance law design for cooperative simultaneous attacks with multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(10): 2439-2447. |
| Click to display the text | |
| [22] |
王肖, 郭杰, 唐胜景, 等. 基于解析剖面的时间协同再入制导[J]. 航空学报, 2019, 40(3): 322565. WANG X, GUO J, TANG S J, et al. Time-cooperative entry guidance based on analytical profile[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(3): 322565. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [23] | CHU H, LI J, DONG Y, et al. Improved MPSP method-based cooperative re-entry guidance for hypersonic gliding vehicles[C]//MATEC Web of Conferences, 2017. |
| [24] |
李征, 彭博, 陈海东, 等.可重复使用航天器时间协同飞行轨迹优化[J/OL]. (2019-11-14)[2019-12-08].计算机仿真, 2020(1): 40-45. LI Z, PENG B, CHEN H D, et al. Time-coordination reentry trajectory design for reusable launch vehicle[J/OL]. (2019-11-14)[2019-12-08].Computer Simulation, 2020(1): 40-45(in Chinese). |
| [25] | BRYSON A E, HO Y C. Applied optimal control[M]. Washington, D.C.: Hemisphere Publishing Corporation, 1975. |
| [26] | PHILLIPS T H. A common aero vehicle (Cav) model, description, and employment guide[R]. Schafer Corporation for AFRL and AFSPC, 2003. |



