2. 北京信息科学与技术国家研究中心(BNRist), 北京 100084
2. Beijing National Research Center for Information Science and Technology(BNRist), Beijing 100084, China
多智能体系统(Multi-Agent System, MAS)是由多个具有感知、认知、控制与行为等能力的智能自主运动体(Agent)通过信息交互组成的群体系统,个体之间通过局部相互作用,使整个系统在宏观上涌现出复杂、有效、强大的智能行为,可以实现单个个体无法实现的功能,在执行协作任务方面具有重要的应用价值,如协作估计[1-3]、协作搜索和协作攻击[4-6]等。其中,多智能体系统的一致性控制问题是一个基础问题,在编队控制[7]、蜂拥控制[8-9]、传感器网络[10]及时钟同步[11]上均有广泛的应用。
一致性控制是指通过设计分布式控制律使得所有个体在某些变量上达成一致。早在20世纪80年代,一些生物学家和物理学家通过建模与仿真以试图发现多个体系统行为背后的机理[12-13]。21世纪初,Fax和Murray将个体之间的局部信息交流建模成有向图,并初步利用图论的知识得到系统稳定的条件[14]。随后,Olfati-Saber和Murray针对固定拓扑和切换拓扑提出了一种一致性控制方法[15-16],从而引发了新一轮一致性问题的研究热潮。到目前为止,一致性控制的研究作为一个研究热点,被广泛地研究[17-20],研究问题涵盖干扰、非线性、时延、噪声、通信协议和最优控制等[21-27]。
目前多数的针对多智能体系统一致性控制的研究未考虑执行器的饱和约束,实际中执行器饱和是普遍存在的,如电机的输出转矩受最大功率的限制,飞机的舵面受物理结构限制等,在一些情况下,为了系统安全会人为加入饱和限制,避免输入过大。饱和环节作为一种典型的非线性环节,给多智能体系统一致性的分析造成了本质性的困难:导致多智能体系统的一致性与系统的初始状态有关。初始状态的微小变化,都可能会改变系统的运动模式。
针对执行器饱和的研究,在单个体中的适用方法包括低增益反馈[28]、抗饱和方法[29]等。其中低增益反馈方法的本质是通过设计很小的增益使得输入控制在饱和界限以内,此时系统简化为线性系统,但是由于增益很小导致系统收敛速度很慢,Lin和Saberi在此基础上进一步提出了高低增益的方法,在低增益的基础上叠加一个高增益[30],利用李雅普诺夫函数证明了该方法的有效性,当增益过大时,输入变量会一直在饱和的上下界处切换,类似最优控制中的Bang-Bang控制。抗饱和方法通过把实际输入信号和理论输入信号的差值作为误差信号,增加反馈环节消除误差信号,实际上是两种控制律的切换,可以得到较好的性质,但是设计较为复杂。此外,存在其他一些方法,如自适应滑模方法,可以处理执行器饱和的约束。
然而,处理单个体系统的方法不能直接用在多智能体系统中,一个重要的原因是:在多智能体系统中,需要考虑个体之间的通信耦合关系,通信拓扑会对系统的稳定性产生影响,如何利用受限的输入量消除通信拓扑造成的影响是其中一个难点。针对这一问题,文献[31-33]针对领航-跟随系统,给出了一种半全局一致的控制律设计方法,分别实现了执行器饱和约束下的状态一致和输出一致。此外,文献[34]和[35]针对全局一致性问题,分别给出了连续时间系统和离散时间系统的一致性控制律设计方法。在这些文献中,都假设系统是有界输入下渐近零可控的(Asymptotically Null Controllable with Bounded Controls, ANCBC),即(A, B)可镇定且A的所有特征根都在左半闭平面(连续系统)或单位圆上或圆内(离散系统)。
基于以上的分析,本文重点研究更具一般性的多智能体系统,在执行器饱和约束下给出控制律的设计方法。主要创新点包括:①针对饱和约束下的离散多智能体系统,设计了一种基于线性矩阵不等式(Linear Matrix Inequality, LMI)的一致性控制律;②引入吸引域对所设计控制律进行评价,并基于LMI给出一种控制参数的优化方法以最大化吸引域;③借助离散黎卡提方程,对LMI解的存在性给出了分析。
符号说明:1n(或0n)表示元素全为1(或0)的n维列向量,0m×n表示m×n维的零矩阵,In表示n×n维的单位矩阵,diag(d0, d1, …, dn)表示以d0, d1, …, dn为对角元素的对角矩阵,ρ(A)和λmax(A)表示矩阵A的谱半径和最大特征根,⊗是Kronecker积,||·||和||·||∞表示矩阵或向量的2-范数和无穷范数。
1 问题描述考虑由N个个体构成的多智能体系统,个体之间的通信用一个有向图G≜(V, E, AG)进行描述,其中V={V1, V2, …, VN}是节点集合,每个节点表示一个个体;E⊂V×V是边集合,边Eij=(Vi, Vj)∈E表示节点i的信息可以传递给节点j;边的总数记为NG,其中Eij和Eji记为一条边;AG=[aij]∈RN×N表示图的邻接矩阵,aii=0,如果Eji∈E,aij=1,否则aij=0。此外,令L=[lij]∈RN×N表示有向图G的拉普拉斯矩阵,定义为lii=∑j≠iaij, lij=-aij, i≠j,当L是对称矩阵时,图G是无向图。如果无向图中任意两个节点之间都存在一条无向路径,那么该无向图是“连通的”。
对于连通的无向图,存在一个正交矩阵T=[T0, T1]使L对角化为TTLT=Λ=diag(0, Φ),其中
考虑由N个个体组成的多智能体系统,每个个体的状态方程为(
| $ {\mathit{\boldsymbol{x}}_i}(k + 1) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i}(k) + \mathit{\boldsymbol{B}}\sigma ({\mathit{\boldsymbol{u}}_i}(k)) $ | (1) |
式中:xi∈Rn和ui∈Rm分别表示状态变量和输入变量。σ(ui)=[σ(ui1), σ(ui2), …, σ(uim)]T是饱和函数,定义为σ(uij)=sign(uij)min{|uij|, 1}。
当执行器存在饱和约束时,多智能体系统能够实现全局一致性的一般假设是(A, B)可镇定并且ρ(A)≤1。当ρ(A)>1时,全局一致性一般难以实现,此时,引入“吸引域”的概念来反映控制律的效果。本文便是针对一般的可镇定系统,设计一致性控制律,同时最大化吸引域。下面首先给出一些基本定义和假设。
定义1 (一致性[36])针对多智能体系统式(1),如果对于任意两个个体i、j∈
| $ \mathop {{\rm{lim}}}\limits_{k \to \infty } \left\| {{\mathit{\boldsymbol{x}}_i}(k) - {\mathit{\boldsymbol{x}}_j}(k)} \right\| = 0 $ | (2) |
则称该多智能体系统达到了一致。
定义2 (吸引域[37])假设系统初值x(0)=x0,系统的解定义为ψ(k, x0),则原点处的吸引域定义为
| $ \mathit{\boldsymbol{D}} = \{ {\mathit{\boldsymbol{x}}_0}|\mathop {{\rm{lim}}}\limits_{k \to \infty } \psi (k,{\mathit{\boldsymbol{x}}_0}) = 0\} $ | (3) |
假设1 多智能体系统的无向图是连通的。
针对多智能体系统式(1),采用一致性控制律形式表示:
| $ {\mathit{\boldsymbol{u}}_i}(k) = \mathit{\boldsymbol{K}}\sum\limits_{j = 1}^N {{a_{ij}}} ({\mathit{\boldsymbol{x}}_i}(k) - {\mathit{\boldsymbol{x}}_j}(k)) $ | (4) |
式中:K为待设计的增益矩阵。
令x=[x1T, x2T, …, xNT]T,利用Kronecker积,可以得到闭环系统动态方程为
| $ \begin{array}{l} \mathit{\boldsymbol{x}}(k + 1) = ({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{A}})\mathit{\boldsymbol{x}}(k) + ({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{B}}) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma ((\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{K}})\mathit{\boldsymbol{x}}(k)) \end{array} $ | (5) |
研究目的在于针对多智能体系统式(1),设计如式(4)所示的一致性控制律,在执行器饱和的约束下,保证系统的一致性,同时优化参数K,最大化吸引域。
2 主要结果首先针对如式(4)所示的一致性控制律,给出其中反馈增益矩阵的设计方法;然后针对饱和约束,给出最大化吸引域下的反馈增益矩阵优化方法。
2.1 一致性控制律设计首先,假设supk(L⊗K)x(k)∞≤1,即控制输入不超过饱和的界,此时系统是一个线性系统。
令y=(TT⊗In)x=[y1T, y2T, …, yNT]T,其中,
| $ \mathit{\boldsymbol{y}}(k + 1) = ({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \otimes \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{y}}(k) $ | (6) |
令z=[y2T, y3T, …, yNT]T=(T1T⊗In)x,式(6)可以进一步转化为
| $ \mathit{\boldsymbol{z}}(k + 1) = ({\mathit{\boldsymbol{I}}_{N - 1}} \otimes \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{z}}(k) $ | (7) |
当z(k)=0n(N-1)时,x(k)满足:
| $ \mathit{\boldsymbol{x}}(k) = (\mathit{\boldsymbol{T}} \otimes {\mathit{\boldsymbol{I}}_n})\mathit{\boldsymbol{y}}(k) = \sqrt {\frac{1}{N}} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_1}(k)}\\ {{\mathit{\boldsymbol{y}}_1}(k)}\\ \vdots \\ {{\mathit{\boldsymbol{y}}_1}(k)} \end{array}} \right] $ |
即所有个体的状态达成一致。因此,通过变量变换,多智能体系统的一致性问题可以转化为一个多输入多输出系统式(7)的稳定性问题。此时,假设条件supk||(L⊗K)x(k)||∞≤1相应转化为supk||(T1Φ⊗K)z(k)||∞≤1。在给出主要结果之前,首先给出两个集合的定义:
| $ \varepsilon (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}},1) = \{ \mathit{\boldsymbol{z}} \in {{\bf{R}}^{(N - 1)n}}:{\mathit{\boldsymbol{z}}^{\rm{T}}}(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{z}} \le 1\} $ | (8) |
| $ \wp (\mathit{\boldsymbol{H}}) = \{ \mathit{\boldsymbol{z}} \in {{\bf{R}}^{(N - 1)n}}:|{H_j}\mathit{\boldsymbol{z}}| \le 1\} $ | (9) |
式中:Hj表示矩阵H的第j行。
定理1 假设1成立,如果存在矩阵Y和矩阵W=P-1>0,使得式(10)对于i=2, 3, …, N均成立:
| $ {\varepsilon (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}},1) \subset \wp ({\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{K}})} $ | (10a) |
| $ {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}^{\rm{T}}} + {\lambda _i}{\mathit{\boldsymbol{Y}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{AW}} + {\lambda _i}\mathit{\boldsymbol{BY}}}&\mathit{\boldsymbol{W}} \end{array}} \right] > 0} $ | (10b) |
则对于初值满足z(0)∈ε(Φ⊗P, 1)的多智能体系统在式(4)所示的控制律下可以实现一致性,其中,反馈增益矩阵K=YW-1。
证明 选取Lyapunov函数:
| $ V(k) = {\mathit{\boldsymbol{z}}^{\rm{T}}}(k)(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{z}}(k) $ | (11) |
不妨设z(k)∈ε(Φ⊗P, 1),由式(10a)可得
即||u(k)||∞=||(L⊗K)x(k)||∞=||(T1Φ⊗K)z(k)||∞≤1, 因此,可得
| $ \begin{array}{l} \Delta V(k) = V(k + 1) - V(k) = {\mathit{\boldsymbol{z}}^{\rm{T}}}(k)(({\mathit{\boldsymbol{I}}_{N - 1}} \otimes \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{BK}}{)^{\rm{T}}}(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}}) \times ({\mathit{\boldsymbol{I}}_{N - 1}} \otimes \mathit{\boldsymbol{A}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{BK}}) - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{z}}(k) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{z}}^{\rm{T}}}(k){\rm{ diag}} ({\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_3}, \cdots ,{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_N})\mathit{\boldsymbol{z}}(k) \end{array} $ | (12) |
式中:Γi=λi(A+λiBK)TP(A+λiBK)-λiP。利用Schur补引理,由不等式(10b)及K=YW-1,可得Γi < 0,由李雅普诺夫稳定性理论可得limk→∞V(k)=0。
此外,由式(10a)和z(0)∈ε(Φ⊗P, 1)可得,
在定理1中,ε(Φ⊗P, 1)是吸引域的一个子集,能够使多智能体系统达到一致的系统初值需要满足z(0)∈ε(Φ⊗P, 1)。通过最大化ε(Φ⊗P, 1)的范围以达到最大化吸引域范围的目的。为了便于描述ε(Φ⊗P, 1)的大小,定义一个椭球体ε(Φ⊗R, 1)={z∈Rn(N-1):zT(Φ⊗R)z≤1},并用max{α}反映ε(Φ⊗P, 1)范围的大小,其中,αε(Φ⊗R, 1)⊂ε(Φ⊗P, 1)。因此,最大化吸引域的问题可以转化为
| $ \begin{array}{l} {\rm{max}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \\ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}},1) \subset \wp ({\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{K}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c2}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}^{\rm{T}}} + {\lambda _i}{\mathit{\boldsymbol{Y}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{AW}} + {\lambda _i}\mathit{\boldsymbol{BY}}}&\mathit{\boldsymbol{W}} \end{array}} \right] > 0\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c3}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \varepsilon (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{R}},1) \subset \varepsilon (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}},1) \end{array} $ | (13) |
对式(13)中的(c1)和(c3)进行分析和变换,进而转化成LMI的形式,便于求解。针对条件(c1),由Φ≤λNIN-1,可得ε(Φ⊗P, 1)⊂ε(λN-1Φ2⊗P, 1),此外,由于
| $ {{\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{K}} = ({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{K}})({\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes {\mathit{\boldsymbol{I}}_n}),} $ |
| $ {\frac{1}{{{\lambda _N}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^2} \otimes \mathit{\boldsymbol{P}} = \frac{1}{{{\lambda _N}}}(\mathit{\boldsymbol{ \boldsymbol{\varPhi} T}}_1^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_n})({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{P}})({\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes {\mathit{\boldsymbol{I}}_n}),} $ |
因此,
| $ \left[ {\begin{array}{*{20}{l}} {\frac{1}{{{\lambda _N}}}}&{{{({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{K}})}_j}}\\ *&{({\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{P}})} \end{array}} \right] \ge 0\;\:j = 1,2, \cdots ,mN $ | (14) |
式中:下标j表示矩阵的第j行; *表示对称元素。
利用Schur补引理,式(14)等价于
| $ \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\lambda _N}}}}&{{\mathit{\boldsymbol{K}}_j}}\\ *&\mathit{\boldsymbol{P}} \end{array}} \right] \ge 0\;\:j = 1,2, \cdots ,m $ | (15) |
进一步转化为
| $ \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\lambda _N}}}}&{{\mathit{\boldsymbol{Y}}_j}}\\ *&\mathit{\boldsymbol{W}} \end{array}} \right] \ge 0\;\:j = 1,2, \cdots ,m $ | (16) |
至此,条件(c1)已经转化为LMI的形式。令
综上,最大化吸引域问题可以转化为求解如下所示LMI组的优化问题,
| $ \begin{array}{l} {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma \\ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{\lambda _N}}}}&{ - {\mathit{\boldsymbol{Y}}_j}}\\ *&{ - \mathit{\boldsymbol{W}}} \end{array}} \right] \le 0\;\:j = 1,2, \cdots ,m\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c2}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{W}}}&*\\ { - \mathit{\boldsymbol{AW}} - {\lambda _i}\mathit{\boldsymbol{BY}}}&{ - \mathit{\boldsymbol{W}}} \end{array}} \right] < 0\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{c3}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{R}}^{ - 1}} \le \gamma \mathit{\boldsymbol{W}} \end{array} $ | (17) |
注1 满足条件z(0)∈ε(Φ⊗P, 1)的初值包含在吸引域中,针对无向连通图有:
| $ \begin{array}{l} \mathit{\boldsymbol{z}}{(0)^{\rm{T}}}(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{z}}(0) = \mathit{\boldsymbol{x}}{(0)^{\rm{T}}}(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{x}}(0) \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{P}})\mathit{\boldsymbol{x}}{(0)^{\rm{T}}}(\mathit{\boldsymbol{L}} \otimes {\mathit{\boldsymbol{I}}_n})\mathit{\boldsymbol{x}}(0) = {\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{P}}) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{E_{ij}} \in \mathit{\boldsymbol{E}},i < j} {{{\left\| {{\mathit{\boldsymbol{x}}_i}(0) - {\mathit{\boldsymbol{x}}_j}(0)} \right\|}^2} \le } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {N_G}{\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{P}}){\rm{ma}}{{\rm{x}}_{i,j,{E_{ij}} \in \mathit{\boldsymbol{E}}}}\{ {\left\| {{\mathit{\boldsymbol{x}}_i}(0) - {\mathit{\boldsymbol{x}}_j}(0)} \right\|^2}\} \end{array} $ | (18) |
因此,多智能体系统满足式(19)的初值条件时:
| $ {\rm{ma}}{{\rm{x}}_{i,j,{E_{ij}} \in \mathit{\boldsymbol{E}}}}\{ \left\| {{\mathit{\boldsymbol{x}}_i}(0) - {\mathit{\boldsymbol{x}}_j}(0)} \right\|\} \le \sqrt {\frac{1}{{{N_G}{\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{P}})}}} $ | (19) |
x(0)被包含在吸引域中,即任意两个互为邻居的个体之间初始状态差值的2-范数不超过
注2 式(17)中的条件(c2)等价于
| $ \begin{array}{l} \mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} - {\lambda _i}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PBK}} - {\lambda _i}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda _i^2{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PBK}} > 0 \end{array} $ | (20) |
如果取K=-c(BTPB+I)-1BTPA,则式(20)转化为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + {c^2}\lambda _i^2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{{({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} + \mathit{\boldsymbol{I}})}^{ - 2}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (2c{\lambda _i} - {c^2}\lambda _i^2){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{{({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} + \mathit{\boldsymbol{I}})}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}} > 0} \end{array} $ | (21) |
则只需Mi≜P-ATPA+(2cλi-c2λi2)·ATPB(BTPB+I)-1BTPA>0即可。∀i=2, 3, …, N, Mi>0均成立可以由Mi≥MN且MN>0得到。由Mi-MN=(λN-λi)[(λN+λi)c2-2c]ATPB(BTPB+I)-1BTPA可得,c≥2/(λN+λ2)时,Mi≥MN。此外,求解MN>0问题可以转化为求解如下所示的修正离散黎卡提方程问题(Q>0):
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} - (2c{\lambda _N} - {c^2}\lambda _N^2){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PB}} \cdot }\\ {{{({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} + \mathit{\boldsymbol{I}})}^{ - 1}} \times {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + \mathit{\boldsymbol{Q}}} \end{array} $ | (22) |
假设(A, B)可镇定,对于任意给定的正定矩阵Q,下面论断成立[38-39]:
1) 如果A的所有特征根都在单位圆内或单位圆上,则对于0 < c < 2/λN,式(22)均存在唯一解。
2) 如果A至少有一个特征根(记为λiu(A))位于单位圆外,并且rank(B)=1时,则对于
3) 式(22)的唯一解满足P=limk→∞P(k),其中P(k)=ATP(k-1)A-(2cλi-c2λi2)ATP(k-1)B(BTP(k-1)B+I)-1BTP(k-1)A+Q。
3 仿真分析1) 多智能体系统1:二阶积分系统
考虑由5个个体构成的多智能体系统,每个个体的系统矩阵为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{0.01}\\ 0&1 \end{array}} \right]}\\ {\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {0.0001}\\ {0.01} \end{array}} \right]} \end{array}} \right. $ |
其中,A的两个特征根均为1,拓扑结构如图 1(a)所示,其中λ2=λ3=1.382 0, λ4=λ5=3.618 0。取R=I2,求解式(17)所示的优化问题,可得
| $ \mathit{\boldsymbol{Y}} = [ - 129.552{\kern 1pt} {\kern 1pt} {\kern 1pt} 9, - 10.044{\kern 1pt} {\kern 1pt} {\kern 1pt} 2], $ |
| $\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 009{\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 028}\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 028}&{0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 6} \end{array}} \right],\gamma = 0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 9, $ |
| $ \mathit{\boldsymbol{K}} = [ - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 54,\;\: - 0.019{\kern 1pt} {\kern 1pt} {\kern 1pt} 6],\alpha = 22.805{\kern 1pt} {\kern 1pt} {\kern 1pt} 1。$ |
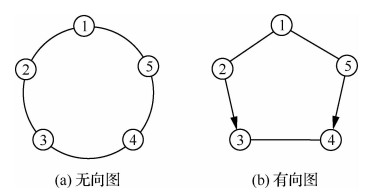
|
| 图 1 多智能体系统拓扑图 Fig. 1 Topology of multi-agent system |
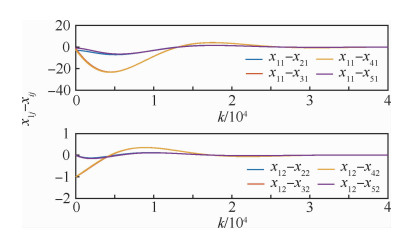
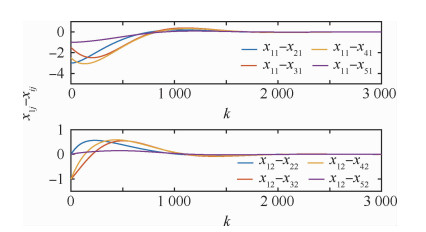
设系统初值为x(0)=[-1, 0, 2, 0, 0.5, 1, 1.5, 1, 0, 0]T,仿真结果如图 2和图 3所示,可以看出,系统最终能够达到一致性。由于反馈增益K较小,导致收敛时间较长,可以通过适当减小α以提高收敛速度。具体方法为:在满足γ≥0.001 9时,固定合适的γ值,求满足LMI组(17)中条件(c1)~(c3)的解。若选取γ=4,可得K=[-0.118 6, -0.310 7],仿真结果如图 4和图 5所示,收敛时间得到缩短。需要注意的是,收敛速度的提高以缩小吸引域为代价,因此,在实际应用中,需要做均衡考虑,而本文给出了该控制框架下所能达到的最大吸引域,便于以此为参考进行控制律的设计。
|
| 图 2 多智能体系统1的x1j-xij变化曲线(i=2, 3, 4, 5, j=1, 2, γ=0.001 9) Fig. 2 Variation of x1j-xij in MAS 1 (i=2, 3, 4, 5, j=1, 2, γ=0.001 9) |
|
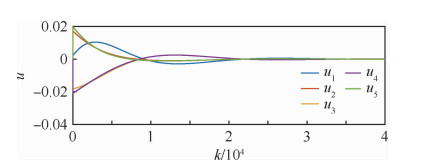
| 图 3 多智能体系统1的输入曲线(γ=0.001 9) Fig. 3 Variation of input variable in the MAS 1 (γ=0.001 9) |
|
| 图 4 多智能体系统1的x1j-xij变化曲线(γ=4) Fig. 4 Variation of x1j-xij in MAS 1 (γ=4) |

|
| 图 5 多智能体系统1的输入曲线(γ=4) Fig. 5 Variation of input variable in MAS 1 (γ=4) |
2) 多智能体系统2:不稳定系统
考虑由5个个体构成的多智能体系统,拓扑结构如图 1(a)所示,每个个体的系统矩阵为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{0.1}\\ {0.15}&{0.5} \end{array}} \right]}\\ {\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {0.2}\\ {0.25} \end{array}} \right]} \end{array}} \right. $ |
其中,A有一个不稳定的特征根1.028 4,取R=I2,求解式(17)所示的优化问题,可得γ=0.025 9, α=6.211 6。适当降低α的值,选取γ=0.08,即α=3.535 5,此时
| $ \mathit{\boldsymbol{Y}} = [ - 1.495{\kern 1pt} {\kern 1pt} {\kern 1pt} 7, - 0.336{\kern 1pt} {\kern 1pt} {\kern 1pt} 3], $ |
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.068{\kern 1pt} {\kern 1pt} 4}&{0.011{\kern 1pt} {\kern 1pt} 6}\\ {0.011{\kern 1pt} {\kern 1pt} 6}&{0.008{\kern 1pt} {\kern 1pt} 0} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} { - 0.106{\kern 1pt} {\kern 1pt} 2,}&{ - 0.020{\kern 1pt} {\kern 1pt} 1} \end{array}} \right] $ |
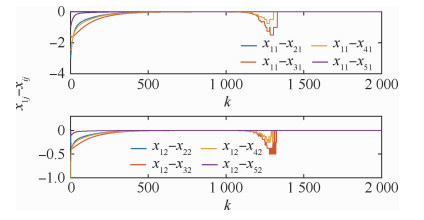
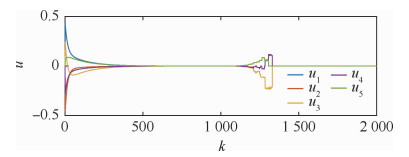
设系统初值为x(0)=[-1, 0, 2, 0, 0.5, 1, 1.5, 1, 0, 0]T,仿真结果如图 6和图 7所示,系统最终能够达到一致性,并且输入量始终维持在饱和界以内。
|
| 图 6 多智能体系统2的x1j-xij变化曲线 Fig. 6 Variation of x1j-xij in MAS 2 |
|
| 图 7 多智能体系统2的输入曲线 Fig. 7 Variation of input variable in MAS 2 |
3) 多智能体系统3:有向图
针对不包含复数特征根的有向图,如果有向图中包含一簇有向生成树,本文所提出的方法依然适用。考虑每个个体的系统矩阵为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{l}} {1.006}&{ - 0.008}\\ {0.006}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.006} \end{array}} \right]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{B}} = \begin{array}{*{20}{c}} {0.019{\kern 1pt} {\kern 1pt} 9}\\ {0.040{\kern 1pt} {\kern 1pt} 2} \end{array}} \end{array}} \right. $ |
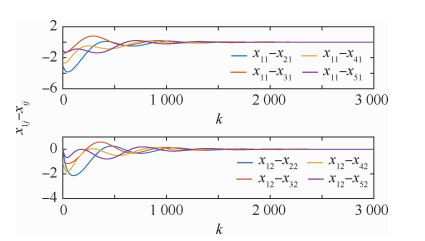
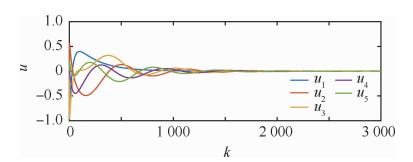
其中,A有一对不稳定的特征根1.006±0.006 9i。拓扑结构如图 1(b)所示,其中λ2=λ3=1, λ4=λ5=3,取R=I2,求解式(17)所示的优化问题,可得γ=0.580 2, α=1.312 8。若选取γ=3,此时K=[0.186 1, -0.498 3]。假设系统初值为x(0)=[-1, 0, 2, 0, 0.5, 1, 1.5, 1, 0, 0]T,仿真结果如图 8和图 9所示,系统最终能够达到一致性。
|
| 图 8 多智能体系统3的x1j-xij变化曲线 Fig. 8 Variation of x1j-xij in MAS 3 |
|
| 图 9 多智能体系统3的输入曲线 Fig. 9 Variation of input variable in MAS 3 |
针对离散的多智能体系统,在执行器存在饱和约束时,设计了一种基于LMI的一致性控制律,并分析了LMI解的存在性条件。在执行器存在饱和约束时,系统的全局一致性一般较难实现,尤其针对本身不稳定的系统。在全局一致性不能实现的情况下,用吸引域的大小对所设计的控制律进行评估,并给出了一种最大化吸引域的参数优化方法。最后,通过两组数值仿真例子,说明了所提出方法的有效性。
| [1] | KWON C, HWANG I. Sensing-based distributed state estimation for cooperative multiagent systems[J]. IEEE Transactions on Automatic Control, 2019, 64(6): 2368-2382. |
| Click to display the text | |
| [2] | SONG W, WANG J, ZHAO S, et al. Event-triggered cooperative unscented Kalman filtering and its application in multi-UAV systems[J]. Automatica, 2019, 105: 264-273. |
| Click to display the text | |
| [3] | LIU Q, WANG Z, HE X, et al. On Kalman-consensus filtering with random link failures over sensor networks[J]. IEEE Transactions on Automatic Control, 2018, 63(8): 2701-2708. |
| Click to display the text | |
| [4] | XIAO H, CUI R, XU D. A sampling-based Bayesian approach for cooperative multiagent online search with resource constraints[J]. IEEE Transactions on Cybernetics, 2018, 48(6): 1773-1785. |
| Click to display the text | |
| [5] | LI P, DUAN H. A potential game approach to multiple UAV cooperative search and surveillance[J]. Aerospace Science and Technology, 2017, 68: 403-415. |
| Click to display the text | |
| [6] | GAO C, ZHEN Z, GONG H. A self-organized search and attack algorithm for multiple unmanned aerial vehicles[J]. Aerospace Science and Technology, 2016, 54: 229-240. |
| Click to display the text | |
| [7] | THUNBERG J, GONCALVES J, HU X. Consensus and formation control on SE(3) for switching topologies[J]. Automatica, 2016, 66: 109-121. |
| Click to display the text | |
| [8] | CUCKER F, SMALE S. Emergent behavior in flocks[J]. IEEE Transactions on Automatic Control, 2007, 52(5): 852-862. |
| Click to display the text | |
| [9] | SOMARAKIS C, BARAS J S. Delay-independent stability of consensus networks with application to flocking[J]. IFAC-PapersOnLine, 2015, 48(12): 159-164. |
| Click to display the text | |
| [10] | JI H, LEWIS F L, HOU Z, et al. Distributed information-weighted Kalman consensus filter for sensor networks[J]. Automatica, 2017, 77: 18-30. |
| Click to display the text | |
| [11] | GARCIA E, MOU S, CAO Y, et al. An event-triggered consensus approach for distributed clock synchronization[C]//Proceedings of the American Control Conference, 2017: 279-284. |
| [12] | REYNOLDS C W. Flocks, herds and schools:A distributed behavioral model[J]. Computer Graphics, 1987, 21(4): 25-34. |
| Click to display the text | |
| [13] | VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75(6): 1226. |
| Click to display the text | |
| [14] | FAX J A, MURRAY R M. Graph Laplacians and stabilization of vehicle formations[C]//IFAC Proceedings Volumes, 2002, 35(1): 55-60. |
| [15] | OLFATI-SABER R, MURRAY R M. Consensus protocols for networks of dynamic agents[C]//Proceedings of the American Control Conference, 2003: 951-956. |
| [16] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. |
| Click to display the text | |
| [17] | REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661. |
| Click to display the text | |
| [18] | MENG Z, REN W, CAO Y, et al. Leaderless and leader-following consensus with communication and input delays under a directed network topology[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(1): 75-88. |
| Click to display the text | |
| [19] | ZHANG F, TRENTELMAN H L, SCHERPEN J M. Fully distributed robust synchronization of networked Lur'e systems with incremental nonlinearities[J]. Automatica, 2014, 50(10): 2515-2526. |
| Click to display the text | |
| [20] | LI Z, CHEN M Z Q, DING Z. Distributed adaptive controllers for cooperative output regulation of heterogeneous agents over directed graphs[J]. Automatica, 2016, 68: 179-183. |
| Click to display the text | |
| [21] | WANG X, LI S, LAM J. Distributed active anti-disturbance output consensus algorithms for higher-order multi-agent systems with mismatched disturbances[J]. Automatica, 2016, 74: 30-37. |
| Click to display the text | |
| [22] | WANG Y, SONG Y, KRSTIC M, et al. Fault-tolerant finite time consensus for multiple uncertain nonlinear mechanical systems under single-way directed communication interactions and actuation failures[J]. Automatica, 2016, 63: 374-383. |
| Click to display the text | |
| [23] | HOU W, FU M, ZHANG H, et al. Consensus conditions for general second-order multi-agent systems with communication delay[J]. Automatica, 2017, 75: 293-298. |
| Click to display the text | |
| [24] | CHENG L, WANG Y, REN W, et al. On convergence rate of leader-following consensus of linear multi-agent systems with communication noises[J]. IEEE Transactions on Automatic Control, 2016, 61(11): 3586-3592. |
| Click to display the text | |
| [25] | MA L, WANG Z, LAM H K. Event-triggered mean-square consensus control for time-varying stochastic multi-agent system with sensor saturations[J]. IEEE Transactions on Automatic Control, 2017, 62(7): 3524-3531. |
| Click to display the text | |
| [26] | WANG L, WANG Z, HAN Q L, et al. Synchronization control for a class of discrete-time dynamical networks with packet dropouts:A coding-decoding-based approach[J]. IEEE Transactions on Cybernetics, 2018, 48(8): 2437-2448. |
| Click to display the text | |
| [27] | JIAO J, TRENTELMAN H L, CAMLIBEL M K. A suboptimality approach to distributed H2 optimal control[J]. IFAC-PapersOnLine, 2018, 51(23): 154-159. |
| Click to display the text | |
| [28] | LIN Z, SABERI A. Semi-global exponential stabilization of linear systems subject to "input saturation" via linear feedbacks[J]. Systems & Control Letters, 1993, 21(3): 225-239. |
| Click to display the text | |
| [29] | BANG H, TAHK M J, CHOI H D. Large angle attitude control of spacecraft with actuator saturation[J]. Control Engineering Practice, 2003, 11(9): 989-997. |
| Click to display the text | |
| [30] | LIN Z, SABERI A. A semi-global low-and-high gain design technique for linear systems with input saturation-stabilization and disturbance rejection[J]. International Journal of Robust and Nonlinear Control, 1995, 5(5): 381-398. |
| Click to display the text | |
| [31] | SU H, CHEN M Z Q, WANG X, et al. Semiglobal observer-based leader-following consensus with input saturation[J]. IEEE Transactions on Industrial Electronics, 2014, 61(6): 2842-2850. |
| Click to display the text | |
| [32] | SU H, QIU Y, WANG L. Semi-global output consensus of discrete-time multi-agent systems with input saturation and external disturbances[J]. ISA Transactions, 2017, 67: 131-139. |
| Click to display the text | |
| [33] | SU H, YE Y, QIN Y, et al. Semi-global output consensus for discrete-time switching networked systems subject to input saturation and external disturbances[J]. IEEE Transactions on Cybernetics, 2019, 49(11): 3934-3945. |
| Click to display the text | |
| [34] | MENG Z, ZHAO Z, LIN Z. On global leader-following consensus of identical linear dynamic systems subject to actuator saturation[J]. Systems & Control Letters, 2013, 62(2): 132-142. |
| Click to display the text | |
| [35] | YANG T, MENG Z, DIMAROGONAS D V, et al. Global consensus for discrete-time multi-agent systems with input saturation constraints[J]. Automatica, 2014, 50(2): 499-506. |
| Click to display the text | |
| [36] | MA C Q, ZHANG J F. Necessary and sufficient conditions for consensusability of linear multi-agent systems[J]. IEEE Transactions on Automatic Control, 2010, 55(5): 1263-1268. |
| Click to display the text | |
| [37] | ZUO Z, WANG Y. On enlarging the domain of attraction for linear systems subject to actuator saturation[J]. International Journal of General Systems, 2008, 37(2): 239-248. |
| Click to display the text | |
| [38] | LI Z, DUAN Z. Cooperative control of multi-agent systems:A consensus region approach[M]. Boca Raton: CRC Press, 2017: 62. |
| [39] | KATAYAMA T. On the matrix Riccati equation for linear systems with random gain[J]. IEEE Transactions on Automatic Control, 1976, 21(5): 770-771. |
| Click to display the text |



