在防空领域，目标的机动性能越来越强，单一导弹很难拦截速度大、机动性强的目标，然而，多枚导弹从不同的方位对同一空中目标进行“围追堵截”能够大大提高拦截概率^[1-3]。因此，为了实现齐射攻击，不断有学者提出攻击时间协同控制的算法，在文献[4]中，针对飞行器寻的问题，该文章提出了一种同时控制攻击时间和攻击角度的制导方法，可用于反舰导弹的有效齐射或协同逼近无人机任务。在文献[5]中，提出了一种考虑导引头视场约束以及攻击时间协同控制算法。在文献[6]中，作者针对导引头视场约束的攻击时间协同制导问题，将比例导引(PNG)法与时间误差有偏项相结合，从而达到各个导弹的剩余攻击时间一致的目的。文献[7]针对导弹协同攻击的问题，作者采用一致性分布式策略，设计了带有满足导引头视场角约束的比例修正项，从而保证了攻击时间和攻击角度的协同。文献[8]基于最优控制理论，研究了多枚导弹协同攻击的最优制导律问题，提出了多枚导弹同时攻击单个目标的新制导律。文献[9]采用最优控制法，并且结合时间调整设计了一种带有时间约束与角度约束的协同制导律。文献[10-11]采用双层的协同制导律设计方法设计了协同制导律，该方法既可以用在集中式的通信拓扑也可用于分布式通信拓扑，通过各枚导弹的剩余制导时间以及弹间通信共享从而完成协同攻击。在文献[12-13]中，针对目标加速度有界但界未知的情况下，基于一致性原理对主从式多智能体协同问题设计了有限时间协同制导律。

滑模理论的提出给制导律的设计提供了一种有效的方法，并且滑模法能够很好地应用到协同制导律的设计中来，结合一致性原理能够保证多枚导弹齐射攻击，并且能够保证导弹以期望的视线角攻击目标^[14-15]。文献[16]分析了3种截获几何形式，并将滑模控制方法引入到比例导引法中从而控制攻击角。文献[17]中的制导律通过将导航比从中段切换到末段来实现攻击角约束，并且在末段引入了观测器和最大升力系数。在文献[18-19]中，为了同时控制攻击时间和攻击角度，作者提出了一种双层设计方案。该方案包括第一层的非奇异滑模制导律和第二层的切换目标策略。在文献[20]中，为了实现攻击时间和落角协同控制，作者设计了超螺旋协同制导律，并用干扰观测器估计目标的机动信息。文献[21-23]在有向通信拓扑结构下，基于一致性原理，作者设计了积分滑模协同制导律，保证了多枚导弹撞击时间的有限时间一致性且保证视线角收敛于期望值。

针对多枚导弹拦截机动目标的问题，采用双层设计方案，基于终端滑模理论以及一致性原理，分别对视线方向以及视线法向进行制导律设计，从而保证多枚导弹之间的时间协同控制。在参考文献[14-23]中，基于滑模法设计了协同制导律，但制导律中采用了符号函数，符号函数的不连续会引起系统的抖振现象。为了解决该问题，本文设计了性能较好的自适应律，可以提高滑模的收敛速度以及滑模制导中由符号函数引起的抖振现象，并且第2节给出了详细的分析。该论文的结构安排如下：第1节给出了多枚导弹拦截同一目标的相对运动学模型，第2节基于滑模理论设计了时间与视线角约束的协同制导律，并给出了理论证明，第3节以三枚导弹拦截同一目标的场景，验证了所设计的制导律的有效性，第4节总结了全文。

1 模型建立

图 1为末制导段导弹拦截机动目标的相对运动三维几何图。图中：OX_IY_IZ_I是参考惯性坐标系；M与T分别代表导弹和目标；R为视线距离；θ_L和ϕ_L是视线角。根据图 1，可以推导出导弹拦截机动目标的三维相对运动学方程：

$ {\ddot R - R\dot \theta _{\rm{L}}^2 - R\dot \phi _{\rm{L}}^2{\rm{co}}{{\rm{s}}^2}{\theta _{\rm{L}}} = {a_{{\rm{LT}}}} - {a_{{\rm{LM}}}}} $	（1）

$ {R{{\ddot \theta }_{\rm{L}}} + 2\dot R{{\dot \theta }_{\rm{L}}} + R\dot \phi _{\rm{L}}^2{\rm{sin}}{\theta _{\rm{L}}}{\rm{cos}}{\theta _{\rm{L}}} = {a_{{\rm{ZT}}}} - {a_{{\rm{ZM}}}}} $	（2）

$ \begin{array}{l} - R{{\ddot \phi }_{\rm{L}}}{\rm{cos}}{\theta _{\rm{L}}} - 2\dot R{{\dot \phi }_{\rm{L}}}{\rm{cos}}{\theta _{\rm{L}}} + 2R{{\dot \phi }_{\rm{L}}}{{\dot \theta }_{\rm{L}}}{\rm{sin}}{\theta _{\rm{L}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{{\rm{YT}}}} - {a_{{\rm{YM}}}} \end{array} $

（3）

式中：[a_LM, a_ZM, a_YM]^T与[a_LT, a_ZT, a_YT]^T分别为视线坐标系下导弹加速度和目标加速度。

为了便于制导律设计，对式(1)~式(3)进行形式上的简化，具体形式为

$ {\ddot R = R\dot \theta _{\rm{L}}^2 + R\dot \phi _{\rm{L}}^2{\rm{co}}{{\rm{s}}^2}{\theta _{\rm{L}}} - {a_{{\rm{LM}}}} + {a_{{\rm{LT}}}}} $	（4）

$ {\left[ {\begin{array}{*{20}{l}} {{{\ddot \theta }_{\rm{L}}}}\\ {{{\ddot \phi }_{\rm{L}}}} \end{array}} \right] = \mathit{\boldsymbol{M}} + \mathit{\boldsymbol{D}} + \mathit{\boldsymbol{Bu}}} $	（5）

式中：$\boldsymbol{M}=\left[\begin{array}{c} -\frac{2 \dot{R}}{R}{\dot{\theta}}_{\mathrm{L}}-\dot{\phi}_{\mathrm{L}}^{2} \sin \theta_{\mathrm{L}} \cos \theta_{\mathrm{L}} \\ -\frac{2 \dot{R}}{R} \dot{\phi}_{\mathrm{L}}+2 \dot{\theta}_{\mathrm{L}} \dot{\phi}_{\mathrm{L}} \tan \theta_{\mathrm{L}} \end{array}\right] $；$ \boldsymbol{M}=\left[\begin{array}{cc} -\frac{1}{R} & 0 \\ 0 & \frac{1}{R \cos \theta_{{\rm L}}} \end{array}\right] ; \boldsymbol{u}=\left[\begin{array}{l} a_{{\rm Z M}} \\ a_{{\rm Y M}} \end{array}\right] ; \quad \boldsymbol{D}=\left[\begin{array}{c} \frac{a_{{\rm Y T}}}{R} \\ -\frac{a_{{\rm Z T}}}{R \cos \theta_{{\rm L}}} \end{array}\right]$。

a_LM与u分别为视线以及视线法向上的控制输入；D为视线法向上由目标加速度引起的系统总干扰。

末制导段，设导弹拦截目标的剩余时间为

$ {t_{{\rm{go}}}} = - \frac{R}{{\dot R}} $	（6）

对式(6)求导可得剩余时间的导数为

$ {\dot t_{{\rm{go}}}} = - 1 + \frac{{{R^2}}}{{{{\dot R}^2}}}\dot \theta _{\rm{L}}^2 + \frac{{{R^2}}}{{{{\dot R}^2}}}\dot \phi _{\rm{L}}^2{\rm{co}}{{\rm{s}}^2}{\theta _{\rm{L}}} - \frac{R}{{{{\dot R}^2}}}{a_{{\rm{LM}}}} + {D_r} $	（7）

式中：$D_{r}=\frac{R}{\dot{R}^{2}} a_{\mathrm{LT}} $为视线方向上的由目标加速度引起的总干扰。

多导弹协同拦截目标是针对每枚导弹设计制导律a_LM和u，使得所有的导弹在同一时间以各自期望的终端视线角命中目标。

式(4)给出了单一导弹拦截目标的相对运动学方程，当n枚导弹拦截同一目标时，第i枚导弹与目标之间的相对运动学方程可以表示为

$ \begin{array}{l} {{\dot t}_{{\rm{go}}i}} = - 1 + \frac{{R_i^2}}{{\dot R_i^2}}\dot \theta _{{\rm{L}}i}^2 + \frac{{R_i^2}}{{\dot R_i^2}}\dot \phi _{{\rm{L}}i}^2{\rm{co}}{{\rm{s}}^2}{\theta _{{\rm{L}}i}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{R_i}}}{{\dot R_i^2}}{a_{{\rm{LM}}i}} + {D_{ri}} \end{array} $

（8）

$ \left[ {\begin{array}{*{20}{l}} {{{\ddot \theta }_{{\rm{L}}i}}}\\ {{{\ddot \phi }_{{\rm{L}}i}}} \end{array}} \right] = {\mathit{\boldsymbol{M}}_i} + {\mathit{\boldsymbol{D}}_i} + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{u}}_i} $	（9）

式中：下标i(i=1, 2, …, n)表示第i枚导弹。为了保证所有导弹能够同时击中目标，需要保证n枚导弹制导时间之间的一致性，即通过弹间信息交互，设计合理的控制输入a_LMi使得各导弹的制导时间t_goi保持一致。

为了方便对式(8)进行制导律设计，引入新的变量：

$ {\tilde a_{{\rm{LM}}i}} = \frac{{R_i^2}}{{\dot R_i^2}}\dot \theta _{{\rm{L}}i}^2 + \frac{{R_i^2}}{{\dot R_i^2}}\dot \phi _{{\rm{L}}i}^2{\rm{co}}{{\rm{s}}^2}{\theta _{{\rm{L}}i}} - \frac{{{R_i}}}{{\dot R_i^2}}{a_{{\rm{LM}}i}} $	（10）

将式(10)代入式(8)可以得到形式上更加简单的多导弹协同三维制导模型，其中$ \widetilde{a}_{\mathrm{LM}i}$为式(11)新的控制输入：

$ {{{\dot t}_{{\rm{go}}i}} = - 1 + {{\tilde a}_{{\rm{LM}}i}} + {D_{ri}}} $	（11）

$ {\left[ {\begin{array}{*{20}{c}} {{{\ddot \theta }_{{\rm{L}}i}}}\\ {{{\ddot \phi }_{{\rm{L}}i}}} \end{array}} \right] = {\mathit{\boldsymbol{M}}_i} + {\mathit{\boldsymbol{D}}_i} + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{u}}_i}} $	（12）

注1  在实际场景中，受到导弹和目标自身尺寸限制以及导弹战斗部的影响，当R=R₀≠0，但是R₀为较小的正的常值时，即属于区域[R_min, R_max]=[0.1, 0.25] m时，导弹即能够成功拦截目标，且视线角θ_Li不为90°，则可以保证系数矩阵B_i是可逆的。

假设1  设目标机动引起的外部干扰D_ri和D_i及D_ri的导数$\dot{D}_{r i} $是有界的，即存在正的常数d_ri、m_ri、ε_1i和ε_2i，使得|D_ri|≤d_ri，$ \left|\dot{D}_{r i}\right|<m_{r}$，|d_1i|≤ε_1i以及|d_2i|≤ε_2i成立。本文中，D_ri和D_i及D_ri的导数$\dot{D}_{r i} $是有界的，但其上界的具体数值是未知的。

引理1^[24]  针对非线性系统：

$ \dot z = f(z,t)\;\:z \in {\bf{R}} $	（13）

假设存在一个连续、正定且径向无界的函数：

$ \dot V(z) \le - \mu V(z) - \lambda {V^\alpha }(z) $	（14）

式中：μ、λ>0且0 < α < 1是常数，那么原点为非线性系统式(14)的全局且有限时间稳定的平衡点。z(t₀)=z₀，t₀是初始时刻，那么系统状态趋近平衡点的时间为

$ T \le \frac{1}{{\mu (1 - \alpha )}}{\rm{ln}}\frac{{\mu {V^{1 - \alpha }}({z_0}) + \lambda }}{\lambda } $	（15）

本节给出了视线坐标系下多枚导弹拦截同一目标的相对运动学方程式(11)和式(12)，接下来将通过对视线方向上的控制输入$\widetilde{a}_{\mathrm{LM}i} $进行设计来保证各枚导弹的剩余时间t_goi达到一致。另一方面通过对视线法向上的控制输入u_i进行设计，使得各枚导弹以不同的期望的视线角攻击目标，这在一定程度上能够避免导弹间在末制导段碰撞，并且发挥各枚导弹最大毁伤能力。

另一方面，多智能体之间的通讯网络通常由无向图或者有向图来表示，在该文中用无向图G=(v, ζ, A)来表示多枚导弹之间的通信关系，其中v是由无向图中所有的节点组成的集合，即本文的n枚导弹，ζ表示节点之间的连线，也就是n枚导弹之间的通信关系，A=[A_ij]∈R^n×n为权重系数矩阵，如果导弹i与导弹j之间能够进行信息通信，则A_ij=1，不能够通信则为A_ij=0。在无向图中A_ij=A_ji。如果任意两个导弹之间均能找到一条线路使得两个导弹之间可以进行信息交互，则该无向连通图是连通的。

在设计有限时间协同制导律之前，首先给出有关多智能体一致性的相关引理。

引理2^[25]  针对某一阶多智能体系统：

$ {\dot x_i} = {u_i} $	（16）

式中：x_i为智能体i的状态；u_i为相应的控制输入。在其通信拓扑结构图G无向且连通时，如果控制输入为

$ {u_i} = {\rm{sgn}}(\sum\limits_{j = 1}^n {{c_{ij}}} ({x_j} - {x_i}))|\sum\limits_{j = 1}^n {{c_{ij}}} ({x_j} - {x_i})){|^{{\delta _i}}} $	（17）

式中：0 < δ_i < 1。则可以保证系统状态x_i可以在有限时间内趋于一致。

2 三维协同制导律设计

在连通的无向通信拓扑图G=(v, ζ, A)以及一致性原理的基础上，设计了有限时间稳定的滑模制导律，并通过李雅普诺夫稳定性理论给出了严格的理论证明。

2.1 视线方向上的协同制导律设计

针对系统模型式(11)，基于积分滑模理论以及选取合适的趋近律，设计了新的有限时间一致性制导律$\widetilde{a}_{\mathrm{LM} i} $，从而保证所有的导弹的剩余拦截制导时间趋于一致。并且通过选取了合理的自适应律进行在线实时的估计未知上界的系统干扰。

令t为当前时刻，t_goi(i=1, 2, …, n)为第i枚导弹拦截目标的剩余时间，则t时刻，第i枚导弹拦截目标的预测时刻为

$ {t_{{\rm{f}}i}} = t + {t_{{\rm{go}}i}} $	（18）

又由于t_goj-t_goi=t_fj-t_fi，所以保证t_fi趋于一致可以保证t_goi达到一致。

对t_fi求导可得：

$ {\dot t_{{\rm{f}}i}} = {\tilde a_{{\rm{M}}ri}} + {d_{ri}} $	（19）

接下来的设计目的即是通过设计$ \widetilde{a}_{\mathrm{M}ri}$，从而保证t_fi趋于一致。在文献[21]的启发下，选取式(20)所示的积分滑模面：

$ \begin{array}{l} s = {t_{{\rm{f}}i}} - {t_{{\rm{f}}i}}(0) + \int_0^t {\left( { - {{\left| {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}}))} \right|}^{{\delta _i}}} \cdot } \right.} \\ \left. { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sign}} \left( {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}})} \right)} \right){\rm{d}}\tau \end{array} $

（20）

式中：t_fi(0)为t_fi的初始值。

基于式(20)，针对式(19)，设计了有限时间收敛的制导律，从而保证有限时间内t_fi达到一致。所设计的制导律为

$ \begin{array}{*{20}{l}} {{{\tilde a}_{{\rm{M}}ri}} = {{\left| {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}}))} \right|}^{{\delta _i}}} {\rm{sign}} \left( {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}})} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {l_i}s - {\omega _i} {\rm{sign}} (s)} \end{array} $

（21）

$ {\dot \omega _i} = - ({\gamma _{0i}} + {\gamma _i}) {\rm{sign}} ({\omega _i} - \frac{{|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}|}}{{{k_{1i}}}} - {k_{2i}}) $	（22）

$ {{{\dot {\tilde s}}_{{\rm{eq}}}} = - \frac{1}{{{T_0}}}{{\tilde s}_{{\rm{eq}}}} + \frac{1}{{{T_0}}} {\rm{sign}} (s)} $	（23）

$ {{{\dot \gamma }_i} = {k_{3i}}\left| {{\omega _i} - \frac{{|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}|}}{{{k_{1i}}}} - {k_{2i}}} \right|} $	（24）

式中：l_i>0；δ_i满足引理1；并且0 < k_1i < 1，k_2i>0，k_3i>0，γ_0i>0；T₀为时间常数，其数值可以选取为充分小的正的常数，则有$\left|\tilde{s}_{\mathrm{eq}}-[\operatorname{sign}(s)]_{\mathrm{eq}}\right| \leqslant O\left(T_{0}\right) \underset{T_{0} \rightarrow 0}{\longrightarrow} 0 $。

注2  在自适应律式(22)~式(24)中，k_is_i可以加快滑模面的收敛速率。ω_isign(s_i)结合自适应律式(22)~式(24)可以补偿未知上界的系统干扰，在式(21)中，其系数ω_i是随着干扰的大小变化而变化的，因此可以一定程度上削弱抖振现象。此外，该趋近律适用范围广泛，在滑模制导律中普遍使用。

定理1  针对视线方向上的弹目相对运动学模型式(11)，选择式(20)作为滑模面，选择式(21)~式(24)为制导律，则各枚导弹拦截目标的制导剩余时间能够保持一致。

证明  由于运动学模型式(11)中的误差D_ri及其导数$\dot{D}_{ri} $是有界的，即存在常数d_ri和m_ri使得|D_ri|≤d_ri以及$\left|\dot{D}_{r i}\right|<m_{r i} $。为了便于制导律设计，定义$\delta=\frac{m_{r i}}{k_{1 i}}-\gamma_{i} $。假设：

$ \vartheta = {\omega _i} - \frac{{|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}|}}{{{k_{1i}}}} - {k_{2i}} $	（25）

考虑新的李雅普诺夫函数，其形式为

$ {V_1} = \frac{1}{2}{\vartheta ^2} + \frac{1}{{2{k_{3i}}}}{\delta ^2} $	（26）

对V₁求导可得：

$ \begin{array}{l} {{\dot V}_1} = \vartheta \dot \vartheta + \frac{1}{{{k_{3i}}}}\delta \dot \delta = \vartheta ({{\dot \omega }_i} - \frac{1}{{{k_{1i}}}}{(|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}|)^\prime }) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta |\vartheta | \le - \vartheta ({\gamma _{0i}} + {\gamma _i}) {\rm{sign}} (\vartheta ) + |\vartheta |\frac{{{m_i}}}{{{k_{1i}}}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta |\vartheta | = ( - {\gamma _{0i}} + \delta )|\vartheta | - \delta |\vartheta | \le 0 \end{array} $

（27）

从不等式(27)可以得出变量ϑ和δ均是有界的，同时，ω_i和γ_i也是有界的。基于拉塞尔不变原理，ϑ_i可以渐近收敛到零，因此，一个有限时间t₀是存在的，使得$ |\vartheta|<\frac{k_{2 i}}{4}$，则：

$ {\omega _i} - \frac{{|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}|}}{{{k_{1i}}}} - {k_{2i}} > - \frac{{{k_{2i}}}}{4} $	（28）

对于任意的t>t₀，有：

$ \begin{array}{*{20}{l}} {{\omega _i} > |{\omega _i}||{{\tilde s}_{{\rm{eq}}}}| + \frac{{1 - {k_{1i}}}}{{{k_{1i}}}}|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}| + \frac{{3{k_{2i}}}}{4} > }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |{d_{ri}}| + \frac{{1 - {k_{1i}}}}{{{k_{1i}}}}|{\omega _i}||{{\tilde s}_{{\rm{eq}}}}| + \frac{{3{k_{2i}}}}{4} > |{d_{ri}}|} \end{array} $

（29）

考虑另外一个李雅普诺夫函数，具体形式为

$ {V_2} = \frac{1}{2}{s^2} $	（30）

对V₂求导可得：

$ \begin{array}{l} {{\dot V}_2} = \dot s\dot s = s({{\tilde a}_{{\rm{LM}}i}} + {D_{ri}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left| {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}})} \right|^{{\delta _i}}} {\rm{sign}} \left( {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}})} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {s( - {l_i}s - {\omega _i} {\rm{sign}} (s) + {D_{ri}}) \le |s||{D_{ri}}| - }\\ {{\omega _i}|s| - {l_i}{s^2} \le - |s|({\omega _i} - {d_{ri}}) - {l_i}{s^2} \le }\\ { - \sqrt 2 ({\omega _i} - {d_{ri}})V_2^{\frac{{\rm{1}}}{{\rm{2}}}} - 2{l_i}{V_2}} \end{array} \end{array} $

（31）

根据引理1，滑模面s可以在有限时间内收敛到零，则也可以在有限时间内收敛到0，则：

$ {\dot t_{{\rm{f}}i}} = - {\left| {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}}))} \right|^{{\delta _i}}} {\rm{sign}} \left( {\sum\limits_{j = 1}^n {{c_{ij}}} ({t_{{\rm{f}}j}} - {t_{{\rm{f}}i}})} \right) $	（32）

根据引理2，t_fi可以在有限时间内趋于一致。定理1得证。

2.2 视线法向上的视线角约束制导律

2.1节设计了制导律$\widetilde{a}_{\mathrm{M}ri} $，保证有限时间内各导弹的剩余制导时间t_goi达到一致。为了保证各导弹能够以期望的视线角拦截目标，针对系统式(12)设计了有限时间视线角约束制导律。

主要设计目的是提出合理的三维制导律使得各个导弹均能够以各自期望的角度拦截目标。令第i枚导弹期望的视线角为$\left[\begin{array}{l} \theta_{\mathrm{Lf}i} \\ \phi_{\mathrm{Lf} i} \end{array}\right] $，则视线角误差为$\boldsymbol{x}_{i}=\left[\begin{array}{l} x_{1 i} \\ x_{2 i} \end{array}\right]=\left[\begin{array}{l} \theta_{\mathrm{L} i}-\theta_{\mathrm{Lf} {i}} \\ \phi_{\mathrm{L}{i}}-\phi_{\mathrm{Lf} i} \end{array}\right] $。采用终端滑模控制原理进行制导律设计，首先选择合适的滑模面，即三维快速非奇异终端滑模面，具体形式为

$ {\mathit{\boldsymbol{\sigma }} = \left[ {\begin{array}{*{20}{l}} {{\sigma _1}}\\ {{\sigma _2}} \end{array}} \right] = {{\mathit{\boldsymbol{\dot x}}}_i} + {\varphi _i}{\mathit{\boldsymbol{x}}_i} + {\beta _i}\mathit{\boldsymbol{f}}({\mathit{\boldsymbol{x}}_i})} $	（33）

$ {\mathit{\boldsymbol{f}}({\mathit{\boldsymbol{x}}_i}) = \left[ {\begin{array}{*{20}{l}} {f({x_{1i}})}\\ {f({x_{2i}})} \end{array}} \right]} $	（34）

$ f({x_{ji}}) = \left\{ {\begin{array}{*{20}{l}} {{r_{1i}}{x_{ji}} + {r_{2i}}x_{ji}^2 {\rm{sign}} ({x_{ji}})}&{|{x_{ji}}| < {\eta _i}}\\ {|{x_{ji}}{|^{{r_i}}} {\rm{sign}} ({x_{ji}})}&{j = 1,2} \end{array}} \right. $	（35）

$ {{r_{1i}} = (2 - {r_i})\eta _i^{r_i^{ - 1}}} $	（36）

$ {{r_{2i}} = ({r_i} - 1)\eta _i^{{r_i} - 2}} $	（37）

式中：r_i、η_i、β_i和φ_i为待设计的正的常值，并且0 < r_i < 1。对滑模面σ进行求导可得：

$ \begin{array}{l} \mathit{\boldsymbol{\dot \sigma }} = {{\mathit{\boldsymbol{\ddot x}}}_i} + {\varphi _i}{{\mathit{\boldsymbol{\dot x}}}_i} + {\beta _i}\mathit{\boldsymbol{\dot f}}({\mathit{\boldsymbol{x}}_i}) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} {{{\ddot \theta }_{{\rm{L}}i}}}\\ {{{\ddot \phi }_{{\rm{L}}i}}} \end{array}} \right] + {\phi _i}\left[ {\begin{array}{*{20}{l}} {{{\dot \theta }_{{\rm{L}}i}}}\\ {{{\dot \phi }_{{\rm{L}}i}}} \end{array}} \right] + {\beta _i}\mathit{\boldsymbol{\dot f}}({\mathit{\boldsymbol{x}}_i}) = }\\ {{\mathit{\boldsymbol{M}}_i} + {\mathit{\boldsymbol{D}}_i} + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{u}}_i} + {\mathit{\boldsymbol{G}}_i}} \end{array} \end{array} $

（38）

式中：

$ {{\mathit{\boldsymbol{G}}_i} = {\varphi _i}\left[ {\begin{array}{*{20}{l}} {{{\dot \theta }_{Li}}}\\ {{{\dot \phi }_{{\rm{L}}i}}} \end{array}} \right] + {\beta _i}\mathit{\boldsymbol{\dot f}}({\mathit{\boldsymbol{x}}_i})} $	（39）

$ {\mathit{\boldsymbol{\dot f}}({\mathit{\boldsymbol{x}}_i}) = \left[ {\begin{array}{*{20}{l}} {\dot f({x_{1i}})}\\ {\dot f({x_{2i}})} \end{array}} \right]} $	（40）

$ \dot f({x_{ji}}) = \left\{ {\begin{array}{*{20}{c}} {{r_{1i}}{{\dot x}_{ji}} + 2{r_{2i}}{x_{ji}}{{\dot x}_{ji}} {\rm{sign}} ({x_{ji}})}&{|{x_{ji}}| < {\eta _i}}\\ {{r_i}|{x_{ji}}{|^{{r_i} - 1}}{{\dot x}_{ji}}}&{j = 1,2} \end{array}} \right. $	（41）

$ {\mathit{\boldsymbol{M}}_i} = \left[ {\begin{array}{*{20}{c}} { - \frac{{2{{\dot R}_i}}}{{{R_i}}}{{\dot \theta }_{{\rm{L}}i}} - \dot \phi _{{\rm{L}}i}^2{\rm{sin}}{\theta _{{\rm{L}}i}}{\rm{cos}}{\theta _{{\rm{L}}i}}}\\ { - \frac{{2{{\dot R}_i}}}{{{R_i}}}{{\dot \phi }_{{\rm{L}}i}} + 2{{\dot \theta }_{{\rm{L}}i}}{{\dot \phi }_{{\rm{L}}i}}{\rm{tan}}{\theta _{{\rm{L}}i}}} \end{array}} \right] $

$ {\mathit{\boldsymbol{B}}_i} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{R_i}}}}&0\\ 0&{\frac{1}{{{R_i}{\rm{cos}}{\theta _{{\rm{L}}i}}}}} \end{array}} \right],{\mathit{\boldsymbol{u}}_i} = \left[ {\begin{array}{*{20}{c}} {{a_{{\rm{ZM}}i}}}\\ {{a_{{\rm{YM}}i}}} \end{array}} \right] $

$ {\mathit{\boldsymbol{D}}_i} = \left[ {\begin{array}{*{20}{c}} {{d_{1i}}}\\ {{d_{2i}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{a_{{\rm{YT}}i}}}}{{{R_i}}}}\\ { - \frac{{{a_{{\rm{ZT}}i}}}}{{{R_i}{\rm{cos}}{\theta _{{\rm{L}}i}}}}} \end{array}} \right] $

为了保证滑模面式(33)快速收敛，并且削弱传统趋近律引入的抖振现象，设计了新的趋近律：

$ \mathit{\boldsymbol{\dot \sigma }} = - {k_i} {\rm{sig}} {(\mathit{\boldsymbol{\sigma }})^{{a_i}}} - {\mathit{\boldsymbol{Q}}_i}({\alpha _i}{\mathit{\boldsymbol{y}}_i} + {\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }})) $	（42）

$ \begin{array}{l} {{\mathit{\boldsymbol{\dot y}}}_i} = \left[ {\begin{array}{*{20}{l}} {{{\dot y}_{1i}}}\\ {{{\dot y}_{2i}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\frac{1}{{{\alpha _i}}}|{s_{1i}}| - {c_i}{y_{1i}}}\\ {\frac{1}{{{\alpha _i}}}|{s_{2i}}| - {c_i}{y_{2i}}} \end{array}} \right]\\ {y_{ji}}(0) > 0,j = 1,2 \end{array} $	（43）

$ {{\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }}) = \left[ {\begin{array}{*{20}{l}} {{\gamma _{0i}}({{\rm{e}}^{{\gamma _{1i}}|{s_{1i}}{|^{{p_i}}}}} - {\gamma _{2i}})}\\ {{\gamma _{00i}}({{\rm{e}}^{{\gamma _{1i}}|{s_{2i}}{|^{{p_i}}}}} - {\gamma _{2i}})} \end{array}} \right]} $	（44）

$ {{\mathit{\boldsymbol{Q}}_i} = \left[ {\begin{array}{*{20}{c}} { {\rm{sign}} ({s_{1i}})}&0\\ 0&{ {\rm{sign}} ({s_{2i}})} \end{array}} \right]} $	（45）

式中：k_i>0，γ_0i、γ_00i和γ_1i是正的常数，并且1>γ_2i>0以及α_i>1；p_i为正的常数。

注3  自适应律式(42)~式(45)中-k_isig(σ)^a_i可以辅助加快滑模面的收敛速度，-Q_i(α_iy_i+M_i(σ))可以有效地削弱由滑模制导律中由符号函数引起的抖振现象。具体的，积分项式(43)可以补偿系统内未知上界的外部扰动，促使滑模面在有限时间内收敛到滑动面。指数项式(44)是一个足够大的增益，当系统状态远离滑模面时，可以缩短补偿扰动的时间，即该项可以加速系统对扰动的响应，并且随着滑模面收敛到零，该项的数值递减直至为零，补偿增益随之降低。也就是说，这种方法可以减少不必要的抖振。

结合所选取的滑模面以及所设计的趋近律式(42)~式(45)，设计了多弹拦截机动目标的视线角约束制导律：

$ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_{1i}} = - \mathit{\boldsymbol{B}}_i^{ - 1}[{\mathit{\boldsymbol{M}}_i} + {\mathit{\boldsymbol{G}}_i} + {k_i} {\rm{sig}} {{(\mathit{\boldsymbol{\sigma }})}^a} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{Q}}_i}({\alpha _i}{\mathit{\boldsymbol{y}}_i} + {\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }}))]} \end{array} $

（46）

定理2  考虑系统式(12)，假设外部干扰D_i是有界的，如果选择式(33)~式(37)作为滑模面，选择式(46)作为制导律，则有以下结论成立：

1) 滑模面σ在有限时间收敛到区域||σ||≤Ω：

$ \varOmega = \sqrt 2 {\left[ {\frac{{{\delta _4}}}{{(1 - {\theta _1}){\delta _3}}}} \right]^{1/(1 + {a_i})}} $	（47）

式中：$ \delta_{1} \geqslant \frac{1}{2} ; \delta_{2} \geqslant 0;$$\delta_{4}=c_{i} \frac{2 \delta_{1}-1}{\delta_{1}} \delta_{2}+\frac{\delta_{1} c_{i}}{2} \boldsymbol{\varepsilon}_{i}^{\mathrm{T}}\cdot \boldsymbol{\varepsilon}_{i}>0$。

2) 视线跟踪角误差θ_Li-θ_Lfi和ϕ_Li-ϕ_Lfi在有限时间内收敛到区域θ_Li-θ_Lfi≤Ω₁和|ϕ_Li-ϕ_Lfi|≤Ω₁，这里Ω₁是充分小的正的常数。

$ {\varOmega _1} = {\rm{max}}\left\{ {{\eta _i},{\rm{min}}\left\{ {{{\left( {\frac{\varOmega }{{{\varphi _i}}}} \right)}^{\frac{1}{2}}},{{\left( {\frac{\varOmega }{{{\lambda _i}}}} \right)}^{\frac{1}{2}}}} \right\}} \right\} $	（48）

3) 视线角速率$ \dot{\theta}_{\mathrm{L} i}$和$ \dot{\phi}_{\mathrm{L}i}$在有限时间内收敛到区域$\left|\dot{\theta}_{\mathrm{L}{i}}\right|<\varOmega_{2} $和$\left|\dot{\phi}_{\mathrm{L}{i}}\right|<\varOmega_{2} $。

$ {\varOmega _2} = {\varphi _i}{\varOmega _1} + {\lambda _i}\varOmega _1^r + \varOmega $	（49）

证明：假设|d_1i|≤ε_1i以及|d_2i|≤ε_2i，那么$ \boldsymbol{\varepsilon}_{i}=\left[\begin{array}{l} \varepsilon_{1 i} \\ \varepsilon_{2 i} \end{array}\right]$。选择式(50)所示的李雅普诺夫函数：

$ {V_3} = \frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }} + \frac{1}{2}{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i}) $	（50）

对V₃进行求导可得：

$ \begin{array}{l} \begin{array}{*{20}{l}} {{{\dot V}_3} = {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }} - {{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}{{\mathit{\boldsymbol{\dot y}}}_i} = {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}[{\mathit{\boldsymbol{D}}_i} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_i} {\rm{sig}} {{(\mathit{\boldsymbol{\sigma }})}^{{a_i}}} - {\mathit{\boldsymbol{Q}}_i}({\alpha _i}{\mathit{\boldsymbol{y}}_i} + {\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }}))] - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _i}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}\left( {\frac{1}{{{\alpha _i}}}\left\| \mathit{\boldsymbol{\sigma }} \right\| - {c_i}{\mathit{\boldsymbol{y}}_i}} \right) \le } \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {k_i}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}} {\rm{sig}} {{(\mathit{\boldsymbol{\sigma }})}^a} + \sum\limits_{j = 1}^2 | {s_{ji}}|{\varepsilon _{ji}} - {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_i}(\alpha {\mathit{\boldsymbol{y}}_i} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }})) - {\alpha _i}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}(\frac{1}{{{\alpha _i}}}\left\| \mathit{\boldsymbol{\sigma }} \right\| - {c_i}{\mathit{\boldsymbol{y}}_i}) \le } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\kern 1pt} - {k_i}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}} {\rm{sig}} {{(\mathit{\boldsymbol{\sigma }})}^{{a_i}}} - {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_i}{\mathit{\boldsymbol{M}}_i}(\mathit{\boldsymbol{\sigma }}) + {\alpha _i}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}} \cdot }\\ \begin{array}{l} {c_i}{\mathit{\boldsymbol{y}}_i} \le - {k_i}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}} {\rm{sig}} {(\mathit{\boldsymbol{\sigma }})^{{a_i}}} - {\rm{min}}({\gamma _{0i}}({{\rm{e}}^{{\gamma _{1i}}|{s_{1i}}{|^{{p_i}}}}} - \\ \begin{array}{*{20}{l}} {{\gamma _{2i}}),{\gamma _{00i}}({{\rm{e}}^{{\gamma _{1i}}|{s_{2i}}{|^{{p_i}}}}} - {\gamma _{2i}}))\left\| \mathit{\boldsymbol{\sigma }} \right\| + {\alpha _i}({\mathit{\boldsymbol{\varepsilon }}_i} - }\\ {{\alpha _i}{\mathit{\boldsymbol{y}}_i}{)^{\rm{T}}}{c_i}{\mathit{\boldsymbol{y}}_i} \le - {2^{(1 + {a_i})/2}}{k_i}{{\left( {\frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)}^{(1 + {a_i})/2}}} \end{array}\\ {c_i}{\alpha _i}{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} \end{array} \end{array} \end{array} $

（51）

对任意的$\delta_{1} \geqslant \frac{1}{2} $存在：

$ \begin{array}{l} {\alpha _i}{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} = - {({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\varepsilon }}_i}) \le \\ - \frac{{2{\delta _1} - 1}}{{2{\delta _1}}}{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i}) + \frac{{{\delta _1}}}{2}\mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_i} \end{array} $

（52）

则：

$ \begin{array}{l} {{\dot V}_3} \le - {2^{(1 + {a_i})/2}}{k_i}{\left( {\frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)^{(1 + {a_i})/2}} - {c_i}\frac{{2{\delta _1} - 1}}{{2{\delta _1}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i}) + \frac{{{\delta _1}{c_i}}}{2}\mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_i} = }\\ \begin{array}{l} - {2^{(1 + {a_i})/2}}{k_i}{\left( {\frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)^{(1 + {a_i})/2}} - {c_i}\frac{{2{\delta _1} - 1}}{{{\delta _1}}} \cdot \\ \begin{array}{*{20}{l}} {{{\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})} \right]}^{(1 + {a_i})/2}} + {c_i}\frac{{2{\delta _1} - 1}}{{{\delta _1}}} \cdot }\\ \begin{array}{l} \left\{ {{{\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})} \right]}^{(1 + {a_i})/2}} - } \right.\\ \left. {\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})} \right]} \right\} + \frac{{{\delta _1}{c_i}}}{2}\mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_i} \end{array} \end{array} \end{array} \end{array} \end{array} $

（53）

如果$ \frac{1}{2}\left(\boldsymbol{\varepsilon}_{i}-\alpha_{i} \boldsymbol{y}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{\varepsilon}_{i}-\alpha_{i} \boldsymbol{y}_{i}\right) \geqslant 1$，则有：

$ \begin{array}{l} {\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})} \right]^{(1 + {a_i})/2}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})} \right] \le 0 \end{array} $

（54）

如果$\frac{1}{2}\left(\boldsymbol{\varepsilon}_{i}-\alpha_{i} \boldsymbol{y}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{\varepsilon}_{i}-\alpha_{i} \boldsymbol{y}_{i}\right)<1 $，则存在正常数δ₂使得：

$ {\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})} \right] \le {\delta _2}} $	（55）

综合以上两种情况，则有：

$ \begin{array}{l} {\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})} \right]^{(1 + {a_i})/2}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\alpha _i}{\mathit{\boldsymbol{y}}_i})} \right] \le {\delta _2} \end{array} $

（56）

把式(56)代入到式(51)并化简得到：

$ \begin{array}{*{20}{l}} {{{\dot V}_3} \le - {\delta _3}{{\left( {\frac{1}{2}\mathit{\boldsymbol{\sigma }}_i^{\rm{T}}{\mathit{\boldsymbol{\sigma }}_i}} \right)}^{(1 + {a_i})/2}} - {\delta _3} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left[ {\frac{1}{2}{{({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})}^{\rm{T}}}({\mathit{\boldsymbol{\varepsilon }}_i} - {\mathit{\boldsymbol{y}}_i})} \right]}^{(1 + {a_i})/2}} + {c_i}\frac{{2{\delta _1} - 1}}{{{\delta _1}}}{\delta _2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\delta _1}{c_i}}}{2}\mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_i} \le - {\delta _3}V_3^{(1 + {a_i})/2} + {\delta _4}} \end{array} $

（57）

式中：$ \delta_{3}=\min \left\{2^{\left(1+a_{i}\right) / 2} k_{i}, c_{i} \frac{2 \delta_{1}-1}{\delta_{1}}\right\} ; \delta_{4}=c_{i}\cdot \frac{2 \delta_{1}-1}{\delta_{1}} \delta_{2}+\frac{\delta_{1} c_{i}}{2} \boldsymbol{\varepsilon}_{i}^{\mathrm{T}} \boldsymbol{\varepsilon}_{i}>0$。

由式(57)可知系统为实际有限时间稳定，即存在正常数θ₁∈(0, 1)，使得滑模变量在有限时间T内收敛到集合D_S内，且T和D_S的满足如下条件：

$ {T \le \frac{{2V_{3,t = 0}^{(1 - {a_j})/2}}}{{{\delta _3}{\theta _1}(1 - {a_i})}}} $

$ {{D_S} = \left\{ {\mathit{\boldsymbol{\sigma }}:\left\| \mathit{\boldsymbol{\sigma }} \right\| \le \sqrt 2 {{\left[ {\frac{{{\delta _4}}}{{(1 - {\theta _1}){\delta _3}}}} \right]}^{1/(1 + {a_i})}}} \right\}} $

式中：V_{3, t=0}表示V₃的初始值。结论1)得证。

情况1：由式(35)可知，若|x_ji|≥η_i, j=1, 2，$s_{j i}=\dot{x}_{j i}+\varphi_{i} x_{j i}+\beta_{1 i}\left|x_{j i}\right| r_{i} \operatorname{sign}\left(x_{j i}\right) $，考虑另一个如式(58)所示的李雅普诺夫函数：

$ {V_4} = x_{ji}^2 $	（58）

对V₄求导可得：

$ \begin{array}{*{20}{l}} {{{\dot V}_4} = {x_{ji}}{{\dot x}_{ji}} = - {x_{ji}}({\varphi _i}{x_{ji}} + {\lambda _i}|{x_{ji}}{|^{{r_i}}} {\rm{sign}} ({x_{ji}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_{ji}}) \le - {\varphi _i}x_{ji}^2 - {\lambda _i}{{(x_{ji}^2)}^{\frac{{1 + {r_i}}}{2}}} + |{x_{ji}}{s_{ji}}|} \end{array} $

（59）

不等式(59)可以简化为

$ {{{\dot V}_4} \le - \left( {{\varphi _i} - \left| {\frac{{{s_{ji}}}}{{{x_{ji}}}}} \right|} \right)x_{ji}^2 - {\lambda _i}{{(x_{ji}^2)}^{\frac{{1 + {r_i}}}{2}}}} $	（60）

$ {{{\dot V}_4} \le - {\varphi _i}x_{ji}^2 - \left( {{\lambda _i} - \left| {\frac{{{s_{ji}}}}{{x_{ji}^{{r_i}}}}} \right|} \right){{(x_{ji}^2)}^{\frac{{1 + {r_i}}}{2}}}} $	（61）

如果$ \varphi_{i}-\left|\frac{s_{j i}}{x_{j i}}\right|>0, x_{j i}$在有限时间收敛到区域$\left|x_{j i}\right| \leqslant\left(\frac{\varOmega}{\varphi_{i}}\right)^{\frac{1}{2}} $。如果$ \lambda_{i}-\left|\frac{s_{j i}}{x_{j i}^{r_i}}\right|>0, x_{j i}$在有限时间收敛到区域$ \left|x_{j i}\right| \leqslant\left(\frac{\varOmega}{\lambda_{i}}\right)^{\frac{1}{2}}$。综上所述，x_ji在有限时间收敛到区域：|x_ji|≤Ω₁=$ \max \left\{\eta_{i}, \min \left\{\left(\frac{\varOmega}{\varphi_{i}}\right)^{\frac{1}{2}}, \left(\frac{\varOmega}{\lambda_{i}}\right)^{\frac{1}{2}}\right\}\right\}$。

情况2：如果|x_ji| < η_i, j=1, 2，σ_j=$\dot{x}_{j i} $+φ_ix_ji+β_1if(x_ji)，可以得到：

$ \begin{array}{*{20}{l}} {{{\dot x}_{ji}} = - {\varphi _i}{x_{ji}} - {\lambda _i}f({x_{ji}}) + {\sigma _j}|{{\dot x}_{ji}}| \le |{\varphi _i}{x_{ji}}| + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |{\lambda _i}f({x_{ji}})| + |{\sigma _j}| \le {\varphi _i}{\eta _i} + {\lambda _i}{\eta _i}^{{r_i}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varOmega \le {\varphi _i}{\varOmega _1} + {\lambda _i}\varOmega _1^{{r_i}} + \varOmega } \end{array} $

（62）

则$\dot{x}_{j i} $在有限时间收敛到区域|$ \dot{x}_{j i}$|≤Ω₂=φ_iΩ₁+λ_iΩ₁^r_i+Ω，也就是说，视线角速率$\dot{\theta}_{\mathrm{L}i} $和$\dot{\varphi}_{{\rm L} i} $分别在有限时间内收敛到区域$ \left|\dot{\theta}_{\mathrm{L} i}\right| \leqslant \varOmega_{2}$和$ \left|\dot{\varphi}_{\mathrm{L} i}\right| \leqslant \varOmega_{2}$，那么，结论2)和3)得证。至此，定理2得证。

注4  本文设计了双层协同制导律式(21)与式(46)，制导律式(21)保证各枚导弹同时拦截目标，制导律式(46)可以保证各枚导弹按照不同的视线角拦截目标，在末制导初始时刻给定各枚导弹适合的期望的攻击视线角可以一定程度上保证各枚导弹不会发生碰撞，并且期望的视线角能够发挥各枚导弹最大的毁伤能力。

3 仿真分析

第2节设计了一种新的协同控制算法，并给出了严格的理论证明。针对三枚导弹拦截同一导弹的情况，本节通过数学仿真验证了所设计的制导律的有效性。其中，三枚导弹的通信情况如图 2所示。

首先在表 1中给出模型的初始仿真条件。目标机动大小：a_LT=50sin(0.5t) m/s²；a_YT=50sin(0.5t) m/s²；a_ZT=50cos(0.5t) m/s²。视线方向上的制导律$ \widetilde{a}_{\mathrm{M}ri}$(i=1, 2, 3)中的参数选取如下：l_i=15，δ_i=0.5并且k_1i=0.9，k_2i=0.01，k_3i=1.2，γ_0i=0.3，T₀=0.05。视线法向上的制导律u_1i(i=1, 2, 3)中的参数选取如下：k_i=1，α_i=2，c_i=0.7，γ_0i=3.5，γ_00i=4.2，γ_1i=0.1，并且γ_2i=0.99，以及α_i>1。

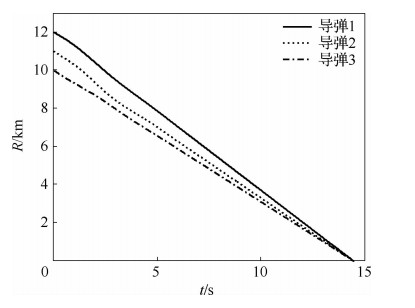
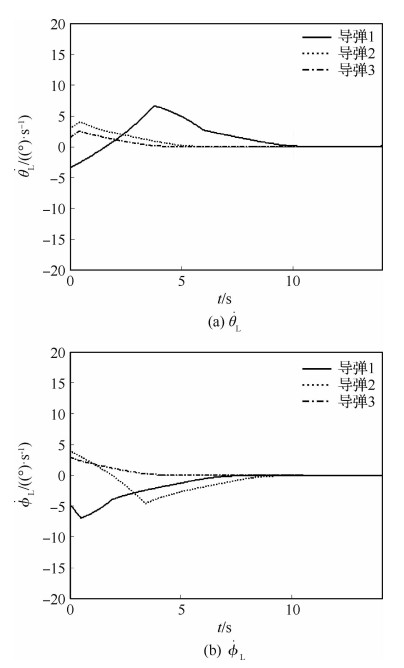
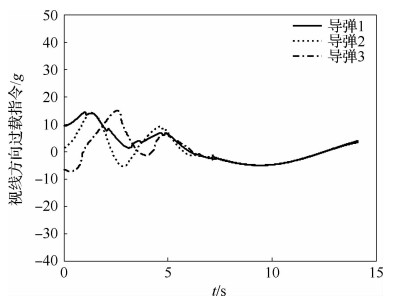
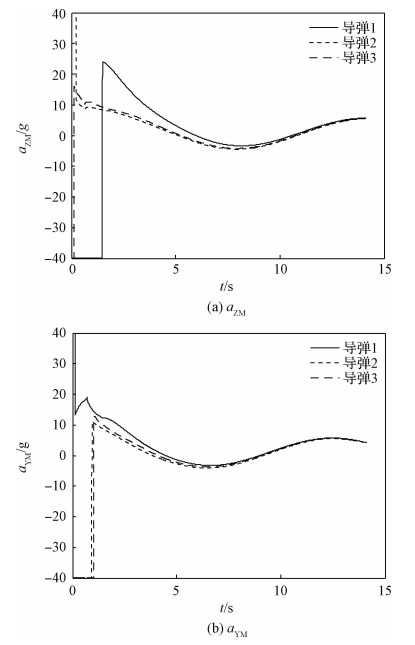
三枚导弹末制导初始位置不同的情况下，采用本文设计的协同制导律，能够保证导弹同时拦截目标，具体数学仿真结果如图 3~图 8所示，图 3给出了三枚导弹的剩余时间，从图中可以看出三枚导弹的剩余时间最终达到一致，图 4给出了弹目视线距离，从图中可以看出三枚导弹同时拦截目标。图 5是视线角随时间变化图，从图中可以看出，三枚导弹视线角速率在有限时间内收敛到零。图 6给出了视线角随时间变化图，从图中可以看出三枚导弹均收敛到了期望的视线角。图 7和图 8给出了导弹过载，图 8是视线法向上的过载，可以看出，视线法向上的过载在末制导开始的前两秒内存在饱和现象，这是由于目标存在5g的机动，并且视线法向方向上的制导律需要保证视线角收敛到期望的数值，但饱和数值在合理范围内，并且饱和现象很快收敛。

文献[20]中, 为了实现攻击时间和落角协同控制，作者设计了超螺旋协同制导律，并用干扰观测器估计目标的机动信息。文献[20]的仿真条件中，初始视线角与期望的视线角最大相差20°，而本文的仿真分析中，初始视线角与期望的视线角也是最大相差20°，对比文献[20]中的剩余时间变化曲线图Fig. 3(c)与本文的图 5~图 6，本文的视线角速率与视线角收敛更快。此外，文献[22]中，基于二阶终端滑模设计了协同制导律，在该文献的仿真分析中，三枚导弹的初始剩余时间最大相差大约8 s，初始视线角与期望的视线角最大相差10°，而本文仿真条件中，三枚导弹的初始剩余时间最大相差超过8 s，初始视线角与期望的视线角最大相差20°，对比文献[22]中的剩余时间变化曲线图Fig. 2(a)与本文的图 3可以看出，本文所设计的制导律能够保证剩余时间快速收敛，对比文献[22]中的Fig. 3(a)和Fig. 3(b)与本文的图 5和图 6相比，本文的视线角速率与视线角收敛更快。并且这两篇论文的制导律中仍然存在符号函数项，传统的方法通常是由连续的饱和函数sat(·)来代替，但符号函数会影响收敛精度，从本文的仿真图可以看出不用符号函数的替代依然能够有效的去除抖振现象。

综上所述，数学仿真验证了所设计制导律的有效性及优越性。

4 结论

1) 基于积分滑模法设计了视线方向上的制导律，该制导律保证了所有导弹同时攻击目标。

2) 基于快速非奇异滑模法设计了视线法向上的制导律，该制导律保证了所有导弹以期望的视线角攻击目标。

3) 对所设计的制导律进行了数学仿真实验，仿真结果表明了所设计制导律的有效性及优越性。