2. 中国电子科技集团公司电子科学研究院, 北京 100041
2. China Academy of Electronics and Information Technology, Beijing 100041, China
随着航空技术的快速发展,固定翼无人机在航空领域扮演着越来越重要的角色,固定翼无人机的吸引力及其在实际中的应用在过去的十年间显著地增加。由于固定翼无人机强机动性的特点,使得固定翼无人机在军事、民用和商业领域的应用前景越来越广阔。同时,由于任务的多样性和复杂性,对固定翼无人机的控制性能的要求越来越高,控制性能的好坏极大影响着无人机飞行的安全性和稳定性。
近年来,针对具有强耦合、强非线性以及快速机动性特点的固定翼无人机,国内外的许多研究人员和学者采用多种控制方法开展了对控制问题的相关研究[1]。2016年,上海交通大学的费爱玲等[2]针对固定翼无人机的四元数模型,采用基于扩张观测器的反步法设计了无人机速度控制器和姿态控制器,实现了对无人机速度和姿态的高精度控制。2015年,哈尔滨工程大学的刘一鸣[3]设计了基于反演法的固定翼无人机自适应控制律,并将该方法与智能自适应PID(Proportion Integral Derivative)方法进行了对比,仿真结果表明,文中所提出的自适应控制方法准确性更高。2016年,TOBB大学的Akyurek等[4]采用H∞方法设计了小型固定翼无人机的姿态控制器,提高了无人机控制系统的鲁棒性。2017年,挪威科技大学的Rotondo等[5]采用线性参数变化模型参考方法针对复杂任务环境需求,设计了固定翼无人机控制器。2016年,美国肯塔基大学的Mullen等[6]考虑无人机在姿态跟踪过程中的参数不确定以及风干扰的影响,采用FDI(Filtered Dynamic Inversion)方法针对小型固定翼无人机设计了姿态控制器,并在飞行试验中将该方法与传统的PI(Proportion Integral)方法进行了对比,试验数据表明,采用FDI方法设计的姿态控制器具有更为优越的控制性能。2016年,南洋理工大学的Hervas等[7]针对固定翼无人机在舰船甲板的着陆问题,考虑随机风干扰的影响,采用基于扩张卡尔曼滤波的滑模控制方法的控制策略设计了控制器。2017年,墨西哥机器人和智能系统中心的Castañeda等[8]采用扩张状态观测器对干扰以及未知状态进行了估计,并基于自适应超螺旋算法设计了姿态控制器和速度控制器,保证了系统的有限时间收敛并有效地减弱了滑模算法中的抖振效应。
当前,自适应滑模控制方法[9-14]被广泛应用到航空航天飞行器的控制器设计中[15-20]。本文考虑固定翼无人机实际飞行过程中的未知干扰、执行器饱和以及强耦合的影响,针对无人机姿态控制和速度控制的不同需求,设计一种新型的自适应多变量螺旋滑模姿态控制器和自适应多变量快速超螺旋滑模速度控制器,进而实现了对固定翼无人机姿态和速度的有限时间快速精确跟踪。主要创新点如下: ①文中设计的自适应多变量螺旋和自适应快速超螺旋算法无需预知系统所受干扰及其导数的上界便可实现对系统的精确稳定控制; ②针对典型的二阶姿态模型,采用自适应多变量螺旋滑模设计姿态控制器,自适应律的引入,有效地抑制了抖振; ③文中设计的新型自适应快速超螺旋速度控制器具有收敛速度快,收敛精度高的优点,适用于固定翼无人机对快速机动性的需求。
1 固定翼无人机模型固定翼无人机姿态运动涉及惯性坐标系和机体坐标系等。相关坐标系的关系如图 1所示。

|
| 图 1 固定翼无人机模型坐标系示意图 Fig. 1 Schematic diagram of referential frames configuration of fixed wing UAV model |
假设飞机为刚体模型、地面坐标系为惯性坐标系,固定翼无人机模型为[8]
| $ {\mathit{\boldsymbol{I\dot \omega }} = - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }} + \mathit{\boldsymbol{M}}} $ | (1) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }} = {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \cdot \mathit{\boldsymbol{\omega }}} $ | (2) |
| $ {\mathit{\boldsymbol{\dot v}} = (\mathit{\boldsymbol{F}} + \mathit{\boldsymbol{T}})/m + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{I}}}\mathit{\boldsymbol{g}} - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{v}}} $ | (3) |
| $ {{{\mathit{\boldsymbol{\dot p}}}^n} = {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{I}}}\mathit{\boldsymbol{v}}} $ | (4) |
式中:m为无人机质量;ω=[p q r]T为无人机的角速度,p为滚转角速度,q为俯仰角速度,r为偏航角速度;Θ=[ϕ θ ψ]T为姿态角,ϕ为滚转角,θ为俯仰角,ψ为偏航角;v=[u v w]T为飞行速度,u为无人机机体坐标系x轴方向的速度,v为无人机机体坐标系y轴方向的速度,w为无人机机体坐标系z轴方向的速度;pn=[xg yg h]T为无人机的位置信息;M=[M1 M2 M3]T为调整无人机姿态的控制力矩, 包含滚转M1、俯仰M2和偏航M33个力矩;F∈R3×1和T=[Tx 0 0]T分别为无人机所受的气动力和发动机提供的推力, Tx为沿机体坐标系x方向推力;RΘ∈R3×3,为转换矩阵,I∈R3×3, 为惯性矩阵,RI∈R3×3表示为
| $ {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = \left[ {\begin{array}{*{20}{c}} 0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }\\ 0&{\frac{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }}{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}}&{\frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }}{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}}\\ 1&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi {\kern 1pt} {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right],\mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} {{I_{xx}}}&0&{{I_{xz}}}\\ 0&{{I_{yy}}}&0\\ {{I_{zx}}}&0&{{I_{zz}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{I}}} = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }\\ { - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi } \end{array}} \right] $ |
由于固定翼无人机的推进系统仅能提供沿机体坐标系x轴方向的推力Tx。所以速度控制器基于空速方程式(5)设计。
| $ \begin{array}{*{20}{l}} {m\dot V = {T_x}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} \beta - D - mg[ - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ]} \end{array} $ | (5) |
式中:V为无人机的空速;α=arctan(w/u)和β=arcsin(u/v)分别为迎角和侧滑角; D为阻力。
在固定翼无人机的控制中,设计飞行控制器的目的是精确跟踪航路点指令pdn,而在实际的控制过程中,通常将pdn解析为空速参考指令Vd和Θd,进而,控制设计的目的可转化为精确跟踪参考指令Vd和Θd。本节针对固定翼无人机控制中的强干扰以及输入饱和问题,基于新型自适应多变量螺旋算法设计二阶姿态控制器;基于与速度子系统相关的空速动态方程,采用自适应快速超螺旋算法设计速度控制器,实现对参考指令的有限时间精确跟踪。控制框图如图 2所示。

|
| 图 2 固定翼无人机控制结构图 Fig. 2 Structure of control scheme of fixed wing UAV |
本节针对姿态子系统式(1)和式(2),考虑执行器饱和以及外界干扰Δdω=[Δdω1 Δdω2 Δdω3]T的影响,设计姿态控制器,定义姿态角跟踪误差为
| $ {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} - {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\rm{d}}} $ | (6) |
式中:Θd为姿态参考指令,基于式(2),对式(6)求导得:
| $ {\mathit{\boldsymbol{\dot e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }} - {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}_{\rm{d}}} = {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \cdot \mathit{\boldsymbol{\omega }} - {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}_{\rm{d}}} $ | (7) |
设
| $ {\mathit{\boldsymbol{\dot z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = {\mathit{\boldsymbol{\dot R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \cdot \mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}{\mathit{\boldsymbol{I}}^{ - 1}}( - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }} + \mathit{\boldsymbol{M}} + \Delta {\mathit{\boldsymbol{d}}_\omega }) - {\mathit{\boldsymbol{ \boldsymbol{\ddot \varTheta} }}_{\rm{d}}} $ | (8) |
考虑固定翼无人机输入饱和的影响,式(8)可转化为式(9)的形式
| $ {\mathit{\boldsymbol{\dot z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = {\mathit{\boldsymbol{\dot R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \cdot \mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}{\mathit{\boldsymbol{I}}^{ - 1}}( - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }} + {\bf{sa}}{{\bf{t}}_M} + \Delta {\mathit{\boldsymbol{d}}_\omega }) - {\mathit{\boldsymbol{ \boldsymbol{\ddot \varTheta} }}_{\rm{d}}} $ | (9) |
式中:satM∈R3×1为非线性饱和特性函数。令satM=f+M=[satM1 satM2 satM3]T,其中,f=[f1 f2 f3]T,表达式为
| $ \begin{array}{*{20}{l}} {{f_i}(i = 1,2,3) = }\\ {\;\:\left\{ {\begin{array}{*{20}{c}} { {\rm{sign}} ({M_i}){M_{{\rm{max}}}} - {M_i}}\\ 0 \end{array}\;\:\begin{array}{*{20}{l}} {|{M_i}| \ge {M_{{\rm{max}}}}}\\ {|{M_i}| < {M_{{\rm{max}}}}} \end{array}} \right.} \end{array} $ | (10) |
其中:Mmax为执行机构所允许的最大力矩值,通过式(10)可得:当控制器产生的力矩|Mi|大于Mmax时,satMi=Mmaxsign(Mi), i=1, 2, 3;当控制器产生的力矩|Mi|小于Mmax时,satMi=Mi,通过函数satM∈R3×1将输出的控制力矩限制在了执行器允许的范围内。
通过上述变换,得到姿态子系统的面向控制模型式(11)
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot e}}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}\\ {{{\mathit{\boldsymbol{\dot z}}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = {\mathit{\boldsymbol{G}}_0} + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}{\mathit{\boldsymbol{I}}^{ - 1}}\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{\rho }}} \end{array}} \right. $ | (11) |
式中:G0和ρ分别为
| $ {{\mathit{\boldsymbol{G}}_0} = {{\mathit{\boldsymbol{\dot R}}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \cdot \mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}{\mathit{\boldsymbol{I}}^{ - 1}}( - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }} + \mathit{\boldsymbol{f}}) - {{\mathit{\boldsymbol{ \boldsymbol{\ddot \varTheta} }}}_{\rm{d}}}} $ |
| $ {{\eta _1} = {\rm{min}}\left( {{\eta _0},\frac{{{\alpha _1}}}{{\sqrt {2{\beta _1}} }}} \right)} $ |
||ρ||≤D,D>0且未知。
基于式(11),采用自适应多变量螺旋算法设计姿态控制器如式(12)所示
| $ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{R}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{ - 1}\mathit{\boldsymbol{I}}\left[ { - {\mathit{\boldsymbol{G}}_0} - {k_1}\left( {\frac{{{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}}{{\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}} + 0.5 \times \frac{{{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}}{{\left\| {{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}}} \right)} \right] $ | (12) |
式中:k1>0为自适应增益,满足式(13)中所示的自适应律:
| $ {\dot k_1} = \left\{ {\begin{array}{*{20}{c}} {{\alpha _1}\sqrt {\frac{{{\beta _1}}}{2}} }&{\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\| \ge {\varepsilon _1}}\\ 0&{\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\| < {\varepsilon _1}} \end{array}} \right. $ | (13) |
其中:α1,β1,ε1为大于零的常数。
将姿态控制律式(12)代入式(11)中,得式(14)
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot e}}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}\\ {{{\mathit{\boldsymbol{\dot z}}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} = - {k_1}\left( {\frac{{{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}}{{\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}} + 0.5 \times \frac{{{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}}{{\left\| {{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}}} \right) + \mathit{\boldsymbol{\rho }}} \end{array}} \right. $ | (14) |
定理1 对于姿态子系统式(1)和式(2),在自适应多变量螺旋滑模控制器式(12)和自适应律式(13)的作用下,选取适当的α1、β1和ε1,姿态子系统可实现有限时间稳定,姿态角跟踪误差可以在有限时间内收敛到原点附近的邻域内。
证明 为证明系统在控制器式(12)~式(13)的作用下可以实现有限时间稳定,选择如下的Lyapunov候选函数
| $ {V_1} = \underbrace {\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{Az}} + \frac{1}{4}{{(\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}})}^2}}_{{V_{10}}} + \underbrace {\frac{1}{{{\beta _1}}}{{({k_1} - k_1^*)}^4}}_{{V_{{\rm{1ad}}}}} $ | (15) |
式中:V10和V1ad为组成V1的2个部分,方便后续进行稳定性分析。
对V10进行稳定性分析。由不等式λmin{A}||z||2≤zTAz≤λmax{A}||z||2(λmin{A}为矩阵的A最小特征值,λmax{A}为矩阵A的最大特征值)可得
| $ \begin{array}{*{20}{l}} {{V_{10}} \le \frac{3}{2}{\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{A}}){{\left\| {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}^2} + \frac{1}{2}({\lambda _{{\rm{max}}}}(\mathit{\boldsymbol{A}}) + \frac{1}{2}){{\left\| {{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}} \right\|}^4}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le {\mathit{\boldsymbol{\chi }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{\chi }} \le {\lambda _{{\rm{max}}}}({\mathit{\boldsymbol{P}}_1})({{\left\| {{\mathit{\boldsymbol{e}}_\theta }} \right\|}^2} + {{\left\| {{\mathit{\boldsymbol{z}}_\theta }} \right\|}^4})} \end{array} $ | (16) |
式中:
| $ {\dot V_{10}} \le - \frac{\vartheta }{{{2^{2/3}}\lambda _{{\rm{max}}}^{3/4}\{ {\mathit{\boldsymbol{P}}_1}\} }}V_{10}^{3/4} = - {\eta _0}V_{10}^{3/4} $ | (17) |
式中:
由式(17)可得
| $ {\dot V_1} \le - {\eta _1}V_1^{3/4} + \tilde \omega $ | (18) |
式中:
| $ {\tilde \omega = \left( { - \frac{1}{{4{\beta _1}}}{{\dot k}_1} + \frac{{{\alpha _1}}}{{4\sqrt {2{\beta _1}} }}} \right)|{k_1} - k_1^*{|^3}} $ |
当
| $ {\dot V_1} \le - {\eta _1}V_1^{3/4} $ | (19) |
当自适应增益k1按照式(13)中的自适应律增长到满足k1>2D时,eΘ可在有限时间内收敛到限定区间ε1内。
2.2 速度控制器设计基于式(5),考虑未知外界干扰Δdv的影响,得到空速误差方程:
| $ {\dot e_v} = \dot V - {\dot V_d} = \gamma u + {\varPhi _1} + {\varPhi _2} $ | (20) |
式中:
根据式(20),设计速度控制器为
| $ \left\{ {\begin{array}{*{20}{l}} {u = - \frac{1}{\gamma }{\varPhi _1} - \frac{1}{\gamma }({k_{v1}}{\xi _1}({\mathit{\boldsymbol{e}}_v}) + {z_1})}\\ {{{\dot z}_1} = - {k_{v2}}{\xi _2}({\mathit{\boldsymbol{e}}_v})} \end{array}} \right. $ | (21) |
ξ1(ev)和ξ2(ev)表示如下:
| $ \left\{ \begin{array}{l} {\xi _1}({\mathit{\boldsymbol{e}}_v}) = \frac{{{\mathit{\boldsymbol{e}}_v}}}{{{{\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|}^{1/2}}}} + {k_{v3}}{\mathit{\boldsymbol{e}}_v}\;\:{k_{v3}} > 0\\ {\xi _2}({\mathit{\boldsymbol{e}}_v}) = \frac{{{\rm{d}}{\xi _1}({\mathit{\boldsymbol{e}}_v})}}{{{\rm{d}}{\mathit{\boldsymbol{e}}_v}}}{\xi _1}({\mathit{\boldsymbol{e}}_v}) = \frac{1}{2} \cdot \frac{{{\mathit{\boldsymbol{e}}_v}}}{{\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{3}{2}{k_{v3}}\frac{{{\mathit{\boldsymbol{e}}_v}}}{{{{\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|}^{1/2}}}} + k_{v3}^2{\mathit{\boldsymbol{e}}_v} \end{array} \right. $ | (22) |
kv3>0为固定增益;kv1, kv2为大于0的自适应增益,
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot k}_{v1}} = \left\{ {\begin{array}{*{20}{c}} {{{\bar k}_{v1}} \cdot \left\| {{\mathit{\boldsymbol{e}}_v}} \right\| \cdot {\rm{sign}} (\left\| {{\mathit{\boldsymbol{e}}_v}} \right\| - {\varepsilon _2})}&{{k_{v1}} > \mu }\\ \mu &{{k_{v1}} \le \mu } \end{array}} \right.}\\ {{k_{v2}} = {\eta _v}{k_{v1}}} \end{array}} \right. $ | (23) |
其中:kv1、ε2、μ和ηv均为大于零的常数。
将式(21)代入式(20)可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_v} = - {k_{v1}}{\xi _1}({\mathit{\boldsymbol{e}}_v}) + {z_v}}\\ {{{\dot z}_v} = - {k_{v2}}{\xi _2}({\mathit{\boldsymbol{e}}_v}) + \Delta {{\dot d}_v}} \end{array}} \right. $ | (24) |
定理2 对于速度子系统,在速度控制器式(21)和自适应增益式(23)的作用下,选取合适的参数ε2、kv3、μ、ηv和kv1,速度子系统的跟踪误差ev可以在有限时间内收敛到零。
证明
采用Lyapunov方法对系统式(24)进行稳定性分析,选择Lyapunov候选函数为
| $ {V_2} = \underbrace {{\zeta ^{\rm{T}}}\mathit{\boldsymbol{P \boldsymbol{\varsigma} }}}_{{V_{20}}} + \underbrace {\frac{1}{{2{\gamma _1}}}{{({k_{v1}} - k_{v1}^*)}^2} + \frac{1}{{2{\gamma _2}}}{{({k_{v2}} - k_{v2}^*)}^2}}_{{V_{{\rm{2ad}}}}} $ | (25) |
式中:ς=[ξ1 zv]T,kv1*和kv2*为大于零的常数,
对式(25)求导得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_2} = {{\mathit{\boldsymbol{ \boldsymbol{\dot \varsigma} }}}^{\rm{T}}}\mathit{\boldsymbol{P \boldsymbol{\varsigma} }} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varsigma} }}}^{\rm{T}}}\mathit{\boldsymbol{P \boldsymbol{\varsigma} }} + \frac{1}{{{\gamma _1}}}({k_{v1}} - k_{v1}^*){{\dot k}_{v1}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{{\gamma _2}}}({k_{v2}} - k_{v2}^*){{\dot k}_{v2}}} \end{array} $ | (26) |
设
| $ {\dot V_{20}} = - 2\xi _1^\prime {\mathit{\boldsymbol{ \boldsymbol{\varsigma} }}^{\rm{T}}}\mathit{\boldsymbol{Q\zeta }} $ | (27) |
式中:
| $ {{q_1} = {k_{v1}}{\lambda ^2} + 4{k_{v1}}\varepsilon - \lambda {k_2} = {a_1}{k_{v1}} - \lambda {k_2}} $ |
| $ \begin{array}{l} {q_2} = \frac{1}{2}( - {\lambda ^2} - 4\varepsilon - \lambda {k_{v1}} + {k_2}) = \\ \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2} \cdot ( - {a_1} - \lambda {k_{v1}} + {k_2}) \end{array} $ |
| $ {{q_3} = \lambda } $ |
其中:a1=λ2+4ε0。
若
| $ {k_2} > 0 \Rightarrow {k_{v2}} > 2\bar \delta \;\:{k_{v1}} > \lambda $ | (28) |
k2的取值范围为
| $ {{k}_{2}}\in [{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}}_{2}},{{\bar{k}}_{2}}]=[{{k}_{v2}}-2\bar{\delta },{{k}_{v2}}+2\bar{\delta }] $ | (29) |
设
| $ {{k}_{v1}}=\lambda +\tau \ \;\tau >0 $ | (30) |
方程det[Q]=0的解为
| $ \left\{ \begin{array}{*{35}{l}} p_{1}^{+}=\lambda {{k}_{v1}}+{{k}_{2}}+2\sqrt{\lambda {{k}_{2}}({{k}_{v1}}-\lambda )} \\ p_{1}^{-}=\lambda {{k}_{v1}}+{{k}_{2}}-2\sqrt{\lambda {{k}_{2}}({{k}_{v1}}-\lambda )} \\ \end{array} \right. $ | (31) |
当p1∈(p1max-, p1min+)时,det[Q]>0。为保证根的存在性,需要满足p1max- < p1min+。设k2=κ2,得到
| $ {{\bar{\delta }}^{2}}<\lambda \tau {{\kappa }^{2}}\Rightarrow {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}}_{2}}>\frac{{{{\bar{\delta }}}^{2}}}{\lambda \tau }\Rightarrow {{k}_{2}}>\frac{{{{\bar{\delta }}}^{2}}}{\lambda \tau }+2\bar{\delta } $ | (32) |
设矩阵P的最小特征值和最大特征值分别为λmin{P}和λmax{P},则式(27)可以转换为式(33)的形式
| $ {\dot V_{20}} = - 2\xi _1^\prime {\left\| \mathit{\boldsymbol{ \boldsymbol{\varsigma} }} \right\|^2}{\lambda _{{\rm{min}}}}\{ \mathit{\boldsymbol{Q}}\} \le - {\gamma _1}V_{20}^{1/2} - {\gamma _2}{V_20} $ | (33) |
式中:
| $ {\dot V_{20}} \le - {\gamma _1}V_{20}^{1/2} $ | (34) |
式(26)可转化为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{{\dot V}_2} \le - {\beta _\eta }V_2^{1/2} + }\\ {\underbrace {( - \frac{1}{{{\gamma _1}}} \cdot k_{v1}^ - \cdot |{\mathit{\boldsymbol{e}}_v}| \cdot {\rm{sign}} (|{\mathit{\boldsymbol{e}}_v}| - \varepsilon ) + {\beta _1}) \cdot |{k_{v1}} - k_{v1}^*|}_{{\zeta _1}} + } \end{array}\\ \underbrace {( - \frac{1}{{{\gamma _2}}} \cdot \eta \cdot k_{v1}^ - \cdot |{\mathit{\boldsymbol{e}}_v}| \cdot {\rm{ sign}} (|{\mathit{\boldsymbol{e}}_v}| - \varepsilon ) + {\beta _2}) \cdot |{k_{v2}} - k_{v2}^*|}_{{\zeta _2}} \end{array} $ | (35) |
式中:βη=min{η1, β1, β2}。
当|ev|>ε2时,kv1和kv2分别以kv1·|ev|和ηvkv1·|ev|的斜率增长,若满足式(36)中所示的条件时,可得ζ1>0,ζ2>0。
| $ {\gamma _1} < \frac{{{{\bar k}_{v1}} \cdot \varepsilon }}{{{\beta _1}}},{\gamma _2} < \frac{{\eta \cdot {{\bar k}_{v1}} \cdot \varepsilon }}{{{\beta _2}}} $ | (36) |
则
仿真中,采用文献[8]中提供的固定翼无人机的六自由度模型以及气动数据,转动惯量I为
| $ \mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} {0.552{\kern 1pt} {\kern 1pt} {\kern 1pt} 8}&0&{0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ 0&{0.633{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5}&0\\ {0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}&0&{1.078{\kern 1pt} {\kern 1pt} {\kern 1pt} 3} \end{array}} \right] $ |
姿态控制器式(12)和式(13)和速度控制器式(21)~式(23)的控制参数如表 1所示,仿真周期为1 ms。
| 姿态控制器 | 速度控制器 | |||
| 参数 | 数值 | 参数 | 数值 | |
| α1 | 12 | μ | 0.02 | |
| β1 | 2 | ε2/(m·s-1) | 0.001 | |
| ε1/(°) | 0.002 | ηv | 2 | |
| kv1 | 10 | |||
| kv3 | 10 | |||
设定姿态干扰dω=[40 40 40]T·sin(3πt/19),速度环的干扰为Δdv=30sin(4πt/19),姿态角的初值为Θ0=[0.6° 1.1°1.7°],姿态角参考值为Θd=[40°51°69°],角速率的初值为ω0=[0.7 0.750.8](°)/s,空速初值为V0=4 m/s,空速参考值为Vd=12 m/s。为了验证本文所提算法的有效性和优越性,将本文所提的算法分别与单变量螺旋算法和文献[16]中的自适应超螺旋算法进行对比。控制参数如下所示:姿态环的单变量螺旋滑模:k1ϕ=k1θ=k1ψ=45;速度环的自适应超螺旋滑模:σT=0.001,ω1=5,r1=5,ε1[16]=2。固定翼无人机控制力矩上界为Mmax=200 N·m。
3.2 仿真结果图 3和图 4分别为自适应多变量螺旋控制器和传统的固定增益螺旋控制器(在图中下标为fixed)的姿态角误差曲线以及姿态角的跟踪曲线,由图 3可以看出,在姿态控制器式(12)和式(13)的作用下,姿态角误差可以在有限时间(< 1.5 s)内收敛到0附近的有限邻域(-0.002°~0.002°)内,与传统螺旋控制器相比,本文所提出的自适应多变量超螺旋控制器精度更高,收敛速度更快,超调更小。

|
| 图 3 姿态角误差曲线 Fig. 3 Errors curves of attitude angle |

|
| 图 4 姿态角跟踪曲线 Fig. 4 Tracking curves of attitude angles |
图 5为力矩变化的曲线,由图中曲线知,采用自适应多变量螺旋滑模产生的力矩M相比于Mfixed抖振更小,且力矩最大值≤Mmax。

|
| 图 5 力矩变化曲线 Fig. 5 Changing curves of control moments |
图 6和图 7分别为在自适应快速超螺旋和自适应超螺旋[16]控制下的速度误差曲线和速度跟踪曲线,由图 6可以看出,在速度控制器式(21)~式(23)的作用下,空速V在1 s内收敛,并且超调很小,空速稳定时的收敛误差在10-3级,相比于自适应超螺旋,本文所提的算法具有更好的控制性能。

|
| 图 6 速度误差曲线 Fig. 6 Changing curves of airspeed errors |

|
| 图 7 速度跟踪曲线 Fig. 7 Tracking curves of airspeed |
图 8为姿态控制器控制增益和速度控制器控制增益的变化曲线,当姿态角跟踪误差小于ε1=0.002时,增益保持在30不变;当速度误差ev小于ε2时,控制增益以较小的斜率减小。
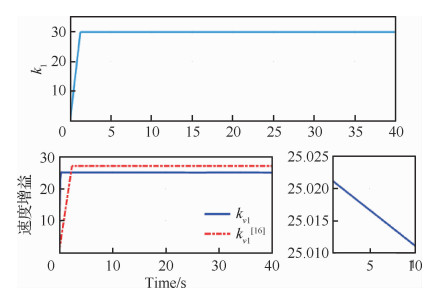
|
| 图 8 速度控制器增益变化曲线 Fig. 8 Changing curves of adaptive-gain in controller |
图 9为推力变化曲线,由图可以看出,推力在开始的1 s内变化较为剧烈,待无人机状态稳定后,推力变化平缓,根据外界扰动,实时变化。而在自适应超螺旋的作用下,后期稳定时,推力的变化更为剧烈。

|
| 图 9 推力变化曲线 Fig. 9 Changing curves of thrust |
本文考虑固定翼无人机飞行过程中的强干扰、不确定以及执行器饱和等问题,基于自适应多变量螺旋滑模和自适应快速超螺旋滑模设计了姿态控制器和速度控制器,有效地解决了干扰以及不确定上界未知时的控制问题,有效地抑制了抖振,简化了控制结构,对参考指令实现快速稳定精确跟踪。在理论上,能较好地适用于固定翼无人机的飞行控制需求。
| [1] |
王彦雄, 祝小平, 周洲. 穿越微下冲气流的飞翼布局无人机控制方法[J]. 航空学报, 2015, 36(5): 1673-1683. WANG Y X, ZHU X P, ZHOU Z. A control method of flying wing UAV for penetration of microburst[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1673-1683. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [2] |
费爱玲, 李柠, 李少远. 固定翼无人机的自抗扰反步控制[J]. 控制理论与应用, 2016, 33(10): 1296-1302. FEI A L, LI N, LI S Y. Active disturbance rejection back-stepping control of fixed-wing unmanned aerial vehicle[J]. Control Theory & Application, 2016, 33(10): 1296-1302. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [3] |
刘一鸣.基于Backstepping自适应的固定翼无人机控制方法研究[D].哈尔滨: 哈尔滨工程大学, 2015. LIU Y M. Study on the control method of fixed-wing UAV based on backstepping adaptive[D]. Harbin: Harbin Engineering University, 2015(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [4] | AKYUREK S, KAYNAK U, KASNAKOGLU C. Altitude control for small fixed-wing aircraft using H ∞, loop-shaping method[J]. IFAC PapersOnLine, 2016, 49(9): 111-116. |
| Click to display the text | |
| [5] | ROTONDO D, CRISTOFARO A, GRYTE K, et al. LPV model reference control for fixed-wing UAVs[J]. IFAC-Papers OnLine, 2017, 50(1): 11559-11564. |
| Click to display the text | |
| [6] | MULLEN J, BAILEY S C C, HOAGG J B. Filtered dynamic inversion for altitude control of fixed-wing unmanned air vehicles[J]. Aerospace Science and Technology, 2016, 54: 241-252. |
| Click to display the text | |
| [7] | HERVAS J R, REYHANOGLU M, TANG H, et al. Nonlinear control of fixed-wing UAVs in presence of stochastic winds[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 33: 57-69. |
| Click to display the text | |
| [8] | CASTAÑEDA H, SALAS-PEÑA O S, DE LEÓN-MORALES J. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV[J]. ISA Transactions, 2017, 66: 226-232. |
| Click to display the text | |
| [9] | SHTESSEL Y B, MORENO J A, FRIDMAN L M. Twisting sliding mode control with adaptation:Lyapunov design, methodology and application[J]. Automatica, 2017, 75: 229-235. |
| Click to display the text | |
| [10] | PLESTAN F, SHTESSEL Y, BREGEAULT V, et al. New methodologies for adaptive sliding mode control[J]. International Journal of Control, 2010, 83(9): 1907-1919. |
| Click to display the text | |
| [11] | SHTESSEL Y, TALEB M, PLESTAN F. A novel adaptive-gain supertwisting sliding mode controller:Methodology and application[J]. Automatica, 2012, 48(5): 759-769. |
| Click to display the text | |
| [12] | EDWARDS C, SHTESSEL Y. Adaptive dual-layer super-twisting control and observation[J]. International Journal of Control, 2016, 89(9): 1759-1766. |
| Click to display the text | |
| [13] | OBEID H, FRIDMAN L M, LAGHROUCHE S, et al. Barrier function-based adaptive sliding mode control[J]. Automatica, 2018, 93: 540-544. |
| Click to display the text | |
| [14] | SHTESSEL Y B, MORENO J A, PLESTAN F, et al. Super-twisting adaptive sliding mode control: A Lyapunov design[C]//49th IEEE Conference on Decision and Control (CDC).Piscataway: IEEE Press, 2010: 5109-5113. |
| [15] | DONG Q, ZONG Q, TIAN B, et al. Adaptive disturbance observer-based finite-time continuous fault-tolerant control for reentry RLV[J]. International Journal of Robust and Nonlinear Control, 2017, 27(18): 4275-4295. |
| Click to display the text | |
| [16] | DONG Q, ZONG Q, TIAN B, et al. Adaptive-gain multivariable super-twisting sliding mode control for reentry RLV with torque perturbation[J]. International Journal of Robust and Nonlinear Control, 2017, 27(4): 620-638. |
| Click to display the text | |
| [17] | GUO Z, ZHAO J, ZHOU M, et al. On a new adaptive multivariable twisting sliding mode control approach and its application[C]//20183rd International Conference on Control and Robotics Engineering (ICCRE).Piscataway: IEEE Press, 2018: 99-103. |
| [18] | ZHANG Y, TANG S, GUO J. Adaptive-gain fast super-twisting sliding mode fault tolerant control for a reusable launch vehicle in reentry phase[J]. ISA Transactions, 2017, 71: 380-390. |
| Click to display the text | |
| [19] | CASTANEDA H, SALAS-PENA O S, DE LEÓN MORALES J. Adaptive super twisting flight control-observer for a fixed wing UAV[C]//2013 International Conference on Unmanned Aircraft Systems (ICUAS). Piscataway: IEEE Press, 2013: 1004-1013. |
| [20] | RAJAPPA S, MASONE C, BVLTHOFF H H, et al. Adaptive super twisting controller for a quadrotor uav[C]//2016 IEEE International Conference on Robotics and Automation (ICRA).Piscataway: IEEE Press, 2016: 2971. |



