2. 军事科学院 国防科技创新研究院, 北京 100071
2. National Innovation Institute of Defense Technology, Academy of Military Sciences, Beijing 100071, China
比例导引律(Proportional Navigation, PN)广泛应用于各种制导武器[1-2]。根据PN的统一方法[3],可以将其分为2大类:以拦截弹速度为参考的PN和以视线为参考的PN。第1类主要包括纯比例导引律(PPN)及其变种[4-11],其指令加速度方向垂直于拦截弹速度方向,主要应用于大气层内拦截制导。第2类PN主要包括真比例导引律(TPN)[12-14]、现实真比例导引律(RTPN)[15-17]、一般真比例导引律(GTPN)[18-20]、理想比例导引律(IPN)[21-23]和一般理想比例导引律(GIPN)[24-26]。对于此类PN,其指令加速度垂直于与视线相关的某个方向,通常用于大气层外拦截[14, 22, 27-31]和交会[32-33]的制导控制。
本文仅讨论拦截问题。根据PN的统一方法[3],TPN是最基本的以视线参考的PN,其指令加速度方向垂直于弹目视线,大小与初始接近速度和弹目视线转率之积成正比。RTPN是TPN的具体实现形式,使用实时的弹目接近速度来代替TPN制导指令中的初始接近速度。GTPN、IPN和GIPN是TPN和RTPN的扩展形式。虽然有学者证明了这3种PN的捕获能力大于TPN和RTPN[18-26],然而它们都有沿视线方向的指令加速度投影,难以实际使用。因而,TPN和RTPN目前仍然是大气层外拦截所实际使用的制导律[27-31]。
在一般大气层外拦截场景中,由于实时弹目接近速度与初始弹目接近速度相比,其变化十分微小,因此RTPN的性能与TPN较为接近。与TPN相比,RTPN在数学上更容易处理和分析,因而有很多学者对RTPN展开了深入的研究。例如,文献[15]得到了二维RTPN对非机动目标和一种加速度大小与弹目接近速度成正比的特殊机动目标的解析解。文献[34]分析了三维RTPN在拦截非机动目标和由IPN制导的机动目标时的性能。文献[35]基于Adomian分解法,推导了二维RTPN的闭合解,并利用数值方法计算了二维RTPN对常加速机动目标的捕获区域。基于修正极坐标系(MPC)和修正极坐标变量(MPV),文献[25]提出了一种相平面方法用于计算三维RTPN对非机动目标和有限机动加速度目标的捕获区域。然而,该机动目标使用的是最大加速度进行机动或者IPN型的机动加速度。
弹道导弹弹头或者航天器总是在尝试发展主动机动突防技术[36-38],这对使用比例导引律进行制导控制的大气层外动能拦截器提出了严峻挑战。RTPN对非机动目标的捕获区域已经得到了深入的研究。然而,已有的大多数文献对RTPN拦截机动目标的捕获区域研究存在一个主要的问题,即所对抗的目标机动加速度形式过于特殊[15, 16, 25, 26, 34-35]。此外,某些关于PN的捕获区域[25-26]需要通过数值方法进行计算,可能由于计算能力限制而不能在弹上实时解算。
文献[17]基于类李雅普诺夫方法[39-42](Lyapunov-like Approach),深入分析了RTPN拦截任意机动目标的捕获区域。文中假设机动目标的加速度方向垂直于弹目视线、加速度大小任意而有界。采用此种假设的原因是,对大气层外拦截而言,目标沿视线方向的机动不足以较大程度地改变拦截几何而难以增大拦截器的脱靶量。本文分析了拦截器在使用RTPN拦截该任意机动目标时所生成的指令加速度的上界,进而利用不等式分析的方法,推导了RTPN的捕获区域。然而,文中所提出的RTPN捕获区域未考虑动能拦截器的过载饱和限制,因而实用性有限。
本文对文献[17]的研究作了进一步拓展,主要作了2方面的改进:
1) 在RTPN拦截任意机动目标指令加速度上限分析结果的基础上,考虑拦截器的饱和过载限制,分析了比例导引系数的可选择范围,以使RTPN的制导指令加速度在拦截过程中总是小于拦截器的饱和机动过载。
2) 采用更为现实的目标捕获定义[14],即弹目相对距离小于容许脱靶量且弹目接近速度的绝对值大于容许碰撞速度的值,基于文献[17]中的不等式分析方法,分别推导了在不考虑和考虑拦截器饱和过载限制时,RTPN对任意机动目标的捕获区域。
本文提出的RTPN对任意机动目标的捕获区域可根据初始时刻弹目相对运动状态进行计算,也可根据实时测量数据进行计算。当弹目相对状态落入捕获区域内时,即可保证具有一定机动过载限制并使用RTPN进行制导控制的动能拦截器实现对论文所假设的任意机动目标的拦截。由于考虑了拦截器饱和过载限制和采用了更现实的目标捕获定义,因而本文提出的捕获区域分析结果相对于文献[17]的结果在理论上具有创新性,在工程上更具有实用性。
1 相对运动方程大气层外拦截时间较短,此时对动能拦截器和目标的弹目相对运动,可以不考虑地球引力和旋转带来的影响。
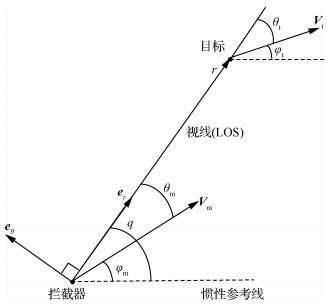
为进一步简化问题,假设拦截器和目标均为质点,并忽略拦截器导引头测量误差和动力学响应延迟,以及执行机构控制偏差与动力学响应延迟,可得到理想的二维拦截几何,如图 1所示。
|
| 图 1 二维拦截几何 Fig. 1 Two-dimensional engagement geometry |
分别以视线(LOS)方向和垂直于视线方向构建极二维视线坐标系( e r, e θ),在该坐标系内二维弹目相对运动方程可表示为[1]
| $ \left\{ {\begin{array}{*{20}{l}} {\dot r - r{{\dot q}^2} = {a_{{\rm{t}}r}} - {a_{{\rm{m}}r}}}\\ {r\ddot q + 2\dot rq = {a_{{\rm{t}}\theta }} - {a_{{\rm{m}}\theta }}} \end{array}} \right. $ | (1) |
式中:r为弹目相对距离;
由于大气层外拦截过程中弹目相对速度极大,目标沿视线方向的机动对突防所起的作用极小,因而可以忽略。因此,可以只考虑目标垂直于视线方向的机动加速度,设
| $ {a_{{\rm{t}}r}} = 0, {a_{{\rm{t}}\theta }} = {a_{\rm{t}}}(t), |{a_{\rm{t}}}(t)| \le \alpha $ | (2) |
式中:α为目标机动加速度的上限,也称为目标的饱和机动过载,设为常数。在实际的拦截任务中,α的值可以根据情报和当前科技水平情况进行分析,在工程应用中可以取得相对保守一些。
对目标的捕获采用文献[14]中的定义:
| $ 0 \le r({t_{\rm{f}}}) < {r_{{\rm{Miss}}}}, \dot r({t_{\rm{f}}}) < {\dot r_{{\rm{Imp}}}} = {v_{r{\rm{Imp}}}} < 0 $ | (3) |
式中:rMiss为容许脱靶量;vrImp为容许碰撞速度。一般情况下,对于大气层外动能拦截,要求rMiss为0.1 m左右,而vrImp为-103 m/s量级。可知,相比于一般采用的捕获定义[3]
| $ r({t_{\rm{f}}}) = 0, \dot r({t_{\rm{f}}}) < 0 $ | (4) |
式(3)的定义更符合实际拦截场景的需要。RTPN的指令加速度垂直于弹目视线[1],与视线转率成正比,即
| $ {a_{{\rm{m}}r}} = 0, {a_{{\rm{m}}\theta }} = N|\dot r|\dot q $ | (5) |
式中:N为RTPN的比例导引系数,工程上通常取3~5[43]。
2 RTPN捕获区分析捕获区域可以认为是一个与目标和拦截器的相对运动状态有关的状态空间,当弹目相对运动状态进入该空间,则其相对运动最终将导致式(3)必然成立,也就意味着将在某个最终时刻tf实现对目标拦截捕获。
2.1 RTPN指令加速度上限在分析RTPN对任意机动目标的捕获区域之前,首先需要给出RTPN在拦截任意机动目标时的指令加速度变化范围,相关结论见定理1。
定理1 对式(1)所示的制导系统,对使用如式(5)所示RTPN的动能拦截器,针对式(2)所示的机动目标,如果拦截过程中弹目接近速度满足:
| $ \dot r(t) < 0, \;\:t \in [0, {t_0}] $ | (6) |
式中:t0∈(0, +∞)为常数;且同时满足比例导引系数
| $ N > 2 $ | (7) |
则式(8)成立:
| $ \begin{array}{*{20}{l}} {|\dot r(t)\dot q(t)| \le \delta = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{max}}\left\{ {|\dot r(0)\dot q(0)|, \frac{\alpha }{{N - 2}}} \right\}, \;\:\forall t \in [0, {t_0}]} \end{array} $ | (8) |
且RTPN的制导指令加速度满足:
| $ |{a_{{\rm{m}}\theta }}| \le N\delta , \;\:\forall t \in [0, {t_0}] $ | (9) |
文献[17]首先给出了定理1及其证明过程。由该定理可知,当N>2时,对任意机动目标,无论能否拦上目标,RTPN的指令加速度都不大于N/(N-2)倍的目标最大机动过载。于是,可根据定理1和所提前预知的目标最大机动能力水平(即α的值),来合理选择拦截器最大机动过载。
2.2 比例导引系数取值范围在拦截过程中,当制导律的指令加速度大于动能拦截器的饱和过载后,拦截器只能以饱和过载进行制导控制,这将导致制导律的拦截性能下降,甚至造成较大的脱靶量。这在实际的大气层外拦截任务中是需要极力避免的。
本文经过分析认为,通过适当选择比例导引系数N,在弹目初始相对运动状态满足一定条件下,可以使RTPN的指令加速度在拦截过程中总是小于拦截器的饱和机动加速度上限,相关结论由定理2给出。
定理2 用如式(5)所示RTPN的动能拦截器,针对式(2)所示的机动目标,如果式(6)成立,且弹目初始相对状态满足:
| $ |\dot r(0)\dot q(0)| \le \frac{{{a_{{\rm{max}}}} - \alpha }}{2} $ | (10) |
同时RTPN的比例导引系数满足:
| $ \frac{{2{a_{{\rm{max}}}}}}{{{a_{{\rm{max}}}} - \alpha }} \le N \le \frac{{{a_{{\rm{max}}}}}}{{|\dot r(0)\dot q(0)|}} $ | (11) |
则式(12)成立:
| $ |{a_{{\rm{m}}\theta }}(t)| \le {a_{{\rm{max}}}}, \;\:\forall t \in [0, {t_0}] $ | (12) |
证明:由式(10)可推导出
| $ \frac{{2{a_{{\rm{max}}}}}}{{{a_{{\rm{max}}}} - \alpha }} \le 2 + \frac{\alpha }{{|\dot r(0)\dot q(0)|}} \le \frac{{{a_{{\rm{max}}}}}}{{|\dot r(0)\dot q(0)|}} $ | (13) |
于是N可以由式(14)确定
| $ \frac{{2{a_{{\rm{max}}}}}}{{{a_{{\rm{max}}}} - \alpha }} \le N \le 2 + \frac{\alpha }{{|\dot r(0)\dot q(0)|}} $ | (14) |
或者
| $ 2 + \frac{\alpha }{{|\dot r(0)\dot q(0)|}} \le N \le \frac{{{a_{{\rm{max}}}}}}{{|\dot r(0)\dot q(0)|}} $ | (15) |
因此,无论通过式(14)还是式(15)选择N,式(7)均满足,再由式(6)成立,可得定理1成立,即式(8)、式(9)成立。
以下分2种情况讨论。第1种情况,若通过式(14)选择N,由其右边不等式可得
| $ |\dot r(0)\dot q(0)| \le \frac{\alpha }{{N - 2}} $ | (16) |
此时δ=α/(N-2)。进而由式(9)可得
| $ |{a_{{\rm{m}}\theta }}| \le \frac{{{N_\alpha }}}{{N - 2}}, \;\:\forall t \in [0, {t_0}] $ | (17) |
再由式(14)左边的不等式,有
| $ \frac{{2{a_{{\rm{max}}}}}}{{{a_{{\rm{max}}}} - \alpha }} \le N \Leftrightarrow \frac{{{N_\alpha }}}{{N - 2}} \le {a_{{\rm{max}}}} $ | (18) |
因此,由式(17)与式(18)可得式(12)成立。
第2种情况,若通过式(15)选择N,由式(15)的左边可得
| $ |\dot r(0)\dot q(0)| \ge \frac{\alpha }{{N - 2}} $ | (19) |
此时
| $ |{a_{{\rm{m}}\theta }}| \le N|\dot r(0)\dot q(0)|, \;\:\forall t \in [0, {t_0}] $ | (20) |
再由式(15)右边可得
| $ N|\dot r(0)\dot q(0)| \le {a_{{\rm{max}}}} $ | (21) |
因此,由式(20)与式(21)可证得式(12)成立。
证明完毕。
由定理2可知,在拦截任意机动目标的过程中,当弹目接近速度为负值(即拦截器与目标在相互接近,
文献[17]给出了在式(4)的目标捕获定义下且不考虑拦截器饱和过载时,RTPN对机动加速度满足式(2)的任意机动目标的捕获区域。然而,式(4)的目标捕获定义在弹目相对距离方面的要求过于严苛,而对弹目接近速度的要求又过于宽泛,因而实用性不强。
本文首先对文献[17]中的定理2作了拓展,分析了在式(3)的目标捕获定义下且不考虑拦截器饱和过载时,RTPN对机动加速度满足式(2)的任意机动目标的捕获区域。接着进一步分析了考虑拦截器饱和过载限制时的RTPN对任意机动目标的捕获区域。
定理3 对式(1)所示的制导系统,对使用如式(5)所示RTPN的动能拦截器,针对式(2)所示的机动目标,如果弹目初始相对状态满足:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot r(0) < 0}\\ {{{\dot r}^2}(0)\left( {1 - \frac{{\dot r_{{\rm{ Imp }}}^4}}{{{{\dot r}^4}(0)}}} \right) > 2{r^2}(0){{\dot q}^2}(0)\left( {1 - \frac{{r_{{\rm{Miss}}}^2}}{{{r^2}(0)}}} \right)} \end{array}} \right. $ | (22) |
且RTPN的比例导引系数满足:
| $ N > 2 + \alpha \sqrt {\frac{{2[{r^2}(0) - r_{{\rm{Miss}}}^2]}}{{{{\dot r}^4}(0) - \dot r_{{\rm{Imp}}}^4}}} $ | (23) |
则必有
| $ \dot r(t) < {\dot r_{{\rm{Imp}}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r(t) > {r_{{\rm{Miss}}}}, \;\:\forall t \in [0, + \infty ) $ | (24) |
如此则必然存在一个终端时刻tf∈(0, +∞),使得式(3)成立,从而实现对目标的拦截。
证明:反证法证明式(24)。假设式(24)不成立,考虑到r和
| $ r({t_3}) > {r_{{\rm{Miss}}}}, \dot r({t_3}) = {\dot r_{{\rm{Imp}}}} $ | (25) |
根据式(22)和式(25),同时考虑到
| $ \begin{array}{l} \dot r(t) < {{\dot r}_{{\rm{Imp}}}} < 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r(t) > {r_{{\rm{Miss}}}} \ge 0\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall t \in [0, {t_3}) \end{array} $ | (26) |
由式(23)和式(26)可知,定理1的前提条件已经满足,可得
| $ |\dot r(t)\dot q(t)| \le \delta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall t \in [0, {t_3}) $ | (27) |
将式(27)代入式(1)的第1式,并考虑到atr=0与amr=0,则有
| $ {\dot r^2}\ddot r = r{(\dot r\dot q)^2} \le r{\delta ^2}, \;\:\forall t \in [0, {t_3}) $ | (28) |
考虑到
| $ {\dot r^3}\frac{{{\rm{d}}\dot r}}{{{\rm{d}}r}} \le r{\delta ^2}, \;\:\forall t \in [0, {t_3}) $ | (29) |
式(29)积分得
| $ \begin{array}{l} {{\dot r}^4}(t) \ge \dot r_0^4 + 2{\delta ^2}({r^2}(t) - r_0^2) = f(r)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall t \in [0, {t_3}) \end{array} $ | (30) |
由r、
| $ {r^2}({t_4}) = {r^2}(0) + \frac{{\dot r_{{\rm{ Imp }}}^4 - {{\dot r}^4}(0)}}{{2{\delta ^2}}} $ | (31) |
考虑到r(t4)的有效性,必然有r2(t4) > rMiss2,可推导出
| $ {\delta ^2} > \frac{{{{\dot r}^4}(0) - \dot r_{{\rm{Imp}}}^4}}{{2({r^2}(0) - r_{{\rm{Miss}}}^2)}} \Rightarrow \delta > \sqrt {\frac{{{{\dot r}^4}(0) - \dot r_{{\rm{Imp}}}^4}}{{2({r^2}(0) - r_{{\rm{Miss}}}^2)}}} $ | (32) |
此时,2种情况需要考虑。
第1种:式(33)
| $ |\dot r(0)\dot q(0)| \le \frac{\alpha }{{N - 2}} $ | (33) |
成立。此时δ=α/(N-2),因此由式(32)可推导出
| $ N < 2 + \alpha \sqrt {\frac{{2({r^2}(0) - r_{{\rm{Miss}}}^2)}}{{{{\dot r}^4}(0) - \dot r_{{\rm{Imp}}}^4}}} $ | (34) |
式(34)与式(23)矛盾,则式(24)成立。且式(33)与式(34)联合必然可以推导出式(22)。
第2种:式(33)不成立,即
| $ |\dot r(0)\dot q(0)| > \frac{\alpha }{{N - 2}} $ | (35) |
此时
| $ {\dot r^2}(0)\left( {1 - \frac{{\dot r_{{\rm{ Imp }}}^4}}{{{r^4}(0)}}} \right) < 2{r^2}(0){\dot q^2}(0)\left( {1 - \frac{{r_{{\rm{Miss}}}^2}}{{{r^2}(0)}}} \right) $ | (36) |
式(36)与式(22)矛盾,则式(24)成立。且式(35)与式(22)联合起来必然可以推导出式(23)。
证明完毕。
根据定理3可以计算出不考虑拦截器饱和机动过载时RTPN对机动目标的捕获区域,以及选择相应的比例导引系数N。当考虑动能拦截器机动过载限制时,RTPN对任意机动目标的捕获区域需根据定理4计算。
定理4 对式(1)所示的制导系统,对使用如式(5)所示RTPN的动能拦截器,针对式(2)所示的机动目标,若弹目初始相对运动状态满足式(10)和式(37):
| $ \left\{ {\begin{array}{*{20}{l}} {{v_r}(0) = \dot r(0) < {v_{r{\rm{Imp}} }} = {{\dot r}_{{\rm{ Imp }}}} < 0}\\ {(v_r^4(0) - v_{r{\rm{Imp}} }^4) > \frac{{({r^2}(0) - r_{{\rm{Miss}}}^2){{({a_{{\rm{max}}}} - \alpha )}^2}}}{2}} \end{array}} \right. $ | (37) |
且RTPN的比例导引系数N由式(11)确定,则式(24)成立,且在拦截过程中有
| $ |{a_{{\rm{m}}\theta }}(t)| \le {a_{{\rm{max}}}}, \;\:\forall t \in [0, + \infty ) $ | (38) |
证明:根据定理2的证明过程,若式(10)成立,则式(13)成立,比例导引系数N可由式(11)来确定。首先,由式(11)左边和式(12)可推导式(22)和式(23),定理2成立,即式(24)成立。
其次,设t0=+∞。式(10)、式(11)和式(24)成立表明定理2成立,即对于t0=+∞,式(12)成立,因此式(38)成立。
证明完毕。
由定理4可知,在二维平面上,当比例导引系数N按式(11)选择时,RTPN对机动目标的捕获区域为式(10)和式(37)所决定的区域。当弹目相对运动状态在初始时刻或者拦截过程中的任意时刻进入该捕获区域后,若采用式(11)来选择RTPN的比例导引系数N,则可使拦截器实现对加速度满足式(2)的任意机动目标的拦截捕获。
为便于计算,可将拦截捕获区域进一步改写为如式(39)~式(41)所示。由式(10)可得
| $ |{v_r}(0){v_\theta }(0)| \le \frac{{r(0)({a_{{\rm{max}}}} - \alpha )}}{2} $ | (39) |
再根据式(37)可得
| $ |{v_r}(0)| > {\left[ {v_{r{\rm{Imp}} }^4 + \frac{{({r^2}(0) - r_{{\rm{Miss}}}^2){{({a_{{\rm{max}}}} - \alpha )}^2}}}{2}} \right]^{\frac{1}{4}}} $ | (40) |
联立式(37)与式(39)可得
| $ |{v_\theta }(0)| < \sqrt {\frac{{v_r^4(0) - v_{r{\rm{Imp}} }^4}}{{2v_r^2(0)\left( {1 - \frac{{r_{{\rm{Miss}}}^2}}{{{r^2}(0)}}} \right)}}} $ | (41) |
实际上,当式(11)、式(39)和式(40)得到满足时,式(41)将自动成立。
注意,根据分析与证明过程可知,本文给出的捕获区域为充分非必要条件,即满足本文给出的定理,必然可以保证对任意机动目标的捕获,但并不意味着不满足本文给出的定理即不能捕获机动目标。实际上,由于拦截任意机动目标问题的非线性,在理论上几乎无法获得目标捕获的充分必要条件。3仿真算例
本节根据实际大气层外拦截场景,通过数值仿真算例,验证本文提出的理论。
设动能拦截器和目标在惯性参考系内的初始状态如表 1所示。
| 变量 | 物理意义 | 初始值 |
| r0/km | 初始相对距离 | 100 |
| q0/(°) | 初始视线角 | 30 |
| rm0/m | 拦截器初始位置 | [0, 0]T |
| vt0/(km·s-1) | 目标初始速度 | 6 |
| vm0(km·s-1) | 拦截器初始速度 | 5 |
| φt0/(°) | 目标初始速度倾角 | 180 |
| IHE/(°) | 初始误差角 | 2 |
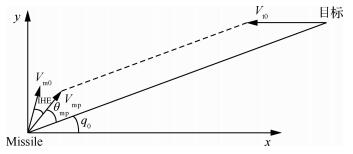
初始拦截几何如图 2所示。其中Vmp表示理想碰撞速度;θmp为理想速度的前置角,即速度方向与视线方向之间的夹角;IHE表示拦截器初始速度与理想碰撞速度之间的偏差角度。
|
| 图 2 初始拦截几何 Fig. 2 Initial engagement geometry |
设目标的饱和机动加速度为α=30 m/s2,拦截器机动加速度上限为amax=60 m/s2。同时,考虑拦截器碰撞所需的容许脱靶量及容许碰撞速度分别为rMiss=0.2 m、vrImp=-4 km/s。根据目标和拦截器的机动过载以及拦截碰撞所需条件,再由式(39)~式(41)可得初始相对距离r0=100 km时的拦截捕获区域,如图 3所示。

|
| 图 3 拦截捕获区域 Fig. 3 Interception capture region |
为方便表述,设
首先,考虑目标机动加速度为常值,加速度形式为atr=0且atθ=30 m/s2。拦截器采用RTPN制导,分别选择比例导引系数N=2.8、4.2、6.0进行数值仿真。不考虑测量误差、控制误差与执行机构响应延迟,当

|
| 图 4 拦截器指令加速度曲线(目标常值机动) Fig. 4 Commanded acceleration curves of interceptor (target with constant maneuver) |
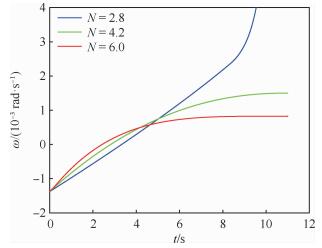
|
| 图 5 视线转率变化曲线(目标常值机动) Fig. 5 Sight of light rate curves (target with constant maneuver) |

|
| 图 6 |vrω|变化曲线(目标常值机动) Fig. 6 Trajectories of |vrω| (target with constant maneuver) |

|
| 图 7 弹目接近速度变化曲线(目标常值机动) Fig. 7 Trajectories of closing speed (target with constant maneuver) |
由图 4可知,导引系数N=2.8时,由RTPN制导的指令加速度在制导后期超过了拦截器的饱和过载,但拦截器采用最大过载进行机动。考虑拦截器过载限制,后期拦截器无法提供有效的指令加速度,导致在拦截末段视线转率的增加,并最终造成的脱靶量很大,这一点由图 5和图 6可以看出。N=4.2情况下,RTPN指令加速度全程都在饱和过载范围之内,表明式(12)成立,即定理2有效。当导引系数N=6.0时,RTPN指令加速度在制导初期就大于拦截器饱和过载,前期拦截器利用自身的饱和过载能力充分降低视线转率,并在末段利用RTPN指令加速度有效碰撞目标。另外在图 7中,除N=2.8情况外,制导过程中随着弹目相对距离的减小,弹目接近速度vr变化极小,vr的绝对值始终远大于容许碰撞速度的绝对值,满足式(24),即定理3成立。以上所取比例导引系数N均满足文献[17]定理2,但文献[17]并未考虑拦截器机动能力大小。因此,当比例导引系数N取2.8时,拦截器在制导后期由于机动性不足而无法拦截到目标。
拦截器脱靶量如表 2所示。
| 导引系数 | 终端脱靶量/m |
| N=2.8 | 45.536 2 |
| N=4.2 | 9.231 8×10-6 |
| N=6.0 | 1.325 4×10-5 |
进一步考虑时变的目标机动加速度,假设atr=0且atθ=[25+5sin(2πt+π/2)] m/s2,目标机动饱和过载保持α=30 m/s2,动能拦截器饱和过载也保持amax=60 m/s2。初始弹目运动状态不变,同样分别取N=2.8,4.2,6.0进行仿真。仿真结果如图 8~图 11所示。
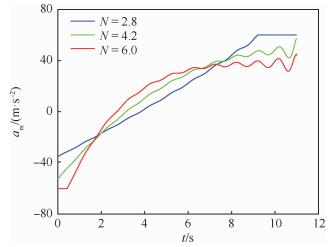
|
| 图 8 拦截器指令加速度曲线(目标正弦机动) Fig. 8 Commanded acceleration curves of interceptor (target with sinusoidal maneuver) |

|
| 图 9 视线转率变化曲线(目标正弦机动) Fig. 9 Sight of light rate curves (target with sinusoidal maneuver) |
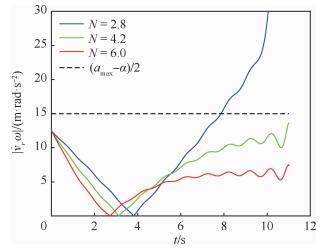
|
| 图 10 |vrω|变化曲线(目标正弦机动) Fig. 10 Trajectories of |vrω| (target with sinusoidal maneuver) |

|
| 图 11 弹目接近速度变化曲线(目标正弦机动) Fig. 11 Trajectories of closing speed (target with sinusoidal maneuver) |
当目标做正弦机动时,RTPN的指令加速度如图 8所示。与上一情况类似,当N取2.8和6.0时,RTPN指令加速度分别在制导初期和后期超过了拦截器饱和过载,而当N在4~4.792 3范围内取值时,指令加速度则始终不超过拦截器饱和过载,这也同样验证了本文提出的定理2。由于拦截器饱和过载限制,当N < 4.0时,在拦截末段拦截器所能提供的加速度无法满足RTPN的指令加速度,导致视线转率突然增加。当N > 4.792 3时,拦截器在刚开始就以饱和过载进行机动,虽然最终能保证拦截到目标,但N值取得过大在制导初期可能会对制导系统产生一定的负荷。
拦截器脱靶量如表 3所示。
| 导引系数 | 终端脱靶量/m |
| N=2.8 | 11.149 5 |
| N=4.2 | 8.958 6×10-6 |
| N=6.0 | 1.338 7×10-5 |
1) 针对大气层外拦截场景,假设目标机动加速度大小任意且有界、方向垂直于弹目视线,深入分析了现实真比例导引律(RTPN)拦截该类目标的捕获区域,证明了当弹目初始相对运动状态进入本文所提出的拦截捕获区后,通过选择合适的比例导引系数N,在拦截器饱和机动过载大于目标最大逃逸机动加速度一定范围的前提下,使用RTPN对动能拦截器进行制导控制,可以使弹目相对距离小于给定的容许脱靶量,同时使弹目接近速度也小于一定的容许碰撞速度,如此即可保证对该类机动目标的拦截捕获。
2) 提出的捕获区域和比例导引系数选择方法可以保证RTPN的指令加速度在拦截过程中不超过动能拦截器的饱和过载限制,具有良好的工程应用能力。
3) 本文分析充分考虑了弹目相对运动的非线性,未采用任何线性化假设和近似,所提出的理论具有全局有效性。
| [1] | SHNEYDOR N A. Missile guidance and pursuit-kinematics, dynamics and control[M]. Chichester: Horwood Publishing, 1998. |
| [2] |
程国采. 战术导弹导引方法[M]. 北京: 国防工业出版社, 1996. CHENG G C. Tactical missile guidance method[M]. Beijing: National Defense Industry Publishing, 1996. (in Chinese) |
| [3] | YANG C D, YANG C C. A unified approach to proportional navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(2): 557-567. |
| Click to display the text | |
| [4] | OH J H, HA I J. Capturability of the three-dimensional pure PNG law[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 491-503. |
| Click to display the text | |
| [5] | OH J H. Solving a nonlinear output regulation problem:Zero miss distance of pure PNG[J]. IEEE Transactions on Automatic Control, 2002, 47(1): 169-173. |
| Click to display the text | |
| [6] | LI K B, SHIN H S, TSOURDOS A, et al. Capturability of 3D PPN against lower-speed maneuvering target for homing phase[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 56(1): 711-722. |
| Click to display the text | |
| [7] | GHOSE S, GHOSE D, RAHA S. Capturability analysis of a 3D Retro-PN guidance law for higher speed nonmaneuvering targets[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 1864-1874. |
| Click to display the text | |
| [8] | GHOSH S, GHOSE D, RAHA S. Capturability of augmented pure proportional navigation guidance against time-varying target maneuvers[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(5): 1446-1461. |
| Click to display the text | |
| [9] | GHOSE S, GHOSE D, RAHA S. Composite guidance for impact angle control against higher speed targets[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 98-117. |
| Click to display the text | |
| [10] |
周觐, 雷虎民, 侯峰, 等. 拦截高速目标的比例与反比例导引捕获区分析[J]. 宇航学报, 2018, 39(9): 1003-1012. ZHOU J, LEI H M, HOU F, et al. Capture region analysis of proportional navigation and retro-proportional navigation guidance for hypersonic target interception[J]. Journal of Astronautics, 2018, 39(9): 1003-1012. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [11] |
王荣刚, 唐硕. 拦截高速运动目标广义相对偏置比例制导律[J]. 西北工业大学学报, 2019, 37(4): 682-690. WANG R G, TANG S. Intercepting higher-speed targets using generalized relative biased proportional navigation[J]. Journal of Northwestern Polytechnical University, 2019, 37(4): 682-690. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [12] | GHOSE D. Capture region for true proportional navigation guidance with nonzero miss-distance[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(3): 627-628. |
| Click to display the text | |
| [13] | GHOSE D. True proportional navigation with maneuvering target[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 229-237. |
| Click to display the text | |
| [14] | LI K B, LIANG Y G, SU W S, et al. Performance of 3D TPN against true-arbitrarily maneuvering target for exoatmospheric interception[J]. Science China Technological Sciences, 2018, 61(8): 1161-1174. |
| Click to display the text | |
| [15] | YUAN P J, CHERN J S. Solution of true proportional navigation for maneuvering and non-maneuvering target[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(1): 268-271. |
| [16] | DHAR A, GHOSE D. Capture region for a realistic TPN guidance law[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(3): 995-1003. |
| Click to display the text | |
| [17] | LI K B, SU W S, CHEN L. Performance analysis of realistic true proportional navigation against maneuvering targets using Lyapunov-like approach[J]. Aerospace Science and Technology, 2017, 69(10): 333-341. |
| Click to display the text | |
| [18] | GHOSE D. On the generalization of true proportional navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 545-555. |
| Click to display the text | |
| [19] | YUAN P J, HSUT S C. Exact closed-form solution of generalized proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1993, 16(5): 963-966. |
| Click to display the text | |
| [20] | YUAN P J, HSUT S C. Solutions of generalized proportional navigation with maneuvering and nonmaneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 30(1): 469-474. |
| Click to display the text | |
| [21] | YUAN P J, CHERN J S. Ideal proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(2): 1161-1165. |
| Click to display the text | |
| [22] | LI K B, ZHANG T T, CHEN L. Ideal proportional navigation for exo-atmospheric interception[J]. Chinese Journal of Astronautics, 2013, 26(4): 976-985. |
| Click to display the text | |
| [23] |
王婷, 周军. 三维理想比例导引律的捕获区域分析[J]. 西北工业大学学报, 2007, 25(1): 83-86. WANG T, ZHOU J. Capture region of 3D ideal proportional navigation[J]. Journal of Northwestern Polytechnical University, 2007, 25(1): 83-86. (in Chinese) |
| Cited By in Cnki (19) | Click to display the text | |
| [24] | YUAN P J, CHEN M J, CHERN J S. Generalized ideal proportional navigation[J]. Proceedings of SPIE, Acquisition, Tracking, and Pointing XⅢ, 1999, 3692: 150-161. |
| Click to display the text | |
| [25] | TYAN F. Unified approach to missile guidance laws:A 3D extension[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1178-1199. |
| Click to display the text | |
| [26] | TYAN F. Capture region of a GIPN guidance law for missile and target with bounded maneuverability[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 201-213. |
| Click to display the text | |
| [27] | MURTAUGH S A, CRIEL H E. Fundamentals of proportional navigation[J]. IEEE Spectrum, 1966, 3(12): 75-85. |
| Click to display the text | |
| [28] | HABLANI H B. Endgame guidance and relative navigation of strategic interceptors with delays[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 82-94. |
| Click to display the text | |
| [29] |
田源, 任章. 大气层外动能拦截器末段导引规律设计[J]. 宇航学报, 2009, 30(2): 474-480. TIAN Y, REN Z. Design of guidance law for exo-atmospheric interceptor during its terminal course[J]. Journal of Astronautics, 2009, 30(2): 474-480. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [30] |
黎克波, 陈磊, 张翼. 真比例导引律的降维分析方法[J]. 国防科技大学学报, 2012, 34(3): 1-5. LI K B, CHEN L, ZHANG Y. Dimension-reduction method of true proportional navigation guidance law[J]. Journal of National University of Defense Technology, 2012, 34(3): 1-5. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [31] | CHEN L, ZHANG B. Novel TPN control algorithm for exo-atmospheric intercept[J]. Journal of System Engineering and Electronics, 2009, 20(6): 1290-1295. |
| [32] | YUAN P J, HSUT S C. Rendezvous guidance with proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(2): 409-411. |
| Click to display the text | |
| [33] | LIU Y H, LI K B, LIANG Y G, et al. Novel augmented proportional navigation guidance law for mid-range autonomous rendezvous[J]. Acta Astronautica, 2019, 162: 526-535. |
| Click to display the text | |
| [34] | YANG C D, YANG C C. Analytical solution of three-dimensional realistic true proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(3): 569-577. |
| Click to display the text | |
| [35] | GARAI T, MUKHOPADHYAY S, GHOSE D. Approximate closed-form solutions of realistic true proportional navigation guidance using the adomian decomposition method[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2009, 223(3): 189-199. |
| Click to display the text | |
| [36] |
雍恩米, 唐国金, 罗亚中. 弹道导弹中段机动突防制导问题的仿真研究[J]. 导弹与航天运载技术, 2005, 277: 13-18. YONG E M, TANG G J, LUO Y Z. Research on maneuvering penetration guidance law of ballistic missile in middle-course flight by simulation method[J]. Missile and Space Vehicles, 2005, 277: 13-18. (in Chinese) |
| Cited By in Cnki (20) | Click to display the text | |
| [37] |
端军红, 高晓光. 卫星对动能拦截器的一种规避策略[J]. 宇航学报, 2011, 32(9): 1953-1962. DUAN J H, GAO X G. An orbit maneuver strategy for the satellite based on evaluating the pregnable area of incoming kinetic kill vehicle[J]. Journal of Astronautics, 2011, 32(9): 1953-1962. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [38] |
王庆普.大气层外弹道导弹弹头机动变轨突防策略研究[D].长沙: 国防科技大学, 2011. WANG Q P. Research on the exo-atmospheric orbit maneuver anti-defense strategy of ballistic missile warhead[D]. Changsha: National University of Defense Technology, 2011(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [39] | HA I J, HUR J S, KO M S, et al. Performance analysis of PNG laws for randomly maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(5): 713-721. |
| Click to display the text | |
| [40] | SONG S H, HA I J. A Lyapunov-like approach to performance analysis of 3-dimension pure PNG laws[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 238-248. |
| Click to display the text | |
| [41] | OH J H, HA I J. Capturability of the three-dimensional pure PNG law[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 491-503. |
| Click to display the text | |
| [42] | LI K B, SHIN H S, TSOURDOS A. Capturability of a sliding mode guidance law with finite time convergence[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(3): 2312-2325. |
| Click to display the text | |
| [43] | ZARCHAN P. Tactical and strategic missile guidance[M]. Reston: AIAA, 2012. |



