随着当代科技的不断进步发展,近年来人们越来越多的将视野投向无人系统的开发与创建。无人机因其成本低廉、无人驾驶、可操作性强等优点,已经渐渐进入现代军事以及民用领域。而无人机编队因其可充分利用每一架无人机的性能并利用多架无人机间相互配合进行协同任务执行等特定优势成为无人机控制方向的热门研究对象。相比旋翼无人机而言,固定翼无人机的控制更为复杂,然而其有着可长距离飞行、大负重以及高速度等不可代替的优势。针对固定翼无人机的编队控制,NASA最早利用风洞试验测试了编队中的气动耦合效应[1],并绘制了紧密编队下的气动参数变化[2]。一些学者从该方面进行了一定的研究并以此建立了相关的无人机紧密编队控制模型[3-5],设计了不同的控制器。如Pachter等[5]所设计的PI控制器;Zhang和Liu[6]为保证位置误差在不确定性以及干扰下的有界性所设计的鲁棒非线性闭环紧密编队控制器;Yu等[7]采用Backstepping控制率以解决无人机尾随系统在执行器故障、输入饱和和尾涡效应下的安全控制问题。国内方面西北工业大学的牟勇飚[8]详细分析了无人机编队的气动耦合效应,提出了一种计算有效风分量和有效风梯度的解决方案;赵峰等[9]利用双机间距误差所设计的PID控制器;刘成功[10]针对传统PID控制器参数整定较为复杂的缺陷所设计的小脑模型神经网络与PID复合控制器;万婧[11]针对模型不确定性所设计的自适应控制器以及滑膜变结构控制器等。
人工势场法是路径规划中应用最为广泛的控制方法,通过建立斥力场和引力场从而引导被控对象抵达目标点。本文将人工势场法和一致性理论相结合,提出了基于人工势场法的编队控制方法并将其应用到无人机紧密编队控制系统中作为间接控制环用以输出僚机理想状态。群智能算法[12]是21世纪初期兴起的一门新兴学科,通过学习大自然中某一生命现象或自然现象实现对问题的最优求解,包含了自学习、自适应以及自组织等特性。近年来不同学者提出了许多群智能算法,如狼群算法(WCA)[13]、果蝇算法(FOA)[14]、人工蜂群(ABC)算法[15]等。但这些算法在实际应用上都存在一定的缺陷,如狼群算法中人工狼信息交流较少,算法全局性较差,而探狼随机搜索又会存在重复探索问题;果蝇算法无法较好处理自变量为负值情况等。鸽群优化(PIO)算法是Duan和Qiao[16]提出的一种新型群智能算法,与其他群优化算法相比具有更新规则简单、适应性强、对优化问题无特殊要求等优点。但基本鸽群算法同样存在收敛性能较差,易于陷入局部最优这一缺点。段海滨等[17]针对该缺陷设计了基于捕食逃逸规则的鸽群算法用来求解无人机紧密编队中的控制输入向量,但其文中没有对改进优化算法进行仿真验证。本文针对基本鸽群算法的该缺陷,通过引入量子更新规则对其进行了一定改进以大幅度增进其寻优性能,在此基础上结合无人机紧密编队模型设计相应的适应度函数作为直接控制环,并利用MATLAB软件对改进的鸽群算法寻优性能进行了仿真测试。
全文的结构为:第1节对无人机编队相对运动系统进行数学建模;第2节对无人机紧密编队条件下的气动耦合效应进行数学建模;第3节针对无人机紧密编队相对运动数学模型,设计出相应的人工势场控制器和改进鸽群控制器,并通过MATLAB仿真验证其控制效果。
1 编队飞行系统建模本节主要考虑长僚机在三维空间内相对位置关系,对无人机控制以及运动学进行数学建模。
1.1 无人机自动驾驶仪模型根据Pachter等[5]的研究,每架无人机都应带有一个无人机自动驾驶仪,其具体可以分为3部分:速度控制仪、航向控制仪以及高度控制仪,速度控制仪与航向控制仪的数学表达式为一个一阶系统。高度控制仪的数学表达式为一个二阶系统:
| $ {\dot V = - \frac{1}{{{\tau _V}}}V + \frac{1}{{{\tau _V}}}{V_{\rm{c}}}} $ | (1) |
| $ {\dot \psi = - \frac{1}{{{\tau _\psi }}}\psi + \frac{1}{{{\tau _\psi }}}{\psi _{\rm{c}}}} $ | (2) |
| $ {\ddot h = - \left( {\frac{1}{{{\tau _{{h_{\rm{a}}}}}}} + \frac{1}{{{\tau _{{h_{\rm{b}}}}}}}} \right)\dot h - \frac{1}{{{\tau _{{h_{\rm{a}}}}}}} \cdot \frac{1}{{{\tau _{{h_{\rm{b}}}}}}}h + \frac{1}{{{\tau _{{h_{\rm{a}}}}}}} \cdot \frac{1}{{{\tau _{{h_{\rm{b}}}}}}}{h_{\rm{c}}}} $ | (3) |
式中:Vc、ψc和hc为输入控制量,τV、τψ、τha和τhb为相关时间常数,具体数值可参考表 1所示的无人机参数。根据其方程解的结构可知,该无人机自动驾驶仪模型可以保证无人机的速度、航向以及高度逐渐趋近于给定的输入控制量,收敛速度与时间常数相关。
| 参数 | 数值 |
| 平均气动压q/(N·m-1) | 2 272.2 |
| 机翼面积S /m2 | 27.9 |
| 翼展b /m | 9.1 |
| 展弦比AR | 3 |
| 升力曲线斜率a | 5.3 |
| 垂尾面积Svt /m2 | 5.1 |
| 垂尾高度 hz /m | 36.6 |
| 垂尾升力曲线斜率avt /(°)-1 | 0.09 |
| 气动效率因子η | 0.95 |
| 速度时间常数τv /s | 5 |
| 航向时间常数τψ /s | 0.75 |
| 高度时间常数τha /s | 0.307 5 |
| 高度时间常数τhb/s | 3.85 |
| 总重量W /N | 111 139 |
| 总质量m /kg | 11 340.7 |
| 空气流速(无人机航速) V /(m·s-1) | 251.5 |
长僚机瞬时平面相对位置关系如图 1所示,采用Leader-Follower编队控制方法[18-19]。其中VL与VW为长僚机的瞬时速度;ψL与ψW为长僚机的瞬时航向角;x为长僚机间的纵向间距;y为长僚机间的横向间距;r为长僚机间的中心间距。根据图 1可以推出:

|
| 图 1 无人机旋转参考系 Fig. 1 Rotating reference frame of wing aircraft |
| $ {\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = {V_{\rm{L}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _{\rm{E}}} + {{\dot \psi }_{\rm{W}}}y - {V_{\rm{W}}}} $ | (4) |
| $ {\frac{{{\rm{d}}y}}{{{\rm{d}}t}} = {V_{\rm{L}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _{\rm{E}}} + {{\dot \psi }_{\rm{W}}}x} $ | (5) |
式中:航向角误差ψE=ψL-ψW。
2 无人机气动耦合效应分析对于固定翼无人机而言,其飞行速度可达几十千米每小时,如此高的速度会在其机翼翼尖产生极为可观的空气涡流,对跟随其后的无人机产生较强的扰动。因此为了更为准确地设计无人机编队控制器,有必要将这种气动耦合影响以数学模型形式给出并加以分析处理。
2.1 无人机涡流数学模型根据文献[5]研究,无人机机翼上的涡流模型类似于两条平行的涡流带。
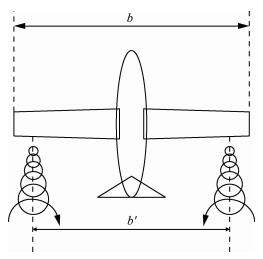
由空气动力学的相关知识可知,无人机在飞行时空气气流会流过机翼从而产生压力差使无人机能飞升,但该压力差在机翼翼尖处会导致气流向内翻转产生涡流从而对其后无人机造成一定影响,如图 2所示。根据文献[11]可知该涡流涡线间的距离b′满足:
|
| 图 2 无人机涡流模型 Fig. 2 Vortex model of UAV |
| $ {b^\prime } = \frac{\pi }{4}b $ | (6) |
式中:b为无人机翼展。假如无人机之间的纵向距离≥2倍无人机翼展,即x≥2b时可以近似认为涡线的长度为无限长[1],此时根据毕奥-萨法尔定律,由涡流引起的速度可以类比因电流元所激发的磁场,因此长机涡流在距离为rc的僚机某点所产生的附加速度可改写为[5]
| $ W = \frac{{{\bar \varPhi} \varGamma }}{{2\pi {r_{\rm{c}}}}} $ | (7) |
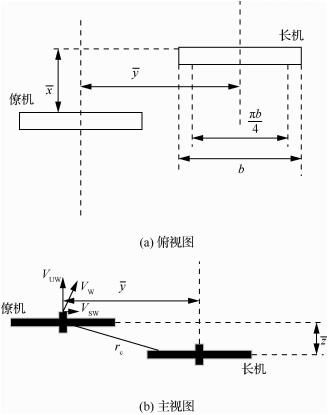
式中:Φ为直交于rc的单位向量;Γ为涡线环量。根据无人机实际形状,该速度可正交分解为一个上洗速度VUW与一个侧洗速度VSW,如图 3(b)所示。图中:x为长僚机间的期望纵向间距;y为长僚机间的期望横向间距;z为长僚机间的期望高度间距;由图 3(a)以及图 3(b)分析可求得僚机的平均上洗速度和平均侧洗速度为
|
| 图 3 双机编队示意图 Fig. 3 View of twin aircraft formation |
| $ \begin{array}{l} {V_{{\rm{U}}{{\rm{W}}_{{\rm{avg}}}}}} = \frac{{{\Gamma _{\rm{L}}}}}{{4\pi b}}\left[ {{\rm{ln}}\frac{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ln}}\frac{{{{\left( {{y^\prime } + \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}} \right]( - \hat z) \end{array} $ | (8) |
| $ \begin{array}{l} {V_{{\rm{S}}{{\rm{W}}_{{\rm{avg}}}}}} = \frac{{{\Gamma _{\rm{L}}}}}{{4\pi {h_z}}}\left[ {{\rm{ln}}\frac{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}} - } \right.\\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ln}}{\kern 1pt} \frac{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}}} \right]\hat y \end{array} $ | (9) |
式中:y′=y/b; z′= z/b为无量纲等效间距;μ2为考虑涡流物理黏度效应所加的校正项。这会带给僚机一个升力变化ΔL、一个阻力变化ΔD以及一个侧向力变化,如图 4所示。图中:α为无人机机翼迎角;Δα为上洗速度影响下的迎角变化量;V′、L′以及D′ 为加入变化量后的对应物理量。由此会导致一个升力增量系数:

|
| 图 4 无人机受力变化侧视图 Fig. 4 Side view of drone force changes |
| $ \begin{array}{l} \Delta {C_{{L_{\rm{W}}}}} = \frac{{{a_W}}}{{\pi {A_{\rm{R}}}}}{C_{{L_{\rm{L}}}}}\frac{2}{{{\pi ^2}}}\left[ {{\rm{ln}}\frac{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\rm{ln}}\frac{{{{\left( {{y^\prime } + \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}} \right] \end{array} $ |
一个阻力增量系数:
| $ \begin{array}{l} \Delta {C_{{D_{\rm{W}}}}} = \frac{1}{{\pi {A_{\rm{R}}}}}{C_{{L_{\rm{L}}}}}{C_{{L_{\rm{W}}}}}\frac{2}{{{\pi ^2}}}\left[ {{\rm{ln}}\frac{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\rm{ln}}\frac{{{{\left( {{y^\prime } + \frac{\pi }{4}} \right)}^2} + {z^2} + {\mu ^2}}}{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}} \right] \end{array} $ |
一个侧向力增量系数:
| $ \begin{array}{l} \Delta {C_Y} = \eta \frac{{{S_{{\rm{vt}}}}}}{S} \cdot \frac{{{a_{{\rm{vt}}}}}}{V} \cdot \frac{{{\varGamma _{\rm{L}}}}}{{4\pi {h_z}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{\rm{ln}}\frac{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ln}}\frac{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}}} \right] \end{array} $ |
提出其中的无量纲函数:
| $ \begin{array}{l} {\sigma _{{\rm{UW}}}}({y^\prime }, {z^\prime }) = \frac{2}{{{\pi ^2}}}\left[ {{\rm{ln}}\frac{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ln}}\frac{{{{\left( {{y^\prime } - \frac{\pi }{4}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{y^{\prime 2}} + {z^{\prime 2}} + {\mu ^2}}}} \right] \end{array} $ |
| $ \begin{array}{l} {\sigma _{{\rm{SW}}}}({y^\prime }, {z^\prime }) = \frac{2}{\pi }\left[ {{\rm{ln}}\frac{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {z^2} + {\mu ^2}}}{{{{\left( {{y^\prime } - \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ln}}\frac{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {z^{\prime 2}} + {\mu ^2}}}{{{{\left( {{y^\prime } + \frac{\pi }{8}} \right)}^2} + {{\left( {{z^\prime } + \frac{{{h_z}}}{b}} \right)}^2} + {\mu ^2}}}} \right] \end{array} $ |
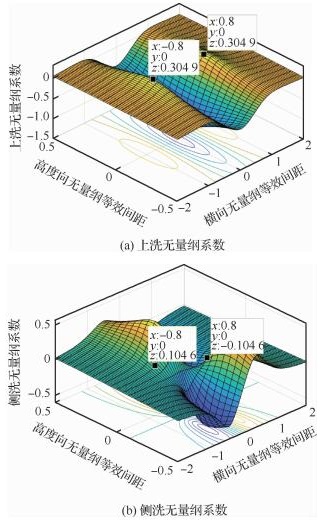
通过MATLAB软件可以绘制以上两函数的三维曲面图,如图 5所示。
|
| 图 5 上洗和侧洗无量纲系数变化示意图 Fig. 5 Schematic diagram of up and side washing dimensionless coefficient changes |
从三维曲面图可以看出在y′=π/4、z′=0时可以获得最大的上洗无量纲系数,此时侧洗无量纲系数有一个较小值。对其在该点分别求3个方向上的偏导同样可知当无人机的侧向间距y=πb/4、高度间距z=0时无人机可以获得最大的升力增量系数、最小的阻力增量系数以及一个较小的侧向力增量系数。则此时根据图 4受力变化可知无人机所获得的升力达到最大、阻力达到最小,处于最优的编队队形。
2.2 加入气动耦合效应无人机紧密编队数学模型根据以上分析可以得出无人机紧密编队中的僚机三维空间状态方程为[1]
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} x\\ {{V_{\rm{W}}}}\\ y\\ {{\psi _{\rm{W}}}}\\ z\\ \zeta \end{array}} \right] = \mathit{\boldsymbol{A}}\left[ {\begin{array}{*{20}{c}} x\\ {{V_{\rm{W}}}}\\ y\\ {{\psi _{\rm{W}}}}\\ z\\ \zeta \end{array}} \right] + \mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} {{V_{{{\rm{W}}_{\rm{c}}}}}}\\ {{\psi _{{{\rm{W}}_{\rm{c}}}}}}\\ {{h_{{{\rm{W}}_{\rm{c}}}}}} \end{array}} \right] + \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {{V_{\rm{L}}}}\\ {{\psi _{\rm{L}}}}\\ {{h_{{{\rm{L}}_{\rm{c}}}}}} \end{array}} \right] $ | (10) |
其中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_{11}}}&{{\mathit{\boldsymbol{A}}_{12}}}&{{\mathit{\boldsymbol{A}}_{13}}}\\ {{\mathit{\boldsymbol{A}}_{21}}}&{{\mathit{\boldsymbol{A}}_{22}}}&{{\mathit{\boldsymbol{A}}_{23}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{11}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}\\ 0&{ - \frac{1}{{{\tau _{{V_{\rm{W}}}}}}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{12}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_y}}}}}, \bar y}&{ - \frac{{\bar y}}{{{\tau _{{V_{\rm{W}}}}}}}G}\\ {\frac{{\bar qS}}{m}\Delta {C_{{D_{{{\rm{W}}_y}}}}}}&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{13}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_z}}}}}, \bar y}&0\\ 0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{21}} = \left[ {\begin{array}{*{20}{l}} 0&0\\ 0&0\\ 0&0\\ 0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{22}} = \left[ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_y}}}}}\bar x}&{\left( {\frac{{\bar x}}{{{\tau _{{\psi _{\rm{W}}}}}}} - {{\bar V}_{\rm{L}}}1} \right)G}\\ {\frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_y}}}}}\frac{1}{G}}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{{{\tau _{{\psi _V}}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\bar qS}}{m}\Delta {C_{{L_{{{\rm{W}}_y}}}}}}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{23}} = \left[ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_z}}}}}\bar x}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}\\ {\frac{{\bar qS}}{{mV}}\Delta {C_{{Y_{{{\rm{W}}_z}}}}}\frac{1}{G}}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{{{\tau _{{h_{\rm{a}}}}}{\tau _{{h_{\rm{b}}}}}}}}&{ - \left( {\frac{1}{{{\tau _{{h_{\rm{a}}}}}}} + \frac{1}{{{\tau _{{h_{\rm{b}}}}}}}} \right)} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&0&0\\ 0&{{{\bar V}_{\rm{L}}}G}&0\\ 0&0&0\\ 0&0&0\\ 0&0&{ - \frac{1}{{{\tau _{{h_{\rm{a}}}}}{\tau _{{h_{\rm{b}}}}}}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&{\frac{{\bar y}}{{{\tau _{{\psi _{\rm{W}}}}}}}G}&0\\ {\frac{1}{{{\tau _{{V_{\rm{W}}}}}}}}&0&0\\ 0&{ - \frac{{\bar x}}{{{\tau _{{\psi _{\rm{W}}}}}}}G}&0\\ 0&{\frac{1}{{{\tau _{{\psi _{\rm{W}}}}}}}}&0\\ 0&0&0\\ 0&0&{\frac{1}{{{\tau _{{h_{\rm{a}}}}}{\tau _{{{\rm{h}}_{\rm{b}}}}}}}} \end{array}} \right] $ |
其中取僚机与长机之间3个方向上的间距以及僚机的正向速度、航向角与纵向速度差作为状态向量X =[x, VW, y, ψW, z, ζ]T;取控制器输出的速度控制量、航向控制量以及高度控制量作为控制向量Y =[VWc, ψWc, hWc]T;取长机的正向速度、航向角以及长机高度控制量作为耦合量Z =[VL, ψL, hLc]T,其具体参数名称及数值设定见表 1。
3 紧密编队控制器设计 3.1 人工势场控制器设计在不考虑无人机的体积时无人机的动力学模型可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}^i} = {v^i}}\\ {{m_i}{{\dot v}^i} = {u^i} - {k_i}{v^i}} \end{array}} \right.i = 1, 2, \cdots , N $ | (11) |
式中:xi为无人机的位置;ki为速度阻尼系数;vi为无人机的速度;mi为无人机的质量;ui 为输入的控制量。
对于每一个无人机编队控制的控制量包括其速度、相邻间距,故其控制量可写为[20]
| $ \begin{array}{*{20}{l}} {{u^i} = - {K_v}\sum\limits_{j \in {{\bf{N}}_i}} {({v^i} - {v^j})} - {K_p}\sum\limits_{j \in {N_i}} {{\nabla _{{x^i}}}} {V^{ij}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {m_i}({v^i} - {v_{{\rm{ end }}}}) + {k_i}{v^i}} \end{array} $ | (12) |
式中:Kv为速度增益系数;Kp为势场增益系数;Ni为无人机的邻接集合;vend为无人机编队稳定速度;Vij为相邻无人机的势场函数;Δ xiVij为对此势场函数求梯度,可看作相邻无人机势场作用力。本文将势场函数设置为
| $ {V^{ij}}(|{x^{ij}}|) = {\rm{ln}}|{x^{ij}}{|^2} + \frac{{d_{ij}^2}}{{|{x^{ij}}{|^2}}} $ | (13) |
式中:xij为无人机间实际间距;dij 为无人机间期望间距。
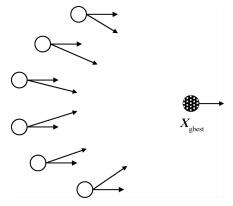
3.2 改进鸽群控制器设计鸽群算法主要由指南针算子和地标算子2个寻优部分组成,指南针算子(图 6)模拟鸽群在导航前期利用地磁进行导航的特性进行寻优迭代:
|
| 图 6 指南针算子模型 Fig. 6 Compass operator model |
| $ \mathit{\boldsymbol{V}}_i^{{N_{\rm{c}}}} = \mathit{\boldsymbol{V}}_i^{{N_{\rm{c}}} - 1}{{\rm{e}}^{ - R \times {N_{\rm{c}}}}} + {\rm{rand}} ({\mathit{\boldsymbol{X}}_{{\rm{gbest}}}} - \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1}) $ | (14) |
| $ \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}}} = \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1} + \mathit{\boldsymbol{V}}_i^{{N_{\rm{c}}}} $ | (15) |
式中:V i为粒子速度向量;X i为粒子位置向量;R为指南针因子;Nc为迭代次数;X gbest为当前所记录的最优解粒子的位置向量。
地标算子(图 7)模拟鸽群在导航后期利用目标点附近的地标建筑进行导航的特性进行寻优迭代:

|
| 图 7 地标算子模型 Fig. 7 Landmark operator model |
| $ \mathit{\boldsymbol{X}}_{{\rm{ center }}}^{{N_{\rm{c}}} - 1} = \frac{{\sum\limits_{i = 1}^{{N^{{N_{\rm{c}}} - 1}}} {\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1}} F(\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1})}}{{{N^{{N_{\rm{c}}} - 1}}\sum\limits_{i = 1}^{{N^{{N_{\rm{c}}} - 1}}} {F(\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1})} }} $ | (16) |
| $ {N^{{N_{\rm{c}}}}} = \frac{{{N^{{N_{\rm{c}}} - 1}}}}{2} $ | (17) |
| $ \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}}} = \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1} + {\rm{rand }}(\mathit{\boldsymbol{X}}_{{\rm{center}}}^{{N_{\rm{c}}} - 1} - \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1}) $ | (18) |
式中:X center为当前所有粒子的中心位置;F(X)为该粒子的适应度值。
受到量子粒子群算法[21]的启发,本文针对其收敛性较差的缺陷对其引入了量子行为更新规则:删去鸽群算法中原有的粒子速度量,改为用量子规则中的波函数表示粒子位置,即粒子的指南针算子更新变为
| $ \alpha = \frac{{(1 - 0.5)({T_1} - t)}}{{{T_1}}} + 0.5 $ | (19) |
| $ \mathit{\boldsymbol{P}} = \frac{{ {\rm{ran}}{{\rm{d}}_1}\mathit{\boldsymbol{X}}_{{\rm{pbes}}{{\rm{t}}_i}}^{{N_{\rm{c}}} - 1} + {\rm{ran}}{{\rm{d}}_2}\mathit{\boldsymbol{X}}_{{\rm{gbest}}}^{{N_{\rm{c}}} - 1}}}{{ {\rm{ran}}{{\rm{d}}_1} + {\rm{ran}}{{\rm{d}}_2}}} $ | (20) |
| $ \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}}} = \mathit{\boldsymbol{P}} \pm \alpha |\mathit{\boldsymbol{X}}_{{\rm{mbest}}}^{{N_{\rm{c}}} - 1} - \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1}|{\rm{ln}}\left( {\frac{1}{{{\rm{rand}}}}} \right) $ | (21) |
式中:α为收缩-扩张系数;T1为指南针算子迭代次数;t为算法当前迭代次数;X mbest为所有粒子的位置平均值。
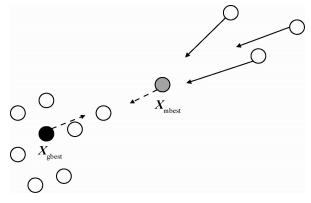
并对地标算子引入学习因子β,利用最优解加快寻优速度,改进地标算子模型如图 8所示。
|
| 图 8 改进地标算子模型 Fig. 8 Improved landmark operator model |
| $ {\beta = {\rm{round}} (1 + {\rm{rand}} )} $ | (22) |
| $ {{\mathit{\boldsymbol{X}}_{{\rm{ne}}{{\rm{w}}_i}}} = \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1} + {\rm{rand}} (\mathit{\boldsymbol{X}}_{{\rm{gbest}}}^{{N_{\rm{c}}} - 1} - \beta \mathit{\boldsymbol{X}}_{{\rm{mbest}}}^{{N_{\rm{c}}} - 1})} $ | (23) |
| $ \mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}}} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_{{\rm{ne}}{{\rm{w}}_i}}}}&{F({\mathit{\boldsymbol{X}}_{{\rm{ne}}{{\rm{w}}_i}}}) < F(\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1})}\\ {\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1}}&{F({\mathit{\boldsymbol{X}}_{{\rm{ne}}{{\rm{w}}_i}}}) > F(\mathit{\boldsymbol{X}}_i^{{N_{\rm{c}}} - 1})} \end{array}} \right. $ | (24) |
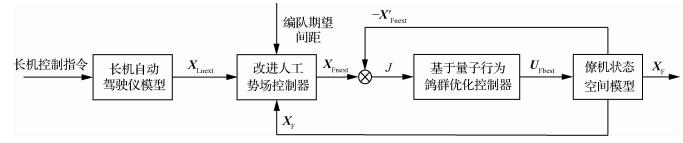
根据以上内容设计了无人机紧密编队控制系统,如图 9所示。由图可知,利用人工势场控制器以及改进鸽群控制器进行无人机紧密编队控制的具体步骤如下:
|
| 图 9 无人机紧密编队控制系统 Fig. 9 UAV tight formation control system |
步骤1 根据提前输入的长机控制量以及当前时刻长机的状态量求出下一时刻长机的状态量,再将编队期望间距、下一时刻长机的状态量以及当前时刻僚机的状态量代入改进人工势场控制器中可以求出下一时刻的理想僚机状态量。
步骤2 将下一时刻僚机的理想状态量X Fnext代入改进鸽群优化控制器中,将基于量子行为改进的鸽群算法中个体位置向量选取为
| $ \mathit{\boldsymbol{X}} = {[{V_{{{\rm{W}}_{\rm{c}}}}}, {\psi _{{{\rm{W}}_{\rm{c}}}}}, {h_{{{\rm{W}}_{\rm{c}}}}}]^{\rm{T}}} $ | (25) |
即僚机下一时刻的控制向量U F,这样选取优化算法变量即可将改进鸽群优化算法和无人机紧密编队模型相结合,利用该向量代入僚机模型式(10)可求出在此控制量控制下的下一时刻僚机状态量X Fnext′ ,并代入适应度函数中:
| $ J = {({\mathit{\boldsymbol{X}}_{{\rm{ Fnext}}}} - \mathit{\boldsymbol{X}}_{{\rm{ Fnext }}}^\prime )^{\rm{T}}}({\mathit{\boldsymbol{X}}_{{\rm{ Fnext }}}} - \mathit{\boldsymbol{X}}_{{\rm{ Fhext }}}^\prime ) $ | (26) |
按照式(19)~式(24)所述更新规则,即改进鸽群优化算法中的指南针算子和地标算子不断迭代寻优更新个体位置向量X,即可找出使设置的适应度函数J最小的僚机控制量U Fbest。
步骤3 将此时刻的改进鸽群优化控制器输出控制量U Fbest代入僚机状态空间模型即可求出下一时刻与理想僚机状态量差距最小的僚机输出状态量。
步骤4 重复执行步骤1~步骤3直至设定的仿真时长结束即完成了无人机紧密编队控制。
3.4 仿真实验及结果分析本文为验证改进鸽群算法的有效性将其与现有的3个鸽群算法做比较:
1) 基本鸽群优化(PIO)算法[16]。
2) 加入混沌、反向以及柯西扰动的自适应鸽群优化(IPIO)算法[22]。
3) 加入收缩因子的自适应鸽群优化(CFPIO)算法[23]。
4) 基于量子行为改进的鸽群优化(QPIO)算法。
其参数设置如表 2所示。并选取了6个常用测试函数如表 3所示。
| 参数 | 数值 |
| 粒子维数D | 10 |
| 种群个数Np | 5D |
| 收缩-扩张系数α | 0.5~1(均匀递减) |
| 指南针算子迭代次数T1 | 800 |
| 地标算子迭代次数T2 | 200 |
| 函数 | 函数名 | 函数表达式 |
| F1 | Sphere | |
| F2 | Schwefel | |
| F3 | Rastrigin | |
| F4 | Griewangk | |
| F5 | Schwefel2.22 | |
| F6 | Schwefel2.21 |
取30次仿真运算结果的最优解(Min)、最次解(Max)、平均解(Mean)以及标准差(STD)作比较,并计算每种算法运行30次所用的平均时间(Tmean),并取其中最优结果一次的优化数据绘制收敛曲线,其仿真结果如表 4以及图 10所示。
| 函数 | PIO | IPIO | CFPIO | QPIO | |
| F1 | Mean | 0.486 9 | 0.128 5 | 0.041 9 | 0 |
| STD | 0.746 1 | 0.461 3 | 0.136 0 | 0 | |
| Min | 0 | 0 | 0 | 0 | |
| Max | 3.240 5 | 2.423 2 | 0.541 7 | 0 | |
| Tmean/s | 1.063 5 | 0.929 7 | 0.996 4 | 1.732 8 | |
| F2 | Mean | 2.236 7 | 0.710 7 | 1.064 8 | 0.067 2 |
| STD | 4.788 7 | 1.582 8 | 2.688 9 | 0.141 7 | |
| Min/10-5 | 1.272 8 | 1.272 8 | 1.272 8 | 1.272 8 | |
| Max | 24.922 0 | 7.430 6 | 14.153 3 | 0.647 5 | |
| Tmean/s | 0.965 1 | 1.031 8 | 1.022 9 | 2.007 3 | |
| F3 | Mean | 0.195 6 | 0.014 5 | 0.004 3 | 0 |
| STD | 0.392 6 | 0.067 4 | 0.015 9 | 0 | |
| Min | 0 | 0 | 0 | 0 | |
| Max | 1.135 9 | 0.364 9 | 0.075 6 | 0 | |
| Tmean/s | 0.938 0 | 1.016 1 | 1.081 8 | 1.814 1 | |
| F4 | Mean | 0.080 3 | 0.057 6 | 0.004 9 | 0.004 2 |
| STD | 0.121 8 | 0.122 5 | 0.005 9 | 0.004 2 | |
| Min | 0.002 5 | 0.002 5 | 0.002 5 | 0.002 5 | |
| Max | 0.557 6 | 0.586 5 | 0.032 2 | 0.024 0 | |
| Tmean/s | 0.994 8 | 1.000 5 | 1.035 4 | 1.968 2 | |
| F5 | Mean | 1.811 5×10-42 | 7.820 0×10-27 | 8.537 5×10-53 | 3.364 6×10-34 |
| STD | 9.785 5×10-42 | 4.283 2×10-26 | 3.647 9×10-52 | 1.748 0×10-33 | |
| Min | 0 | 0 | 1.294 5×10-98 | 1.647 3×10-64 | |
| Max | 5.361 8×10-41 | 2.346 0×10-25 | 1.912 5×10-51 | 9.584 6×10-33 | |
| Tmean/s | 1.007 8 | 1.042 2 | 1.135 4 | 1.926 0 | |
| F6 | Mean | 0.580 7 | 0.212 3 | 0.180 2 | 1.284 9×10-32 |
| STD | 0.755 6 | 0.415 8 | 0.569 6 | 7.037 6×10-32 | |
| Min | 0 | 0 | 1.879 7×10-99 | 0 | |
| Max | 2.938 2 | 1.584 5 | 2.925 5 | 3.854 7×10-31 | |
| Tmean/s | 1.056 8 | 1.104 2 | 1.193 2 | 1.860 9 | |

|
| 图 10 各适应度函数收敛曲线 Fig. 10 Convergence curves of fitness functions |
通过仿真结果可以看出:
1) 在不同函数条件下本项目所提出的改进鸽群算法基本上在4个评价指标中均为最优,说明本项目所提出的算法寻优性能较其他算法有较大提升,且其寻优稳定性较好。
2) 在仿真所用平均时间这一项上,原始鸽群优化算法较其他算法表现更好,但基本相差不大,说明现存的改进鸽群优化算法基本上都是以牺牲一定的收敛时长来显著提升其收敛性能。这也说明了如何在保证收敛时长基本不变的条件下提升算法的寻优性能是此优化算法值得进一步研究的方向。
3) 由收敛曲线可以看出本项目所提出改进鸽群优化算法收敛速度较传统鸽群优化算法有较大提升,在几种改进算法的比较上也是速度最快的,基本上在迭代的前100次以内就可以满足一般的寻优要求。
随后本文选取了10架无人机,其中首架无人机为长机,其余均为僚机,队形为斜“一”字形的编队方案。即采用后一架僚机处于前一架僚机的斜后方以其为所跟随的长机策略。
仿真条件为紧密编队,长机控制可分为2个阶段:第1阶段为前15 s长机航向控制指令由零均匀减为-30°,随后稳定飞行5 s;第2阶段再在20~35 s期间由-30°均匀增加至零度并保持此控制指令至仿真时长。仿真时长设置为60 s,步长为0.02 s,得到了如图 11所示仿真结果,其中红线代表长机、绿线代表僚机,速度和航向用不同颜色曲线表示,每幅图共10条收敛曲线。无人机初始值及控制量设置如表 5所示。

|
| 图 11 仿真结果 Fig. 11 Simulation results |
| 状态名称 | 控制量 | 长机 | 僚机 |
| 速度/(m·s-1) | 251.5 | 0 | 0 |
| 航向/(°) | -30 | 0 | 0 |
| 高度/m | 13 716 | 0 | 0 |
| 横向间距/m | 18.3 | 18.3 | |
| 侧向间距/m | 7.2 | 7.2 | |
| 纵向间距/m | 0 | 0 |
通过仿真结果可以看出:
1) 仿真开始无人机编队可以很快到达指定高度,随着仿真时长增加,长机按照指定控制指令进行变化,而僚机根据所设计的控制器输出控制量进行相应编队。
2) 从图 11(a)可以看出在x和y方向上编队收敛程度较好,而z方向上随着仿真时长的增加误差不断减小;从图 11(b)可以看出仿真时长结束后所形成的编队队形,10架无人机排成斜“一”字形编队。
3) 从图 11(c)可以看出机群速度拟合程度较好,在整个编队过程中僚机与长机的速度能始终保持一致;从图 11(d)可以看出对于航向方向上由于长机增加了扰动,僚机的航向存在一定的波动,但始终保持在误差允许范围内。
以此证明了本文所设计的控制系统对于多无人机紧密编队控制的有效性。
4 结论本文重点研究了无人机紧密编队的队形控制问题。
1) 针对无人机紧密编队所产生的气动耦合效应进行了数学建模,分析了无人机紧密编队的理论最优队形。
2) 在此基础上设计了人工势场控制器以及改进鸽群控制器,经过仿真验证证实了该控制器对于无人机紧密编队控制的有效性,可以提高无人机紧密编队的可靠性,使无人机在不同控制指令下快速形成设定编队队形并保持队形不变。
| [1] | JENNIFER L H, JAMES E M, NORMA V C. The NASA Dryden flight test approach to an aerial refueling system: NASA/TM-2005-212859[R]. Washington, D.C.: NASA, 2015. |
| [2] | BANGASH Z, SANCHEZ R, AHMED A, et al. Aerodynamics of formation flight[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2004. |
| [3] | BUZOGANY L E, PACHTER M, AZZO J J D. Automated control of aircraft in formation flight[C]//Guidance, Navigation and Control Conference. Reston: AIAA, 1992. |
| [4] | PROUD A W, MEIR P, JOHN J D A. Close formation flight control: AIAA-1999-4207[R]. Reston: AIAA, 1999: 1231-1246. |
| [5] | PACHTER M, D'SZZO J J, PROUD A W. Tight formation flight control[J]. Journal of Guidance, Control, and Dynamic, 2001, 24(2): 246-254. |
| Click to display the text | |
| [6] | ZHANG Q R, LIU H H T. Robust nonlinear control of close formation flight[EB/OL]. (2019-04-16)[2019-12-01].https: arxiv.org/abs/1094.07479v1. |
| [7] | YU Z, QU Y, ZHANG Y. Safe control of trailing UAV in close formation flight against actuator fault and wake vortex effect[J]. Aerospace Science and Technology, 2018, 77(6): 189-205. |
| Click to display the text | |
| [8] |
牟勇飚.无人机编队中的气动耦合问题研究[D].西安: 西北工业大学, 2006: 30-45. MOU Y B. Research on aerodynamic coupling in UAV formation[D]. Xi'an: Northwestern Polytechnical University, 2006: 30-45(in Chinese). |
| Cited By in Cnki (29) | Click to display the text | |
| [9] |
赵锋, 杨伟, 杨朝旭. 无人机紧密编队飞行控制仿真研究[J]. 航空科学技术, 2012(5): 18-21. ZHAO F, YANG W, YANG C X. Close formation flight control of UAVs[J]. Aeronautical Science Technology, 2012(5): 18-21. (in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [10] |
刘成功.无人机仿生紧密编队飞行控制技术研究[D].南京: 南京航空航天大学, 2009: 21-33. LIU C G. Research on biomimetic close formation flight control of UAVs[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009: 21-33(in Chinese). |
| Cited By in Cnki (15) | Click to display the text | |
| [11] |
万婧.无人机自主编队飞行控制系统设计方法及应用研究[D].上海: 复旦大学, 2009: 39-63. WAN J. Research on design method and application of UAV autonomous formation flight control system[D]. Shanghai: Fudan University, 2009: 39-63(in Chinese). |
| Cited By in Cnki (33) | Click to display the text | |
| [12] |
ENGELBRECHT A, 谭营. 计算群体智能基础[M]. 北京: 清华大学出版社, 2009: 1-15. ENGELBRECHT A, TAN Y. Fundamentals of computational swarm intelligence[M]. Beijing: Tsinghua University Press, 2009: 1-15. (in Chinese) |
| [13] | LIU C G, YAN X H, LIU C Y, et al. The wolf colony algorithm and its application[J]. Chinese Journal of Electronics, 2011, 20(2): 210-216. |
| [14] | PAN W T. A new fruit fly optimization algorithm:Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74. |
| Click to display the text | |
| [15] | KARABOGA D. An idea based on honey bee swarm for numerical optimization[D]. Erciyes: Erciyes University, 2005. |
| [16] | DUAN H B, QIAO P. Pigeon-inspired optimization:A new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Computing & Cybernetics, 2014, 7: 24-37. |
| Click to display the text | |
| [17] |
段海滨, 邱华鑫, 范彦铭. 基于捕食逃逸鸽群优化的无人机紧密编队协同控制[J]. 中国科学:技术科学, 2015, 45(6): 559-572. DUAN H B, QIU H X, FAN Y M. Unmanned aerial vehicle close formation cooperative control based onpredatory escaping pigeon-inspired optimization[J]. Scientia Sinica Technologica, 2015, 45(6): 559-572. (in Chinese) |
| Cited By in Cnki (37) | Click to display the text | |
| [18] |
王晶, 顾维博, 窦立亚. 基于Leader-Follower的多无人机编队轨迹跟踪设计[J]. 航空学报, 2020, 41(S1): 723728. WANG J, GU W B, DOU L Y. Leader-Follower formation control of multiple UAVs with trajectory tracking design[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S1): 723728. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] |
张民, 夏卫政, 黄坤, 等. 基于Leader-Follower编队的无人机协同跟踪地面目标制导律设计[J]. 航空学报, 2018, 39(2): 321497. ZHANG M, XIA W Z, HUANG K, et al. Guidance law for cooperative tracking of a ground target based on leader-follower formation of UAVs[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 321497. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [20] |
杨宇.多机器人编队群集运动控制的研究[D].武汉: 华中科技大学, 2007: 21-40. YANG Y. Research on formation and flocking control of multiple robots[D]. Wuhan: Huazhong University of Science and Technology, 2007: 21-40(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [21] |
孙俊. 量子行为粒子群优化:原理及其应用[M]. 北京: 清华大学出版社, 2011: 31-51. SUN J. Quantum-behaved PSO:Principles and applications[M]. Beijing: Tsinghua University Press, 2011: 31-51. (in Chinese) |
| [22] |
周雨鹏.基于鸽群算法的函数优化问题求解[D].长春: 东北师范大学, 2016: 6-23. ZHOU Y P. A pigeon-inspired algorithm for function optimization problems[D]. Changchun: Northeast Normal University, 2016: 6-23(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [23] |
郭瑞, 赵汝鑫, 吴海舟, 等. 具有收缩因子的自适应鸽群算法用于函数优化问题[J]. 物联网技术, 2017(5): 91-94. GUO R, ZHAO R X, WU H Z, et al. Adaptive pigeon group algorithm with contraction factor for function optimization[J]. Internet of Things Technologies, 2017(5): 91-94. (in Chinese) |
| Cited By in Cnki | Click to display the text |



