复合材料加筋壁板在轴压载荷作用下,主要的失效模式为屈曲破坏[1-2]。在实际工程应用中,受加工精度及材料性能的影响,复合材料的力学性能较金属材料分散性大,其几何尺寸、物理属性等参数具有不可忽视的不确定性[3]。虽然每个参数的波动很小,但其综合作用可能会改变加筋壁板的后屈曲特性。因此,在复合材料加筋壁板的设计中应充分考虑各种不确定性因素。
目前,考虑不确定性因素对结构模型验证问题,国内外已有大量的学者开展了相关的研究工作。Ben和Thacker对不确定性模型和试验结果比较的度量方法进行了梳理和分析[4]。Christopher和William对考虑不确定性的科学计算研究框架进行了综述,并通过一个超声速喷管流动模型论述了不确定性分析的主要流程[5];Lee等针对机身结构所用的复合材料加筋壁板进行了参数不确定性和结构鲁棒性研究[6];李湘郡等针对C-C复合材料的分散性进行了详细的研究[7];Li等考虑了边界不确定性,对一个承受轴向载荷的梁进行了试验与分析方法的验证[8]。同样考虑边界不确定性的研究工作还有Isaac[9]、Marc[10]等。而Daniel和Sonny针对一个通讯卫星结构进行了不确定性传播的研究[11]。
近年来,国内相关学者在不确定性问题和模型验证方面也表现出了极大的兴趣,如李维重点论述了主、客观不确定性在模型中的传播问题,开展了灵敏度分析、不确定性量化等研究工作[12];聂小华和吴存利总结了考虑不确定性因素的模型验证常用方法,并针对一个化铣整体壁板的屈曲问题,采用面积度量法进行了有限元模型的验证[13]。解江等开展了T700/环氧3234的复合材料圆管吸能特性不确定性研究,获得了对吸能特性具有显著影响的参数[3]。陈学前等讨论了工程普遍存在的装配不确定性问题,并以组合梁和根部柔性梁为例,开展了不确定性参数识别、量化、模型验证等问题的研究[14-15]。张冬冬和郑宗勇等采用响应面方法对复杂结构的不确定性分析进行了深入研究[16-17]。张保强等采用贝叶斯模型进行不确定性的分析和模型修正[18-21]。
对于考虑不确定性因素的复合材料加筋壁板分析模型的验证问题,由于构件在服役条件下需要考虑的不确定性因素较多,开展相关的工程实验具有复杂性,目前现有的相关文献仍然缺乏。本文针对复合材料加筋壁板后屈曲有限元模型,建立了一种考虑不确定性因素模型评估方法,并系统介绍了分析方法和流程。最后利用该分析方法和流程,对加筋壁板分析模型进行实验验证和确认。本文研究形成的模型验证方法为大型飞机虚拟试验高精度建模提供参考。
1 考虑不确定性参数模型验证方法 1.1 参数显著性分析复合材料加筋壁板结构的不确定性参数较多,需要选取那些对分析结果影响较大的参数。本文利用正交试验设计方法构建正交表,并采用方差分析法进行参数的显著性分析。
在方差分析中,对因素xi(i=1, 2, …, n),给定显著水平α (通常取α=0.01和α=0.05),从F分布表上查Fα值,即求上α分位点。如果F值Fi>Fα,则认为因素xi对结果的影响是显著的[22]。
1.2 代理模型不确定性分析实质上是一个大量、随机模拟的过程,基于传统有限元方法对结构后屈曲分析时,其单次分析成本较高,若直接采用有限元模型进行不确定性分析,耗时昂贵。在工程中,一般采用代理模型进行不确定性分析。为获得满足精度的代理模型,通常需要选择样本点,构建样本空间。
中心组合试验设计作为代理模型研究中常用的构造样本空间的试验设计方法,其试验点分布见图 1。通常由3部分试验组成,首先是对每个因素(n个)2个水平值(最高和最低水平),共2n次试验;其次在相对于中心点单个因素偏移±α处各进行一次试验,试验次数为2n次;第3部分试验是在中心点(0,0,…,0)作nc次重复试验,由于数值计算试验的结果不存在物理试验那样的不确定性,所以对数值试验来说,这一步只作一次试验,即nc=1,3部分试验次数共为N=2n+2n+nc次。由于该方法设计时可分批进行,在某种程度上降低了试验次数。
|
| 图 1 两因素和三因素中心组合试验点分布 Fig. 1 Test point distributions of two-factor and three-factor central composite designs |
代理模型构建采用Kriging模型。虽然二阶多项式响应面模型表达形式直观、操作方便,但若参数较多,采用多项式响应面时,响应面方程较为复杂,反而降低预测精度,而Kriging模型可以很好地解决多参数的代理模型。该方法在描述非线性程度较高的问题中具有更好的预测效果,尤其针对本文所涉及的后屈曲特性的分析计算。
Kriging模型是基于统计的插值模型[23],包含回归部分与随机过程2部分:
| $ \mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{F}}^{\rm{T}}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{\beta }} + \mathit{\boldsymbol{Z}}(\mathit{\boldsymbol{x}}) $ | (1) |
式中:F (x)为x的多项式,用于模拟全局近似;β为回归系数;Z (x)为正态随机函数,用于模拟局部偏差,Z (x)具有以下统计特性,均值、方差、协方差分别为:
| $ {E(\mathit{\boldsymbol{Z}}(\mathit{\boldsymbol{x}})) = 0} $ | (2) |
| $ { {\rm{var}} (\mathit{\boldsymbol{Z}}(\mathit{\boldsymbol{x}})) = {\sigma ^2}} $ | (3) |
| $ \begin{array}{*{20}{c}} {{\rm{Cov}} (\mathit{\boldsymbol{Z}}({\mathit{\boldsymbol{x}}_i}), \mathit{\boldsymbol{Z}}({\mathit{\boldsymbol{x}}_j})) = {\sigma ^2}[{\mathit{\boldsymbol{R}}_{ij}}({\theta _k}, x_i^k, x_j^k)]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i, j \in \{ 1, 2, \cdots , m\} ;k \in \{ 1, 2, \cdots , n\} } \end{array} $ | (4) |
其中:σ2为方差;R ij(θ, x i, x j)为以θ为参数的相关系数矩阵,本文取高斯函数作为相关系数矩阵,即
| $ {\mathit{\boldsymbol{R}}_{ij}}({\theta _k}, x_i^k, x_j^k) = {\rm{exp}}( - {\theta _k}|x_i^k - x_j^k{|^2}) $ | (5) |
由最大似然估计可以得到方差σ2、相关系数矩阵参数θk和回归系数β *:
| $ {{\sigma ^2} = \frac{{{{(\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\beta }})}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\beta }})}}{m}} $ | (6) |
| $ {{\mathit{\boldsymbol{\beta }}^*} = {{({\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{F}})}^{ - 1}}({\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{Y}})} $ | (7) |
式中:R为相关系数矩阵。参数θk可以视为因素xk对响应影响程度的测量。用Kriging模型对非样本点xnew的预测响应与方差为
| $ {\mathit{\boldsymbol{\hat y}}({x_{{\rm{new}}}}) = {\mathit{\boldsymbol{f}}^{\rm{T}}}{\mathit{\boldsymbol{\beta }}^*} + {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}^*}} $ | (8) |
| $ {{{\hat \sigma }^2}({x_{{\rm{new}}}}) = {\sigma ^2}[1 + {\mathit{\boldsymbol{D}}^{\rm{T}}}{{({\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{F}})}^{ - 1}}\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}}]} $ | (9) |
式中:
| $ {{r_i}({\theta _k}, x_{{\rm{ new }}}^k, x_i^k) = {\rm{exp}}( - {\theta _k}|x_{{\rm{ new }}}^k - x_i^k{|^2})} $ | (10) |
| $ {{\mathit{\boldsymbol{\gamma }}^*} = {\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{\beta }}^*})} $ | (11) |
| $ {\mathit{\boldsymbol{D}} = {\mathit{\boldsymbol{f}}^{\rm{T}}} - {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}}} $ | (12) |
式中:r、f为将预测点处值xnew分别代入相关系数矩阵R和回归部分F得到的向量或矩阵。
无论选用何种代理模型,都需要对代理模型的拟合程度进行检验。这里选用R2检验,R2越接近1说明响应面方程拟合度越好。即
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^m {{{({y_i} - {{\hat y}_i})}^2}} }}{{\sum\limits_{i = 1}^m {{{({y_i} - \bar y)}^2}} }} $ | (13) |
式中:
通过构建显著参数与结构响应指标之间的响应面,就确定了两者之间的函数关系,对显著参数进行大量抽样,并利用蒙特卡罗模拟可获得响应指标的概率分布。
1.4 基于试验数据的模型验证方法对复合材料加筋壁板模型的验证可从2个层面比较分析:第1个层面,从模型本身上讲,可选取典型试验件的试验结果作为对比对象,通过分析屈曲破坏试验的失效模式和典型的载荷-应变曲线来确定分析与试验的一致性。
第2个层面,从具有统计意义的量化指标上进行验证分析。在工程应用中,常用的验证指标主要有:均值比较、假设检验、贝叶斯方法以及面积度量方法[4, 13]。由于本文所研究的复合材料加筋壁板试验数据较少,不具有统计特征,因此,在进行模型验证时,将主要采取均值比较的方法,并结合假设检验进行验证。
均值比较可采用如下方式计算:
| $ Z = \left| {\frac{{E({Y_{{\rm{mod}}}}) - E({Y_{{\rm{exp}}}})}}{{E({Y_{{\rm{exp}}}})}}} \right| \times 100\% $ | (14) |
通过均值比较可获得模型预测值Ymod与试验值Yexp的集中程度[13],在此基础上,利用响应指标的概率分布,获得95%置信度时置信区间,从而确定预测值与试验值的离散情况。
1.5 模型验证流程综合以上分析方法,考虑不确定性参数的模型验证流程如图 2所示。首先对不确定参数进行显著性分析,进行参数的筛选。然后借助中心组合试验设计和Kriging模型构建代理模型,并基于该模型进行蒙特卡罗随机模拟,获取结构响应特性概率分布。最后,基于试验数据进行模型验证,以确定模型的可靠性。
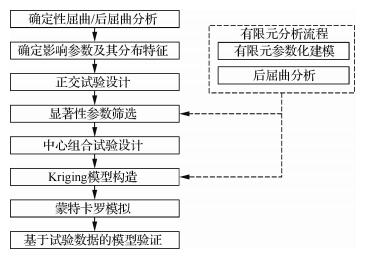
|
| 图 2 模型验证流程 Fig. 2 Model validation process |
基于上述模型验证方法和流程,对复合材料加筋壁板后屈曲模型进行验证。
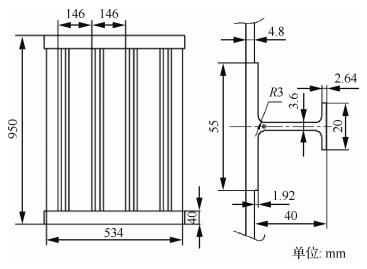
2.1 结构简介复合材料加筋壁板由蒙皮和4个“工”字形筋条组成。几何尺寸如图 3所示,纵向长度为950 mm,横向长度为534 mm,筋条间距为146 mm,筋条和蒙皮采用胶接连接。各个部位铺层如表 1所示,单层厚度为0.12 mm。

|
| 图 3 加筋壁板几何参数 Fig. 3 Geometric parameters of stiffened panel specimens |
| 组件 | 铺层信息 |
| 蒙皮 | [45/0/-45/90/±45/02/452/0/-452/0/452/90/-452/0]s |
| 下缘条 | [45/03/-45/90]s |
| 腹板 | [45/02/45/02/-45/90/-45/02/-45/02/45]s |
| 自由缘条 | [45/02/-45/02/-45/02/-45/90]s |
试件材料为复合材料CCF300/BA9916,界面胶层为J116。
2.2 试验结果对复合材料加筋壁板进行轴压试验,采用在试验件端部加压方式进行,为防止试件受压两端压劈和保证压力分布均匀,试验件端部采用玻璃钢加强片及专用夹具将试件端头侧面夹紧,并在翼肋的位置上由刀口对试件提供支持。将试验件及夹具放在压力试验机平台上,试验件加载形心位置调正压心,使试验机平台的中心线与加筋壁板横截面形心轴对齐。试验加载方式及支持状态如图 4所示。

|
| 图 4 试验加载方式及支持 Fig. 4 Test loading mode and supporting |
共进行了5个试验件的破坏试验,获得了5组破坏载荷,相关结果如表 2所示。本试验数据来源于中国飞机强度研究所研发的加筋壁板试验数据库,该数据库收录了各类试验产生的模型数据、试验数据以及对应的描述性报告[24]。
| 试验件编号 | 1# | 2# | 3# | 4# | 5# | 均值 |
| 破坏载荷/kN | 1 148 | 1 226 | 1 196 | 1 184 | 1 188 | 1 188.4 |
筋条和蒙皮选用壳单元模拟,界面胶层采用内聚力单元模拟,内聚力单元与壳间采用共节点连接方式模拟。为了准确模拟复合材料的失效过程,采用Hashin失效准则,并设置损伤演化规律。
复合材料加筋壁板有限元边界如图 5所示,远离加载端边界固支,次端部边界约束U1、U2,翼肋边界约束壁板节点Y向自由度,非加载边自由。有限元模型节点总数为13 181个,单元总数为10 368个。

|
| 图 5 复合材料加筋壁板有限元模型边界条件 Fig. 5 Finite element model boundary condition of stiffened composite panel |
为确定对指标具有显著影响的参数,选取复合材料加筋壁板的几何参数、材料参数以及加载参数(加载点X方向坐标、形心高度)等作为不确定性参数。对于材料参数,本研究所对复合材料CCF300/BA9916按照相关标准进行了测试,获得了统计测试结果;对于几何参数分布取为公差范围内的正态分布;加载参数的取值根据加载设备的精度来确定。各个参数的均值和标准差见表 3。
| 参数类型 | 参数意义 | 均值 | 标准差 |
| 几何参数 | 壁板单层厚度Tl/mm | 0.12 | 0.001 2 |
| 筋条下缘条宽度Ws1/mm | 55 | 0.55 | |
| 筋条上缘条宽度Ws3/mm | 20 | 0.2 | |
| 筋条腹板高度HS/mm | 40 | 0.4 | |
| 筋条间距B/mm | 146 | 1.46 | |
| 翼肋间距Lrib/mm | 630 | 6.3 | |
| 材料参数 | 1方向弹性模量E11/MPa | 129 000 | 6 450 |
| 2方向弹性模量E22/MPa | 9 820 | 491 | |
| 泊松比ν12 | 0.311 | 0.016 | |
| 12方向剪切模量G12/MPa | 5 290 | 264.5 | |
| 13方向剪切模量G13/MPa | 5 290 | 264.5 | |
| 23方向剪切模量G23/MPa | 3 430 | 171.5 | |
| 纤维方向拉伸强度XT/MPa | 1 720 | 86 | |
| 纤维方向压缩强度XC/MPa | 1 230 | 61.5 | |
| 垂直于纤维方向拉伸强度YT/MPa | 70 | 3.5 | |
| 垂直于纤维方向压缩强度YC/MPa | 220 | 11 | |
| 剪切强度S/MPa | 134 | 6.7 | |
| 加载参数 | 加载点X向坐标Xdisp/mm | 292 | 8.76 |
| 截面形心高度HRP/mm | 9.805 | 0.294 |
复合材料加筋壁板后屈曲特性的计算,初始参数共计19个,包含几何参数、材料参数以及加载参数。针对这19个变量,选用L54(326)型正交表进行显著性参数分析,选取极限载荷作为试验指标,利用有限元分析计算设计矩阵的试验结果。
通过正交表的方差分析,获得各个参数的F值如图 6所示,查表Fα的区间为[3.251 9, 5.229],根据此区间,判断对极限载荷具有显著影响的参数分别为:①沿纤维方向弹性模量E11;②壁板单层厚度Tl;③纤维方向压缩强度XC;④筋条间距B;⑤筋条上缘条宽度Ws3;⑥剪切模量G12;⑦筋条下缘条宽度Ws1。
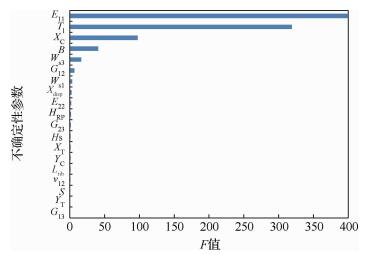
|
| 图 6 不确定性参数显著性分析 Fig. 6 Significance analysis of uncertain parameters |
通过以上分析,获得对后屈曲极限载荷具有显著影响的参数有7个,采用中心组合试验设计方法进行试验设计时,需要安排79次试验。将试验矩阵对应的参数值输入有限元模型,得到样本点对应的后屈曲载荷。
利用上述获得的样本,建立Kriging模型。对应Kriging模型,回归部分采用二次回归模型,相关函数为Gauss函数。在模型建立后,对模型进行R2检验,可得R2=1.00,满足精度要求。
针对该模型设计10组样本进行测试,测试结果,见表 4。由表 4可见,选取10组样本进行测试,其相对误差均在10%以内,说明构造的Kriging模型具有较高的精度,可代替复合材料加筋壁板后屈曲有限元的计算。
| 样本编号 | 后屈曲有限元结果/N | Kriging模型计算结果/N | 相对误差/% |
| 1 | 1 352 430 | 1 326 512 | -1.92 |
| 2 | 1 295 830 | 1 293 201 | -0.2 |
| 3 | 1 261 520 | 1 259 545 | -0.16 |
| 4 | 1 226 060 | 1 225 546 | -0.04 |
| 5 | 1 191 520 | 1 191 236 | -0.02 |
| 6 | 1 156 610 | 1 156 550 | -0.01 |
| 7 | 1 120 850 | 1 121 487 | 0.06 |
| 8 | 1 084 740 | 1 086 187 | 0.13 |
| 9 | 1 113 880 | 1 050 470 | -5.69 |
| 10 | 1 075 690 | 1 014 336 | -5.7 |
根据1.4节所述模型验证方法,首先从第1个层面进行验证。图 7、图 8分别为1#试验件的破坏状态和典型部位的载荷-应变曲线。分析图 7可见,在轴压载荷作用下,复合材料加筋壁板最终的失效状态为中间2根筋条发生压溃断裂,而且第2根筋条比第3根筋条更早的出现压溃。有限元分析的破坏区域和破坏顺序与试验结果保持一致。
|
| 图 7 试验与分析破坏状态对比 Fig. 7 Failure state comparison of test and analysis |

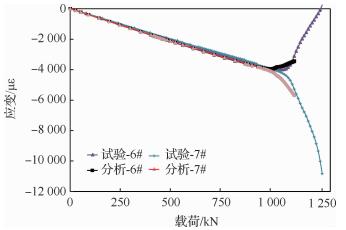
|
| 图 8 试验与分析的载荷-应变曲线 Fig. 8 Load-strain curves of test and analysis |
由图 8分析可知,载荷-应变曲线首先是线性发展,在达到一个较大的载荷1 033 kN后,曲线斜率发生小幅变化,这意味着结构开展出现初始屈曲。当载荷继续增大时,结构逐步向后屈曲模式演变,直到结构发生屈曲破坏,载荷-应变曲线开始拐折。此时即为结构最终的承载能力,极限载荷为1 148 kN。从曲线上看,试验与分析破坏模式基本一致,且关键部位的应变数据对比较好。
从统计意义上进行验证,利用表 3的参数分布进行多次抽样,并代入Kriging模型进行计算。当抽样次数达到30 000次时,后屈曲载荷均值可获得稳定的统计结果。此时,后屈曲载荷分布直方图如图 9所示,图中“*”为试验结果。对计算结果统计分析,获得后屈曲载荷平均值为1 174.77 kN,标准差47.80 kN,95%置信度时置信区间为[1 081.1,1 268.5] kN。试验均值为1 188.4 kN,分析与试验均值的相对误差为1.15%,可见,具有较高的一致性。

|
| 图 9 后屈曲载荷直方图和试验结果 Fig. 9 Histogram of post-buckling loads and test results |
1) 模型验证中充分考虑了材料组分和几何尺寸的不确定性,从而避免因随机因素干扰对模型可靠与否做出错误的判断。
2) 不确定参数的选择通过参数显著性分析来实现。为了保证计算精度和效率,选取对模型预测结果具有较大影响的参数,而去除影响小的参数。
3) 文中提出了考虑不确定因素的复合材料加筋壁板后屈曲分析有限元模型验证方法和流程,从模型本身和统计学2个层面对模型进行了验证,具有一定工程实用性,可以对复合材料结构线性和非线性有限元模型进行确认。
| [1] |
张国凡, 段世慧, 吴存利. 基于有限元的加筋板结构后屈曲分析方法研究[J]. 强度与环境, 2013, 40(2): 43-50. ZHANG G F, DUAN S H, WU C L. Method research for post-buckling analysis of stiffened structure base on FEM[J]. Structure & Environment Engineering, 2013, 40(2): 43-50. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [2] |
汪厚冰, 林国伟, 韩雪冰, 等. 复合材料帽形加筋登板剪切屈曲性能[J]. 航空学报, 2019, 40(8): 222889. WANG H B, LIN G W, HAN X B, et al. Shear buckling performance of composite hat-stiffened panels[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(8): 222889. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [3] |
解江, 冯振宇, 赵彦强, 等. 含随机不确定参数复合材料薄壁结构吸能特性评估方法研究[J]. 振动与冲击, 2015, 34(22): 109-114. XIE J, FENG Z Y, ZHAO Y Q, et al. Evaluation method based on probability for energy-absorbing composite structures with uncertain parameters[J]. Journal of Vibration and Shock, 2015, 34(22): 109-114. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [4] | BEN H, THACKER T L P.A simple probabilistic validation metric for the comparison of uncertain model and test results[C]//The 16th AIAA Non-Deterministic Approaches Conference.Reston: AIAA, 2014. |
| [5] | CHRISTOPHER J R, WILLIAM L O. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(2011): 2131-2144. |
| Click to display the text | |
| [6] | LEE M C W, DONALD W K, RICHARD D, et al. A study on the robustness of two stiffened composite fuselage panels[J]. Composite Structures, 2010, 92: 223-232. |
| Click to display the text | |
| [7] |
李湘郡, 李彦斌, 郭飞, 等. C/C复合材料的压缩强度分布与可靠性评估[J]. 航空学报, 2019, 40(8): 222853. LI X J, LI Y B, GUO F, et al. Compression strength distribution and reliability assessment of C/C composites[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(8): 222853. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [8] | LI S Z, EDWIN R, KRISTOF M, et al. Vibration-based estimation of axial force for a beam member with uncertain boundary conditions[J]. Journal of Sound and Vibration, 2013, 332: 795-806. |
| Click to display the text | |
| [9] | ISAAC E, CLÉMENT S. Remedy to overestimation of classical interval analysis:Analysis of beams with uncertain boundary conditions[J]. Shock and Vibration, 2012, 20(2012): 143156. |
| Click to display the text | |
| [10] | MARC P M, CHRISTIAN S, JAVIER A. Nonparametric stochastic modeling of structures with uncertain boundary conditions/coupling between substructures[J]. AIAA Journal, 2013, 51(6): 1296-1308. |
| Click to display the text | |
| [11] | DANIEL C K, SONNY N. Propagation of uncertainty in test-analysis correlation of substructured spacecraft[J]. Journal of Sound and Vibration, 2011, 330: 1211-1224. |
| Click to display the text | |
| [12] |
李维.基于不确定性分析与模型验证的计算模型可信性研究[D].西安: 西北工业大学, 2015. LI W. Credibility of computational mode based on uncertainty analyses and model verification[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [13] |
聂小华, 吴存利. 考虑不确定性因素的有限元屈曲模型验证[J]. 力学与实践, 2017, 39(5): 460-467. NIE X H, WU C L. Validation and confirmation of static finite element model by considering uncertainties[J]. Mechanics in Engineering, 2017, 39(5): 460-467. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [14] |
陈学前, 肖世富, 刘信恩. 不确定性因素结构的有限元建模与确认[J]. 噪声与振动控制, 2013, 33(5): 26-29. CHEN X Q, XIAO S F, LIU X E. Finite element modeling and validating of structural uncertainty factors[J]. Noise and Vibration Control, 2013, 33(5): 26-29. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [15] |
陈学前, 肖世富, 刘信恩, 等. 根部柔性梁的不确定性建模与确认[J]. 力学与实践, 2012, 34(1): 52-56. CHEN X Q, XIAO S F, LIU X E, et al. The uncertain modeling and validation for a cantileverwith flexible root[J]. Mechanics in Engineering, 2012, 34(1): 52-56. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [16] |
张冬冬, 郭勤涛. Kriging响应面代理模型在有限元模型确认中的应用[J]. 振动与冲击, 2013, 32(9): 187-191. ZHANG D D, GUO Q T. Application of Kriging response surface in finite element model validation[J]. Journal of Vibration and Shock, 2013, 32(9): 187-191. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] |
郑宗勇.复杂联接结构非线性有限元精确建模和模型确认方法研究[D].南京: 南京航空航天大学, 2010. ZHENG Z Y. Study on nonlinear finite element precise modeling and model validation methods of complex joint structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [18] |
张保强.热结构不确定性动力学仿真及模型确认方法研究[D].南京: 南京航空航天大学, 2012. ZHANG B Q. Uncertainty simulation of thermal structural dynamics and model validation method research[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). |
| Cited By in Cnki (9) | Click to display the text | |
| [19] |
赵亮, 杨战平. 考虑认知不确定性的模型确认贝叶斯因子法[J]. 计算机应用研究, 2016, 33(2): 473-477. ZHAO L, YANG Z P. Bayer factor for model validation under epistemic uncertainty[J]. Application Research of Computers, 2016, 33(2): 473-477. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [20] |
刘伯权, 刘喜, 吴涛. 基于共轭先验分布的深受弯构件受剪承载力概率模型分析[J]. 工程力学, 2015, 32(4): 169-177. LIU B Q, LIU X, WU T. Probabilistic shear strength model for deep flexural members based on conjugate prior distribution[J]. Engineering Mechanics, 2015, 32(4): 169-177. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [21] |
韩芳, 钟冬望, 汪君. 基于贝叶斯法的复杂有限元模型修正研究[J]. 振动与冲击, 2012, 31(1): 39-43. HAN F, ZHONG D W, WANG J. Complicated finite element model updating based on Bayesian method[J]. Journal of Vibration and Shock, 2012, 31(1): 39-43. (in Chinese) |
| Cited By in Cnki (46) | Click to display the text | |
| [22] |
王岩, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012: 153-203. WANG Y, SUI S L. Experimental design and MATLAB data analysis[M]. Beijing: Tsinghua University Press, 2012: 153-203. (in Chinese) |
| [23] |
郑建强, 向锦武, 罗漳平, 等. 民机机身下部结构耐撞性优化设计[J]. 航空学报, 2012, 33(4): 640-648. ZHENG J Q, XIANG J W, LUO Z P, et al. Crashworthiness optimization of civil aircraft subfloor structure[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(4): 640-648. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [24] |
关德新.某型飞机平尾壁板选型试验研究[R].西安: 中国飞机强度研究所, 2009. GUAN D X. Research on the style-selection test of a aircraft horizontal tail panel[R]. Xi'an: Aircraft Strength Research Institute of China, 2009(in Chinese). |



