2. 昆明理工大学 云南省内燃机重点实验室, 昆明 650500
2. Yunnan Province Key Laboratory of Internal Combustion Engines, Kunming University of Science and Technology, Kunming 650500, China
基于气体润滑技术的空气静压轴承具有高速、精密、低摩擦的特点,因而被广泛应用在惯导陀螺马达、空间模拟装置、低速伺服转台等航空航天领域[1-2]。特别是在大型高精度空气静压轴承转台中,作为核心部件的空气静压轴承不仅要保障转台实现极高的回转精度,同时要求振动小、噪声低,并且具有高稳定性和耐振动冲击能力。支撑部件的间隙、支撑刚度和不平衡分布等动力学参数和气动流场气动力等随着工作条件和支撑系统状态变化而变化,使得系统结构振动具有非线性时变特征,因此,对空气轴承动力学特性要求更为严格。根据冲击射流理论和气动弹性力学可知,气膜入口在一定流速的来流作用下,气浮块会受到流向以及横向的周期性变化的脉动压力,作为一个弹性支撑,脉动压力会引起结气浮块在平衡位置发生周期性振动,这种振动又会反过来改变气膜内流场结构[3]。气膜流体与固体气浮轴承之间相互耦合的涡激振动沿着流场运动方向传播,不仅影响系统的定位精度和进给精度,也会降低整个系统的加工精度和检测精度[4-5]。特别是当轴承表面负载分布不均匀时,载荷的重力不再通过支撑气膜的形心。轴承表面产生横倾角,气膜厚度不再均匀,导致气膜压力分布发生变化,并在侧向推力平面上产生压力分量。同时,轴承支撑面倾斜引发气膜流场变化,不仅会引起较大的轴承间隙测量误差,当局部涡激振动强度增强或与外界干扰信号发生谐振时,则会引起气膜失稳,甚至引发气锤现象[6-7]。因此,提高空气静压轴承的倾斜刚度和阻尼系数及研究载荷分布对气膜流场的影响对提高空气轴承稳定性和使用精度具有重要意义。
国内外学者在这方面做了大量有益探索,其中一部分学者通过研究空气静压轴承的静/动态倾侧特性进行了理论分析。Majumdar和Singh[8]对传统的多个凹槽止推轴承进行了深入比较,给出了方形凹槽止推轴承性能的设计曲线。在此基础上Singh和Rao[9-10]研究了偏置载荷作用下空气静压多孔矩形止推轴承的静态倾斜特性,对不同工作参数的静态特性进行了数值计算,并给出了气浮倾斜特性随气浮块形状、不同工作条件的变化规律。Al-bender和Brussel[11]采用小扰动法对圆形空气静压轴承的动态倾斜特性进行了研究,得到了倾斜刚度和阻尼系数随工作气膜改变的影响规律。Nakamura和Yoshimoto [12-13]研究了带有复合节流器的空气静压止推轴承倾斜力矩作用下的线性导轨系统中的静态倾斜特性,并与传统的小孔节流器止推轴承的特性进行比较,阐明了复合节流器空气静压止推轴承的实用性。然而,在实际气浮工作中,由于热变形、结构变形或工作偏载误差等原因,轴承不对中运动导致气膜厚度和压力分布不均匀,导致空气静压轴承静压刚度显著降低,对气浮系统的运动精度有很大的影响,甚至气浮支撑不稳定[14-16]。此外,空气静压推力轴承的刚度和阻尼等动态特性发生变化,也会引起气浮系统的微振动。Long和Deng[17]采用有限体积法计算了不同倾角下轴承的侧向力,研究了不同气腔直径和深度在发生倾斜角时对轴承的横向力产生的影响。Yoshimoto等[18]从理论和实验上研究了轴倾斜运动下带有复合节流器的空气静压矩形双垫推力轴承的动态特性。Jiang等[19-20]利用线性扰动建立了轴承的雷诺方程,研究了轴承参数对轴承静、动态特性的影响,并分析了多孔介质对空气轴承动刚度和阻尼系数的影响。Xu和Jiang[21]建立了3自由度气动静力推力轴承模型,并得到了轴承的稳定性、不平衡响应和强迫响应,全面研究了倾角和转速对轴承动态刚度和阻尼系数的影响。虽然国内外学者就空气静压轴承的偏载和动特性开展了相关的研究,但是主要集中在数值模拟和动特性系数(动刚度和动阻尼)的分析上,而对载荷分布与稳定性之间的关系与成因缺乏充分的解释和分析。
因此,本文以圆盘形中心供气小孔节流空气静压轴承为对象,基于涡激振动原理和振荡流体力学理论,在求解非定常流体力学方程的基础上,对空气静压止推轴承表面载荷分布不均匀时气浮倾斜特性随工作条件的变化规律开展研究。从理论和实验两方面研究空气静压止推轴承的微振动,并分析了倾斜力矩对轴承气膜内部涡动能量的影响,给出了不同工况下轴承偏载及正载下的工作条件和参数要求,明确偏载特性对空气静压止推轴承稳定性的影响因素及其相关结论。
1 理论模型空气静压轴承通过节流器形成的压力在气膜内形成压力梯度,气体流场的变化引起气膜内发生气旋涡动从而引发涡流激振效应。对于轴承的动特性和稳定性分析,归根到底取决于轴承气膜内流动激振的分析。现有研究气膜内流体动力学问题的方法是建立在雷诺方程基础上的,但是由于气膜厚度在微米级,传统方法认为速度参数沿气膜厚度方向变化,而压力沿气膜厚度方向不变,从而对Navier-Stokes方程进行定常简化,这样得到的雷诺方程本质是一个定常的方程。为了将雷诺方程应用于求解轴承的动态特性,就必须将流动参数与时间变量关联起来。采用振荡流体力学原理分析气膜激振,首先求解气膜内不做振动或涡动时的流场(即:定常场),然后以定常参数作为已知值再求解气膜的振荡流场(即:振荡速度场和振荡压力场),通过对气膜表面振荡压力的积分,即可得到作用在轴承表面的非定常流动力。由于微幅简谐振荡流的特点,可以将非定常参数表示为定常参数与振幅参数的关系,因此,用于描述空气静压轴承工作气膜流场特性的非定常连续方程、动量方程、能量方程等就可以转化为相应的振幅连续方程,振幅动量方程和振幅能量方程等,从而构成振荡流体力学的基本方程。
当空气轴承负载重心稍微偏离气膜形心导致气浮轴承发生倾斜时,气膜流场特性参数分布跟随改变,直接影响气膜支撑系统静态和动态特性。
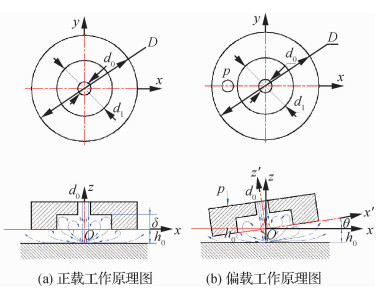
图 1所示为圆盘型中心供气小孔节流空气静压止推轴承在表面载荷分布发生偏载前后的结构示意图及相关参数:轴承外径D=200 mm;供气孔直径d0=0.2 mm;气腔直径d1=3 mm;气腔深度δ=0.2 mm;环境压力pa=0.1 MPa;供气压力ps=0.2~0.5 MPa;气膜间隙h=10~40 μm;环境温度T=293 K;气体动力黏度η=1.833×10-5 Pa·s;气体密度ρ=1.205 kg/m3;气体常数R=288 J/(kg·K)。
如图 1(a)所示,气膜流场的入口是位于圆盘型气浮轴承中心的小孔节流器,气源气体从供气孔径向均匀的呈直线向外流出,形成均匀的压力气膜。由于流动是径向的,根据流动连续性原理,通过坐标系内任意分度圆圆柱的流量Q都相等:
|
| 图 1 空气静压止推轴承示意图 Fig. 1 Schematic diagram of aerostatic bearing |
| $ Q = 2\pi \sqrt {{x^2} + {y^2}} {v_{\rm{r}}} $ | (1) |
式中:vr为半径方向流速。即
| $ {v_{\rm{r}}} = \frac{Q}{{2\pi \sqrt {{x^2} + {y^2}} }} = \sqrt {{u^2} + {v^2}} $ | (2) |
其中:u和v分别为沿x和y方向的气流速度。
根据流函数的定义并令积分常数为零,可得此时供气孔处流函数:
| $ \varphi = \pm \frac{Q}{{2\pi }}{\rm{arctan}}\frac{y}{x}\;\:\frac{{{d_0}}}{2} < x < \frac{D}{2},\frac{{{d_0}}}{2} < y < \frac{D}{2} $ | (3) |
根据射流理论可知,高压气体从供气孔流出就会与周围介质发生剧烈的动量交换和紊动扩张,在流体的外边界形成速度不连续的间断面,并将周围原有静止的气体分子卷吸到射流过程中,从而形成涡旋,从图 1中可以看到气旋集中发生在过渡区并沿着壁面射流区流出,在气腔底部中心定义坐标系Oxy,气体沿供气孔z方向流动,当气体通过过渡区后,射流方向发生改变,流动速度沿x和y方向运动。定义气腔高度为δ,气膜厚度为h,正载下气膜厚度为h0, 则供气出口总的冲击高度为h=δ+h0。
当正载工作时如图 1(a)所示,轴承气膜内x、y方向的速度[22]为
| $ u = \left\{ {\begin{array}{*{20}{l}} { - \frac{1}{{2u}} \cdot \frac{{\partial p}}{{\partial x}} \cdot z({h_0} + \delta - z) + \frac{{{u_2} - {u_1}}}{{h + \delta }} \cdot z + {u_1}}&{0 < \sqrt {{x^2} + {y^2}} < \frac{{{d_1}}}{2}}\\ { - \frac{1}{{2u}} \cdot \frac{{\partial p}}{{\partial x}} \cdot z({h_0} - z) + \frac{{{u_2} - {u_1}}}{h} \cdot z + {u_1}}&{\frac{{{d_1}}}{2} < \sqrt {{x^2} + {y^2}} < \frac{D}{2}} \end{array}} \right. $ | (4) |
| $ v = \left\{ {\begin{array}{*{20}{l}} { - \frac{1}{{2u}} \cdot \frac{{\partial p}}{{\partial y}} \cdot z({h_0} + \delta - z) + \frac{{{v_2} - {v_1}}}{{h + \delta }} \cdot z + {v_1}}&{0 < \sqrt {{x^2} + {y^2}} < \frac{{{d_1}}}{2}}\\ { - \frac{1}{{2u}} \cdot \frac{{\partial p}}{{\partial y}} \cdot z({h_0} - z) + \frac{{{v_2} - {v_1}}}{h} \cdot z + {v_1}}&{\frac{{{d_1}}}{2} < \sqrt {{x^2} + {y^2}} < \frac{D}{2}} \end{array}} \right. $ | (5) |
式中:p为压力;μ为气体黏度(Pa·s);u1,u2,v1,v2为轴承两侧面在x,y方向上的运动速度(m/s),当z=0时,u=u1,v=v1,当z=h+δ,u=u2,v=v2。
根据动量守恒可知,过渡区中压力分布规律[23]可以表示为
| $ p = {p_{\rm{m}}} \cdot {\rm{exp}}\left( { - 0.693\frac{{{y^2}}}{{{h^2}}}} \right) $ | (6) |
式中:pm为轴线压力,则p应满足:
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left( {{{({h_0} + \delta )}^3}p\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{{({h_0} + \delta )}^3}p\frac{{\partial p}}{{\partial y}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {12\mu \frac{\partial }{{\partial t}}(p({h_0} + \delta )) + }\\ {6\mu \left[ {({u_1} + {u_2})\left( {\frac{{\partial (p({h_0} + \delta ))}}{{\partial x}} + } \right.} \right.}\\ {\left. {\left. {({v_1} + {v_2})\frac{{\partial (p({h_0} + \delta ))}}{{\partial y}}} \right)} \right]} \end{array} \end{array} $ | (7) |
其中:半径要求
壁面射流区中p满足:
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}\left( {h_0^3p\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {h_0^3p\frac{{\partial p}}{{\partial y}}} \right) = 12\mu \frac{\partial }{{\partial t}}(p{h_0}) + }\\ {6\mu \left[ {({u_1} + {u_2})\frac{{\partial (p{h_0})}}{{\partial x}} + ({v_1} + {v_2})\frac{{\partial (p{h_0})}}{{\partial y}}} \right]} \end{array} $ | (8) |
其中:半径要求
当偏载工作时如图 1(b)所示,Oxy面沿O点发生偏移,气浮块一侧抬高另一侧降低,偏移量为
| $ {h_{{\rm{eff}}}} = \left\{ {\begin{array}{*{20}{l}} {h + \Delta h}\\ {h - \Delta h} \end{array}} \right. $ | (9) |
则壁面射流区中p满足:
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left( {{{({h_{{\rm{eff}}}})}^3}p\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{{({h_{{\rm{eff}}}})}^3}p\frac{{\partial p}}{{\partial y}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {12\mu \frac{\partial }{{\partial t}}(p{h_{{\rm{eff}}}}) + }\\ {6\mu \left[ {({u_1} + {u_2})\frac{{\partial (p{h_{{\rm{eff}}}})}}{{\partial x}} + ({v_1} + {v_2})\frac{{\partial (p{h_{{\rm{eff}}}})}}{{\partial y}}} \right]} \end{array} \end{array} $ | (10) |
其中:半径要求
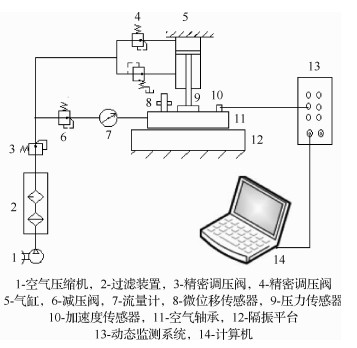
实验原理图如图 2所示,实验中主要测试空气静压轴承的承载力和气膜刚度的大小以及空气静压轴承自激微振动特性及幅频特性。对不同工作条件下的微振动大小进行测量并对比研究。微振动测试装置主要由气源、过滤器、加载装置、检测装置和数据处理部分等组成。
|
| 图 2 气浮微振动测试原理图 Fig. 2 Schematic of air floatation micro-vibration test |
实验时被测空气静压轴承水平置于00级大理石隔振平台上,气源压力气体经过过滤装置除去气体中水分、灰尘等杂质,并经SMC高精密调压阀输送到气路中。采用气缸加载的方式控制负载的大小,通过控制气缸的进气量和压力调节对气浮轴承施加的负载压力,气浮轴承承载由压力传感器测得。随着供气压力的变化,相同负载条件下气膜厚度会随之改变,气膜厚度由微位移传感器测得;为保证气膜厚度可控可测,实时根据供气压力大小调整负载大小,以保证气膜厚度精确可控。微振动信号由贴敷在轴承表面的3个单轴加速度传感器(PCB Piezotronics)检测。为检测三维气旋对气浮轴承表面的作用效果,分别在气膜高度方向和垂直气膜方向上布置两组加速度传感器。数据处理部分采用比利时公司的LMS动态检测系统。
2.2 实验条件及设备实验条件为标况大气压、室温25 ℃、湿度40%~50%,隔振平台为00级花岗石平台,三轴方向的固有频率均为1.2~2.0 Hz。
图 3为气浮微振动测试实验台和相关设备。测试实验台由振动测试和数据采集装置组成,如图 3 (a)所示实验台采用光学隔振平台,气源装置采用空气压缩机,经过高精密过滤减压组件后,将高压气体同时通入加载气缸和气浮轴承中,耗气量由流量计得到。图 3(b)为实验测试部分。测得微振动信号由频谱仪实时采集和记录,处理后最终显示在PC屏幕上。如图 3(c)所示:压力传感器(BSHS-1)读取气缸垂直作用在气浮轴承上的承载力大小;气膜厚度由微位移传感器(DGC-8ZG/D,精度0.01 μm)测得;LMS(SCADAS)共12个通道,前端升级动态检测系统的频率采集范围是0~40 MHz,扫描精度±2%;微振动信号由2个单轴PCB加速度传感器检测,具体型号分别为:① LW195334,灵敏度为100.8 mV/g,BIAS级别为11.0 VDC;②LW195333,灵敏度为99.6 mV/g,BIAS级别为11.1 VDC。

|
| 图 3 气浮微振动测试装置 Fig. 3 Micro vibration test of air floatation |
搭建微振动测试平台如图 3(a)所示,为了验证微振动的产生原因主要是由三维气旋波动引起的,将2个单轴方向PCB传感器安装在气浮块的上表面和周向侧面如图 3(c)所示,从而总结出空气静压轴承在不同工作条件及不同方向上的幅频特性。当空气静压轴承表面载荷分布不均匀时,等效在轴承表面发生偏载作用,导致整个气膜内湍动气流不对称流动。实验进一步对比分析了发生不同偏载时,空气静压轴承微振动特性的变化规律及分布载荷位置对空气静压轴承微振动的影响。标定实验后,每组测试数据重复3~5次,偏离平均值较大的数值舍去。图 4所示为分布载荷测试示意图,在轴承背面标识出不同半径的分布圆(图 4(a)),根据偏载情况选择合适的配重砝码布置于相应的力臂分布圆上,从而等效出载荷分布不均匀时在轴承表面形成的偏载力矩。图 4(b)及图 4(c)分别为配重砝码和等效偏载作用效果。

|
| 图 4 分布载荷测试示意图 Fig. 4 Schematic diagram of partial load moment test |
表 1所示为空气静压轴承在不同载荷重量及分布位置的载荷力矩数据表,a、b、c、d 4个点如4(a)所示,每个作用点上分布相应质量砝码后对空气静压轴承施加的载荷如表中数据所示。例如当a、b两点同时作用2 kg载荷后,则轴承受到载荷力矩为3 N·m。同理,当轴承上施加多个载荷或者不同方向上作用载荷时,可以根据力矩矢量叠加原理求得作用在轴承上的载荷力矩。发生偏载时,气膜内局部气阻和气容的变化可以消耗更多的湍流动能。因此,有必要着重研究载荷分布在不均匀时气膜内部涡激振动的敏感因素。
| 不同载荷下 偏载力矩/kg |
载荷力矩/(N·m) | |||
| a | b | c | d | |
| 0.5 | 0.25 | 0.5 | 1 | 2.5 |
| 1 | 0.5 | 1 | 2 | 5 |
| 2 | 0.75 | 1.5 | 3 | 7.5 |
| 5 | 1 | 2 | 4 | 10 |
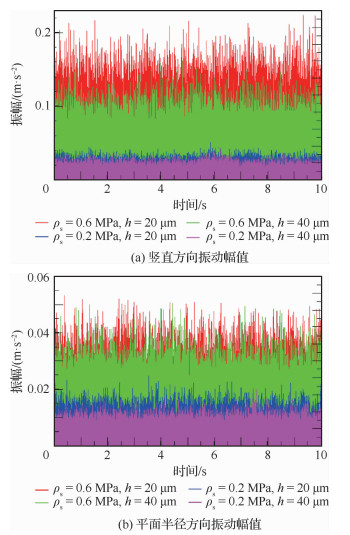
根据数值模拟及实验观察分析,气膜内的涡激振动是由于三维的气流湍动和壁面之间的耦合作用引起的,所以空气轴承在工作过程中表现的微振动也是三维方向的。如图 5所示:在竖直方向和平面半径方向上,ps=0.2 MPa和ps=0.6 MPa下,大供气压力下振动幅值明显比小供气压力下的振动幅值大,且相同条件下沿竖直方向的微振动幅值远大于沿平面半径方向的微振动幅值。其次,较小的气膜厚度会带来更大的振动强度。
|
| 图 5 不同供气压力下的时域对比图 Fig. 5 Time domain comparison chart with different gas supply pressure |
由于气浮支承的振动受供气压力的影响较大,供气压力越大气膜振动越大,而气膜厚度的改变对微振动的影响主要对沿垂直高度方向上的微振动幅值增强较明显,而对沿平面半径方向的微振动影响相对较小,因为气膜厚度变化在竖直方向上给气旋(特别是压力腔内主旋)形成和发展提供了一定的变化空间和发展裕量。另一方面,在不同供气压力及不同轴向时,小气膜厚度(h=20 μm)的微振动幅值比大气膜厚度(h=40 μm)的微振动幅值略大。这是因为,当轴承气膜较大时,气膜内部的气旋可以很好地释放,从而引起支撑气膜局部振动更小;而当气膜较小时,气膜被压缩区域的局部压力增加,整个流场内部气流不稳定,导致微振动幅值增大。
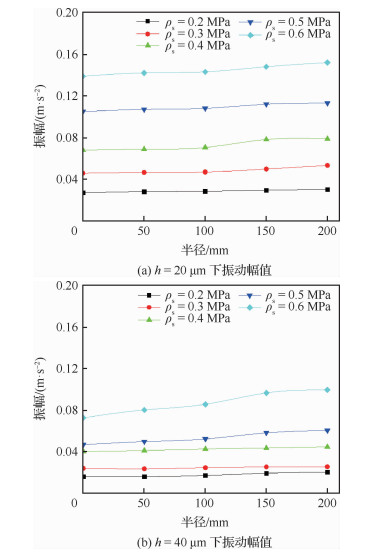
进一步对比图 6中不同气膜高度下垂直方向微振动强度可以发现:当加入5 kg偏置载荷下,载荷位移分布和供气压力不同时,支撑气膜的刚度和内部气阻也不相同,此时即使发生相同的偏载,其影响也不同。
|
| 图 6 不同载荷分布下的气膜振动幅值 Fig. 6 Vibration amplitudes of gas films with different load distributions |
随着供气压力的增大,气膜振动幅值逐渐增大;并且在相同供气压力下,大气膜(h=40 μm)下的振动幅值小于小气膜(h=20 μm)时的振动幅值。另一方面,在小气膜(h=20 μm)下载荷分布对气膜振动幅值不敏感,这时随着偏载位置的改变,振动幅值略有增大;而在大气膜(h=40 μm)下,当供气压力在中低压(ps≤0.4 MPa)时,气膜对偏载影响不大,而当高供气压力(ps>0.4 MPa)下,随着分布载荷偏移位置的增大,振动强度逐渐增强。
由于在供气孔入口进入气膜内部流场的过程中存在气体速度矢量由竖直方向向平面方向转变,根据动量矩方程可知,空气轴承必然会受到流场对轴承表面的作用力,伴随急变流湍动涡旋。进入气膜以后,在沿半径方向移动和发展的过程中,气旋和壁面之间的耦合作用形成了涡激振动。随着气膜的逐渐增大,涡激发展越充分,则传递给气浮块平面的能量越少。如果气膜越小,则发展受到气浮块约束,涡动不能很好地释放,则此时把自身涡动能传递给了气浮块,所以振动变大。
如图 7所示:竖直方向和水平方向上的固有频率和主要倍频分布大体一致,这主要是由于在同一个气浮块的相同方向上,其固有频率相同,主要的振动频率范围也相一致。从整体上对比可以看出竖直方向上的固有频率及主要倍频相接近,而水平方向上的固有频率及倍频差别较大,这是因为竖直方向气体的流动自由度被限制住;而水平方向的气膜流场跟大气相同,压力气体可以自由流动所造成的。

|
| 图 7 不同供气压力下的气浮支承振动频域信号 Fig. 7 Frequency-domain signals of air floatation at different gas supply pressure |
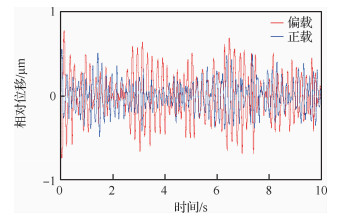
不同供气压力下气膜对偏载的敏感性是不同的,由于高压气体在发生偏载时,气膜内各处高度不再统一,导致气膜内湍动气流不对称流动。如图 8所示:当h=20 μm,ps=0.6 MPa,作用5 kg偏置载荷下,当轴承发生偏载时,其振动幅值和正载时相比,偏载作用导致轴承微振动平均幅值由0.44 μm增加到0.53 μm,轴承的微振动强度明显增大。这是因为:轴承表面发生偏载时引起支撑气膜局部厚度不均匀,在压差驱动下,高压区气体迅速向低压区涌动,增大了气膜内的湍动强度及流场内的涡动能量,导致振动幅值增大。
|
| 图 8 振动时域特性 Fig. 8 Vibration domain comparison chart |
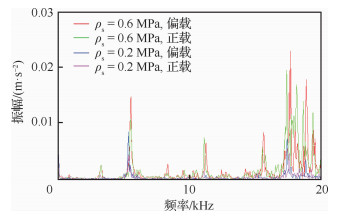
进一步分析轴承微振动的频率特性,如图 9所示:相同供气压力下虽然轴承表面载荷分布发生变化,但偏载对微振动的固有频率和主要倍频分布影响不大,微振动各阶峰值频率基本稳定在一个相近的范围内。但是供气压力对空气静压轴承微振动的频域特征影响比较明显,当供气压力较低时,气浮轴承在气膜脉动压力作用下产生的微振动的主要频率均有所下降。这是由于,供气压力较小时气膜内整体能量水平较低,气膜流场通过涡激作用对气浮块实时做功输入的能量也较低;随着供气压力增大,压力能一定程度补充气腔内部局部压降造成的黏性阻力损失,同时对气浮块做功程度增强,从而提高了轴承微振动的固有频率和低阶峰值频率。
|
| 图 9 不同供气压力下的的振动频域特性 Fig. 9 Vibration frequency-domain comparison at different gas supply pressure |
由于载荷偏置的出现,使得气浮轴承表面的受力中心发生改变,不再通过支撑系统的质心,形成偏载力矩,导致此时支撑气膜的动态阻尼变小,使得振动一定程度地增加。
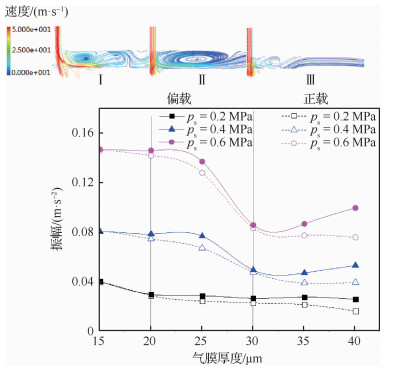
如图 10所示:当载荷均匀分布时,随着气膜厚度的增加,微振动幅值整体降低;当载荷分布不均匀时,随着气膜厚度的增加,微振动幅值先降低后增长。其中,当(h≤20 μm)时,不管是否发生偏载,微振动幅值接近;随着气膜厚度增加,当(20 μm < h≤30 μm)时可以发现,发生偏载造成的微振动幅值显著大于载荷分布时的微振动幅值;随着气膜厚度进一步增加,当(30 μm < h)后可以发现,载荷均匀分布的微振动幅值进一步减小,而发生偏载造成的微振动幅值却迅速增大。
|
| 图 10 不同供气压力下气膜振动幅值 Fig. 10 Vibration amplitudes of gas film under different gas supply pressure |
特别值得注意的是,当气膜厚度(h≥35 μm)以后,随着供气压力的增大,由于偏载造成的微振动幅值较载荷均匀分布时差值显著增大。
综上,对应不同气膜厚度下气腔对称面上的速度矢量图,可以按振动情况划分3个区域,即:① Ⅰ区:涡旋不充分区(h≤20 μm);② Ⅱ区:涡旋发展区(20 μm < h≤ 30 μm);③ Ⅲ区:涡旋释放区(30 μm < h)。
综上可见:气膜流场的流动特性和能量传递过程,特别是流场内高压区的湍流涡动及其能量分布,才是决定轴承自激微振动强度和稳定性的最根本依据。不同工况下,载荷的施加及分布形式均会影响静压轴承的微振动强度和工作稳定性。所以,在设计和使用空气静压轴承的过程中,对于空气轴承微振动的分析一定要从流场分析入手,结合具体的结构参数和使用条件,在保证承载和刚度要求的前提下,合理选择供气压力和工作气膜厚度;在载荷分布不均匀或者发生偏载时,更要使各个参数之间良好匹配,这样才能保证气浮支撑系统实现高精度和良好的稳定性。
4 结论本文主要通过实验测试及理论分析相结合的方法分析了载荷分布对气膜三维微振动特性的影响,比较了气膜涡激振动在各个方向上的时域和频域特性。研究发现:不同工况下偏置载荷对轴承微振动的影响不尽相同。
1) 对于空气静压止推轴承,气膜内的涡激振动是由流场内三维气旋形成的涡流形成的。而空气静压轴承的微振动成因,核心是气膜流场流动特性。气膜高压区内局部雷诺数较大,湍流程度较高,带来流场能量的迅速转化和发展。只有当高压区涡动能较低,及涡量分布均匀分散时,形成的涡激效应才能有效减小。反之,则会破坏系统的稳定程度。
2) 轴承表面载荷分布不均匀会增加空气静压轴承的微振动强度。对于小孔节流空气静压轴承而言,相同工况下,随着气膜厚度的增加,振动幅值逐渐减小。在较大气膜下,当供气压力增加到一定时,随着分布载荷偏移位置的增加,振动强度逐渐增强;且高供气压力对微振动影响更敏感。所以在发生偏载下,为减小轴承的振动强度,提高工作稳定性,必须使用较小的供气压力。
3) 轴承气膜内的涡激振动强度会随着供气压力和气膜厚度的增加而增加。相同气供气压力下气体的稠密性降低,导致气膜振动强度降低,而偏置载荷的加入使得气浮轴承气膜流场更为复杂,特别在气膜厚度较大时,气膜的气容量增加,导致偏载对气浮振动强度影响更加明显。
| [1] | WEN Z P, WU J W, TAN J B. An adaptive modeling method for multi-throttle aerostatic thrust bearing[J]. Tribology International, 2019. |
| [2] | MAAMARI N, KREBS A, WEIKERT S, et al. Stability and dynamics of an orifice based aerostatic bearing with a compliant back plate[J]. Tribology International, 2019, 138: 279-296. |
| Click to display the text | |
| [3] |
龙威, 王继尧, 李法社, 等. 空气静压止推轴承自激微振动数值分析及实验研究[J]. 振动与冲击, 2019, 38(16): 224-232. LONG W, WANG J Y, LI F S, et al. Numerical analysis and experimental research on self-excited micro-vibration of aerostatic thrust bearings[J]. Journal of Vibration and Shock, 2019, 38(16): 224-232. (in Chinese) |
| Cited By in Cnki (67) | Click to display the text | |
| [4] |
杜建军, 刘墩, 张国庆, 等. 带有圆周方向均压槽的静压气体止推轴承的气锤自激[J]. 润滑与密封, 2010, 35(1): 9-12. DU J J, LIU T, ZHANG G Q, et al. Study of self-excited vibration for externally pressurized gas thrust bearing with circumferential groove[J]. Lubrication Engineering, 2010, 35(1): 9-12. (in Chinese) |
| Cited By in Cnki (67) | Click to display the text | |
| [5] |
薛义璇, 陆金生, 侯志勇. 基于Fluent的小孔节流式空气静压轴承特性研究[J]. 自动化与仪表, 2019, 34(4): 70-74. XUE Y X, LU J S, HOU Z Y, et al. Investigation on characteristics of orifice-type aerostatic bearing based on fluent[J]. Automation & Instrumentation, 2019, 34(4): 70-74. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [6] |
黄泽中, 尹洋, 李佳, 等. 气体静压高速电主轴稳定性研究[J]. 现代机械, 2018(1): 1-6. HUANG Z Z, YIN Y, LI J, et al. Study on the stability of high-speed aerostatic motorized spindle[J]. Modern Machinery, 2018(1): 1-6. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [7] |
刘暾.圆盘形平面止推气体轴承的气锤自激[C]//2008年中国空间科学学会空间机电与空间光学专业委员会学术年会论文集, 2008: 64-67. LIU T. Air hammer self-excitation of disc-shaped planar thrust gas bearing[C]//2008 Annual Meeting of the Space Electromechanical and Space Optics Committee of the Chinese Academy of Space Sciences, 2008: 64-67(in Chinese). |
| [8] | MAJUMDAR B C, SINGH K C. Analysis of aerostatic thrust bearings with offset load[J]. International Journal of Machine Tool Design & Research, 1973, 13(2): 65-76. |
| Click to display the text | |
| [9] | SINGH K C, RAO N S. Static characteristics of aerostatic porous rectangular thrust bearings with offset load[J]. Journal of Lubrication Technology, 1983, 105(1): 143-146. |
| Click to display the text | |
| [10] | RAO N S. Analysis of aerostatic porous rectangular thrust bearings with offset loads[J]. Wear, 1980, 59(2): 333-344. |
| Click to display the text | |
| [11] | AL-BENDER F, BRUSSEL H V. Tilt characteristics of circular centrally fed aerostatic bearings[J]. Tribology International, 1992, 25(3): 189-197. |
| Click to display the text | |
| [12] | NAKAMURA T, YOSHIMOTO S. Static tilt characteristics of aerostatic rectangular double-pad thrust bearings with compound restructures[J]. Tribology International, 1996, 29(2): 145-152. |
| Click to display the text | |
| [13] | NAKAMURA T, YOSHIMOTO S. Static tilt characteristics of aerostatic rectangular double-pad thrust bearings with double row admissions[J]. Tribology International, 1997, 30(8): 605-611. |
| Click to display the text | |
| [14] | AL-BENDER F, BRUSSEL H V. Tilt characteristics of circular centrally fed aerostatic bearings[J]. Tribology International, 1992, 25(3): 189-197. |
| Click to display the text | |
| [15] | ANDRES S L A. Analysis of hydrostatic journal bearings with end seals[J]. Journal of Tribology, 1992, 114(4): 802-811. |
| Click to display the text | |
| [16] | NAKAMURA T, YOSHIMOTO S. Static tilt characteristics of aerostatic rectangular double-pad thrust bearings with double row admissions[J]. Tribology International, 1997, 30(8): 605-611. |
| Click to display the text | |
| [17] | LONG W, DENG M M. Study on tilt properties of orifice-compensated aerostatic thrust bearings[J]. Advanced Materials Research, 2012, 605-607: 1492-1495. |
| Click to display the text | |
| [18] | YOSHIMOTO S, TAMURA J, NAKAMURA T. Dynamic tilt characteristics of aerostatic rectangular double-pad thrust bearings with compound restrictors[J]. Tribology International, 1999, 32(12): 731-738. |
| Click to display the text | |
| [19] | JIANG S, YANG S, YIN Z, et al. Static and dynamic characteristics of externally pressurized annular porous gas thrust bearings[J]. Proceedings of the Institution of Mechanical Engineerings Part J-Journal of Engineeving Tribology, 2016, 230(10): 1221-1230. |
| Click to display the text | |
| [20] | MAJUMDAR B C. Dynamic characteristics of externally pressurized rectangular porous gas thrust bearings[J]. Journal of Tribology, 1976, 98(1): 141. |
| Click to display the text | |
| [21] | XU C, JIANG S. Dynamic analysis of a motorized spindle with externally pressurized air bearings[J]. Journal of Vibration and Acoustics, 2015, 137(4): 041001. |
| Click to display the text | |
| [22] |
龙威.平面空气静压轴承承载特性研究[D].哈尔滨: 哈尔滨工业大学, 2010: 15-19. LONG W. Study on loading characteristics of orifice compensated aerostatic thrust bearing[D]. Harbin: Harbin Institute of Technology, 2010: 15-19(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [23] |
裴浩, 龙威, 杨少华, 等. 空气静压轴承微振动形成机理分析[J]. 振动与冲击, 2018, 37(5): 71-78. PEI H, LONG W, YANG S H, et al. Formation mechanism of micro-vibration in aerostatic bearings[J]. Journal of Vibration and Shock, 2018, 37(5): 71-78. (in Chinese) |
| Cited By in Cnki | Click to display the text |



