随着智能材料与结构技术的发展,智能化已成为飞行器结构发展的重要趋势。“变形机翼”概念的提出最早可以追溯到1916年,美国就有人提出“变形机翼”的专利申请,而美国航空航天局于1979年与波音公司才签订合同,发展柔性复合材料“自适应变形机翼”[1]。这种飞行器能够根据飞行环境、飞行任务等的需要通过内置的传感器、作动器和控制系统进行自适应变形,灵活控制飞行航迹、飞行高度和飞行速度等参数,以实现飞行器的最优飞行性能[1-2]。而变形监测是变形控制实现的前提,变形监测把结构的实时形状信息,反馈给结构控制系统,以实现对结构精确变形的控制,因此具有重大的研究意义。
传统的基于光学成像法的结构变形测量方法已经不能满足飞行器结构实时变形监测的要求。基于应变的变形监测方法采用的应变片或光纤光栅传感器更加小型化、轻量化,可埋入结构表层,适应较复杂的结构,因此更加适用于航空航天飞行器等结构的变形监测[3-5]。
已发展的基于应变监测的变形重构方法主要分为3类。美国德莱顿飞行研究中心的Ko等提出的Ko位移理论基于经典材料力学假设和梁结构变形几何、物理关系,利用分段方式将大跨度梁结构变形问题转化为求和问题,算法简单,但计算精度依赖于应变传感器的布置密度[6-8]。波音结构及环境监测实验室的Foss等基于模态叠加理论提出模态转换算法,通过结构的应变阵型矩阵和相应的位移阵型矩阵计算得到位移-应变转换矩阵,结合应变传感系统测得的结构应变场实现结构位移场的重构。该方法常用于动载环境下的变形重构,需要预先知道结构各阶模态[9-11]。美国航空航天局兰利研究中心Tessler等基于最小二乘变分方程提出了逆向有限元法。常规的有限元分析通常是已知给结构施加的载荷或者位移,然后计算结构的应力应变响应。而所谓“逆向有限元”法中的“逆”是指已知量与未知量之间的反转,已知的是结构的应变响应,然后反推结构的位移。该方法是基于弹性力学Mindlin中厚板理论(考虑横向剪切变形)以及最小位能原理,建立逆向有限单元,通过最小二乘变分方程求解结构应变场和位移场之间的传递函数,解决应变转换为位移的逆向问题[12-15]。之后逐步研究提出了各类逆向单元模型以适用不同的结构形式,如四节点逆壳单元iQS4[16]、适用于复合材料结构的三角形逆壳单元[17],并且应用到船体结构[18-19]和风力叶片[20]等结构的变形监测。
为了比较上述3种不同的变形监测方法各自的重构效果,Gherlone等开展了针对翼形板在承受弯扭组合的载荷下的变形试验与变形重构研究,试验结果表明逆向有限元法重构精度最高[21]。
自适应变形机翼作为一种典型的自适应智能结构,主要包含机翼柔性蒙皮、变形驱动构件和承力构件3个部分。变形驱动构件驱动承力构件发生偏转,机翼柔性蒙皮所围成的翼型形状随之发生改变。服役过程中所受外载荷形式多样,逆向有限元法能适应不同的结构形式,而且无需结构诸如模态信息等自身属性信息以及外载荷信息,同时还能对结构的全局位移进行重构,是一种有前景的、适用于变形机翼的变形重构方法。
由于变形机翼表面受气动载荷作用,不便于直接在机翼蒙皮表面布置应变传感系统,目前还没有针对鱼骨结构这种真实复杂机翼结构的变形重构研究,大多针对机翼翼型的变形重构研究是将整个机翼简化成简单的翼形板、梁结构,然后采用基于应变信息的变形监测方法进行重构[22-23]。本文首次针对真实复杂机翼鱼骨结构进行变形重构研究,提出基于逆向有限元算法与位移分段叠加思想的变形监测方法,根据Mindlin中厚板变形理论建立四节点逆壳单元,采用应变传感系统测得结构表面应变分布作为算法输入,然后基于最小二乘变分方程求解结构应变场和位移场之间的传递函数,重构鱼骨结构的变形形状,为反演机翼翼型变形形状提供方法。
1 机翼鱼骨变形重构方法本文将基于逆向有限元算法重构机翼鱼骨的变形,其基本过程如下:首先对鱼骨结构的结构形式和主要受载形式进行分析,将鱼骨结构进行分段,采用合适的变形理论构建逆向单元,然后建立鱼骨结构的逆向有限元模型并展开分析。基于逆向有限元算法对每一分段位移进行重构,最终将各分段重构位移结果进行分段叠加,得到整个鱼骨的位移分布。
1.1 鱼骨结构分析自适应变形机翼作为一种典型的自适应智能结构,常用形状记忆合金弹簧驱动内部鱼骨结构发生变形使得机翼进行偏转,鱼骨支撑着整个机翼的翼型,表征了机翼的基本形状,因此重构鱼骨结构的变形形状将为推演机翼形状奠定基础。
图 1所示为拟开展方法验证研究的自适应变形机翼模型,机翼主要承力构件为鱼骨结构,内部由形状记忆合金驱动器驱动机翼上下偏转变形,如图 2所示,鱼骨结构由航空硬铝7050制造,长宽高尺寸为500 mm×30 mm×3 mm,该结构主要分为主梁和驱动装置安装固定分叉2个部分,前者用于承受来自机翼的载荷与变形,后者用于安装驱动主梁变形的形状记忆合金弹簧,其中主梁主要承受弯曲变形、拉压变形和横向剪切变形。如图 3所示为鱼骨结构偏转变形示意图,分叉之间连接有驱动弹簧,通过弹簧的伸缩来控制鱼骨结构的偏转变形。鱼骨作为机翼的主要承力构件,支撑着整个机翼的翼型形状,分叉顶端与机翼蒙皮相连接,当驱动鱼骨发生偏转变形时,鱼骨会带动机翼蒙皮形状随之发生改变。

|
| 图 1 自适应变形机翼 Fig. 1 Self-adaptive morphing wing |

|
| 图 2 鱼骨结构实物图 Fig. 2 Physical structure of fishbone |

|
| 图 3 鱼骨偏转变形 Fig. 3 Deformation of fishbone |
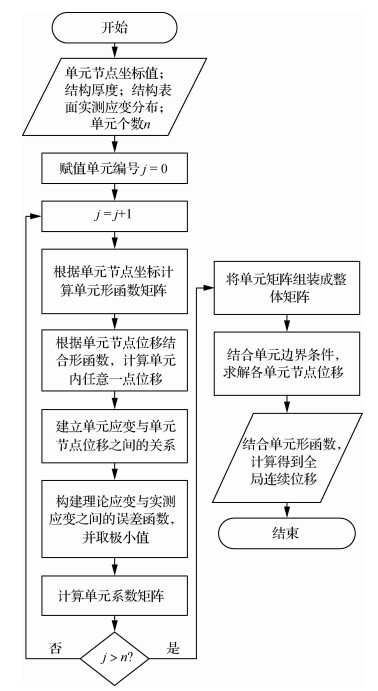
逆向有限元算法重构位移的基本过程如图 4所示。首先采用基础变形理论构建逆向单元,理论上建立结构所受应变与位移之间的关系,并用形函数线性插值的方法,将单元内任意一点的位移用单元各个节点位移表示,然后用单元节点位移结合形函数表示理论上的单元应变分布。用n(n>0)个逆向单元划分被测结构,同时通过在结构表面布置应变传感系统,实测获得结构表面应变分布。构建单元内理论应变与实测应变之间的最小二乘误差函数,求误差函数取得极小值时的位移分布,即为与实测应变分布对应的位移分布。然后将单元1~n内的节点的局部位移通过有限元组装步骤转换成结构整体位移,解决应变转换为位移的逆向问题。结合插值形函数可以将各单元节点位移转换成单元内任意一点的位移,从而重构整个区域的连续位移分布。
|
| 图 4 逆向有限元算法流程图 Fig. 4 Flowchart of inverse finite element method |
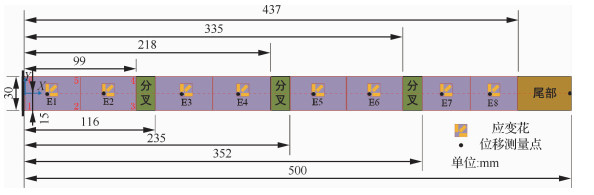
鱼骨结构主梁部分为矩形平面板壳结构,因此本文采用逆向平面壳单元划分鱼骨结构。适用于鱼骨主梁外形的常用单元有:三节点平面逆壳单元和四节点平面逆壳单元。考虑到三节点平面逆壳单元为常应变单元,单元内应变为常数,而四节点逆壳单元内应变呈线性变化,更加贴近于结构实际应变状态[12]。图 5所示为鱼骨主梁部分逆向有限元模型及其逆向单元划分示意图,其中,E1~E8表示单元编号,XYZ表示建立在鱼骨固定端的全局坐标系,其中Z轴方向垂直于主梁平面竖直向上。
|
| 图 5 鱼骨主梁俯视平面及传感器布局 Fig. 5 Vertical view of fishbone and layout of strain sensors |
鱼骨主梁结构厚度(3 mm)与板平面内最小尺寸(30 mm)的比例为0.1,可划分为中厚板结构。对于变形机翼的鱼骨这种中厚板结构,载荷可分解为平行于中面XY平面的纵向载荷和垂直于XY平面的横向载荷。纵向载荷引起的应力、应变和位移,可按平面应力问题求解。横向载荷将使薄板弯曲,引起的应力、应变以及位移按薄板弯曲问题求解[7]。
鱼骨在服役过程中主要受横向载荷作用,相比经典变形理论,Mindlin板变形理论考虑了横向剪切变形,误差更小,因此采用Mindlin板变形理论构建逆向单元。该变形理论认为变形前中面的发现,在变形后仍保持直线,但不垂直于变形后的中性面[9]。这样计入横向剪切的影响后,中性面法线的转角θx、θy和θz不仅是由中性面挠度的偏导数∂w/∂y、∂w/∂x产生,还包含了板的剪切变形γyz和γxz,因此要附加考虑自由度θx、θy,而θz是为了方便矩阵运算事先考虑的,没有实际意义。基于Mindlin板变形理论构建的四节点逆向壳单元,如图 6所示。xyz为建立在四节点单元内中性面上、且原点在四边形形心位置的局部坐标系,u、v和w分别是该局部坐标系下x、y和z方向的位移,θx、θy和θz分别为绕x、y和z轴方向的转角。单元厚度为2h,点1,2,3,4分别为单元的4个节点,位于结构的中性面上。

|
| 图 6 四节点逆壳单元 Fig. 6 Four-node quadrilateral inverse-shell element |
| $ \left\{ {\begin{array}{*{20}{l}} {u = {u_0} + z{\theta _{{y_0}}}}\\ {v = {v_0} - z{\theta _{{x_0}}}}\\ {w = {w_0}} \end{array}} \right. $ | (1) |
式中:u0、v0和w0分别表示与点(x, y, z)对应的中性面上点(x, y, 0)在x、y、z方向的位移;θx0和θy0表示中性面上点(x, y, z)绕+x轴和+y轴方向的旋转角度,其中z方向的位移w沿壳的厚度方向z∈[-h, +h]不变化。
根据经典有限元分析理论,单元内任意一点的位移(u, v, w, θx, θy)可由单元内4个节点的位移和转角的线性插值表示,对于二维平面壳单元,不考虑绕z轴方向的转角θz,但为方便计算补充了自由度θz[11]。
每个单元包含4个节点,各个节点的位移向量可表示为
| $ \mathit{\boldsymbol{u}}_i^e = {\left[ {\begin{array}{*{20}{l}} {{u_i}}&{{v_i}}&{{w_i}}&{{\theta _{xi}}}&{{\theta _{yi}}}&{{\theta _{zi}}} \end{array}} \right]^{\rm{T}}} $ | (2) |
式中:单元节点位移矩阵ue可表示为
| $ {\mathit{\boldsymbol{u}}^e} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}}_1^e}&{\mathit{\boldsymbol{u}}_2^e}&{\mathit{\boldsymbol{u}}_3^e}&{\mathit{\boldsymbol{u}}_4^e} \end{array}} \right]^{\rm{T}}} $ | (3) |
结构表面拉压和弯曲的组合应变εb以及截面横向剪切应变εs可表示为
| $ {\mathit{\boldsymbol{\varepsilon }}_{\rm{b}}} = {\left[ {\begin{array}{*{20}{l}} {{\varepsilon _{xx}}}&{{\varepsilon _{xy}}}&{{\gamma _{xy}}} \end{array}} \right]^{\rm{T}}} $ | (4) |
| $ {\mathit{\boldsymbol{\varepsilon }}_{\rm{s}}} = {\left[ {\begin{array}{*{20}{l}} {{\gamma _{xz}}}&{{\gamma _{yz}}} \end{array}} \right]^{\rm{T}}} $ | (5) |
根据线弹性理论[9],结构表面应变εb可以表示为面内拉压应变e(ue)与弯曲应变k(ue)的线性组合。且进一步可用四节点逆壳单元的形函数的偏导数矩阵Bm、Bk与单元节点位移矩阵ue表示,如式(6)所示,矩阵Bm、Bk的详细计算表达式见文献[12]。
| $ {\mathit{\boldsymbol{\varepsilon }}_{\rm{b}}} = \mathit{\boldsymbol{e}}({\mathit{\boldsymbol{u}}^e}) + z\mathit{\boldsymbol{k}}({\mathit{\boldsymbol{u}}^e}) = {\mathit{\boldsymbol{B}}^m}{\mathit{\boldsymbol{u}}^e} + z{\mathit{\boldsymbol{B}}^k}{\mathit{\boldsymbol{u}}^e} $ | (6) |
此外,结构所受截面横向剪切应变εs可用四节点单元形函数的偏导数矩阵Bs与单元节点位移矩阵ue表示,如式(7)所示,矩阵Bs的详细计算表达式见文献[12]。
| $ {\mathit{\boldsymbol{\varepsilon }}_{\rm{s}}} = \mathit{\boldsymbol{g}}({\mathit{\boldsymbol{u}}^e}) = {\mathit{\boldsymbol{B}}^s}{\mathit{\boldsymbol{u}}^e} $ | (7) |
式中:形函数的偏导数矩阵Bm、Bk、Bs的详细计算表达式见文献[12]。
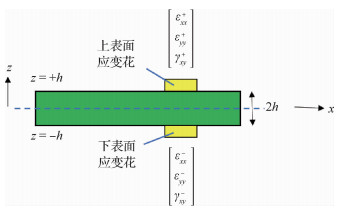
1.4 基于应变的变形重构方法逆向有限元法需要测得结构上下表面的应变,如图 7所示。测得应变表示为(εxx+, εyy+, γxy+)j,(εxx-, εyy-, γxy-)j,其中j=1, 2,…,n,n为单元内应变传感器个数,上标“+”’和“-”分别表示结构的上下表面,2h为结构厚度。测得的结构表面离散应变与结构平面应变以及弯曲应变之间的关系如式(8)~式(10)所示[12]。
|
| 图 7 单元内应变测量结构表面离散应变分布示意图 Fig. 7 Discrete strain measurement on surface of structure inside the element |
| $ \mathit{\boldsymbol{e}}_j^\varepsilon = \frac{1}{2}\left( {{{\left[ {\begin{array}{*{20}{c}} {\varepsilon _{xx}^ + }\\ {\varepsilon _{yy}^ + }\\ {\gamma _{xy}^ + } \end{array}} \right]}_i} + {{\left[ {\begin{array}{*{20}{c}} {\varepsilon _{xx}^ - }\\ {\varepsilon _{yy}^ - }\\ {\gamma _{xy}^ - } \end{array}} \right]}_i}{\kern 1pt} {\kern 1pt} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,n $ | (8) |
| $ \mathit{\boldsymbol{k}}_j^\varepsilon = \frac{1}{{2h}}\left( {{{\left[ {\begin{array}{*{20}{c}} {\varepsilon _{xx}^ + }\\ {\varepsilon _{yy}^ + }\\ {\gamma _{xy}^ + } \end{array}} \right]}_i} - {{\left[ {\begin{array}{*{20}{c}} {\varepsilon _{xx}^ - }\\ {\varepsilon _{yy}^ - }\\ {\gamma _{xy}^ - } \end{array}} \right]}_i}{\kern 1pt} {\kern 1pt} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,n $ | (9) |
式中:eiε为中厚板中性面拉压应变;kiε为中厚板中性面弯曲应变,方程中上标ε表示实验所测得离散应变值。因此,应变向量εj可表示为
| $ {\mathit{\boldsymbol{\varepsilon }}_j} = \mathit{\boldsymbol{e}}_j^\varepsilon + z\mathit{\boldsymbol{k}}_j^\varepsilon $ | (10) |
横向剪切应变gjε不能由表面应变直接计算得到,需要通过其他的辅助程序计算,但对于薄壳结构,所受横向剪切应变相比平面应变和弯曲应变很小,因此本文中将实测横向剪切应变视为0。
逆向有限元法重构结构变形需要构建实测应变与理论应变之间的最小二乘误差函数。然后求误差函数对单元节点位移的极小值,得到理论上该单元各节点的位移值;当误差函数取得极小值时,则认为此时求得的单元节点位移分布即为对应此时结构实测应变状态下的实际位移分布。
单元内理论应变与实测应变的误差函数Φe(ue)包含平面应变、弯曲应变以及横向剪切应变3个部分,可表示为
| $ \begin{array}{l} {\varPhi _e}({\mathit{\boldsymbol{u}}^e}) = {\left\| {\mathit{\boldsymbol{e}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{e}}^\varepsilon }} \right\|^2} + {\left\| {\mathit{\boldsymbol{k}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{k}}^\varepsilon }} \right\|^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda {\left\| {\mathit{\boldsymbol{g}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{g}}^\varepsilon }} \right\|^2} \end{array} $ | (11) |
式中:λ为罚参数(0 < λ≪1),其大小与测量数据与理论分析结果之间的相关程度有关[10],代表着主梁横截面yz所承受弯曲应变、平面拉压应变和横向剪切应变之间的比例关系。经理论计算,鱼骨结构所受横向剪切变形相比弯曲和平面拉压变形小很多。横向剪切应变与拉压应变或弯曲应变之间的比值约为10-5,因此本文中罚参数λ取10-5,来控制横向剪切变形与弯曲变形、拉压变形之间的比例关系。
| $ {\left\| {\mathit{\boldsymbol{e}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{e}}^\varepsilon }} \right\|^2} = \frac{1}{n}\iint\limits_{{A^e}} {\sum\limits_{j = 1}^n {{{(\mathit{\boldsymbol{e}}{{({\mathit{\boldsymbol{u}}^e})}_j} - \mathit{\boldsymbol{e}}_j^\varepsilon )}^2}{\rm{d}}x{\rm{d}}y} } $ | (12) |
| $ {\left\| {\mathit{\boldsymbol{k}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{k}}^\varepsilon }} \right\|^2} = \frac{{{{\left( {2h} \right)}^2}}}{n}\iint\limits_{{A^e}} {\sum\limits_{j = 1}^n {{{(\mathit{\boldsymbol{k}}{{({\mathit{\boldsymbol{u}}^e})}_j} - \mathit{\boldsymbol{k}}_j^\varepsilon )}^2}{\rm{d}}x{\rm{d}}y} } $ | (13) |
| $ {\left\| {\mathit{\boldsymbol{g}}({\mathit{\boldsymbol{u}}^e}) - {\mathit{\boldsymbol{g}}^\varepsilon }} \right\|^2} = \frac{1}{n}\iint\limits_{{A^e}} {\sum\limits_{j = 1}^n {{{(\mathit{\boldsymbol{g}}{{({\mathit{\boldsymbol{u}}^e})}_j} - \mathit{\boldsymbol{g}}_j^\varepsilon )}^2}{\rm{d}}x{\rm{d}}y} } $ | (14) |
式中:n>0是单元内应变传感器的数量;积分域Ae为单元内整个区域。
对误差函数Φe(ue)关于位移向量ue求偏导,并令其为零,求解方程得到误差函数Φe(ue)的极小值。
| $ \frac{\partial }{{\partial {\mathit{\boldsymbol{u}}^e}}}{\varPhi _e}({\mathit{\boldsymbol{u}}^e}) = {\mathit{\boldsymbol{k}}^e}{\mathit{\boldsymbol{u}}^e} - {\mathit{\boldsymbol{f}}^e} = {\bf{0}} $ | (15) |
通过计算得到
| $ {\mathit{\boldsymbol{k}}^e}{\mathit{\boldsymbol{u}}^e} = {\mathit{\boldsymbol{f}}^e} $ | (16) |
式中:矩阵ke与fe按式(17)和式(18)计算
| $ \begin{array}{l} {\mathit{\boldsymbol{k}}^e} = \iint\limits_{{A^e}} {[{{({\mathit{\boldsymbol{B}}^m})}^{\rm{T}}}{\mathit{\boldsymbol{B}}^m} + {{(2h)}^2}{{({\mathit{\boldsymbol{B}}^k})}^{\rm{T}}}{\mathit{\boldsymbol{B}}^k}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda {({\mathit{\boldsymbol{B}}^s})^{\rm{T}}}{\mathit{\boldsymbol{B}}^s}]{\rm{d}}x{\rm{d}}y \end{array} $ | (17) |
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}^e} = \frac{1}{n}\int\limits_{{A^e}} {\sum\limits_{i = 1}^n {[{{({\mathit{\boldsymbol{B}}^m})}^{\rm{T}}}\mathit{\boldsymbol{e}}_i^\varepsilon + {{(2h)}^2}{{({\mathit{\boldsymbol{B}}^k})}^{\rm{T}}}\mathit{\boldsymbol{k}}_i^\varepsilon } } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda {({\mathit{\boldsymbol{B}}^s})^{\rm{T}}}\mathit{\boldsymbol{g}}_i^\varepsilon ]{\rm{d}}x{\rm{d}}y \end{array} $ | (18) |
将上述单元内求得的矩阵按照式(19)~式(21)做坐标变换,并将各个单元矩阵按照标准的有限元整体组装步骤组装成整体矩阵,将每个单元的系数矩阵中的每个元素按其脚标编号对应叠加成整体系数矩阵。
| $ {\mathit{\boldsymbol{K}} = \sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {{{({\mathit{\boldsymbol{T}}^e})}^{\rm{T}}}} {\mathit{\boldsymbol{k}}^e}{\mathit{\boldsymbol{T}}^e}} $ | (19) |
| $ {\mathit{\boldsymbol{F}} = \sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {{{({\mathit{\boldsymbol{T}}^e})}^{\rm{T}}}} {\mathit{\boldsymbol{f}}^e}} $ | (20) |
| $ {\mathit{\boldsymbol{U}} = \sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {{{({\mathit{\boldsymbol{T}}^e})}^{\rm{T}}}} {\mathit{\boldsymbol{u}}^e}} $ | (21) |
式中:nel为逆向单元个数;Te为坐标转换矩阵。本文中鱼骨主梁为平面结构,因此单元局部坐标系与整体位移坐标系为同一坐标系,不需要进行坐标转换,只需要进行单元矩阵的组装,最终可得到
| $ \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}} $ | (22) |
式中:方程式左边的K矩阵是一个对称矩阵,与应变测量值无关,与应变测量点所在逆向单元的单元节点位置和应变测量点位置有关,再结合单元边界条件,系数矩阵K将简化为一个正定矩阵,求逆后可得到单元节点的全局位移U。
1.5 鱼骨结构分段位移叠加鱼骨分叉根部与主梁结合部位由于外形复杂、凹凸不平导致实验时无法在该位置布置应变传感器而不能获得应变分布,因此得将该部分单独进行处理,进行等效和简化。下面对该部分的结构形式和受力特性展开分析。
鱼骨主梁平面部分的截面积S1为30 mm×3 mm,从左至右3个分叉截面积S2、S3、S4分别为65 mm×30 mm、45 mm×30 mm、25 mm×30 mm,因此相比主梁平面部分的截面积S1,分叉部分截面积大很多。
考虑到鱼骨结构表面应变和位移受弯曲变形的影响最大,因此针对鱼骨结构在弯曲变形下结构表面的应力应变值可按式(23)、式(24)计算:
| $ {\sigma = \frac{M}{W}} $ | (23) |
| $ {W = \frac{{b{h^2}}}{6}} $ | (24) |
式中:M为弯矩; W为抗弯刚度; b为矩形截面宽度; h为矩形截面高度。
应力与截面高度的平方成反比,以高度为25 mm的截面S4为例,其高度是截面高度为3 mm的S1的8倍,在同等载荷作用下,分叉根部与主梁结合部的应力约为主梁平面部分应力值的1/64。而应变与应力呈线性关系,在鱼骨结构向下偏转15°的情况下,鱼骨结构表面的最大应变值不超过3 000 με,故分叉根部与主梁结合部的应力小于50 με。此外,还考虑到分叉根部与主梁结合部分的长度只有20 mm,因此该部分的局部变形很小。
根据以上对该部分的应力应变特性分析结果,本文中将其简化为刚体,该部分只发生刚体转动,而不发生内部弯曲和拉压变形。
此外,鱼骨尾部外形形状复杂,同样无法布置应变传感器测量表面应变,需要进行单独处理。而尾部靠近加载位置,所承受弯矩很小,所产生的内部弯曲和拉压变形很小,因此本文同样将鱼骨尾部视为刚体,只发生刚体转动。
针对鱼骨结构的实际复杂外形布局,在对鱼骨进行变形重构时,分叉根部将鱼骨分割成多个分段,每一段长度尺寸如图 5所示。因此,在重构鱼骨变形时应该从鱼骨固定端开始,每个分段按照原逆向有限元法求解局部位移分布,然后限制几个刚体分段(分叉和鱼骨尾部分段)的各个自由度与前一分段的末尾位移的自由度保持一致,最后将局部位移分布矩阵组装成整体位移分布矩阵,即为结构整体的位移分布。数学计算过程如下:
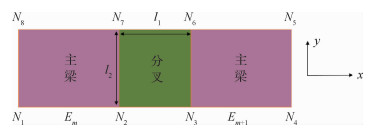
如图 8所示为鱼骨主梁平面俯视图的分叉与主梁结合部分示意图,Em、Em+1分别表示两个间隔开来的逆向单元。N1,N2,…,N8分别表示这2个逆向单元的各个节点编号,l1和l2分别为分叉部分的宽度和高度尺寸。
|
| 图 8 分叉与主梁结合部分示意图 Fig. 8 Combined part of bifurcate and girder |
根据式(22)求解得到的第m个单元内各个节点的全局位移ume
| $ \mathit{\boldsymbol{u}}_m^e = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}}_m^{{N_1}}}&{\mathit{\boldsymbol{u}}_m^{{N_2}}}&{\mathit{\boldsymbol{u}}_m^{{N_7}}}&{\mathit{\boldsymbol{u}}_m^{{N_8}}} \end{array}} \right] $ | (25) |
式中:节点N2和N7的位移可表示为
| $ \mathit{\boldsymbol{u}}_m^{{N_2}} = {\left[ {\begin{array}{*{20}{l}} {{u^{{N_2}}}}&{{v^{{N_2}}}}&{{w^{{N_2}}}}&{\theta _x^{{N_2}}}&{\theta _y^{{N_2}}}&{\theta _z^{{N_2}}} \end{array}} \right]^{\rm{T}}} $ | (26) |
| $ \mathit{\boldsymbol{u}}_m^{{N_7}} = {\left[ {\begin{array}{*{20}{l}} {{u^{{N_7}}}}&{{v^{{N_7}}}}&{{w^{{N_7}}}}&{\theta _x^{{N_7}}}&{\theta _y^{{N_7}}}&{\theta _z^{{N_7}}} \end{array}} \right]^{\rm{T}}} $ | (27) |
则紧邻的分叉刚体分段的位移um+1e里的各位移自由度分别可表示为
| $ \mathit{\boldsymbol{u}}_{m + 1}^e = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}_m^{{N_2}}}&{\mathit{\boldsymbol{u}}_m^{{N_3}}}&{\mathit{\boldsymbol{u}}_m^{{N_6}}}&{\mathit{\boldsymbol{u}}_m^{{N_7}}} \end{array}} \right] $ | (28) |
式中:由于将分叉部分视为刚体,只发生刚体转动,而无内部弯曲和拉压变形,因此节点N3和N6的位移可表示为
| $ \mathit{\boldsymbol{u}}_m^{{N_3}} = \left[ {\begin{array}{*{20}{c}} {{u^{{N_2}}} + {l_1} \cdot \theta _z^{{N_2}}}\\ {{v^{{N_2}}} + {l_2} \cdot \theta _z^{{N_2}}}\\ {{w^{{N_2}}} - {l_1} \cdot \theta _x^{{N_2}} - {l_2} \cdot \theta _y^{{N_2}}}\\ {\theta _x^{{N_2}}}\\ {\theta _y^{{N_2}}}\\ {\theta _z^{{N_2}}} \end{array}} \right] $ | (29) |
| $ \mathit{\boldsymbol{u}}_m^{{N_6}} = \left[ {\begin{array}{*{20}{c}} {{u^{{N_7}}} + {l_1} \cdot \theta _z^{{N_7}}}\\ {{v^{{N_7}}} + {l_2} \cdot \theta _z^{{N_7}}}\\ {{w^{{N_7}}} - {l_1} \cdot \theta _x^{{N_7}} - {l_2} \cdot \theta _y^{{N_7}}}\\ {\theta _x^{{N_7}}}\\ {\theta _y^{{N_7}}}\\ {\theta _z^{{N_7}}} \end{array}} \right] $ | (30) |
然后以分叉分段右边界作为起始固定端(固定端的位移不为0,以节点N3和N6位移情况为边界条件)继续用逆向有限元算法计算分叉后的其他部分的位移分布ui+2e,…, une,以此类推,最终重构得到整个鱼骨的位移分布情况。
2 变形重构实验如图 9所示为变形机翼鱼骨结构实验装置,鱼骨左端用螺栓固定在支撑座上,右端自由。

|
| 图 9 鱼骨结构实验装配图 Fig. 9 Assembly diagram of fishbone during experiment |
本文将分叉之间的主梁部分划分为2个四节点逆向单元,单元尺寸为50 mm×30 mm,并在每个单元的形心位置布置一个应变传感器,如图 5所示,应变传感器采用BE120-3CA电阻式45°三轴应变花,上表面应变传感器从右至左依次编号为1~8,下表面应变传感器从右至左依次编号为9~16。位移测量系统选用的是高度数显卡尺,位移测量点如图 5中黑色圆点所示。
变形重构实验系统如图 10所示,实验中采用ST24多通道应变数据采集系统,测试中采样率为50 Hz。实验中通过在鱼骨主梁自由端悬挂砝码对结构施加集中载荷,分别施加3.6 N/7.1 N/10.6 N的竖直向下作用力,使得鱼骨分别对应向下偏转5°/10°/15°。

|
| 图 10 鱼骨结构变形重构实验系统 Fig. 10 Experimental system for deformation reconstruction of fishbone |
采集各个变形状态下鱼骨主梁结构上下表面的应变分布,其中沿主梁延伸方向的轴向应变εxx+受鱼骨变形影响最大,其分布情况如图 11所示。
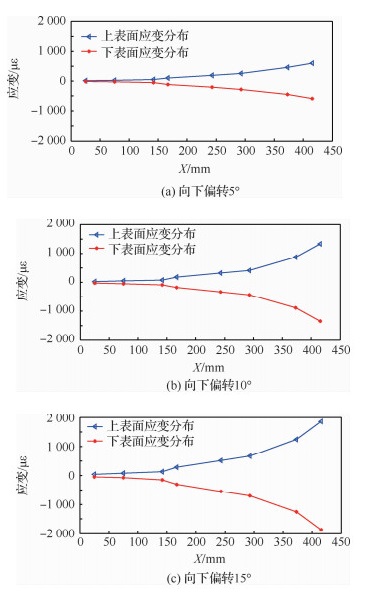
|
| 图 11 鱼骨结构表面应变测量结果 Fig. 11 Results of strain measurement of fishbone surface |
实测鱼骨表面应变分布后,按照式(17)~式(18),计算各个逆向单元的系数矩阵ke和fe。在机翼偏转15°的情况下,以单元E2为例,如图 5中数字标记为该分段内单元节点编号情况,可计算得到其单元系数矩阵k2e和f2e为
| $ \mathit{\boldsymbol{f}}_2^e = {\left[ {\begin{array}{*{20}{c}} {2.86 \times {{10}^{ - 4}}}\\ {7.35 \times {{10}^{ - 5}}}\\ \vdots \\ { - 3.58 \times {{10}^{ - 6}}}\\ 0 \end{array}} \right]_{24 \times 1}} $ | (31) |
| $ \begin{array}{l} \mathit{\boldsymbol{k}}_2^e = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} {2.25 \times {{10}^{ - 3}}}&{8.14 \times {{10}^{ - 3}}}& \cdots &{3.69 \times {{10}^{ - 5}}}\\ {5.51 \times {{10}^{ - 3}}}&{6.63 \times {{10}^{ - 3}}}& \cdots &{2.33 \times {{10}^{ - 5}}}\\ \vdots & \vdots &{}& \vdots \\ {4.42 \times {{10}^{ - 3}}}&{3.10 \times {{10}^{ - 3}}}& \cdots &{7.29 \times {{10}^{ - 6}}} \end{array}} \right]_{24 \times 24}} \end{array} $ | (32) |
将分段1内各个单元的系数矩阵组装成整体矩阵K和F,同时考虑到分段1左端固支,节点1和6的所有位移分量均为0。求得该分段的2个单元内6个节点的位移值U为
| $ \mathit{\boldsymbol{U}} = {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ {0.082}\\ 0 \end{array}} \right]_{36 \times 1}} $ | (33) |
表 1所示为向下偏转15°各分段末尾位移计算结果。
| 分段编号 | u/mm | v/mm | w/mm | θx/rad | θy/rad |
| 1 | 4.045 | 0 | 10.264 | 0.004 | 0.082 |
| 2 | 3.817 | 0 | 7.318 | 0.004 | 0.072 |
| 3 | 3.608 | 0 | 6.917 | 0.004 | 0.060 |
| 4 | 3.330 | 0 | 5.420 | 0.003 | 0.053 |
按照式(29)和式(30)所示将各分段位移叠加,计算得到鱼骨结构的所有逆向单元节点的位移,通过单元形函数插值得到结构任意一点的位移值。
图 12所示为重构算法获得的整个鱼骨位移分布与高度数显卡尺的实测结果的对比情况。偏转角是用机翼自由端末端竖直方向的位移除以鱼骨原轴向长度对应的角度来计算。表 2中给出的当机翼向下偏转5°/10°/15°时,自由端末尾的位移重构绝对误差和偏转角误差。结果表明本文所研究的逆向有限元法能够较为精确地重构机翼鱼骨结构位移,可以用于自适应变形机翼结构实时变形监测。
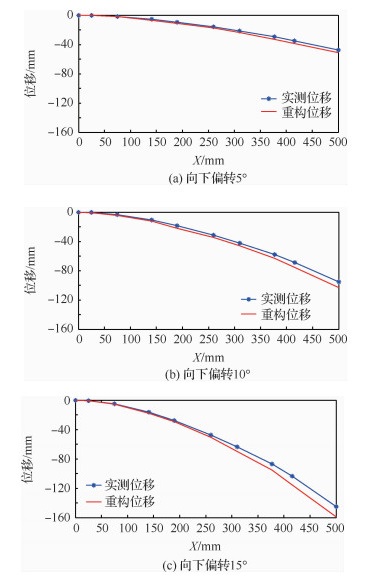
|
| 图 12 重构位移与实测位移对比曲线 Fig. 12 Comparison of reconstructive displacement and measured displacement |
| 偏转角度/(°) | 位移绝对误差/cm | 偏转角误差/(°) |
| 5 | 0.58 | 0.67 |
| 10 | 1.27 | 1.46 |
| 15 | 1.73 | 1.91 |
1) 针对自适应智能结构变形监测的需求,本文提出了一种基于逆向有限元算法和位移分段叠加思想的变形重构方法,实现对航空自适应变形机翼鱼骨结构的变形重构。
2) 实验验证结果表明,自适应变形机翼在分别偏转5°/10°/15°的情况下,机翼末端的位移重构误差不超过1.73 cm,因此验证了该方法在变形机翼这种自适应智能结构的变形重构研究中的有效性和准确性。
| [1] | CHOPRA I. Review of state of art of smart structures and integrated systems[J]. AIAA Journal, 2012, 40(11): 2145-2187. |
| Click to display the text | |
| [2] | YIN W, FU T, LIU J, et al. Structural shape sensing for variable camber wing using FBG sensors[J]. Journal of Mechanics of Materials and Structures, 2010, 5(2): 341-367. |
| Click to display the text | |
| [3] |
陆宇平, 何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10): 1906-1911. LU Y P, HE Z. A survey of morphing aircraft control systems[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1906-1911. (in Chinese) |
| Cited By in Cnki (94) | Click to display the text | |
| [4] | YI J, ZHU X, ZHANG H, et al. Spatial shape reconstruction using orthogonal fiber Bragg grating sensor array[J]. Mechatronics, 2012, 22(6): 679-687. |
| Click to display the text | |
| [5] |
冷劲松, 孙健, 刘彦菊. 智能材料和结构在变体飞行器上的应用现状与前景展望[J]. 航空学报, 2013, 35(1): 29-45. LENG J S, SUN J, LIU Y J. Application status and future prospect of smart materials and structures in morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2013, 35(1): 29-45. (in Chinese) |
| Cited By in Cnki (28) | Click to display the text | |
| [6] |
袁慎芳, 闫美佳, 张巾巾, 等. 一种适用于梁式机翼的变形重构方法[J]. 南京航空航天大学学报, 2014, 46(6): 825-830. YUAN S F, YAN M J, ZHANG J J, et al. Shape reconstruction method of spar wing structure[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(6): 825-830. (in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [7] | KO W L, JACKSON R H. Multilayer theory for delamination analysis of a composite curved bar subjected to end forces and end moments[J]. Composite Structures, 1989, 19: 173-198. |
| Click to display the text | |
| [8] | WANG Z, WANG J, SUI Q, et al. Deformation reconstruction of a smart Geogrid embedded with fiber Bragg grating sensors[J]. Measurement Science and Technology, 2015, 26(12): 125202. |
| Click to display the text | |
| [9] | FOSS G C, HAUGSE E D. Using modal test results to develop strain to displacement transformations[J]. Aerospace Science and Technology, 2007, 10: 16-29. |
| Click to display the text | |
| [10] | TESSLER A, SPANGLER J. An inverse finite element method for application to structural health monitoring[J]. Journal of Composite Materials, 2009, 43(9): 1051-1081. |
| Click to display the text | |
| [11] | KEFAL A, OTERKUS E. Displacement and stress monitoring of a Panamax containership using inverse finite element method[J]. Ocean Engineering, 2016, 119: 16-29. |
| Click to display the text | |
| [12] | KEFAL A, OTERKUS E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method[J]. Ocean Engineering, 2016, 112: 33-46. |
| Click to display the text | |
| [13] | GHERLONE M, CERRACCHIO P, MATTONE M, et al. Shape sensing of 3D frame structures using an inverse finite element method[J]. International Journal of Solids and Structures, 2012, 49(22): 3100-3112. |
| Click to display the text | |
| [14] | ALBANESI A, BRE F, FACHINOTTI V, et al. Simultaneous ply-order, ply-number and ply-drop optimization of laminate wind turbine blades using the inverse finite element method[J]. Composite Structures, 2018, 184: 894-903. |
| Click to display the text | |
| [15] | KEFAL A, YILDIZ M. Modeling of sensor placement strategy for shape sensing and structural health monitoring of a wing-shaped sandwich panel using inverse finite element method[J]. Sensors, 2017, 17(12): 2775. |
| Click to display the text | |
| [16] | PAPA U, RUSSO S, LAMBOGLIA A, et al. Health structure monitoring for the design of an innovative UAS fixed wing through inverse Finite Element Method (iFEM)[J]. Aerospace Science and Technology, 2017, 69: 439-448. |
| Click to display the text | |
| [17] | KIM H, HAN J, BANG H. Real-time deformed shape estimation of a wind turbine blade using distributed fiber Bragg grating sensors[J]. Wind Energy, 2014, 17(9): 1455-1467. |
| Click to display the text | |
| [18] | KEFAL A, OTERKUS E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method[J]. Ocean Engineering, 2016, 112: 33-46. |
| Click to display the text | |
| [19] | KEFAL A, YILDIZ M. Modeling of sensor placement strategy for shape sensing and structural health monitoring of a wing-shaped sandwich panel using inverse finite element method[J]. Sensors, 2017, 17(12): 2775-2786. |
| Click to display the text | |
| [20] | LIU M, WANG L, YUN K, et al. Study on the deformation measurement and reconstruction of heavy-duty machine column based on FBG sensor[J]. Smart Structures and Materials, 2013, 10(2): 88-100. |
| Click to display the text | |
| [21] | GHERLONE M, CERRACCHIO P, MATTONE M. Shape sensing methods:Review and experimental comparison on a wing-shaped plate[J]. Progress in Aerospace Sciences, 2018, 99: 56-63. |
| Click to display the text | |
| [22] | LI L, ZHONG B S, LI W Q, et al. Structural shape reconstruction of fiber Bragg grating flexible plate based on strain modes using finite element method[J]. Journal of Intelligent Material Systems and Structures, 2017, 5(12): 104-125. |
| Click to display the text | |
| [23] | MIELOSZYK M, SKARBEK L, KRAWCZUK M, et al. Application of fibre Bragg grating sensors for structural health monitoring of an adaptive wing[J]. Smart Materials & Structures, 2011, 20(12): 125-144. |
| Click to display the text |



