2. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191;
3. 上海卫星工程研究所, 上海 200240;
4. 湖南大学 信息科学与工程学院, 长沙 410082
2. School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China;
3. Shanghai Institution of Satellite Engineering, Shanghai 200240, China;
4. College of Computer Science and Electronic Engineering, Hunan University, Changsha 410082, China
脉冲到达时间(Time-of-Arrival, TOA)是X射线脉冲星导航的基本观测量[1-2]。航天器上的X射线探测器收集X射线脉冲星辐射的光子[3],经历元折叠形成累积脉冲轮廓[4-5],再结合标准脉冲轮廓、脉冲星计时模型等信息估计脉冲到达时间。但航天器运动和脉冲星周期跃变[6]等导致接收到的脉冲信号周期发生变化,使得按固有周期累积的脉冲轮廓发生畸变,进而导致脉冲TOA发生漂移。脉冲周期估计对脉冲TOA高精度估计具有重要意义,目前已成为一个研究热点。
脉冲星周期估计方法可分为2类:一类利用脉冲星TOA漂移估计周期误差;另一类根据脉冲轮廓畸变反演周期误差,是目前的主流方法。
基于脉冲星TOA漂移的周期误差估计的基本思路如下:建立周期误差与脉冲星TOA漂移之间的关系模型。在此基础上,利用最小二乘法估计TOA与周期误差[7-8];利用天文信息补偿[9]或优化卡尔曼滤波器,如:EKF-CMBSEE(Extended Kalman Filter-Correlated Measurement Bias and State Estimation Error)[10]、跟踪滤波器[11],以达到抑制周期误差影响的目的。
基于轮廓畸变的脉冲星周期估计方法的基本思路如下:尝试按不同周期折叠脉冲星信号,得到一系列畸变脉冲累积轮廓,然后找出畸变度最小的脉冲累积轮廓,其对应的周期就是固有周期。如:时域χ2法、快速折叠法[12]、傅立叶频谱法[13]、循环平稳信号相干统计量法[14]、最大相关方差搜索法[15]、基于Lomb的χ2算法[16]、脉冲轮廓熵算法[17]和轮廓特征法[18]等。上述方法无一例外都需要尝试按不同周期折叠脉冲星信号。但是,脉冲星辐射信号数据量庞大,导致计算量大等问题,不适合星载计算机在轨运行。
压缩感知(Compressed Sensing,CS)[19-20]是一种新兴的信号处理方法,对稀疏信号的处理能力很强,恰巧脉冲星信号是典型的稀疏信号。近年来,基于CS的脉冲星信号处理成为一个研究热点[21-23]。基于快速傅里叶变换-压缩感知(FFT-CS)的脉冲星周期快速估计方法[24]利用CS压缩脉冲星辐射信号,再直接根据脉冲星轮廓畸变度估计脉冲固有周期。该方法避免了多次脉冲星信号折叠,大幅减少了计算量,使得脉冲星周期在轨估计成为可能。
但是,傅立叶变换将信号能量分散在数量庞大的傅立叶级数中。FFT-CS采用低频傅立叶变换,所需的傅立叶级数仍然上千,这导致测量矩阵尺寸极大。为提高计算速度,必须大幅减小尺寸。经验模态分解(Empirical Mode Decomposition, EMD)[25-26]根据原始信号的固有特征,自适应地将其分解成有限个固有模态函数(Intrinsic Mode Function,IMF)。IMF包含了原始信号不同时间尺度的局部特征信号。而脉冲轮廓畸变度这一微弱局部特征可体现在某些IMF中。与傅立叶变换相比,IMF数量大幅减少,仅为101~102量级。因此,本文将IMF构成的测量矩阵替换FFT-CS中的低频傅立叶变换矩阵,提出了一种基于EMD-CS的脉冲星周期超快速估计方法,旨在保持估计精度的同时,减小计算量,加快运行速度。
1 最优IMF测量矩阵为减小测量矩阵尺寸,本文利用EMD分解得到的IMF构造测量矩阵来替代低频傅立叶矩阵,并在此基础上提出了一种EMD-CS方法。EMD-CS方法的基本流程与FFT-CS方法类似,二者唯一不同在于测量矩阵。本节重点研究测量矩阵。
在CS中,测量矢量的获取是通过测量矩阵来实现的。通常,测量矩阵尺寸越小,计算量越少。因此寻找一种测量矩阵,用更少的测量次数达到预期的结果变得尤为重要。
为了实现这个目标,本文提出了最优IMF测量矩阵,思路如下:MD个不同畸变程度的脉冲轮廓hm经EMD分解后,得到一系列IMF{FIMm, n},m=0, 1, …,MD-1为畸变脉冲轮廓序号;n=0, 1, …,Nm-1为每个畸变脉冲轮廓EMD分解得到的IMF序号, 其中:Nm为最大IMF序号,对于不同畸变轮廓,Nm也不同。
将这一系列IMF序列组合而成一个IMF原始测量矩阵Φ0(MIMF×N),N为一个脉冲周期内的脉冲间隔数;MIMF为不同畸变轮廓分解的IMF序列数总和, 可表示为
| $ {M_{{\rm{IMF}}}} = \sum\limits_m {{N_m}} $ | (1) |
Φ0可以表示为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_0} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{F}}_{{\rm{IM}}}^0}&{\mathit{\boldsymbol{F}}_{{\rm{IM}}}^1}& \cdots &{\mathit{\boldsymbol{F}}_{{\rm{IM}}}^m}& \cdots &{\mathit{\boldsymbol{F}}{{_{{\rm{I}}{{\rm{M}}^{\rm{D}}}}^M}^{ - 1}}} \end{array}} \right]^{\rm{T}}} $ | (2) |
式中:FIMm为第m个IMF测量子矩阵,表达式为
| $ \mathit{\boldsymbol{F}}_{{\rm{IM}}}^m = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}_{{\rm{IM}}}^{m,0}}&{\mathit{\boldsymbol{F}}_{{\rm{IM}}}^{m,1}}& \cdots &{\mathit{\boldsymbol{F}}_{{\rm{IM}}}^{m,n}}& \cdots &{\mathit{\boldsymbol{F}}{{_{{\rm{IM}}}^{m,{N_m}}}^{ - 1}}} \end{array}} \right]^{\rm{T}}} $ | (3) |
虽然IMF包含了各个畸变脉冲轮廓的所有趋势分量,但脉冲轮廓畸变度这一微弱局部特征只体现在某些IMF中。因此,迭代剔除冗余的IMF序列尤为必要,可以减小测量矩阵的尺寸。例如:残差函数,它代表每个畸变轮廓的平均趋势,无法体现脉冲轮廓畸变,构造测量矩阵中应剔除此序列。除了剔除残差函数,去除哪些IMF序列会对提高精度更有帮助,成为一个值得考虑的问题。本文根据仿真结果,利用迭代剔除法解决这一问题,详见4.2节。采用迭代剔除法将FIMm的第ne行删掉,估计精度更高,即
| $ \mathit{\boldsymbol{F}}_{{\rm{IM}}}^m({n_{\rm{e}}},:) = [ \bullet ] $ | (4) |
式中:ne∈ZE,ZE为删除的IMF序号集合,元素个数为NE。删除冗余的IMF后,即可得到第m个最优IMF测量子矩阵FEm,将测量子矩阵组合构成最优IMF测量矩阵ΦE(MEIMF×N维):
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{E}}} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{F}}_{\rm{E}}^0}&{\mathit{\boldsymbol{F}}_{\rm{E}}^1}& \cdots &{\mathit{\boldsymbol{F}}_{\rm{E}}^m}& \cdots &{\mathit{\boldsymbol{F}}{{_{{{\rm{E}}^{\rm{D}}}}^M}^{ - 1}}} \end{array}} \right]^{\rm{T}}} $ | (5) |
MEIMF的值为
| $ {M_{{\rm{EIMF}}}} = \sum\limits_m {{N_m}} - {M_{\rm{D}}}{N_E} $ | (6) |
由式(1)和式(6)可看出,ΦE的尺寸小于Φ0。
迭代剔除法在地面进行,筛选得到的最优IMF测量矩阵存入器载计算机,无需在轨筛选。
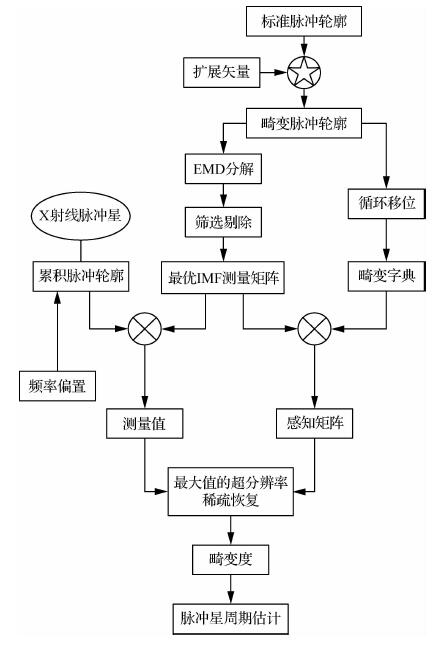
2 EMD-CS本节将介绍EMD-CS方法估计脉冲星周期的整个算法流程,如图 1所示分成4个模块:①最优IMF测量矩阵的设计;②畸变字典的构造;③脉冲频率初始偏置;④最大元素的超分辨率稀疏恢复。其中,最优IMF测量矩阵已经在第1节中描述。下面将介绍其他3个模块:
|
| 图 1 所提算法流程图 Fig. 1 Flowchart of proposed algothim |
1) 畸变字典的构造
文献[24]已证明,畸变脉冲轮廓可视为标准脉冲轮廓与门函数的循环互相关。因此,构造了MD个不同畸变度的脉冲轮廓hm,表达式为
| $ {\mathit{\boldsymbol{h}}_m} = {\mathit{\boldsymbol{G}}_m} \otimes \mathit{\boldsymbol{h}} $ | (7) |
式中:Gm(N×1维)为扩散矢量;m为畸变脉冲轮廓序号;h(N×1维)为标准脉冲轮廓;⊗表示循环互相关。Gm满足:
| $ {\mathit{\boldsymbol{G}}_m}(n) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{m}}&{0 \le n \le m - 1}\\ 0&{m \le n \le N - 1} \end{array}} \right. $ | (8) |
从式(7)和式(8)可看出,Gm相当于MD个宽度不同的矩形窗。脉冲星轮廓畸变度定义为畸变宽度与一个脉冲周期内的周期间隔数N之比,即m/N。随着m增大,矩形窗变宽,脉冲累积轮廓的畸变度变大。
脉冲星导航常用于深空探测巡航段,此时的轨道模型近似于线性的[10],所以可把脉冲星周期误差视为非时变的。式(8)所建立的模型适用于这种情况。
将第m个畸变脉冲轮廓循环移位构成第m个畸变脉冲轮廓子字典φm(N×P维),表达式为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varphi }}_m} = \{ {\mathit{\boldsymbol{\varphi }}_{mi}}(t)|{\mathit{\boldsymbol{\varphi }}_{mi}}(t) = {\mathit{\boldsymbol{h}}_m}(t \pm i)\} }\\ {i = 0,1, \cdots ,(P - 1)/2} \end{array} $ | (9) |
式中:P为最大相位偏移量;φmi(t)为子字典φm中的第i个原子;hm(t)为第m个畸变脉冲轮廓。可将MD个子字典φm合成一个三维矩阵字典Ψ(N×P×MD维)。
2) 脉冲频率初始偏置
累积脉冲轮廓是根据脉冲固有周期T0将脉冲星辐射光子进行折叠而形成的,这一过程称为历元折叠。但是,多普勒效应以及脉冲星周期跃变会使航天器接收到的脉冲周期存在误差ΔT,与频率偏移之间的关系可表示为
| $ \Delta f = - \Delta T/T_0^2 = - \Delta Tf_0^2 $ | (10) |
式中:Δf为频率偏移;f0为固有频率。
文献[24]已经证明,不能直接根据脉冲星轮廓畸变辨别Δf的正负号。为了解决此问题,引入脉冲星周期偏移Toffset,且满足Toffset≫ΔT。这样,-Toffset+ΔT和-Toffset-ΔT的符号都是负号,但幅度不同。所以,脉冲轮廓按照周期T0-Toffset+ΔT进行历元折叠形成累积脉冲轮廓。
3) 基于最大值的超分辨率稀疏恢复
在压缩感知中,信号稀疏恢复是通过感知矩阵与测量矢量相匹配,根据最大匹配值实现的。感知矩阵T是最优IMF测量矩阵与字典的乘积:
| $ \mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{E}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} $ | (11) |
式中:T的尺寸为MEIMF×P×MD。
测量矢量y(MEIMF×1维)的获得方式为
| $ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{E}}}\mathit{\boldsymbol{\tilde h}} $ | (12) |
式中:
感知矩阵与测量矢量的乘积为匹配矩阵S,S可表示为
| $ \begin{array}{l} \begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}(i,j) = \mathit{\boldsymbol{T}}{{(:,i,j)}^{\rm{T}}}\mathit{\boldsymbol{y}}}\\ {i = 1,2, \cdots ,P;} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,{M_{\rm{D}}} \end{array} $ | (13) |
S的最大值对应的相位和畸变度的索引值分别
| $ [\tilde p,\tilde m] = \mathop {{\rm{ argmax }}}\limits_{i,j} (\mathit{\boldsymbol{S}}(i,j)) $ | (14) |
为了使估计更加准确,运用基于最大值的超分辨率稀疏恢复:
| $ \hat m = \frac{{\tilde m - 0.5[{\rm{max}}({\mathit{\boldsymbol{S}}_{\tilde m + 1}}) - {\rm{max}}({\mathit{\boldsymbol{S}}_{\tilde m - 1}})]}}{{{\rm{max}}({\mathit{\boldsymbol{S}}_{\tilde m + 1}}) + {\rm{max}}({\mathit{\boldsymbol{S}}_{\tilde m - 1}}) - 2\mathit{\boldsymbol{S}}(\tilde p,\tilde m)}} $ | (15) |
式中:
| $ \Delta \hat f = \frac{{\hat m}}{{N{T_{{\rm{obs}}}}}} $ | (16) |
式中:Tobs为观测时间。相应的脉冲周期估计误差Δ
| $ \Delta \hat T = {T_{{\rm{ offset }}}} - \Delta \hat fT_0^2 = {T_{{\rm{ offset }}}} - T_0^2\frac{m}{{N{T_{{\rm{ obs }}}}}} $ | (17) |
本节分析EMD-CS方法的计算复杂度。在该方法中,脉冲星轮廓累积、测量矢量获取和匹配在航天器上运行。其中,脉冲星累积过程可在脉冲星信号的观测时间内进行。而测量矢量获取和匹配是在观测结束后才进行的。考虑到航天器高速飞行的影响,需尽快完成这2个过程,才能保证算法的实时性。因此,本文分析二者计算复杂度即可。
测量矢量的获取由式(12)确定。最优IMF测量矩阵尺寸为MEIMF×N,脉冲累积轮廓为长度为N。这需要MEIMF×(2N-1)MAC,MAC(Multiply/Accumulate Computation)表示加法乘法的计算次数。
匹配由式(13)确定。测量矢量与一个原子匹配,所需计算量为2MEIMF-1 MAC。字典中原子个数为MD×P。测量矢量与字典匹配所需计算量是(2MEIMF-1)×MD×P MAC。
总计算量为MEIMF×(2N-1)+(2MEIMF-1)×MD×P≈2MEIMF×(N+MD×P) MAC。
以上可以看出,计算量与MEIMF呈正比关系。若能大幅减小MEIMF,计算量也将大幅减少。此外,与FFT-CS相比,EMD-CS仅有实数部分,计算量将更小。
4 仿真实验将基于EMD-CS的脉冲星周期估计方法与基于FFT-CS的周期估计进行仿真比较。首先,筛选出最优的测量矩阵,并分析其有限等距性质;其次,将其与基于FFT-CS的脉冲星周期估计方法作比较,体现本文方法的优越性;再次,分析脉冲星和背景噪声的光子流量密度、X射线探测器面积以及观测时间对脉冲星周期估计精度的影响。
4.1 仿真条件脉冲星数据来自于欧洲脉冲星网(EPN),仿真实验在处理器为英特尔Core i5-7500@3.40 GHz四核、内存为8 GB的计算机上运行。最大畸变度MD=21,即构造21个脉冲星畸变轮廓,最大相位偏移量P=21。仿真条件如表 1所示。
| 仿真条件 | 具体数值 |
| 脉冲星 | PSR B0531+21 |
| 周期/ms | 33.4 |
| 辐射光子流量/(ph·cm-2·s-1) | 1.54 |
| 背景噪声流量/(ph·cm-2·s-1) | 0.005 |
| 脉冲星间隔数 | 33 400 |
| 时间分辨率/μs | 1 |
| 探测器面积/cm2 | 400 |
| 观测时间/s | 1 000 |
| 脉冲星周期偏移值/ps | 334 |
将21个脉冲星畸变轮廓经EMD分解,得到的一系列IMF{FIMm, n}中Nm=9~12, MIMF=211。若用Φ0作为测量矩阵,脉冲星周期估计误差为90.624 7 ps。本文采用迭代剔除法筛选部分IMF,即剔除部分IMF后,将剩下的IMF构成最优测量矩阵ΦE。
表 2给出了剔除某些IMF的脉冲星周期估计误差,表的首行和首列表示剔除的IMF序号。从表 2可以看出,若是剔除第1个IMF,脉冲星周期估计误差大,所以必须保留第1个IMF;而同时剔除残差和第5个IMF时,误差最小(70.177 8 ps)。
| 单位:ps | |||||||||||||||||||||||||||||
| 剔除序号 | 第0行 | 第1行 | 第2行 | 第3行 | 第4行 | 第5行 | 第6行 | 第7行 | 第8行 | ||||||||||||||||||||
| 第0行 | 76.127 7 | 245.761 | 75.926 4 | 77.160 6 | 77.180 4 | 70.177 8 | 70.382 4 | 70.930 2 | 77.147 4 | ||||||||||||||||||||
| 第1行 | 245.761 | 269.504 | 286.024 | 268.287 | 258.423 | 235.983 | 237.471 | 252.797 | 257.397 | ||||||||||||||||||||
| 第2行 | 75.926 4 | 286.024 | 84.354 6 | 84.295 2 | 84.631 8 | 79.236 3 | 77.550 0 | 76.870 2 | 86.341 2 | ||||||||||||||||||||
| 第3行 | 77.160 6 | 268.287 | 84.295 2 | 85.641 6 | 85.958 4 | 80.566 2 | 78.480 6 | 76.520 4 | 86.552 4 | ||||||||||||||||||||
| 第4行 | 77.180 4 | 258.423 | 84.631 8 | 85.958 4 | 85.618 5 | 81.529 8 | 77.939 4 | 77.441 1 | 85.763 7 | ||||||||||||||||||||
| 第5行 | 70.177 8 | 235.983 | 79.236 3 | 80.566 2 | 81.529 8 | 80.645 4 | 76.629 3 | 73.619 7 | 87.301 5 | ||||||||||||||||||||
| 第6行 | 70.382 4 | 237.471 | 77.550 0 | 78.480 6 | 77.939 4 | 76.629 3 | 77.345 4 | 67.221 0 | 81.328 5 | ||||||||||||||||||||
| 第7行 | 70.930 2 | 252.797 | 76.870 2 | 76.520 4 | 77.441 1 | 73.619 7 | 67.221 0 | 76.230 0 | 75.477 6 | ||||||||||||||||||||
| 第8行 | 77.147 4 | 257.397 | 86.341 2 | 86.552 4 | 85.763 7 | 87.301 5 | 81.328 5 | 75.477 6 | 86.295 0 | ||||||||||||||||||||
本文保留第1个IMF,剔除残差和第5个IMF后,在剩下的IMF中继续实施剔除操作,仿真结果如表 3所示。从表 3中可以看出,剔除第6和第7个IMF,误差最小(62.224 8 ps)。表 4给出了剔除第5、6、7个IMF以及残差之后的周期估计。实验结果表明,再剔除第3和第8个IMF,估计误差更小(57.063 6 ps)。表 5给出了在此基础上,4次剔除之后的结果。此次剔除,使得误差增大。因此,本文将IMF剔除第3、5、6、7、8个IMF以及残差之后的IMF序列组合成最优IMF测量矩阵ΦE,该矩阵尺寸为85×33 400。相对于原始测量矩阵Φ0,该矩阵的尺寸大大减少,而精度也得到了提高。
| 单位:ps | |||||||||||||||||||||||||||||
| 剔除序号 | 第2行 | 第3行 | 第4行 | 第6行 | 第7行 | 第8行 | |||||||||||||||||||||||
| 第2行 | 69.062 4 | 69.036 0 | 69.342 9 | 66.161 7 | 65.640 3 | 69.418 8 | |||||||||||||||||||||||
| 第3行 | 69.036 0 | 70.224 0 | 70.065 6 | 67.389 3 | 65.868 0 | 70.111 8 | |||||||||||||||||||||||
| 第4行 | 69.342 9 | 70.065 6 | 69.719 1 | 66.960 3 | 65.056 2 | 69.943 5 | |||||||||||||||||||||||
| 第6行 | 66.161 7 | 67.389 3 | 66.960 3 | 70.356 0 | 62.224 8 | 71.194 2 | |||||||||||||||||||||||
| 第7行 | 65.640 3 | 65.868 0 | 65.056 2 | 62.224 8 | 71.920 2 | 71.491 2 | |||||||||||||||||||||||
| 第8行 | 69.418 8 | 70.111 8 | 69.943 5 | 71.194 2 | 71.491 2 | 76.550 1 | |||||||||||||||||||||||
| 单位:ps | |||||||||||||||||||||||||||||
| 剔除序号 | 第2行 | 第3行 | 第4行 | 第8行 | |||||||||||||||||||||||||
| 第2行 | 60.003 9 | 59.862 0 | 60.089 7 | 57.086 7 | |||||||||||||||||||||||||
| 第3行 | 59.862 0 | 60.825 6 | 62.115 9 | 57.063 6 | |||||||||||||||||||||||||
| 第4行 | 60.089 7 | 62.115 9 | 61.680 3 | 57.297 9 | |||||||||||||||||||||||||
| 第8行 | 57.086 7 | 57.063 6 | 57.297 9 | 57.136 2 | |||||||||||||||||||||||||
| 单位:ps | |||||||||||||||||||||||||||||
| 剔除序号 | 第2行 | 第4行 | |||||||||||||||||||||||||||
| 第2行 | 57.264 9 | 57.637 8 | |||||||||||||||||||||||||||
| 第4行 | 57.637 8 | 57.621 3 | |||||||||||||||||||||||||||
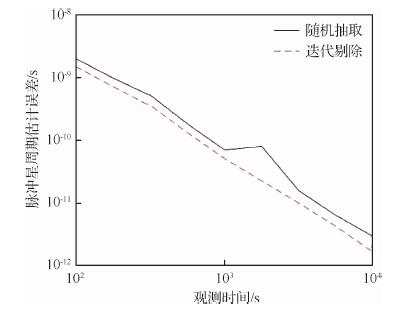
为了体现迭代剔除法的优越性,将迭代剔除后的最优测量矩阵与随机抽取85个IMF组成的测量矩阵进行比较。图 2给出了观测时间为100~10 000 s时,2种测量矩阵的脉冲星周期估计误差对比。与随机抽取相比,本文方法得出的测量矩阵可使脉冲星周期估计误差更小。
|
| 图 2 迭代剔除与随机抽取的对比 Fig. 2 Comparison between iteration elimination and random selection |
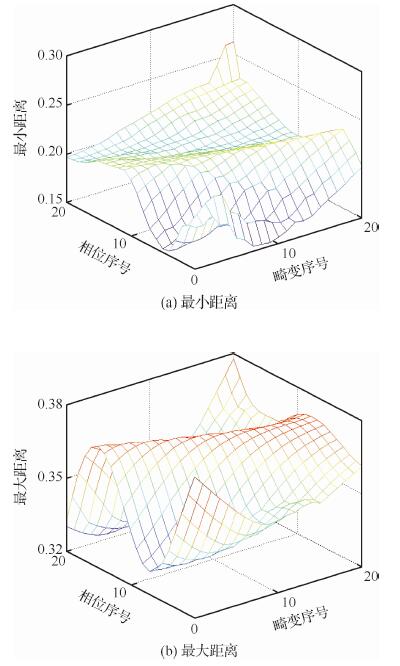
本节研究IMF测量矩阵是否满足有限等距性质(Restricted Isometry Property, RIP)。每个测量矢量与其他测量矢量之间的最大距离与最小距离如图 3所示。从图中可以看出,单个测量矢量的最小距离在0.15~0.27之间,最大值在0.32~0.38之间,波形起伏小。这表明算法性能几乎与累积轮廓的相位和畸变度无关。因此,等距常量为0.85,测量矩阵满足1阶RIP。
|
| 图 3 测量矢量之间的距离 Fig. 3 Distance between measurement vectors |
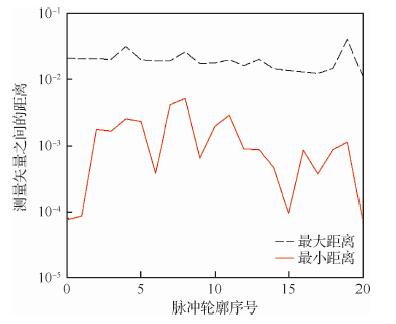
接着,又研究了利用单个轮廓EMD分解,构造测量矩阵。从图 4中可以看出,最大距离与最小距离相差约1~2个数量级,差距大。虽然测量矩阵也满足1阶RIP,但是,最小距离太小,易受噪声干扰。
|
| 图 4 单个轮廓对应的测量矢量距离最值 Fig. 4 Extreme distance between measurement vectors for single profile |
本文将基于EMD-CS的脉冲周期估计方法与FFT-CS方法进行对比,实验结果如表 6所示。
| 参数 | EMD-CS | FFT-CS | |||
| 矩阵行数 | 85 | 85 | 1 999 | 2 499 | 3 499 |
| 误差/ps | 57.9 | 279 | 95.8 | 57.5 | 41.8 |
| 时间/s | 0.002 1 | 0.003 0 | 0.012 7 | 0.015 5 | 0.024 4 |
从表 6可看出,随着测量矩阵行数的增加,FFT-CS的估计误差减小。若测量矩阵行数为85,FFT-CS的估计误差为279 ps,远大于EMD-CS的57.9 ps。若要达到58 ps的精度,FFT-CS需要的矩阵尺寸为2 499×33 400,远大于EMD-CS的85×33 400。
从运行时间上看,当测量行数都为85的时候,FFT-CS方法运行时间是0.003 0 s,EMD-CS方法运行时间是0.002 1 s,若要达到EMD-CS方法中测量行数是85时候的精度,FFT-CS方法所需运行时间是0.015 5 s。
因此,EMD-CS只需较小的测量矩阵就可以获得较高的估计精度,且运行速度更快,明显优于FFT-CS方法。此外,当测量矩阵行数较大(上千)运行,FFT-CS的运行时间与矩阵行数几乎成正比,符合理论分析结论。
值得一提的是,器载计算机的计算能力有限,因此,这2种算法在轨运行时间必将大幅增长。所以,缩短运行时间是有一定实际意义的。
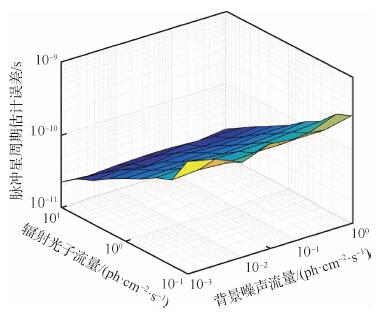
4.5 光子流量密度脉冲星辐射光子流量密度和背景噪声流量密度是影响脉冲星周期估计精度的重要因素。本节研究两者对周期估计精度的影响,结果如图 5所示。从图 5中可以看出,脉冲星周期估计误差随背景噪声的增大而增大;而随辐射光子流量密度的增大而减小。
|
| 图 5 不同流量下的周期估计误差 Fig. 5 Period estimation error with different fluxes |
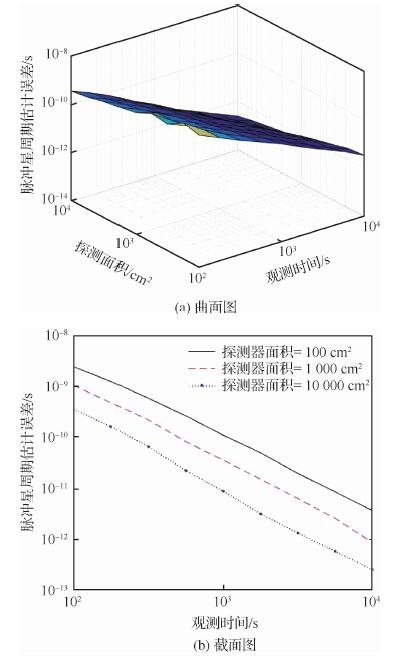
X射线探测器面积和观测时间均为脉冲星周期估计精度的影响因素。本节给出了二者与脉冲周期估计误差的关系,仿真结果如图 6所示。由图 6(a)可看出,观测时间和探测器面积的增加均能减小脉冲星周期估计误差。因此,增加X射线探测器面积与观测时间,有助于提高精度。
|
| 图 6 不同探测器面积和观测时间下的周期估计误差 Fig. 6 Period estimation error with different sensor's areas and observation times |
为便于分析,本文在100 cm2、1 000 cm2、10 000 cm2这3种典型的探测器面积下研究估计误差,如图 6(b)所示。可以看出,X射线探测器面积增大2个数量级,脉冲星周期估计精度提高约一个数量级。观测时间延长2个数量级,脉冲星周期估计精度提高约3个数量级。因此,相比于增加探测器面积,延长观测时间更加有利于提高估计精度。
值得一提的是,本文方法并未考虑延长观测时间所带来的轨道外推误差影响。这是因为本文方法适用于深空探测巡航段,此时的轨道模型近似于线性的[10],轨道外推误差的影响可忽略不计。若在环绕段长时间观测,利用天文测角信息补偿[9]是一个较好的选择。
5 结论本文提出了一种基于EMD-CS的脉冲星周期超快速估计方法。考虑到IMF包含了脉冲轮廓畸变度这一微弱局部特征,该方法利用畸变脉冲轮廓的IMF构造测量矩阵,使得采样率大幅下降,从而提高计算速度。该方法具有以下优点:
1) 计算量小,约2 ms。究其原因,一方面,与FFT-CS类似,EMD-CS仅利用一个累积轮廓进行估计,避免了多次脉冲信号累积;另一方面,与FFT-CS相比,测量矩阵尺寸减小了一个数量级以上,降低了采样和匹配估计的计算量。
2) 估计精度高。在相同测量矩阵尺寸下,EMD-CS的估计精度优于FFT-CS。若要二者达到相同精度,FFT-CS的测量矩阵比EMD-CS大一个数量级以上。
3) 纯实数运算。EMD无虚数运算,IMF为实数。与FFT-CS相比,EMD-CS进一步降低了计算复杂度。
4) 原信号长度不受限制。哈达玛矩阵的阶数N应满足N、N/12、N/20必须是2的整数次幂。由于尺寸受限,实际难与脉冲轮廓长度匹配,无法完成采样。而IMF长度必与原信号相等。
综上,基于EMD-CS的脉冲星周期超快速估计方法计算量小,估计精度高,适合于深空探测在轨计算。
基于EMD-CS的脉冲星周期超快速估计方法适用于时不变的轨道模型。而环绕段、捕获段等是时变的,如何在时变段实现脉冲星周期估计是一个值得研究的问题。
| [1] |
杨廷高. X射线脉冲星脉冲到达航天器时间测量[J]. 空间科学学报, 2008, 28(4): 330-334. YANG T G. Determination of X-ray pulsar pulse time of arrival at spacecraft[J]. Chinese Journal of Space Science, 2008, 28(4): 330-334. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [2] |
林晴晴, 帅平, 黄良伟, 等. 一种高精度的X射线脉冲星导航TOA估计方法[J]. 宇航学报, 2016, 37(6): 704-710. LIN Q Q, SHUAI P, HUANG L W, et al. A high precision TOA estimation method for X-ray pulsar-based navigation system[J]. Journal of Astronautics, 2016, 37(6): 704-710. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [3] | SHEIKH S I, PINES D J, RAY P S, et al. Spacecraft navigation using X-ray pulsars[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 49-63. |
| Click to display the text | |
| [4] | EMADZADEH A A, SPERER J L. X-Ray pulsar-based relative navigation using epoch folding[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2317-2328. |
| Click to display the text | |
| [5] | ZHANG H, XU L P. An improved phase measurement method of integrated pulse profile for pulsar[J]. Science China, 2011, 54(9): 2263-2270. |
| Click to display the text | |
| [6] |
孙海峰, 包为民, 方海燕, 等. X射线脉冲轮廓稳定性对导航精度的影响[J]. 物理学报, 2014, 63(6): 441-448. SUN H F, BAO W M, FANG H Y, et al. Effect of stability of X-ray pulsar profiles on range measurement accuracy in X-ray pulsar navigation[J]. Acta Physica Sinica, 2014, 63(6): 441-448. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [7] | SONG J N, XU G D, DONG L M, et al. Pulse period estimation method based on TOA information[J]. Acta Photonica Sinica, 2017, 46(5): 16-25. |
| Click to display the text | |
| [8] | LIU J, WU J, XIONG L, et al. Fast position and velocity determination for pulsar navigation using NML and LSM[J]. Chinese Journal of Electronics, 2017, 26(6): 1325-1329. |
| Click to display the text | |
| [9] |
褚永辉, 王大轶, 熊凯, 等. X射线脉冲星导航测量延时补偿方法研究[J]. 宇航学报, 2012, 33(11): 1617-1622. CHU Y H, WANG D Y, XIONG K, et al. Research on measurement time-delay compensation on X-ray pulsar-based navigation[J]. Journal of Astronautics, 2012, 33(11): 1617-1622. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [10] | LIU J, FANG J C, KANG Z W, et al. Novel algorithm for X-ray pulsar navigation against doppler effects[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 228-241. |
| Click to display the text | |
| [11] | HUANG L W, LIANG B, ZHANG T. Pulse phase and doppler frequency estimation of X-ray pulsars under conditions of spacecraft and binary motion and its application in navigation[J]. Science China, Physics, Mechanics and Astronomy, 2013, 56(4): 848-858. |
| Click to display the text | |
| [12] | LYNE A G, GRAHAM-SMITH F. Book review:Pulsar astronomy[J]. Journal of the British Astronomical Association, 1999, 109(1): 145. |
| [13] | BURNS W R, CLARK B G. Pulsar search techniques[J]. Astronomy & Astrophysics, 1969, 2(1): 280-287. |
| [14] |
李建勋, 柯熙政. 基于循环平稳信号相干统计量的脉冲星周期估计新方法[J]. 物理学报, 2010, 59(11): 8304-8310. LI J X, KE X Z. Period estimation method for weak pulsars based on coherent statistic of cyclostationary signal[J]. Acta Physica Sinica, 2010, 59(11): 8304-8310. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [15] |
李建勋, 柯熙政, 赵宝升. 一种脉冲星周期的时域估计新方法[J]. 物理学报, 2012, 61(6): 537-543. LI J X, KE X Z, ZHAO B S. A new time-domain estimation method for period of pulsars[J]. Acta Physica Sinica, 2012, 61(6): 537-543. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] |
周庆勇, 姬剑锋, 任红飞. 非等间隔计时数据的X射线脉冲星周期快速搜索算法[J]. 物理学报, 2013, 62(1): 525-532. ZHOU Q Y, JI J F, REN H F. The quick search algorithm of pulsar period based on unevenly spaced timing data[J]. Acta Physica Sinica, 2013, 62(1): 525-532. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] | ZHANG H, XU L P, XIE Q. Modeling and doppler measurement of X-ray pulsar[J]. Science China (Physics, Mechanics & Astronomy), 2011, 54(6): 1068-1076. |
| Click to display the text | |
| [18] |
谢强, 许录平, 张华. 基于轮廓特征的X射线脉冲星信号多普勒估计[J]. 宇航学报, 2012, 33(9): 1301-1307. XIE Q, XU L P, ZHANG H, et al. Doppler estimation of X-ray pulsar signals based on profile feature[J]. Journal of Astronautics, 2012, 33(9): 1301-1307. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| Click to display the text | |
| [20] | BOYER C, BIGOT J, WEISS P. Compressed sensing with structured sparsity and structured acquisition[J]. Applied & Computational Harmonic Analysis, 2019, 46(2): 312-350. |
| Click to display the text | |
| [21] |
苏哲, 许录平, 甘伟. 基于压缩感知的脉冲星轮廓构建算法[J]. 中国科学:物理学力学天文学, 2011, 41(5): 681-684. SU Z, XU L P, GAN W. Pulsar profile construction algorithm based on compressed sensing[J]. Scientia Sinica (Physica, Mechanica & Astronomic), 2011, 41(5): 681-684. (in Chinese) |
| Cited By in Cnki (13) | Click to display the text | |
| [22] |
康志伟, 吴春艳, 刘劲, 等. 基于两级压缩感知的脉冲星时延估计方法[J]. 物理学报, 2018, 67(9): 285-292. KANG Z W, WU C Y, LIU J, et al. Pulsar time delay estimation method based on two-level compressed sensing[J]. Acta Physica Sinica, 2018, 67(9): 285-292. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [23] | SHEN L R, LI X P, SUN H F, et al. A robust compressed sensing based method for X-ray pulsar profile construction[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(10): 4379-4385. |
| Click to display the text | |
| [24] | LIU J, YANG Z H, KANG Z W, et al. Fast CS-based pulsar period estimation method without tentative epoch folding and its CRLB[J]. Acta Astronautica, 2019, 160(1): 90-100. |
| Click to display the text | |
| [25] | HUANG N E, ZHENG S, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| Click to display the text | |
| [26] | TAI G, DENG Z. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing[J]. Applied Acoustics, 2017, 127(1): 46-62. |
| Click to display the text |



