在分布式多传感器多目标跟踪系统[1-2]中,航迹关联(即判断航迹“同源”)是进行信息融合的基础。然而传感器开机时机或采样周期的不同往往导致航迹是异步不等速率[3-4]的,这增大了航迹关联的难度。
为解决此问题,文献[5]提出一种基于最小二乘法的关联算法;文献[6]利用顺序成对关联思想,将关联问题转化为广义似然比检验;文献[7]借助变异蚁群算法解决了最小二乘多维分配问题。文献[8]组合距离分布直方图特征,引入机器学习进行特征提取,对航迹插值处理进行时间对齐;文献[9]利用滤波插值补偿全局估计,构造反馈序列,进行自适应航迹关联。文献[10]利用插值重构,将测量值与滤波值统一,用伪测量校准时间后再使用经典分配法进行关联。通过衡量航迹集合之间的最优次模式分配(OSPA)距离[11],文献[12]提出一种基于滑窗OSPA距离的航迹关联算法,但对于不等速率采样情况下的异步航迹关联仍需作同步处理。
无论是最小二乘拟合还是拉格朗日插值,异步不等速率航迹关联问题的传统解决思路是先通过时域配准[13]将航迹时刻统一,再利用内插外推的方法得到等长航迹序列进行关联。但时域配准会增加算法运算量,且在同步化过程中,估计值的误差会发生传播,这种传播与滤波误差有一定相关性,难以进行描述和衡量,从而影响关联性能。
文献[14]引入灰理论[15],用区间灰数表征异步特性,提出了航迹灰关联算法;文献[16]通过区实混合序列变换,将航迹序列灰化,利用灰色系统分析进行关联;文献[17]使用动态时间规划,从整体上考虑航迹形状的相似性进行关联。文献[18]则将不同航迹公共测量时间区间划分为时间窗,计算时间窗权重,应用D-S证据理论或Bayes理论进行关联。
文献[16-18]无需时域配准对异步航迹进行关联,但算法均是以航迹间距离为依据,根据航迹整体形状相似性或相对位置进行关联。在实际的航迹交叉、分叉和合并[12, 19]现象中,航迹交叉点或航迹分叉合并前后的平行阶段,依靠局部航迹间的距离进行航迹关联往往会导致错误关联。
为避免以局部航迹距离为判据带来的错误关联,本文将航迹序列作为数据集进行处理,利用分段混合航迹序列的离散度来判断2条航迹的接近程度。该方法无需时域配准,未引入新误差,可直接对异步不等速率航迹进行关联,并且航迹序列的分段处理可有效解决航迹交叉、分叉和合并问题。
1 数据集的离散度度量定义1 混合数据集的离散度
对任意2个数值型数据集X={x1, x2, …, xM}和Y={y1, y2, …, yN},记(X, Y)=X∪Y为混合数据集,称
| $ \Delta (X,Y) = \left\{ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\Pi _M^{nN}} V({X_{\Pi _M^{nN}}} \cup nY) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{max}}}\limits_{\Pi _M^{nN}} V(X_{\Pi _M^n}^{\rm{c}} \cup {Y_{\Pi _N^m}}),M \ge N\\ \Delta (Y,X),M < N \end{array} \right. $ | (1) |
为混合数据集的离散度。
式中:n=INTL[M/N];INTL[x]表示不大于x的最大整数;m=M mod N,y mod x表示y除以x的余数;∪为集合“并”运算。
对数据集X={x1, x2, …, xp},有nX={nx1, nx2, …, nxp}
| $ {X_{\Pi _p^q}} = \{ x_j^\pi |x_j^\pi \in X,j = 1,2, \cdots ,q\} $ |
式中:∏pq表示从数据集X的p个元素中任取q个元素;X∏cpq=X-X∏pq;V(X)=
| $ \bar x = \sum\limits_{i = 1}^p {{x_i}} /p,s = \sqrt {\sum\limits_{i = 1}^p {{{({x_i} - \bar x)}^2}} /p} $ |
假设由2部雷达对公共观测区域内的多个目标进行跟踪,雷达标号为s、w,所得航迹标号集合为
| $ {U_s} = \{ 1,2, \cdots ,{m_s}\} ,{U_w} = \{ 1,2, \cdots ,{m_w}\} $ | (2) |
记
| $ {\hat \lambda _{ij}} = \Delta (\hat X_s^i,\hat X_w^j) $ | (3) |
为
| $ {\lambda _{ij}} = \Delta (X_s^i,X_w^j) $ | (4) |
的估计。
式中:Xsi、Xwj为雷达s所观测目标i和雷达w所观测目标j的真实状态;
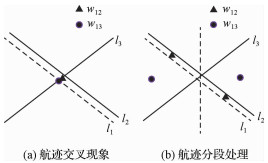
由于离散度表征数据离散程度,航迹交叉现象会对判别产生干扰。如图 1(a)所示,当航迹l2、l3存在交叉现象时,航迹l1与航迹l2、l3的几何中心w12、w13几乎重合,由于几何对称性,航迹点的离散度基本相同,此时无法判断航迹l2、l3与l1的关联情况。但若如图 1(b)所示,将航迹序列分段,则产生的两段子序列几何中心不再重合,航迹l1与航迹l2关于几何中心w12的平均离散度小于航迹l1与航迹l3关于几何中心w13的平均离散度,可以正确判断航迹l1与航迹l2关联。
|
| 图 1 交叉和分段处理示意图 Fig. 1 Schematic diagram of cross and segmentation |
故针对航迹交叉问题,只需对航迹序列进行分段,再根据定义1分别计算各航迹序列的离散度
定义2 航迹序列的分段划分
对航迹序列X={x1, x2, …, xM}进行n段划分,可得
| $ \begin{array}{*{20}{c}} {X \to \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} = \{ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (1),\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (2), \cdots ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (n)\} = }\\ {\{ \{ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} (1)\} ,\{ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} (2)\} , \cdots ,\{ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} (n)\} \} } \end{array} $ |
如果满足:
| $ \left\{ {\begin{array}{*{20}{l}} {M \ge n}\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (i) \cap \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (j) = \emptyset ,i \ne j}\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (1) \cup \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (2) \cup \cdots \cup \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (n) = X}\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} (j) = \{ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} (j)\} = \left( {{x_i}|i \in \left( {\frac{{j - 1}}{n}M,\frac{j}{n}M} \right]} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,n} \end{array}} \right. $ |
则称为航迹序列的分段划分。
由定义2可知,经过划分可将航迹序列分为n段子序列。
假设由2部雷达和1个融合中心构成信息融合系统,对公共观测区域内的多个目标进行跟踪。设T为融合中心的一个处理周期,在第k个处理周期[(k-1)T, kT]内,雷达s, w上报的航迹数目分别为ms、mw。在第k个处理周期内上报的航迹集合ζs(k)记为
| $ {\zeta _s}(k) = \{ \zeta _s^1(k),\zeta _s^2(k), \cdots ,\zeta _s^i(k), \cdots ,\zeta _{{s^s}}^m(k)\} $ |
式中:ζsi(k)为雷达s的第i条航迹,i∈{1, 2, …, ms}。
设2部雷达异步,采样速率不一致但恒定,则在融合中心的同一处理周期内,2部雷达上报航迹的航迹点数目不同,即航迹序列的长度不同,假设来自雷达s的第i条航迹包含ni个航迹点。由于采样周期不一致,雷达上报航迹的次数亦不同,假设在同一处理周期内雷达s上报a次航迹,来自雷达s第b次上报的航迹集合中第i条航迹记为
| $ \begin{array}{l} \zeta _s^i(k + b) = \{ \hat X_s^i(k + b + {f^1}),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat X_s^i(k + b + {f^2}), \cdots ,\hat X_s^i(k + b + {f^{{n^i}}})\} \end{array} $ |
式中:k+b+fp为雷达s在第k个处理周期内第b次上报航迹集合中第i条航迹第p个航迹点的时间标记;
在同一处理周期内对多次上报的同批号航迹集合作并集处理,即
| $ \begin{array}{l} \zeta _s^i(k) = \zeta _s^i(k + 1) \cup \zeta _s^i(k + 2) \cup \cdots \cup \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \zeta _s^i(k + a) = \{ \hat X_s^i(k + 1 + {f^1}),\hat X_s^i(k + 1 - 1)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {f^2}), \cdots ,\hat X_s^i(k + a + {f^{{n^i}}})\} \end{array} $ |
处理后雷达s的第i条航迹记为
| $ \begin{array}{l} \zeta _s^i(k) = \{ \hat X_s^i(k + f_s^1),\hat X_s^i(k + f_s^2), \cdots ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat X_s^i(k + f_{{s^s}}^{{n^i}})\} \end{array} $ |
式中:nsi=a×ni。
假设对雷达s、w的航迹集合作并集处理后,来自雷达s的每条航迹包含的航迹点数目记为nsi,来自雷达w的每条航迹包含的航迹点数目记为nwj(nsi≠nwj),根据定义2,对每条航迹序列进行分段划分,得到分段航迹序列。
根据nwj/nsi取值的不同,给出不等长航迹序列分段过程中的分段原则:
1) 确保分段后同一组对比序列具有相同的段数,分段数目为nj=INTL[nwj/nsi]+2。
2) 序列分段时,尽可能保证每个分段航迹子序列所含航迹点数目相等。
3) 尽量避免某分段航迹子序列只包含单一航迹点。
4) 原则优先级为:
根据以上原则,可保证分段后每组对比子序列航迹点数目之比与原始序列航迹点数目之比基本不变;并确保航迹序列至少分为2段,避免中心交叉问题。
2.3 分段航迹序列离散度的计算本文以二维情况为例,若航迹序列的航迹点包含x、y、ẋ、ẏ共4个分量,则先分别求解对于每一个分量航迹序列的离散度,再对多个分量离散度进行加权融合得到总离散度指标。
取雷达w的mw条航迹作为比较航迹,雷达s的第i条航迹作为参考航迹。由于每条航迹的航迹点数目不同,根据分段原则,共有mw种分段方式,每种分段方式对应一条比较航迹和参考航迹。
例如在第1个位移分量x上定义分段航迹序列矩阵为Ψx:
| $ {{\mathit{\boldsymbol{{ }\!\!\varPsi\!\!\text{ } }}}_{x}}=\left[ \begin{matrix} \overset\frown{X_{w}^{1}}(1) & \cdots & \overset\frown{X_{w}^{1}}(p) & \cdots & \overset\frown{X_{w}^{1}}({{n}_{1}}) & 0 & 0 \\ \overset\frown{X_{s,1}^{i}}(1) & \cdots & \overset\frown{X_{s,1}^{i}}(p) & \cdots & \overset\frown{X_{s,1}^{i}}({{n}_{1}}) & 0 & 0 \\ \vdots & {} & \vdots & {} & \vdots & \vdots & \vdots \\ \overset\frown{X_{w}^{k}}(1) & \cdots & \overset\frown{X_{w}^{k}}(p) & \cdots & \overset\frown{X_{w}^{k}}({{n}_{1}}) & \cdots & \overset\frown{X_{w}^{k}}({{n}_{k}}) \\ \overset\frown{X_{s,k}^{i}}(1) & \cdots & \overset\frown{X_{s,k}^{i}}(p) & \cdots & \overset\frown{X_{s,k}^{i}}({{n}_{1}}) & \cdots & \overset\frown{X_{s,k}^{i}}({{n}_{k}}) \\ \vdots & {} & \vdots & {} & {} & \vdots & \vdots \\ \overset\frown{X_{w}^{j}}(1) & \cdots & \overset\frown{X_{w}^{j}}(p) & \cdots & \cdots & \overset\frown{X_{w}^{j}}({{n}_{j}}) & 0 \\ \overset\frown{X_{s,j}^{1}}(1) & \cdots & \overset\frown{X_{s,j}^{1}}(p) & \cdots & \cdots & \overset\frown{X_{s,j}^{1}}({{n}_{j}}) & 0 \\ \vdots & {} & \vdots & {} & {} & \vdots & \vdots \\ \overset\frown{X_{{{w}^{w}}}^{m}}(1) & \cdots & \overset\frown{X_{{{w}^{w}}}^{m}}(p) & \cdots & \cdots & 0 & 0 \\ \overset\frown{X_{s,{{m}_{w}}}^{i}}(1) & \cdots & \overset\frown{X_{s,{{m}_{w}}}^{i}}(p) & \cdots & \cdots & 0 & 0 \\ \end{matrix} \right] $ | (5) |
式中:nj=INTL[nwj/nsi]+2, j=1, 2, …, mw;nk=max{n1, n2, …, nmw};
分段航迹序列矩阵Ψx为2mw×nk维,每一行表示每一条航迹在分量x上的分段子序列集合;奇数行元素来源于比较航迹,偶数行元素来源于参考航迹。由于分段数目不同,矩阵各行元素数目不同,故各行缺失元素用0做补齐处理。
根据定义1中对数据集离散度的定义,可计算得到参考航迹和比较航迹的离散度矩阵为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_x} = {{[{\delta _{e,f}}]}_{{m_w} \times {n_k}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\delta _{1,1}}}&{{\delta _{1,2}}}& \cdots &{{\delta _{1,{n_k}}}}\\ {{\delta _{2,1}}}&{{\delta _{2,2}}}& \cdots &{{\delta _{2,{n_k}}}}\\ \vdots & \vdots &{}& \vdots \\ {{\delta _{{m_w}}},1}&{{\delta _{{m_w}}},2}& \cdots &{{\delta _{{m_w}}},{n_k}} \end{array}} \right]} \end{array} $ | (6) |
式中:
| $ \begin{array}{*{35}{l}} {{\delta }_{e,f}}=\Delta (\overset\frown{X_{w}^{e}}(f),\overset\frown{X_{s,e}^{i}}(f)) \\ e=1,2,\cdots ,{{m}_{w}};f=1,2,\cdots ,{{n}_{k}} \\ \end{array} $ | (7) |
进而可以计算在位移分量x上,来源于雷达s的第i条航迹与来源于雷达w的第j条航迹的离散度,记为
| $ {{\lambda }_{x}}=\lambda (\overset\frown{X_{w}^{j}},\overset\frown{X_{s,j}^{i}})=\frac{1}{{{n}_{j}}}\sum\limits_{f=1}^{{{n}_{j}}}{{{\delta }_{j,f}}} $ | (8) |
考虑到位移分量与速度分量具有相关性(导数关系),并且物理意义的不同导致不同属性分量间的滤波精度不易比拟,故仅采用位移分量进行关联。
同理,可以列出在位移分量y上的分段航迹序列矩阵Ψy,相应求解航迹在位移分量y上的离散度,记为λy。对位移分量的航迹离散度进行加权融合,得到在第k个处理周期内参考航迹i(i∈Us)和比较航迹j(j∈Uw)之间的总离散度为
| $ {\lambda _{ij}} = {\alpha _1}{\lambda _x} + {\alpha _2}{\lambda _y} $ | (9) |
式中:加权系数α1、α2为非负实数,且满足α1+α2=1的约束条件。其数值大小取决于滤波精度,精度越高,权重越大。记状态滤波协方差矩阵中位移分量x、y的滤波误差分别为σx、σy,则加权系数为
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} = \frac{{1/|{\sigma _x}|}}{{1/|{\sigma _x}| + 1/|{\sigma _y}|}}}\\ {{\alpha _2} = \frac{{1/|{\sigma _y}|}}{{1/|{\sigma _x}| + 1/|{\sigma _y}|}}} \end{array}} \right. $ | (10) |
根据所用的指标量离散度λij,可推广为广义经典分配法。对于雷达s、w上报的ms、mw条航迹分别计算离散度,构成ms×mw维矩阵,由此将问题转化为全体航迹的分类问题。
令
| $ {\vartheta _{ij}} = \left\{ {\begin{array}{*{20}{l}} 1\\ 0 \end{array}} \right. $ | (11) |
式中:ϑij=1表示航迹i与航迹j关联;ϑij=0表示二者不关联。目标函数记为
| $ L(k) = \sum\limits_i^{{m_s}} {\sum\limits_j^{{m_w}} {{\vartheta _{ij}}} } {\lambda _{ij}}(k) $ | (12) |
则形成二维分配问题
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {{\rm{min}}}\limits_{{\vartheta _{ij}}} \sum\limits_i^{{m_s}} {\sum\limits_j^{{m_w}} {{\vartheta _{ij}}} } {\lambda _{ij}}(k)}\\ {\sum\limits_{j = 1}^{{m_w}} {{\vartheta _{ij}}} = 1\quad \forall i = 1,2, \cdots ,{m_s}}\\ {\sum\limits_{i = 1}^{{m_s}} {{\vartheta _{ij}}} = 1\quad \forall j = 1,2, \cdots ,{m_w}} \end{array}} \right. $ | (13) |
此类二维分配问题,存在匈牙利算法、拍卖算法等经典解决方法,此处不再赘述。分配问题的本质为约束条件下求解目标函数最值的问题,求解算法的不同,求解中多义性的具体表现也不尽相同。
在求解分配问题时,若存在2组及以上不同的分配方案使得目标函数L(k)最小值相等,则设置二次检验环节进行处理。记2组(2组以上情况类似)分配方案的最小目标函数为L1、L2,2组分配方案中航迹的分段数目矩阵记为NL1、NL2, 分段数目为nijL1、nijL2,若L1=L2,则令
| $ n_{ij}^{{L_1}} = n_{ij}^{{L_1}} + 1,n_{ij}^{{L_2}} = n_{ij}^{{L_2}} + 1 $ | (14) |
然后按照2.3节重复计算步骤,直至分配方案呈现唯一性。
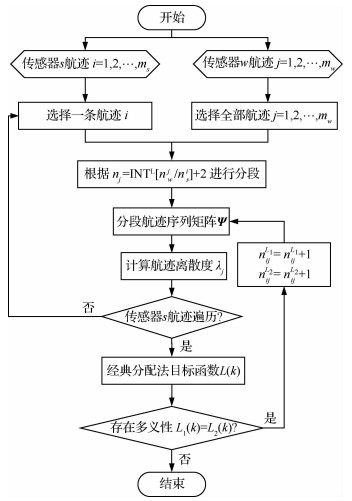
分段数目的增加会细化数据处理程度,放大局部航迹的离散度差异,提高度量精度,能有效解决多义性问题。算法的流程如图 2所示。
|
| 图 2 算法流程图 Fig. 2 Flowchart of algorithm |
假设由2部异地配置的2D雷达构成的跟踪系统对公共区域进行观测,目标批数为20批,持续观测时间为30 s。雷达1、2位置坐标分别为(0, 0) km, (100, 0) km,雷达1的采样时间间隔为T1=0.2 s,雷达2的采样时间间隔为T2=0.5 s,并且雷达2比雷达1晚开机0.2 s。
目标运动模型采用二维平面匀速直线运动模型,目标初始方向在0~2π rad内随机分布,目标初始速度在200~400 m/s内随机分布。雷达1的测距和测角误差分别为σr1=150 m、σθ1=0.03 rad;雷达2的测距和测角误差分别为σr2=180 m、σθ2=0.02 rad。
进行M次Monte Carlo仿真实验,采用正确关联率对航迹关联结果进行评价:
| $ {\rm{Ec}}(k) = \frac{{\sum\limits_{i = 1}^M {{C_i}} (k)}}{{MN}} $ | (15) |
式中:Ci(k)为第k个处理周期内正确关联的航迹数目;M为Monte Carlo仿真实验的次数;N为每次仿真实验的目标航迹数目。
3.2 算法性能比较与分析在仿真环境中,进行100次Monte Carlo仿真实验。在不同条件下对本文算法与文献[5]中算法和文献[16]中算法进行比较。
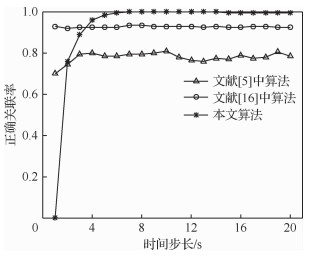
图 3给出了在仿真环境中3种算法关联结果的比较。可以看出,本文算法的正确关联率最高,但在采样初期,本文算法关联效果较差。这是由于本文算法的离散度属于统计学度量,采样初期数据点较少,对关联的正确性造成了很大影响。但影响持续时间较短,算法可以很快收敛至最佳关联效果。
|
| 图 3 不同算法的正确关联率对比 Fig. 3 Comparison of correct associating rates of different algorithms |
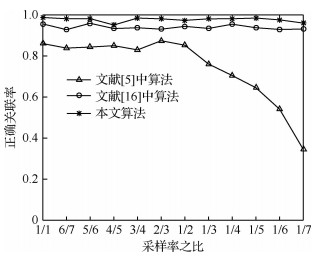
在仿真环境的基础上,改变2部雷达的采样频率之比,图 4给出了不同采样频率之比对3种算法的影响。本文算法利用同源航迹数据集波动性小的特点进行关联判定,只关乎航迹点的同源性,航迹点数目(满足一定统计学数据量)并不会对关联结果产生影响,故雷达采样频率不一致对本文算法无显著影响。从图 4中可以看出,随着采样频率相差越来越大,文献[5]中算法的正确关联率下降较为明显,而本文算法和文献[16]中算法的正确关联率并无明显变化,与理论结果吻合。
|
| 图 4 关联结果随采样率之比的变化 Fig. 4 Variation of correlation results with changing ratio of sampling rate |
在仿真环境的基础上,根据不同信噪比,改变参数中噪声的幅值,模拟强杂波干扰。从图 5中可以看出,随着信噪比的减小,文献[5]中算法的正确关联率迅速下降;本文算法和文献[16]中算法的正确关联率起初并无明显变化,在信噪比低于28 dB后有明显下滑,且文献[16]中算法的下滑趋势较快。

|
| 图 5 关联结果随信噪比的变化 Fig. 5 Variation of correlation results with changing SNR |
表 1给出了不同采样周期和开机时延下本文算法的平均正确关联率。可以看出,采样周期增大,算法正确关联率有小幅度下降;开机时延并未产生明显影响。这是由于采样周期越长,数据量越少,对离散度的刻画越不准确;而一定范围内的开机时延只造成数据点在时间上的错位,并不影响数据分布的离散度。
| 雷达2开机时延/s | 正确关联率 | ||
| T1=0.2 s, T2=0.4 s |
T1=0.5 s, T2=1 s |
T1=1.1 s, T2=2 s |
|
| 0.1 | 0.930 1 | 0.914 9 | 0.875 7 |
| 0.2 | 0.928 9 | 0.916 6 | 0.890 1 |
| 0.3 | 0.924 1 | 0.915 8 | 0.885 4 |
表 2给出了不同噪声分布形式下本文算法的正确关联率。可以看出,噪声的分布形式对本文算法没有影响。综合表 1和表 2可知,本文算法在多种情景下均保持较高的正确关联率,稳定性较佳。
| 噪声分布形式 | 高斯分布 | 瑞利分布 | 指数分布 | 均匀分布 |
| 正确关联率 | 0.922 6 | 0.921 7 | 0.916 2 | 0.918 4 |
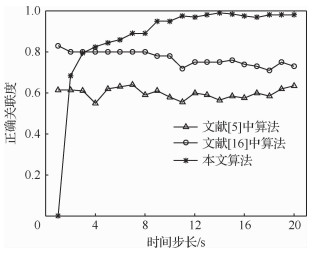
在仿真环境的基础上,调整目标数目、初始位置和初始速度,模拟目标在二维平面上航迹交叉、分叉和合并的情况。当观测区域中的目标航迹存在大量交叉、分叉和合并现象时,以航迹间距离作为关联依据的传统算法,在交叉点或平行阶段容易发生错误关联。从图 6可以看出,文献[5]和文献[16]中算法的正确关联率相较于匀速直线模型有所下降;而本文算法由于不依赖距离进行判定,故仍保持较佳的关联效果。
|
| 图 6 航迹存在分叉合并时的正确关联率对比 Fig. 6 Comparison of correct associating rates of track bifurcation merging |
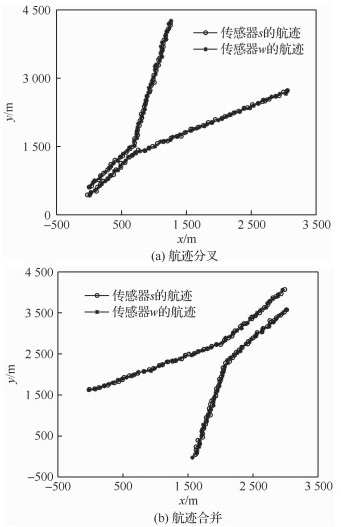
图 7(a)仿真了航迹分叉过程。在开始时刻雷达s、w所观测2目标进行平行飞行,距离较近,后分别转向,改为独立飞行。图 7(b)则仿真了2目标航迹合并过程。开始2目标相距较远,后组成编队平行飞行,距离拉近。
|
| 图 7 航迹分叉与合并示意图 Fig. 7 Schematic diagram of track bifurcation and merging |
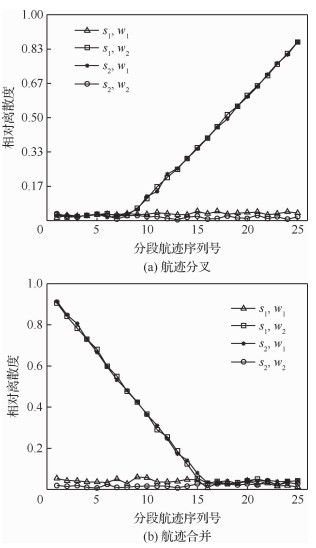
图 8仿真了航迹分叉和合并过程中同源航迹{s1, w1}、{s2, w2}和非同源航迹{s1, w2}、{s2, w1}对应的各分段航迹相对离散度的变化趋势。为直观反映本文算法对处理目标运动状态发生突变现象的灵敏程度,细化航迹序列分段为25段予以说明。
|
| 图 8 分段航迹序列离散度的变化 Fig. 8 Variation of segmented track sequence dispersion |
从图 8(a)中可以看出,在目标进行平行飞行时,同源航迹和非同源航迹的相对离散度均较小,无法进行有效的航迹关联。但目标航迹分叉后,同源航迹{s1, w1}、{s2, w2}的相对离散度并未产生变化,而非同源航迹{s1, w2}、{s2, w1}的相对离散度却迅速增大。
同样,从图 8(b)中可以看出独立飞行时非同源航迹{s1, w2}、{s2, w1}的相对离散度较大,同源航迹{s1, w1}、{s2, w2}的离散度较小;但随着航迹的合并,非同源航迹的相对离散度迅速下降,接近同源航迹的相对离散度。
从航迹交叉合并现象的仿真实验中可以看出,测度分段航迹离散度的方法可以迅速对航迹状态突变做出反应,即算法在解决航迹状态突变问题中具有灵敏度高的特点。即使航迹存在平行飞行阶段,只要对各分段航迹的离散度取平均,依旧可以进行准确的航迹关联。
3.4 算法复杂度分析图 9给出了3种算法耗时的比较。可以看出,随着目标航迹数目的增加,3种算法的CPU耗时均呈增加趋势,但本文算法耗时高于文献[16]中算法,远高于文献[5]中算法。

|
| 图 9 不同算法的耗时对比 Fig. 9 Comparison of time consumption of different algorithms |
以等长航迹序列关联为例,假设有m条比较航迹与1条参考航迹进行关联,各航迹均包含n个航迹点,数据类型为实数类型,计算各算法运算量,如表 3所示。显然,本文算法运算量要高于文献[16]中算法。
1) 本文提出一种基于分段序列离散度的异步航迹关联算法,给出离散度的具体度量指标和不等长航迹序列的分段划分规则,并针对多义性问题给出二次检验方法。
2) 本文算法无需时域配准,可在多种环境下直接对异步不等速率航迹进行准确关联,具有稳定性。算法不受噪声分布的影响,且噪声强度对算法的影响相对较小,具有良好的抗杂波干扰性。
3) 本文算法可有效分辨航迹交叉、分叉和合并等复杂情况。
| [1] |
何友, 王国宏, 关欣. 信息融合理论及应用[M]. 北京: 电子工业出版社, 2010: 178-265. HE Y, WANG G H, GUAN X. Information fusion theory with applications[M]. Bejing: Publishing House of Electronics Industry, 2010: 178-265. (in Chinese) |
| [2] |
潘泉, 梁彦, 杨峰, 等. 现代目标跟踪与信息融合[M]. 北京: 国防工业出版社, 2009: 65-77. PAN Q, LIANG Y, YANG F, et al. Modern target tracking and information fusion[M]. Bejing: National Defense Industry Press, 2009: 65-77. (in Chinese) |
| [3] | ZHU H, LEUNG H, YUEN K V. A joint data association, registration, and fusion approach for distributed tracking[J]. Information Sciences, 2015, 324: 186-196. |
| Click to display the text | |
| [4] | ZHU H Y, WANG C. Joint track-to-track association and sensor registration at the track level[J]. Digital Signal Processing, 2015, 41: 48-59. |
| Click to display the text | |
| [5] |
朱洪艳, 韩崇昭, 韩红. 分布式多传感信息融合系统的异步航迹关联方法[J]. 控制理论与应用, 2004, 21(3): 453-456. ZHU H Y, HAN C Z, HAN H. Asynchronous track-to-track association method in distributed multi-sensor information fusion system[J]. Control Theory and Applications, 2004, 21(3): 453-456. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [6] | KAPLAN L, BAR-SHALOM Y, BLAIR W. Assignment costs for multiple sensor track-to-track association[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 655-677. |
| Click to display the text | |
| [7] |
郭蕴华, 袁成. 一种异步航迹关联的变异蚁群算法[J]. 电子学报, 2012, 40(11): 2200-2205. GUO Y H, YUAN C. A mutation ant colony algorithm for the asynchronous track correlation[J]. Acta Electronica Sinica, 2012, 40(11): 2200-2205. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [8] |
徐亚圣, 丁赤飚, 任文娟, 等. 基于直方统计特征的多特征组合航迹关联[J]. 雷达学报, 2019, 8(1): 25-35. XU Y S, DING C B, REN W J, et al. Multi-feature combination track-to-track association based on histogram statistics feature[J]. Journal of Radars, 2019, 8(1): 25-35. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [9] | CHENG C, WANG J F. Algorithm for multi-sensor asynchronous track-to-track fusion[C]//6th International Symposium on Neural Networks, 2009. |
| [10] | CHENG C. Asynchronous multisensor track association algorithm and simulation[J]. Procedia Environmental Sciences, 2011, 10(Part B): 1109-1114. |
| Click to display the text | |
| [11] | SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457. |
| Click to display the text | |
| [12] |
刘伟峰, 文成林. 基于OSPA距离的航迹关联方法[J]. 航空学报, 2012, 33(6): 1083-1092. LIU W F, WEN C L. A track association algorithm based on the OSPA distance[J]. Acta Aeronautica et Astronautica Sincia, 2012, 33(6): 1083-1092. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [13] | ZHU H, HAN C, HAN H, et al. The algorithm and simulations for the asynchronous track association[C]//Sixth International Conference on Information Fusion. Piscataway: IEEE Press, 2003. |
| [14] |
衣晓, 张怀巍, 曹昕莹, 等. 基于区间灰数的分布式多目标航迹关联算法[J]. 航空学报, 2013, 34(2): 352-360. YI X, ZHANG H W, CAO X Y, et al. A track association algorithm for distributed multi-target system based on gray numbers[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 352-360. (in Chinese) |
| Cited By in Cnki (21) | Click to display the text | |
| [15] |
邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002: 158-161. DENG J L. Grey system theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 158-161. (in Chinese) |
| [16] |
衣晓, 韩健越, 张怀巍, 等. 基于区实混合序列相似度的异步不等速率航迹关联算法[J]. 航空学报, 2015, 36(4): 1212-1220. YI X, HAN J Y, ZHANG H W, et al. Asynchronous track-to-track association algorithm based on similarity degree of interval-real sequence[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1212-1220. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] | YANG Y T, LIANG Y, YANG Y, et al. Asynchronous track-to-track association algorithm based on dynamic time warping distance[C]//201534th Chinese Control Conference. Piscotaway: IEEE Press, 2015. |
| [18] |
石教华. 利用时间窗权重进行航迹关联[J]. 火力与指挥控制, 2014(10): 78-80. SHI J H. Using the weight in time widow to associate tracks[J]. Fire Control and Command Control, 2014(10): 78-80. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] |
李洋, 张靖. 基于自适应滑动窗均值OSPA航迹关联算法[J]. 电子学报, 2016, 44(2): 115-119. LI Y, ZHANG J. Track fusion based on the mean OSPA distance with an adaptive sliding window[J]. Acta Electronica Sinica, 2016, 44(2): 115-119. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [20] |
王文森. 变异系数-一个衡量离散程度简单而有用的统计指标[J]. 中国统计, 2007(6): 43-44. WANG W S. Coefficient of variation-a simple and useful statistical measure of dispersion[J]. China Statistics, 2007(6): 43-44. (in Chinese) |
| Cited By in Cnki (93) | Click to display the text |



