2. 合肥工业大学 土木与水利工程学院, 合肥 230009
2. College of Civil Engineering, Hefei University of Technology, Hefei 230009, China
连续体结构拓扑优化设计指在给定的区域内,寻求结构的某种布局(如结构有无孔洞、孔洞位置、数量和结构连接方式等),使其能够在满足指定约束条件下的设计目标最优[1-2]。拓扑优化在早期研究中以全局性性能如结构柔顺度、振动频率为设计指标,发展到考虑局部应力、疲劳损伤等性能,从解决工程实际问题的角度出发,以改善结构综合性能[3]。
位移或变形量是结构产品刚度的重要衡量指标。Rong等[4-5]在拓扑优化设计中引入多点位移约束,实现了对结构变形的控制。Huang和Xie[6]提出采用柔顺度目标和节点位移约束以实现对全局和局部刚度的控制。Zuo和Xie[7]提出一个全局化位移指标,采用双向进化式拓扑优化方法实现了结构刚度设计。Qiao和Liu[8]提出了几何平均位移指标用于衡量拓扑优化结构的刚度。Li和Kim[9]从工程实际出发,提出了多相材料结构位移约束下的轻量化设计列式和求解算法。Long等[10]提出了多点位移约束拓扑优化问题的二次规划列式与求解算法。针对局部翘曲变形,朱继宏等[11]提出了多点保形的概念,用来衡量多点间相对位移变化程度和变形协调。基于保形指标的拓扑优化设计方法在考虑变形方向性、谐响应振动和几何非线性问题中得到进一步拓展[12-14]。
在工程问题中,有一类工程结构承受分布力载荷作用,例如受风载荷的建筑、承受气动力的飞行翼面、舵体等[3]。此类结构承载表面的节点变形量需要满足刚度设计要求。由于承载面节点数目庞大,并且在优化迭代过程中,最大位移发生的位置会发生变化,若采用多点位移约束的处理方式,不仅敏度求解中的伴随工况数量庞大,有限元分析计算量大,而且会造成约束方程数目增多而难以优化求解。
针对上述问题,提出考虑承载面最大位移约束的拓扑优化模型。遵循独立连续映射(Independent Continuous Mapping, ICM)建模方法[15-16],引入倒变量中间变量,将原有拓扑优化问题转换为一系列严格正定的二次规划问题,并采用高效、稳健的序列二次规划算法求解。将提出模型获得的优化结果与传统的体积比约束下柔顺度最小化列式结果、多点位移约束下体积最小化结果做对比,说明提出列式与求解方法的可行性和优越性。
1 体积比约束下的拓扑优化列式在现有的拓扑优化方法中,以体积比为约束、柔顺度最小化为目标的拓扑优化列式最为典型,数学表达式为[1]
| $ \begin{array}{l} {\rm{find}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\rho }}\\ {\rm{minimize}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c = {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{u}}\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {V(\mathit{\boldsymbol{\rho }}) \le f{V_0}}\\ {\mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}}\\ {0 < {\rho _{{\rm{min}}}} \le {\rho _e} \le 1\quad e = 1,2, \cdots ,{N_{\rm{E}}}} \end{array}} \right. \end{array} $ | (1) |
式中: ρ 为密度矢量; 分量ρe为单元e的相对密度值,用于表征单元e的有无;c为系统柔顺度值;K 、u 和 F 分别为总刚度阵、位移列阵和载荷列阵;V和V0分别为优化后体积和初始结构体积;f为设定体积比;密度下限ρmin用于避免结构分析中的数值奇异性,这里取值ρmin=10-3;NE为设计域内单元总数。
SIMP插值模型通过建立弹性模量(或刚度阵)与密度变量的假设关系,驱使在优化过程中密度变量向0或1靠近,其表达式为[1]
| $ {\mathit{\boldsymbol{k}}_e} = \rho _e^p\mathit{\boldsymbol{k}}_e^0 $ | (2) |
式中: k e和 k e0分别为惩罚单元刚度阵和初始单元刚度阵;p为惩罚因子,这里取值p=3。
柔顺度c对密度变量ρe的一阶导数为[1]
| $ \frac{{\partial c}}{{\partial {\rho _e}}} = - {\mathit{\boldsymbol{U}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _e}}}\mathit{\boldsymbol{U}} = - \mathit{\boldsymbol{u}}_e^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{k}}_e}}}{{\partial {\rho _e}}}{\mathit{\boldsymbol{u}}_e} $ | (3) |
式中:u e为单元e的位移列阵。拓扑优化列式(1)在得到结构响应量敏度的前提下,将敏度数值代入到连续型优化算法,即可实现优化求解。在拓扑优化研究领域中,常见的优化求解算法有准则法(Optimality Criteria, OC)[17]、凸线性化(Convex Linearization, CONLIN)[18]、移动渐进线法(Method of Moving Asymptotes, MMA)[19-20]等。
2 考虑承载面最大位移约束的拓扑优化列式 2.1 拓扑优化列式尽管列式(1)在拓扑优化研究领域得到了广泛的应用,但存在着以下缺点[1]:①柔顺度值缺乏工程意义;②体积比是人为给定的数值,但实际工程应用中,拓扑优化结果仅用于结构传力路径的确定,工程可用的结构需要进一步通过尺寸优化、形状优化等后续工作完成。
对于承受分布载荷的工程结构,承载面的变形量需要进行严格控制。假设承载面上每一个节点位移满足约束限值,以结构轻量化设计为目标的拓扑优化列式为
| $ \begin{array}{l} {\rm{find}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\rho }}\\ {\rm{minimize}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} V/{V_0}\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{d_j} \le \bar d{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,J}\\ {\mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}}\\ {0 < {\rho _{{\rm{min}}}} \le {\rho _e} \le 1\quad e = 1,2, \cdots ,{N_{\rm{E}}}} \end{array}} \right. \end{array} $ | (4) |
式中:dj为承载面第j自由度对应的位移值;d为许用位移限值。式(4)为常见的多点位移约束列式。若节点位移约束数量较多,则会造成伴随方程数计算量增大和难以优化求解的两重困难。
为了解决上述困难,这里提出的解决方案是采用承载面上最大节点位移约束取代多点位移约束方程,即
| $ \begin{array}{l} {\rm{find}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\rho }}\\ {\rm{minimize}}:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} V/{V_0}\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{\rm{max}}\left( {{d_j}} \right) \le \bar d{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,J}\\ {\mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}}\\ {0 < {\rho _{{\rm{min}}}} \le {\rho _e} \le 1\quad e = 1,2, \cdots ,{N_{\rm{E}}}} \end{array}} \right. \end{array} $ | (5) |
式(5)中的最大值函数具有不可导性,从而无法利用现有的连续型优化算法求解。受最大应力约束拓扑优化问题的启发[21-22],此问题可采用包络函数包括KS函数、p范数(p-norm)和p平均(p-mean)函数对最大值函数进行连续光滑处理,这里选择采用KS函数,最大值约束的代理模型为
| $ {d^{{\rm{KS}}}} = \frac{1}{\mu }{\rm{ln}}\left( {\sum\limits_j {{{\rm{e}}^{\mu \frac{{{d_j}}}{{\bar d}}}}} } \right) \le 1 $ | (6) |
式中:μ为KS包络函数参数,并满足:
| $ \mathop {{\rm{lim}}}\limits_{\mu \to \infty } {d^{{\rm{KS}}}} = \mathop {{\rm{lim}}}\limits_{\mu \to \infty } \frac{1}{\mu }{\rm{ln}}\left( {\sum\limits_j {{{\rm{e}}^{\mu \frac{{{d_j}}}{{\bar d}}}}} } \right) = 1 $ | (7) |
根据数值经验,当μ取值较大时,容易引起优化求解中的数值振荡;当μ取有限值时,包络函数值与真实最大值之间具有一定的差异性。为了消除这种差异性,引入修正系数以调整两者间的关系,即[23-24]
| $ {\tilde d^{{\rm{KS}}}} = {c^{{\rm{KS}}}} \cdot {d^{{\rm{KS}}}} \le 1 $ | (8) |
式中:cKS为调整系数,数学表达式为
| $ {c^{{\rm{KS}}}} = \frac{{{\rm{max}}({d_j})}}{{\bar d \cdot {d^{{\rm{KS}}}}}} $ | (9) |
对式(6)求偏导可得
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}} = \frac{{{{\rm{e}}^{\mu \frac{{{d_j}}}{{\bar d}}}}}}{{\bar d\sum\limits_i {{{\rm{e}}^{\mu \frac{{{d_j}}}{{\bar d}}}}} }} $ | (10) |
由链式求导法则得
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {\rho _e}}} = \sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot \frac{{\partial {d_j}}}{{\partial {\rho _e}}} $ | (11) |
自由度j对应的位移表达为位移向量的函数,即
| $ \left\{ {\begin{array}{*{20}{l}} {{d_j} = \mathit{\boldsymbol{\alpha }}_j^{\rm{T}}\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{\alpha }}_j^{\rm{T}} = \left[ {\begin{array}{*{20}{l}} 0&0& \cdots &1&0& \cdots \end{array}} \right]} \end{array}} \right. $ | (12) |
将式(12)代入到式(11)可得
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {\rho _e}}} = \sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot \frac{{\partial \mathit{\boldsymbol{\alpha }}_j^{\rm{T}}\mathit{\boldsymbol{u}}}}{{\partial {\rho _e}}} = \sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot \mathit{\boldsymbol{\alpha }}_j^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\rho _e}}} $ | (13) |
对平衡方程 Ku = F 两边求导可得
| $ \mathit{\boldsymbol{K}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\rho _e}}} + \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _e}}}\mathit{\boldsymbol{u}} = \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial {\rho _e}}} $ | (14) |
假设载荷 F 与密度变量无关,则
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\rho _e}}} = - {\mathit{\boldsymbol{K}}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _e}}}\mathit{\boldsymbol{u}} $ | (15) |
将式(15)代入到式(13)中可得
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {\rho _e}}} = \sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot \mathit{\boldsymbol{\alpha }}_j^{\rm{T}}\left( { - {\mathit{\boldsymbol{K}}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _e}}}\mathit{\boldsymbol{u}}} \right) $ | (16) |
建立伴随方程
| $ \mathit{\boldsymbol{K\lambda }} = {\left[ {\sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot \mathit{\boldsymbol{\alpha }}_j^{\rm{T}}} \right]^{\rm{T}}} = \sum\limits_j {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {d_j}}}} \cdot {\mathit{\boldsymbol{\alpha }}_j} $ | (17) |
式中:λ 为伴随向量,则敏度表达式为
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {\rho _e}}} = - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _e}}}\mathit{\boldsymbol{u}} $ | (18) |
由式(18)可得,当采用提出的最大位移指标时,伴随方程对应一次有限元分析,相比较多点位移约束问题,可以大大减少伴随方程求解计算量。
2.3 独立连续映射法显式化过程与常见拓扑优化方法不同,ICM以各类结构响应量为约束,重量最小化为目标。通常情况下,柔顺度、节点位移和应力等各类结构响应量难以求其二阶敏度,在获取一阶敏度信息的情况下,可获取其一阶近似表达。在引入倒变量情形下,目标体积函数可以解析获取对设计变量的二阶敏度值。综合目标函数和约束函数的近似表达,可构建出二次规划问题的模型,配合稳健高效的序列二次规划(Sequential Quadratic Programming, SQP)算法求解。本节将遵循ICM建模方法,实现目标函数和约束函数的显式化表达。
定义设计变量为密度变量ρe的倒数函数,即
| $ {x_e} = \frac{1}{{\rho _e^p}} $ | (19) |
由此推导体积函数对设计变量的一和二阶敏度表达式为
| $ {\frac{{\partial V}}{{\partial {x_e}}} = - \frac{1}{p}x_e^{ - (1/p + 1)}{v_e}} $ | (20a) |
| $ {\frac{{{\partial ^2}V}}{{\partial x_e^2}} = \frac{{p + 1}}{{{p^2}}}x_e^{ - (1/p + 2)}{v_e}} $ | (20b) |
式中:ve为单元e的体积。
由式(20b)组成的海塞矩阵(Hessian)的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \\ \frac{{p + 1}}{{{p^2}}}\left[ {\begin{array}{*{20}{c}} {x_1^ - (\frac{1}{p} + 2){v_1}}&0& \cdots &0\\ 0&{x_2^ - (\frac{1}{p} + 2){v_2}}& \cdots &0\\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &{x_{{N_{\rm{E}}}}^{ - (1/\alpha + 2)}{v_{{N_{\rm{E}}}}}} \end{array}} \right] \end{array} $ | (21) |
与优化列式(4)对比可知,若直接采用ρe作为设计变量,体积函数对密度变量ρe的一阶敏度为常数,二阶敏度为0。当采用倒变量形式的设计变量xe时,由式(21)易得,海塞矩阵非对角线元素为0且对角线元素恒定大于0,即海塞矩阵严格正定且具有可分离性质。
利用链式求导法则可得
| $ \frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {x_e}}} = - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_e}}}\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\lambda }}_e^{\rm{T}}\frac{{{\mathit{\boldsymbol{k}}_e}}}{{{x_e}}}{\mathit{\boldsymbol{u}}_e} $ | (22) |
式中:λ e为单元伴随向量。
基于上述敏度信息,位移约束函数采用一阶泰勒展开得到显式表达式:
| $ {c^{{\rm{KS}}}} \cdot \left[ {d_0^{{\rm{KS}}} + {{\sum\limits_{e = 1}^{{N_{\rm{E}}}} {\left. {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {x_e}}}} \right|} }_{\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}^{(l)}}}}({x_e} - x_e^{(l)})} \right] \le 1 $ | (23) |
式中:上标l代表第l轮优化迭代。
体积目标函数采用二阶泰勒展开得到显式表达式,并忽略其中的常数项可得
| $ \begin{array}{l} {\rm{find}}:\mathit{\boldsymbol{x}}\\ {\rm{minimize}}:{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{x}} + \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Hx}}\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}}\\ {{c^{{\rm{KS}}}} \cdot \left[ {d_0^{{\rm{KS}}} + {{\sum\limits_{e = 1}^{{N_{\rm{E}}}} {\left. {\frac{{\partial {d^{{\rm{KS}}}}}}{{\partial {x_e}}}} \right|} }_{\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}^{(l)}}}}({x_e} - x_e^{(l)})} \right] \le 1}\\ {1 \le {x_e} \le \rho _{{\rm{min}}}^{ - \alpha }\quad e = 1,2, \cdots ,{N_{\rm{E}}}} \end{array}} \right. \end{array} $ | (24) |
式中:矩阵 B 与体积函数的一阶敏度相关。优化列式(24)是标准的二次规划模型,为了克服拓扑优化中设计变量庞大的困难,通常转化为对偶模型并采用SQP求解[15-16, 25],优化迭代至与体积比相对变化率满足收敛条件,即
| $ |{V^{(l)}} - {V^{(l - 1)}}|/{V^{(l)}} \le \varepsilon $ | (25) |
收敛率ε通常为1‰。
借鉴数字图像处理中的过滤技术消除拓扑优化中常见的棋盘格现象,具体过程可参考文献[15-16, 24]。值得注意的是,由于过滤平均的影响,将导致结构边界存在着一定数量的灰度单元。
3 数值算例与讨论本节采用数值算例来验证提出模型的可行性和有效性。在各算例中,材料的弹性模量和泊松比值分别为1 MPa和0.3,平面结构厚度为1 mm,单元尺寸为1 mm。初始结构的单元密度值取1,即设计区域全部为实体材料。
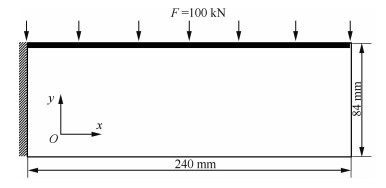
算例1 如图 1所示的长悬臂梁结构,结构尺寸为240 mm×84 mm,顶部4层单元为非设计区域,即单元密度值恒定为1。左端全部固定,顶部受到总载荷值为100 kN的力作用,载荷均匀分布在各个节点上。假设顶层y方向最大位移许用值为8 mm。KS函数参数μ=20。采用提出的拓扑优化列式和求解算法,所得到的拓扑优化结果如图 2所示。
|
| 图 1 长悬臂梁结构示意图 Fig. 1 Illustration of long cantilever structure |

|
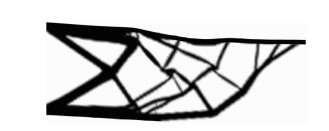
| 图 2 所提方法的拓扑优化结果 Fig. 2 Optimized topology obtained from the proposed method |
由图 2可知,拓扑优化结果顶部的变形尽可能保持水平且上下起伏,这表明可能多处节点的位移达到约束限值。最终结构体积比为0.309,最大节点位移值为7.999 mm。
为了验证提出方法的有效性,采用拓扑优化列式(5)和MMA算法求解,拓扑优化结果如图 3所示。
|
| 图 3 采用拓扑优化列式(5)和MMA算法的拓扑结果 Fig. 3 Optimized topology obtained from Eq.(5) and MMA algorithm |
由图 2和图 3对比可知,2种不同方法下的拓扑优化结果及变形特点类似。MMA算法求解下的最优结构体积比为0.310,最大节点位移值为8.001 mm。上述结果也表明,本文提出的优化列式具有可行性。
为了对比与传统拓扑优化结果的异同,以体积比0.309为约束条件,采用刚度最大化列式(1),得到的拓扑优化结果如图 4所示,优化结构顶部受载区域最大位移为10.167 mm,比设定的许用位移值8 mm大27.1%。顶面结构变形保持为直线,朝着自由端倾斜,这与图 2和图 3中最优结构的变形特点明显不同。上述结果表明,传统的刚度最大化列式(1)不具有控制局部最大变形的能力。

|
| 图 4 拓扑优化列式(1)下的拓扑优化结果 Fig. 4 Optimized topology using Eq.(1) |
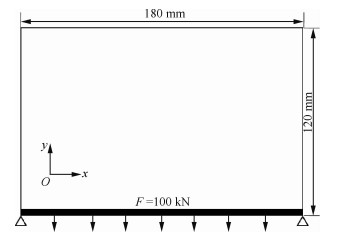
算例2 如图 5所示的平面结构,结构尺寸为180 mm×120 mm,底部4层单元为非设计区域,即单元密度值恒定为1, 下端两角点全约束。下端面受到合力F=100 kN作用,载荷均匀分配到下端面每个节点上,假设底层y方向最大位移许用值为8 mm,最优拓扑与结构变形如图 6所示。
|
| 图 5 平面结构示意图 Fig. 5 Illustration of plane structure |

|
| 图 6 所提列式下的拓扑优化结果与变形 Fig. 6 Optimized topology obtained from the proposed equation |
为了对比与多点位移约束下拓扑优化结果的异同,设置底部距离左端点1/6,2/6,3/6,4/6和5/6长度位置点位移约束条件,形成多点位移约束拓扑优化列式,同样采用ICM方法求解[15-16],最优拓扑与结构变形如图 7所示。位移约束设置位置对应的节点位移均达到许用值8 mm,但底部最大节点位移为9.433 mm,这说明即使采用多点位移约束,也无法严格控制承载面内每一点的变形。值得注意的是,多点位移约束的敏度分析包含5个伴随工况,即对应5次结构有限元计算,而本文提出的优化列式将多点位移约束凝聚为单约束函数,仅包含1个伴随工况。上述结果证明了提出方法的有效性和优越性。

|
| 图 7 多点位移约束下的拓扑优化结果 Fig. 7 Optimized topology obtained from multiple nodal displacement constraints |
算例3 三维结构如图 8所示,结构尺寸为90 mm×40 mm×28 mm,底部四角点全约束,顶部受到总载荷F=26 390 kN的力作用,载荷均匀分配到上端面每个节点上。顶部2层单元为非设计区域,即单元密度值恒定为1。设顶部区域y向最大许用位移为18 mm。采用提出的方法得到的拓扑优化结果如图 9(a)所示,最优结构体积比为0.125,承载面最大节点位移为17.996 mm;设定0.125为体积比约束, 采用柔顺度最小优化列式(1), 拓扑优化结果如图 9(b)所示,承载面最大节点位移为19.056 mm。

|
| 图 8 三维结构示意图 Fig. 8 Illustration of 3D structure |

|
| 图 9 不同列式下的拓扑优化结果 Fig. 9 Optimized topology obtained from different equations |
由图 9可知,不同的拓扑优化列式下对应的拓扑优化结果有所不同。类似于二维结构,本文提出方法对对该三维结构具有控制承载面最大位移的效果。即在相同的材料用量下,采用柔顺度最小化目标,优化结构的节点最大位移值超过许用位移值约5.89%。算例结果证明了提出列式和优化求解算法在三维结构优化问题中的适用性。
4 结论针对工程中受分布载荷的连续体结构,提出承载面最大位移约束下的拓扑优化设计模型。该模型通过KS包络函数实现了多点位移最大值的凝聚,推导了相应的敏度表达式。基于ICM方法,形成了具有正定可分离海塞矩阵的二次规划列式,采用序列二次规划法优化求解,得到以下结论:
1) 与传统的体积比约束下柔顺度最小化列式对比,提出方法具有控制局部区域最大位移的效果。优化结果证明了提出方法的有效性。
2) 与多点位移约束对比,提出方法更精确、有效控制承载面的最大变形量。且将多点位移约束凝聚为单一约束,不仅减少了伴随工况计算工作量,且有利于优化求解。
3) 提出的优化列式和相应求解算法有望在几何非线性位移约束问题中进一步拓展。
| [1] | MAUTE K, SIGMUND O. Topology optimization approaches[J]. Structural and Multidisciplinary Optimization, 2013, 48(6): 1-25. |
| Click to display the text | |
| [2] | DEATON J D, GRANDHI R V. A survey of structural and multidisciplinary continuum topology optimization:Post 2000[J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 1-38. |
| Click to display the text | |
| [3] | ZHU J, ZHANG W, XIA L. Topology optimization in aircraft and aerospace structures[J]. Archives of Computational Methods in Engineering, 2016, 23(4): 595-622. |
| Click to display the text | |
| [4] | RONG J H, YI J H. A structural topological optimization method for multi-displacement constraints and any initial topology configuration[J]. Acta Mechanica Sinica, 2010, 26(5): 735-744. |
| Click to display the text | |
| [5] |
俞燎宏, 荣见华, 唐承铁, 等. 基于可行域调整的多相材料结构拓扑优化设计[J]. 航空学报, 2018, 39(9): 222023. YU L H, RONG J H, TANG C T, et al. Multi-phase material structural topology optimization design based on feasible domain adjustment[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(9): 222023. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [6] | HUANG X, XIE Y M. Evolutionary topology optimization of continuum structures with an additional displacement constraint[J]. Structural and Multidisciplinary Optimization, 2010, 40(1-6): 409-416. |
| Click to display the text | |
| [7] | ZUO Z H, XIE Y M. Evolutionary topology optimization of continuum structures with a global displacement control[J]. Computer Aided Design, 2014, 56: 58-67. |
| Click to display the text | |
| [8] | QIAO H T, LIU S. Topology optimization by minimizing the geometric average displacement[J]. Engineering Optimization, 2013, 45(1): 1-18. |
| Click to display the text | |
| [9] | LI D, KIM I Y. Multi-material topology optimization for practical lightweight design[J]. Structural and Multidisciplinary Optimization, 2018, 58(3): 1081-1094. |
| Click to display the text | |
| [10] | LONG K, WANG X, GU X. Local optimum in multi-material topology optimization and solution by reciprocal variables[J]. Structural and Multidisciplinary Optimization, 2018, 57(3): 1283-1295. |
| Click to display the text | |
| [11] | ZHU J, LI Y, ZHANG W, et al. Shape preserving design with structural topology optimization[J]. Structural and Multidisciplinary Optimization, 2016, 53: 893-906. |
| Click to display the text | |
| [12] | LI Y, ZHU J, ZHANG W, et al. Structural topology optimization for directional deformation behavior design with orthotropic artificial weak element method[J]. Structural and Multidisciplinary Optimization, 2018, 57(3): 1251-1266. |
| Click to display the text | |
| [13] | LI Y, ZHU J, WANG F, et al. Shape preserving design of geometrically nonlinear structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2019, 59(4): 1033-1051. |
| Click to display the text | |
| [14] | CASTRO M S, SILVA O M, LENZI A, et al. Shape preserving design of vibrating structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2018, 58(3): 1109-1119. |
| Click to display the text | |
| [15] |
隋允康. 建模变换优化-结构综合方法新进展[M]. 大连: 大连理工大学出版社, 1996. SUI Y K. Modelling, transformation and optimization-new developments of structural synthesis method[M]. Dalian: Dalian University of Technology Press, 1996. (in Chinese) |
| [16] |
隋允康, 叶红玲. 连续体结构拓扑优化的ICM方法[M]. 北京: 科学出版社, 2013. SUI Y K, YE H L. Continuum topology optimization methods ICM[M]. Beijing: Science Press, 2013. (in Chinese) |
| [17] | SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization, 2001, 21(2): 120-127. |
| Click to display the text | |
| [18] | FLEURY C, BRAIBANT V. Structural optimization:A new dual method using mixed variables[J]. International Journal for Numerical Methods in Engineering, 1986, 23: 409-428. |
| Click to display the text | |
| [19] | SVANBERG K. The method of moving asymptotes-a new method for structural optimization[J]. International Journal for Numerical Methods in Engineering, 1987, 24: 359-373. |
| Click to display the text | |
| [20] | BRUYNEEL M, DUYSINX P, FLEURY C. A family of MMA approximations for structural optimization[J]. Structural and Multidisciplinary Optimization, 2002, 24(4): 263-276. |
| Click to display the text | |
| [21] | CHENG G D, GUO X. ε-relaxed approach in structural topology optimization[J]. Structural Optimization, 1997, 13(4): 258-266. |
| Click to display the text | |
| [22] | DUYSINX P, BENDSE M P. Topology optimization of continuum structures with local stress constraints[J]. International Journal for Numerical Methods in Engineering, 1998, 43(8): 1453-1478. |
| Click to display the text | |
| [23] | YANG D, LIU H, ZHANG W, et al. Stress-constrained topology optimization based on maximum stress measures[J]. Computers and Structures, 2018, 198: 23-29. |
| Click to display the text | |
| [24] | LONG K, WANG X, LIU H. Stress-constrained topol ogy optimization of continuum structures subjected to harmonic force excitation using sequential quadratic programming[J]. Structural and Multidisciplinary Optimization, 2019, 59(5): 1747-1759. |
| Click to display the text | |
| [25] |
龙凯, 谷先广, 王选. 基于多相材料的连续体结构动态轻量化设计方法[J]. 航空学报, 2017, 38(10): 221022. LONG K, GU X G, WANG X. Lightweight design method for continuum structure under vibration using multiphase materials[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 221022. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text |



