2. 大连理工大学 机械工程学院, 大连 116024
2. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
加筋壳结构具有较高的比强度和比刚度,在飞机机身[1]、运载火箭贮箱[2]和飞行器舱段[3]等航空航天结构中应用十分广泛。其服役过程主要处于轴压工况下,主要的破坏形式是整体失稳[4]。为了进一步提高加筋壳结构的抗失稳能力,学者们[5-6]提出了多级加筋壳这种新颖的加筋结构形式,其主要通过非均匀分布的筋条布局实现加筋壳结构的轻量化设计及高承载需求。为了准确预测加筋壳结构的极限承载力水平,需要基于高精度的有限元方法对结构进行后屈曲分析,如显式动力学方法。与实验结果对比后发现显式动力学后屈曲分析方法具有较高的预测精度和计算稳定性[7],但由于显式动力学计算耗时较大,限制了其在大规模优化设计中的应用。对于多级加筋壳结构,更加复杂的加筋形式将进一步增加显式动力学后屈曲分析的计算成本,如何对其进行快速的屈曲分析及优化成为了亟待解决的技术难题。
对于加筋筒壳的屈曲分析问题,等效刚度法[8](Smeared Stiffener Method, SSM)是一种代表性的解析的结构等效方法,而由于SSM没有考虑筋条偏心导致的拉弯耦合刚度,使得屈曲载荷的预测结果易产生不准确的现象[9-10]。相比解析方法,数值等效方法具有预测精度高和适用性广的优点,最常用的周期性单胞结构数值等效方法有代表体元法[11-12]和渐近均匀化法[13]等。Cheng等[14-15]建立了渐近均匀化快速数值实现(Numerical Implementation of Asymptotic Homogenization, NIAH)方法,可以在保证渐近均匀化法预测精度的前提下极大地提高分析效率。
代理模型技术能有效地降低计算成本,通过建立代理模型并结合启发式算法[16]可以进一步提高分析优化效率和寻优能力。Rikards等[17]基于RSM代理模型和遗传算法进行复合材料加筋筒壳后屈曲载荷的全局优化研究,在提高效率的同时保证了模型的高精度。郝鹏[18]、Zhao[19]和王博[20]等基于RBF代理模型和遗传算法,分别对T型多级加筋壳、多级三角形加筋筒壳和双层蒙皮多级加筋壳开展了结构优化设计。但对于复杂的多级加筋壳结构优化问题,构造精确的代理模型需要进行大量的样本点采样,仍需要耗费巨大的计算资源,例如Tian等[21]在较高精度的多级加筋壳代理模型构造中需耗费702 h进行样本点抽样,这是优化设计中难以承受的。
近年来,变保真度模型(Variable-Fidelity Model, VFM)技术得到了广泛应用,VFM通过把高保真度模型(High-Fidelity Model, HFM)和低保真度模型(Low-Fidelity Model, LFM)以某种合理的方式结合起来,综合了HFM的高精度和LFM的计算成本廉价两个特性,能够有效的节约计算资源。Han等[22-24]提出了基于梯度增强型Kriging的VFM、基于分层Kriging的VFM以及基于CoKriging的VFM等,在代理模型、飞行器设计和气动优化等领域取得了较为重大的突破。宋保维等[25]基于Han等[26]提出的样本点更新策略结合交叉算子方法建立了VFM,能够精确的预测自主水下航行器的流体动力参数。黄礼铿等[27]利用Co-Kriging方法构造了一种高效的VFM,并通过气动优化算例验证了该方法在优化中的高效性与实用性。Zhou等[28-29]等提出一种根据已有信息主动学习进行加点的VFM构造方法,并通过数值算例和工程算例验证了方法的通用性。刘蔚[30]采用VFM对7 000 m载人潜水器的载人耐压球壳结构子系统进行计算分析。但针对多级加筋壳这种复杂的薄壁结构的后屈曲分析问题,是一个有潜力的VFM应用场景,国内外目前还未针对多级加筋壳后屈曲分析给出有效的VFM构建方法,包括HFM与LFM的建立方式,合适的样本点更新策略等,亟待开展研究。
针对多级加筋壳结构的后屈曲极限承载力预测问题建立了VFM,并基于最大RMSE加点准则在VFM最大误差处进行样本点更新。结果表明建立的VFM能高效且准确地预测多级加筋壳结构的后屈曲极限承载力。同时还讨论了合适的LFM建立方式对VFM精度的重要性。
1 多级加筋壳HFM与LFM建立方法 1.1 HFM建立方法基于精细有限元模型的显式动力学方法进行结构极限承载力的计算,将计算结果作为HFM。显式动力学方法可以模拟轴压实验的准静态加载过程,进而准确模拟结构后屈曲行为,预测得到结构极限承载力,该方法稳健、不存在收敛性问题[31],其控制方程为
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{a}}_t} = \mathit{\boldsymbol{F}}_t^{{\rm{ext}}} - \mathit{\boldsymbol{F}}_t^{{\rm{int}}} - \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{V}}_t} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{U}}_t} $ | (1) |
式中:M代表质量阵;a代表节点加速度矢量;C代表阻尼阵;K代表刚度阵;V代表节点速度矢量;U代表节点位移矢量;t代表时间;Ftext(ext表示exterior)代表外力矢量;Ftint(int表示interior)代表内力矢量。
1.2 LFM建立方法对于加筋筒壳结构,周期性单胞结构的等效刚度系数可以基于渐近均匀化数值等效方法进行求解。根据经典的渐近均匀化理论[13],周期性单胞结构的等效刚度系数Aij、Bij和Dij的求解公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{A_{ij}} = \frac{1}{{|\varOmega |}}\int_\varOmega {{{(\mathit{\boldsymbol{\varepsilon }}_i^0 - \mathit{\boldsymbol{\varepsilon }}_i^*)}^{\rm{T}}}} \mathit{\boldsymbol{c}}(\mathit{\boldsymbol{\varepsilon }}_j^0 - \mathit{\boldsymbol{\varepsilon }}_j^*){\rm{d}}\varOmega }\\ {{B_{ij}} = \frac{1}{{|\varOmega |}}\int_\varOmega {{{(\mathit{\boldsymbol{\varepsilon }}_i^0 - \mathit{\boldsymbol{\varepsilon }}_i^*)}^{\rm{T}}}} \mathit{\boldsymbol{c}}(\mathit{\boldsymbol{\bar \varepsilon }}_j^0 - \mathit{\boldsymbol{\bar \varepsilon }}_j^*){\rm{d}}\varOmega }\\ {{D_{ij}} = \frac{1}{{|\varOmega |}}\int_\varOmega {{{(\mathit{\boldsymbol{\bar \varepsilon }}_i^0 - \mathit{\boldsymbol{\bar \varepsilon }}_i^*)}^{\rm{T}}}} \mathit{\boldsymbol{c}}(\mathit{\boldsymbol{\bar \varepsilon }}_j^0 - \mathit{\boldsymbol{\bar \varepsilon }}_j^*){\rm{d}}\varOmega } \end{array}} \right. $ | (2) |
式中:Ω代表周期性单胞结构的体积;c代表弹性矩阵,下标i、j∈{1, 2, 6};εi0表示单位面内应变场;εi0表示单位弯曲应变场;εi*表示特征面内应变场;ε i*表示特征弯曲应变场。
渐近均匀化方法的传统数值求解方法需要在每个单元上进行积分求解支反力和应变能。当周期性单胞结构中含有微结构时,为了准确分析结构性能,需要针对微结构划分大量单元。此时,传统数值求解方法需要进行大量的单元积分求解,计算成本将大幅度增加。为了提高渐近均匀化方法的求解效率,Cheng[14]和Cai[15]等建立了渐近均匀化方法的快速数值求解方法,将周期性单胞结构的等效刚度系数用一种更简洁的方式来进行计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{A_{ij}} = \frac{1}{{|\varOmega |}}{{(\mathit{\boldsymbol{\chi }}_i^0 - \mathit{\boldsymbol{a}}_i^*)}^{\rm{T}}}({\mathit{\boldsymbol{f}}_j} - \mathit{\boldsymbol{P}}_j^*)}\\ {{B_{ij}} = \frac{1}{{|\varOmega |}}{{(\mathit{\boldsymbol{\chi }}_i^0 - \mathit{\boldsymbol{a}}_i^*)}^{\rm{T}}}({{\mathit{\boldsymbol{\bar f}}}_j} - \mathit{\boldsymbol{\bar P}}_j^*)}\\ {{D_{ij}} = \frac{1}{{|\varOmega |}}{{(\mathit{\boldsymbol{\bar \chi }}_i^0 - \mathit{\boldsymbol{\bar a}}_i^*)}^{\rm{T}}}({{\mathit{\boldsymbol{\bar f}}}_j} - \mathit{\boldsymbol{\bar P}}_j^*)} \end{array}} \right. $ | (3) |
式中:χ i0、χ i0表示节点面内位移场和弯曲位移场;ai*、ai*表示特征面内位移场和特征弯曲位移场;fj、fj表示单胞结构节点面内支反力场和弯曲支反力场;Pj*、Pj*表示特征面内支反力场和特征弯曲支反力场。
式(3)中的每个系数均可基于商用有限元软件计算得出,无须采用传统渐近均匀化方法中的复杂积分求导,从而加筋单胞的等效刚度系数Aij、Bij和Dij可以快速获得。
基于上述刚度等效方法,对多级加筋壳次筋进行等效,然后基于显式动力学方法进行后屈曲分析,以此作为LFM。由于上述方法既等效了结构又保留了后屈曲分析,建立的LFM可以在保证较高效率的同时获得结构的后屈曲特性,称此方法为混合方法。
1.3 HFM与LFM预测精度和计算效率开展算例研究来对比HFM与LFM的预测精度与计算效率。算例所采用的多级加筋壳模型几何参数如下:不可变参数包括多级加筋壳直径D=3 000.0 mm和多级加筋壳高度L=2 000.0 mm;可变参数包括蒙皮厚度ts、主筋高度hj、主筋厚度trj、轴向主筋数目Naj、环向主筋数目Ncj、次筋高度hn、次筋厚度trn、主筋格栅中的轴向次筋数目Nan和主筋格栅中的环向次筋数目Ncn。蒙皮和筋条的材料属性如表 1所示。可变参数的变量设计空间如表 2所示。进行显式动力学分析的加载时间为200 ms,加载总位移为20 mm。边界条件设置如下:底端固支,顶端约束除轴向位移外的其余自由度,并将顶端面所有节点刚性耦合至参考点,在参考点上施加轴压位移载荷直至结构发生坍塌。
| 属性 | 弹性模量/ MPa |
泊松比 | 屈服强度/ MPa |
抗拉强度/ MPa |
伸长率 |
| 数值 | 70 000 | 0.33 | 563 | 630 | 0.07 |
| 变量 | 下限值 | 上限值 |
| ts/mm | 2.5 | 5.5 |
| trj/mm | 3.0 | 12.0 |
| trn/mm | 3.0 | 12.0 |
| hj /mm | 15.0 | 30.0 |
| hn /mm | 6.0 | 15.0 |
| Ncj | 3 | 9 |
| Ncn | 1 | 4 |
| Naj | 20 | 50 |
| Nan | 1 | 4 |
HFM和LFM的有限元模型示意如图 1所示。基于拉丁超立方抽样(Latin Hypercube Sampling, LHS)方法在设计空间抽取20个样本点,并基于HFM和LFM分别计算样本点的极限承载力,其数据相关性如图 2所示,两组数据的相关系数为0.97,表明LFM与HFM计算结果有较强的相关性。HFM的计算时长约为1.67 h,而LFM的计算时长仅约为0.083 h,表现出较高的分析效率。可以看出,LFM具有较高的预测精度和效率。
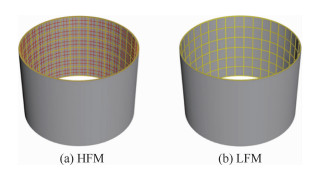
|
| 图 1 多级加筋壳HFM与LFM示意图 Fig. 1 Illustration of HFM and LFM of hierarchical stiffened shells |

|
| 图 2 HFM和LFM的相关性分析 Fig. 2 Correlation analysis results of HFM with LFM |
Benjamin等[32]总结了3种对HFM和LFM进行结合的方式,分别是自适应(Adaptation)、融合(Fusion)与过滤(Filtering)。自适应方法在计算过程中采用自适应策略,利用来自HFM的信息增强LFM;融合方法通过对LFM和HFM数据进行评估,以某种方式将LFM和HFM结合起来;过滤方法在对LFM滤波器进行测评之后调用HFM数据。
融合方法是较为常用的VFM结合方法,又称为桥函数法,可分为加法式[33]、乘法式[33]与综合式[34-35]。基于加法式桥函数构建VFM:
| $ {y_{{\rm{VFM}}}} = {y_{{\rm{LF}}}}(x) + \delta (x) $ | (4) |
通过在LFM(yLF)的基础上加入桥函数δ(x),得到VFM (yVFM)。
2.2 高斯过程回归高斯过程回归(Gaussian Process Regression, GPR)是使用高斯过程先验对数据进行回归分析的非参数模型[36]。高斯过程是一个随机过程,对处理小样本、非线性、高维数等复杂问题有较好的拟合效果。
高斯过程的表达式为
| $ f(\mathit{\boldsymbol{x}})\backsim {\rm{ GP}} (m(\mathit{\boldsymbol{x}}),k(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}^\prime })) $ | (5) |
式中:f(x)表示满足联合高斯分布的任意假设函数;m(x)表示均值函数;k(x, x′)表示协方差函数,GP表示高斯过程。
假设自变量为x,因变量为y,加入噪声ε即可建立高斯回归过程模型,即
| $ \mathit{\boldsymbol{y}} = f(\mathit{\boldsymbol{x}}) + \mathit{\boldsymbol{\varepsilon }} $ | (6) |
式中:ε~N(0, σn2In)为满足高斯分布的白噪声;σn2为噪声方差;In是单位阵。
由式(5)和式(6)可得观测值y的先验分布:
| $ \mathit{\boldsymbol{y}}\backsim N(m(\mathit{\boldsymbol{x}}),k(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}^\prime }) + \sigma _n^2{\mathit{\boldsymbol{I}}_n}) $ | (7) |
根据贝叶斯原理,GP在给定数据集内建立先验函数,并在测试数据集中转变为后验分布,观测值y与预测值f*的联合高斯分布为
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{y}}\\ {{\mathit{\boldsymbol{f}}_*}} \end{array}} \right]\backsim N\left( {0,\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{X}},\mathit{\boldsymbol{X}}) + \sigma _n^2{\mathit{\boldsymbol{I}}_n}}&{\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_*})}\\ {\mathit{\boldsymbol{K}}({\mathit{\boldsymbol{X}}_*},\mathit{\boldsymbol{X}})}&{\mathit{\boldsymbol{K}}({\mathit{\boldsymbol{X}}_*},{\mathit{\boldsymbol{X}}_*})} \end{array}} \right]} \right) $ | (8) |
式中:K(X, X)表示N×N的核矩阵,其元素为Kij=k(xi, xj);X表示输入样本;X*表示待预测输入值。
于是GPR方程可写为
| $ {{\mathit{\boldsymbol{f}}_*}|\mathit{\boldsymbol{X}},\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{X}}_*}\backsim N({\mathit{\boldsymbol{m}}_*},\mathit{\boldsymbol{K}}({\mathit{\boldsymbol{f}}_*},{\mathit{\boldsymbol{f}}_*}))} $ | (9) |
| $ {{\mathit{\boldsymbol{m}}_*} = \mathit{\boldsymbol{K}}({\mathit{\boldsymbol{X}}_*},\mathit{\boldsymbol{X}}){{(\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{X}},\mathit{\boldsymbol{X}}) + \sigma _n^2{\mathit{\boldsymbol{I}}_n})}^{ - 1}}\mathit{\boldsymbol{y}}} $ | (10) |
| $ \begin{array}{l} \mathit{\boldsymbol{K}}({\mathit{\boldsymbol{f}}_*},{\mathit{\boldsymbol{f}}_*}) = \mathit{\boldsymbol{K}}({\mathit{\boldsymbol{X}}_*},{\mathit{\boldsymbol{X}}_*}) - \mathit{\boldsymbol{K}}({\mathit{\boldsymbol{X}}_*},\mathit{\boldsymbol{X}}) \cdot \\ \quad {(\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{X}},\mathit{\boldsymbol{X}}) + \sigma _n^2{\mathit{\boldsymbol{I}}_n})^{ - 1}}\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_*}) \end{array} $ | (11) |
式中:f*是GPR模型的输出;m*为预测值的均值;K(f*, f*)表示输出预测值的后验方差。预测值的后验方差可以用来度量预测结果的不确定性,即可信程度。
2.3 样本点更新策略及精度评价指标基于代理模型的优化方法,国际上已发展了多种加点准则[37],其中基于最大均方根误差(Root Mean Square Error, RMSE)方法的加点准则是提高代理模型全局精度最好的准则[38]。前面已经提到,GPR不仅可以预测未知点处的响应值,还可以预测未知点处的RMSE,对于VFM,其未知点处的均方根误差为LFM的误差与桥函数的误差之和:
| $ {\rm{RMSE}} (x) = {\rm{RMSE}} ({y_{{\rm{LF}}}}(x)) + {\rm{RMSE}} (\delta (x)) $ | (12) |
通过在迭代时加入RMSE值最大的样本点,即可不断提高模型的整体精度。具体加点原理通过简单一维测试函数展示。如图 3(a)所示,初始时高保真样本点只有3个,可以看到蓝色线表示的VFM与黄色线表示的真实模型存在一定的差距。通过在RMSE最大处加入3个样本点,如图 3(b)所示,VFM曲线已经和真实模型接近,只有局部存在少量误差。当样本点数量增加到6个时,如图 3(c)所示,VFM曲线已基本和真实模型重合,红色线表示的均方根误差也都处于较小值,模型的整体精度有较明显的提升。
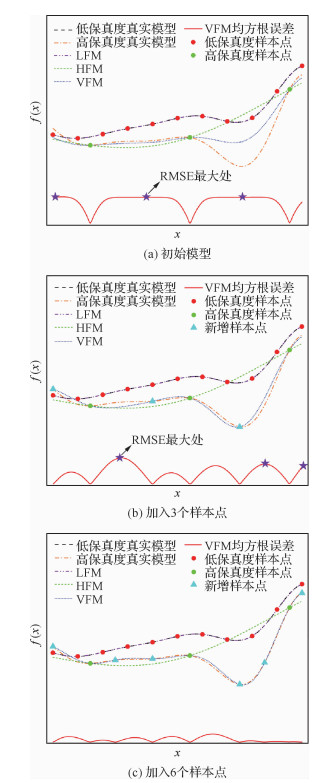
|
| 图 3 基于最大RMSE自适应加点示意图 Fig. 3 Illustration of procedure for maximal RMSE-based adaptive updating approach |
采用RMSE和R2作为代理模型精度的评价指标:
| $ { {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({y_i} - {{\hat y}_i})}^2}} } } $ | (13) |
| $ {R^2} = 1 - \frac{{\sum\nolimits_{i = 1}^N {{{({y_i} - {{\hat y}_i})}^2}} }}{{\sum\nolimits_{i = 1}^N {{{({y_i} - {{\tilde y}_i})}^2}} }} $ | (14) |
式中:N代表样本总数;yi表示真实值;
VFM的构建方法如图 4所示,主要步骤包括:
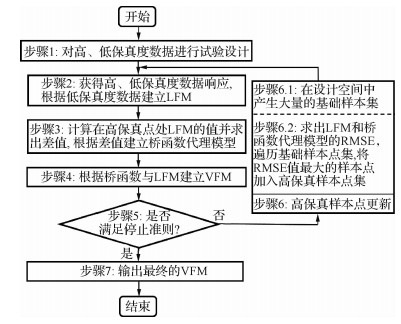
|
| 图 4 VFM构建流程 Fig. 4 Flowchart of constructing VFM |
步骤1 对高、低保真度数据进行试验设计,本文使用LHS进行抽样,以得到分布相对均匀的高、低保真度样本点。
步骤2 基于第1节中的方法分别获得高、低保真度样本点处的响应,并根据低保真度数据基于GPR构建LFM。
步骤3 先计算LFM在高保真度样本点处的响应,然后得到该处的LFM响应与HFM结果的差值,根据差值建立桥函数代理模型。
步骤4 根据桥函数代理模型与LFM构建VFM。
步骤5 检验是否满足停止准则。若满足,则跳转至步骤7;若不满足,则继续步骤6。
步骤6 根据样本点更新策略加入新样本点。首先,在步骤6.1中,在设计空间中通过LHS方法产生1 000组样本点,构成基础样本集。然后,在步骤6.2中,分别求出LFM和桥函数代理模型的误差指标RMSE,并将两者求和。遍历1 000组样本点对应的RMSE,将RMSE值最大的样本点作为新样本点加入高保真度样本点集中,跳转至步骤2。
步骤7 输出满足要求的VFM。
3 多级加筋壳VFM构建结果HFM的预测精度与样本点数目的关系如表 3所示,柱状图形式如图 5所示。可以看出随着高保真样本点的增加,HFM的整体精度也随之增加。当代理模型精度较高(R2=0.951)时,需要计算100个高保真样本点的响应以构造代理模型,计算成本较大。

|
| 图 5 HFM精度与高保真样本点数量的关系 Fig. 5 Relationship between accuracy of HFM and number of high-fidelity sample points |
| 高保真 样本点数 |
20 | 40 | 60 | 80 | 100 |
| RMSE | 2 394.8 | 1 659.8 | 1 276.9 | 1 231.9 | 1 173.7 |
| R2 | 0.796 | 0.902 | 0.942 | 0.946 | 0.951 |
基于混合方法建立的LFM的预测精度与样本点数目的关系如表 4所示,绘制成柱状图形式如图 6所示。当低保真度样本点的数量为200时,代理模型RMSE为1 742.2,R2为0.892。可以看出,若继续增加样本点数量,LFM的精度也无明显提高。
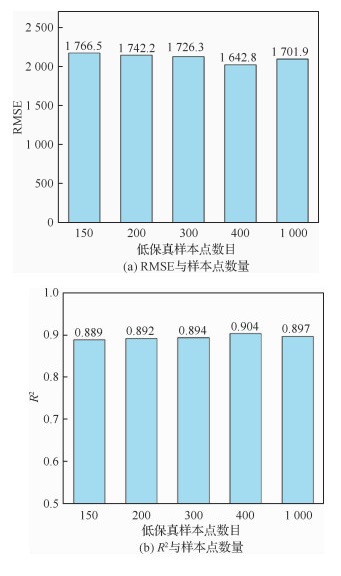
|
| 图 6 LFM精度与低保真样本点数量的关系 Fig. 6 Relationship between accuracy of LFM and number of low-fidelity sample points |
| 低保真样本点数 | 150 | 200 | 300 | 400 | 1 000 |
| RMSE | 1 766.5 | 1 742.2 | 1 726.3 | 1 642.8 | 1 701.9 |
| R2 | 0.889 | 0.892 | 0.894 | 0.904 | 0.897 |
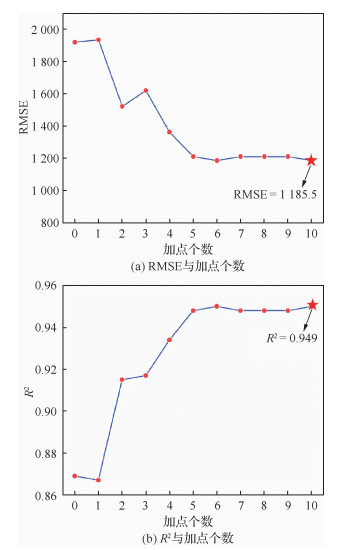
选取20个高保真样本点与200个低保真样本点构建的VFM作为基准,通过第2节所提出的样本点更新策略进行加点,设定的收敛准则为新增样本点数目不超过10个。加点个数与VFM精度关系如图 7所示,随着样本点的不断更新,VFM精度也不断提高,收敛时RMSE为1 185.5,相比加点前降低38.2%;收敛时R2为0.949,相比加点前提高9.2%。
|
| 图 7 加点个数与VFM精度的关系 Fig. 7 Relationship between accuracy of VFM and number of updating sample points |
由表 5可知,上述根据自适应加点构建的VFM的R2为0.949,100个HFM的R2为0.951,两者精度水平较为接近,而前者的计算时间只需4 000 min,相比100个HFM降低了60%的计算耗时。若直接采用30HFM+200LFM构建VFM,计算耗时也为4 000 min,但其RMSE为1 521.5,相比自适应加点方法构建的VFM增加了28.3%,R2为0.915,相比自适应加点方法构建的VFM降低了3.6%,表明了加点策略的有效性。
| 代理模型样本点 | RMSE | R2 | 计算耗时/min |
| 20HFM | 2 394.7 | 0.796 | 2 000 |
| 100HFM | 1 173.7 | 0.951 | 10 000 |
| 200LFM(基于混合方法) | 1 742.2 | 0.892 | 1 000 |
| 20HFM+200LFM (基于混合方法) |
1 919.0 | 0.869 | 3 000 |
| 30HFM+200LFM (基于混合方法) |
1 521.5 | 0.915 | 4 000 |
| 20HFM+200LFM (基于混合方法)+10VFM (基于最大RMSE加点) |
1 185.5 | 0.949 | 4 000 |
| 200LFM(基于NSSM) | 3 099.8 | 0.658 | 20 |
| 20HFM+200LFM (基于NSSM) |
2 276.7 | 0.815 | 2 020 |
| 30HFM+200LFM (基于NSSM) |
2 216.5 | 0.825 | 3 020 |
| 20HFM+200LFM (基于NSSM)+10VFM (基于最大RMSE加点) |
2 075.7 | 0.847 | 3 020 |
综合来看,基于RMSE的自适应加点方法构建的VFM可以在满足精度要求的同时有效地节约计算成本。
4 面向后屈曲问题LFM建立方法讨论在VFM的构建过程中需要先建立HFM和LFM,LFM有多种建立方式[39]。针对不同的实际问题,如何建立合适的LFM是一个具有挑战性的难题,建立不恰当的LFM可能会导致构建的VFM精度不如直接使用HFM[40]。如前文所说,多级加筋壳结构后屈曲极限承载力的预测是一个高度非线性和复杂的问题,建立合适的LFM对于VFM效率和精度尤为重要。
除了1.2节中介绍的混合方法,通常思路是通过刚度等效的方式对筋条进行等效以降低计算成本,再通过瑞利-里兹法得到其线性屈曲载荷,Wang等[41]针对多级加筋筒壳结构基于NIAH方法和瑞利-里兹法建立了NSSM方法,可以快速预测多级加筋壳的线性屈曲载荷和屈曲模态,但该方法只能预测线性阶段承载能力,无法获得后屈曲特性。本节将以基于NSSM方法建立的LFM与1.2节中基于混合方法建立的LFM进行对比,以讨论这两种LFM对于构建VFM的精度的影响。
NSSM方法的流程主要包括3步[42]:第1步,从多级加筋壳结构中提取出代表性单胞结构,进行有限元建模;第2步,基于NIAH方法计算单胞结构的等效刚度系数Aij、Bij和Dij;第3步,将上述等效刚度系数代入至瑞利-里兹公式,计算得出整体型屈曲载荷值。本节将第3节中的200个LFM样本点基于NSSM方法重新计算,构建的相关代理模型精度结果如表 5所示。
由表 5可知,尽管基于NSSM方法建立的LFM在计算耗时上有所降低,但其200个低保真度样本点构建的LFM的R2精度只有0.658,远低于基于混合方法构建的LFM。原因是NSSM方法只预测线性屈曲阶段,没有预测到后屈曲阶段高度非线性和复杂性的信息,因此造成了较大的误差。相比之下,基于混合方法建立的LFM,可以有效预测后屈曲阶段,R2达到0.892,表现出更高的预测精度。由1.3节内容可知,基于混合方法所建立的LFM和HFM在设计空间内具有高度相关性,是一种能较准确描述极限承载力变化趋势的LFM。同时可以发现,基于NSSM方法建立的LFM构建的VFM及其加点后结果与混合方法相比均精度较差,并没有达到理想的高精度效果。由此可见,选取合适的LFM对于高精度VFM的建立具有重要意义。
5 结论1) 以精细有限元模型和显式动力学算法建立了多级加筋壳的HFM,并基于混合方法建立了多级加筋壳的LFM。在此基础上,借助于桥函数实现了HFM与LFM的连接,并基于GPR方法构建了适用于多级加筋壳的VFM。
2) 基于RMSE更新策略在VFM误差最大处持续更新样本点,使得VFM精度进一步提高。多级加筋壳算例结果表明,在达到同样的高精度要求时,基于本文提出方法构建的VFM相比于基于直接通过HFM抽样的代理模型降低了约60%的计算成本,将有助于提高多级加筋壳后屈曲分析及优化效率。
3) 验证了基于混合方法建立LFM的有效性,表明了对于后屈曲分析问题LFM应选取可捕捉后屈曲阶段的LFM,而只能计算线性屈曲的LFM对于建立后屈曲问题的VFM作用不大。
后续将基于提出的VFM开展多级加筋壳高效优化方法研究。
| [1] | LENE F, DUVAUT G, OLIVIER-MAILHE M, et al. An advanced methodology for optimum design of a composite stiffened cylinder[J]. Composite Structures, 2009, 91(4): 392-397. |
| Click to display the text | |
| [2] | HAO W, YING Y, WEI Y, et al. Adaptive approximation-based optimization of composite advanced grid-stiffened cylinder[J]. Chinese Journal of Aeronautics, 2010, 23(4): 423-429. |
| Click to display the text | |
| [3] |
吴振强, 程昊, 张伟, 等. 热环境对飞行器壁板结构动特性的影响[J]. 航空学报, 2013, 34(2): 334-342. WU Z Q, CHENG H, ZHANG W, et al. Effects of thermal environment on dynamic properties of aerospace vehicle panel structures[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 334-342. (in Chinese) |
| Cited By in Cnki (54) | Click to display the text | |
| [4] | SHI S S, SUN Z, REN M F, et al. Buckling resistance of grid-stiffened carbon-fiber thin-shell structures[J]. Composites Part B:Engineering, 2013, 45(1): 888-896. |
| Click to display the text | |
| [5] | WANG B, HAO P, LI G, et al. Generatrix shape optimization of stiffened shells for low imperfection sensitivity[J]. Science China Technological Sciences, 2014, 57(10): 2012-2019. |
| Click to display the text | |
| [6] |
马建峰, 陈五一, 赵岭, 等. 基于蜻蜓膜翅结构的飞机加强框的仿生设计[J]. 航空学报, 2009, 30(3): 562-569. MA J F, CHEN W Y, ZHAO L, et al. Bionic design of aircraft reinforced frame based on structure of dragonfly wing[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(3): 562-569. (in Chinese) |
| Cited By in Cnki (29) | Click to display the text | |
| [7] | WANG B, DU K F, HAO P, et al. Numerically and experimentally predicted knockdown factors for stiffened shells under axial compression[J]. Thin-Walled Structures, 2016, 109: 13-24. |
| Click to display the text | |
| [8] | CHEN H J, TSAI S W. Analysis and optimum design of composite grid structures[J]. Journal of Composite Materials, 1996, 30(4): 503-534. |
| Click to display the text | |
| [9] | JONES R M. Buckling of circular cylindrical shells with multiple orthotropic layers and eccentric stiffeners[J]. AIAA Journal, 1968, 6(12): 2301-2305. |
| Click to display the text | |
| [10] | SADEGHIFAR M, BAGHERI M, JAFARI A A. Buckling analysis of stringer-stiffened laminated cylindrical shells with nonuniform eccentricity[J]. Archive of Applied Mechanics, 2011, 81(7): 875-886. |
| Click to display the text | |
| [11] | QUEK S C, WAAS A M, SHAHWAN K W, et al. Analysis of 2D triaxial flat braided textile composites[J]. International Journal of Mechanical Sciences, 2003, 45(6-7): 1077-1096. |
| Click to display the text | |
| [12] | MARTINEZ O A, SANKAR B V, HAFTKA R T, et al. Micromechanical analysis of composite corrugated-core sandwich panels for integral thermal protection systems[J]. AIAA Journal, 2007, 45(9): 2323-2336. |
| Click to display the text | |
| [13] | LEE C Y, YU W. Homogenization and dimensional reduction of composite plates with in-plane heterogeneity[J]. International Journal of Solids and Structures, 2011, 48(10): 1474-1484. |
| Click to display the text | |
| [14] | CHENG G D, CAI Y W, XU L. Novel implementation of homogenization method to predict effective properties of periodic materials[J]. Acta Mechanica Sinica, 2013, 29(4): 550-556. |
| Click to display the text | |
| [15] | CAI Y W, XU L, CHENG G D. Novel numerical implementation of asymptotic homogenization method for periodic plate structures[J]. International Journal of Solids and Structures, 2014, 51(1): 284-292. |
| Click to display the text | |
| [16] |
丛明煜, 王丽萍. 现代启发式算法理论研究[J]. 高技术通讯, 2003, 13(5): 105-110. CONG M Y, WANG L P. Survey on the theory of meta-heuristic algorithms[J]. High Technology Letters, 2003, 13(5): 105-110. (in Chinese) |
| Cited By in Cnki (98) | Click to display the text | |
| [17] | RIKARDS R, ABRAMOVICH H, AUZINS J, et al. Surrogate models for optimum design of stiffened composite shells[J]. Composite Structures, 2004, 63(2): 243-251. |
| Click to display the text | |
| [18] |
郝鹏, 王博, 李刚, 等. T型截面多级加筋柱壳的缺陷敏感性及优化研究[J]. 工程力学, 2015, 32(8): 223-228. HAO P, WANG B, LI G, et al. Imperfection sensitivity analysis and optimization of hierarchical stiffened shells with T-section stiffeners[J]. Engineering Mechanics, 2015, 32(8): 223-228. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [19] | ZHAO Y N, CHEN M J, YANG F, et al. Optimal design of hierarchical grid-stiffened cylindrical shell structures based on linear buckling and nonlinear collapse analyses[J]. Thin-Walled Structures, 2017, 119: 315-323. |
| Click to display the text | |
| [20] |
王博, 杜凯繁, 郝鹏, 等. 考虑几何缺陷的轴压双层蒙皮加筋柱壳结构设计[J]. 中国科学:物理学, 力学, 天文学, 2018, 48(1): 1-8. WANG B, DU K F, HAO P, et al. Design of sandwich-walled cylindrical shell structure[J]. Science China Physica, Mechanica & Astronomica, 2018, 48(1): 1-8. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [21] | TIAN K, WANG B, ZHANG K, et al. Tailoring the optimal load-carrying efficiency of hierarchical stiffened shells by competitive sampling[J]. Thin-Walled Structures, 2018, 133: 216-225. |
| Click to display the text | |
| [22] | HAN Z H, GÖRTZ S, ZIMMERMANN R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function[J]. Aerospace Science and Technology, 2013, 25(1): 177-189. |
| Click to display the text | |
| [23] | HAN Z H, GÖRTZ S. Hierarchical kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(9): 1885-1896. |
| Click to display the text | |
| [24] | HAN Z H, ZIMMERMAN R, GÖRTZ S. Alternative cokriging method for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1205-1210. |
| Click to display the text | |
| [25] |
宋保维, 王新晶, 王鹏. 基于变保真度模型的AUV流体动力参数预测[J]. 机械工程学报, 2017, 53(18): 176-182. SONG B W, WANG X J, WANG P. Aerodynamic optimization based on multi-fidelity surrogate[J]. Journal of Mechanical Engineering, 2017, 53(18): 176-182. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [26] | HAN Z H, GÖRTZ S, HAIN R. New results in numerical and experimental fluid mechanics VII[M]. Berlin: Springer Berlin Heidelberg, 2010: 17-25. |
| [27] |
黄礼铿, 高正红, 张德虎. 基于变可信度代理模型的气动优化[J]. 空气动力学学报, 2013, 31(6): 783-788. HUANG L Q, GAO Z H, ZHANG D H, et al. Aerodynamic optimization based on multi-fidelity surrogate[J]. Acta Aerodynamica Sinica, 2013, 31(6): 783-788. (in Chinese) |
| Cited By in Cnki (239) | Click to display the text | |
| [28] | ZHOU Q, SHAO X, JIANG P, et al. An active learning metamodeling approach by sequentially exploiting difference information from variable-fidelity models[J]. Advanced Engineering Informatics, 2016, 30(3): 283-297. |
| Click to display the text | |
| [29] | ZHOU Q, SHAO X, JIANG P, et al. An active learning variable-fidelity metamodelling approach based on ensemble of metamodels and objective-oriented sequential sampling[J]. Journal of Engineering Design, 2016, 27(4-6): 205-231. |
| Click to display the text | |
| [30] |
刘蔚.多学科设计优化方法在7000米载人潜水器总体设计中的应用[D].上海: 上海交通大学, 2007: 105-122. LIU W. Application of MDO method to 7000m HOV general design[D]. Shanghai: Shanghai Jiao Tong University, 2007: 105-122(in Chinese). |
| Cited By in Cnki (40) | Click to display the text | |
| [31] | TIAN K, WANG B, HAO P, et al. A high-fidelity approximate model for determining lower-bound buckling loads for stiffened shells[J]. International Journal of Solids and Structures, 2018, 148: 14-23. |
| Click to display the text | |
| [32] | BENJAMIN P, KAREN W, MAX G. Survey of multifidelity methods in uncertainty propagation, inference, and optimization[J]. SIAM Review, 2018, 60(3): 550-591. |
| Click to display the text | |
| [33] | HAFTKA, RAPHAEL T. Combining global and local approximations[J]. AIAA Journal, 1991, 29(9): 1523-1525. |
| Click to display the text | |
| [34] | KEANE A J. Cokriging for robust design optimization[J]. AIAA Journal, 2012, 50(11): 2351-2364. |
| Click to display the text | |
| [35] | PERDIKARIS P, VENTURI D, ROYSET J O, et al. Multi-fidelity modelling via recursive co-kriging and Gaussian-Markov random fields[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2015, 471(2179): 1-22. |
| Click to display the text | |
| [36] | RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge: MIT Press, 2006: 7-31. |
| [37] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| Cited By in Cnki (32) | Click to display the text | |
| [38] |
刘俊.基于代理模型的高效气动优化设计方法及应用[D].西安: 西北工业大学, 2015: 60-65. LIU J. Efficient surrogate-based optimization method and its application in aerodynamic design[D]. Xi'an: Northwestern Polytechnical University, 2015: 60-65(in Chinese). |
| [39] | PARK C, HAFTKA R T, KIM N H. Remarks on multi-fidelity surrogates[J]. Structural and Multidisciplinary Optimization, 2017, 55(3): 1029-1050. |
| Click to display the text | |
| [40] | FERNÁNDEZ-GODINO M G, PARK C, KIM N H, et al. Issues in deciding whether to use multifidelity surrogates[J]. AIAA Journal, 2019, 57(5): 2039-2054. |
| Click to display the text | |
| [41] | WANG B, TIAN K, HAO P, et al. Numerical-based smeared stiffener method for global buckling analysis of grid-stiffened composite cylindrical shells[J]. Composite Structures, 2016, 152: 807-815. |
| Click to display the text | |
| [42] |
田阔.基于多保真度建模的多层级筒壳屈曲分析及优化方法研究[D].大连: 大连理工大学, 2018: 66-70. TIAN K. Research on buckling analysis and optimization methods of hierarchical cylindrical shells based on multi-fidelity modeling[D]. Dalian: Dalian University of Technology, 2018: 66-70(in Chinese). |
| Cited By in Cnki | Click to display the text |



