由鲨鱼皮衍生出来的仿生表面结构在航空发动机叶片、整体叶盘等转动构件表面的形成对于提高其减阻、降噪、抗疲劳等服役性能具有重要的影响;同时钛合金材料具有比重小、比强度高、韧性高、疲劳裂纹扩展速率低、耐腐蚀性好等优点[1],作为轻质材料被广泛应用于上述转动构件的设计中,其加工后的型面精度和表面纹路、粗糙度、显微硬度、残余应力、亚表层组织等表面完整性特征对上述钛合金转动构件的疲劳寿命、气流动力性和使用性能影响巨大,因此研究钛合金仿生表面的加工方法具有重要意义。
由于叶片具有复杂的型面和较弱的刚度,因此主要通过砂带磨削等精密加工方法来保证叶片的最后精度。但对于砂带磨削仿生表面的形成与砂带单颗粒模型和砂带多颗粒磨削方法的关系, 目前尚未揭示,因而提出基于单颗粒模型的航发叶片砂带磨削微观仿生锯齿状表面形成方法及试验。
对于鲨鱼皮仿生表面的加工可分为两种[2],一种是直接复刻鲨鱼皮的表面盾鳞结构,另一种是基于鲨鱼皮表面结构衍生出来的设计制备的沟槽。对于后一种方法,针对沟槽结构具有代表性的加工方法有磨削加工技术。Xie[3-4]等利用金刚石砂轮在单晶硅上干磨出微沟槽,并且发现微沟槽的形状与砂轮上的金刚石磨粒状参数有关,如金刚石磨粒的前角,磨粒尖端的半径的大小等。Denkena等[5]提出了磨削轮沟槽结构加工方法,即多轮廓磨削法。该方法在制备磨削轮的效率和工艺稳定性上具有优势,通过这种工艺能够很有效率地加工沟槽结构,但磨削法成形的沟槽结构较为粗糙,容易形成毛刺。Brinksmeier和Schönemann[6]采用金刚石微凿切加工出了不连续的微观结构,如微型立方体和V型沟槽;研究发现,可加工显微结构的尺寸主要受加工相关形状偏差的限制,增加结构尺寸对表面光洁度没有明显的影响;然而,大尺寸结构的加工会导致切削力的线性增加。
针对航发钛合金叶片等零部件的表面精密磨削加工,国内外采用了磨料流[7-8]、砂带磨削以及手工抛光等方法,对于提升叶片表面完整性具有一定的作用。砂带磨削兼具磨削和抛光的双重作用,其工艺灵活性高、适应性强,且其柔性磨削的特性在型面平滑过渡方面具有独特的拟合效果[9]。鉴于上述特性,目前砂带磨削技术已经成功应用于航发叶片的精密磨削中,成为提高其表面完整性的有效加工技术之一[10]。Eckart和Florian[11-12]以及Xu等[13]采用了机器人辅助砂带磨削的方法进行了涡轮叶片精密加工,并通过力控的方法实现加工过程的自适应从而提高了加工效率、加工精度和叶片表面质量。张雷等[14]对航发叶片双曲面砂带磨削工艺、恒力磨削方法等进行了研究,提出了叶片双曲面砂带磨削力的精确控制方法。肖贵坚等[15]提出了一种面向型面精度一致性的砂带磨削新方法, 一方面通过砂带周期性的往复运动结合自锐式磨削原理, 实现型面铣削残差层的高效去除; 另一方面通过砂带周期性的自动更新, 保证各叶片的型面精度在同一截面具有高一致性。阐述并建立了面向型面精度一致性的砂带磨削新方法及其磨削控制方程。Xiao和Huang[16]对航发叶片边缘当量自适应砂带磨削方法进行了研究,对砂带磨削后的表面粗糙度进行了分析,结果表明在砂带磨削后表面粗糙度≤0.25 μm,且表面呈现压应力状态;蔺小军等[17]采用柔性抛光技术和控制抛光轴矢量来实现砂带与叶片型面的有效贴合,砂带磨削技术的发展极大地提高了叶片表面加工的质量。
由上述分析可以看出,对于鲨鱼皮仿生表面的加工,大多采用砂轮磨削的方式,国内外缺少砂带磨削仿生表面的形成和对叶片、整体叶盘等零件仿生表面加工的研究。本文将针对叶片鲨鱼皮仿生表面进行研究,首先,分析了微观仿生锯齿状表面典型结构特征,基于单颗粒砂带磨削模型,研究了单颗粒砂带磨削去除机理;然后,建立了砂带磨削多颗粒参数化数学模型,提出微观仿生锯齿状表面砂带磨削方法;最后,以钛合金叶片型面为对象,搭建以钛合金为典型材料的微观仿生锯齿状表面砂带磨削基础实验平台,进行微观仿生锯齿状表面的试验验证。
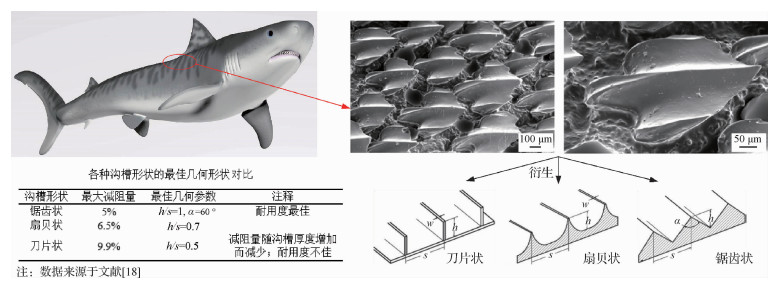
1 微观仿生锯齿状表面磨削机理 1.1 单颗粒数学模型及其磨削特征分析图 1中各种沟槽形状的最佳几何形状对比数据主要来源于Bechert等[18]的研究,其中h为沟槽高度、s为沟槽宽度、α为沟槽的夹角、w为沟槽尖端平面宽度。对于锯齿状沟槽结构而言,最大减阻量可达5%左右,是耐用度最佳的结构之一,最佳几何参数为:h/s=1,α=60°;对于刀刃状沟槽结构而言,最大减阻量可达9.9%左右,是减阻量最优的结构之一,且减阻量的大小随着沟槽厚度的增加而减小,耐用度不佳,最佳几何参数为:h/s=0.5。
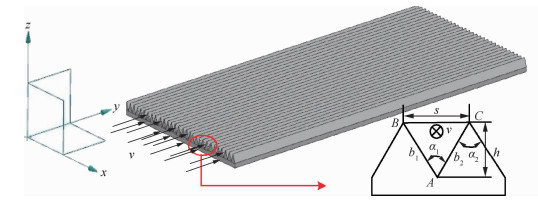
刀片型结构具有最佳减阻效果但容易失稳,在实际中锯齿结构因其具有几何稳定性而被广泛采用,其具体结构参数设计如图 2所示[19],其中α1为沟槽底角,α2为锯齿沟槽顶角,v为流体线速度,b1、b2为承载边受力长度,A、B、C为其中一个锯齿状三角形的3个顶点。类似于鲨鱼皮表面沟壑结构,承载面是试件在流体中直接接触并且承受力的一面,其二维截面正视图中对应的边为承载边,承载边的大小直接决定了承载面面积的大小,当流体中承载面的受力不变的情况下,增大承载边的长度可以增加承载面的面积,从而可以减轻承载面所受的压强,相应的可以减少微观锯齿状仿生表面的阻力。
如图 2所示,在ΔABC中,由三角形余弦定理以及面积公式可以得到b1、b2与s、h、α1之间的关系式为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}{b_1}{b_2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\alpha _1} = \frac{1}{2}sh}\\ {b_1^2 + b_2^2 - 2{b_1}{b_2}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\alpha _1} = {s^2}} \end{array}} \right. $ |
化简可得
| $ \left\{ {\begin{array}{*{20}{l}} {{b_1}{b_2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\alpha _1} - sh = 0}\\ {b_1^2 + b_2^2 - 2{b_1}{b_2}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\alpha _1} - {s^2} = 0} \end{array}} \right. $ |
可得承载边长度b1、b2由s、h、α1表达的关系式为
| $ \left\{ {\begin{array}{*{20}{l}} {{b_1} = [ sh{\kern 1pt} {\kern 1pt} {\rm{cot}}{\alpha _1} + 0.5{s^2} - 0.5s({s^2} + 4{h^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 4hs{\kern 1pt} {\rm{cot}}{\alpha _1}{)^{0.5}}{]^{0.5}}}\\ {{b_2} = sh{\kern 1pt} {\kern 1pt} {\rm{csc}}{\alpha _1}[ sh{\kern 1pt} {\kern 1pt} {\rm{csc}}{\alpha _1} + 0.5{s^2} - 0.5s \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{({s^2} - 4{h^2} + 4hs{\kern 1pt} {\rm{cot}}{\alpha _1})}^{0.5}}{]^{0.5}}} \end{array}} \right. $ |
通过调整参数s、h、α1的大小,可以对承载边b1、b2进行控制,从而对微观锯齿状仿生表面的减阻等性能进行调控。
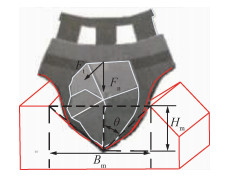
要实现上述特征表面的磨削,需要进一步探究单颗粒磨削的表面形成过程,在此基础上来研究微观仿生锯齿状表面砂带磨削的方法。在砂带磨削材料去除原理研究中,重庆大学黄云等在《现代砂带磨削技术及工程应用》一书中研究了单颗磨粒切刃切除材料的原理模型,分析了单颗磨粒切刃切除材料运动过程中的材料去除机理,如图 3所示,其中Ft为单颗磨粒切向力,Fn为单颗磨粒法向接触压力,2θ为磨粒锥顶角,Bm为与磨粒进给垂直方向最大宽度,Hm为磨痕断面最大谷底高度。
|
| 图 3 砂带磨削单颗粒模型 Fig. 3 Single particle model for belt grinding |
磨粒切刃在材料表面的平均最大磨痕断面面积为
| $ {A_{\rm{m}}}{(x)_{{\rm{max}}}} = \frac{1}{{\pi {\rm{tan}}{\kern 1pt} {\kern 1pt} \theta }}\left( {\frac{{3{F_{\rm{n}}}}}{{2mk{\kern 1pt} {\rm{HV}}}} - {A_{\rm{i}}}} \right) $ | (1) |
磨痕断面最大谷底高度为
| $ {H_{\rm{m}}} = \left( {\sqrt {\frac{{3{F_{\rm{n}}}}}{{2\pi mk{\kern 1pt} {\rm{HV}}}}} - \sqrt {\frac{{{A_{\rm{i}}}}}{\pi }} } \right){\rm{cot}}{\kern 1pt} {\kern 1pt} \theta $ | (2) |
又因为
| $ {B_{\rm{m}}} = \sqrt {\frac{{6{F_{\rm{n}}}}}{{\pi mk{\kern 1pt} {\rm{HV}}}}} $ | (3) |
将式(3)代入式(2)推出Hm与Bm的关系:
| $ {H_{\rm{m}}} = \left( {\frac{{{B_{\rm{m}}}}}{2} - \sqrt {\frac{{{A_{\rm{i}}}}}{\pi }} } \right){\rm{cot}}\theta $ | (4) |
式中:HV为材料的维氏硬度;k为磨粒与工件相互作用影响因子,通常取1.08;Ai为磨粒端部小平面面积;m为接触区切刃密度。
从式(2)可以看出,磨痕断面最大谷底高度Hm同Fn、m、HV有关。当被加工材料确定后,材料所对应的维氏硬度为一定值,Hm、Fn和m呈幂函数分布,Fn越大、m越小,得到的Hm也越大。从式(4)可以看出,最大谷底高度Hm和最大宽度Bm之间存在线性关系。
单颗粒砂带磨削材料去除机理已经充分地证明了砂带磨削可以有效的控制Hm和Bm,因此,采用砂带磨削达到了形成理想微观仿生锯齿状表面的条件。在试验中为了控制Hm和Bm的大小,形成微观仿生锯齿状表面,可以通过改变Fn、m、vp等工艺参数来实现,同时m与P呈反比例关系,故可以用P表示m。
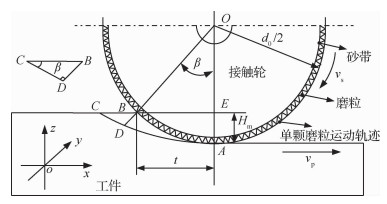
1.2 砂带磨削多颗粒磨削去除模型图 4中取磨削平面中垂直于磨具系统轴线的横剖面图进行分析,砂带以线速度vs绕着直径为d0的接触轮中心进行旋转,工件以线速度vp沿x轴方向做匀速进给运动。在运动经过时间t时,磨具系统中砂带由A点转动到B点,转动了β角,工件由C点运动到B点,此时在多颗粒共同作用下完成从接触工件到切削的整个过程,图中区域ABCD就是多颗磨粒共同作用去除的部分材料。
|
| 图 4 砂带磨削多颗粒切削运动示意图 Fig. 4 Schematic diagram of belt grinding movement of multi particles |
从多颗磨粒共同作用去除材料的整个过程中分析可得,去除材料的最大厚度为BD,同时在时间t内,参与切削的磨粒总数为
| $ {h_{\rm{c}}} = BD/(\widehat {AB}{\kern 1pt} {b_{\rm{c}}}m) $ | (5) |
由于磨削过程为微量切削,且切削时间t较小,故而将ΔBCD近似看成一个以角∠CDB为直角的直角三角形,由几何知识可得
| $ BD = BC{\kern 1pt} {\rm{sin}}{\kern 1pt} \beta $ |
由于砂带和工件在同一时间t内运动,故可以得:
又因为在直角三角形ΔOBE中,根据几何知识可得
| $ \begin{array}{*{20}{l}} {{\rm{cos}}\beta = OE/OB = ({d_0}/2 - {H_{\rm{m}}})/({d_0}/2) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({d_0} - 2{H_{\rm{m}}})/{d_0}} \end{array} $ |
由此,可以推出:
| $ {\rm{sin}}\beta = \sqrt {1 - {\rm{co}}{{\rm{s}}^2}\beta } = 2\sqrt {{H_{\rm{m}}}/{d_0} - H_{\rm{m}}^2/d_0^2} $ |
联系砂带磨削系统中实际情况,通常接触轮的直径d0远大于Hm,故Hm2/d02可近似忽略不计,所以得到
| $ {h_{\rm{c}}} = \frac{{2{v_{\rm{p}}}}}{{{v_{\rm{s}}}m{b_{\rm{c}}}}}\sqrt {{H_{\rm{m}}}/{d_0}} $ | (6) |
正如前文研究中的假设,在研究分析过程中忽略砂带的单颗粒磨损的影响,故由式(4)可得砂带中的单颗粒磨削沟槽最大深度为
| $ {H_{\rm{m}}} = \sqrt {\frac{{3{F_{\rm{n}}}}}{{2\pi mk{\kern 1pt} {\rm{HV}}}}} {\rm{cot}}\theta $ | (7) |
将式(7)代入式(6)可得砂带中单颗磨粒的最大切削深度为
| $ {h_{\rm{c}}} = {K_{\rm{c}}}{v_{\rm{p}}}v_{\rm{s}}^{ - 1}F_{\rm{n}}^{1/4} $ | (8) |
式中: Kc为单颗粒切削深度系数,由此可以看出,在砂带磨削磨具系统参数不变的情况下,砂带磨削中的hc与vp和Fn成正比,与vs成反比。其表达式为
| $ {K_{\rm{c}}} = {24^{1/4}}{\pi ^{ - 1/4}}b_{\rm{c}}^{ - 1}{m^{ - 5/4}}d_0^{ - 1/2}{k^{ - 1/4}}{\rm{H}}{{\rm{V}}^{ - 1/4}}{\rm{co}}{{\rm{t}}^{1/2}}\theta $ | (9) |
从式(9)可以看出,砂带中的单颗粒切削深度系数Kc与m、θ、k、bc、HV等有关。
为了研究砂带磨削参数化数学模型, 将hc作为微观仿生锯齿状表面的深度h;将Bm作为微观仿生锯齿状表面的宽度s;将2θ近似为微观仿生锯齿状表面的夹角α1;从而得到微观仿生锯齿状表面砂带磨削参数化计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {h = {h_{\rm{c}}} = {K_{\rm{c}}}{v_{\rm{p}}}v_{\rm{s}}^{ - 1}F_{\rm{n}}^{1/4}}\\ {{K_{\rm{c}}} = {{24}^{1/4}}{\pi ^{ - 1/4}}b_{\rm{c}}^{ - 1}{m^{ - 5/4}}d_0^{ - 1/2}{k^{ - 1/4}}{\rm{H}}{{\rm{V}}^{ - 1/4}}{\rm{co}}{{\rm{t}}^{1/2}}\theta }\\ {s = {B_{\rm{m}}} = \sqrt {\frac{{6{F_{\rm{n}}}}}{{\pi mk{\rm{HV}}}}} }\\ {{\alpha _1} = 2\theta } \end{array}} \right. $ | (10) |
从单颗粒磨削参数化数学模型中可以看出,砂带磨削形成微观仿生锯齿状表面沟槽的高度与工件进给速度、砂带旋转速度、磨削正压力以及磨具系统的固有参数等有关,微观仿生锯齿状沟槽的宽度与磨削正压力以及磨具系统的固有参数有关,其夹角主要与砂带磨粒的形状有关。
2 微观仿生锯齿状表面磨削规划及其实验 2.1 叶片微观仿生锯齿状表面砂带磨削方法为实现微观仿生锯齿状表面的磨削,设计了如图 5所示的砂带磨削运动方案。数控磨床通过接触杆控制接触轮并使之紧贴砂带与工件表面接触而产生力Fn,同时磨床主轴带动砂带的高速旋转而与工件表面产生力Ft,在力Fn与力Ft共同作用下实现砂带的磨削过程。

|
| 图 5 微观仿生锯齿状表面砂带磨削方法 Fig. 5 Micro bionic zigzag surface using belt grinding method |
其磨削运动形式主要是接触杆带动磨头以恒定进给速度vp、进给步距P在试件表面沿着Y轴方向做周期为T的往复运动,运动距离为试件长度L,与此同时砂带主轴以线速度vs旋转,并通过接触杆对试件表面施加恒定接触力F,保证砂带可以与试件表面有效的贴合,从而进行材料有效地去除。通过施加在接触杆/轮上的力F带动砂带冲击式的磨削运动,实现砂带微切削快速累积运动,既快速去除余量又能保证粗糙度,使铣削残差层得以高效的去除,同时在表面形成微观仿生锯齿状。
如图 5所示,试件在运动过程中,受接触杆作用,由式(10)可以得出,微观仿生锯齿状沟槽的高度h同力Fn呈幂函数分布。为计算方便,本试验选择了φ=90°(即,砂带和接触杆/轮垂直方向施加力于试件表面)进行后续砂带磨削试验。
在砂带磨削过程中,磨头进给循环周期T由3部分时间组成:①磨头在试件长度方向来回直线进给运动时间;②磨头抬起落下的缓冲时间;③试件进给步距P的时间,故T可计算得:
| $ \left\{ {\begin{array}{*{20}{l}} {T = {t_1} + {t_2} + {t_3}}\\ {{t_1} = \frac{{2L}}{{{v_{\rm{p}}}}},{t_2} = \frac{{2{h_1}}}{{{v_{\rm{步}}}}},{t_3} = \frac{P}{{{v_{\rm{步}}}}}} \end{array}} \right. $ | (11) |
式中:L为试件长度;h1为磨头抬离工件表面高度;v步为机床步进电机进给线速度。
2.2 实验装置及其方法选用某型号航空发动机压气机钛合金叶片进行微观仿生锯齿状表面砂带磨削实验验证,实验采用由重庆三磨海达磨床有限公司和重庆大学共同研制的七轴六联动自适应数控砂带磨床作为加工磨床,磨床具体结构如图 6所示。

|
| 图 6 MGY5540A-7NC数控砂带磨床 Fig. 6 MGY5540A-7NC CNC belt grinding machine |
由于砂带磨削过程中接触轮本身具有的弱刚性及磨床U轴在Z轴方向上具有一定范围内的弹性运动,使得该磨床在对叶片等复杂曲面加工过程中具有一定的“柔性”特征。该砂带磨床的核心是具有补偿功能的数控砂带磨具系统,该磨具系统主要由砂带、接触轮、接触杆等组成。磨具系统与叶片的接触为浮动接触,磨头的微小位移不会给叶片带来大幅度磨削压力的改变。该数控砂带磨床不仅可以使砂带和叶片进行有效的贴合,而且还可以最大程度地避免磨削过程中过切和过磨现象的产生。
本文对单颗粒模型磨削参数的分析验证了微观仿生锯齿状表面磨削的可行性;然后通过单颗粒模型计算了实际多颗粒砂带理论上磨削的可行性和推导了微观仿生锯齿状表面参数的理论计算公式;最后进行相关的试验,检测所加工出来的微观仿生锯齿状表面参数,与理论计算出来的沟槽宽度s、沟槽高度h和实际的磨粒夹角α1进行分析验证,具体如图 7所示。
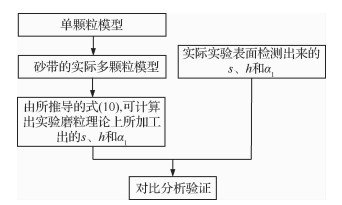
|
| 图 7 研究思路流程 Fig. 7 Chart of research idea |
图 8为砂带磨削微观仿生锯齿状表面示意图。结合实际的航发钛合金叶片表面粗糙度要求[1],拟加工表面参数选定为s=5~10 μm,h= 5~10 μm和α1=60°[20]。由此可以推出砂带磨粒大小应在50~100 μm之间,根据厂商粒度型号的分类,选用粒度号为P240的磨粒(其磨粒大小为60 μm)。使用3M陶瓷氧化铝XK870F粒度号为P240和金字塔237AA粒度号为P240的砂带,并采用表 1的工艺参数来进行磨削实验验证。砂带磨削素有“冷态磨削”之称,故本次实验磨削条件为干磨。

|
| 图 8 砂带磨削微观仿生锯齿状表面示意图 Fig. 8 Schematic diagram of micro bionic zigzag surface using belt grinding |
| 磨削 区域 |
磨削压力 /N |
进给速度 /(m·s-1) |
砂带线速 度/(m·s-1) |
进给步距 /mm |
| 型面 | 10 | 0.005 | 10 | 0.40 |
为了更直观有效地反映砂带磨削后的微观仿生锯齿状表面结构参数,采用扫描电子显微镜SEM和形状测量激光显微镜VKL-X1000分别拍摄试件表面的二维和三维形貌,同时,结合三维模型重构理论中的曲面拟合方法对试件拍摄后的微观仿生锯齿状三维形貌结构参数进行数据采集,来分析表面形貌的参数。
二维形貌是对试件表面分布状态以及形态的一种直观性表达,可以通过扫描电子显微镜拍摄图片后进行观察。对陶瓷氧化铝砂带磨削后的表面进行后期的分析处理,得到砂带磨削后微观仿生锯齿状表面SEM二维形貌,如图 9所示。从图 9中可以直观地看出表面结构分布较均匀,锯齿形沟槽结构,且测得图形中沟槽宽度在5.5 μm左右。

|
| 图 9 磨削后微观仿生锯齿状SEM二维形貌表面 Fig. 9 SEM of two-dimensional morphology of micro bionic zigzag surface after belt grinding |
三维形貌是对试件表面微观仿生锯齿状结构分布状态以及形态的一种直观性表达,可以通过形状测量激光显微镜VKL-X1000拍摄图片后进行观察。分别对试件磨削前后的表面三维形貌图进行后期的分析处理,结果如图 10和图 11所示,对比试件磨削前后三维形貌表面,可以看出磨削之后的表面减少了表面凸凹不平和表面烧伤等缺陷,表面质量得到了提高。
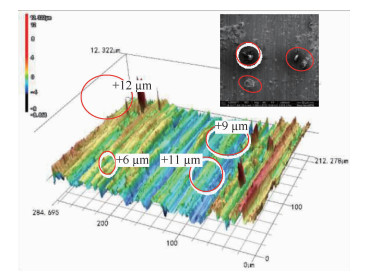
|
| 图 10 砂带磨削前表面微观三维图 Fig. 10 Three-dimensional morphology surface before belt grinding |
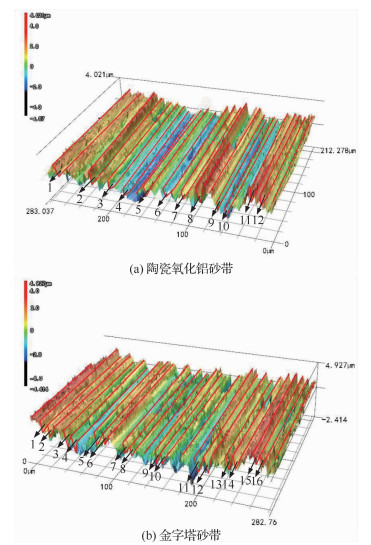
|
| 图 11 砂带磨削后微观仿生锯齿状表面三维图 Fig. 11 Three dimensional morphology of micro bionic zigzag surface after belt grinding |
将图 11中用序号标出的沟槽进行参数测量分析对比,用1.2节中式(10)算出的理论微观仿生锯齿状表面沟槽宽度s、沟槽高度h和实际的磨粒夹角α1与实际测得的参数进行对比,得到图 12。
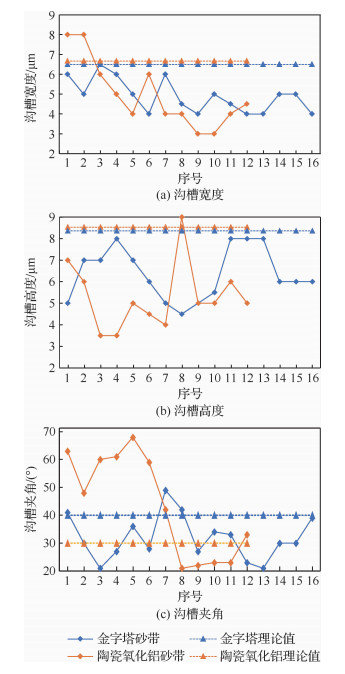
|
| 图 12 两种砂带磨削表面参数对比 Fig. 12 Comparison of surface processed by two kinds of belt grinding parameters |
由图 12(a)和图 12(b)对比发现,实际的沟槽宽度s和沟槽高度h都明显小于理论值,这是由于叶片的弱刚性和接触轮的弹性所造成的。在磨削过程中,叶片由于受磨削力的影响,在磨削时会产生一定的弯曲变形,接触轮在接触叶片磨削的区域也会产生弹性变形,使得实际磨粒磨削的去除材料深度比理论的小,从而磨削所产生的表面尺寸实际值比理论值小;并且在磨削过程中存在着磨粒的磨损现象,使得磨粒变小,进一步影响了实际磨削产生的微观仿生锯齿状表面尺寸。磨粒的磨损主要是由于磨粒的切削刃被磨平或者断裂,使得h与理论值的差距比s与理论值的差距大。由图 12(a)和图 12(b)还可以看出,金字塔砂带磨削出来的沟槽宽度s和沟槽高度h总体上比陶瓷氧化铝小,这是由于金字塔砂带有着独特的金字塔结构,氧化铝/碳化硅矿砂,树脂胶,表面加有助磨剂,使得金字砂带的磨粒磨损比陶瓷氧化铝砂带小,实际磨削效果更好。
对于沟槽夹角α1,由于在砂带磨削过程中的磨粒磨损和磨粒大小的不均匀性,使得沟槽夹角有明显的波动,且陶瓷氧化铝相对于理论值的波动性更大。明显的用金字塔砂带磨削出来的微观仿生锯齿状表面沟槽夹角α1更小而且沟槽宽度、高度和夹角一致性更好,磨削表面线路更细致均匀,如图 13所示,这是由于金字塔砂带的磨粒分布和大小更均匀,说明了微观仿生锯齿状表面的参数与砂带磨粒分布和大小有相关性。

|
| 图 13 两种砂带形貌示意图 Fig. 13 Schematic diagram of morphology of two kinds of belts |
砂带磨削后的微观仿生锯齿状表面主要以锯齿形沟槽为主,其中沟槽的宽度在2.5 ~8 μm之间,平均值为4.91 μm;沟槽的高度在3.5~9 μm之间,平均值为5.91 μm;沟槽的夹角在28°~68°之间,平均值为42.3°。
4 结论1) 对微观仿生表面典型结构进行了分析,提出了将锯齿形沟槽结构作为叶片的微观仿生锯齿状表面。通过对单颗粒的砂带磨削去除机理的研究,建立了砂带磨削多颗粒参数化数学模型。最后,搭建了以钛合金为典型材料的微观仿生锯齿状表面砂带磨削基础实验平台。
2) 通过砂带磨削方法实现了微观仿生锯齿状表面的形成;砂带磨削后的叶片表面减少了凸凹不平和烧伤等缺陷,表面质量得到了提高;砂带表面磨粒分布情况能影响微观仿生锯齿状表面沟槽形成的大小和均匀性。对砂带磨削后的叶片表面进行检测,结果表明通过砂带磨削方法实现的微观仿生锯齿状表面以锯齿形沟槽为主。
| [1] |
丁文锋, 奚欣欣, 占京华, 等. 航空发动机钛材料磨削技术研究现状及展望[J]. 航空学报, 2019, 40(6): 022763. DING W F, XI X X, ZHAN J H, et al. Research status and future development of grinding technology of titanium materials for aero-engine[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(6): 022763. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [2] |
马付良, 曾志翔, 高义民, 等. 仿生表面减阻的研究现状与进展[J]. 中国表面工程, 2016, 29(1): 7-15. MA F L, ZENG Z X, GAO Y M, et al. Research status and progress of bionic surface drag reduction[J]. China Surface Engineering, 2016, 29(1): 7-15. (in Chinese) |
| Cited By in Cnki (36) | Click to display the text | |
| [3] | XIE J, XIE H F, LIU X R, et al. Dry micro-grooving on Si wafer using a coarse diamond grinding[J]. International Journal of Machine Tools and Manufacture, 2012, 61: 1-8. |
| Click to display the text | |
| [4] | ZHANG S J, ZHOU Y P, ZHANG H J, et al. Advances in ultra-precision machining of micro-structured functional surfaces and their typical applications[J]. International Journal of Machine Tools and Manufacture, 2019, 142: 16-41. |
| Click to display the text | |
| [5] | DENKENA B, KOEHLER J, WANG B. Manufacturing of functional riblet structure by profile grinding[J]. CIRP Journal of Manufacturing Science and Technology, 2010, 9(3): 14-26. |
| Click to display the text | |
| [6] | BRINKSMEIER E, SCHÖNEMANN L. Generation of discontinuous microstructures by diamond micro chiseling[J]. CIRP Annals-Manufacturing Technology, 2014, 63(1): 49-52. |
| Click to display the text | |
| [7] |
高航, 李世宠, 付有志, 等. 金属增材制造格栅零件磨粒流抛光[J]. 航空学报, 2017, 38(10): 421210. GAO H, LI S C, FU Y Z, et al. Abrasive flow machining of additive manufactured metal grilling parts[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 421210. (in Chinese) |
| Cited By in Cnki (22) | Click to display the text | |
| [8] |
高航, 吴鸣宇, 付有志, 等. 流体磨料光整加工理论与技术的发展[J]. 机械工程学报, 2015, 51(7): 174-187. GAO H, WU M Y, FU Y Z, et al. Development of theory and technology in fluid abrasive fining technology[J]. Journal of Mechanical Engineering, 2015, 51(7): 174-178. (in Chinese) |
| Cited By in Cnki (55) | Click to display the text | |
| [9] | WANG W, YUN C. A path planning method for robotic belt surface grinding[J]. Chinese Journal of Aeronautics, 2011, 24(4): 520-526. |
| Click to display the text | |
| [10] |
黄云, 肖贵坚, 邹莱. 整体叶盘抛光技术的研究现状及发展趋势[J]. 航空学报, 2016, 37(7): 2045-2064. HUANG Y, XIAO G J, ZOU L. Current situation and development trend of polishing technology for blisk[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2045-2064. (in Chinese) |
| Cited By in Cnki (36) | Click to display the text | |
| [11] | ECKART U, FLORIAN H. Improving efficiency in robot assisted belt grinding of high performance materials[J]. Advanced Materials Research, 2014, 907: 139-149. |
| Click to display the text | |
| [12] | ECKART U, FLORIAN H, MARCEL M, et al. Applicability of industrial robots for machining and repair processes[J]. Procedia CIRP, 2013, 11: 234-238. |
| Click to display the text | |
| [13] | XU X H, ZHU D H, ZHANG H Y, et al. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2368-2382. |
| Click to display the text | |
| [14] |
张雷, 周宛松, 卢磊, 等. 抛光力实时控制策略研究[J]. 东北大学学报(自然科学版), 2015, 36(6): 853-857. ZHANG L, ZHOU W S, LU L, et al. Research on real-time control strategies of polishing force[J]. Journal of Northeastern University (Nature Science), 2015, 36(6): 853-857. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [15] |
肖贵坚, 黄云, 尹浩. 面向型面精度一致性的整体叶盘砂带磨削新方法及实验研究[J]. 航空学报, 2016, 37(5): 1666-1676. XIAO G J, HUANG Y, YIN H. Experimental research of new belt grinding method for consistency of blisk profile and surface precision[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1666-1676. (in Chinese) |
| Cited By in Cnki (18) | Click to display the text | |
| [16] | XIAO G J, HUANG Y. Equivalent self-adaptive belt grinding for the real-R edge of an aero-engine precision-forged blade[J]. The International Journal of Advanced Manufacturing Technology, 2016, 83(9-12): 1697-1706. |
| Click to display the text | |
| [17] |
蔺小军, 杨艳, 吴广, 等. 面向叶片型面的五轴联动柔性数控砂带抛光技术[J]. 航空学报, 2015, 36(6): 2074-2082. LIN X J, YANG Y, WU G, et al. Flexible polishing technology of five-axis NC abrasive belt for blade surface[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 2074-2082. (in Chinese) |
| Cited By in Cnki (25) | Click to display the text | |
| [18] | BECHERT D W, BRUSE M, HAGE W, et al. Experiments on drag reducing surfaces and their optimization with an adjustable geometry[J]. Journal of Fluid Mechanics, 1997, 338: 59-87. |
| Click to display the text | |
| [19] | XIAO G J, HE Y, HUANG Y, et al. Shark-skin-inspired micro-riblets forming mechanism of TC17 titanium alloy with belt grinding[J]. IEEE Access, 2019, 7(1): 107636-107648. |
| Click to display the text | |
| [20] | CLAUDIA C B, SCHULZ U. Shark skin inspired riblet structures as aerodynamically optimized high temperature coatings for blades of aeroengines[J]. Smart Materials & Structures, 2011, 20(9): 094016. |