2. 西北工业大学 航空学院, 西安 710072;
3. 中国空气动力研究与发展中心, 绵阳 621000;
4. 中国飞机强度研究所, 西安 710065
2. School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China;
3. China Aerodynamics Research and Development Center, Mianyang 621000, China;
4. China Aircraft Strength Research Institute, Xi'an 710065, China
大迎角(Angle of Attack, AoA)机动飞行能够迅速改变飞机的速度矢量与机头指向、抢占有利的攻击位置、并率先发动攻击。同时还能将自己飞机的位置始终处于对手转弯半径的内侧,可有效规避敌方武器系统的攻击、形成战术上的绝对优势。采用鸭翼前置与全动V型双垂尾布局的气动设计方案,可充分实现其良好的大迎角机动可控飞行,可充分发挥新一代战斗机的超机动性等先进战技指标。因此,在中国先进战斗机研制的双垂尾结构设计中,充分利用了这种先进设计方案对飞机整体性能带来的优势。
在大迎角飞行时,飞机前机身高强度的脱体涡破裂会导致后机身V型全动垂尾发生严重的抖振[1-2]。V尾抖振不仅会大幅降低结构的疲劳寿命,使结构过早产生疲劳裂纹甚至断裂破坏,增加飞机的维护成本,降低机群的出勤率,还会严重影响飞机的飞行控制性能和飞行品质,并造成仪表显示判读困难,武器火控系统的瞄准、跟踪和射击精度严重降低,限制了飞机的机动飞行包线,降低了新一代战斗机超机动性能的发挥。更有甚者,严酷的抖振环境还可能导致机载设备功能失效,使飞机失去控制,造成飞机失事。因此,在中国先进战斗机结构平台设计中,能否解决好大迎角机动飞行导致的V尾抖振问题,将对新一代战斗机先进战技性能的发挥、提高V尾结构的抗振动疲劳寿命以及降低飞机的结构维护成本产生严重的影响。
美国在第三、第四代先进战斗机的研制过程中都普遍遭遇到了不同程度的V尾抖振问题,如美国的F-18A/B型战斗机在服役不久(不足3个月),就发现在数次大迎角飞行后,V尾根部结构产生了疲劳裂纹,究其原因是由于V尾抖振引起的[3]。
在美国F-35验证机的大迎角试飞中,当迎角达到18°,马赫数0.75时,尾翼产生了严重的抖振,过载达到了极限载荷条件,不得已结束了该次机动飞行。从最近美国国防部公开的资料显示,V尾抖振仍然是困扰F-35飞机设计定型的5个重要遗留问题之一,在很长一段时间内都不能进行迎角≥20°的飞行验证[4]。在美国F/A-22飞机研制过程中也花费了大量的人力、物力和财力来研究解决翼面抖振动强度设计和振动/声疲劳问题[5]。
直到2012年,美国还在对F-15、F/A-18E/F、F-35、F/A-22飞机的V尾抖振问题继续开展深入的研究。从美国近年来公开发表的技术文献看,对V尾抖振问题的研究除了涉及大迎角飞行时前机身脱体涡破裂引发抖振的机理研究外,他们还重点开展了对尾翼抖振响应预计与计算流体力学(Computational Fluid Dynamics, CFD)仿真分析方法、抖振动态载荷风洞试验测试与飞行试验的相关性分析技术、V尾抖振响应减缓的自适应主动控制方法以及翼面抖振动强度、疲劳强度分析与试验验证方法的系统深入研究。
纵观中国在尾翼结构抖振动强度设计与试验研究方面所开展的工作,由于中国自主研制的全动V尾布局先进战斗机、无人机起步较晚,基础研究相对薄弱,因而对V尾抖振问题的发生机理、抖振风洞试验方法以及V尾结构抖振动强度设计分析方法与动态疲劳试验验证方法等关键技术的研究,都缺乏充分的技术储备,与美国等航空技术先进国家相比还有较大的差距。因此,如何建立先进有效的技术手段解决好高性能战斗机在大迎角机动飞行时V尾结构的抖振问题,将是中国先进战斗机V尾结构动强度设计中不可回避的重大技术难题,也将关系到新一代战斗机先进战技性能的发挥。本项目研究工作就是针对这一工程应用背景而开展的。
1 全动V尾抖振风洞试验“刚性/弹性”组合模型的风洞试验方法V尾布局先进战斗机在做大迎角机动飞行时,尤其是在跨声速区进行盘旋和收敛转弯机动时,前机身分离的脱体涡破裂后打到V尾上会导致V尾发生严重的抖振。破裂的高强度脱体涡包含有各种尺度的非线性混合涡流,频率成份复杂,采用数值仿真方法获得抖振载荷的时间周期较长,在型号的初步设计阶段,完成V尾抖振动强度分析所需要的翼面加速度响应和脉动压力动态载荷主要依靠风洞试验获取。对于高机动性先进战斗机其飞行包线远远超出抖振起始边界,抖振风洞试验中需要弄清在这些飞行状态下V尾结构的抖振动响应与动态载荷。在V尾布局抖振模型风洞试验中,通常将一侧V尾模型设计成刚性模型,在其翼面两侧布置成对的贴片式脉动压力传感器测量时域脉动压力差,再转换到飞机尺度作为V尾结构动强度计算的动态载荷输入。而另一侧V尾模型则设计成动力相似(或结构相似)的弹性模型。弹性模型可以在风洞试验中直观地反映翼面抖振响应随迎角、速压的变化趋势,直接验证抖振响应减缓控制措施的效果,测量的动响应和V尾根部弯矩、扭矩等动态载荷还能够直接按照相似比例尺转换得到飞机尺度结构的动响应量值以及动态内力载荷[3]。因此,在型号研制中,分别进行了全机低速与跨声速的V尾“刚性/弹性”组合模型的抖振风洞试验,给出了把抖振风洞试验动态测试结果向飞机尺度进行相似转换的原理与方法,主要研究工作体现在以下几个方面。
1.1 V尾弹性/刚性抖振模型风洞试验结果向飞机尺度相似转换的原理与方法全机状态V尾抖振风洞试验是获取大迎角机动飞行时前机身脱体涡破裂后在双V尾翼面分布的非定常脉动压力载荷特征与频谱特性最直接有效的方法。与常规的定常气动力测压模型以及颤振模型设计与试验方法不同,前者是采用全刚性模型进行试验,测压结果可以用气流参数的无量纲化处理方法向飞机尺度转换,不涉及动态载荷的频谱特性转换;后者是采用全机弹性动力相似模型进行试验,试验测试结果、特别是结构响应的频率特性是按照结构动力学分析方法获得向飞机尺度相似转换的公式。而全机状态抖振风洞试验模型需要使用刚性V尾模型(左侧)和弹性动力相似V尾模型(右侧)的组合模型进行试验(见图 1),首先需要理论推导出在同一风洞试验流场条件下测量的破裂脱体涡流场激励频率与弹性V尾结构响应频率是否协调统一,才能够按照动力相似的弹性模型设计方法,设计抖振风洞试验模型并用于试验,建立把试验动态测试结果(非定常气动力/结构响应)向飞机尺度协调匹配的相似转换关系,得出用于飞机V尾结构抖振动强度分析的动载荷输入条件。
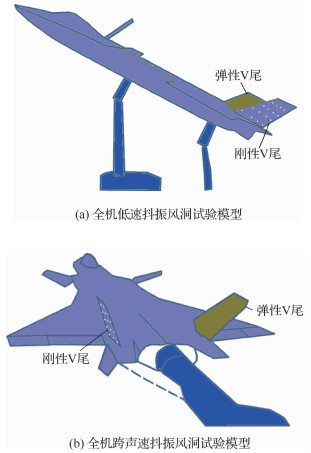
|
| 图 1 全机状态V尾抖振风洞试验(刚/弹)组合模型 Fig. 1 Complete aircraft V-tail buffet (rigid/ elastic) hybrid model for wind tunnel test |
通过分析国外相关技术文献,动态流场参数的相似转换准则是按照“斯特劳哈尔数(减缩频率)”相等原理。对于引起V尾抖振的前机身脱体涡破裂形成的非定常流场脉动压力,通过理论分析确认,在刚性V尾模型上测量的脉动压力主导频率可以按照颤振风洞试验与计算分析中使用的“减缩频率”相等的原则进行换算[6],即
| $ {{\eta _{\rm{m}}} = \frac{{{\omega _{\rm{m}}}{L_{\rm{m}}}}}{{{V_{\rm{m}}}}} = \frac{{{\omega _{\rm{a}}}{L_{\rm{a}}}}}{{{V_{\rm{a}}}}} = {\eta _{\rm{a}}}} $ | (1) |
| $ {{K_\omega } = \frac{1}{{{K_L}}} \cdot \frac{{{V_{\rm{m}}}}}{{{V_{\rm{a}}}}} = \frac{1}{{{K_L}}}{{({K_q}/{K_\rho })}^{\frac{1}{2}}}} $ | (2) |
式中:ηm、ωm、Lm、Vm分别为模型尺度的减缩频率、圆频率、特征长度、风洞的风速;ηa、ωa、La、Va分别为飞机尺度的减缩频率、圆频率、特征长度、飞行速度;Kω、Kq、Kρ、KL分别为频率、速压、密度和长度比例尺。
按照量纲分析原理推导的弹性V尾模型频率比例尺为
| $ {{K_\omega } = \frac{{{{({K_q}/{K_\rho })}^{\frac{1}{2}}}}}{{{K_L}}}} $ | (3) |
它反映了模型V尾的前几阶固有频率与飞机V尾固有频率的相似比例关系。由式(2)和式(3)可以看出,在同一风洞试验流场中,刚性V尾模型测量的非定常流激励频率与弹性模型的结构响应频率转换比例尺是协调一致的。在此基础上进一步推导出了抖振风洞试验测量的脉动压力与结构响应向飞机尺度的相似转换关系及比例尺为
频率:$f_{\mathrm{ia}}=\frac{L_{\mathrm{m}} V_{\mathrm{a}}}{L_{\mathrm{a}} V_{\mathrm{m}}} f_{\mathrm{im}}$
时间:$t_{\mathrm{a}}=\frac{V_{\mathrm{m}} L_{\mathrm{a}}}{L_{\mathrm{m}} V_{\mathrm{a}}} t_{\mathrm{m}}$
功率谱密度:
| $ {{\varphi _{\rm{a}}} = {{({L_{\rm{a}}}/{L_{\rm{m}}})}^4}{{({\rho _{\rm{a}}}/{\rho _{\rm{m}}})}^2}{{({V_{\rm{a}}}/{V_{\rm{m}}})}^3}{\varphi _{\rm{m}}}} $ |
脉动压力均方根值:KCR=(KmKω2)/KL=Kq
脉动压力功率谱密度:
| $ {{K_{{\rm{CP}}}} = (K_{\rm{m}}^2K_\omega ^3)/K_L^2 = {K_L}{{({K_\rho }K_q^3)}^{1/2}}} $ |
加速度均方根值:Kar=KLKω2=Kq/(KρKL)
加速度功率谱密度:
| $ {{K_{{\rm{ap}}}} = K_L^2K_\omega ^3 = {{({K_q}/{K_\rho })}^{3/2}}/{K_L}} $ |
弯/扭矩均方根值:KMR=KL2KmKω2=KL3Kq
弯/扭矩功率谱密度:
| $ {{K_{{\rm{MP}}}} = K_L^4K_{\rm{m}}^2K_\omega ^3 = K_L^7K_\rho ^{1/2}K_q^{3/2}} $ |
式中:Km、KCR、KCP、Kar、Kap、KMR、KMP分别为质量、脉动压力均方值、脉动压力功率谱密度、加速度均方值、加速度功率谱密度、弯/扭矩均方值、弯/扭矩功率谱密度的相似转换比例尺。fia、ta、φa为飞机尺度的频率、时间及功率谱密度函数,fim、tm、φm分别为模型尺度的频率、时间及功率谱密度函数。
1.2 低速、高速抖振风洞试验V尾翼面脉动压力相关性分析全机低速抖振风洞试验在8 m×6 m低速风洞进行(模型示意图见图 1(a)),全机高速抖振风洞试验在2.4 m×2.4 m跨声速风洞完成(模型示意图见图 1(b))。
为获取左侧刚性V尾内、外侧表面的脉动压力分布规律,根据V尾翼面压力梯度沿展向及弦向的变化情况,把翼面分成若干个区域。在V尾翼面内、外侧表面对应的每个小块面积上成对布置脉动压力传感器(见图 2和图 3)用以测量翼面的脉动压力差。利用右侧弹性V尾模型可测得V尾翼尖抖振加速度响应时间历程(见图 3)。
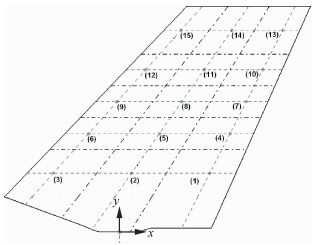
|
| 图 2 V尾翼面脉动压力传感器布置 Fig. 2 Locations of V-tail fluctuating pressure transducers |

|
| 图 3 抖振风洞试验刚/弹性V尾模型的数据测量 Fig. 3 Data measurement of rigid/elastic V-tail model in buffet wind tunnel test |
把低、高速风洞试验典型状态测量的脉动压力频谱与幅值按照相似比例尺转换到某飞行高度的飞机尺度进行比较(见图 4)可以看到:①主导频率分布基本一致;②脉动压力幅值分布也基本相似,低速试验与高速试验相比,转换的压力幅值偏高,试验结果偏保守。

|
| 图 4 低速、高速风洞试验结果比较 Fig. 4 Comparison between low and high speed wind tunnel test results |
对比其他状态的试验结果,都呈现出类似的规律,这里不再赘述。由此可见,按照相似变换原理,用低速试验结果预测高亚声速状态V尾翼面脉动压力特性是可行的。
通过模型抖振风洞试验,根据获得的弹性V尾翼尖加速度响应随迎角变化曲线(见图 5),可准确预计出垂尾抖振起始边界,从而理清脱体涡破裂形成的非定常分离流的激励频率与结构响应频率的关系,并获得了V尾翼面的脉动压力动态载荷分布(见图 6)(图中CH1~CH15为测试通道),得到了V尾翼尖加速度响应随迎角与马赫数的变化规律。试验结果应用于指导飞机V尾及支持结构的刚度设计,使V尾结构的固有频率避开在大迎角飞行时脱体涡破裂形成的非定常分离流激励的主导频率,达到降低V尾抖振结构响应、提高结构抗振动疲劳性能的动强度设计目的。V尾翼尖加速度响应转换到飞机尺度,用于指导飞机大迎角试飞。

|
| 图 5 全机状态V尾(刚/弹)组合模型抖振风洞试验结果 Fig. 5 Buffet wind tunnel test results of complete aircraft V-tail (rigid/ elastic) hybrid model |
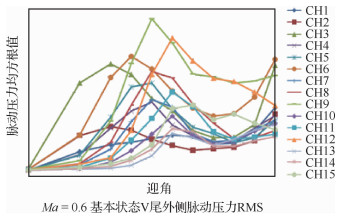
|
| 图 6 V尾翼面内、外侧脉动压力分布随迎角变化 Fig. 6 Pressure distribution vs angle of attack at inside and outside of V-tail |
基于计算流体力学/计算结构动力学(CFD/CSD)耦合求解技术的V尾抖振响应计算方法与颤振CFD/CSD计算方法有很大的不同,在颤振CFD翼面响应计算中,非定常气动力计算只需要考虑翼面运动产生的非定常气动力,也就是翼面近壁的流场特性,不需要提供远场分离流脱体涡的流场信息,湍流模型采用基于雷诺平均(Reynolds Average Navier-Stockes,RANS)模式就可以得到较为满意的计算结果。而在V尾抖振响应CFD计算中,不仅需要求解翼面近壁的小尺度湍流,更需要准确地描述前机身脱体涡破裂后产生的非定常空间流场结构。若采用基于传统涡黏性假设的RANS湍流模型来预计翼面抖振的空间三维复杂非定常流动,由于RANS湍流模型模化了大部分的湍流结构,得到偏大的湍流黏性系数抑制了非定常涡的发展,无法准确地对分离流场进行细致地刻画,它只对工程中计算翼面近壁湍流较为适用[7]。而大涡模拟方法(Large Eddy Simulation,LES)是通过求解滤波后Navier-Stoke方程,它只模化了亚格子尺度小涡,相比RANS模式,LES方法能精确求解大范围的气流分离和不稳定流动,因此LES方法在很大程度上解决RANS方法对远场分离流动模拟能力的不足问题,但同时LES方法在计算近壁湍流时也存在需要进行壁函数修正、鲁棒性较高的壁函数很难获得、壁面湍流计算网格太大等问题,因此LES并不适合用来计算工程壁面湍流。为了克服LES和RANS各自的缺点,解决V尾抖振CFD/CSD耦合求解中对空间分离流场与翼面近壁的非定常气动力都需要准确数值模拟的计算难点,研究应用了基于RANS/LES混合算法(也称为DES(Detached Eddy Simulation)混合算法)求解大迎角飞行时的远场与近壁非定常气动力高精度数值计算方法[8]。RANS/LES方法其本质是采用LES方法预测复杂流场中的大范围分离流动,而在壁面边界层内部采用RANS方法计算近壁湍流。通过理论推导,在剪切应力输运(Shear Stress Transport,SST)湍流模式基础上构造了适用于大迎角分离流场精确计算的控制方程和数值计算方法,该控制方程在壁面区域表现出RANS方程的性能,而在流动大分离区域则表现出LES方程的性能。应用所开发的高精度数值计算方法对先进战斗机飞机1:10跨声速风洞试验模型进行了典型大迎角试验状态的计算分析(见图 7)。
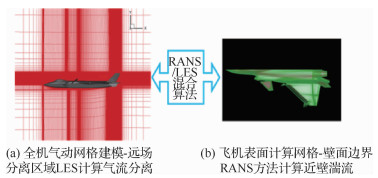
|
| 图 7 RANS/LES混合算法气动模型 Fig. 7 RANS/LES hybrid algorithm aerodynamic model |
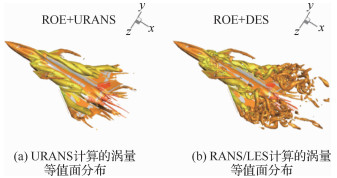
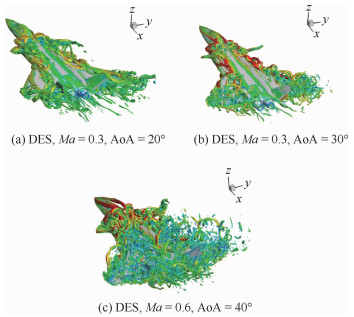
从计算结果对比可以看到(见图 8),采用非定常雷诺平均Navior-Stokes(Unsteady Reynolds Average Navier-Stokes, URANS)方程计算方法只能得到大尺度的涡结构,在V尾翼面附近对非定常涡流的捕获能力较差,而采用RANS/LES算法不论在前、中机身还是V尾翼面近壁都可以得到丰富的涡结构。图 9为用RANS/LES算法得到的模型飞机在不同迎角状态下脱体涡流场空间分布。
|
| 图 8 URANS与RANS/LES计算结果对比 Fig. 8 Compare of URANS and RANS/LES results (Ma=0.3、迎角30°) (Ma=0.3, angle of attack 30°) |
|
| 图 9 不同迎角状态下脱体涡流场空间分布 Fig. 9 Detached vortex flow field spatial distribution with different angle of attack |
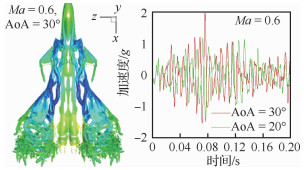
要把通过RANS/LES混合算法计算出的V尾远场与近壁非定常气动力与结构运动方程联合求解来获取翼面结构的抖振响应仍需解决许多关键技术难点。与翼面颤振响应CFD/CSD求解方法相比,V尾抖振响应是多模态耦合振动位移的叠加,具有翼面振动位移大和非定常流场激励频带宽的特性。颤振时域计算只需要分别对某个模态坐标计算到广义位移发散即可得到颤振点,计算过程中翼面的位移相对较小,动态网格的更新与变形相对容易。针对翼面抖振响应位移变形大、非定常流场激励频带宽、结构位移多模态耦合等特点,通过改进RANS/LES非定常气动力计算的时间推进精度,对气动与结构耦合求解方程的内部迭代算法进行优化设计,并采用混合背景网格映射的动态网格变形技术对翼面大变形后流场计算网格进行变形更新[9],建立了基于RANS/LES混合算法的V尾抖振响应CFD/CSD高效高精度计算方法与流程(见图 10),并通过先进战斗机跨声速风洞试验模型的计算与风洞试验结果对比证明(见表 1),计算精度较RANS算法有大幅提高。使用该算法能够计算分析大迎角飞行时前机身脱体涡的生成、演化规律与涡流轨迹,优化垂尾展向位置设计,避免与分离流场的主涡线轨迹重合,同时可以计算得到V尾结构的抖振响应,以减少风洞试验次数(见图 11)。

|
| 图 10 V尾抖振响应CFD/CSD高效高精度计算方法与流程 Fig. 10 CFD/CSD efficient and high precision calculation method and flowchart for V-tail buffet response |
| 马赫数 | 迎角/(°) | 翼尖后缘加速度响应均方根值误差/% |
| 0.6 | 20 | -4.7 |
| 0.8 | 20 | -5.2 |
| 0.3 | 30 | 3.4 |
| 0.6 | 30 | -6.3 |
|
| 图 11 V尾翼尖广义坐标下的加速度响应 Fig. 11 Acceleration response of V-tail in generalized coordinates |
在对V尾抖振风洞试验模型的抖振响应压电控制系统设计过程中,最初选择了线性二次最优(Linear Quadratic Regulator, LQR)控制方法。但在进行垂尾模型地面控制模拟试验时发现,用LQR控制方法存在以下问题:①由于LQR控制是一种全维状态反馈控制,这种类型的控制器以全维状态变量作为反馈信号,在实际试验时需要同时测量所有的状态反馈量,而实际中无法实现对所需的全维状态量的观测。该方法只对固定频率的激励信号具有较好的控制性能,但对于像V尾抖振这样的宽带随机激励,该控制系统的自适应能力较差;②基于最优控制的LQR控制方法的鲁棒性较差,因为LQR控制器是通过求解泛函极值使得目标函数式最小从而获得控制器的。通过这种最优控制得到控制系统的稳定裕度比较低,对参数的变化比较敏感,试验中微小的参数变化可能会直接导致控制器偏离其原来设计的最优状态,因此在试验时对应每个试验状态的变化都需要花费大量的时间重新调整控制系统参数才能达到较好的控制效果,可见LQR控制方法的工程适用性较差,不能满足型号试验的要求。
因此,参考基于经典的正位置反馈(Positive Position Feedback, PPF)控制方法,建立了基于对被控系统传递函数进行辨识的正加速度反馈(Positive Acceleration Feedback, PAF)控制方法,完成了对V尾抖振模型的压电控制系统设计。
PAF控制方法具有以下优点:①不需要精细的控制系统模型,只需根据系统的固有频率和相位关系设计控制补偿器;②控制系统通过引入二阶补偿器构成新的闭环系统,可以根据劳斯-赫尔维茨稳定性判据或李雅普诺夫稳定性判据获得系统稳定边界,指导控制器参数的选择;③在具体实施时,可以通过适当地选取增益确定系统的稳定裕度,使得当抖振载荷作用于V尾结构造成系统参数变动的情况下,依然能够获得良好的控制效果,控制的自适应能力较强;④控制系统通过补偿器辅助系统与被控对象构成新的闭环系统,可在结构的主要固有频率处大幅提高系统的阻尼比,直接降低结构的抖振响应,同时辅助系统的引入并不会对原系统的稳定性造成影响。
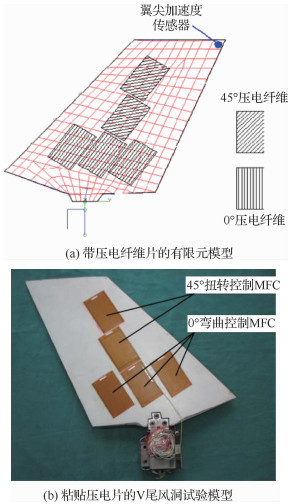
3.1 正加速度反馈控制方法的建立首先建立V尾结构的动力学有限元模型,计算翼面结构在一弯与一扭模态处的“模态应变”,选择在翼面蒙皮应变最大部位粘贴压电纤维片(见图 12)。根据压电纤维材料的力/电耦合本构关系,应用热弹性比拟原理对垂尾复材蒙皮贴有压电纤维的板单元赋予热膨胀系数来模拟压电效应。用NASTRAN软件的热弹性分析模块计算出单位温度变化下结构的变形向量(也称作Ritz向量),把Ritz向量与模态振型向量Φ组合成结构缩减向量,再利用设计的MATLAB程序组装就得到带压电纤维结构的动力学方程,进而计算得到翼面响应反馈点的频响函数,用于建立V尾抖振系统的压电主动控制方程[10]。
|
| 图 12 V尾翼面压电纤维与传感器布置 Fig. 12 Arrangement of V-tail piezoelectric fiber and sensor |
用V尾翼尖结构加速度响应作为反馈给控制系统的反馈信号,则基于PAF控制方法的基本原理如下:
假设每个通道视为一个单自由度振动系统:
| $ {\ddot x + 2\zeta {\omega _{\rm{n}}}\dot x + \omega _{\rm{n}}^2x = u} $ | (4) |
式中:x为系统的状态变量,如位移;u为控制输入;ζ为系统的阻尼比;ωn为系统的固有频率。
设计正加速度反馈控制器为
| $ {\left\{ {\begin{array}{*{20}{l}} {\ddot x + 2{\zeta _{\rm{f}}}{\omega _{\rm{f}}}{\kern 1pt} {\kern 1pt} \dot z + \omega _{\rm{f}}^2{\kern 1pt} z = g{\kern 1pt} \ddot x}\\ {u = g{\kern 1pt} \ddot z} \end{array}} \right.} $ | (5) |
式中:z为控制器的状态变量;g为一个增益常数;ζf为控制器阻尼常数;ωf为控制器频率。将式(4)和式(5)组合,可以得到基于PAF控制方法的系统控制方程为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} 1&{ - g}\\ { - g}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\ddot x}\\ {\ddot z} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {2\zeta {\omega _{\rm{n}}}}&0\\ 0&{2{\zeta _{\rm{f}}}{\omega _{\rm{f}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot z} \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\omega _n^2}&0\\ 0&{\omega _{\rm{f}}^2} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x\\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ 0 \end{array}} \right] \end{array} $ | (6) |
要使系统稳定必须使得式(6)第1项的系数矩阵正定。因此系统增益g必须满足g2 < 1,考虑到加速度正反馈,系统增益满足的条件实际为
| $ {0 < g < 1} $ | (7) |
则控制器传递函数有
| $ {\frac{{X(s)}}{{Z(s)}} = \frac{{g{s^2}}}{{{s^2} + 2{\zeta _{\rm{f}}}{\omega _{\rm{f}}}s + \omega _{\rm{f}}^2}}} $ | (8) |
式中:X(s)和Z(s)分别为x和z的拉氏变换。
应用设计反馈控制系统可以使被控对象构成新的闭环系统,该系统在结构共振频率附近的阻尼比ζc可近似的表示为$\zeta+\frac{g}{4 \zeta_{\mathrm{f}}}$。
上述分析可以看到反馈系统的引入能够大幅提高闭环系统的阻尼比,能够起到降低结构抖振响应的作用,同时控制系统的引入并不会对系统的稳定性造成影响,也提高了控制系统的鲁棒性[11]。
3.2 基于PAF控制方法的控制系统设计与仿真PAF控制方法除了可以增大闭环系统的阻尼比外,还可通过对V尾结构响应贡献最大的一弯模态和一扭模态设计独立的控制器与补偿器,使闭环控制器的传递函数在设计点处(V尾一阶弯曲频率和一阶扭转频率)的相位与被控系统传递函数在该点处的相位相反,这样来达到降低结构抖振响应的目的。
具体的设计步骤是通过安置在V尾翼尖的加速度传感器输出加速度反馈信号,这一信号先用于被控系统传递函数辨识,然后加速度响应信号分为2路(g1、g2)分别经过带通滤波器Cb滤波后,分离出一弯、一扭振动信号输入到控制器Claw1和Claw2(见图 13),Claw1为V尾一阶弯曲控制器(其前置放大器增益为K1);Claw2为垂尾一阶扭转控制器(其前置放大器增益为K2)。Claw1和Claw2中都包括了加速度反馈控制的二阶控制器和因作动器/传感器非共位布置造成的延迟补偿器。控制器输出经加法器和系统输入u1和u2相加后输入到高压功放,放大的信号分别输入到V尾翼面根部和中部的压电纤维作动器,压电作动器产生的作动力与抖振载荷一起作用于V尾结构[12]。
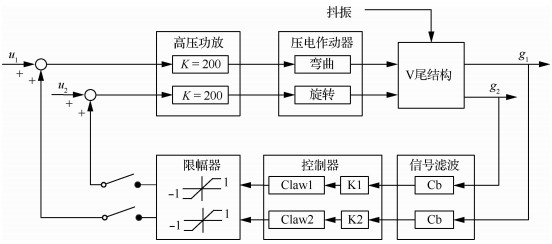
|
| 图 13 V尾模型抖振响应PAF控制系统设计框图 Fig. 13 Block diagram of PAF control system for V-tail model buffet response |
2个反馈通道信号的传递函数在设计点处的相位与被控系统(辨识系统)传递函数相位对比见图 14,在此点处控制系统实际获得的相位差均接近反相要求的180°。
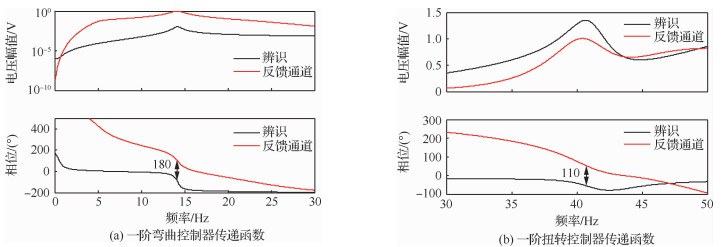
|
| 图 14 控制系统传递函数相位与被控系统(辨识系统)传递函数相位对比 Fig. 14 Comparison of transfer function phases between control system and controlled system (recognized system) |
通过先进战斗机验证机V尾抖振模型低速风洞试验,验证了采用压电抖振控制技术对V尾抖振响应的抑制效果,最终使V抖振最严重状态的翼尖振动加速度响应降低约25%(见图 15)。
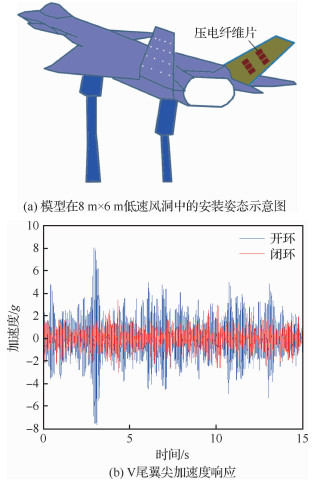
|
| 图 15 先进战斗机V尾抖振响应控制低速风洞试验 Fig. 15 Low speed wind tunnel test for advanced fighter V-tail buffet response control |
美国在F-35、F-22第四代战斗机研制中吸取了F-18等飞机的经验教训,在整个设计与试验流程中都充分考虑了V尾抖振载荷对结构寿命的影响,在全机疲劳试验载荷谱中抖振载荷占全部载荷循环的比例高达34%[5]。
在充分消化和吸收国外抖振动态疲劳载荷谱编制先进技术的基础上[4],针对中国先进战斗机的飞行包线和任务剖面,提出了一种适合中国高性能战斗机的抖振动态疲劳载荷谱编制方法与试验实施方案,解决了试验中常规疲劳机动载荷谱与抖振载荷谱的叠加问题。建立了中国新一代先进战斗机考虑V尾抖振载荷的全机疲劳载荷谱编制方法与试验实施手段。
4.1 V尾抖振频率分布与AoA-sf参数表计算V尾抖振刚性模型风洞试验用于测量垂尾翼面的脉动压力分布。在翼面各个分区的内、外侧翼面对位布置压力传感器,测量脉动压力差并进行谱分析。然后按照以下公式转换到飞机尺度[13]:
| $ {\frac{{{\varphi _{\rm{m}}}({\omega _{\rm{m}}})}}{{{{(1/2{\rho _{\rm{m}}}V_{\rm{m}}^2)}^2}}}\left( {\frac{{{V_{\rm{m}}}}}{{{L_{\rm{m}}}}}} \right) = \frac{{{\varphi _{\rm{a}}}({\omega _{\rm{a}}})}}{{{{(1/2{\rho _{\rm{a}}}V_{\rm{a}}^2)}^2}}}\left( {\frac{{{V_{\rm{a}}}}}{{{L_{\rm{a}}}}}} \right)} $ | (9) |
在飞机V尾动力有限元模型上选择脉动压力测量对应点,输入在各个迎角(AoA)、马赫数Ma(或速压q)状态下测量的输入点a的自功率谱密度(Sa)、输入点a、b的互功率密度(Sab),计算出翼尖参考点的加速度响应(或结构内力动态载荷),对响应再进行功率谱分析找出对应的结构振动主导频率f,这样就可以获得编谱需要的抖振AoA-q-f参数表[14](见表 2)
| AoA/(°) | f/Hz | |||
| q=10~30 kPa | q=20~50 kPa | q=50~70 kPa | q=70~90 kPa | |
| 18 | 16.0 | 21.0 | 42.0 | 65.0 |
| 30 | 15.5 | 18.2 | 40.3 | 63.0 |
在全机基本机动谱中对各级过载系数选择对称拉起或急剧机动对称等典型基本机动,使用飞行品质模拟器(Flight Quality Simulator, FQS)对这些机动进行模拟分析,得出完成该机动的时间、马赫数Ma、迎角和速压等参数。再由基本机动谱的各级过载循环次数就可以得到在不同速压(q)、迎角(AoA)状态V尾抖振的总时间t。把模拟计算的全部结果汇入AoA-q-t表中(见表 3)。
| AoA/(°) | t/s | |||
| q=10~30 kPa | q=20~50 kPa | q=50~70 kPa | q=70~90 kPa | |
| 18 | 2 500.0 | 2 000.0 | 4560.0 | 2 651.0 |
| 30 | 2 800.0 | 2 400.0 | 4 800.0 | 2 726.0 |
把表 2与表 3的数据相乘就得到在1 000飞行小时内各个迎角状态机动飞行时V尾抖振的总循环次数。在得到了总的抖振循环次数后还需要把它返回叠加到机动载荷循环中。具体方法是在基本机动谱中选择与表 3各个状态对应的各过载级中的对称拉起机动层,进而施加抖振载荷循环(见图 16)。
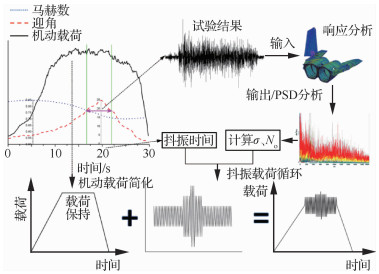
|
| 图 16 机动载荷叠加抖振载荷方法示意图 Fig. 16 Sketch map of superposition of maneuver-load and buffet-load |
抖振载荷在转换到时域之后,载荷循环数将非常大,远大于战斗机的机动载荷谱循环数。这对分析和试验都带来困难,太多的载荷循环会造成试验周期很长,增加试验成本投入,反过来又影响到研制进度。因此需要研究对简单叠加后的载荷循环进行简化,以编制适用于时域范围的分析和试验载荷谱。
大量的试验和实测数据证明,抖振响应是典型的窄带随机过载,即抖振峰/谷服从高斯分布。大量的研究也表明,抖振载荷幅值xa的概率密度函数为Rayleigh分布[15]:
| $ {f({x_a}) = \frac{{{x_a}}}{{{\sigma ^2}}}{{\rm{e}}^{ - \frac{1}{2}{{\left( {\frac{{x_a^2}}{\sigma }} \right)}^2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_a} > 0} $ | (10) |
Rayleigh分布如图 17所示,σ取响应时间历程的均方根值(RMS)作为估计量。
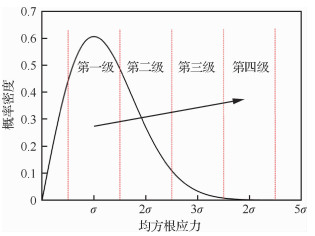
|
| 图 17 Rayleigh分布 Fig. 17 Rayleigh distribution |
由材料的基本S-N曲线和Miner损伤累计准则,可以根据抖振载荷幅值分布得到损伤值:
| $ {{D_{{\rm{ buff }}}} = T\frac{{{N_0}}}{C}\int_0^\infty {{f_a}} ({x_a}){{({x_a})}^n}{\rm{d}}{x_a}} $ | (11) |
式中:n为材料寿命指数;T为抖振时间;N0为随机抖振过程每秒产生的峰值(零值穿越数的一半);C为材料常数。代入Rayleigh分布,令y=xa,整理后的损伤公式为[16]
| $ {{D_{{\rm{ buff }}}} = T\frac{{{N_0}}}{C}{\sigma ^n}\int_0^\infty {{y^{n + 1}}} {{\rm{e}}^{ - \frac{{{y^2}}}{2}}}{\rm{d}}y} $ | (12) |
抖振为高频重复载荷,相同的时间段内抖振载荷循环数远大于机动载荷循环,为了便于分析和试验,需要对载荷谱进行简化,但要保证损伤的等效。
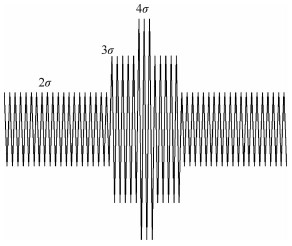
具体简化方法为:确定若干典型的抖振载荷循环,然后将整个抖振历程的损伤折算到这些典型循环,可以从Rayleigh分布的特征出发研究如何确定典型载荷状态。为此选取4种典型的抖振载荷幅值:1σ、2σ、3σ、4σ。将0.5σ~1.5σ间的总损伤折算到1σ、1.5σ~2.5σ间的总损伤折算到2σ、2.5σ~3.5σ间的总损伤折算到3σ、3.5σ~4.5σ间的总损伤折算到4σ。由于第一级典型状态1σ,折算后的循环仍然较多,将其对应区间折算到4σ,最终保留三级。各级载荷的等效关系为[17]
| $ \left\{ \begin{array}{l} T\frac{{{N_0}}}{C}{\sigma ^n}\int_{1.5}^{2.5} {{y^{n + 1}}} {{\rm{e}}^{ - \frac{{{y^2}}}{2}}}{\rm{d}}y = \frac{{{N_{p2\sigma }}}}{C} \cdot {(2\sigma )^n}\\ T\frac{{{N_0}}}{C}{\sigma ^n}\int_{2.5}^{3.5} {{y^{n + 1}}} {{\rm{e}}^{ - \frac{{{y^2}}}{2}}}{\rm{d}}y = \frac{{{N_{p3\sigma }}}}{C} \cdot {(3\sigma )^n}\\ T\frac{{{N_0}}}{C}{\sigma ^n}\left( {\int_{0.5}^{1.5} {{y^{n + 1}}} {{\rm{e}}^{ - \frac{{{y^2}}}{2}}}{\rm{d}}y + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\int_{3.5}^{4.5} {{y^{n + 1}}} {{\rm{e}}^{ - \frac{{{y^2}}}{2}}}{\rm{d}}y} \right) = \frac{{{N_{p4\sigma }}}}{C} \cdot {(4\sigma )^n} \end{array} \right. $ | (13) |
式中:Np2σ、Np3σ、Np3σ分别为p2σ、p3σ、p4σ载荷幅值下的等效循环数,取整数。
取铝合金和钛合金S-N幂函数曲线的指数n=4进行分析,对式(13)积分后可得到各级抖振的循环数:
| $ \left\{ {\begin{array}{*{20}{l}} {{N_{p{\kern 1pt} 2\sigma }} = 0.25T{N_0}}\\ {{N_{p{\kern 1pt} 3\sigma }} = 0.033{\kern 1pt} {\kern 1pt} {\kern 1pt} 5T{N_0}}\\ {{N_{p{\kern 1pt} 4\sigma }} = 0.005T{N_0}} \end{array}} \right. $ | (14) |
最后将载荷按照低高低的顺序进行组合,形成类似程序块谱的形状[17],如图 18所示。
|
| 图 18 简化后的抖振谱 Fig. 18 Simplified buffet load |
很明显,取2σ时等效后的循环数缩减到原循环数的1/4,取3σ可以缩减到原循环数1/30,取4σ可以缩减到原循环数1/200,因此达到了简化循环的目的。
最终考虑机动和抖振叠加的载荷循环简化为图 19所示的3种情况之一[18]:
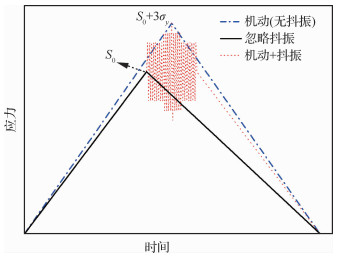
|
| 图 19 机动载荷叠加抖振载荷方法示意图 Fig. 19 Sketch of superposition methods of maneuver load and buffet load |
1) 整个过程不发生抖振,只有机动载荷循环(黑色实线)。
2) 抖振发生,但抖振载荷循环的损伤可忽略,考虑叠加形成的最大载荷循环(蓝色虚线)。
3) 考虑最大载荷叠加的载荷循环,同时抖振不可忽略,等效为等幅循环(虚线)。
4.4 考虑叠加机动载荷和抖振载荷谱编制的应用基于上述机动载荷与抖振载荷的叠加方法以及载荷循环的简化原理,根据飞机任务剖面的机动定义,编制考虑叠加机动和抖振载荷谱的具体编制流程如图 20所示。
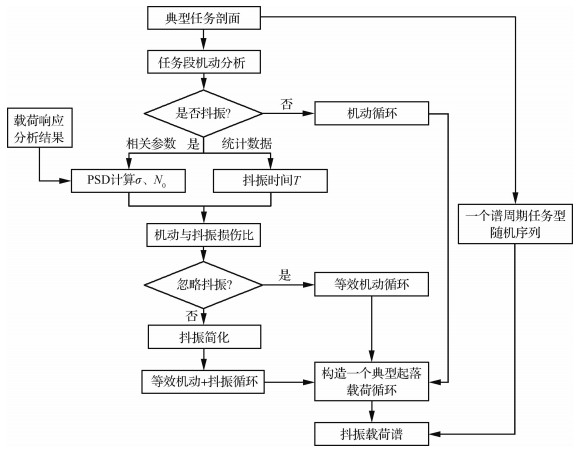
|
| 图 20 抖振和机动载荷叠加的编谱流程 Fig. 20 Flowchart of spectrum produce of maneuver-load and buffet-load superposition |
根据已知结构部位的机动载荷历程和相关抖振参数,判断是否发生抖振。如果不满足抖振发生条件则只考虑机动载荷;若满足抖振条件则根据有限元响应分析结果确定响应的σ、N0,根据大量的统计数据计算各类机动的抖振时间。再计算抖振载荷相对于机动载荷的损伤比例,可忽略的(损伤比≤2%)只考虑抖振和机动载荷叠加形成的最大载荷循环;不可忽略的(损伤大>2%),采用等损伤简化,然后形成等效机动载荷循环和简化后的抖振载荷循环。多个机动组合成一个完整起落的典型载荷循环[19](见图 21)。在全机疲劳试验中,只需要考虑V尾抖振载荷对后机身支持结构的寿命影响。在试验机上左侧V尾用假件代替,按照1 000飞行小时分块施加V尾根部转轴处的弯矩机动载荷谱与简化后的抖振等幅谱[20]。
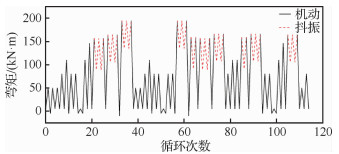
|
| 图 21 一个完整起落的典型疲劳载荷循环谱 Fig. 21 Typical load cyclic spectrum of one take-off and landing |
在单独V尾抖振疲劳试验中,重点需要考核抖振载荷对V尾翼面结构疲劳寿命的影响。因此,首先需要设计满足动力学特性相似的支持夹具,使V尾在夹具上安装后的前4阶固有频率与飞机状态V尾频率满足设计误差要求[21](见图 22)。
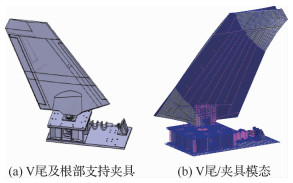
|
| 图 22 V尾动力学相似支持夹具与垂尾模态 Fig. 22 V-tail dynamic similar fixture and the calculated V-tail mode |
试验中采用循环加载的方式分别施加常规疲劳机动载荷与抖振动态载荷。以1 000飞行小时为一个循环,即加载1 000个飞行小时的机动谱后,加载1 000个飞行小时的抖振谱,以此循环。
应用卡板-杠杆系统施加单纯的机动载荷(见图 23)。施加抖振载荷谱时,需要同时在V尾翼面上施加对应的机动载荷(均值载荷),这就需要设计特殊的气囊加载装置,使加载时气囊装置给V尾翼面提供的附加刚度对翼面固有频率的影响必须要在可接受的误差范围内[22]。V尾抖振动态疲劳载荷由液压作动器单点施加在V尾翼面上,通过布置在翼尖后缘的加速度传感器来控制激振力的谱型与量值使其满足试验要求。设计完成的单独V尾叠加机动静载的抖振疲劳试验加载系统如图 24所示。
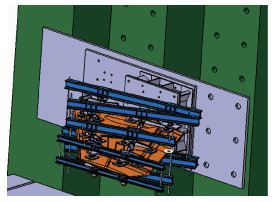
|
| 图 23 常规机动疲劳试验加载系统 Fig. 23 Loading system for conventional maneuver fatigue test |
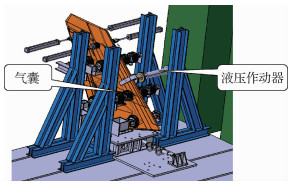
|
| 图 24 叠加机动静载的抖振疲劳试验加载系统 Fig. 24 Loading system for buffet fatigue test superposition with maneuver static load |
全动V尾布局先进战斗机的垂尾抖振动强度设计与试验验证关键技术研究工作在国内属首次开展,本文建立了一套V尾结构抗抖振动强度设计与试验验证的理论分析技术、设计准则和试验方法。在先进战斗机验证机试制试飞中,应用该项技术成果对飞机在大迎角飞行状态的V尾抖振载荷、抖振响应进行了准确的预计,完成了在全飞行包线对V尾结构的抖振动强度评估,成功解决了验证机大迎角试飞过程中V尾翼尖抖振加速度超限情况下的结构动强度分析问题,确保了试飞安全。
在先进战斗机的后续研发设计中,应用本项目研究在理论仿真分析与试验验证方面所取得的技术成果,对前机身脱体涡破裂后的流场结构、频谱特性、涡流线轨迹进行了准确的预测,在此基础上对V尾结构进行了优化迭代设计。使大迎角试飞过程中V尾翼尖抖振加速度响应在验证机的基础上有大幅降低,提升了飞机的飞行品质,确保了先进战斗机高机动性先进战技指标的发挥,还大幅提高了V尾结构抗抖振疲劳性能,直接降低飞机使用维护成本,延长了结构检修周期,提高了机群的战斗出勤率。
| [1] | LEE B H K, BROWN D. Wind tunnel studies of F/A-18 tail buffet[J]. Journal of Aircraft, 1992, 29(1): 146-152. |
| Click to display the text | |
| [2] |
李劲杰, 杨青, 肖春生, 等. 边条翼布局流场及其双垂尾抖振特性研究[J]. 航空学报, 2006, 27(3): 395-398. LI J J, YANG Q, XIAO C S, et al. Investigation of flow and twin-vertical tail buffet characteristics of leading-edge extension configuration[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 395-398. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [3] | HEALEY M D. F/A-18 E/F vertical tail buffet design, analysis and test[C]//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2003. |
| [4] | CHRIS M. Incorporation of buffet into the F-35 full scale durability tests spectra[R].F-35-Structural Integrity Program, 2006. |
| [5] | CHRISTONPHER L B. Buffet fatigue sequence generation from F-22 flight test data using frequency domain methods[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston: AIAA, 2007. |
| [6] | PATEL S R. F/A-22 vertical tail buffet strength certification[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2005. |
| [7] | YEHIA M R. Numerical investigation of tail buffet on F-18 aircraft[C]//10th Applied Aerodynamics Conference, 1992. |
| [8] | KEN G. Computational analysis of FA-18 tail buffet[C]//20th Atmospheric Flight Mechanics Conference, 1995. |
| [9] | BRAFORD E G. Computational prediction of nose-down control for F/A-18E at high alpha[J]. Journal of Aircraft, 2008, 45(5): 1661-1668. |
| Click to display the text | |
| [10] |
王巍.压电结构振动主动控制及在尾翼抖振响应控制中的应用[D].西安: 西北工业大学, 2009: 30-35. WANG W. Application of piezoelectric structural vibration active control and its application to the control of vertical tail buffeting response[D]. Xi'an: Northwestern Polytechnical University, 2009: 30-35(in Chinese). |
| [11] | MORES R W. Active control of F/A-18 vertical tail buffeting using piezoelectric actuators[C]//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston: AIAA, 2003. |
| [12] | ASHLEY H. Further study of active control for fin buffet alleviation with application to F-22: WL-TR-97-3073[R]. 1997. |
| [13] | WILLIAM D A. F/A-22 high angle of attack buffet-test adequacy analysis[C]//22nd Applied Aerodynamics Conference and Exhibit Providence, 2004. |
| [14] | HEWWITT R L. Spectrum editing for a full-scale fatigue test of a fighter aircraft wing with buffet loading[C]//ASTM Special Technical Publication, Fatigue Testing and Analysis Under Variable Amplitude Loading Conditions, 2003. |
| [15] | CONSER D P, KEYS G L. F/A-18 production ASPJ vertical tail dynamic fatigue test FT98 test spectra development: MDC 91B0424[R]. St.LouiS: McDonnell Douglas Corporation, 1992. |
| [16] | HEALEY M D. F/A-18E/F vertical tail dynamic fatigue test ESD03 test spectra development: MDC 93B0168[R]. St. Loui S: McDonnell Douglas Corporation, 1995. |
| [17] | MOLENT L A D. Buffet loads and structural redundancy considerations inertial tail fatigue monitoring programs[C]//International Aerospace Congress, 1999. |
| [18] | SHETA E F. Control of twin-tail buffet responses using normal leading-edge blowing: AIAA-2000-4227[R].Reston: AIAA, 2000. |
| [19] | SHETA E F, HUTTSELL L J. Numerical analysis of F/A-18 vertical tail buffeting[C]//19th AIAA Applied Aerodynamics Conference Anaheim.Reston: AIAA, 2001. |
| [20] | FERMAN M A, PAGEL S R. A unified approach to buffet response of fighter aircraft empennage: AGARD Report CP-483[R]. Sorrento: North Atlantic Treaty Organization, 1990. |
| [21] | SHAH G H, GRAFTON S B, GUYNN M D, et al. Effect of vortex flow characteristics on tail buffet and high angle of attack aerodynamics of a twin tail fighter configuration[C]//High Angle of Attack Technology Conference.Washington, D.C.: NASA, 1990. |
| [22] | ANDERSON W D, PATEL S R, BLACK C L. Low speed wind tunnel buffet testing on the F/A-22[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2004. |



