2. 南京航空航天大学 自动化学院, 南京 210016
2. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
过失速机动是飞机超出设计包线的非常规机动动作,其内涵是飞机飞行迎角远大于失速迎角后,按控制指令要求,快速改变飞行速度和航向姿态的特殊战术机动。过失速机动也称为“超机动”,其在近距离空战格斗中具有重要意义,是先进战斗机的重要性能标志[1-2]。
多年来,过失速/大迎角飞行问题,包括非线性/非定常空气动力建模[3-4]与参数辨识[5]、推力矢量技术[6-7]、飞推一体化控制[8-10]等,一直是航空界关注的热点和难点问题。西方发达国家多年前开展了X-31、F-18 High Alpha Research Vehicle (HARV)等验证机的研究和飞行试验,美国F-22、F35等四代机和俄罗斯Su-35等先进战斗机都具备了超机动能力,可以在过失速条件下实现多种复杂且有实战意义的机动。从过失速机动技术验证机到具备超机动能力的战斗机,过失速条件下的飞行大气数据传感是一个必须跨越的难题。过失速条件下的飞行大气数据传感技术的重要性不仅体现在大气数据是飞机飞行状态的实时反馈信息,更在于该技术是过失速机动飞行控制理论、方法与技术验证的基准——针对过失速机动所开展的大量飞行力学建模与飞行控制律研究无不以迎角(AOA)、侧滑角(AOS)、总静压、真空速等大气数据能够精确测量为前提。
飞机的飞行大气参数通常由大气数据系统提供,大气数据系统提供的迎角、侧滑角、总压、静压,以及进一步计算得到的马赫数、气压高度、空速等一系列参数是飞机飞行控制与安全飞行的关键参数。目前,可提供飞行大气参数的大气数据有集中式、嵌入式、分布式等多种结构形式,先进战斗机大多采用基于智能探头的分布式大气数据系统。已有的大气数据系统在常规飞行包线范围内能较好地完成测量任务,但在过失速条件下,由于气流分离、强耦合,大气数据系统的压力测量失效等原因,即使是在飞行试验中加装机头校准风标与探头,也不足以完全胜任过失速机动下的大气数据测量需求。因此,探索和研究满足过失速机动飞行控制需求的大气数据测量、融合与估计方法,对先进战斗机超机动能力的实战化至关重要。
大气数据是飞机与周围大气之间相对关系的表征,机载导航系统输出的导航参数是飞机相对当地地理坐标系的运动关系,风速风向等参数则是某一区域内的大气相对地理系的风场信息。大气数据、飞机的地理导航参数、风场信息之间具有内在的关联。对大气参数、导航参数、风场信息三者的时/空关联特性的融合应用,是解决过失速/大迎角条件下的大气数据传感器问题的有效技术途径。
基于多源信息融合思想估计大气数据的方法利用飞机的结构参数和飞行过程中航电系统获取的测量信息,通过设计信息融合算法,实现对大气数据的实时估计。基于上述思想获得大气数据方法的信息系统也被称为虚拟大气数据系统、计算大气数据系统[11-12]。目前,开展此类研究主要包括美、欧、俄等,近年来,随着新型先进战斗机的研发,中国在该领域的研究也取得了显著进展[13-14]。
本文面向过失速机动对大气数据系统提出的挑战和对大气数据传感的需求,开展大气参数估计,基于中国推力矢量技术验证机的数据,对所研究的方法进行验证。
1 方法介绍 1.1 过失速机动飞行试验的大气数据特性分析随着中国推力矢量技术的研究与应用,战斗机的操控能力发生了质的变化。推力矢量技术验证机安装了分布式大气数据系统和机头风标空速管,完成了眼镜蛇机动、赫伯斯特机动、直升机机动、大迎角360°滚转机动、榔头机动等多个标志性的超机动动作飞行试验。
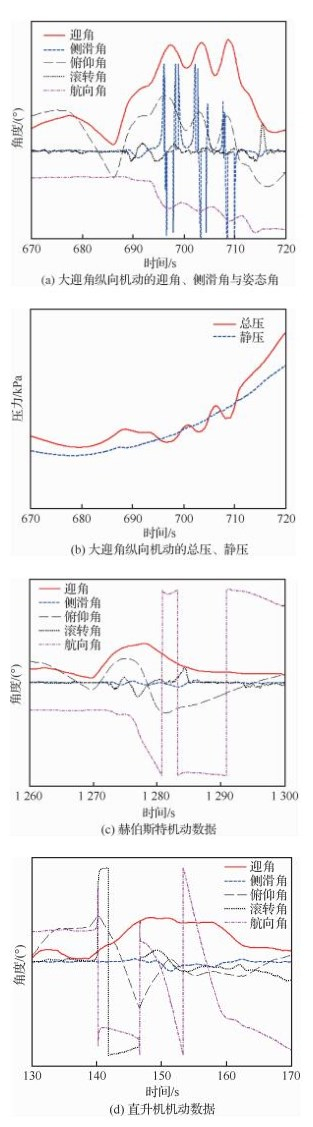
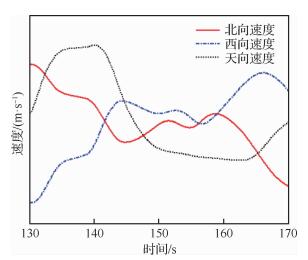
图 1为典型过失速机动飞行过程的数据曲线,机动过程包括大迎角纵向机动、赫伯斯特机动、直升机机动等,图 2为直升机机动的三维速度曲线。其中,迎角、侧滑角由机头空速管的风标测得,姿态角、速度由机载惯性/卫星组合导航系统测得,这些参数清晰地反映了相关过失速机动的飞行过程与飞行状态,机动过程中飞行迎角最大超过100°、水平飞行速度最小为4 m/s,飞行包线得到了显著扩展,表明了飞机的超机动飞行能力。
|
| 图 1 过失速机动迎角、侧滑角、总静压、姿态角曲线 Fig. 1 Variation curves of measured AOA, AOS, total and static pressure, attitude angles in post-stall maneuver |
|
| 图 2 直升机机动的三维速度曲线 Fig. 2 3D speed curves in helicopter maneuver |
从图 1和图 2的飞行数据曲线可以看出,大迎角条件下,尤其是迎角达到90°时,气流与空速管垂直、与侧滑角风标的旋转轴平行,在该飞行状态下,飞机纵向机动过程中,气流扰动导致风标在旋转范围内大幅度摆动,侧滑角风标失效。
总压是气流被阻滞速度到零时的压力,为气流的静压与动压之和,按飞机的实际飞行过程,总压应该大于静压。从图 1(b)可以发现,在迎角90°附近,飞机纵向机动时,机头空速管压力传感器测得的总压出现了比静压小的情况,表明在过失速机动状态下,总压、静压测量系统已不能准确反映飞机的真实总压、静压关系。这一现象并不是压力传感器测量精度问题,而是由于过失速机动状态,总静压受感器所反映的局部气流关系不能代表飞机飞行中的复杂总静压总体关系。
从图 1(c)赫伯斯特机动和图 2直升机机动的飞行数据曲线可以进一步发现,飞行过程中,迎角虽然持续处于接近90°的情况下,但侧滑角曲线比较平滑,与图 1(c)的结果相比,更进一步表明了过失速机动中大气数据测量面临的不确定性问题。
上述情况充分表明了过失速机动飞行中,飞机表面流体的复杂性,其非定常、迟滞等特性综合影响着迎角、侧滑角、总压、静压等大气参数的测量。
1.2 过失速机动大气数据融合估计方案过失速机动飞行中,飞行迎角超过甚至远大于临界失速迎角,在远超过安全飞行包线的情况下完成大角速率机动。实际飞行过程表明,在时间维度上,过失速机动是相对较短时间(通常在30 s左右)内的动态过程,从空间维度上看,过失速机动是在一个相对较小的空间范围(水平和高度各约2000 m的变化)内完成的。
如图 3所示,过失速机动过程与其前后的常规飞行状态是连续的飞行过程,过失速机动过程的时空特性与常规飞行状态之间的连续性是本文大气数据融合估计方法的基础条件。

|
| 图 3 飞行状态转换过程示意图 Fig. 3 Schematic diagram of flight state transition process |
本文所提出的大气数据融合估计方法是风场信息与大气数据的交替融合与估计方法,包括以下步骤:
1) 在常规飞行状态,基于机载惯性/卫星组合导航系统和大气数据系统的输出信息,估计风场参数。
2) 进入过失速机动后,停止风场参数的估计,在过失速机动的飞行时间和空间范围内,冻结风场参数。
3) 利用冻结的风场参数、机载惯性/卫星导航系统的导航参数,进行大气参数估计,包括迎角与侧滑角的计算。
4) 基于飞行数据,训练深度神经网络,利用深度神经网络对迎角复杂非线性误差进行补偿。
5) 在迎角、侧滑角基础上,进一步计算过失速机动状态下的真空速、马赫数、静温、总压、静压等大气参数。
6) 过失速机动过程结束、恢复常规飞行状态后,大气数据系统恢复有效性,开始风场信息的估计与更新。
该方案对参数的估计性能主要取决于风场信息估计的准确性、冻结的风场信息与过失速飞行过程中风场信息的时空关联程度、补偿迎角误差的深度神经网络对非定常/非线性流场影响的拟合精度及其泛化能力等因素。
2 基于风场模型的风场信息滤波飞机的真空速和地速是相对于2个不同坐标系下的飞机速度。真空速是飞机相对于空气的运动速度,一般由大气数据系统通过敏感空气压力获得,而地速是相对于惯性系的运动速度,可直接利用惯性导航或组合导航系统获得。根据以上定义,可知真空速、地速和风速之间可以构成矢量三角形。
设飞机的俯仰角、滚转角和航向角分别为θ、φ、ψ,该姿态角表征的机体系b(采用GB/T14410—2008关于机体系坐标轴指向定义:x轴为沿着机身纵轴向前,y轴指向右侧,z轴垂直于机身平面向下)到导航系n(“北东地”地理坐标系)的姿态转移矩阵为Cbn,某一位置的风在地理坐标系的速度为三维风速矢量Vwn(严格意义上,风场的信息是三维风速矢量的空间分布随时间的变化),飞机相对空气运动的速度为真空速VTb,飞机相对地理坐标系的速度为地速VGn,则地速、真空速与风速三者之间的矢量关系为
| $ \mathit{\boldsymbol{V}}_{\rm{W}}^{\rm{n}} = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}}{\kern 1pt} \mathit{\boldsymbol{V}}_{\rm{W}}^{\rm{b}} = \mathit{\boldsymbol{V}}_{\rm{G}}^{\rm{n}} - \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}}{\kern 1pt} \mathit{\boldsymbol{V}}_{\rm{T}}^{\rm{b}} $ | (1) |
考虑到飞机在进行角运动时,由于杆臂效应,不同位置的速度不同,式(1)中的VGn可由惯性/卫星组合直接输出的飞机质心线速度VG, 0n,以及机体系下的三维角速度矢量ω与杆臂向量R的叉乘矢量合成得到,即
| $ \mathit{\boldsymbol{V}}_{\rm{G}}^{\rm{n}} = \mathit{\boldsymbol{V}}_{{\rm{G, 0}}}^{\rm{n}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{R}} $ | (2) |
根据气流和机体坐标系之间的转换关系[11, 14],可将真空速在机体系下的3个分量表示为
| $ \mathit{\boldsymbol{V}}_{\rm{T}}^{\rm{b}} = \left[ {\begin{array}{*{20}{l}} {v_{{\rm{T, }}x}^{\rm{b}}}\\ {v_{{\rm{T, }}y}^{\rm{b}}}\\ {v_{{\rm{T, }}z}^{\rm{b}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{V_{\rm{T}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }\\ {{V_{\rm{T}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }\\ {{V_{\rm{T}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\kern 1pt} {\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha } \end{array}} \right] $ | (3) |
式中:α为飞机迎角;β为飞机侧滑角,是大气数据系统输出的关键参数,也是大气数据融合方法需要估计的重要参数。
式(1)仅反映飞机所在位置处的局部风场信息的测量关系,无法全面反映飞机所在区域一定范围和一段时间内的完整信息。为了更加准确地获得更多有效风场信息,基于大气监测的风场模型可作为风场估计的状态模型。
考虑变化风场由平均风和大气紊流组成,即
| $ \mathit{\boldsymbol{V}}_{\rm{W}}^{\rm{n}} = \mathit{\boldsymbol{V}}_{{\rm{W, c}}}^{\rm{n}} + \mathit{\boldsymbol{V}}_{{\rm{W, t}}}^{\rm{n}} $ | (4) |
式中:平均风VW, cn为三维风场的稳定分量,
实际应用中,滤波器模型中的系数需要根据飞行试验和相关的气象观测进行校准。
采用上述风场的状态模型与局部风场的观测信息,可实现对飞机所处区域的风和风的变化率进行估计,在此基础上,可实现对风的短时间预测。
此外,在风场参数估计阶段,还需根据气压高度与惯性/卫星组合导航系统的高度,计算气压高度修正值Hbc=Hp-HI,静温修正值Tbc=Ts-T(Hp),其中Hp为气压高度;HI为惯性高度;Ts为大气静温;T(Hp)为标准大气静温。
3 基于冻结风场和导航数据的大气数据计算模型进入过失速机动时,风场滤波估计暂停更新,风场信息作为已知信息使用。因此,在获得风场信息和导航数据的情况下,根据大气数据的物理测量原理,对大气数据系统的测量模型进行重新编排。过失速机动中,大气数据的融合估计计算模型为
| $ \mathit{\boldsymbol{V}}_{\rm{T}}^{\rm{b}} = \mathit{\boldsymbol{C}}_{\rm{n}}^{\rm{b}}(\mathit{\boldsymbol{V}}_{\rm{G}}^{\rm{n}} - \mathit{\boldsymbol{V}}_{\rm{W}}^{\rm{n}}) $ | (5) |
| $ \alpha = {\rm{arctan}}\frac{{V_{{\rm{T}}, z}^{\rm{b}}}}{{V_{{\rm{T}}, y}^{\rm{b}}}} $ | (6) |
| $ \beta = {\rm{arctan}}\frac{{V_{{\rm{T}}, x}^{\rm{b}}}}{{\sqrt {{{(V_{{\rm{T}}, y}^{\rm{b}})}^2} + {{(V_{{\rm{T}}, z}^{\rm{b}})}^2}} }} $ | (7) |
| $ {V_{\rm{T}}} = \sqrt {{{(V_{{\rm{T}}, x}^{\rm{b}})}^2} + {{(V_{{\rm{T}}, y}^{\rm{b}})}^2} + {{(V_{{\rm{T}}, z}^{\rm{b}})}^2}} $ | (8) |
| $ {H_{\rm{p}}} = {H_{\rm{I}}} + {H_{{\rm{bc}}}} $ | (9) |
| $ {P_{\rm{s}}} = {P_{\rm{b}}}{\rm{exp}}\left( {\frac{{ - {g_{\rm{n}}}}}{{R{T_{\rm{b}}}}}({H_{\rm{p}}} - {H_{\rm{b}}})} \right) $ | (10) |
| $ {T_{\rm{s}}} = T({H_{\rm{p}}}) + {T_{{\rm{bc}}}} $ | (11) |
| $ {T_{\rm{t}}} = {T_{\rm{s}}}(1 + 0.2M{a^2}) $ | (12) |
| $ Ma = \frac{{{V_{\rm{T}}}}}{{72.164{\kern 1pt} {\kern 1pt} {\kern 1pt} 86\sqrt {{T_{\rm{s}}}} }} $ | (13) |
| $ {P_{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{P_{\rm{s}}}}}{{{{(1 + 0.2M{a^2})}^{ - 3.5}}}}}&{Ma \le 1}\\ {{P_{\rm{s}}} \cdot 1.2M{a^2} \cdot {{\left( {\frac{{7.2M{a^2}}}{{7M{a^2} - 1}}} \right)}^{2.5}}}&{Ma > 1} \end{array}} \right. $ | (14) |
式中:Vtb为真空速;Ps为静压;Pb为相应层下界大气压力;Tb为相应层下界大气温度;Hb为相应层下界高度;gn为自由落体标准加速度;R为专用气体常数;Tt为大气总温;Ma为马赫数;Pt为总压。
4 基于深度多层神经网络的迎角误差补偿方法前述融合估计方法对大部分大气参数都可以实现有效估计,弥补过失速机动过程中迎角、侧滑角、总压、静压等测量失效的问题。试飞验证阶段,机头安装风标空速管,通常情况下,此阶段以风标输出信号为真迎角(迎角参考基准),可对融合估计的迎角进行建模修正,修正模型通常为多项式解析模型或神经网络模型等。
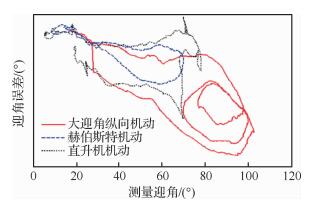
过失速机动过程中,飞机的空气动力学、飞行动力学都处于非定常、强非线性状态,按式(6)估计得到的迎角误差与测量迎角的关系曲线如图 4所示,3个机动分别为大迎角纵向机动、机赫伯斯特机动、直升机机动。从曲线看,融合迎角的误差随测量迎角变化规律,表现出了映射关系的不确定性、强非线性、大迟滞等突出特性。
|
| 图 4 计算迎角的误差与测量迎角的对应曲线 Fig. 4 Curves of error of calculated AOA with change of measured AOA |
图 4中表现出来的明显迟滞现象除了受到角速率产生的杆臂效应影响外,还受到大迎角机动过程中气流非定常现象的显著影响,以及动静压与迎角、侧滑角误差之间深度耦合的影响。上述特性在多架次飞行试验的同类机动中,具有较好的重复性,与机动动作的角速率、持续时间以及高度变化密切相关。
针对过失速大迎角状态,初步融合得到迎角偏差较大,超过10%,需要进行建模修正。修正模型的选择需要综合考虑问题的属性、拟合对象的复杂度、模型的特点特性、模型的表征能力等因素。常用对复杂非线性拟合建模方法有反向传播(BP)、径向基函数(RBF)神经网络、支持向量机等,理论证明BP神经网络单隐层,具有对任意非线性函数的逼近能力;RBF神经网络用径向基函数作为隐层单元的“基”构成隐含层空间,将输入矢量直接映射到隐空间,网络的输出是隐单元输出的线性加权。支持向量机是具有稀疏性和稳健性的分类器,通过核方法定义函数内积为核函数,用于解决非线性分类、回归拟合等问题。上述方法理论体系完备,已有大量的成功应用,然而,针对本文的迎角误差的建模修正,都有不能全面反映误差的不确定性、强非线性、大迟滞、非定常、模型参数耦合等特性。
神经网络技术的新发展为针对复杂问题的建模提供了新的思路和视角。21世纪初,国外有学者通过研究解决了多层神经网络训练的难题[15], 学术界和工业界对深度神经网络的研究不断取得突破。
深度神经网络(DNN)是神经网络和深度学习理论相结合出现的新型机器学习神经网络[15-16]。相对于经典的神经网络,在宏观网络结构上,深度神经网络的“深”表现为层数更多;在神经元的微观层次上,改用修正线性单元(ReLU)作为激活函数,避免了神经网络层数增加带来的梯度消失问题;在神经网络训练方面,增加了无监督预训练,为有监督学习提供初始条件[17-19]。深度神经网络通过构建具有多隐层的机器学习模型,侧重于挖掘和学习数据中的隐含特征,通过逐层特征变换,将样本在原空间的特征表示,通过多层次组合的思想,变换到一个新特征空间。
随着层数的增加,深度神经网络对复杂模型的建模能力增强,特征表征挖掘能力增强,同时有效改善了梯度消失、梯度爆炸等问题。基于这一特性,本文采用深度神经网络(多个隐含层)作为迎角偏差建模的工具。在具体应用中,既要避免网络层次过多导致的梯度消失问题,又要关注深度神经网络层次结构与拟合对象特性之间的匹配性。针对迎角误差强非线性、大迟滞的特点,本文从深度神经网络的输入物理量、网络层数、网络节点数量、过失速机动类型对迎角误差拟合的影响等角度,对深度神经网络的应用进行研究。
1) 训练数据集合构建
训练数据集对神经网络的训练性能至关重要,本文的数据集来自于基于中国推力矢量过失速机动飞行的大量飞行试验数据,总飞行近百架次,其中60%~70%架次的数据用于构建本文的深度神经网络训练数据集,其余架次的数据用于验证模型的适应性。
针对过失速机动运动特征和运动耦合,进行分类,第1类是眼镜蛇、榔头等大迎角条件下的纵向机动,第2类是过失速条件下,横侧向机动,如赫伯斯特、大迎角360°滚转、直升机机动等。深度神经网络的训练数据集合包括作为拟合对象的迎角偏差和作为网路输入的马赫数、融合迎角、融合侧滑角、俯仰角、滚转角、真航向角、机体系的三轴角速度、飞行高度、天向速度等信息,根据阶段的过程,分段组合。
训练数据集合决定了深度神经网络模型的输入与输出,针对过失速机动过程迎角的误差修正,所设计的深度神经网络的输出为迎角偏差。分析过失速机动的动态过程,可以发现与迎角有关的物理量包括:马赫数、融合迎角、融合侧滑角、俯仰角、滚转角、真航向角、俯仰角速率、滚转角速率、偏航角速率等。此外,由于大气静压、大气温度以及风速矢量与飞行高度有关,而在过失速机动中飞行高度通常有明显的变化,因此,在本文研究中,天向速度和高度的输入,有利于深度神经网络对天向运动的特征进行识别。
2) 深度神经网络层数和节点数迭代训练
深度神经网络的结构取决于待学习的问题对象复杂度,但两者之间并没有确切的确定依据。因此,在深度神经网络的应用中,为了确定网络隐藏层结构,需要多次迭代调整深度神经网络的层数和隐藏层神经元个数,对过失速机动的融合迎角偏差与飞行参数构建的数据集合进行训练,并以输出层误差的平方差大小(损失函数)作为评价标准,用于评估网络结构对过失速机动的迎角误差建模与补偿问题的适应性。
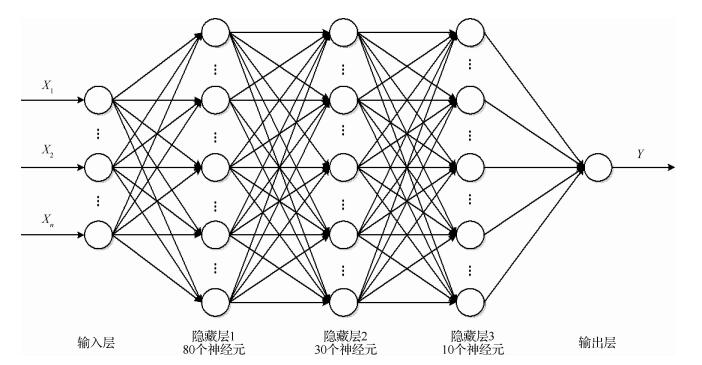
表 1为深度多层感知器神经网络隐藏层结构试探迭代过程,每个结果为训练7次的平均值。通过表 1可以发现,当隐藏层神经元个数分别为80、30、10时,训练效果与深度神经网络复杂度的综合效果满足过失速机动迎角误差建模修正的应用需求。
| 第1隐层 节点数 |
第2隐层 节点数 |
第3隐层 节点数 |
损失 函数 |
| 80 | 30 | 5 | 0.36 |
| 100 | 30 | 5 | 0.67 |
| 80 | 50 | 5 | 0.46 |
| 100 | 50 | 5 | 0.24 |
| 80 | 30 | 10 | 0.20 |
| 100 | 30 | 10 | 0.26 |
| 80 | 50 | 10 | 0.31 |
| 100 | 50 | 10 | 0.52 |
经过多轮迭代进行优化设计的深度神经网络的总体结构如图 5所示。
|
| 图 5 过失速机动融合迎角的偏差修正深度神经网络结构图 Fig. 5 Structural chart of depth neural network for post-stall maneuvering correction of fusion angle of attack |
为了验证冻结风场条件下的过失速大气数据融合与补偿估计方法的有效性和可行性,本文基于飞行试验数据,进行离线计算分析。验证数据来自于训练集之外的多组飞行数据,鉴于篇幅,下面分析中给出的曲线为验证集中的一组。
1) 风速估计与风场冻结的误差分析
图 6为飞机进行过失速大迎角机动前,由论文风速滤波方法得到的20 s时间内的北向、西向和天向风速。

|
| 图 6 过失速大迎角纵向机动前的风速估计曲线 Fig. 6 Estimated wind speed before post-stall longitudinal maneuver at high AOA |
根据飞机飞行速度大小,空间跨度可到1500 m以上,与完成过失速机动的空间区域范围量级相当。图 6中,北向风速和天向风速较稳定,西向风速的变化达到5 m/s(对应的水平风速矢量和的变化量约为3 m/s)。
通常适合飞行的气象条件下,大气环境相对平稳,图 6的结果具有代表性,冻结风场所造成的风速误差可认为在5 m/s的量级,从速度量级上看,该速度误差虽然和1.1节所述过失速机动过程的最小水平速度在一个量级上,但从飞机总速的角度看,相对于过失速机动结束后的三维速度矢量和的量级,相对误差约7%,该误差在分解后对迎角、侧滑角的估计的影响将更小。
2) 迎角融合与补偿分析
图 7为融合迎角与真迎角的曲线,曲线包括大迎角纵向机动和赫伯斯特机动的迎角曲线。图中曲线包括真迎角、冻结风场条件下根据速度矢量计算的融合迎角、采用训练好的深度神经网路对融合迎角进一步修正后的迎角,通过对比可以发现,经过融合计算与深度神经网络修正得到的迎角,与风标传感器的真迎角一致。

|
| 图 7 典型过失速机动的融合迎角与真迎角曲线 Fig. 7 Curves of fused AOA and true AOA in typical post-stall maneuvers |
图 8给出了大迎角纵向机动过程中,冻结风场后由式(6)得到的融合迎角与真迎角的误差曲线、训练后的深度神经网络对该误差的拟合曲线,以及采用深度神经网络的迎角误差输出量修正融合迎角后的迎角误差曲线。对深度神经网络修正后的迎角进行误差统计,误差均方差为0.5°,误差最大值不大于2.3°。

|
| 图 8 大迎角纵向机动的迎角误差拟合与补偿残差曲线 Fig. 8 Curves of AOA error fitting and residual in longitudinal maneuver with high AOA |
将迎角误差修正深度神经网络作用于由多架次飞行数据构成的验证集,可得到各架次、各机动动作的修正结果,进行统计分析。统计结果见表 2。从统计结果看,本文所提出的迎角融合估计与深度神经网络补偿相结合的方法可有效解决过失速机动中的迎角测量难题。
| 机动类型 | 融合迎角 最大相对 误差/(°) |
融合迎角+ DNN补偿 后的最大 相对误差/(°) |
融合迎角+ DNN补偿 后误差均 方差/(°) |
| 大迎角纵向机动 | 0.13 | 0.02 | 0.5 |
| 赫伯斯特机动 | 0.08 | 0.03 | 0.4 |
| 直升机机动 | 0.19 | 0.03 | 0.4 |
| 榔头机动 | 0.12 | 0.03 | 0.5 |
| 大迎角360°滚转 | 0.12 | 0.02 | 0.4 |
3) 总静压与侧滑角的融合估计结果分析
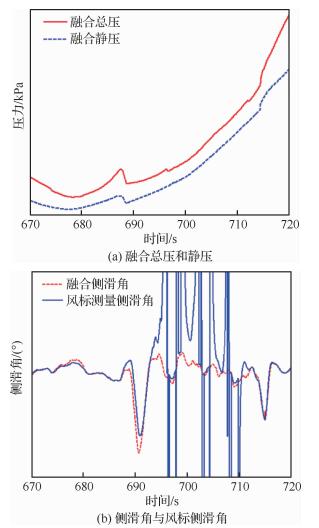
图 9给出了大迎角纵向机动的总静压和侧滑角融合结果,大迎角纵向机动中,总压、静压和侧滑角的直接测量受显著影响。从曲线可以看出,融合得到的总静压与机动前后的总压、静压保持了连续的趋势,分别反映了飞机的速度与高度的变化情况,在测量的总压、静压系统失效情况下,基于冻结的风场数据和地速、高度等信息,可以得到满足飞机过失速机动飞行所需要的总压、静压信息。基于数据融合的侧滑角方法,相对于侧滑角风标传感器,更适合于过失速大迎角机动的飞行过程。
|
| 图 9 大迎角纵向机动时总压、静压和侧滑角曲线 Fig. 9 Curves of fused total pressure, static pressure and fused AOS in longitudinal maneuver with high AOA |
1) 过失速机动为瞬态过程,基于过失速机动前的常规飞行状态估计的风场信息,在过失速机动过程中,冻结风场信息在时间连续性和空间关联性方面的假设合理,飞行试验数据支持了上述假设的合理性。
2) 进入过失速机动状态后,基于冻结的风速信息、地速和惯性姿态、导航参数,可以融合得到总压、静压、迎角、侧滑角等大气参数,相对于大气数据测量得到的信息,融合估计得到参数更符合过失速机动物理过程。
3) 以试飞状态风标传感器的真迎角为基准,对直接融合得到的迎角信息的误差进行研究,利用深度神经网络对复杂非线性问题的拟合能力,对迎角偏差进行拟合,表明:通过过失速飞行状态下的融合迎角和补偿,多个典型过失速机动飞行过程的迎角误差优于2.3°。
4) 风标传感器测量的真实迎角依然受到大迎角气动非定常现象的影响,但为了方便进行对比说明,仍然采用该迎角作为比较的基准。后续需要进行气动非定常对机头空速管风标测量误差的定量研究。
本文研究的方法可以有效解决过失速机动中的大气数据传感问题,对先进战斗机过失速机动的研究和实战化具有重要的意义。
| [1] |
朱纪洪, 张尚敏, 周池军, 等. 飞机超机动状态动力学特征及对控制系统的挑战[J]. 控制理论与应用, 2014, 31(12): 1650-1662. ZHU J H, ZHANG S M, ZHOU C J, et al. Dynamic characteristics and challenges for control system of super-maneuverable aircraft[J]. Control Theory & Applications, 2014, 31(12): 1650-1662. (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [2] |
史忠科. 高性能飞机发展对控制理论的挑战[J]. 航空学报, 2015, 36(8): 2717-2734. SHI Z K. Challenge of control theory in the presence of high performance aircraft development[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2717-2734. (in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [3] |
汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. WANG Q, QIAN W Q, DING D. A review of unsteady aerodynamic modeling of aircraft at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. (in Chinese) |
| Cited By in Cnki (16) | Click to display the text | |
| [4] | HYDE D, BROWN F, SHWEYK K, et al. High angle of attack static and dynamic modeling methods for flight dynamics loss of control research[C]//2018 AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2018. |
| [5] |
张婉鑫, 朱纪洪. 大迎角非定常气动参数辨识研究[J]. 清华大学学报(自然科学版), 2017, 57(7): 673-679. ZhANG W X, ZHU J H. Unsteady aerodynamic identification of aircraft at high angle of attack[J]. Journal Tsinghua University (Science and Technology), 2017, 57(7): 673-679. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [6] | SHI J P, LV Y X, QU X B, et al. A coordinated control method of thrust vector and aerodynamic surfaces based on control allocation technology[C]//2018 18th International Conference on Control, Automation and Systems, 2018. |
| [7] |
汤伟, 黄勇, 傅澔. 推力矢量对飞机大迎角动态气动特性的影响[J]. 航空学报, 2018, 39(4): 121648. TANG W, HUANG Y, FU H. Effect of thrust vector on dynamic aerodynamic characteristics of aircraft at high angle of attack[J]. Acta Aeronautica et Astronatica Sinica, 2018, 39(4): 121648. (in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [8] | HARRIS J. F-35 flight control law design, development and verification[C]//2018 Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2018. |
| [9] |
陈海, 何开锋, 钱炜褀, 等. 基于扩展L1自适应的战斗机大迎角非线性控制[J]. 控制与决策, 2017, 32(8): 1403-1408. CHEN H, HE K F, QIAN W Q, et al. L1 adaptive augmentation for high angle of attack nonlinear control of fighter[J]. Control and Decision, 2017, 32(8): 1403-1408. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [10] |
叶辉, 吴庆宪, 陈谋. 非定常条件下大迎角机动控制[J]. 哈尔滨工业大学学报, 2016, 48(4): 84-90. YE H, WU Q X, CHEN M. Control of high angle of attack maneuver under unsteady aerodynamic condition[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 84-90. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [11] |
陆辰, 李荣冰, 刘建业, 等. 气动模型及导航信息辅助的大气参数估计方法[J]. 控制与决策, 2018, 33(3): 491-496. LU C, LI R B, LIU J Y, et al. Air data estimation method aided by aerodynamic model and navigation information[J]. Control and Decision, 2018, 33(3): 491-496. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [12] | NEBULA F, PALUMBO R, MORANI G. Virtual air data: A fault-tolerant approach against ADS failures[C]//AIAA Infotech at Aerospace Conference, Reston: AIAA, 2013: 1-14. |
| [13] | LANGELAAN J W, SPLETZER J, MONTELLA C, et al. Wind field estimation for autonomous dynamic soaring[C]//2012 IEEE International Conference on Robotics and Automation. Piscataway: IEEE Press, 2012: 16-22. |
| [14] | LI R B, LU C, LIU J Y, et al. Air data estimation algorithm under unknown wind based on information fusion[J]. Journal of Aerospace Engineering, 2018, 31(5): 04018072. |
| Click to display the text | |
| [15] |
焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年:回顾与展望[J]. 计算机学报, 2016, 39(8): 1697-1716. JIAO L C, YANG S Y, LIU F, et al. Seventy years beyond neural networks:Retrospect and prospect[J]. Chinese Journal of Computer, 2016, 39(8): 1697-1716. (in Chinese) |
| Cited By in Cnki (550) | Click to display the text | |
| [16] |
曾毅, 刘成林, 谭铁牛. 类脑只能研究的回顾与展望[J]. 计算机学报, 2016, 39(1): 212-222. ZENG Y, LIU C L, TAN T N. Retrospect and outlook of brain-inspired intelligence research[J]. Chinese Journal of Computer, 2016, 39(1): 212-222. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] |
陈建廷, 向阳. 深度神经网络训练中梯度不稳定线型研究综述[J]. 软件学报, 2018, 29(7): 2071-2091. CHEN J T, XIANG Y. Survey of unstable gradients in deep neural network training[J]. Journal of Software, 2018, 29(7): 2071-2091. (in Chinese) |
| Cited By in Cnki (35) | Click to display the text | |
| [18] |
高晓光, 李新宇, 岳勐琪, 等. 基于深度学习的地空导弹发射区拟合算法研究[J]. 航空学报, 2019, 40(9): 322858. GAO X G, LI X Y, YUE M Q, et al. Fitting algorithm of ground-to-air missile launching area based on deep learning[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(9): 322858. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] |
朱虎明, 李佩, 焦李成, 等. 深度神经网络并行化研究综述[J]. 计算机学报, 2018, 41(8): 1862-1881. ZHU H M, LI P, JIAO L C, et al. Review of parallel deep neural network[J]. Chinese Journal of Computer, 2018, 41(8): 1862-1881. (in Chinese) |
| Cited By in Cnki (42) | Click to display the text |



