大迎角机动能力作为现代战斗机的重要性能指标，在近距离空战中对战斗机快速改变机头指向以提高作战效能和生存几率具有重要意义^[1]。在大迎角机动过程中，飞机背风面流场结构会发生剧烈变化，导致气动力呈现强烈的非线性、非定常特性^[2]，并由此引发了如非定常气动力偏离^[3]等一系列的大迎角空气动力学问题，这对飞机大迎角飞行时的稳定性和可操纵性提出了极大的挑战^[4]。

目前对战斗机大迎角非定常气动特性的研究主要还依赖于风洞试验模拟。由于大迎角非定常气动力无法像小迎角时通过有限次数的风洞试验建立数据库插值获得，因此必须在合理地设计试验方法获取试验数据的基础上建立非定常气动力模型，以获得飞机任意运动状态下的气动力，进而准确分析大迎角气动性能、预测气动力失稳进入偏离的可能性。在此基础上进行过失速机动、尾旋进入/改出等状态的飞行动力学分析、飞行仿真，为控制律设计提供参考依据，并为飞行模拟器提供比较准确的非定常气动力。

近年来，国内外学者围绕大迎角非定常气动力建模方法开展了大量的研究工作。但到目前为止，相关的研究都还处于理论阶段，距离实际工程应用还有一定的距离^[5-6]，且目前的研究大多依赖单自由度风洞试验开展，未充分考虑飞机过失速机动中的多轴耦合特性，因此如何建立能准确反映飞机大迎角多自由度耦合运动中的非定常气动特性且工程适用的非定常气动力模型依然是目前飞机设计、空气动力学、飞行力学等相关领域研究者们共同关注的热点问题之一。

本文简要介绍了目前大迎角非定常气动力建模研究在工程应用中存在的一些问题。针对这些问题，基于偏航-滚转耦合运动风洞试验结果提出了一种大迎角横航向非定常气动力${\dot \beta } $模型。探讨了该模型通过线性化处理进行频率拓展并与目前工程实践中使用的气动导数方法兼容指导飞行动力学分析的可行性。使用该模型计算了不同运动形式中的横航向气动力并进行了飞行仿真研究，验证了该气动力模型的大迎角非定常气动力预测精度，展示了该模型良好的工程适用能力。

1 非定常气动力模型研究现状

到目前为止，国内外学者基于不同原理发展了各种非定常气动力模型，具有代表性的如非线性阶跃响应模型^[7-9]及其各种简化形式^[10-11]、Fourier泛函分析模型^[12-14]、状态空间模型^[15-17]、微分方程模型^[18-21]等，以及模糊逻辑^[22-24]、神经网络^[25-27]、支持向量机^[28-29]等人工智能类模型，在相关研究中都表现出了较高的非定常气动力预测精度。但同时这些非定常气动力模型还存在着诸如对风洞试验方法要求严苛、表达形式过于复杂、系统参数辨识困难以及缺乏明确的物理意义等不足，极大地限制了它们的使用前景。此外，目前的相关研究似乎更关注气动力模型对风洞试验数据的拟合精度，而常常忽视了非定常气动力模型在飞机设计过程中指导偏离敏感性分析、控制律设计等工程实践活动的实际需要。从公开的研究结果来看，微分方程模型因其表达形式更容易与运动方程联立以解决飞行动力学问题，相比其他非定常气动力模型具有更强的工程应用前景，其线性化形式能很好地兼容于现有的工程方法进行大迎角纵向^[30-31]和横航向^[32]的模态分析和增稳控制律设计研究。但在实际应用中，微分方程模型依然存在一些局限。例如作为其主要建模参数的特征时间常数τ在物理意义上表征迟滞效应，因此在参数辨识过程应保证为正值，但文献[32]中对一种飞翼模型进行横航向气动参数识别时，在大迎角状态下出现了τ为负值的情况，文中未就此种情况进行详细解释。此外，有研究显示^[33-34]在大迎角大振幅运动特别是耦合运动中，特征时间常数并非常值。因此如何将微分方程模型应用于大振幅多自由度耦合运动还有待开展进一步的研究。

由于理论研究中的非定常气动力模型无法有效指导工程设计，气动导数仍然是目前飞机大迎角气动特性研究过程中必须的空气动力参数。以横航向气动力矩系数为例，飞机任意运动状态下的气动力为

$ \begin{array}{*{20}{l}} {{C_i} = {C_{i0}} + {C_{i\beta }}\beta + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({C_{ip}} + {C_{i\dot \beta }}{\rm{sin}}{\kern 1pt} {\kern 1pt} \alpha )\bar p + ({C_{ir}} - {C_{i\dot \beta }}{\rm{cos}}\alpha )\bar r} \end{array} $

（1）

式中：C_i=C_l、C_n分别为滚转力矩系数、偏航力矩系数；C_i0为零侧滑力矩系数；C_iβ为静稳定导数；β为侧滑角；p和r分别为无量纲的滚转、偏航角速度；C_ip和C_ir为旋转导数(直接阻尼导数)；${C_{\dot i\beta }} $为非定常导数(加速度导数)。式(1)通常简写为

$ {C_i} = {C_{l0}} + {C_{l\beta }}\beta + {C_{lp}}\bar p + {C_{lr}}\bar r $	（2）

这种表达形式简称为动导数模型，在常规飞行迎角范围内已被广泛使用并验证。

为了研究飞机尾旋运动中的非定常气动力，研究者们又在动导数模型中加入了通过旋转天平试验^[35]获得的旋转速率导数项：

$ {C_i} = {C_{i0}} + {C_{i\beta }}\beta + {C_{ip}}\bar p + {C_{ir}}\bar r + {C_{i\omega }}\bar \omega $	（3）

式中：C_iω为旋转速率导数；ω为绕体轴旋转角速度在风轴上投影的无量纲形式。这种表达形式也被称为混合模型。

目前工程实践中普遍认为大迎角非定常气动力是由迎角、侧滑角速率${\dot \alpha } $和$ {\dot \beta }$贡献的。由于常规动导数中旋转导数和非定常导数通常以组合形式出现，并将其简单等效为旋转速率的影响，因此传统气动导数模型被认为是“准定常”的。为了提高气动导数模型对非定常气动力的描述精度，不少研究机构开展了通过升沉/侧移运动机构将非定常导数与旋转导数分离的研究^[36-39]，但目前工程领域对于如何使用非定常导数还没有形成广泛的共识^[40]。此外，有研究机构通过复杂的试验平台单独获得了旋转导数，将其与升沉/侧移试验获得的非定常导数相加，结果与组合导数在中、大迎角区域存在较大偏差^[41-42]，具体原因还不明确。

另外，常规动导数是通过小振幅试验获得的，试验频率选择没有统一的标准。而大量研究表明动导数在大迎角范围内与运动频率和振幅密切相关^[43-44]，因此近年来有学者提出了使用Duhamel积分法^[45]、单圈平均法^[46]以及线性拟合法^[47]等从大振幅动态试验中提取动导数的方法，获得了较好的结果。对于运动频率的影响，有学者提出使用减缩频率建立动导数试验频率和实际飞行等效频率间的联系^[48]，但在实际飞机运动中获取等效频率的方法需要考虑当前飞行状态前“若干”时间步长内的状态，这一过程具有很大的随意性，且很可能产生误导^[49]，因此如何获得频率相关的动导数仍是目前相关领域的研究重点之一。

此外，本文作者团队^[50]的研究显示，基于单自由度试验的动导数无法准确反映大迎角耦合运动中的非定常气动迟滞特性。而Wang等^[51]的研究则展示了F-16XL验证机试飞中出现的一种未预测到的横向扰动现象，该现象无法通过以往的单自由度气动力模型仿真复现。因此，基于多自由度耦合运动风洞试验开展大迎角非定常气动力建模研究显得十分必要。然而由于试验设备限制等原因，现有的相关研究大多仍基于单自由度运动开展。德国荷兰风洞(DNW)正通过使用多自由度运动平台(MPM)^[52]开展耦合运动中的气动导数辨识研究，获得了一种形式复杂的非线性气动导数模型^[53]。目前该研究只完成了俯仰-偏航耦合运动中的气动导数辨识工作，耦合滚转运动的相关研究还未开展。事实上在飞机飞行过程中，副翼、方向舵的偏转都会同时产生偏航和滚转力矩，飞机很难保持纯粹的单自由度偏航或滚转运动，因此偏航-滚转耦合更为常见和复杂。试验研究表明^[54]飞机在大迎角横航向耦合运动中的气动迟滞特性会随耦合程度的不同而剧烈变化，而目前对于横航向耦合运动中的非定常气动力建模研究还有待开展。

综上所述，目前的大迎角非定常气动力模型研究还存在诸多不足，还应充分考虑多自由度耦合的影响，进一步提高模型预测精度以满足工程应用需求。此外，所建立的非定常气动力模型还应具有简洁的表达形式和清晰的物理意义，并能通过适当的方法与飞机运动方程联立，以满足稳定性分析、控制律设计等工程应用的实际需要。

2 非定常气动力$ {\dot \beta }$模型 2.1 偏航-滚转耦合运动风洞试验

目前国内外学者对于大迎角非定常气动力建模的研究大多基于单自由度风洞试验，对于多自由度耦合特别是偏航-滚转耦合运动的相关研究则开展较少。以南京航空航天大学NH-2风洞中进行的某战斗机构型模型大迎角偏航-滚转耦合运动风洞试验为基础，进行了横航向非定常气动力的建模研究。风洞试验支撑迎角θ_j范围为20°~70°，试验频率f范围为0~0.7 Hz。

试验中，通过引入参数耦合比η来表征横航向运动的耦合程度：

$ \eta = \left| {{\kern 1pt} {\kern 1pt} \frac{r}{p}{\kern 1pt} {\kern 1pt} } \right| $	（4）

式中：r为偏航角速度；p为滚转角速度。在试验中可以通过分别调整偏航、滚转运动振幅获得期望的耦合比数值。在每个支撑迎角下，选取了7组耦合比使其α-β曲线能均匀地分布在从单自由度滚转到单自由度偏航的整个横航向运动区域，以充分反映偏航-滚转耦合效应对非定常气动力的影响。图 1给出了支撑迎角20°时7组耦合比运动中的α-β曲线，其他支撑迎角下类似。试验结果表明，当η≥10时，运动产生的气动力与单自由度偏航运动中的气动力已基本一致，因此本文均使用η=10代表单自由度偏航运动。

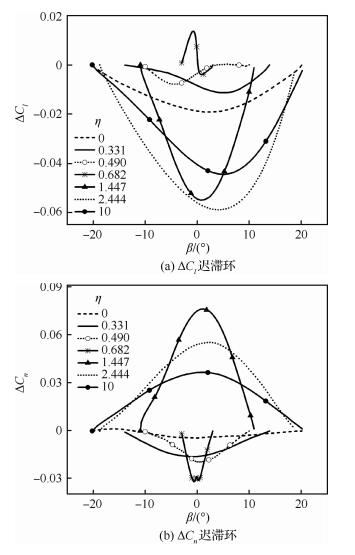
试验结果显示，对于本文研究的试验模型，从支撑迎角35°开始，部分耦合比运动中的横航向气动力迟滞环呈现明显的“8”字形。图 2给出了该支撑迎角下，频率为0.5 Hz时各组耦合运动中侧滑角从负到正变化的半个周期内的横航向力矩系数动态增量(从动态试验值中扣除静态值)。在耦合比η≈tanθ_j附近，滚转力矩系数会在侧滑角较小时发生阻尼特性(数值正负，负的滚转力矩和正的偏航力矩表示动态气动力呈正阻尼特性)的突变。

由于篇幅所限，具体试验细节与其他支撑迎角下的试验结果参见文献[54]。

2.2 建模方法

飞机运动中的动态气动力是由旋转矢量Ω和速度矢量V引起的。在飞行动力学分析中，和旋转相关的参数是快变分量，比与平移运动相关的慢变分量对飞机动态稳定性的影响更大^[55-56]，且目前的风洞试验大多以转动运动形式开展，因此本文主要研究旋转矢量产生的非定常气动力，并以偏航、滚转力矩系数为主要对象进行讨论。

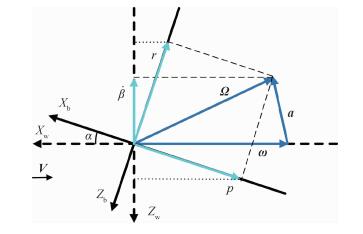
对于旋转矢量Ω，其对飞机动态气动特性的影响由它的模(旋转速率的快慢)和方向(引起的飞机姿态变化)两部分构成。在横航向运动中，Ω是滚转、偏航角速度的合矢量。如图 3所示，首先将其按模的大小$ \left| \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right| = \sqrt {{p^2} + {y^2}} $投影到速度轴上，得到向量ω。于是由飞机旋转运动引起的动态气动力可以分解为分别由向量ω和a两部分产生。图中下标b表示体轴系坐标轴，下标w表示风轴系坐标轴。

同时，侧滑角速率${\dot \beta } $是矢量Ω在速度轴垂直轴上的投影，而ω为绕速度轴转动的矢量，不会引起侧滑角的变化，因此${\dot \beta } $与矢量a可以建立一一对应的关系，该部分气动力即为由Ω引起的姿态变化${\dot \beta } $产生。于是，横航向运动中的动态气动力可以分解为旋转矢量的模贡献的非定常气动力和旋转矢量引起的姿态变化${\dot \beta } $贡献的非定常气动力两部分。

在建模过程中，矢量Ω产生的非定常气动力可以由偏航-滚转耦合运动风洞试验获得。向量ω产生的气动力可以直接由旋转天平试验(偏航-滚转耦合的一种特殊形式)获得。两部分相减即可得到${\dot \beta } $产生的非定常气动力。于是，${\dot \beta } $模型中的气动力可以表示为

$ \begin{array}{*{20}{l}} {{C_i} = {C_{i,{\rm{ static }}}}(\alpha ,\beta ) + \Delta {C_{i,\dot \beta }}(\alpha ,\beta ,\dot \beta ,\eta ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {C_{i,\omega }}(\alpha ,\beta ,\omega )} \end{array} $

（5）

式中：i=l, n；C_{i, static}为静态气动力；$ \Delta {C_{i, \dot \beta }}$和δC_iω, _ω分别为由${\dot \beta } $和ω产生的气动系数动态增量；括号中为各分量的建模参数(其中ω为矢量的模，ω指向来流方向时ω数值为正)，建模过程中可以使用代数多项式拟合算法、模糊逻辑算法、神经网络算法等不同方法建立非定常气动力数据库。本文采用代数多项式拟合方法进行气动力建模。

相比传统气动导数模型，${\dot \beta } $模型充分考虑了偏航-滚转耦合效应对飞机大迎角横航向气动阻尼特性的影响。此外，混合模型中的旋转矢量投影方式具有一定的随意性，最常用的为垂直投影，在扣除相应的旋转天平试验结果后其余的动态气动力仍由常规动导数表示，这种方法放大了旋转矢量的模对气动力的“准定常”影响而弱化了姿态变化${\dot \beta } $对横航向非定常气动力的贡献。而${\dot \beta } $模型的分解方法能彻底将旋转矢量的大小和方向对横航向气动力的影响(类似于动导数概念中的直接阻尼导数和非定常导数两项的影响)分离开来。

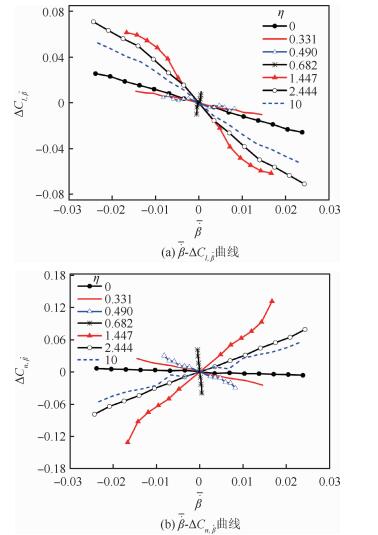
图 4给出了支撑迎角35°时，不同耦合比运动中β=0°处由${\dot \beta } $引起横航向非定常气动力曲线，横坐标为无量纲化的侧滑角速率($\bar{\dot{\beta }}=\dot{\beta }b/2V$，b为模型展长，V为试验风速)。可以看到，图中曲线是近似线性的，其斜率与动导数概念中的非定常导数类似。不同的是，通过侧移运动获得的非定常导数在每一迎角下是唯一的，而通过模型获得的非定常气动力曲线斜率在大迎角状态下会随耦合比的不同而呈现明显的区别，甚至反号。由此可见，模型相比气动导数模型更能准确体现大迎角耦合运动中的非定常气动特性。

2.3 运动频率的拓展

运动频率是影响大迎角非定常气动力的重要因素。由于试验设备的限制，偏航-滚转耦合运动风洞试验中的模型运动频率可能达不到高机动动作中的实际频率，而${\dot \beta } $模型中非定常项的线性特性为运动频率的拓展提供了可能。

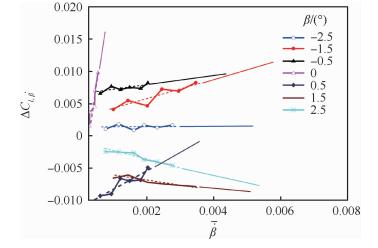
以图 2中迟滞环形状最复杂的η=0.682运动中的滚转力矩系数为例，首先对不同侧滑角下的$\bar{\dot{\beta }}-\Delta {{C}_{l,\dot{\beta }}}$曲线进行延伸，图 5给出了该耦合比运动中部分侧滑角下的曲线及其线性延长线。当运动频率大于试验频率时，首先求出运动参数${\dot \beta } $，再按其无量纲值在相应侧滑角的延长线上获得对应的气动力矩系数。而模型中的准定常项来源于旋转天平试验，其旋转速率通常已经足够大，可以根据相应的旋转角速度ω直接获得。于是可以得到需求频率下的动态气动力。

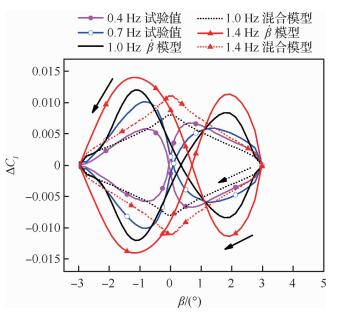
图 6给出了该组耦合比运动将频率拓展到1.0 Hz和1.4 Hz后的滚转力矩系数迟滞环，同时给出了使用混合模型的计算结果。可以看到，模型拓展的这两组超出试验频率范围的运动中的滚转力矩系数迟滞环变化规律与试验频率下一致，且“8”字环各部分的方向与小频率试验值完全一致。而混合模型计算结果为一个单方向的迟滞环，随着频率的增大只是单纯地扩大了迟滞环的面积，并不能准确反映该运动规律中随侧滑角变化的气动阻尼特性。可见，相比常规动导数方法，模型对超出试验频率的运动状态中的非定常气动力预测结果更为可信。

3 ${\dot \beta } $模型的验证

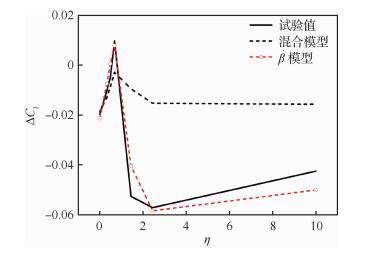
为了研究上述非定常空气动力${\dot \beta } $模型的适用性，将几种不同类型试验方法获得的试验数据和模型计算结果进行比较。由于目前对于偏航-滚转耦合运动中的非定常气动力建模研究还未开展，工程实践中依然使用传统气动导数模型进行相关气动力的计算，同时给出了相对更能反映横航向耦合效应的混合模型计算结果进行对比。

3.1 拟合样本数据

分别使用${\dot \beta } $模型和混合模型计算图 2中β=0°处的滚转力矩系数，如图 7所示。可以看到混合模型计算结果的量值在大部分耦合比区域与试验值有较大差距，更重要的是，混合模型无法准确反映滚转力矩在η≈tanθ_j区域内阻尼特性的突变，这很可能会在偏离敏感性分析和飞行仿真中导致错误结果。${\dot \beta } $模型无论在量值大小还是阻尼特性方面都能准确地反映该迎角下非定常气动力随耦合比变化的规律，相比混合模型精度更高

由于${\dot \beta } $模型的样本数据来自偏航-滚转耦合运动风洞试验，而使用各种气动力模型反算样本数据得到的结果通常与样本数据吻合度都很高，对于验证模型的准确性没有太大的说服力。因此，下文将使用${\dot \beta } $模型计算不同来源、不同运动方式的风洞试验中的气动力并与试验数据进行比较，以验证${\dot \beta } $模型的适用性，所有原始试验数据来自于中国航空工业空气动力研究院。

3.2 “不协调”运动

在小迎角常规机动中，出于使飞机进行协调转弯的考虑，通常横航向运动中滚转角速度和偏航角速度是同号的(国标坐标系下)。然而在大迎角过失速机动过程中，不可避免地会出现p和r异号的飞行状态。这种运动状态简称为“不协调”运动。

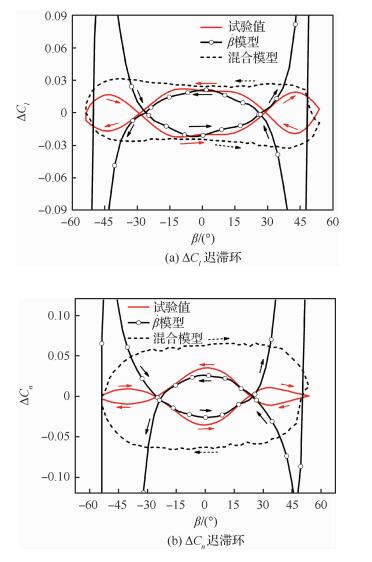
图 8给出了一组支撑迎角50°，频率0.6 Hz的“不协调”运动中的横航向气动力矩系数动态增量，同时给出了模型和混合模型的计算值。该运动规律为

$ \left\{ {\begin{array}{*{20}{l}} {{\psi _j} = {{40}^\circ }{\rm{cos}}(2\pi ft)}\\ {{\phi _j} = {{40}^\circ }{\rm{cos}}(2\pi ft)} \end{array}} \right. $	（6）

在“不协调”运动中，侧滑角最大振幅达到了±55°左右，不论是滚转力矩系数还是偏航力矩系数，其动态阻尼特性都随侧滑角变化而反复变化，试验值都由3个不同方向的迟滞环构成。由于${\dot \beta } $模型样本数据中最大侧滑角约±20°(如图 2所示)，因此${\dot \beta } $模型计算不协调运动中侧滑角远超样本数据范围的气动力时，其计算结果逐渐发散。但${\dot \beta } $模型准确地反映出了滚转力矩系数迟滞环在β=±30°左右出现的交点，且计算值迟滞环各部分方向与试验值完全一致，即模型能准确反映横航向气动力随侧滑角的阻尼变化规律。而在－30° < β < 30°范围内，模型计算结果能很好地与试验值吻合。对于侧滑角β >30°时的气动力，可以通过采用更大振幅的偏航-滚转耦合运动试验数据进行建模，从根本上解决${\dot \beta } $模型在计算超大侧滑角下气动力时数值发散的问题。因此，${\dot \beta } $模型总体上能准确反映“不协调”运动中的横航向非定常气动特性。

相比之下，混合模型计算结果都是单方向迟滞环。对于滚转力矩迟滞环，在侧滑角较小时其方向和数值大小都与试验值较为一致。在超大侧滑角下，混合模型计算值虽然没有出现数值发散的情况，但也没有准确反映真实的阻尼特性变化。对于偏航力矩系数迟滞环，在小侧滑角范围内，试验值迟滞环方向显示偏航力矩呈发散特性，但混合模型计算值是呈收敛性的。

总的来说，不论对于“协调”还是“不协调”偏航-滚转耦合运动中的横航向非定常气动力，${\dot \beta } $模型计算结果相比混合模型都更为准确。

3.3 旋转流场叠加单自由度运动 3.3.1 旋转流场下的滚转运动

继续比较旋转流场中叠加单自由度滚转运动时的横航向气动力矩系数。该试验在旋转天平动态试验台上实现，试验支撑迎角为50°，运动频率为0.4 Hz，运动规律为

$ \left\{ {\begin{array}{*{20}{l}} {\omega = 2\pi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rad}}/{\rm{s}}}\\ {{\phi _j} = {{30}^\circ }{\rm{cos}}(2\pi ft)} \end{array}} \right. $	（7）

事实上，该运动也属于偏航-滚转耦合运动。由于前文混合模型计算值与试验值比较结果已经充分说明在大迎角范围内该方法并不能准确反映横航向气动力的迟滞特性，因此混合模型的计算结果不再讨论。

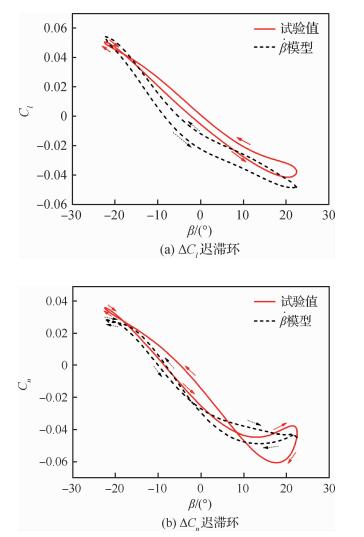
图 9分别给出了运动过程中滚转力矩系数和偏航力矩系数的试验值和${\dot \beta } $模型计算值的比较结果。在β∈[－22.5°, －18.8° ]区间内，滚转力矩系数试验值有一个很小的顺时针迟滞环，虽然${\dot \beta } $模型并没有反映这一微小变化，但在绝大部分侧滑角范围内，模型计算值与试验值迟滞环方向一致，都为逆时针方向。

偏航力矩系数迟滞环较为复杂，由3个不同方向的迟滞环组成。虽然试验值中在β=8°附近的迟滞环交点在计算值中左移至β=0°附近，但总体上${\dot \beta } $模型很好地复现了迟滞环方向的变化规律，各部分阻尼特性与试验值一致。

3.3.2 旋转流场下的偏航运动

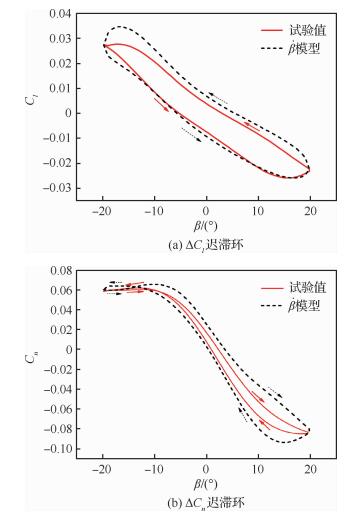
图 10给出了旋转流场叠加单自由度偏航运动中的模型计算值与试验值的对比结果，该运动支撑迎角同样为50°，频率为0.4 Hz，运动规律为

$ \left\{ {\begin{array}{*{20}{l}} {\omega = 2\pi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rad}}/{\rm{s}}}\\ {{\phi _j} = {{30}^\circ }{\rm{cos}}(2\pi ft)} \end{array}} \right. $	（8）

由于滚转力矩系数迟滞环较为简单，因此${\dot \beta } $模型计算结果与试验值重合度极好，且迟滞环方向一致。偏航力矩系数在较大的负侧滑角时有一个逆时针的小迟滞环，其余侧滑角区域为明显的顺时针稳定的迟滞环。${\dot \beta } $模型很好地计算出了“8”字形迟滞环，交点位置也较为准确，总体上准确地反映偏航力矩的大小和阻尼特性。

总的来说，使用${\dot \beta } $模型计算旋转流场下叠加单自由度滚转或偏航运动中横航向气动力，计算结果不论是气动力矩系数的量值还是其阻尼特性都能较准确地与试验值吻合。

上述的算例本质上都是不同形式的偏航-滚转耦合运动，结果表明${\dot \beta } $模型能很好地反映飞机在不同形式大迎角横航向运动中的非定常气动特性。

3.4 纵向与横航向耦合运动

在实际大迎角机动飞行中，飞机运动大多是多自由度耦合的，而${\dot \beta } $模型是基于不同支撑迎角下的偏航-滚转耦合运动风洞试验结果建立的，并没有考虑纵向运动与横航向运动的耦合效应，因此有必要对${\dot \beta } $模型在纵向运动中的使用限制进行评估。

3.4.1 俯仰-滚转耦合运动

首先使用${\dot \beta } $模型计算俯仰-滚转耦合运动中的横航向气动力矩系数，试验迎角变化范围为0°~80°，滚转机构角变化范围为±40°，运动频率为0.8 Hz，运动规律为

$ \left\{ {\begin{array}{*{20}{l}} {{\alpha _j} = {{40}^\circ } - {{40}^\circ }{\rm{cos}}(2\pi ft)}\\ {{\phi _i} = {{40}^\circ }{\rm{cos}}(2\pi ft)} \end{array}} \right. $	（9）

由于本文主要研究动态运动对非定常气动特性的影响，使用${\dot \beta } $模型计算俯仰-滚转耦合运动中的滚转、偏航力矩系数时，静态气动力直接从俯仰运动风洞试验结果中提取得到。

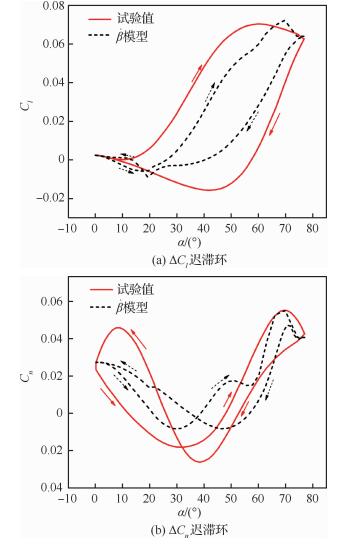
图 11给出了${\dot \beta } $模型计算值与试验值的比较结果。

对于滚转力矩系数，${\dot \beta } $在迎角很小时，风洞试验值几乎没有迟滞，而${\dot \beta } $模型计算结果在迎角小于18°时有一个逆时针的迟滞环，但迟滞环面积不大。当迎角大于18°以后${\dot \beta } $，模型计算结果形成的迟滞环总体面积略小于风洞试验结果，但两者迟滞环方向是一致的。

对于偏航力矩系数，${\dot \beta } $模型计算得到的迟滞环交点处的迎角值相比试验结果略有增大。在25°~45°的迎角区域，计算值迟滞环曲线整体比试验值有所上移。

总体而言，${\dot \beta } $模型能较好地复现俯仰-滚转耦合运动中横航向的非定常气动迟滞特性。

3.4.2 俯仰-偏航耦合运动

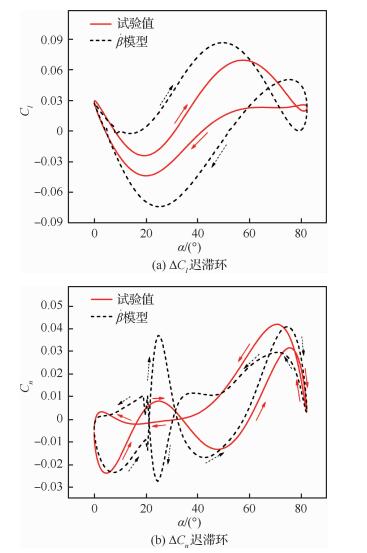
图 12给出了俯仰-偏航耦合运动中的横航向气动力试验值与${\dot \beta } $模型计算结果。运动规律为

$ \left\{ {\begin{array}{*{20}{l}} {{\alpha _j} = {{40}^\circ } - {{40}^\circ }{\rm{cos}}(2\pi ft)}\\ {{\psi _j} = {{40}^\circ }{\rm{cos}}(2\pi ft)} \end{array}} \right. $	（10）

运动频率为0.8 Hz。同样地，运动过程中静态气动力直接提取自纵向运动风洞试验结果。

相比俯仰-滚转耦合运动，俯仰-偏航耦合运动形式相对简单，因此对横航向非定常气动力的影响更小，${\dot \beta } $模型基本上能准确反映滚转力矩与偏航力矩随迎角变化的阻尼特性改变情况。整体而言，${\dot \beta } $模型计算得到的滚转力矩系数和偏航力矩系数在部分迎角区域内的迟滞环面积稍大于试验值，且迟滞环交点稍微有所偏移，但计算值与试验值的迟滞环方向是一致的。

相比偏航-滚转耦合运动，${\dot \beta } $模型对于纵向与横航向耦合运动中横航向非定常气动力的计算结果与试验值略有差别，分析其原因可能为

1) ${\dot \beta } $模型在建模过程中并未计入俯仰运动对横航向非定常气动力的影响，因此可能在计算横航向气动力的过程中引入了误差。

2) 本文中${\dot \beta } $模型的建模样本数据支撑迎角范围为20°~70°，因此在计算迎角远离该区域的气动力时可能会存在一定的误差。

但即便如此，${\dot \beta } $模型也已经能较准确地反映各类不同运动中的气动迟滞特性。而在飞行仿真等实际应用中，气动力的动态阻尼特性相比其量值对分析结果的准确性更为重要，因此${\dot \beta } $模型可以满足实际工程设计中的精度要求。

综上所述，大量计算值与试验值的比较表明，使用${\dot \beta } $模型计算各类不同运动中的横航向非定常气动力得到的结果是可信的。本文采用在不同迎角下分别进行偏航-滚转耦合运动风洞试验，将横航向运动与纵向运动解耦再进行非定常气动力建模的思路是可行的。

3.5 尾旋运动

尾旋是飞机最危险的失控运动之一，对于每个新型飞机都必须要进行尾旋动力学的研究，并在设计阶段就充分考虑如何防止飞机进入尾旋，研究进入尾旋后的动力学特性以及改出尾旋的相应措施。目前研究尾旋的手段一般有立式风洞试验、大比例尺遥控模型试飞、真机试飞以及使用气动力模型进行数值仿真等，而混合模型是工程实践中研究飞机尾旋特性最常用的气动力模型。因此，本节分别使用混合模型与${\dot \beta } $模型进行尾旋仿真研究，并与立式风洞试验结果进行比较，验证${\dot \beta } $模型在尾旋研究中的适用性。

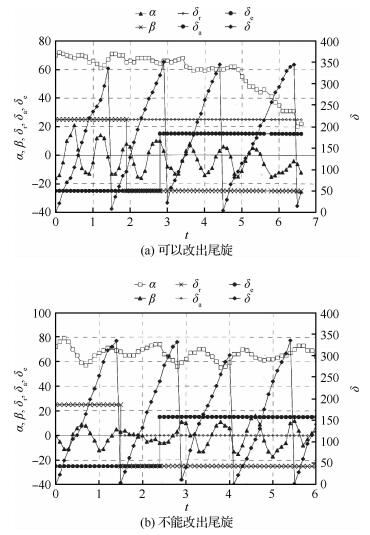
立式风洞试验结果^[57]表明，对于本文研究的试验模型，当其进入平均迎角70°左右的平尾旋(左尾旋)时，必须先反向偏转副翼和方向舵，待飞机旋转运动明显减缓时迅速偏转升降舵使飞机低头才能改出尾旋(如图 13(a)所示)。而如果将副翼偏转归零，仅反向偏转方向舵则无法改出尾旋，而是进入一个迎角振荡幅度更小、侧滑角振荡幅度更大的尾旋(如图 13(b)所示)。图中δ_r、δ_a和δ_e分别表示方向舵、副翼和升降舵偏转量；δ为航向角变化量。

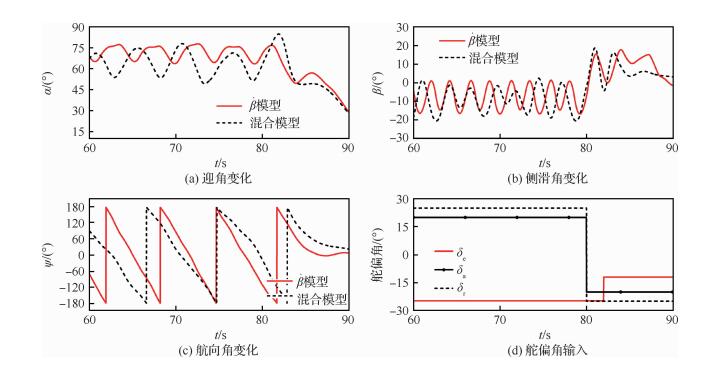
分别使用${\dot \beta } $模型和混合模型对图 13(a)中同时偏转副翼和方向舵改出尾旋的情形进行仿真，结果如图 14所示。在立式风洞试验中，模型是直接投放的，由于缺少投放初始时刻的旋转角速度等相关运动参数，仿真无法从相同的尾旋状态直接开始，本文通过将飞机从小迎角定直平飞中快速拉起，然后同时偏转副翼和方向舵使飞机进入平均迎角、侧滑角以及尾旋周期(对于缩比模型，尾旋中的时间尺度约为全尺寸飞机的$1/\sqrt K $，K为缩比因子，在本次立式风洞试验中K=12)与立式风洞试验一致的尾旋状态。由于进入尾旋的方式不同，仿真结果与试验结果的舵面偏转量稍有区别，但这对尾旋状态没有本质的影响，也不影响本文对尾旋改出的研究，因此图 14中并未给出尾旋的进入过程，以便于直观对比仿真结果与试验结果。

${\dot \beta } $模型仿真结果显示当飞机进入平均迎角与试验结果一致(约70°)的稳定左尾旋时，尾旋周期约6 s(根据缩比关系这与试验结果基本一致)，侧滑角振幅略小于试验结果，但平均值差别不大。而混合模型仿真结果显示稳定尾旋阶段迎角振幅较大，平均值约65°，尾旋周期约8 s，侧滑角振荡幅度也略小于试验值。根据尾旋稳定阶段的迎角、侧滑角以及尾旋周期等参数可以判断两种模型所仿真的尾旋状态与立式风洞结果基本一致。

通过先反向偏转副翼和方向舵，2 s后推杆的方式，两种模型都显示飞机可以顺利改出尾旋。总体来说，对于这种可以改出尾旋的状态，${\dot \beta } $模型仿真结果与立式风洞试验结果几乎完全一致。混合模型仿真结果除了纵向振荡幅度和尾旋周期略大于试验值，基本能反映改出尾旋过程中的相关特征。${\dot \beta } $模型和混合模型仿真结果并未显示出本质上的差异。

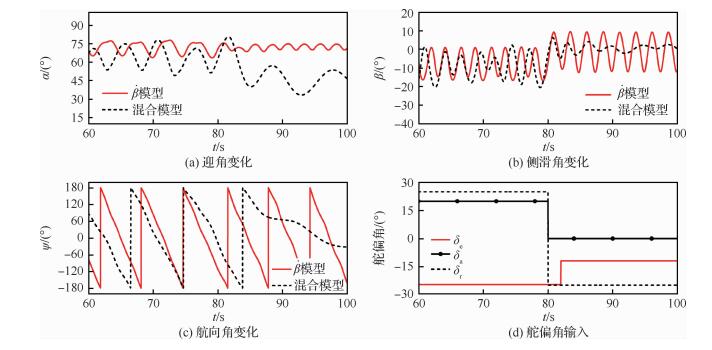
图 15分别给出了两种模型对于试图通过单独偏转方向舵使飞机改出尾旋的情形进行仿真的结果。仿真中飞机进入尾旋的方式以及尾旋状态与前一算例相同。当飞机进入稳定的尾旋状态后，将副翼归零，同时反向偏转方向舵，2 s后向前推杆。

可以看到，混合模型仿真结果显示飞机直接改出了尾旋。事实上，混合模型只需要直接松杆使副翼和方向舵偏转归零，而并不用反向偏转舵面即可直接改出尾旋，由于篇幅原因这里不再给出具体的状态曲线。

${\dot \beta } $模型仿真结果显示飞机进入了另一种尾旋，并且纵向振幅大幅减小，而侧滑角振荡幅度大为增加，这与图 13(b)中的立式风洞试验结果完全一致。

通过对比可以发现，基于偏航-滚转耦合运动风洞试验数据建立的${\dot \beta } $模型在进行尾旋仿真时比基于小振幅动导数风洞试验和旋转天平试验的混合模型更能准确反映尾旋过程中的细节特征。

4 ${\dot \beta } $模型在飞行动力学分析中的应用 4.1 横航向偏离敏感性分析

进行飞行动力学分析、指导大迎角偏离敏感性分析和控制律设计等实际工程应用是非定常气动力建模研究的重要任务之一，也是目前大多数非定常气动力模型面向的工程问题。

在${\dot \beta } $模型中，气动力由静态项、绕速度轴旋转引起的“准定常”项和${\dot \beta } $引起的非定常项组成。其中，静态项、绕风轴旋转项可以直接使用传统的静稳定导数、旋转速率导数表示。对于非定常项，在每个迎角下是β、${\dot \beta } $和η的函数，由第2节的讨论可知当侧滑角和耦合比固定时它是近似线性的。因此，${\dot \beta } $模型可以在不同侧滑角、不同耦合比下表示成局部线性化形式：

$ {{C}_{i}}={{C}_{i0}}+{{C}_{i\beta }}\beta +C_{i\dot{\beta }}^{\prime }\bar{\dot{\beta }}+{{C}_{i\omega }}\bar{\omega } $	（11）

式中：i=l、n。需要注意的是，其中${{C'}_{\dot i\beta }} $是图 4和图 5中气动力非定常项的曲线斜率，而非动导数概念中的非定常导数。

在横航向运动中，有

$ {\dot \beta = p{\kern 1pt} {\rm{sin}}\alpha - r{\kern 1pt} {\rm{cos}}\alpha } $	（12a）

$ {\omega = p{\kern 1pt} {\rm{cos}}\alpha + r{\kern 1pt} {\rm{sin}}\alpha } $	（12b）

将式(12)与式(11)联立，可以将${\dot \beta } $模型表示成线性化形式：

$ \begin{array}{*{20}{l}} {{C_i} = {C_{i0}} + {C_{i\beta }}\beta + (C_{i\dot \beta }^\prime {\rm{sin}}\alpha + {C_{i\omega }}{\rm{cos}}\alpha )\bar p + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - C_{i\dot \beta }^\prime {\rm{cos}}\alpha + {C_{i\omega }}{\rm{sin}}\alpha )\bar r} \end{array} $

（13）

式(13)与传统动导数模型表达形式十分类似，将括号中的项理解为不同耦合比运动中名义上的“动导数”，即可实现${\dot \beta } $模型与现有工程设计方法的衔接，进而指导稳定性分析和增稳控制律设计，使${\dot \beta } $模型具备了较好的工程适用性。

分别使用${\dot \beta } $模型和混合模型对本文所研究的飞机进行横航向偏离敏感性分析。通过忽略长周期螺旋模态使横航向运动方程降为三阶，根据开环特征方程系数可得飞机横航向稳定条件为^[58]

$ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\dot \beta }} = - \left( {{C_{lp}} + \frac{{{I_x}}}{{{I_z}}}{C_{nr}}} \right) > 0}\\ {{\sigma _\beta } = {C_{n\beta }}{\rm{cos}}\alpha - \frac{{{I_z}}}{{{I_x}}}{C_{l\beta }}{\rm{sin}}\alpha > 0}\\ {{\sigma _\omega } = {C_{l\beta }}{C_{n\omega }} - {C_{n\beta }}{C_{l\omega }} > 0}\\ {R = {\sigma _{\dot \beta }}{\sigma _\beta } - {\sigma _\omega } > 0} \end{array}} \right. $

（14）

将静稳定导数、旋转速率导数、传统动导数和通过${\dot \beta } $模型获得的名义动导数代入式(14)，即可获得各迎角下的横航向稳定性判据。

图 16给出了较典型的4个迎角下的稳定性分析结果，其中σ_β和σ_ω只与静稳定导数和旋转速率导数有关，因此两种模型分析结果相同。

对于${\dot \beta } $模型，其分析结果显示当迎角小于或等于30°时，飞机横航向是稳定的。从迎角35°开始，飞机在部分耦合比区域内会出现横航向失稳。而混合模型在每个迎角下只有唯一一组判断结果，在这4个迎角下都显示飞机是动态稳定的。此外，混合模型分析结果与${\dot \beta } $模型中单独滚转和单独偏航两组状态下的分析结果较为接近，这可能与常规动导数获取自这两种单自由度运动有关。

4.2 纵向振荡中的侧向扰动仿真

在F-16XL试飞研究中发现^[51]，当飞机在迎角10°~30°之间振荡时给予一个横向小扰动，当扰动消除后，随着迎角的振荡运动，每当迎角接近30°附近，侧滑角都会出现3°左右的振荡。这种偏离现象无法通过传统偏离敏感性分析方法预测，也无法通过现有的单自由度模型进行理论解释或仿真复现。

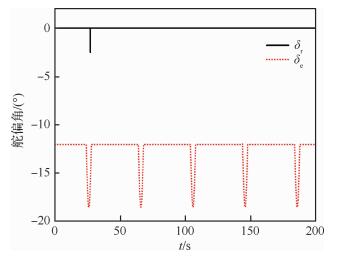
本文认为这种侧向扰动现象与图 16中呈现的飞机在大迎角部分耦合比区域内横航向失稳的特性有关。为验证这一设想，针对本文所研究的飞机设计了一种类似的运动进行仿真分析。鉴于前文中${\dot \beta } $模型预测的偏离临界迎角为35°，因此设计的运动首先以迎角22°迎角平飞进入，通过正弦脉冲式操纵升降舵使迎角最大值达到约37°。当迎角第一次达到35°时，通过偏转方向舵-2.5°并保持0.2 s给予飞机一个侧向小扰动，舵面操纵规律如图 17所示。

图 18分别给出了${\dot \beta } $模型和混合模型的仿真结果。${\dot \beta } $模型仿真结果显示当飞机进入纵向振荡后，每当迎角接近35°时，侧滑角相应地会产生约-3°的振荡，这与F-16XL试飞中出现的现象几乎完全一致。而混合模型给出的仿真结果显示，只有在方向舵给出扰动的瞬间，飞机出现了约0.2°的侧滑角抖动，当扰动撤销后，侧滑角振荡迅速消失，并不再随迎角的变化而产生变化，这也与文献[51]中的仿真结果一致。

两种气动力模型仿真结果的区别可以从两者的偏离动态判据分析结果中发现一些端倪。混合模型预测结果显示仿真迎角区域内飞机横航向动态稳定，而${\dot \beta } $模型预测结果显示飞机在迎角35°的一小段耦合比区域内会出现横航向失稳。这段耦合比区域内，${\dot \beta } $模型的训练样本数据对应的偏航-滚转耦合运动试验只有一组。为了证明这种侧向扰动现象是由这段不稳定耦合比区域内的非定常横航向气动力矩引起的，将这组试验数据从${\dot \beta } $模型样本数据中剔除，其余气动力和舵面操纵规律保持不变，侧滑角变化规律仿真结果如图 19所示，与混合模型几乎完全一致。

由此证明，该扰动现象正是由大迎角状态下部分耦合比区域内横航向动态失稳引起的。以往的非定常气动力模型由于模糊了耦合比对非定常气动力阻尼特性的影响，因此无法准确预测或复现该现象。同时，这也证明了${\dot \beta } $模型在不同耦合比下进行局部线性化处理进行飞行动力学分析是合理且准确的。

与偏离敏感性分析方法类似，通过将${\dot \beta } $模型进行线性化处理还能将其应用于控制律设计的相关研究^[59]，由于篇幅限制本文不再展开叙述。

5 结论

1) 相比传统气动导数模型，${\dot \beta } $模型能清楚地将分别由绕体轴旋转矢量的模产生的“准定常”气动力与旋转矢量引起的姿态变化${\dot \beta } $产生的非定常气动力完全分离开。相比传统动导数方法，该建模方法能更准确地描述${\dot \beta } $对大迎角横航向气动力的非定常影响，同时能简单有效地进行运动频率的拓展。

2) 对于不同形式横航向耦合运动中的气动力计算以及尾旋仿真研究结果显示，由于充分考虑了偏航-滚转耦合效应对大迎角非定常气动特性的影响，${\dot \beta } $模型相比混合模型具有更高的非定常气动力预测精度。

3) 使用${\dot \beta } $模型计算了纵向与横航向耦合运动中的偏航、滚转力矩系数，与风洞试验值的对比结果表明，${\dot \beta } $模型能准确反映这类运动中的非定常气动力迟滞特性，本文采用的将横航向运动与纵向运动解耦再进行非定常气动力建模的思路是可行的。在后期研究中加入$ {\dot \alpha }$的影响可以进一步提高${\dot \beta } $模型的精度。

4) ${\dot \beta } $模型结构简单、物理意义清晰，其特殊的气动力分解方法使其具备进行局部线性化的能力，从而能与现有的偏离敏感性分析、控制律设计工程方法相兼容。使用${\dot \beta } $模型仿真复现并理论解释了F-16XL试飞中出现的侧向扰动现象，这是以往的非定常气动力模型无法实现的。相比目前基于单自由度运动的非定常气动力模型，${\dot \beta } $模型不仅具有较高的精度，还具有较好的工程适用前景。