近年来,随着美国太空探索技术公司的猎鹰-9(Falcon 9)火箭一子级多次成功返回及重复使用,垂直起降可重复使用运载火箭子级返回技术由于可大幅降低航天发射成本、减少航天发射周期,引起了国内外学者的广泛关注[1-2]。火箭子级返回过程中,需要利用有限的控制能力实现大范围减速,且满足过程约束和苛刻的定点垂直着陆终端约束(如:位置、速度、航迹角等)[3]。同时,要尽量减少燃料消耗以提高火箭运载能力并应对突发情况。除此之外,火箭在着陆返回时最小推力通常要远大于火箭自身重力,因此火箭无法靠悬停等动作调整位置与姿态,而必须持续减速,这对制导控制也提出了更高的要求。子级返回制导可描述为复杂多约束条件下的最优控制问题,传统的上升段或经典再入制导方法难以直接应用。
早年间已经有大量关于有动力软着陆制导方法的研究,文献[4-5]针对月面着陆问题,将加速度表示为时间的二次函数,实时计算闭环形式的解析制导律,但无法应对推力限幅的情况[6];之后几十年间,数值方法和近似方法被逐渐提出,非线性最优控制被越来越多地应用到火箭垂直软着陆制导问题上。Sostaric和Rea[7]将Legendre伪谱法应用到火星和月球多约束定点着陆制导问题上,将最优控制问题转换为非线性规划问题进行求解。但非线性规划求解耗时长,收敛速度慢,无法应用于在线制导,而开环优化又无法克服模型误差和干扰等问题。
近年来,Acikmese等[8-9]将凸优化方法成功应用于火星软着陆问题,为火箭有动力回收着陆段制导提供了新的思路。由于凸优化算法具有计算效率高的特点[10],在飞行器轨迹优化和制导中逐渐得到越来越多的应用。Liu和Lu[11]提出针对非凸约束的逐次线性化方法,将非凸约束转化为凸约束,最终将非线性最优控制问题转化为二阶锥规划问题进行求解,并成功用于航天器交会对接、轨道转移等问题。由于上述所涉及的最优控制问题相对较为简单,不涉及气动非线性,所以能够较方便地实现凸化和求解。然而,很多飞行器制导问题需要考虑气动力的影响,控制方式也更为复杂,需要同时对推力的大小和方向进行设计。一种常用的方法是逐次逼近,利用序列凸优化进行迭代求解,如:路钊利用序列凸优化方法求解高超声速再入轨迹规划问题[12];张志国等提出火箭回收着陆段的在线序列凸优化方法,并结合滚动时域控制策略在线实时更新状态信息,提高凸优化制导方法的精度和鲁棒性[13]。基于逐次逼近的求解方法,可直接在小范围内对非线性动力学等式约束进行线性化,通过序列凸优化实现逐次逼近,无需对原问题进行前期繁琐的凸化和变换,实现简单,但该方法的效果在很大程度上依赖于模型的形式与复杂程度,对于许多模型存在迭代不容易收敛的问题,尤其是考虑气动力的复杂模型。而且,当状态量和约束较多时,求解效率达不到目前在线制导的要求。
针对以上问题,Liu等[14]指出凸优化完全依赖线性化无法保证求解性能,尤其对于再入轨迹优化这类非线性较强的问题,提出逐次线性化和松弛技术以更合理地对再入轨迹优化问题进行凸化。进一步地,Liu[15]针对火箭返回着陆问题,考虑气动力引入的非凸性,通过引入变量替换、松弛等凸化技术,较好地解决了序列线性近似逼近方法难以收敛的问题。显然,通过引入合理的凸化和变换对最优控制模型进行裁剪,明显改善了凸优化求解的性能,但凸化工作具有较强的经验性,不同的问题凸化变换处理方法可能完全不同,即使形式上非常相似的2个问题,凸化处理方式也很难照搬,且凸化上细微的不合理,都极有可能导致求解不收敛,通用性与工程应用性较差,工程人员难以快捷地应用。
火箭垂直软着陆制导问题为一典型的约束落角、落速与落点位置的制导问题,工程常用的带落角约束的比例导引方法[16]能较好地处理落角和落点位置约束,且产生的飞行轨迹平滑,但无法解决落速约束以及控制约束,而凸优化能有效处理各种约束[17]。为了充分利用凸优化求解效率高且能处理多约束的优势,同时避免凸优化收敛困难和前期复杂繁琐的凸化变换,提高凸优化在求解火箭垂直软着陆制导问题时的收敛性和通用性,本文提出将带落角约束的比例导引和凸优化进行结合,实现火箭垂直软着陆制导。将火箭的运动分解为法向运动和切向运动,将带落角约束的广义比例导引方法应用到火箭的法向制导上,产生相应的攻角控制火箭着陆,使其满足落点和落角约束。同时,将凸优化和滚动时域控制方法应用到火箭的切向制导上,充分利用凸优化的快速性,使软着陆问题满足落速和推力控制约束。由于将火箭的运动分解为切向和法向控制,落点和落角约束在法向非常方便地得以满足,而切向控制的凸优化求解在基准轨迹近似策略下动力学模型得以大为简化,仅包含速度、推力和质量状态量和推力控制量,无需对模型进行复杂繁琐的凸化剪裁处理,求解效率和收敛性大为改善。而且,针对任意约束末速度的推力优化问题,均可结合该模型与凸优化方法进行求解。因此,相比于现有的凸优化方法,提出的制导方法具有更强的工程适用性。
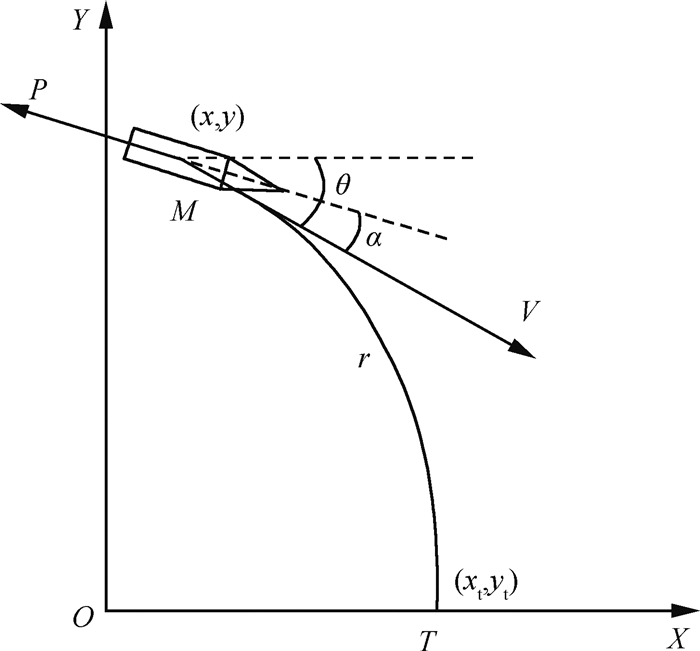
1 问题描述 1.1 火箭有动力着陆段动力学模型图 1为火箭子级降落段二维几何关系图,图中OXY为惯性坐标系,M为火箭返回体。火箭返回体位置为(x, y),速度为V,返回所经过的路径为r,航迹角为θ(速度方向与水平方向的夹角),攻角为α(火箭速度方向与火箭轴向方向的夹角)。T为火箭期望落点(xt, yt),P为火箭推力,其方向为火箭轴向的反方向。
|
| 图 1 火箭子级降落段纵向平面几何关系图 Fig. 1 Geometric diagram of rocket landing in longitudinal plane |
由此建立火箭返回体着陆段的纵向平面质点动力学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = - \frac{{P {\rm{cos}} \alpha + {F_{\rm{D}}}}}{m} - g {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }\\ {\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \frac{{P {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha + {F_{\rm{Y}}}}}{{mV}} - \frac{{g {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}{V}}\\ {\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = V {\rm{cos}}{\kern 1pt} {\kern 1pt} \theta }\\ {\frac{{{\rm{d}}y}}{{{\rm{d}}t}} = V {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }\\ {\frac{{{\rm{d}}r}}{{{\rm{d}}t}} = V}\\ {\frac{{{\rm{d}}m}}{{{\rm{d}}t}} = - \frac{P}{{{I_{{\rm{sp}}}}}}} \end{array}} \right. $ | (1) |
式中:g为地球表面重力系数;FD为气动阻力;FY为气动升力;Isp为火箭燃料的比冲; m为火箭质量。
FD和FY的表达式分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\rm{D}}} = \frac{1}{2}\rho {V^2}{S_{{\rm{ref}}}}{C_D}}\\ {{F_{\rm{Y}}} = \frac{1}{2}\rho {V^2}{S_{{\rm{ref}}}}C_{\rm{L}}^\alpha \alpha } \end{array}} \right. $ | (2) |
式中:Sref为参考面积;CD为阻力系数;CLα为升力系数关于攻角α的导数,这里将气动升力视作攻角α的线性函数;ρ为大气密度,表示为
| $ \rho = {\rho _0}{{\rm{e}}^{ - \beta y}} $ | (3) |
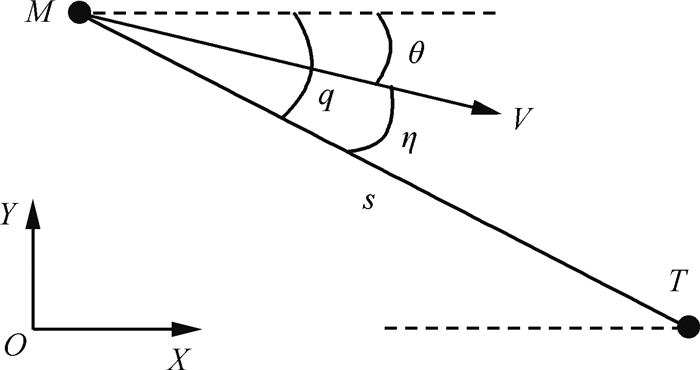
火箭返回定点着陆的制导问题涉及火箭与目标落点的相对运动,图 2为纵向平面内“箭-目”相对运动的二维几何关系图,其中“箭-目”视线角为q、火箭速度与“箭-目”连线间的夹角为η、“箭-目”距离为s。
|
| 图 2 纵向平面“箭-目”相对运动几何关系图 Fig. 2 Geometric diagram of "rocket-target" relative motion in longitudinal plane |
“箭-目”相对运动学方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}s}}{{{\rm{d}}t}} = - V {\rm{cos}}{\kern 1pt} {\kern 1pt} \eta }\\ {\frac{{{\rm{d}}q}}{{{\rm{d}}t}} = \frac{{V {\rm{sin}}{\kern 1pt} {\kern 1pt} \eta }}{s}}\\ {\eta = q - \theta } \end{array}} \right. $ | (4) |
火箭垂直返回着陆制导通过调整发动机的推力大小和箭体的攻角,对火箭加以控制,使其在尽可能降低燃料消耗的情况下,满足各类约束,如:初始位置和速度、终端速度和航迹角等,降落到预定着陆点,并且能够抵抗一定的干扰。其中,推力的方向由攻角和航迹角决定,因此控制量为推力大小P和攻角α。
制导过程中需要满足的约束包括以下几类:
1) 始端约束
| $ \left\{ {\begin{array}{*{20}{l}} {V({t_0}) = {V_0}}\\ {\theta ({t_0}) = {\theta _0}}\\ {x({t_0}) = {x_0}}\\ {y({t_0}) = {y_0}}\\ {m({t_0}) = {m_0}} \end{array}} \right. $ | (5) |
2) 终端约束
返回任务要求火箭以接近0的速度和几乎垂直的航迹角降落在指定落点。
| $ \left\{ {\begin{array}{*{20}{l}} {V({t_{\rm{f}}}) = {V_{\rm{f}}}}\\ {\theta ({t_{\rm{f}}}) = {\theta _{\rm{f}}}}\\ {x({t_{\rm{f}}}) = {x_{\rm{t}}}}\\ {y({t_{\rm{f}}}) = {y_{\rm{t}}}} \end{array}} \right. $ | (6) |
3) 控制约束
火箭的控制能力有限,因此其攻角一般限制在一定范围内,以防止过于剧烈的姿态变化;火箭的推力通常也会约束在一定范围内。
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _{{\rm{ min }}}} \le \alpha \le {\alpha _{{\rm{ max }}}}}\\ {{P_{{\rm{ min }}}} \le P \le {P_{{\rm{ max }}}}} \end{array}} \right. $ | (7) |
本文提出的火箭垂直着陆在线制导方案将火箭飞行的法向控制与切向控制分离,将带落角约束的广义比例导引方法应用于法向控制,将在线滚动时域凸优化应用于切向控制。对于火箭垂直着陆制导问题,沿速度切向的火箭主推力分量和气动阻力主要决定了火箭的切向运动,沿速度法向的火箭推力分量和气动升力主要决定了火箭的法向运动。带落角约束的广义比例导引制导律可有效解决火箭着陆的落角与落点约束,且形式解析、实现简单,但无法满足火箭的着陆的速度约束和推力范围约束。为此,在切向运动上,利用凸优化方法快速规划推力,使之满足落速约束。同时在滚动时域控制架构下实时更新状态信息,实现在线制导。
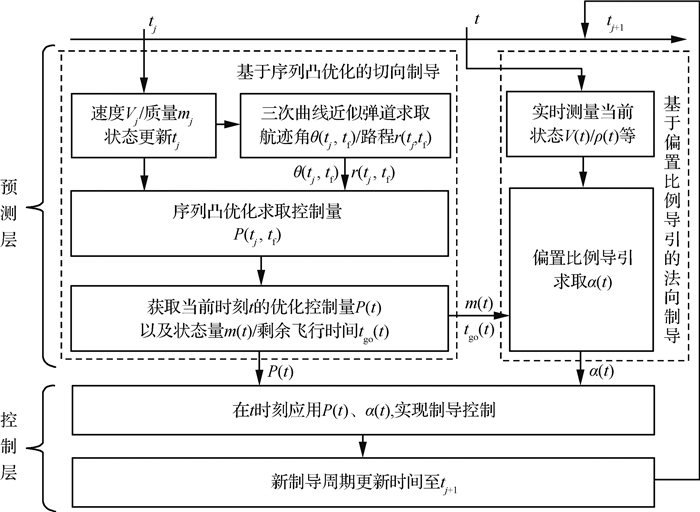
图 3为本文提出的火箭垂直着陆制导方案的流程图。对于切向控制,在每个制导周期开始,进行终端速度约束下的凸优化求解,求取最优推力序列(预测),同时在当前制导周期将对应时域的推力序列作用于火箭动力学(控制),并将预测的需用状态(推力P、质量m、剩余飞行时间tgo)传递给法向控制;等到下一个制导周期到来,更新火箭当前的飞行状态参数,开始新的制导周期的预测和控制。对于法向控制,获取当前实测的状态(速度V、大气密度ρ),以及无法直接实测、需要依靠凸优化预测的状态量(推力P、质量m、剩余飞行时间tgo),生成需用攻角,控制火箭以要求的落角降落于指定点。
|
| 图 3 火箭垂直着陆制导方案流程图 Fig. 3 Flow-chart of rocket vertical landing guidance |
采用文献[18]中的基于多项式函数的落角约束比例导引律:
| $ {a_{\rm{B}}} = (n + 2)V\dot q - n\frac{{V{\theta _{\rm{f}}}}}{{{t_{{\rm{go}}}}}} $ | (8) |
式中:
基于上述制导律可给出火箭的法向需用过载指令,火箭的法向控制最终体现在攻角α指令上,攻角指令产生的法向控制力主要来自火箭推力在速度方向法向上产生的分力,另外攻角还会附加产生垂直于速度方向的气动升力。因此,由攻角产生的法向加速度an为
| $ {a_{\rm{n}}} = \frac{{\frac{1}{2}\rho {V^2}SC_L^\alpha \alpha - P {\rm{sin}} \alpha }}{m} $ | (9) |
由于本文所研究的问题涉及的攻角约束在一小范围,可看作一小量,因此sin α≈α。基于式(8)和式(9),可得需用攻角为
| $ \alpha = \frac{{{a_{\rm{B}}}m}}{{\frac{1}{2}\rho {V^2}SC_L^\alpha - P}} $ | (10) |
制导指令在执行过程中需要当前的状态信息,如速度V、质量m和推力P等,其中速度可通过传感器实时测出;质量m、推力P和剩余飞行时间tgo将通过切向的滚动时域凸优化在当前制导周期求解获得。经过上述方法可使火箭获得实际攻角指令,控制火箭在满足落角约束的同时降落在指定位置。关于tgo的计算将在2.2.2节中进行具体介绍。
2.2 基于凸优化和滚动时域控制的推力在线规划 2.2.1 速度切向运动模型的简化为了通过控制推力使速度在着陆时刚好降至0附近,本文提出将火箭垂直返回的切向运动制导从火箭制导的动力学模型中剥离出来,采用序列凸优化方法对推力进行快速优化,并结合滚动时域控制方法,在制导飞行过程中进行多周期的状态更新和重新规划,以消除误差与干扰。
根据式(1),剥离出与速度相关的式子,与速度V相关的量包括推力P、路程r和质量m,有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = - \frac{{P {\rm{cos}}{\kern 1pt} {\kern 1pt} \alpha + {F_{\rm{D}}}}}{m} - g {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }\\ {\frac{{{\rm{d}}r}}{{{\rm{d}}t}} = V}\\ {\frac{{{\rm{d}}m}}{{{\rm{d}}t}} = - \frac{P}{{{I_{{\rm{sp}}}}}}} \end{array}} \right. $ | (11) |
式(11)中以时间t为自变量,但火箭飞行至落点的时间无法提前确定,为了避免对飞行时间寻优,提高凸优化求解的效率,且考虑到路程r单调递增,将r作为自变量,将式(11)中的第1和第3个方程分别除以第2个方程,有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}V}}{{{\rm{d}}r}} = - \frac{{P {\rm{cos}}{\kern 1pt} {\kern 1pt} \alpha + {F_{\rm{D}}}}}{{mV}} - \frac{{g {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }}{V}}\\ {\frac{{{\rm{d}}m}}{{{\rm{d}}r}} = - \frac{P}{{V{I_{{\rm{sp}}}}}}} \end{array}} \right. $ | (12) |
式(12)中,涉及未知变量θ、α以及气动阻FD。FD的表达式见式(2),其中ρ与高度y有关,而高度y是未知项。攻角α通过式(10)求出,此项无法提前估计。由于攻角是小量,认为cos α≈1。进一步,若能将θ与y表示为自变量r的函数,式(12)所示模型便可以进行优化求解。为此,将式(12)变为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}V}}{{{\rm{d}}r}} = - \frac{{P + {F_{\rm{D}}}(r)}}{{mV}} - \frac{{g {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta (r)}}{V}}\\ {\frac{{{\rm{d}}m}}{{{\rm{d}}r}} = - \frac{P}{{V{I_{{\rm{sp}}}}}}} \end{array}} \right. $ | (13) |
2.2.1节中为了便于凸优化求解,进行了自变量替换,而求解出的控制量最终应当是时间t的函数。基于凸优化求解出的V(r)和r可反解出时间t:
| $ t(r) = \int_0^r V (r){\rm{d}}r $ | (14) |
火箭垂直返回任务在速度法向上采取约束落角的偏置比例导引制导方法,如式(10)所示。可以注意到偏置比例导引中需要的tgo是未知的,tgo的估计精度直接决定了末端落角能否收敛至期望落角。剩余飞行时间tgo在很大程度上是由火箭的速度切向运动决定的,这部分运动由序列凸优化求解,而通过式(14)对变量t的反求可知,飞行过程中的任意点上剩余飞行时间是很容易得到的。基于滚动时域控制的思想,在路径上每一个状态更新点时初始时间为t=0,由式(14)可求出预计到达落点的飞行时间为
| $ t_{{\rm{go}}}^0 = \int_0^R V (r){\rm{d}}r $ | (15) |
式中:tgo0为从当前制导周期状态更新点飞行至落点的求解飞行时间,积分上限R的计算将在2.2.3节中给出。
式(15)积分的求解过程并非复杂,对于已知总的飞行路程R,由于凸优化求解出的最优状态量是离散的,离散分段数为N,则式(15)中的积分可以简单表示为
| $ t_{{\rm{go}}}^0 = \sum\limits_{i = 1}^N {\frac{T}{{{V_i}}}} $ | (16) |
式中:T为凸优化求解中自变量r的离散周期; Vi为第i个离散点上的速度。
已知状态更新点至路径上任意一点已经飞过了时间tpass,那么剩余飞行时间应当为
| $ {t_{{\rm{go}}}} = t_{{\rm{go}}}^0 - {t_{{\rm{pass}}}} $ | (17) |
这样便可以通过速度切向的优化求解估算出法向制导需要的预估剩余飞行时间。
2.2.3 基准轨迹生成分析可知,在进行凸优化求解的过程中,若要求解推力P、速度V与质量m,关键是要获得较为准确的自变量r和相应的θ(r)与y(r),但目前尚无法预知未来飞行轨迹的任何数据。为此,本文提出提前构建一条基于三次多项式的“基准轨迹”,以近似实际飞行轨迹。之所以使用三次多项式近似“基准轨迹”,原因有两点。首先,在轨迹较为平滑的前提假设下,在滚动时域控制的每一个制导周期,轨迹x=f(y)可由初始点位置(x0, y0)与航迹角θ0(这些初始状态由火箭当前状态决定)、终点位置(xf, yf)与航迹角θf(这些终端状态为火箭着陆的约束值)大致确定,共4个已知量(y0, θ0, yf, θf)刚好能确定一个三次多项式函数,因此这里没有选择二次多项式或更高阶(>3)的多项式。
另外,使用多项式形式能保证快速生成基准轨迹,大为降低切向制导凸优化求解的复杂度与计算量。虽然三次多项式近似必然存在偏差,但该轨迹仅用于为凸优化提供参考轨迹数据,此处导致的误差可以通过滚动时域控制的闭环制导策略进行消除,而且实际的飞行轨迹很大程度上由偏置比例导引确定。另一方面,对于工程实际而言,对制导算法的稳定性和实时性要求更为迫切,基于三次多项式近似轨迹进行凸优化所得轨迹虽非最优,但是能在满足各种约束的情况下,提供一个可行的近乎最优的解,也是非常有意义的。
设轨迹曲线函数x=f(y)为
| $ x = {k_{\rm{a}}}{y^3} + {k_{\rm{b}}}{y^2} + {k_{\rm{c}}}y + {k_{\rm{d}}} $ | (18) |
对式(18)求导得
| $ {x^\prime } = 3{k_{\rm{a}}}{y^2} + 2{k_{\rm{b}}}y + {k_{\rm{c}}} $ | (19) |
由于初始位置(x0, y0)和初始航迹角θ0、终点位置(xf, yf)和终点航迹角θf=-90°已知,便可计算初始点和终点的斜率。将这些信息代入式(18)和式(19),可得
| $ \left\{ {\begin{array}{*{20}{l}} {{x_0} = {k_{\rm{a}}}y_0^3 + {k_{\rm{b}}}y_0^2 + {k_{\rm{c}}}{y_0} + {k_{\rm{d}}}}\\ {{x_f} = {k_{\rm{a}}}y_{\rm{f}}^3 + {k_{\rm{b}}}y_{\rm{f}}^2 + {k_{\rm{c}}}{y_{\rm{f}}} + {k_{\rm{d}}}}\\ {\frac{1}{{ {\rm{tan}}{\kern 1pt} {\kern 1pt} {\theta _0}}} = 3{k_{\rm{a}}}y_0^2 + 2{k_{\rm{b}}}{y_0} + {k_{\rm{c}}}}\\ {0 = 3{k_{\rm{a}}}y_{\rm{f}}^2 + 2{k_{\rm{b}}}{y_{\rm{f}}} + {k_{\rm{c}}}} \end{array}} \right. $ | (20) |
求解上述线性方程组,可得三次多形式轨迹曲线中的系数为
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{\rm{a}}} = 2\frac{{{x_{\rm{f}}} - {x_0}}}{{y_0^3}} + \frac{1}{{y_0^2 {\rm{tan}}{\kern 1pt} {\kern 1pt} {\theta _0}}}}\\ {{k_{\rm{b}}} = \frac{{{x_0} - {x_{\rm{f}}}}}{{y_0^2}} - {k_{\rm{a}}}{y_0}}\\ {{k_{\rm{c}}} = 0}\\ {{k_{\rm{d}}} = {x_{\rm{f}}}} \end{array}} \right. $ | (21) |
采用上述方法求解由初始点至落点的三次多项式曲线,完成对实际飞行轨迹的近似,从而近似预测θ(r)与y(r)。设飞行轨迹近似曲线为C(y, x),可求取曲线上r和θ:
| $ \left\{ {\begin{array}{*{20}{l}} {r = \int_{{y_0}}^y {\sqrt {1 + {x^\prime }{{(y)}^2}} } {\rm{d}}y}\\ {\theta = {\rm{arctan}} \frac{1}{{{x^\prime }}}} \end{array}} \right. $ | (22) |
由于路程r为自变量,基于式(22)可求出近似的θ(r)和y(r)。至此,式(13)的简化模型就能进行优化求解。另外,优化中需要给定自变量r的范围[0, R],可根据式(23)得到r的最大值,即:近似轨迹曲线的总路程为
| $ R = \int_{{y_0}}^{{y_f}} {\sqrt {1 + {x^\prime }{{(y)}^2}} } {\rm{d}}y $ | (23) |
基于2.2.1~2.2.3节的描述,建立带末速约束的最优控制问题P1:
| $ \begin{array}{*{20}{l}} {{P_1}:{\rm{ Find }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P(r)}\\ {{\rm{Min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J = \int_0^R {{P^2}} (r){\rm{d}}r} \end{array} $ |
| $ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{\rm{Eq}}{\rm{. }}(13)}\\ {{P_{{\rm{ min }}}} \le P \le {P_{{\rm{ max }}}}}\\ {V(0) = {V_0}}\\ {m(0) = {m_0}}\\ {V(R) = {V_{\rm{f}}}} \end{array}} \right. $ | (24) |
式(24)中的优化目标没有明确的实际物理意义,但与火箭制导能量最省的目标一致。而且,对于本项目的凸优化求解,其中的约束都将转化为线性约束,目标函数将离散为二次型函数,这将有利于获得更加光滑的便于实际工程应用的控制量。
2.2.5 非线性约束的凸化处理首先对非线性动力学等式约束式(13)进行凸化,为书写方便将式(13)简写为
| $ \mathit{\boldsymbol{\dot X}}(r) = \mathit{\boldsymbol{f}}(\mathit{\boldsymbol{X}}(r),\mathit{\boldsymbol{U}}(r)) = {[{f_1},{f_2}]^{\rm{T}}} $ | (25) |
式中:X=[V, m],U=[P]。
设某参考轨迹上状态和控制量分别为Xref(k)=[Vk, mk]T和P(k)=Pk(k=0, 1, 2, …)。以下统一将Xref(k)记为Xk,在参考轨迹处对非线性状态方程(25)进行一阶泰勒展开,得
| $ \mathit{\boldsymbol{\dot X}}(r) = {\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{X}}(r) + {\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{U}}(r) + {\mathit{\boldsymbol{C}}_k} $ | (26) |
式中:各项系数矩阵中的下角标k表示对应第k条参考轨迹,分别表示为
| $ \begin{array}{l} {{\rm{A}}_k} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. {\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial V}}}&{\frac{{\partial {f_1}}}{{\partial m}}}\\ {\frac{{\partial {f_2}}}{{\partial V}}}&{\frac{{\partial {f_2}}}{{\partial m}}} \end{array}} \right]} \right|_{{\mathit{\boldsymbol{X}}_k},{\mathit{\boldsymbol{U}}_k}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\frac{{{P_k} - {F_{{\rm{D}}k}}}}{{{m_k}V_k^2}} + \frac{{g {\rm{sin}} {\theta _k}}}{{{V_k}}}}&{\frac{{{P_k} + {F_{{\rm{D}}k}}}}{{m_k^2{V_k}}}}\\ {\frac{{{P_k}}}{{{I_{{\rm{sp}}}}V_k^2}}}&0 \end{array}} \right] \end{array} $ |
| $ {{\rm{B}}_k} = {\left. {\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial P}}}\\ {\frac{{\partial {f_2}}}{{\partial P}}} \end{array}} \right]} \right|_{{\mathit{\boldsymbol{X}}_k},{\mathit{\boldsymbol{U}}_k}}} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{V_k}{m_k}}}}\\ { - \frac{1}{{{I_{{\rm{sp}}}}{V_k}}}} \end{array}} \right] $ |
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_k} = \mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{X}}_k} - {\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{U}}_k} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} { - \frac{{\partial {f_1}}}{{\partial V}}{V_k} - \frac{{\partial {f_1}}}{{\partial m}}{m_k} - \frac{{\partial {f_1}}}{{\partial P}}{P_k}}\\ { - \frac{{\partial {f_2}}}{{\partial V}}{V_k} - \frac{{\partial {f_2}}}{{\partial m}}{m_k} - \frac{{\partial {f_2}}}{{\partial P}}{P_k}} \end{array}} \right]} \end{array} $ |
在经过凸化处理的式(26)基础上,进一步进行离散化。设离散周期为T,离散周期数为N,则状态方程离散为
| $ \mathit{\boldsymbol{X}}(i + 1) = \mathit{\boldsymbol{A}}(i)\mathit{\boldsymbol{X}}(i) + \mathit{\boldsymbol{B}}(i)\mathit{\boldsymbol{U}}(i) + \mathit{\boldsymbol{C}}(i) $ | (27) |
式中:A(i)=TAk+I2(I2为2×2的单位矩阵),B(i)=TBk,C(i)=TCk。
经过凸化和离散化处理后,形成二阶锥规划问题P2, 即
| $ \begin{array}{*{20}{l}} {{P_2}:{\rm{ Find }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P(r)}\\ {{\rm{Min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J = \sum\limits_{i = 1}^N {P_i^2} } \end{array} $ |
| $ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot X}}(r) = {\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{X}}(r) + {\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{U}}(r) + {\mathit{\boldsymbol{C}}_k}}\\ {{P_{{\rm{ min }}}} \le P \le {P_{{\rm{ max }}}}}\\ {V(1) = {V_0}}\\ {m(1) = {m_0}}\\ {V(N) = {V_{\rm{f}}}} \end{array}} \right. $ | (28) |
上述凸优化问题可采用序列凸优化算法[15, 19-20]进行求解。用于凸化动力学方程的“序列凸优化”方法目前在诸多问题中都有应用并取得了较好的效果。但是其收敛性的证明非常困难,基本不可能[21]。目前只能通过仿真手段针对具体的问题从仿真结果去判断序列线性近似方法的收敛性,如:是否在有限迭代次数内收敛至给定误差限[19]。从第3节展示的数值仿真结果可以看出,序列线性近似方法对于本文涉及的火箭着陆制导问题具有很好的收敛性。
2.2.6 基于滚动时域在线优化的制导算法上述优化模型(式(28))在推导构建中进行了若干简化和近似,如:攻角小量处理、基于三次多项式的飞行轨迹近似、凸化中动力学方程的序列线性近似等,这将不可避免地导致优化模型与原问题模型存在一定的偏差。此外,火箭返回过程中存在诸多随机不确定性因素,如:推力偏差、气动数据偏差和风干扰等。仅进行一次序列凸优化求解的开环制导方式无法应对上述模型误差与不确定性因素,进而导致较大制导误差。为此,将凸优化与滚动时域控制进行结合,形成闭环优化制导。在每个制导周期内,利用凸优化对推力进行快速规划,得到未来所有时刻的推力指令,并在下一周期应用该指令;到达制导周期节点后,更新当前飞行状态作为优化初始状态,并在下一周期内使用更新后的初始状态迅速进行新一次的序列凸优化求解,求解出新的未来所有时刻推力指令,以此类推直到火箭着陆。
3 仿真分析下面给出一组带落角与落速约束的火箭垂直返回着陆仿真算例,表 1为火箭的基本参数,表 2为火箭返回段的初始状态参数和垂直着陆落点约束要求。
| 参数 | 数值 |
| 火箭参考面积Sref/m2 | 7.07 |
| 火箭推进剂比冲Isp/(m·s-1) | 2 958 |
| 阻力系数CD | 2 |
| 升力系数随攻角导数CLα | 2 |
| 推力范围[Pmin, Pmax]/kN | [1 200, 2 400] |
| 攻角范围[αmin, αmax]/(°) | [-10, 10] |
| 参数 | 数值 |
| 初始速度V0/(m·s-1) | 253 |
| 初始航迹角θ0/(°) | -75 |
| 初始横坐标x0/m | 0 |
| 初始纵坐标y0/m | 1 950 |
| 初始质量m0/kg | 80 000 |
| 期望降落速度Vf/(m·s-1) | 0 |
| 期望落角θf/(°) | -90 |
| 期望落点横坐标xf/m | 360 |
| 期望落点纵坐标yf/m | 0 |
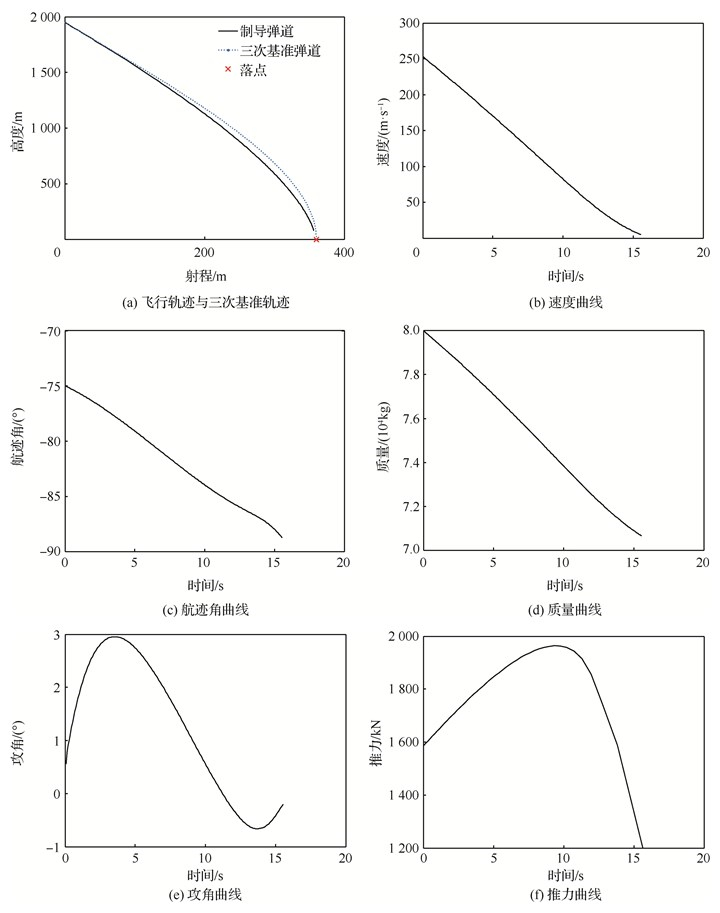
偏置比例导引设置比例系数n=3。为验证序列凸优化的有效性,首先不使用闭环滚动时域控制策略,而是只在轨迹初始位置进行一次开环序列凸优化。对于序列凸优化,设定优化状态、控制变量的离散点数均为50,凸优化算法采用内点法(ipopt)。在使用双核四线程i3 550 CPU、8 G内存的普通台式机上进行仿真测试。序列凸优化求解共迭代6次后满足收敛条件,求解时间每次迭代约0.3 s,凸优化求解一次耗时约1.8 s。图 4(a)~图 4(f)展示了基于开环序列凸优化与偏置比例导引的实际制导轨迹、速度、航迹角、质量变化、攻角和推力曲线。表 3给出了轨迹终端落点约束的满足情况。
|
| 图 4 基于比例导引和开环凸优化的制导仿真曲线 Fig. 4 Simulation results of proportional guidance and open-loop convex optimization based guidance |
| 参数 | 期望数值 | 实际数值 |
| 期望降落速度Vf/(m·s-1) | 0 | 5.16 |
| 期望落角θf/(°) | -90 | -88.77 |
| 期望落点横坐标xf/m | 360 | 356.2 |
| 期望落点纵坐标yf/m | 0 | 77 |
从图 4和表 3中可以看到,所得的控制量推力P始终在要求的约束范围内,但落点速度、落角与落点均出现了一定的偏差。上述偏差产生的原因是本文建立的凸优化模型(式(28))在推导构建中进行了若干简化和近似,如:攻角小量处理、基于三次多项式的基准轨迹近似、凸化中动力学方程的序列线性近似等,这些都将不可避免地导致优化模型与原问题模型存在一定的偏差,进而导致开环优化存在误差。图 4(a)展示了实际开环制导轨迹与凸优化所用到的三次多项式基准轨迹,可以看到二者存在一定的偏差,但是偏差不明显。基准轨迹为凸优化提供航迹角θ(r)、高度y(r)和飞行轨迹距离R必备数据,保证火箭制导切向与法向的解耦,基准轨迹近似带来的偏差成为开环制导出现偏差的主要原因之一。这些近似带来的制导偏差包括基准轨迹近似偏差,可通过结合滚动时域控制的闭环制导策略得以消除。而且,在闭环制导的每个制导周期,基准轨迹会自动更新,将更加贴合实际飞行轨迹,这在3.2节的仿真结果中会得到证实。
3.2 基于偏置比例导引与闭环凸优化的在线制导仿真从3.1节的仿真可见,开环凸优化将导致较大的制导误差。因此,本节将对基于偏置比例导引与闭环凸优化的制导进行测试。3.1节中已经提到每次凸优化求解耗时约1.8 s,仿真中只需要保证各周期优化求解时间小于制导周期时间即可。在本节仿真中设定滚动时域优化制导周期为2 s。
仿真依然使用表 1和表 2中设定的参数值。表 4给出了火箭返回闭环制导下落点的满足情况,相关的仿真结果如图 5所示。
| 参数 | 期望数值 | 实际数值 |
| 降落速度Vf/(m·s-1) | 0 | 0.01 |
| 落角θf/(°) | -90 | -89.95 |
| 落点横坐标xf/m | 360 | 359.99 |
| 落点纵坐标yf/m | 0 | 0.93 |
|
| 图 5 闭环滚动时域凸优化制导仿真结果 Fig. 5 Simulation results of closed-loop convex optimization based guidance |
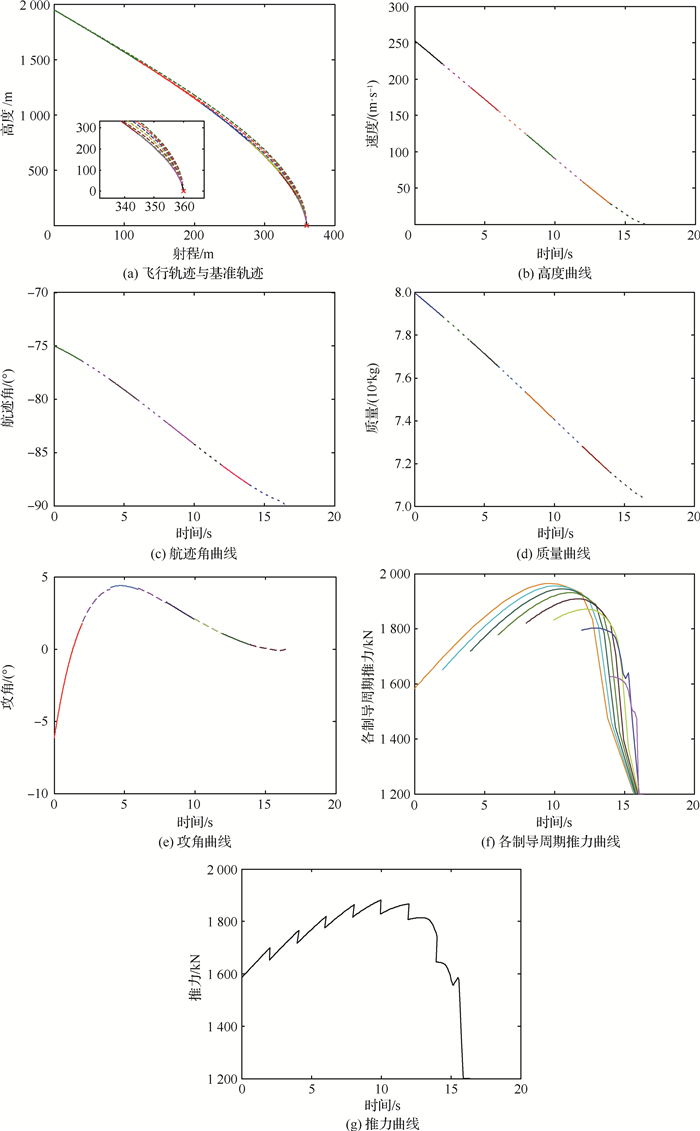
图 5中间隔使用不同的颜色和线型以区别各个制导周期的状态曲线。其中,图 5(a)中实线为闭环制导轨迹,同颜色虚线为相同制导周期内所生成的基准轨迹,可以看出随着制导周期的往前推进,基准轨迹与实际轨迹越来越接近,偏差越来越小,到最后一个制导周期,二者几乎重合。这也验证了滚动凸优化制导策略在消除偏差方面的有效性,同时也再次印证采用三次多项式近似基准轨迹的方案是合理可行的。图 5(f)为各制导周期中序列凸优化求解出的推力曲线(从当前制导周期开始时刻到飞行结束),在各状态更新点经过状态更新后,再次进行序列凸优化以更新推力优化结果。图 5(g)为实际飞行中火箭应用的推力指令,也就是各制导周期内序列凸优化求解所得的最优推力指令的第一个序列,显然推力始终在约束的范围。从表 4中可以看到,最终实际降落速度为0.01 m/s、落角为-89.95°,实际落点横坐标与期望值相差几乎可以忽略,实际落点纵坐标与期望相差不到1 m,落速、落角与落点约束的满足情况均远优于开环凸优化。基于滚动时域序列凸优化和偏置比例导引的火箭垂直返回制导在落角约束、落点速度和落点偏差上都可以获得令人满意的结果。
此外,采用序列凸优化方法求解切向最优推力,每个制导周期迭代次数为4~6次,且迭代均满足收敛误差要求。从图 5的仿真曲线也能看出序列凸优化方法求解火箭切向制导问题能满足各类约束,实现精确的定点着陆,具有很好的收敛性。
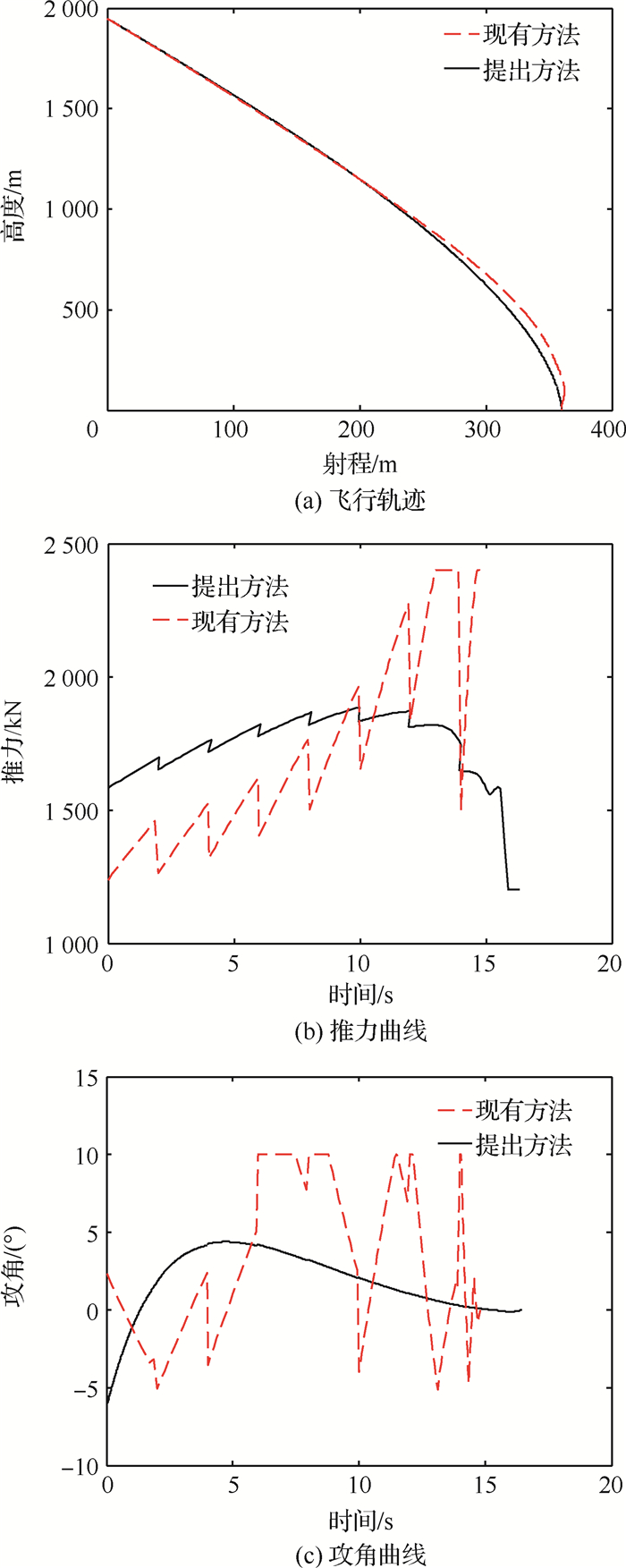
为了展示本文提出的切向和法向分开制导方法的优势,考虑完全同样的火箭软着陆动力学问题,设定同样的制导周期、状态和控制变量离散数量,采用滚动时域控制结合序列凸优化方法[15, 19, 20](本文简称为现有方法)直接对火箭垂直着陆制导问题进行求解,同时获取最优推力和攻角。图 6为本文提出的制导方法与现有方法所得的飞行轨迹、推力、攻角曲线的对比图。
|
| 图 6 两种方法的仿真曲线对比 Fig. 6 Simulation curves of two methods |
图 6中黑色实线表示本文提出方法的结果,虚线为现有滚动序列凸优化方法的结果。从图 6(b)和图 6(c)中可以看到,使用提出的基于偏置比例导引与滚动凸优化的制导方法所得的控制量(推力和攻角)曲线较为平滑,更加适合于工程应用;现有方法直接采用滚动凸优化,所得控制量曲线震荡较为剧烈。而且,从图 6(a)中可以看出,提出方法的飞行轨迹更为平滑,原因在于该方法下火箭的法向运动基本由偏置比例导引决定,而偏置比例导引已经被证明某些性能指标下具有最优性,且所得控制量均匀平滑,飞行轨迹较为平直[16]。而且,由于切向和法向分开制导,并引入三次多项式基准轨迹近似策略实现切向和法向的解耦,火箭切向运动的最优控制模型大为简化,状态变量减少,优化控制变量仅为推力P,模型线性化带来的偏差影响更小,因此凸优化求解更为容易。现有方法直接对包含法向和切向的最优控制模型进行线性化凸化,由于模型状态量和控制量多,状态的耦合更强,线性化带来的偏差影响更大,凸优化求解必然更加困难。
表 5展示了2种方法仿真飞行时间、优化算法用时、各周期迭代次数和制导周期平均优化算法用时的对比。本文的所有算例均使用MATLAB语言进行编程仿真,仿真使用的计算机处理器为i3 550双核处理器,内存为8 G。从中可以看出本文提出方法的优化算法总用时15.2 s,共8个制导周期,平均每个制导周期优化用时为1.9 s、优化迭代4~6次。现有方法优化算法总用时37.2 s,8个制导周期,平均每个制导周期优化用时为4.65 s、每个周期优化迭代大约8~10次,在当前计算环境下用时已经超出了设定的制导周期。由此可见,本文提出的制导方法计算速度更快,而且所生成的控制量曲线更加平滑,具有更强的工程适用性;现有方法虽然能保证各类约束的满足,但是所得的攻角和推力曲线均出现大幅振荡,且优化迭代次数多、收敛慢,求解效率低。
| 方法 | 飞行时间/s | 总用时/s | 平均迭代次数 | 周期平均用时/s |
| 提出的方法 | 16.3 | 15.2 | 4.8 | 1.9 |
| 现有方法 | 14.8 | 37.2 | 8.7 | 4.65 |
提出的方法具有更快的计算速度,原因是提出的方法将导弹制导分为切向和法向控制,法向采用解析式的高效比例导引,切向的最优控制问题仅包含推力控制量,涉及3个状态量(V、m、P),使用序列凸优化方法离散点为50,设计变量个数为3×50=150。现有方法直接采用序列凸优化方法,涉及状态量V、θ、x、y、m、t和控制量P和α,共8×50=400个。除此之外,状态变量个数的不同导致动力学线性化之后的线性等式约束的数目也存在很大差距。表 6给出了2种方法凸优化求解中优化变量和约束的数目,可见提出方法的优化变量和约束的数目都要明显小于现有方法。提出方法由于将切向和法向分开制导,切向凸优化优化变量的个数以及约束的个数都明显减少,有利于降低计算量;而且切向凸优化模型得以简化,线性化带来的影响更小,每个制导周期收敛所需迭代次数更少,因此计算耗时显著减少。
| 方法 | 设计变量数量 | 约束数量 |
| 提出的方法 | 150 | 201 |
| 现有方法 | 400 | 605 |
本文提出了一种基于偏置比例导引和序列凸优化的火箭返回垂直软着陆制导方法。仿真结果表明:
1) 法向采用偏置比例导引,使火箭着陆满足落点与落速要求。
2) 切向采用滚动时域凸优化模型,结合本文提出的三次曲线拟合轨迹方法,保证火箭着陆的末速度约束,经仿真验证具有足够的精度。
3) 本文将提出方法与目前已有的滚动时域序列凸优化方法进行对比,以更少的计算时间和计算量解决火箭垂直着陆问题,且具有更好的收敛性,所产生的控制指令更为平滑,工程上更容易实现。
| [1] | DENEU F, MALASSIGNE M, LE-COULS O, et al. Promising solutions for fully reusable two-stage-to-orbit configurations[J]. Acta Astronautica, 2005, 56(8): 729-736. |
| Click to display the text | |
| [2] |
高朝辉, 张普卓, 刘宇, 等. 垂直返回重复使用运载火箭技术分析[J]. 宇航学报, 2016, 37(2): 145-152. GAO Z H, ZHANG P Z, LIU Y, et al. Analysis of vertical landing technique in reusable launch vehicle[J]. Journal of Astronautics, 2016, 37(2): 145-152. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [3] | ALEXANDER N, VLADIMIR N. Reusable space planes challenges and control problems[J]. IFAC-Paperonrime, 2016, 49(17): 480-485. |
| Click to display the text | |
| [4] | MEDITCH J S. On the problem of optimal thrust programming for a lunar soft landing[J]. IEEE Transactions on Automatic Control, 1964, 9(4): 477-484. |
| Click to display the text | |
| [5] | MIELE A. The Calculus of variations in applied aerodynamics and flight mechanics[J]. Mathematics in Science & Engineering, 1962, 5: 99-170. |
| [6] | KLUMPP A R. Apollo lunar descent guidance[J]. Automatica, 1974, 10(2): 133-146. |
| Click to display the text | |
| [7] | SOSTARIC R, REA J. Powered descent guidance methods for the moon and mars[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2005. |
| [8] | ACIKMESE B, PLOEN S R. Convex programming approach to powered descent guidance for mars landing[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1353-1366. |
| Click to display the text | |
| [9] | BLACKMORE L, ACIKMESE B, SCHARF D P. Minimum-landing-error powered-descent guidance for mars landing using convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1161-1171. |
| Click to display the text | |
| [10] | NESTEROV Y E, TODD M J. Self-scaled barriers and interior-point methods for convex programming[J]. Mathematics of Operations Research, 1997, 22(1): 1-42. |
| Click to display the text | |
| [11] | LIU X F, LU P. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 750-765. |
| Click to display the text | |
| [12] |
路钊.高超声速飞行器再入末段轨迹在线优化[D].哈尔滨: 哈尔滨工业大学, 2014: 39-74. LU Z. Online trajectory optimization for the terminal stage of retry hypersonic vehicles[D]. Harbin: Harbin Institute of Technology, 2014: 39-74(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [13] |
张志国, 马英, 耿光有, 等. 火箭垂直回收着陆段在线制导凸优化方法[J]. 弹道学报, 2017, 29(1): 9-16. ZHANG Z G, MA Y, GENG G Y, et al. Convex optimization method used in the landing-phase online guidance of rocket vertical recovery[J]. Journal of Ballistics, 2017, 29(1): 9-16. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [14] | LIU X F, SHEN Z, LU P. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance Control & Dynamics, 2015, 39(2): 1-15. |
| [15] | LIU X F. Fuel-optimal rocket landing with aerodynamic controls[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(1): 65-77. |
| Click to display the text | |
| [16] |
宋建梅, 张天桥. 带末端落角约束的变结构导引律[J]. 弹道学报, 2001, 13(1): 16-20. SONG J M, ZHANG T Q. The passive homing missiles variable structure proportional navigation with terminal impact angular constraint[J]. Journal of Ballistics, 2001, 13(1): 16-20. (in Chinese) |
| Cited By in Cnki (89) | Click to display the text | |
| [17] | TOH K C, TODD M J. SDPT3-a MATLAB software package for semidefinite programming[J]. Optimization Methods & Software, 1999, 11(1-4): 545-581. |
| Click to display the text | |
| [18] |
马爽, 杨军, 袁博. 基于多项式函数求解的落角约束制导律[J]. 导航定位与授时, 2018, 5(5): 43-47. MA S, YANG J, YUAN B. Impact angle constraint guidance law proposed by polynomial function[J]. Navigation Positioning & Timing, 2018, 5(5): 43-47. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] | DINH Q T, SAVORGNAN C, DIEHL M. Real-time sequential convex programming for nonlonear model predictive control and applications to a hydro-power plant[C]//2012 Decision & Control & European Control Conference. Piscataway: IEEE Press, 2012. |
| [20] | JIANG H, AN Z, YU Y N, et al. Cooperative guidance with multiple constraints using convex optimization[J]. Aerospace Science and Technology, 2018, 79: 426-440. |
| Click to display the text | |
| [21] | LU P, LIU X. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 375-389. |
| Click to display the text |



