2. 天津市非线性动力学与控制重点实验室, 天津 300350;
3. 北京电子工程总体研究所, 北京 100854
2. Tianjin Key Laboratory of Nonlinear Dynamics and Control, Tianjin 300350, China;
3. Beijing Institute of Electronic System Engineering, Beijing 100854, China
为了满足存储、运输过程中节省空间的要求,很多飞行器会采用折叠舵面结构,如舰载飞机机翼、导弹弹翼等。但由于加工生产中的超差、装配误差以及使用磨损等因素,折叠舵面中不可避免地存在着间隙。间隙非线性是折叠舵面结构最为常见的一种集中式结构非线性,它的存在会改变折叠舵面的刚度特性,进而对飞行器的气动弹性特性(包括颤振特性和动力学响应)产生重要影响[1-3]。赵永辉和胡海岩[4]研究了操纵面自由度具有间隙的二元翼段颤振特性,发现铰链间隙的存在会使机翼发生极限环振荡和跳跃。Gold和Karpel[5]研究了具有铰链间隙非线性的控制面对飞机飞行的影响,发现铰链刚度的间隙非线性会引起飞机结构的极限环振荡。Behal和Rao[6]基于有限元建立含间隙非线性的三元机翼模型,研究了副翼结构特性的变化对机翼颤振特性的影响。迟圣威[7]建立了可折叠机翼的有限元模型,研究铰链折叠角和刚度变化对颤振特性的影响,结果表明在铰链刚度和折叠角的改变过程中颤振的不稳定分支会发生改变。Abdelkefi等[8]采用三次多项式表征间隙的非线性连接刚度,并基于实验数据对二元翼段的非线性连接刚度进行了分析。
近年来,一些学者基于模态综合法[9]对折叠舵面动态特性进行了分析。Kim[10]和Bae[11]等运用模态综合法和恢复力曲面法对典型折叠舵面结构进行了分析,发现结构间隙非线性可以由分段双线性连接刚度表示。全祎倬和方明霞[12]利用自由界面模态综合法得到机翼颤振特性,结果表明随着马赫数的提高,飞行器的颤振速度呈下降趋势,而颤振频率的变化不明显。倪迎鸽等[13]采用模态综合法,分析了具有间隙非线性的折叠机翼的气动弹性,结果表明在间隙量很小的情况下,极限环也不可避免。杨宁[14-15]和Wu[16-17]等采用双协调自由界面模态综合法,建立并分析了多自由度结构非线性折叠翼面的动力学特性。
目前,国内外学者围绕含间隙折叠舵面的动态特性分析进行了大量研究,但仍存在诸多问题有待解决。在运用模态综合法分析含间隙折叠舵面动态特性时,现有研究大多建立在已知连接界面处间隙非线性连接刚度的假设下,而真实结构的间隙非线性连接刚度往往是未知或难以测量的。本文在对含间隙折叠舵面的结构动力学特性进行分析的基础上,采用模态综合法对折叠舵面的有限元模型进行降阶,进而通过模型修正得到连接界面处的间隙非线性连接刚度,完成含间隙折叠舵面的非线性动力学模型建立,为开展含间隙折叠舵面的非线性动态特性分析提供技术基础。
1 折叠舵面的有限元模型 1.1 折叠舵面结构折叠舵面结构分为内舵和外舵2部分,内舵和外舵通过销轴连接,内舵根部固定,用以模拟与弹体的连接,如图 1所示。

|
| 图 1 折叠舵面结构 Fig. 1 Structure of a folding fin |
销轴间隙产生的非线性恢复力-位移关系由图 2所示,其中间隙非线性特性由间隙尺寸δ和接触刚度Kθ这2个参数来描述[18]。其表达式为

|
| 图 2 间隙非线性刚度特性 Fig. 2 Freeplay nonlinear stiffness characteristics |
| $ f(\theta ) = \left\{ {\begin{array}{*{20}{l}} {{K_\theta }(\theta - \delta )}&{\theta > \delta }\\ 0&{ - \delta \le \theta \le \delta }\\ {{K_\theta }(\theta + \delta )}&{\theta < - \delta } \end{array}} \right. $ | (1) |
式中:θ为转角;f(θ)为力矩。当间隙量δ=0 rad时,力矩变为关于θ的线性函数。
折叠舵面的材料选择铝合金材料,材料属性如表 1所示。
| 弹性模量/Pa | 泊松比 | 密度/(kg·m-3) |
| 7.1×1010 | 0.33 | 2.77×103 |
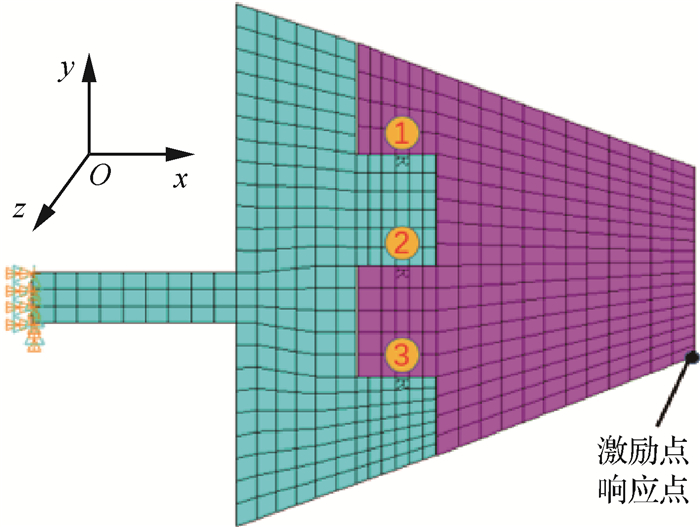
采用不同厚度的壳单元对折叠舵面的内舵和外舵进行建模,如图 3所示。由于实际结构的内舵和外舵之间通过销轴连接,因此在建模这个环节,销轴的建模最为重要。分析结构的物理特性,可将实际结构简化为3组铰链连接。利用MPC多点约束单元将铰链连接处除了绕y轴转动的自由度以外,其他的自由度全部约束,实现对内外舵面销轴连接的模拟。图 3给出了3组铰链的编号及位置,由于铰链①不提供绕y轴转动的刚度,结构绕y轴转动刚度仅由铰链②和铰链③提供,因此令铰链②和铰链③绕y轴转动刚度为Kθ,铰链①绕y轴转动刚度恒为零。
|
| 图 3 折叠舵面的有限元模型 Fig. 3 Finite element model of folding fin |
动态子结构法可以从量级上大幅度减缩系统的自由度而不改变问题的本质,其基本思想是:把大型复杂系统人为地抽象成若干个子结构,先对自由度较少的子结构进行动态分析,保留其低阶主要模态信息,再根据各个子结构的界面协调条件,组装成整个系统的动态特性[19]。
对于含间隙折叠舵面,间隙的变化会改变结构的非线性动力学特性,需要相应的非线性动力学处理手段来建模与分析。本节采用双协调自由界面模态综合法[16]建立非线性折叠舵面的子结构模型,该模型可以将铰链连接处非线性自由度保留在最终的广义坐标中,便于求解分析。
2.1 子结构动力学方程折叠舵面由内舵和外舵通过铰链连接而成,因此可以将模型分为2个子结构,其中内舵为子结构a,外舵为子结构b。假设子结构离散后的有限元模型是n自由度无阻尼系统,其动力学方程为
| $ \mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{f}}_J} $ | (2) |
式中:M和K分别质量和刚度矩阵;f为节点力列阵(只有对应界面自由度的位置才有非零元素);fJ为界面力列阵;BT为投影矩阵[20]。
传统自由界面模态综合法减缩自由度时,仅保留了低阶主模态Φk,略去了全部高阶主模态影响,故综合出来的结果误差较大。而在双协调自由界面模态综合法中,引入剩余模态Ψd来表示这些高阶主模态[21]。即分别使用低阶保留模态Φk和剩余模态Ψd进行自由度减缩:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{k}}}{\mathit{\boldsymbol{p}}_{\rm{k}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}{\mathit{\boldsymbol{p}}_{\rm{d}}} $ | (3) |
式中:pk和pd分别为保留和剩余模态坐标。
第1次坐标变换,将式(3)代入子结构动力学方程式(2)中并左乘[Φk Ψd]T,得到子结构的主模态均关于其质量阵正交归一的运动方程。
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{\rm{k}}}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{M}}_{\rm{k}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\ddot p}}}_{\rm{k}}}}\\ {{{\mathit{\boldsymbol{\ddot f}}}_J}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{\rm{k}}}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{K}}_{\rm{d}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_{\rm{k}}}}\\ {{\mathit{\boldsymbol{f}}_J}} \end{array}} \right\} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {[{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{k}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}]^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{f}}_J} \end{array} $ | (4) |
式中:界面力fJ和保留模态坐标pk一样,也是一种广义坐标,且界面力fJ根据界面协调条件在模态综合时被消去; Ik和Md分别为保留和剩余质量阵;Λk和Kd分别为保留和剩余刚度阵。
2.2 子结构的剩余模态对于工程结构,一般只能计算得到结构的低阶保留主模态Φk,不能获得结构的高阶模态。下面给出在只保留低阶主模态Φk的情况下,求解剩余模态Ψd的途径[19, 22]。
当子结构无刚体模态时
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}} = {\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}} - \mathit{\boldsymbol{G}} $ | (5) |
式中:G为子结构柔度矩阵。
当子结构有刚体模态时,K-1不存在,所以不能用式(5)计算剩余模态。为此,必须首先把刚体模态分离出来。此时剩余模态Ψd表达式为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{CK}}_{{\rm{CC}}}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{B}}^{\rm{T}}} - \mathit{\boldsymbol{G}} $ | (6) |
式中:Γ=I-ΦRΦRT为子结构的投影矩阵,ΦR为子结构的刚体模态;KCC=CTKC,C为有、无刚体位移列阵的转换矩阵。在计算G时,保留模态集中仅需要考虑弹性主模态。
2.3 刚弹混合连接的双协调条件将子结构a和b模态坐标下的运动方程式(4)合并
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde M}}}_a}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde M}}}_b}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\ddot p}}}_a}}\\ {{{\mathit{\boldsymbol{\ddot p}}}_b}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde K}}}_a}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde K}}}_b}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_a}}\\ {{\mathit{\boldsymbol{p}}_b}} \end{array}} \right\} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {([{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{k}}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}]{\mathit{\boldsymbol{B}}^{\rm{T}}}{)_a}}&{}&{\bf{0}}\\ {}&{\bf{0}}&{([{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{k}}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}]{\mathit{\boldsymbol{B}}^{\rm{T}}}{)_b}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{f}}_{{a_J}}}}\\ {{\mathit{\boldsymbol{f}}_{bJ}}} \end{array}} \right\} \end{array} $ | (7) |
式中:pa=[pak faJ];pb=[pbk fbJ]。由于间隙非线性的存在,相应的界面自由度之间存在弹性连接,界面相应的自由度间并不相等,而是存在着一定的差值δ。但界面力是作用力与反作用力,仍然存在着相等的关系,则协调条件为[15-17]
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_{aJr}} = {\mathit{\boldsymbol{u}}_{bJr}}}\\ {{\mathit{\boldsymbol{u}}_{aJe}} = {\mathit{\boldsymbol{u}}_{bJe}} + \mathit{\boldsymbol{\delta }}}\\ {{\mathit{\boldsymbol{f}}_{aJ}} = - {\mathit{\boldsymbol{f}}_{aJ}}} \end{array}} \right. $ | (8) |
式中:r代表刚性连接;e代表弹性连接。
由于转角自由度差值δ与保留模态广义坐标无关,因此也作为广义坐标保留在最终方程中,为消除广义坐标中不独立的坐标,对方程进行第2次坐标变换,可表示为
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{a{\rm{k}}}}}\\ {{\mathit{\boldsymbol{f}}_{aJ}}}\\ {{\mathit{\boldsymbol{p}}_{b{\rm{k}}}}}\\ {{\mathit{\boldsymbol{f}}_{bJ}}} \end{array}} \right\} = \mathit{\boldsymbol{T}}\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{a{\rm{k}}}}}\\ {{\mathit{\boldsymbol{p}}_{b{\rm{k}}}}}\\ \mathit{\boldsymbol{\delta }} \end{array}} \right\} $ | (9) |
式中:坐标变换矩阵T为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&{\bf{0}}&{\bf{0}}\\ { - \mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{ar}}}\\ {{\mathit{\boldsymbol{B}}_{ae}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{a{\rm{k}}}}}&{\mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{br}}}\\ {{\mathit{\boldsymbol{B}}_{be}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{b{\rm{k}}}}}&{\mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{l}} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]}\\ {\bf{0}}&\mathit{\boldsymbol{I}}&{\bf{0}}\\ {\mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{ar}}}\\ {{\mathit{\boldsymbol{B}}_{ae}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{a{\rm{k}}}}}&{\mathit{\boldsymbol{ - E}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{br}}}\\ {{\mathit{\boldsymbol{B}}_{be}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{b{\rm{k}}}}}&{\mathit{\boldsymbol{ - E}}\left[ {\begin{array}{*{20}{l}} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]} \end{array}} \right] $ |
其中:
| $ \mathit{\boldsymbol{E}} = {\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{ar}}}\\ {{\mathit{\boldsymbol{B}}_{ae}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{a{\rm{d}}}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{br}}}\\ {{\mathit{\boldsymbol{B}}_{be}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{b{\rm{d}}}}} \right)^{ - 1}} $ |
通过此种变换方法,仅需要在对应弹性连接的位置引入弹性连接刚度,大大缩减了计算量。
2.4 系统的整体动力学方程应用双协调条件式(8)及变换矩阵式(9)对运动方程式(7)进行坐标变换,消去它们之间的相关坐标,可得到广义坐标均独立的整体动力学方程:
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde M}}}_a}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde M}}}_b}} \end{array}} \right]\mathit{\boldsymbol{T}}\left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot p}}}_{a{\rm{k}}}}}\\ {{{\mathit{\boldsymbol{\ddot p}}}_{b{\rm{k}}}}}\\ {\mathit{\boldsymbol{\ddot \delta }}} \end{array}} \right\} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{\mathit{\boldsymbol{T}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde K}}}_a}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde K}}}_b}} \end{array}} \right]\mathit{\boldsymbol{T + }}\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{k}}_{\rm{e}}}} \end{array}} \right]} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{a{\rm{k}}}}}\\ {{\mathit{\boldsymbol{p}}_{b{\rm{k}}}}}\\ \mathit{\boldsymbol{\delta }} \end{array}} \right\} = {\bf{0}} \end{array} $ | (10) |
式中:ke为弹性连接刚度。
由弹性自由度协调关系得,fbJ=keδ。在式(10)中恢复力与广义位移均显示表达,当恢复力为非线性恢复力时,恢复力可以表示为fbJ=knon(δ)δ(knon为间隙非线性刚度),即非线性连接刚度与元件两端转角自由度差值的乘积。
由于方程式(10)计算得到的响应是广义坐标下的响应,因此还需要对得到的响应进行2次坐标变换,得到物理坐标下结构的动态响应:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_a}}\\ {{\mathit{\boldsymbol{u}}_b}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {[{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{a{\rm{k}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{a{\rm{d}}}}]}&{\bf{0}}&{}\\ {\bf{0}}&{[{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{b{\rm{k}}}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{b{\rm{d}}}}]} \end{array}} \right]\mathit{\boldsymbol{T}}\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{a{\rm{k}}}}}\\ {{\mathit{\boldsymbol{p}}_{b{\rm{k}}}}}\\ \mathit{\boldsymbol{\delta }} \end{array}} \right\} $ | (11) |
在仅保留子结构a和b前5阶弹性模态的情况下,检验折叠舵面子结构模型的精度。有限元模型和子结构模型的铰链连接处采用相同的线性连接刚度(间隙为零)Kθ,在不同的连接刚度情况下,对比了整体结构前5阶固有频率,如表 2所示。可以看出经过子结构法减缩的系统能够对有限元模型的模态进行较好地逼近。
| 连接刚度/(N·m·rad-1) | 有限元模型/Hz | 子结构模型/Hz | 误差/% |
| 16.72 | 15.81 | 5.44 | |
| 58.81 | 60.28 | 2.44 | |
| 10 | 94.02 | 95.31 | 1.37 |
| 132.40 | 132.42 | 0.02 | |
| 416.20 | 415.34 | 0.21 | |
| 44.26 | 44.73 | 1.06 | |
| 62.90 | 64.50 | 2.48 | |
| 103 | 132.40 | 132.42 | 0.02 |
| 176.76 | 178.01 | 0.71 | |
| 459.98 | 456.27 | 0.81 |
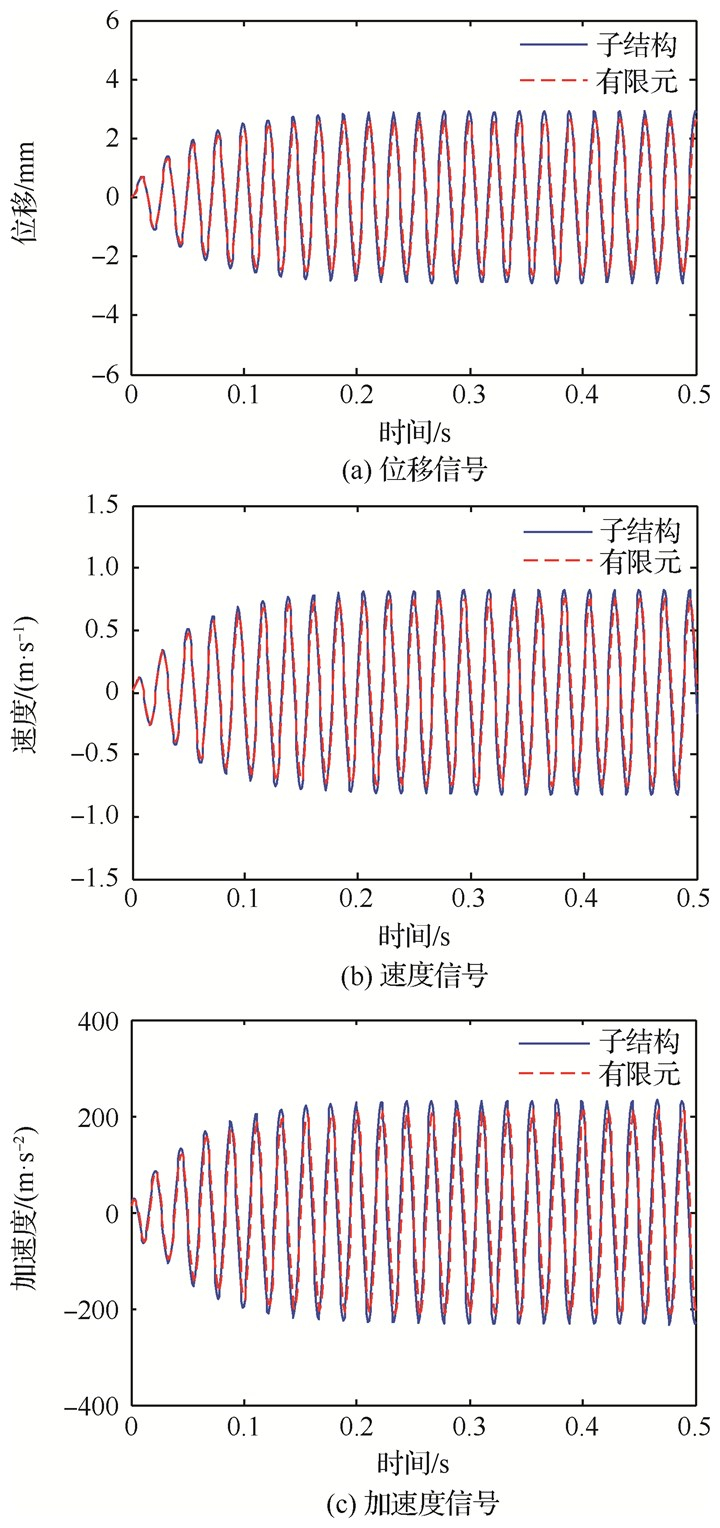
在线性连接刚度为103 N·m/rad和相同正弦激励下,对比有限元模型与子结构模型的响应。激励点与响应点位置如图 3所示,计算得到的响应信号如图 4所示。可以看出,子结构模型和有限元模型的响应信号吻合较好,即降阶后的子结构模型可用于表征有限元模型的动力学特性。
|
| 图 4 响应信号对比 Fig. 4 Comparison of response signals |
分别使用振动台和力锤对不含间隙的折叠舵面进行扫频和模态实验。进行模态实验时,采用力锤激励,在折叠舵面上布置9个测点,如图 5所示。为了消除传感器附加质量对结构固有频率的影响,使用振动台进行扫频实验,仅在图 5所示激励点处布置1个传感器。

|
| 图 5 折叠舵面的实验装置 Fig. 5 Experimental setup of folding fin |
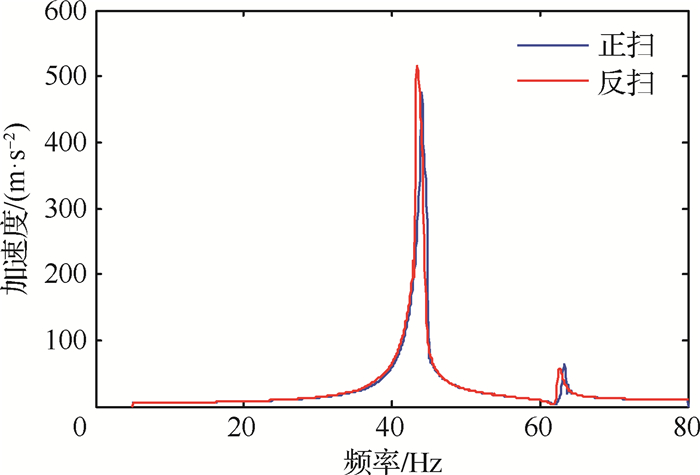
首先使用振动台对不含间隙折叠舵面进行扫频实验,得到结构前2阶固有频率分别为44.08 Hz和63.28 Hz,如图 6所示。
|
| 图 6 线性实验扫频曲线(δ=0) Fig. 6 Experimental linear sweep curves (δ=0) |
由于在有限元模型中把实际结构的销轴简化为MPC多点约束单元,因此连接刚度Kθ为实际结构的等效连接刚度。通过模态实验结果直接修正有限元模型的等效刚度,计算量大,不易操作[23]。因此选用子结构模型的动力学方程(10)对连接刚度进行修正。通过模型修正得到等效线性连接刚度为590 N·m/rad,在该连接刚度下对比了不同模型的前2阶固有频率,如表 3所示。在等效线性连接刚度下,通过有限元模型和子结构模型得到的固有频率计算值与不含间隙折叠舵面的实验结果十分接近。
| 模态阶数 | 模态实验/Hz | 有限元/Hz | 子结构/Hz |
| 1 | 44.08 | 43.59 | 43.73 |
| 2 | 63.28 | 62.64 | 64.12 |
其次使用力锤激励对折叠舵面进行模态实验,获取其前2阶模态振型,并与有限元计算结果进行对比,如图 7和图 8所示。由图可知,虽然实验布置的测点数目有限,模态振型的实验结果相对粗糙,但模态振型的有限元计算结果与实验结果基本吻合。综上,通过子结构模型修正得到的等效线性连接刚度能够较好地描述真实结构的连接特性,所建立的动力学模型可用于折叠舵面的动力学响应预测。

|
| 图 7 第1阶模态振型对比 Fig. 7 Comparison of the first mode shapes |

|
| 图 8 第2阶模态振型对比 Fig. 8 Comparison of the second mode shapes |
此外,观察结构前2阶振型可以看出,结构第1阶振型是弯曲模态,第2阶振型是扭转模态。结合表 2不同连接刚度下前2阶固有频率的对比结果,可以看出连接刚度主要影响结构第1阶弯曲模态频率,对第2阶扭转模态频率影响相对较小。
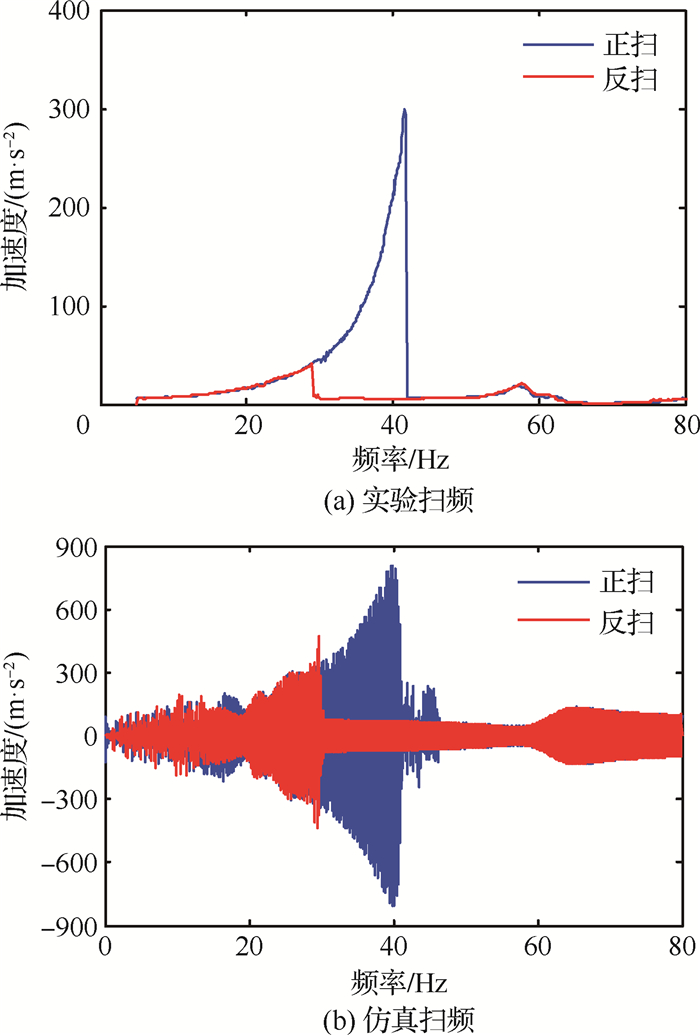
3.3 非线性动态特性分析在不同的间隙下,将图 2所示的分段刚度取为等效线性连接刚度590 N·m/rad,即将等效线性连接刚度与间隙值组合,得到不同间隙下的非线性连接刚度。基于子结构模型对不同间隙下的折叠舵面进行仿真扫频,对比仿真和实验扫频结果,如图 9~图 11所示。

|
| 图 9 线性仿真扫频曲线(δ=0 rad) Fig. 9 Curves of simulated linear sweep (δ=0 rad) |

|
| 图 10 非线性扫频曲线(δ=0.013 rad) Fig. 10 Curves of nonlinear sweep (δ=0.013 rad) |
|
| 图 11 非线性扫频曲线(δ=0.04 rad) Fig. 11 Curves of nonlinear sweep (δ=0.04 rad) |
表 4定量对比了在不同间隙下仿真与实验的扫频结果。随着间隙的增大,结构前2阶频率对应的峰值位置逐渐降低,但第1阶频率处出现了明显的非线性跳跃现象,正扫与反扫的峰值位置逐渐分离,而第2阶频率正扫与反扫的峰值位置基本重合。仿真与实验扫频结果基本吻合,验证了非线性动力学模型的精度及其在含间隙折叠舵面非线性动态特性分析中的可行性。
| 间隙大小/rad | 第1阶频率峰值/Hz | 第2阶频率峰值/Hz | |||||
| 实验 | 仿真 | 误差/% | 实验 | 仿真 | 误差/% | ||
| 0正扫 | 44.08 | 44.25 | 0.38 | 63.28 | 65.4 | 3.35 | |
| 0反扫 | 43.49 | 43.2 | 0.67 | 63.28 | 65.4 | 3.35 | |
| 0.013正扫 | 43.35 | 42.98 | 0.86 | 61.93 | 64.14 | 3.57 | |
| 0.013反扫 | 42.52 | 41.84 | 1.63 | 61.93 | 64.14 | 3.57 | |
| 0.04正扫 | 41.77 | 39.38 | 6.07 | 57.65 | 61.52 | 6.71 | |
| 0.04反扫 | 29.05 | 30.04 | 3.30 | 57.65 | 61.52 | 6.71 | |
1) 采用双协调自由界面模态综合法对非线性连接系统的线性主体部件有限元模型进行减缩,可降低模型规模,提高计算效率。
2) 针对本文中的折叠舵面结构,结构的线性连接刚度可通过模型修正获得,而间隙非线性连接刚度可由得到的等效线性连接刚度和间隙值组合而成。
3) 实验验证了所建立非线性动力学模型的精度,为开展含间隙折叠舵面的非线性动态特性分析提供了技术基础。
| [1] | DOWELL E H, TANG D. Nonlinear aeroelasticity and unsteady aerodynamics[J]. AIAA Journal, 2002, 40(9): 1697-1707. |
| Click to display the text | |
| [2] |
丁千, 陈予恕. 机翼颤振的非线性动力学和控制研究[J]. 科技导报, 2009, 27(2): 53-61. DING Q, CHEN Y S. Non-linear dynamic and control of flutter of airfoil[J]. Science and Technology Review, 2009, 27(2): 53-61. (in Chinese) |
| Cited By in Cnki (40) | Click to display the text | |
| [3] |
刘芳, 丁千. 含间隙折叠舵面的主共振响应分析[J]. 航空动力学报, 2016, 31(12): 2965-2971. LIU F, DING Q. Primary resonance response analysis on folding rudder with gaps[J]. Journal of Aerospace Power, 2016, 31(12): 2965-2971. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [4] |
赵永辉, 胡海岩. 具有操纵面间隙非线性二维翼段的气动弹性分析[J]. 航空学报, 2003, 24(6): 521-525. ZHAO Y H, HU H Y. Aeroelastic analysis of a two-dimensional airfoil with control surface freeplay nonlinearity[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(6): 521-525. (in Chinese) |
| Cited By in Cnki (81) | Click to display the text | |
| [5] | GOLD P, KARPEL M. Reduced-size aeroservoelastic modeling and limit-cycle-oscillation simulations with structurally nonlinear actuators[J]. Journal of Aircraft, 2008, 45(2): 471-477. |
| Click to display the text | |
| [6] | BEHAL A, RAO D. Adaptive control for a nonlinear wing section with multiple flaps[J]. Journal of Guidance, Control and Dynamics, 2006, 29(3): 744-750. |
| Click to display the text | |
| [7] |
迟圣威.折叠翼颤振理论分析和计算方法[D].南京: 南京航空航天大学, 2011: 11-17. CHI S W. Theoretical and computational flutter study for folding wing configuration[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 11-17(in Chinese). |
| [8] | ABDELKEFI A, VASCONCELLOS R, MARQUES F D, et al. Modeling and identification of freeplay nonlinearity[J]. Journal of Sound and Vibration, 2012, 331(8): 1898-1907. |
| Click to display the text | |
| [9] |
向树红, 邱吉宝, 王大钧. 模态分析与动态子结构方法新进展[J]. 力学进展, 2004, 34(3): 289-303. XIANG S H, QIU J B, WANG D J. The resent progresses on modal analysis and dynamic sub-structure methods[J]. Advances in Mechanics, 2004, 34(3): 289-303. (in Chinese) |
| Cited By in Cnki (202) | Click to display the text | |
| [10] | KIM D, BAE J, LEE I, et al. Dynamic model establishment of a deployable missile control fin with nonlinear hinge[J]. Journal of Spacecraft and Rockets, 2005, 42(1): 66-77. |
| Click to display the text | |
| [11] | BAE J, KIM D, SHIN W, et al. Nonlinear aeroelastic analysis of a deployable missile control fin[J]. Journal of Spacecraft and Rockets, 2004, 41(2): 264-271. |
| Click to display the text | |
| [12] |
全炜倬, 方明霞. 超音速飞行器翼——身组合体的颤振研究[J]. 噪声与振动控制, 2010, 30(6): 1-4. QUAN W Z, FANG M X. Flutter study of wing-fuselage combination of supersonic aircrafts[J]. Noise and Vibration Control, 2010, 30(6): 1-4. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [13] |
倪迎鸽, 侯赤, 万小朋, 等. 具有结构非线性的折叠机翼气动弹性分析[J]. 振动与冲击, 2016, 35(18): 165-171. NI Y G, HOU C, WAN X P, et al. Aeroelastic analysis of a folding wing with structural nonlinearities[J]. Journal of Vibration and Shock, 2016, 35(18): 165-171. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [14] |
杨宁, 吴志刚, 杨超, 等. 折叠翼的结构非线性颤振分析[J]. 工程力学, 2012, 29(2): 197-204. YANG N, WU Z G, YANG C, et al. Flutter analysis of a folding wing with structural nonlinearity[J]. Engineering Mechanics, 2012, 29(2): 197-204. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [15] | YANG N, WANG N, ZHANG X, et al. Nonlinear flutter wind tunnel test and numerical analysis of folding fins with freeplay nonlinearities[J]. Chinese Journal of Aeronautics, 2016, 29(1): 144-159. |
| Click to display the text | |
| [16] | WU Z G, YANG N, YANG C. Identification of nonlinear multi-degree-of freedom structures based on Hilbert transformation[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(9): 1725-1736. |
| Click to display the text | |
| [17] | WU Z G, YANG N, YANG C. Identification of nonlinear structures by the conditioned reverse path method[J]. Journal of Aircraft, 2015, 52(2): 373-386. |
| Click to display the text | |
| [18] |
胡海岩, 赵永辉, 黄锐. 飞机结构气动弹性分析与控制研究[J]. 力学学报, 2016, 48(1): 1-27. HU H Y, ZHAO Y H, HUANG R. Studies on aeroelastic analysis and control of aircraft structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 1-27. (in Chinese) |
| Cited By in Cnki (19) | Click to display the text | |
| [19] |
王文亮, 杜作润, 陈康元. 模态综合技术短评和一种新的改进[J]. 航空学报, 1979(3): 32-51. WANG W L, DU Z R, CHEN K Y. A short commentary for modal synthesis techniques and a novel improvement[J]. Acta Aeronautica et Astronautica Sinica, 1979(3): 32-51. (in Chinese) |
| Cited By in Cnki (117) | Click to display the text | |
| [20] |
王永岩. 动态子结构方法理论及应用[M]. 北京: 科学出版社, 1999. WANG Y Y. Theory and application of dynamic substructure method[M]. Beijing: Science Press, 1999. (in Chinese) |
| [21] | RUBIN S. Improved component-mode representation for structural dynamic analysis[J]. AIAA Journal, 1975, 13(8): 995-1006. |
| Click to display the text | |
| [22] |
应祖光, 邱吉宝, 潭志勇. 精确剩余模态及其综合技术[J]. 振动工程学报, 1996, 9(1): 38-46. YING Z G, QIU J B, TAN Z Y. Exact residual modes and their synthesis techniques[J]. Journal of Vibration Engineering, 1996, 9(1): 38-46. (in Chinese) |
| Cited By in Cnki (30) | Click to display the text | |
| [23] | NOËL J P, KERSCHEN G. Nonlinear system identification in structural dynamics:10 more years of progress[J]. Mechanical Systems and Signal Processing, 2017, 83(15): 2-35. |



