代理模型方法最早是由Morris[1]在1972年提出的,由于Sacks等[2]在这方面的卓越成果使得代理模型方法在20世纪90年代末得以流行。近年来,基于代理模型的优化(Surrogate-Based Optimization, SBO)以其高效性、全局性和广泛的适用性,被广泛应用于结构优化、气动优化、多学科优化、航天航空工程和机械工程等学科中[3-8]。
在基于Kriging模型的SBO过程中,新样本的选择对于整个SBO过程的效率、鲁棒性和优化质量都有很大的影响[3]。常用的样本选择方法有如下几种:基于模型预测目标值、基于模型误差、基于期望提高(Expected Improvement, EI)函数、基于可能性提高函数、基于下置信域边界[9]。由于基于EI的取样能够同时权衡设计空间的局部勘测和全局搜索,并且其建模时获得的误差函数能够被直接应用于EI函数值的计算,该取样方法被广泛应用于SBO过程。
当前,受限于样本总数的限制,更有效的取样方法成为研究热点之一[10-15]。一种有效的平衡局部勘测和全局搜索的方式是确定一个包含全局最优的空间,然后在取样迭代过程中不断地对该空间的大小进行动态调整,并在该变化的空间内进行取样和建模。Cheng和Wang将信赖域的概念引入基于二次响应面的SBO过程,并且通过模式搜索在子空间中取样,特别适于处理高维优化问题[16]。Guo等使用粒子群进化算法生成大量的低成本样本,此后采用模糊C均值聚类对这些样本进行分类来确定关注的空间,然后从该空间的粒子中选择新的样本[17]。Qiu等发展了一种多级设计空间缩减方法,采用了自组织规划来确定初始缩减空间,然后利用模糊聚类方法缩减初始设计空间到一个相对小的空间[18]。Shi等将模糊C均值聚类方法引入基于径向基函数(Radial Basis Function, RBF)模型的优化,并采用支持向量基来确定低成本样本的聚类中心,用以缩减设计空间[19]。Dong等在SBO过程中,采用了Kriging和二次响应面模型,并选择二次响应面模型的全局最优点和Kriging模型的几个局部最优点作为样本细化过程的新增样本。同时,为了平衡模型的全局和局部精度,K均值聚类方法被用以寻找样本密度比较稀疏的区域,以便于通过样本细化过程提高模型的全局精度[20]。王超等提出了引入期望提高阈值的混合选点方法,并采用扩大设计变量范围和多轮优化的方法对设计空间进行重构,提出了自适应设计空间扩展的代理模型方法[21]。Li和Pan将信赖域方法引入SBO过程来自适应地改变动态取样的设计空间的大小,可以提高代理模型的局部精度[22]。
综上所述,为了进一步提高代理模型的局部和全局精度,更好地适应于具有多极值、强非线性的优化问题,本文在一般的SBO方法的基础上,发展了一种能够自适应序列取样的高效全局优化算法。在自适应取样过程中,利用模糊C均值聚类方法将设计空间划分成若干子空间,并据此对设计空间进行缩减,然后在缩减后的设计空间中利用最大化EI函数和最小化模型预测(Minimizing Surrogate Prediction, MSP)目标来选择新的样本更新代理模型。上述所发展的方法命名为SBO-FCM。本文将该方法用于多个解析算例的求解,验证了算法的正确性和有效性;并进一步将其用于气动优化实例的求解,以检验算法的效率和实用性。
1 基于代理模型的优化算法一般的, 具有m个设计变量、Mc个非线性约束的优化问题的数学模型可以表示为
| $ \begin{array}{l} {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ f\left( \mathit{\boldsymbol{x}} \right)\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{g_j}(\mathit{\boldsymbol{x}}) \le 0}&{j = 1,2, \cdots ,{M_{\rm{c}}}}\\ {x_i^{\rm{L}} \le {x_i} \le x_i^{\rm{U}}}&{i = 1,2, \cdots ,m} \end{array}} \right. \end{array} $ | (1) |
式中:gj(x)为第j个非线性约束;xiL和xiU分别为设计变量的上下边界。本模型中,假设获得目标函数和非线性约束的代价比较大。因此,采用SBO方法求解上述问题可以提高优化效率。
一般的SBO方法过程包括初始取样、高精度模型分析、代理模型建模、动态取样和优化,具体的流程见图 1。其中,初始取样主要采用试验设计(Design of Experiment, DoE)方法[2],从取样的均匀性上对方法进行选取和设置。高精度模型分析可以采用试验或高精度数值仿真方法,直接或间接获得样本的目标函数值。代理模型建模是基于当前样本及其目标函数值,建立一个可以代替高精度模型来预测目标函数的代理模型。当代理模型精度不够时,需要通过样本细化准则生成新的样本并添加到原有样本库中,更新代理模型。在样本细化过程中循环添加样本,直到基于所有样本建立的代理模型的精度满足要求。最后,利用最终的代理模型来预测目标函数,进行优化。
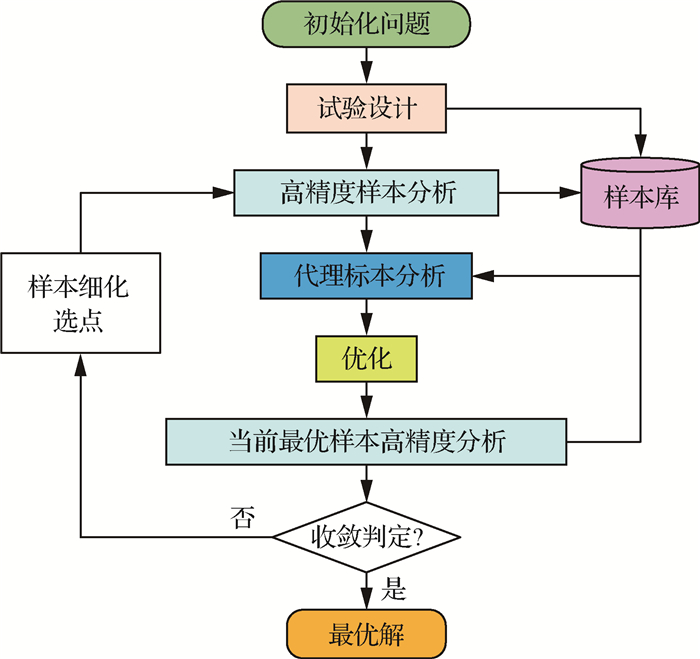
|
| 图 1 一般的SBO方法流程图 Fig. 1 Flowchart of common SBO procedure |
在本文所发展的SBO优化方法中,代理模型采用了Kriging模型[23]。Kriging模型是一种基于统计理论建立的插值模型。如果要为一个未知函数y(x): Rm→R建立Kriging模型,其中x为设计变量,需要首先利用试验设计方法生成一组样本S=[x1, x2, …, xn]T∈Rn×m。然后,通过高精度分析工具获得每个样本对应的响应值y=[y1, y2, …, yn]T∈Rn。最后,利用样本和对应的响应值建立Kriging模型,可以表示为
| $ \hat y(\mathit{\boldsymbol{x}}) = \hat \mu + {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{y}} - {\bf{1}}\hat \mu ) $ | (2) |
式中:
| $ {R_{i,j}} = {\rm{exp}} \left( { - \sum\limits_{l = 1}^m {{\theta _l}} |x_i^l - x_j^l{|^2}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i,j = 1,2, \cdots ,n $ | (3) |
其中:θl为Kriging模型的第l个未知相关参数; m为设计变量个数。
对于一组给定的相关参数θ (可以通过最大化似然函数的对数求得),Kriging模型的预测递归参数
| $ \left\{ {\begin{array}{*{20}{l}} {\mu = \frac{{{{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{y}}}}{{{{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}{\bf{1}}}}}\\ {\hat \sigma _{\rm{C}}^2 = \frac{{{{(\mathit{\boldsymbol{y}} - {{\bf{1}}_\mu })}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{y}} - {{\bf{1}}_\mu })}}{n}} \end{array}} \right. $ | (4) |
进一步求解可以获得Kriging模型的误差
| $ {s^2}(\mathit{\boldsymbol{x}}) = \hat \sigma _{\rm{C}}^2\left[ {1 - {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}} + \frac{{{{\left( {1 - {{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}}} \right)}^2}}}{{{{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}{\bf{1}}}}} \right] $ | (5) |
模糊C均值聚类是一种软聚类,最早是在1973年由Bezdek和Christian提出的[24],是对简单聚类方法的改进,能够尽可能保证每类中个体的差异性最小。假设当前用于聚类的数据集为xk(k=1, 2, …, Np),对应的目标函数值为fk(k=1, 2, …, Np)。如果要将当前Np个样本聚合成Nc个类,每个类中心和其他样本的差异性可以表示为
| $ J(\mathit{\boldsymbol{U}},\mathit{\boldsymbol{V}}) = \sum\limits_{k = 1}^{{N_{\rm{p}}}} {\sum\limits_{i = 1}^{{N_{\rm{c}}}} {{{({\mathit{\boldsymbol{u}}_{ik}})}^d}} } {\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right\|^2} $ | (6) |
式中:vi为第i个类中心;uik为第i个类中的第k个样本到该类中心的权重,即隶属度系数;U为对Np个样本的模糊划分;d为大于1的常数,通常取2。式(6)通常存在一个局部最小值,因此可以通过求解如下的优化问题来获得Nc个聚类,即获得U和V,表达式为
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{U,V}}} J(\mathit{\boldsymbol{U,V}})\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum _{i = 1}^{{N_{\rm{c}}}}{\mathit{\boldsymbol{u}}_{ik}} = 1 \end{array} $ | (7) |
式(7)中的优化问题可以利用拉格朗日乘子法求解,根据极值存在的必要条件,可以计算得到类中心和隶属度系数,表达式为
| $ {\mathit{\boldsymbol{v}}_i} = \sum\limits_{k = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{u}}_{ik}^d} {\mathit{\boldsymbol{x}}_k}/\sum\limits_{k = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{u}}_{ik}^d} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,{N_{\rm{c}}} $ | (8) |
| $ {\mathit{\boldsymbol{u}}_{ik}} = 1/\sum\limits_{j = 1}^{{N_{\rm{c}}}} {{{\left( {\frac{{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right\|}}{{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_j}} \right\|}}} \right)}^{\frac{2}{{d - 1}}}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\mathit{\boldsymbol{u}}_{ik}} \le 1 $ | (9) |
聚类实现的具体流程描述如下:
步骤1 设置类数目Nc≥2,小量ε>0,初始化种群的中心V0,设置最大迭代步Kmax和初始迭代步ks=0。
步骤2 如果ks < Kmax,根据式(9)计算隶属度矩阵Uk。
步骤3 通过求解式(8)更新聚类中心Vk+1。
步骤4 如果‖Vk+1-Vk‖≤ε,停止迭代,输出聚类中心Vk和隶属度矩阵Uk;否则,更新迭代步ks=ks+1,回到步骤2。
步骤5 根据每个样本对于不同类的隶属度系数,将其划分到不同的类,划分原则是:第k个样本xk归属于最大的uik对应的类(即对应的i)。
图 2为采用模糊C均值聚类方法对100个2-D空间中的样本进行聚类的示例。其中,100个样本由Maximin拉丁超立方设计[25]生成,类的数目Nc=3。图 2(a)中,3种不同颜色代表不同的类,每个类的中心用不同的符号标出。对比于图 2(b)可见,类的划分与输入数据的空间特征相关。此示例的输入为设计变量和其对应的目标函数值,因此类的划分同时考虑了样本的空间分布和目标函数大小的分布。
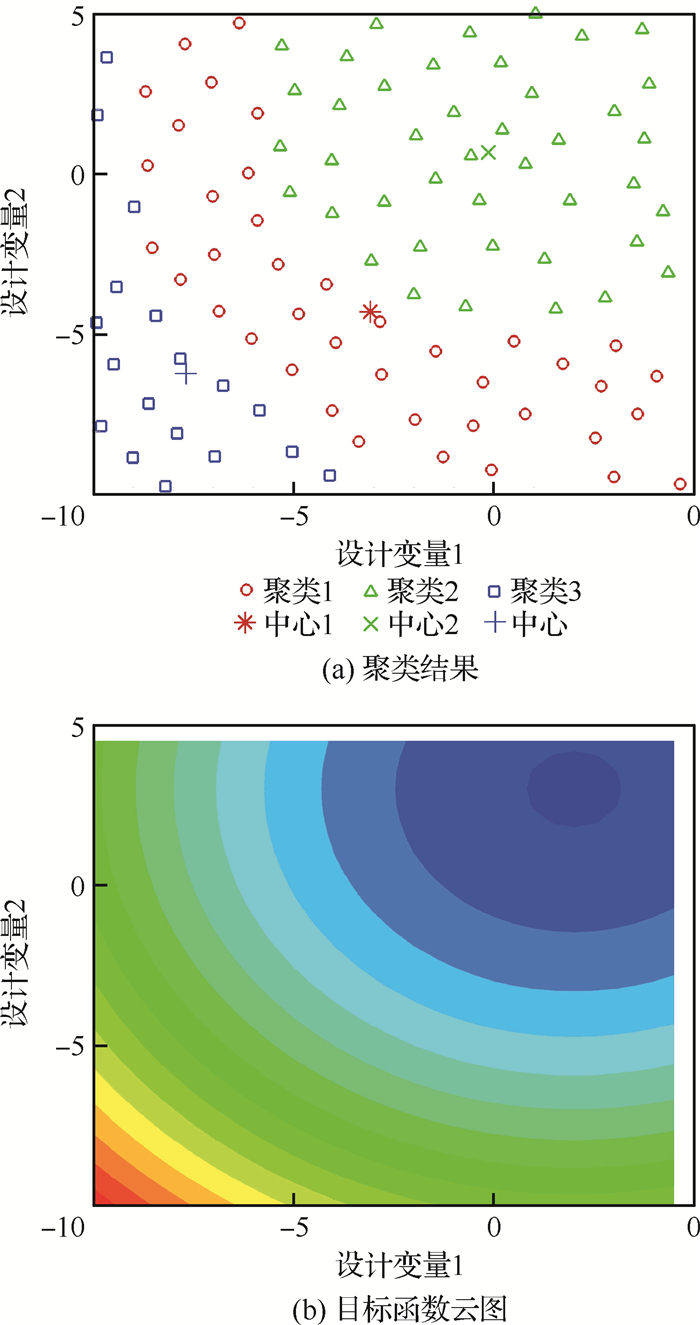
|
| 图 2 100个2-D样本聚类示例 Fig. 2 Example for 100 clustered samples in 2-D |
SBO中的样本细化方法必须具有自适应性。为了进一步提高代理模型的局部精度,本文发展了基于聚类的自适应样本细化方法。该过程可以分为以下4步:①在当前设计空间内生成伪样本,并缩减伪样本数量;②对缩减后的伪样本进行聚类,生成子空间;③在子空间内选择新的样本;④对子空间进行聚合,生成新的设计空间。本文所发展的SBO-FCM方法的流程如图 3所示。由于前面对一般的SBO过程已经进行了描述,这里只对改进的自适应取样过程进行讲解。
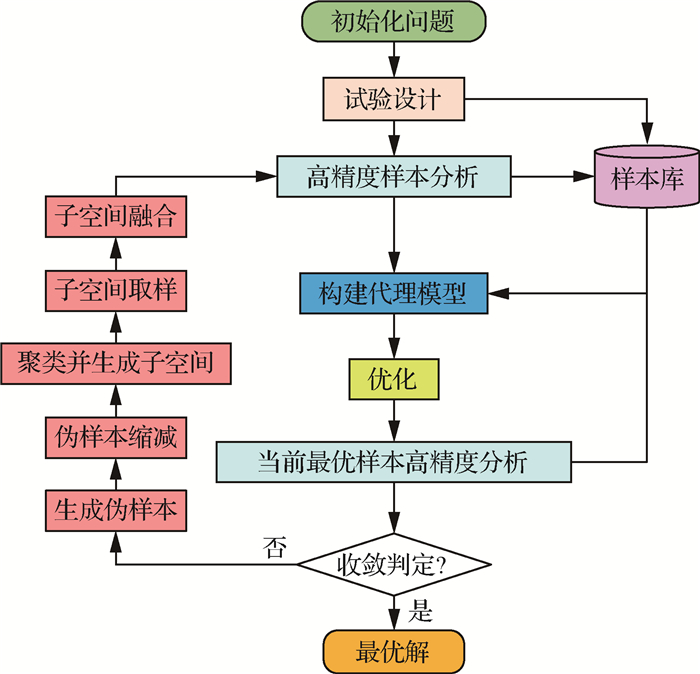
|
| 图 3 SBO-FCM方法流程 Fig. 3 Flowchart of SBO-FCM |
1) 伪样本生成和缩减
在SBO过程中,初始迭代过程中的高精度样本数量不足,不适合于聚类分析。因此,本文采用伪样本来进行聚类,即首先在当前设计空间内利用随机拉丁超立方设计(Random Latin Hypercube Design, RLHD)生成Np个伪样本,并通过代理模型预测获得所有伪样本的目标函数值。然后,通过如下操作对Np个伪样本进行缩减,以尽可能地缩减子空间的范围。
① 计算伪样本的目标函数均值fm=
② 根据定义的缩减阈值系数tr,计算目标函数阈值ft=tr(fmax-fmin),其中0 < tr≤1,fmax和fmin分别为当前伪样本中的最大目标和最小目标。
③ 对比目标函数均值和目标函数阈值,确定被删除的伪样本的目标函数值下限,即fd=max(fm, ft)。
④ 删除所有目标函数值大于fd的伪样本,剩余的Nr个伪样本用于聚类分析。
一般而言,缩减阈值系数可以控制设计空间被删除部分的大小,阈值系数越小,剩余伪样本所在的设计空间大小可能越小。但是,为了保证有足够的伪样本用于聚类分析,并且阻止设计空间的迅速减小,采用目标函数下限来筛选被删除的伪样本更加合理。
2) 聚类分析
之后采用上述的模糊C均值聚类方法对剩余的Nr个伪样本进行聚类分析,最多可以生成Nc个类(初始设置的类个数)。每个类中的伪样本可以构成一个子空间,有Nc个类就有Nc个子空间,可以用于下一步样本细化选点。
3) 样本细化
在自适应的SBO过程中,需要在迭代过程中不断添加新的样本来更新代理模型,以提高模型的全局和局部精度。上述过程被称为样本细化过程。不同于一般的SBO方法,本文不在整个设计空间内取样,而是在聚类分析形成的若干子空间内采用样本细化策略来选择新的样本,这样可以一次添加多个样本,既充分利用计算机的并行能力,又适应于非线性强,具有多极值的复杂问题。本文所使用的样本细化策略包括:基于EI函数的取样、基于MSP的取样和混合取样方法。
Jones等在1998年提出了EI准则[26],如果当前的最优目标函数值为fmin,与某点预测目标函数的差为Δy=ymin-
| $ E[I(\mathit{\boldsymbol{x}})] = \left\{ {\begin{array}{*{20}{l}} {\Delta y\varPhi (\Delta y/s) + s\varphi (\Delta y/s)}&{s > 0}\\ 0&{s = 0} \end{array}} \right. $ | (10) |
式中:Φ和φ分别表示标准正态函数的积分分布函数和概率密度函数。因此,通过最大化EI函数选点的过程可以表述为
| $ \begin{array}{l} {\rm{max}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E\left[ {I\left( \mathit{\boldsymbol{x}} \right)} \right]\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_i^{\rm{L}} \le {x_i} \le x_i^{\rm{U}}\quad i = 1,2, \cdots ,m \end{array} $ | (11) |
基于MSP的取样为最小化模型预测目标函数值,该过程可以表述为
| $ \begin{array}{l} {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat y\left( \mathit{\boldsymbol{x}} \right)\\ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_i^{\rm{L}} \le {x_i} \le x_i^{\rm{U}}\quad i = 1,2, \cdots ,m \end{array} $ | (12) |
混合取样方法将上述两种方法进行组合,而且可以在不同的样本细化迭代步中选择使用。由于子空间可能存在交叠的情况,这可能导致在不同的子空间获得的新样本相同或者极其相近,因此,需要对这些相同或相近样本进行剔除。
4) 子空间融合
最后,将若干子空间进行融合,生成新的设计空间,作为下一步迭代的输入。
5 算例分析 5.1 解析算例本文采用了6个带有边界约束的低维和高维解析算例对方法进行了测试和验证。6个算例的具体介绍如下。
2-D Branin(BR)函数具有3个极值,分别位于(-π, 12.275), (π, 2.275)和(9.424 8, 2.475),对应的全局最优目标函数值为0.397 9。优化问题可以表示为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) = [{x_2} - 5.1{{(0.5{x_1}/\mathsf{π} )}^2} + (5/\mathsf{π} ){x_1} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{]^2} + 10[1 - 0.125(1/\mathsf{π} )] {\rm{cos}} {x_2} + 10} \end{array}\\ \ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 5,10];{x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [0,15] \end{array} $ | (13) |
2-D的Rosenbrock(RB)函数具有一条长的脊线,会给搜索带来极大的困难。该问题的全局最优点位于(1, 1),对应的最优解为0。优化问题的数学模型为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) = 100{{({x_2} - x_1^2)}^2} + {{({x_1} - 1)}^2}}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_1},{x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 5,10]} \end{array} $ | (14) |
2-D Griewank(GN)函数具有极强的非线性,在设计空间内具有非常多的局部极值点,但是只有一个全局极值点位于(0, 0),其目标函数值为0。优化问题如下
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^2 {x_i^2} /200 - \prod\limits_{i = 1}^2 { {\rm{cos}} } ({x_i}/\sqrt i ) + 1}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 100,100]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2} \end{array} $ | (15) |
2-D Rastringin(RS)函数也具有很强的非线性,有多个局部极值,但只有一个全局最优解(0, 0),对应的目标函数值为0。优化问题的数学模型为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( \mathit{\boldsymbol{x}} \right) = 20 + \sum\limits_{i = 1}^2 {[x_i^2 - 10 {\rm{cos}} (2\mathsf{π} {x_i})]} }\\ \ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 1,1]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2} \end{array} $ | (16) |
6-D Hartmann(HN6)函数具有6个局部极值,由于函数的非线性和多变量的特点,寻找全局最优点变得困难。该问题只有一个全局最优解(0.201 7, 0.150 0, 0.476 9, 0.275 3, 0.311 7, 0.657 3),对应的目标函数值为-3.322。优化问题如下,系数见文献[27]:
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( \mathit{\boldsymbol{x}} \right) = - \sum\limits_{j = 1}^4 {{b_j}{\rm{exp}}\left[ { - \sum\limits_{i = 1}^6 {{a_{ji}}{{\left( {{x_i} - {p_{ji}}} \right)}^2}} } \right]} }\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [0,1]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,6} \end{array} $ | (17) |
16-D(F16)高维测试算例有16个设计变量,是个非线性函数,最优点对应的函数值为25.878。优化问题表述为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{16} {\sum\limits_{j = 1}^{16} {{a_{ij}}} } (x_i^2 + {x_i} + 1)(x_j^2 + {x_j} + 1)}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 1,0]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,16} \end{array} $ | (18) |
式中:系数aij可以通过文献[27]获得。
为了评估SBO-FCM方法,本文还采用了基于EI的代理模型优化方法(SBO-EI)和基于MSP的代理模型优化方法(SBO-MSP)对上述算例进行了求解。初始的试验设计样本数目根据文献[9],确定方法为:当问题的维度m ≤6时,取(m+1)(m+2)/2个样本;当问题维度m>6时,取2m个样本作为初始样本。
上述算例用每种方法都重复求解了30次,以测试求解方法的鲁棒性。每种方法求解不同问题获得的最优解的均值、30个最优解的方差如表 1所示。结果表明,SBO-FCM方法得到的最优解均值是最好的,也是最接近于解析解的,特别是对于非线性很强的问题,例如GN函数、RS函数,SBO-FCM的效果会明显优于SBO-EI和SBO-MSP。从方差上看,SBO-FCM方法获得的30次解的方差最小,表明该方法的鲁棒性较好。
| 测试函数 | 实验设计 | SBO-FCM | SBO-EI | SBO-MSP | |||||
| 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | ||||
| BR | 6 | 0.397 8 | 2.820 6×10-9 | 0.398 4 | 1.462×10-6 | 0.662 2 | 3.986 0×10-1 | ||
| RB | 6 | 0.003 6 | 1.974 8×10-4 | 0.021 7 | 9.028 6×10-3 | 0.702 8 | 2.428 5 | ||
| GN | 6 | 0.043 9 | 6.419 1×10-2 | 0.095 2 | 1.759 9×10-2 | 0.380 4 | 3.102 2×10-1 | ||
| RS | 6 | -1.996 0 | 4.888 6×10-4 | -1.561 6 | 4.799 2×10-1 | -1.460 0 | 5.840 7×10-1 | ||
| HN6 | 28 | -3.269 0 | 6.576 2×10-3 | -3.168 7 | 5.328 3×10-2 | -3.165 6 | 6.336 7×10-2 | ||
| F16 | 32 | 25.875 6 | 5.814 9×10-7 | 25.876 5 | 4.122 1×10-6 | 25.878 8 | 2.404 2×10-5 | ||
图 4中的箱线图也证明了SBO-FCM方法具有较好的鲁棒性。图示表明,对于低维且非线性的一般的多极值问题,例如BR函数,3种SBO都具有较好的鲁棒性。对于低维但具有较强非线性RB、GN和RS函数,SBO方法的鲁棒性都有所下降;但是相比而言SBO-FCM的鲁棒性是下降较小的,在三者中最好。当问题的维度提高时,即使优化问题的非线性一般,3种SBO的鲁棒性也都会明显下降,但是SBO-FCM依然在三者中最好。
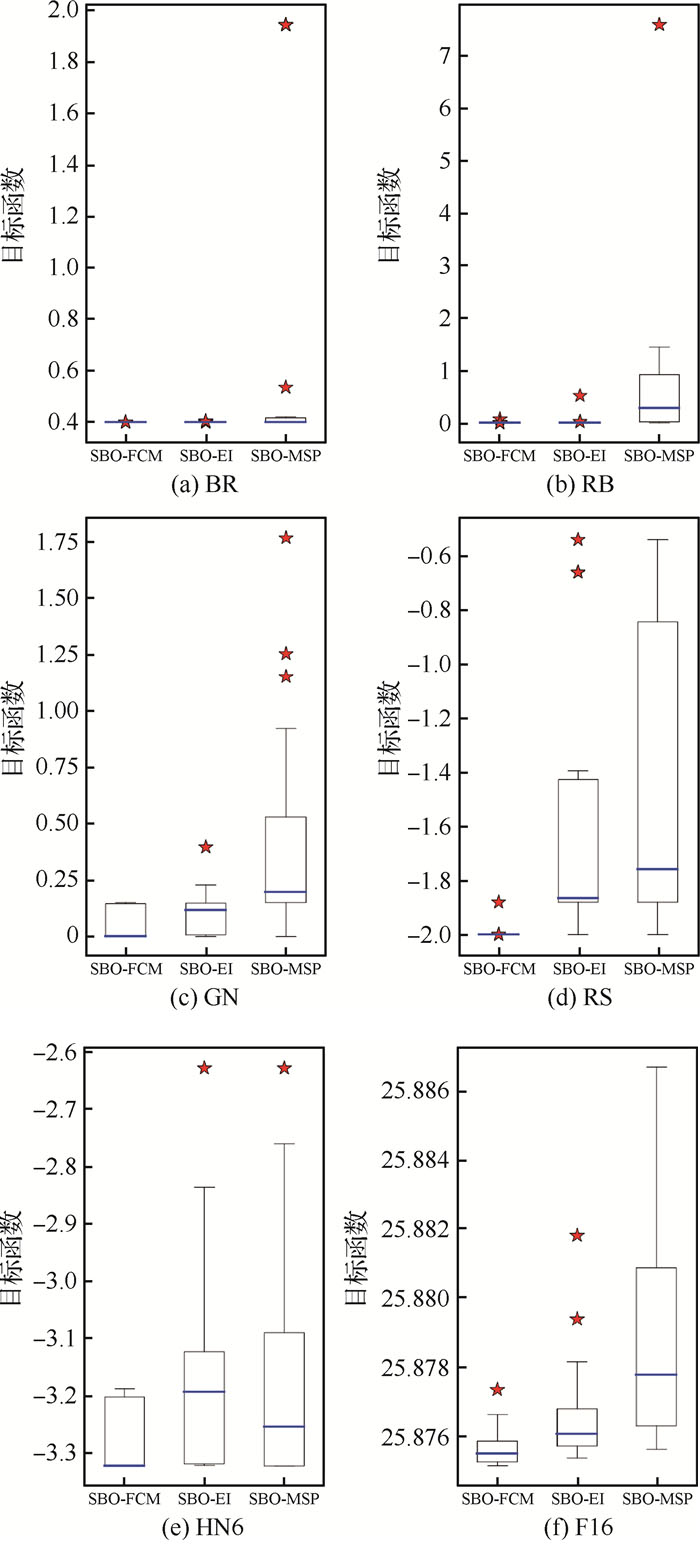
|
| 图 4 解析算例箱线图 Fig. 4 Box plots of analytical tests |
每种SBO方法30次重复求解解析算例的平均函数调用次数和样本细化迭代次数在表 2中进行了对比。
| 测试函数 | SBO-FCM | SBO-EI | SBO-MSP | |||||
| 函数调用次数 | 样本迭代次数 | 函数调用次数 | 样本迭代次数 | 函数调用次数 | 样本迭代次数 | |||
| BR | 87.77 | 25.77 | 48.00 | 36.70 | 83.10 | 59.03 | ||
| RB | 247.60 | 73.00 | 125.60 | 75.37 | 351.17 | 226.17 | ||
| GN | 215.63 | 40.00 | 596.27 | 309.23 | 376.03 | 244.70 | ||
| RS | 168.60 | 17.97 | 47.80 | 30.00 | 78.40 | 50.60 | ||
| HN6 | 112.73 | 26.27 | 71.73 | 34.37 | 68.40 | 148.70 | ||
| F16 | 106.23 | 22.57 | 84.50 | 47.13 | 96.23 | 26.88 | ||
对于SBO-EI和SBO-MSP而言,样本迭代的每个迭代步中,只添加一个新的样本;对于SBO-FCM而言,由于样本细化每个迭代步划分的子空间内样本数量过少,无法建立代理模型,以及子空间有交叠区,可能选择了相同的新增样本,因此每个迭代步添加的新样本数量并不相同。从总函数调用次数看,大多数情况,SBO-FCM总是需要最多的函数调用次数。但是,对比样本细化迭代次数,SBO-FCM在多数情况下是明显好于其他2种SBO方法的,因为SBO-FCM在一个迭代步中能够选择多个新增样本,并且可以充分利用计算机资源对样本进行并行求解(如果需要高精度分析,例如CFD)。上述分析说明SBO-FCM方法对于具有强非线性的问题具有很好的求解效率。
样本细化过程的自适应性,可以通过图 5展示的BR和RS函数优化得到的样本分布来进行分析。图中所示的样本分布为每种SBO方法在30次求解中获得一次最佳最优解次。可以发现:① SBO-MSP方法是一种局部方法,其添加的样本集中在局部极值附近;因此,在初始样本很少,不能充分描述整个设计空间的情况下,或者目标函数非线性很强,具有很多极值的情况下,很容易陷入局部最优;② SBO-EI是一种全局优化方法,因为EI函数权衡了模型局部和全局精度,但是对于强非线性和很多极值的问题,其全局能力下降,如图 5(b3)所示,很可能得到一个局部最优结果;③ SBO-FCM方法在平衡全局和局部搜索能力上是最好的,其添加的样本基本覆盖了所有极值存在的区域,如图 5(b1)和5(b2)对比所示。相比而言,SBO-FCM方法的样本细化过程具有很好的自适应性,能够同时对模型的全局和局部精度进行改进。

|
| 图 5 BR和RS函数优化样本分布 Fig. 5 Distribution of samples after optimizing BR and RS functions |
综上分析,解析算例证明了所发展的SBO-FCM方法的正确性;此外算例对比表明,SBO-FCM具有较高的效率、很好的鲁棒性和自适应性,适应于求解具有强非线性、多极值的优化问题。
5.2 气动优化实例为了进一步检验方法的应用性能,本文将SBO-FCM方法应用于RAE2822翼型减阻优化问题的求解,气动优化计算的状态为迎角α=2.31°,马赫数Ma=0.729,雷诺数Re=6.4×106。此外,要求优化得到的翼型升力系数均不小于基准翼型,最大相对厚度不小于9.5%。优化问题的数学模型表示为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ {C_D}\left( \mathit{\boldsymbol{x}} \right)}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{C_L}(\mathit{\boldsymbol{x}}) \ge 0.723}\\ {t(\mathit{\boldsymbol{x}}) \ge 0.095}\\ {{x_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 0.01,0.01]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,10} \end{array}} \right.} \end{array} $ | (19) |
式中: CD和CL分别表示阻力系数和升力系数; t表示翼型最大相对厚度,无量纲化的翼型长度为1。设计矢量x具有10个设计变量,是由Hicks-Henne参数化方法对翼型进行参数化得到的,表示基函数的系数,来控制翼型形状的改变,如图 6所示,1-10代表了10个控制系数分布在上下翼面的所在位置。
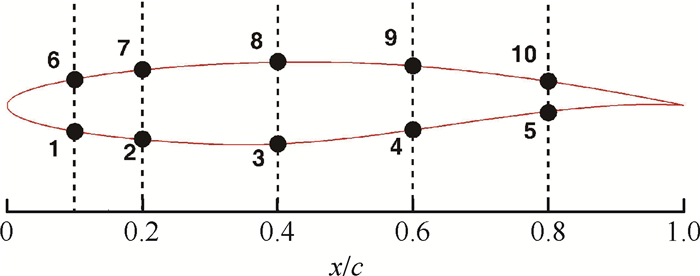
|
| 图 6 RAE2822翼型参数化 Fig. 6 Parameterization of RAE2822 airfoil |
翼型的网格(网格Ⅰ)由商业软件Pointwise生成,为混合网格,一共22 842个网格单元,第1层附面层网格高度为1.0×10-5,网格如图 7所示。为了证明网格的收敛性,本文对比了另外2套网格(网格Ⅱ和网格Ⅲ),其差异主要在翼面附近网格的密度。2套网格的附面层高度与第1套网格相同,网格单元数量分别为13 285和52 237。CFD计算采用的是开源代码SU2[28],来求解Navier-Stokes方程,湍流模型为Spalart-Allmaras方程模型。
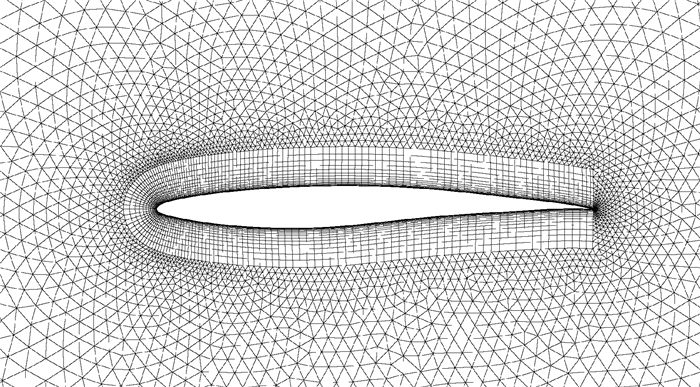
|
| 图 7 RAE2822中等尺度网格(网格Ⅰ) Fig. 7 Medium-scale mesh of RAE2822 airfoil (grid Ⅰ) |
CFD计算结果对比如表 3所示。结果表明,中等尺度的网格(网格Ⅰ)和细网格(网格Ⅲ)的气动计算结果较为接近,其相对误差小于1%,因此采用网格Ⅰ对问题进行优化。在优化过程中,新翼型的网格采用RBF网格变形方法获得。
| 参数 | 网格Ⅲ(细) | 网格Ⅰ(中) | 网格Ⅱ(粗) |
| 单元数目 | 52 237 | 22 842 | 13 285 |
| 升力系数 | 0.740 633 | 0.735 969 | 0.720 269 |
| 阻力系数 | 0.013 606 | 0.013 494 | 0.013 435 |
| 相对升力误差/% | 0.630 | 2.570 | |
| 相对阻力误差/% | 0.823 | 1.257 |
此外,CFD计算求解的精度通过求解RAE2822翼型的流场来进行检验。如图 8所示,计算得到的压力系数分布与试验数据吻合得很好,证明求解器具有足够的精度。
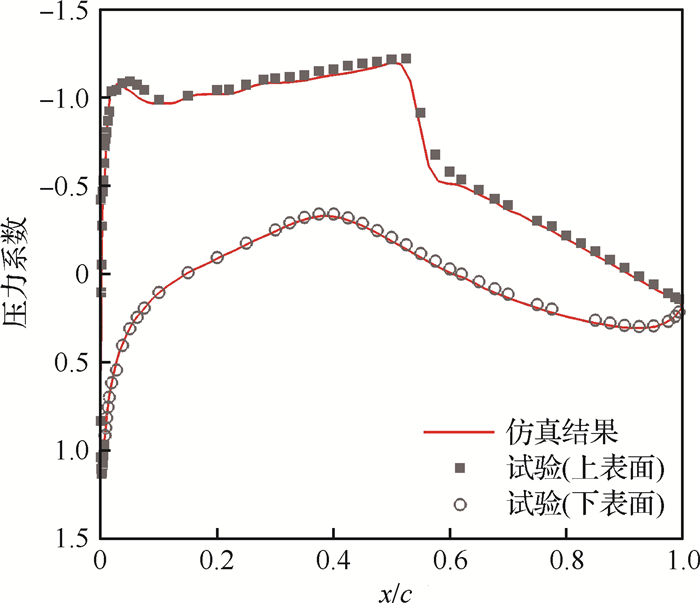
|
| 图 8 RAE2822翼型压力系数分布与试验数据对比 Fig. 8 Comparison of pressure coefficient distribution of RAE2822 airfoil with experimental data |
对于采用的SBO方法,根据(m+1)(m+2)/2推荐的样本数量,采用RLHD试验设计方法生成了66个初始样本,并且利用CFD对这些样本进行了计算。优化采用的3种SBO方法都是基于相同的初始样本进行的。此外,本文还采用了差分进化(Differential Evolutionary, DE)算法[29]和改进的非线性单纯形法(SubPlex)对该气动优化问题进行求解,以对比优化方法的效率和优化质量。其中,DE设置的种群大小为20,代数为100;SubPlex设置的最大迭代次数为1 000,收敛标准为1.0×10-6。
不同优化算法求解得到的结果如表 4所示。DE需要上千次的高精度分析,但是这并不能改善其局部搜索能力差的缺点;SubPlex获得了较好的结果,因其在设计空间的多个子空间内进行局部搜索,所以局部搜索能力较DE要好,但是仍然需要调用上千次CFD分析。相比而言,SBO方法调用的CFD分析次数大大减少,其中SBO-EI的局部勘测能力略显不足;SBO-Hybrid的局部勘测能力要好一些,因为在基于EI选择新样本的同时,还加入的基于MSP的策略选择新的样本,可以加强模型的局部精度;SBO-FCM获得的最优外形的阻力系数最小,但是调用CFD分析197次(包括初始试验设计方法的CFD分析次数),而样本细化迭代次数只有64次。
| 外形/优化方法 | 阻力系数/Count | CFD分析次数 | 样本细化迭代次数 | 升力系数 | 最大相对厚度 |
| 基准外形 | 134.50 | 0.723 | 12.10 | ||
| SubPlex | 101.56 | 1 130 | 221 | 0.723 | 9.56 |
| DE | 105.45 | 2 000 | 100 | 0.733 | 10.56 |
| SBO-EI | 102.91 | 78 | 38 | 0.743 | 9.86 |
| SBO-Hybrid | 100.85 | 139 | 100 | 0.723 | 9.72 |
| SBO-FCM | 99.81 | 197 | 64 | 0.723 | 9.52 |
图 9对比了优化得到的外形的压力系数分布和几何外形。鉴于表 4中的优化结果,图中只对比了SubPlex、SBO-Hybrid和SBO-FCM得到的外形。可以发现,优化后得到的外形在压力恢复段只出现了弱激波,原始基准外形的强激波被抹平,且SBO-Hybrid和SBO-FCM优化后的外形上表面的激波更弱。从几何外形上看,SBO-FCM得到的最优外形的最大相对厚度前移,这有利于保持高的负压力峰值。
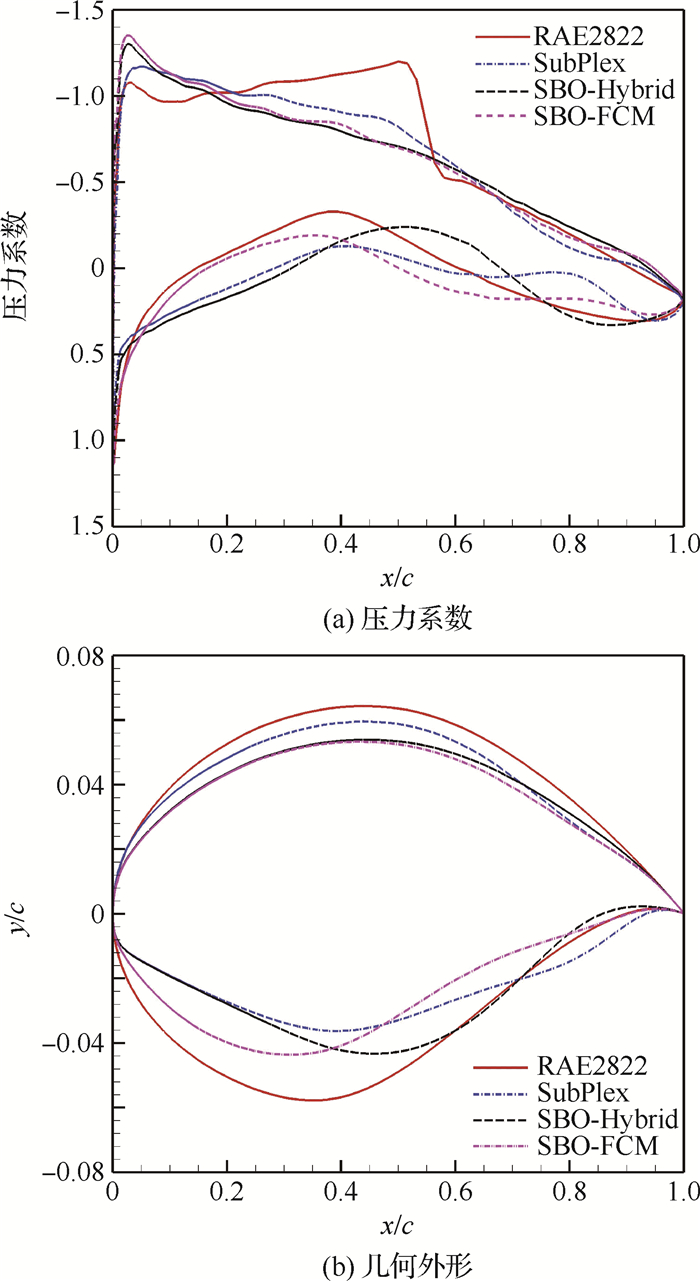
|
| 图 9 优化后的压力系数和几何外形对比 Fig. 9 Comparison of optimum pressure coefficients and geometries |
图 10对比了SBO-FCM得到的最优外形和基准外形的压力场云图。很明显,基准外形的上翼面中部偏后一点的位置存在强激波,压力等值线在该处集中汇聚;而优化后的翼型上表面中部附近的压力等值线分布的较均匀,不存在强激波,说明了最优外形的确具有更小的波阻。
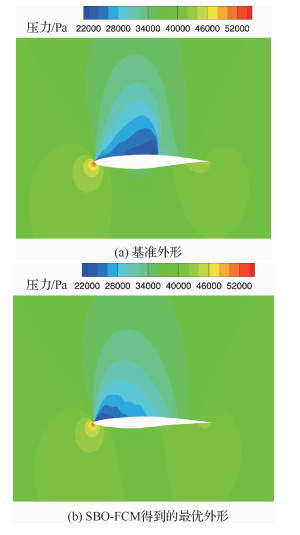
|
| 图 10 SBO-FCM得到的最优外形与基准外形的压力场云图对比 Fig. 10 Comparison of contours of baseline and optimized geometry by SBO-FCM |
为了分析SBO-FCM通过聚类划分子空间能够加强空间勘测能力并加快样本细化过程的速度,图 11对不同SBO方法中的样本在不同设计变量构成的空间内的分布以及样本响应值的云图进行了对比。
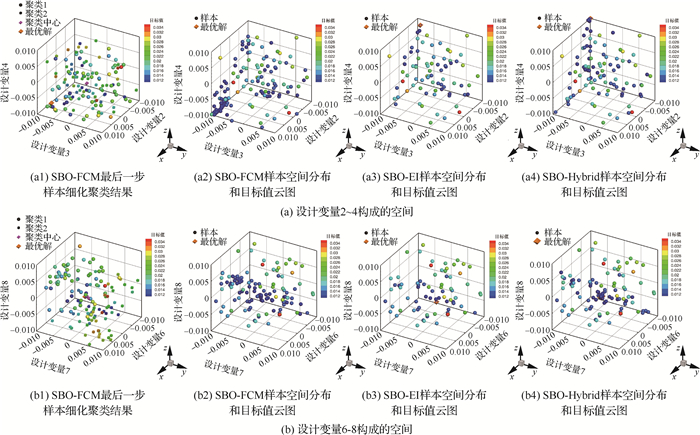
|
| 图 11 不同SBO方法的样本在不同设计变量构成的空间中的分布对比 Fig. 11 Comparison of infills by different SBO methods within spaces expanded by defferent design variable |
图 11(a1)展示了SBO-FCM最后一步样本细化迭代中的聚类结果:圆球表示聚类1中的伪样本,立方体表示聚类2中的伪样本,样本的颜色代表模型预测的响应值;橙色八面体为寻优得到的最优解。可以发现,在设计变量2~4所构成的空间内,2个类的伪样本是相互掺混的,说明这3个设计变量对目标影响的非线性程度很高。此外,掺混的类空间会导致2个子空间范围都较大,同时在子空间取样可以提高样本细化过程的全局勘测能力。相应地,图 11(a2)显示在设计变量2~4构成的空间内,至少有3个子区域存在极值,分别位于图的中上部、左下侧和中间偏右侧一点的位置;寻得的最优点位于左下侧的区域。
图 11(a3)展示的样本分布是由SBO-EI方法获得的,样本响应值云图说明空间可能存在2个极值区域,分别位于图中上部和中间偏右侧,而寻得的最优解位于中上部,说明SBO-EI方法在处理非线性强的问题时全局勘测能力不足。图 11(a4)展示了SBO-Hybrid方法的样本分布,图示表明:空间中可能存在3个极值区域,但是所找到的极值位于图中上部;此外,SBO-Hybrid寻得的最优点与SBO-EI寻得的最优点的3个变量相似,说明SBO-Hybrid对于具有强非线性的复杂问题,其局部的挖掘能力略显不足。
图 11(b)展示了设计变量6~8构成空间内的样本分布。图 11(b1)给出了SBO-FCM最后一步样本细化迭代中聚类的结果,图中符号的意义与前述相同。可以发现,2个类的伪样本基本上位于2个独立的子区域中,说明这3个设计变量对目标的影响相对独立。这样,在子空间加点时,更容易发现多极值区间,同样可以提高样本细化的全局勘测能力。图 11(b2)~图 11(b4)对比了不同方法分析的样本的空间分布和响应值云图。可以发现,除了试验设计的样本,3种方法在样本细化过程中添加了更多的目标响应值小的样本。SBO-FCM通过子空间加点,目标响应值小的样本聚集在2个局部区域;SBO-EI添加的目标响应值小的样本较分散;SBO-Hybrid添加的目标响应值小的样本集中在一个区域。3种方法找到的6~8这3个设计变量的最优点的值很接近,说明变量对目标影响的相关性较小时,优化过程的难度减小;但是样本分布表明SBO-EI的全局勘测能力最差,SBO-FCM的全局勘测能力较好。
设计变量6~8位于翼型上表面,如图 6所示。从图 9可以发现,设计变量6~8的变化趋势与图 11(b1)中2个类空间相对独立。SBO-FCM寻得的最优外形的设计变量2与设计变量3、4的变化趋势相反;相应地,图 11(a1)中类空间是掺混的。但是,SBO-EI和SBO-Hybrid寻优得到的外形的设计变量4与设计变量2、3相反。设计变量2~4对目标影响相关性大的特性会使优化问题变复杂,这可能是不同方法得到的最优外形在下表面差异较大的原因。根据上述分析,SBO-FCM的全局勘测和局部挖掘能力都强于SBO-EI和SBO-Hybrid,说明SBO-FCM更适合于求解非线性强的复杂问题。
6 结论1) SBO方法在求解优化问题时,可以大大减少高精度分析模型的调用次数,提高优化过程的效率。但是针对具有强非线性或者高维设计空间的优化问题,SBO-EI的局部勘测能力呈现不足。
2) 采用聚类分析算法对设计空间缩减后的伪样本进行聚类,可以捕捉多个具有共性的子空间,然后在子空间中通过EI和MSP准则选择样本,并进行相似样本剔除,可以提高样本细化过程的自适应性。
3) 经过了聚类分析后最后融合的新设计空间在样本细化过程中也会自适应地发生缩减,这有利于提高建模效率和模型的精度。
4) 解析算例测试证明SBO-FCM方法具有很好的全局探索和局部勘测能力,适用于强非线性和多设计变量的问题。此外,SBO-FCM方法还具有很好的鲁棒性和较高的效率,可以充分利用计算资源进行多样本的并行计算。
5) 优化实例证明SBO-FCM在求解具有强非线性的气动优化问题上,仍然具有较高的效率,其样本细化过程保持良好的自适应特性,可以获得很高的优化质量。
| [1] | MORRIS A J. Structural optimization by geometric programming[J]. International Journal of Solids & Structures, 1972, 8(7): 847-864. |
| [2] | SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science, 1989, 4(4): 409-423. |
| Click to display the text | |
| [3] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:Review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| Cited By in Cnki (32) | Click to display the text | |
| [4] |
乔建领, 韩忠华, 宋文萍, 等. 基于代理模型的高效全局低音爆优化设计方法[J]. 航空学报, 2018, 39(5): 67-80. QIAO J L, HAN Z H, SONG W P, et al. An efficient surrogate-based global optimization for low boom design[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 67-80. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [5] |
韩忠华, 张瑜, 许晨舟, 等. 基于代理模型的大型民机机翼气动优化设计[J]. 航空学报, 2019, 40(1): 522398. HAN Z H, ZHANG Y, XU C Z, et al. Aerodynamic optimization design of large civil aircraft wings using surrogate-based model[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522398. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [6] |
周旺仪, 白俊强, 乔磊, 等. 变弯翼型与增升装置多目标气动优化设计研究[J]. 西北工业大学学报, 2018, 36(1): 83-90. ZHOU W Y, BAI J Q, QIAO L, et al. A study of multi-objective aerodynamic optimization design for variable camber airfoils and high lift devices[J]. Journal of Northwestern Polytechnical University, 2018, 36(1): 83-90. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [7] | LIU B, GROUT V, NIKOLAEVA A. Efficient global optimization of actuator based on a surrogate model assisted hybrid algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5712-5721. |
| Click to display the text | |
| [8] | IULIANA E. Global optimization of benchmark aerodynamic cases using physics-based surrogate models[J]. Aerospace Science & Technology, 2017, 67: 273-286. |
| Click to display the text | |
| [9] | FORRESTER A I J, SÓBESTER A, KEANE A J. Engineering design via surrogate modeling:A practical guide[M]. Reston, VA: AIAA, 2008: 77-106. |
| [10] | LIU H, ONG Y S, CAI J. A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design[J]. Structural and Multidisciplinary Optimization, 2018, 57(1): 393-416. |
| Click to display the text | |
| [11] | LI C N, BREZILLON J, GÖRTZ S. A hybrid approach for surrogate-based aerodynamic optimization with constraints[C]//2011 EUROGEN: Eccomas Thematic Conference, 2011: 84-87. |
| [12] | MACKMAN T J, ALLEN C B, GHOREYSHI M, et al. Comparison of adaptive sampling methods for generation of surrogate aerodynamic models[J]. AIAA Journal, 2013, 51(4): 797-808. |
| Click to display the text | |
| [13] | CHAUDHURI A, HAFTKA R T. Efficient global optimization with adaptive target setting[J]. AIAA Journal, 2014, 52(7): 1573-1577. |
| Click to display the text | |
| [14] | LIU H, ONG Y S, CAI J. A Survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design[J]. Structural and Multidisciplinary Optimization, 2017(6): 1-24. |
| Click to display the text | |
| [15] | KAMINSKY A L, WANG Y, PANT K, et al. Adaptive sampling techniques for surrogate modeling to create high-dimension aerodynamic loading response surfaces[C]//2018 Applied Aerodynamics Conference. Reston: AIAA, 2018 |
| [16] | CHENG G H, WANG G G. Trust region based MPS method for global optimization of high dimensional design problems: AIAA-2012-1590[R]. Reston: AIAA, 2012. |
| [17] | GUO X S, LONG T, WU D, et al. RBF metamodel assisted global optimization method using particle swarm evolution and fuzzy clustering for sequential sampling: AIAA-2014-2305[R]. Reston: AIAA, 2014. |
| [18] | QIU H, XU Y J, GAO L, et al. Multi-stage design space reduction and metamodeling optimization method based on self-organizing maps and fuzzy clustering[J]. Expert Systems with Applications, 2016, 46: 180-195. |
| Click to display the text | |
| [19] | SHI R H, LIU L, LONG T, et al. Sequential radial basis function using support vector machine for expensive design optimization[J]. AIAA Journal, 2017, 55(1): 214-227. |
| Click to display the text | |
| [20] | DONG H C, SONG B W, WANG P, et al. Surrogate-based optimization with clustering-based space-exploration for expensive multimodal problems[J]. Structural and Multidisciplinary Optimization, 2018, 57(4): 1553-1577. |
| Click to display the text | |
| [21] |
王超, 高正红, 张伟, 等. 自适应设计空间扩展的高效代理模型气动优化设计方法[J]. 航空学报, 2018, 39(7): 121745. WANG C, GAO Z H, ZHANG W, et al. Efficient surrogate-based aerodynamic design optimization method with adaptive design space expansion[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121745. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [22] | LI C N, PAN Q F. Adaptive optimization methodology based on Kriging modeling and a trust region method[J]. Chinese Journal of Aeronautics, 2019, 32(2): 281-295. |
| Click to display the text | |
| [23] | LI C N. A surrogate-based framework with hybrid refinement strategies for aerodynamic shape optimization[D]. Cologne: Library and Information Base of German Aerospace Center, 2013: 37-52. |
| [24] | BEZDEK J C, CHRISTIAN J. Fuzzy mathematics in pattern classification[D]. New York: Cornell University, 1973: 142-147. |
| [25] | WU D, LONG T, WANG Y, et al. A sequential maximin latin hypercube sampling method and its application to aircraft design: AIAA-2015-3095[R]. Reston: AIAA, 2015. |
| [26] | JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. |
| Click to display the text | |
| [27] | LI Y, LIU L, LONG T, et al. Metamodel-based global optimization using fuzzy clustering for design space reduction[J]. Chinese Journal of Mechanical Engineering, 2013, 26(5): 928-939. |
| Click to display the text | |
| [28] | PALACIOS F, ECONOMON T D, ALONSO J J. Large-scale aircraft design using SU2[C]//AIAA Aerospace Sciences Meeting. Reston: AIAA, 2015. |
| [29] | QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. |
| Click to display the text |



