2. 北京航空航天大学 交通科学与工程学院, 北京 100083
2. School of Transportations Science and Engineering, Beihang University, Beijing 100083, China
非线性动态逆(Nonlinear Dynamic Inversion,NDI)控制作为一种非线性控制方法,通过对消非线性项来精确线性化系统,进而利用线性控制律设计方法来设计控制律,该方法在飞行控制领域中得到了广泛的应用[1]。但其对系统的精确模型依赖度高导致鲁棒性不足。国内外有许多学者对动态逆方法的鲁棒性问题进行了研究,一部分研究[2-4]采用神经网络等智能控制方法对模型偏差进行补偿,还有部分研究[5-7]将NDI与鲁棒控制方法结合进行设计。这些方法设计的控制器结构较为复杂,阶次较高,不利于工程实现。20世纪末,Bugajski和Enns[8],Bacon等[9]提出了一种动态逆的控制方法,利用增量形式的控制方程,通过状态量的速率即角加速度反馈来降低控制律对于被控对象模型的依赖性,提高了鲁棒性。
在非线性增量动态逆(Incremental Nonlinear Dynamic Inversion,INDI)方法的基础之上,研究者等进行了相关的研究工作,将其广泛地应用于飞行控制领域[10-12]。INDI方法依赖角加速度反馈,而一般飞控系统无法直接测量角加速度,针对INDI对于角加速度反馈的需求,有各种角加速度估计方法被提出。常规的方法是利用角速度差分结合低通滤波进行角加速度估计,但低通滤波带来的时间延迟会影响系统的稳定性,对此,Koschorke等[13]研究了时间延迟对INDI闭环系统稳定性的影响,Smeur等[14]和周池军等[15]利用低通滤波估计角加速度的同时,对控制量进行滤波补偿。Bacon和Ostroff[16]、陈海兵等[17]利用几何方法估计角加速度,但此方法数值求解较为复杂,不利于工程应用。尹航等[18]利用卡尔曼滤波(Kalman Filter,KF)估计角加速度,通过仿真实验证明了该方法的有效性。
本文针对小型三旋翼无人机(Unmanned Aerial Vehicle,UAV)飞行平台,在增量动态逆控制方法的基础之上,利用飞控惯性测量单元测得的角速度通过卡尔曼滤波角加速度估计器实时提供角加速度反馈,分回路设计了姿态控制器,并利用基于模型的控制系统设计方法将控制器实现。最后,通过试飞试验验证基于角加速度估计器的增量动态逆控制方法的有效性和鲁棒性。
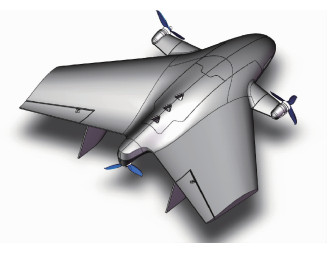
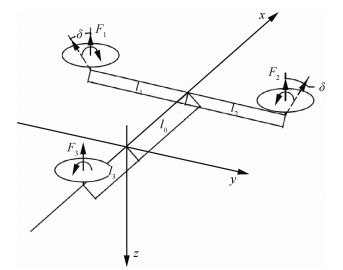
1 三旋翼动力学模型本文所采用的三旋翼无人机模型如图 1所示。其简化模型的受力分析,如图 2所示。图中:F1、F2、F3为3个电机产生的拉力,为克服3个电机转动产生的偏航力矩,前2个电机为可倾转差动设计;δ为前2个电机的差动角;l0为1号、2号电机连线到重心的距离;l1和l2为1号、2号电机到x轴的距离;l3为3号电机到重心的距离。
|
| 图 1 无人机模型 Fig. 1 UAV model |
|
| 图 2 受力分析图 Fig. 2 Diagram of force analysis |
机体轴系下的三旋翼姿态转动动力学方程为
| $ \left\{ \begin{array}{l} \dot p = \frac{{qr}}{{{I_x}}}\left( {{I_y} - {I_z}} \right) + \left( {{F_1}{l_1}\cos\delta - {F_2}{l_2}\cos\delta } \right)\\ \dot q = \frac{{rp}}{{{I_y}}}\left( {{I_z} - {I_x}} \right) + \left( {{F_1}\cos\delta + {F_2}\cos\delta } \right){l_0} - {F_3}{l_3}\\ \dot r = \frac{{pq}}{{{I_z}}}\left( {{I_x} - {I_y}} \right) + c{F_3} - \left( {{F_1}{l_1}\sin\delta + {F_2}{l_2}\sin\delta } \right) \end{array} \right. $ | (1) |
定义控制输入量和简化后三旋翼无人机的转动惯量矩阵分别为
| $ \mathit{\boldsymbol{u}} = {\left[ {{F_1},{F_2},{F_3},\delta } \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} {{I_x}}&{}&{}\\ {}&{{I_y}}&{}\\ {}&{}&{{I_z}} \end{array}} \right] $ |
式中:p、q、r为无人机绕机体轴转动的角速度。
2 三旋翼控制系统设计 2.1 增量动态逆控制律考察的飞机非线性动力学系统方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right)}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right)} \end{array}} \right. $ | (2) |
式中:x为n维状态量;u为p维控制输入;y为m维输出。
设某一时刻的状态量和输入量分别为(x0, u0),则在(x0, u0)的某邻域内,非线性状态方程可利用泰勒一阶展开近似为
| $ \begin{array}{l} \mathit{\boldsymbol{\dot x}} \approx \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_0}} \right) + \mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right) + \\ \;\;\;\;\;\frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}{\left( {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right)} \right)_{{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0}} \right) + \\ \;\;\;\;\;\frac{\partial }{{\partial \mathit{\boldsymbol{u}}}}\mathit{\boldsymbol{g}}{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right)_{{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}}}\left( {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_0}} \right) \end{array} $ | (3) |
(x0, u0)点的状态方程为
| $ {{\mathit{\boldsymbol{\dot x}}}_0} = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_0}} \right) + \mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right) $ | (4) |
定义2个偏导数为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}\left( {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right)} \right)\\ \mathit{\boldsymbol{B}} = \frac{\partial }{{\partial \mathit{\boldsymbol{u}}}}\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right) \end{array} \right. $ | (5) |
式(3)可整理为
| $ \mathit{\boldsymbol{\dot x}} \approx {{\mathit{\boldsymbol{\dot x}}}_0} + \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\Delta \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{B}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\Delta \mathit{\boldsymbol{u}} $ | (6) |
输出方程对时间求导可得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot y}} = \frac{{\partial \mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right)}}{{\partial \mathit{\boldsymbol{x}}}}\mathit{\boldsymbol{\dot x}} \approx \\ \;\;\;\;\;{\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}\left( {{{\mathit{\boldsymbol{\dot x}}}_0} + \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\Delta \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{B}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\Delta \mathit{\boldsymbol{u}}} \right) \end{array} $ | (7) |
设期望的飞机闭环动态特性为
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{u}} = {\left( {{\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}\mathit{\boldsymbol{B}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)} \right)^{ - 1}} \cdot \\ \;\;\;\;\;\;\left( {{{\mathit{\boldsymbol{\dot y}}}_{\rm{d}}} - {\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}{{\mathit{\boldsymbol{\dot x}}}_0} - {\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\Delta \mathit{\boldsymbol{x}}} \right) \end{array} $ | (8) |
当控制律的解算频率足够高,步长足够小时,状态量的增量Δx相对于控制输入的增量Δu来说是高阶小量,故可略去,则增量动态逆控制律为
| $ \Delta \mathit{\boldsymbol{u}} = {\left( {{\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}\mathit{\boldsymbol{B}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)} \right)^{ - 1}}\left( {{{\mathit{\boldsymbol{\dot y}}}_{\rm{d}}} - {\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{x}}}{{\mathit{\boldsymbol{\dot x}}}_0}} \right) $ | (9) |
一般来说,控制输入的维数p大于输出维数m,故(hxB (x0, u0))-1为广义右逆。控制律中不显含非线性状态项f(x),降低了控制律对于飞机本体数学模型的依赖,使得控制律对于飞机本体数学模型中的参数摄动具有一定的鲁棒性。同时,采用增量式的控制律算法,使得控制律需要利用到状态量的导数,在三旋翼姿态控制中意味着需要角加速度反馈量,因此需要利用到第3节所提到的角加速度估计器。
2.2 控制律设计对于本文所研究的被控对象即三旋翼无人机的姿态控制而言,被控对象的动力学方程如式(1)所示。
定义 状态量x= Ω =[p, q, r]T,控制输入为u=[F1, F2, F3, δ]T,输出为y= x = Ω。故由式(9)可得相应的增量动态逆控制律为
| $ \Delta \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{u}}_0}} \right)\left( {{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_{\rm{d}}} - {{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_{\rm{0}}}} \right) $ | (10) |
式中:B-1(x0, u0)为矩阵B的广义右逆;
根据三旋翼无人机姿态控制的特性,基于以上的增量动态逆控制律,对姿态控制进行双回路控制律设计。
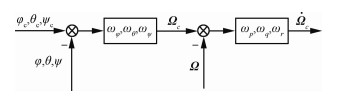
外回路包括姿态角回路(慢回路)和角速度回路(快回路),控制框图如图 3所示。ωφ、ωθ、ωψ和ωp、ωq、ωr分别表示姿态角回路和角速度回路的带宽。快回路带宽一般为慢回路带宽的3~5倍,具体设置为:ωφ=ωθ=ωψ=3 rad/s,ωp=ωq=ωr=10 rad/s;下标c表示指令。
|
| 图 3 外回路控制框图 Fig. 3 Block diagram of outer loop control |
|
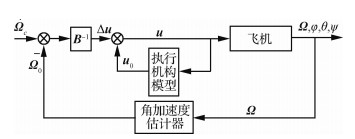
| 图 4 内回路控制框图 Fig. 4 Block diagram of inner loop control |
内回路即为角加速度回路,采用增量动态逆控制律,控制框图如图 4所示,u0为上一采样时刻的控制输入量,因为无法直接反馈实际电机的拉力和舵机偏转的角度,因此加入执行机构模型模拟电机和舵机的动力学环节,同时加入角加速度估计器实时地估计飞机的角加速度。
3 角加速度估计器设计 3.1 基于卡尔曼滤波器的角加速度估计INDI是一种对于模型参数不敏感的鲁棒非线性控制方法,该方法利用角加速度反馈进行解算,而一般飞控硬件采用惯性测量单元测量角速度,没有角加速度传感器直接测量角加速度。直接利用角速度差分得到的角加速度噪声过大,无法用于控制律的解算,因此需要利用传感器的信号估计出角加速度信号。传统的方式是直接对传感器的角速度信号进行差分,然后再进行低通滤波。在此基础之上,本文利用KF进行角加速度的实时估计。
1) 运动学模型
以俯仰角加速度的估计为例,模型为线性模型,状态量为x=[q,
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_{k + 1}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_k} + \mathit{\boldsymbol{Q}}}\\ {{\mathit{\boldsymbol{z}}_{k + 1}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}_{k + 1}} + \mathit{\boldsymbol{R}}} \end{array}} \right. $ | (11) |
式中:
2) 滤波估计过程[19]
角加速度估计的过程即卡尔曼滤波器的递推求解过程,故可以用于控制律中进行实时的角加速度反馈。
① 一步状态更新,根据上一采样时刻估计出的状态量经过状态转移矩阵得出一步状态量估计值:
| $ {{\mathit{\boldsymbol{\hat x}}}_{k + 1/k}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_k} $ | (12) |
② 状态误差协方差一步更新,求解出状态误差协方差阵经过一步状态更新并引入过程噪声之后的估计值:
| $ {{\mathit{\boldsymbol{\hat P}}}_{k + 1/k}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{P}}_k}{\mathit{\boldsymbol{F}}^{\rm{T}}} + \mathit{\boldsymbol{Q}} $ | (13) |
③ 求解使得状态量估计为最小方差无偏估计的卡尔曼增益K:
| $ {\mathit{\boldsymbol{K}}_{k + 1}} = {{\mathit{\boldsymbol{\hat P}}}_{k + 1/k}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{H}}{{\mathit{\boldsymbol{\hat P}}}_{k + 1/k}}{\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}}} \right)^{ - 1}} $ | (14) |
④ 根据卡尔曼增益进行状态量和协方差的校正:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{k + 1/k + 1}} = {{\mathit{\boldsymbol{\hat x}}}_{k + 1/k}} + {\mathit{\boldsymbol{K}}_{k + 1}}\left( {{\mathit{\boldsymbol{z}}_{k + 1}} - \mathit{\boldsymbol{H}}{{\mathit{\boldsymbol{\hat x}}}_{k + 1/k}}} \right)\\ {{\mathit{\boldsymbol{\hat P}}}_{k + 1/k + 1}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}\mathit{\boldsymbol{H}}} \right){{\mathit{\boldsymbol{\hat P}}}_{k + 1/k}} \end{array} \right. $ | (15) |
3) 角加速度估计结果
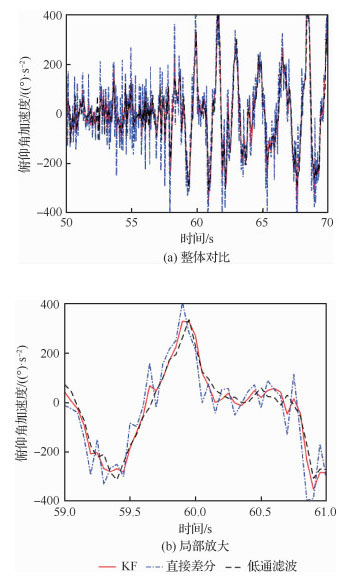
根据三旋翼飞行平台实际试飞过程中测量的俯仰角速度q,分别利用直接差分、直接差分加低通滤波、卡尔曼滤波器估计3种方法得到相应的角加速度,并进行比较,如图 5所示。
|
| 图 5 角加速度估计对比图 Fig. 5 Diagram of angular acceleration estimate |
可见,对角速度信号进行直接差分会将噪声放大,采用传统的差分加低通滤波则会带来一定的延迟,而用KF进行角加速度估计可以去除高频噪声并保证较小的延迟。
3.2 角加速度估计的时间延迟互相关函数是信号分析里衡量2个信号之间相互关联程度的函数。可以通过求取互相关函数得到2个相似信号之间的时间延迟。
对于连续信号定义为
| $ {r_{{\rm{fg}}}}\left( \tau \right) = \int_0^T {f\left( t \right)g\left( {t + \tau } \right){\rm{d}}t} $ | (16) |
即将g(t)对时间轴原点进行翻转后与f(t)作卷积。
对于离散时间序列定义为
| $ {r_{xy}}\left( m \right) = \sum\limits_{n = 0}^N {x\left( n \right)y\left( {n + m} \right)} \;\;\;\;m \in {\bf{Z}} $ | (17) |
它表示序列x(n)不动,将y(n)在时间轴上向左或右移动m个采样间隔后与序列x(n)相乘后求和,得到平移m之后的对应互相关函数值rxy(m),该值越大表示此时两信号越相似。因此可以通过互相关函数曲线上的峰值点得出2个相似信号之间的时间延迟。
定义归一化的互相关函数,互相关函数越接近1表示此时两信号越相似。
| $ {R_{xy}}\left( m \right) = \frac{{\sum\limits_{n = 0}^N {x\left( n \right)y\left( {n + m} \right)} }}{{\sum\limits_{n = 0}^N {x\left( n \right)x\left( n \right)} }}\;\;\;m \in {\bf{Z}} $ | (18) |
考察利用卡尔曼滤波得到的角加速度估计值和传统差分加低通滤波分别带来的时间延迟。选择直接进行数值差分得到的角加速度信号作为基准信号,认为此信号无时间延迟,分别计算2种方法与基准信号之间的互相关函数来比较两者的时间延迟。数据来源同3.1节中数据。
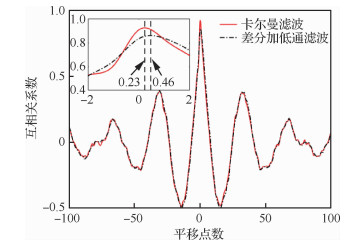
由图 6结果可知,KF方法的时间延迟为0.23个采样间隔,而差分加低通滤波方法的时间延迟为0.46个采样间隔(由于两者延迟都小于1个采样间隔,故求取互相关函数之后采用插值的方法得到了平移非整数采样间隔点的互相关函数值)。故结果表明,采用KF进行角加速度估计可以去除高频噪声并保证较小的延迟。
|
| 图 6 时间延迟对比 Fig. 6 Comparison of time delay |
为验证增量动态逆控制律和角加速度估计器的可行性,本文进一步基于小型三旋翼无人机平台开展了飞行试验,试验所用三旋翼无人机平台如图 7所示,其基本参数如表 1所示。

|
| 图 7 无人机实物图 Fig. 7 Picture of UAV |
| 参数 | 数值 |
| 飞机总重m/kg | 0.82 |
| 翼展b/m | 0.73 |
| 机身总长/m | 0.62 |
| 螺旋桨型号 | 6535 |
| 单个电机最大拉力/N | 6.5 |
| Ixx/(kg·m2) | 0.018 8 |
| Iyy/(kg·m2) | 0.03 |
| Izz/(kg·m2) | 0.013 |
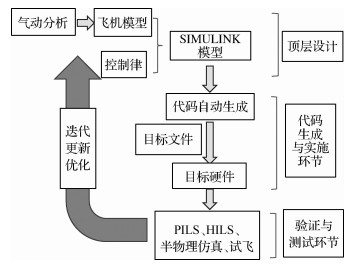
无人机飞控硬件平台为雷迅pixhack V3,内置3组IMU冗余设计(包含3组加速度计、3组陀螺仪、1组电子罗盘、2组数字气压计)。飞行控制律设计平台为MATLAB/SIMULINK,利用基于模型的设计方法[20],在SIMILINK中搭建好控制器仿真模型之后,通过SIMULINK代码自动生成技术生成可执行文件到目标硬件中,并进行试飞测试等等。具体流程如图 8所示。
|
| 图 8 控制律设计流程图 Fig. 8 Diagram of control law design |
三旋翼无人机姿态控制试验在室内无风条件下进行。测试姿态角的跟踪情况,验证角加速度估计器和增量动态逆控制律的有效性。
1) 三轴姿态响应
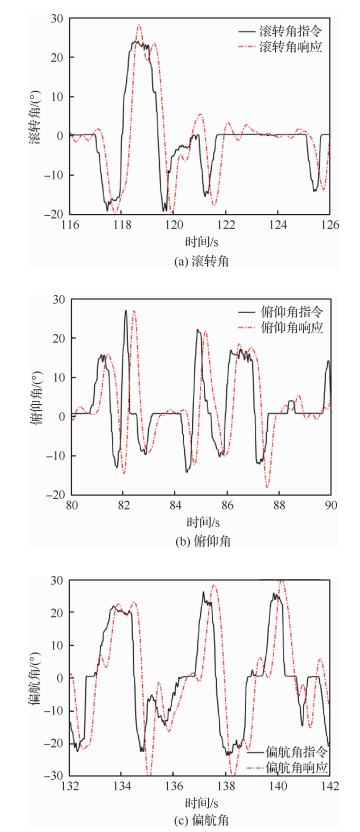
图 9为三轴姿态响应仿真图。
|
| 图 9 三轴姿态响应 Fig. 9 Three-axis attitude response |
2) 鲁棒性测试
在三旋翼无人机平台上附加重物,改变飞行器的重心位置,测试姿态角的跟踪情况,同时与常规PID控制律进行对比,考察INDI控制律对于飞机本体模型参数摄动的鲁棒性。
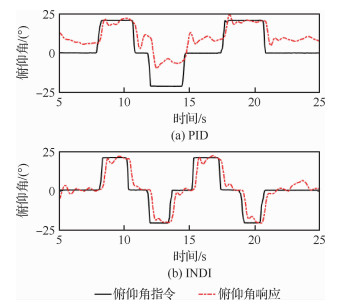
重心位置摄动俯仰角跟踪情况如图 10所示。改变三旋翼其中一个动力单元的螺旋桨的尺寸,以达到改变执行机构效能的目的,考察控制律对于执行机构效能摄动的鲁棒性。
|
| 图 10 重心位置摄动测试结果 Fig. 10 Robust test results at center of gravity |
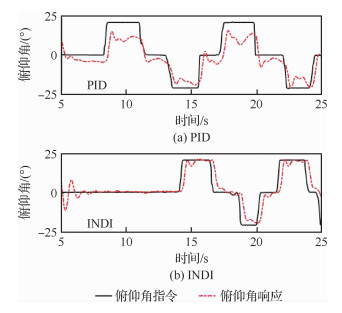
动力效能摄动俯仰角跟踪情况如图 11所示。可以明显看出,在重心位置和动力效能有较大摄动时,常规PID控制律存在很大的稳态误差,无法很好地跟踪指令,而基于角加速度反馈的增量动态逆控制律由于降低了对飞机本体模型的敏感度,故仍能实现很好的指令跟踪效果,具有较好的鲁棒性。
|
| 图 11 动力效能摄动测试结果 Fig. 11 Robust test results of power efficiency |
3) 指令跟踪
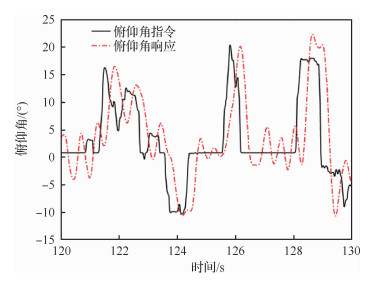
图 12为俯仰角、俯仰角速度以及俯仰角加速度的指令跟踪情况。图 13为利用角速度差分加低通滤波进行角加速度估计得到的俯仰角指令跟踪情况。

|
| 图 12 指令跟踪结果 Fig. 12 Command tracking results |
|
| 图 13 差分加低通滤波指令跟踪结果 Fig. 13 Command tracking results using low-pass filter |
试飞数据显示,俯仰角、俯仰角速度和俯仰角加速度均能够很好的跟踪指令,响应动态良好。俯仰角响应与俯仰角指令之间的时间延迟约为0.3 s,与姿态角回路3 rad/s的带宽一致。稳定点附近有小幅的2 °左右的振荡,该振荡是由传感器噪声以及气动-结构耦合振动等因素导致。角加速度响应通过角加速度估计器实时估计得到,可以看出,2种角加速度估计方法均能达到控制效果,利用本文的角加速度估计器可以在滤除高频噪声的同时保证较小的时间延迟,保障了更好的稳定性。
5 结论1) INDI控制律可以运用于实际飞行器的控制中,并且对飞机本体模型参数摄动具有很好的鲁棒性。
2) 角加速度估计器为INDI控制律提供必需的角加速度信息,为控制律的实现提供了一种工程上的解决途径。
3) 基于卡尔曼滤波的角加速度估计方式在滤除高频噪声的基础上带来的时间延迟更小。
| [1] | REINER J, BALAS G J. Robust dynamic inversion for control of highly maneuverable aircraft[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(1): 18-24. |
| Click to display the text | |
| [2] | KIM B, CALISE A. Nonlinear flight control using neural networks[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 97-105. |
| Click to display the text | |
| [3] |
朱家强, 朱纪洪, 郭锁凤, 等. 基于神经网络的鲁棒自适应逆飞行控制[J]. 控制理论与应用, 2005, 22(2): 182-188. ZHU J Q, ZHU J H, GUO S F, et al. Neural network based robust dynamic inversion flight control[J]. Control Theory & Applications, 2005, 22(2): 182-188. (in Chinese) |
| Cited By in Cnki (63) | Click to display the text | |
| [4] | XU B, YANG C, SHI Z. Reinforcement learning output feedback NN control using deterministic learning technique[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(3): 635-641. |
| Click to display the text | |
| [5] | SMIT Z M, CRAIG I K. Robust flight controller design using H∞ loop-shaping and dynamic inversion techniques: AIAA-1998-4132[R]. Reston, VA: AIAA, 1998. |
| [6] | ITO D, WARD D T, VALASEK J. Robust dynamic inversion controller design and analysis for the X-38[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Restion, VA: AIAA, 2001: 4380. |
| Click to display the text | |
| [7] |
范子强, 方振平. 过失速机动飞机的鲁棒非线性飞行控制律设计[J]. 航空学报, 2002, 23(3): 193-196. FAN Z Q, FANG Z P. Robust, nonlinear control design for a poststall maneuver aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(3): 193-196. (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [8] | BUGAJSKI D, ENNS D. A dynamic inversion based control law with application to high angle of attack research vehicle[C]//Proceeding of AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 1990: 826-839. |
| Click to display the text | |
| [9] | BACON B J, OSTROFF A J, JOSHI S M. Reconfigurable NDI controller using inertial sensor failure detection & isolation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(4): 1373-1383. |
| Click to display the text | |
| [10] | SIEBERLING S, CHU Q P, MULDER J A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(6): 1732-1742. |
| Click to display the text | |
| [11] | SIMPLICIO P, PAVEL M D, KAMPEN E J V, et al. An acceleration measurements-based approach for helicopter nonlinear flight control using incremental nonlinear dynamic inversion[J]. Control Engineering Practice, 2013, 21(8): 1065-1077. |
| Click to display the text | |
| [12] |
郑积仕, 蒋新华, 陈兴武. 增量非线性动态逆小型无人机速度控制[J]. 系统工程与电子技术, 2013, 35(9): 1923-1927. ZHENG J S, JIANG X H, CHEN X W. Velocity control design for the small UAV based on the incremental non-linear dynamic inversion[J]. Systems Engineering and Electronics, 2013, 35(9): 1923-1927. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [13] | KOSCHORKE J, FALKENA W, KAMPEN E J V, et al. Time delayed incremental nonlinear control[C]//AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2013. |
| Click to display the text | |
| [14] | SMEUR E J, CHU Q P, CROON G C. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(3): 450-461. |
| Click to display the text | |
| [15] |
周池军, 朱纪洪, 袁夏明, 等. 考虑作动器动态补偿的飞机增量滤波非线性控制[J]. 控制理论与应用, 2017, 34(5): 594-600. ZHU C J, ZHU J H, YUAN X M, et al. Incremental filtered nonlinear control for aircraft with actuator dynamics compensation[J]. Control Theory & Applications, 2017, 34(5): 594-600. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] | BACON B J, OSTROFF A J. Reconfigurable flight control Using nonlinear dynamic inversion with a special accelerometer implementation[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston, VA: AIAA, 2000. |
| Click to display the text | |
| [17] |
陈海兵, 张曙光, 方振平. 加速度反馈的隐式动态逆鲁棒非线性控制律设计[J]. 航空学报, 2009, 30(4): 597-603. CHEN H B, ZHANG S G, FANG Z P. Implicit NDI robust nonlinear control design with acceleration feedback[J]. Acta Aeronautica et Astronautica, 2009, 30(4): 597-603. (in Chinese) |
| Cited By in Cnki (20) | Click to display the text | |
| [18] |
尹航, 朱纪洪, 周池军, 等. 基于Kalman预报观测器的增量动态逆控制[J]. 清华大学学报:自然科学版, 2014, 54(12): 1534-1538. YIN H, ZHU J H, ZHOU C J, et al. Incremental dynamic inversion control with Kalman prediction observers[J]. Journal of Tsinghua University (Science and Technology), 2014, 54(12): 1534-1538. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [19] | RUDOLF E K. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82: 35-45. |
| Click to display the text | |
| [20] |
孙忠潇. Simulink仿真及代码生成技术入门到精通[M]. 北京: 北京航空航天大学出版社, 2015: 350-357. SUN Z X. Simulink simulation and code generation technique[M]. Beijing: Beihang University Press, 2015: 350-357. (in Chinese) |



