2. 海军工程大学 舰船与海洋学院, 武汉 430033;
3. 海军工程大学 舰船综合电力国防科技重点实验室, 武汉 430033
2. College of Naval Architecture&Marine Engineering, Naval University of Engineering, Wuhan 430033, China;
3. National Key Laboratory for Vessel Integrated Power System Technology, Naval University of Engineering, Wuhan 430033, China
现代航天、航空等领域的武器、装备以及战储器材通常具有“长期贮存、一次使用”的特点,如某重点型号设定的服役年限为30年,分解到元器件级要求其贮存期为32年。元器件经长期贮存会出现主要参数漂移、材料性能下降等问题[1]。随着贮存时间的增长,元器件性能的变化必然给其所属单元带来影响,导致贮存单元及装备可用数量降低。装备贮存单元的完好情况直接影响着保障部门日常维护保养工作能否正常开展,也决定着装备的完好数量能否满足要求。
针对贮存期内各类单元性能下降及故障对装备造成的影响,国内外开展了大量研究。在考虑不同环境及使用条件下的可靠性评估方面,文献[2]研究了非恒定温度场合性能退化型部件贮存可靠性评估模型。文献[3]研究了火箭等航天装备在贮存和运输阶段的可靠度评估问题。文献[4]基于Bootstrap算法对贮存系统的可靠度进行了置信限评估。文献[5-7]基于导弹多部件退化数据,开展导弹关键性能参数研究,给出多部件竞争失效的可靠度评估模型。在考虑不同类型、不同可靠性结构的寿命单元可靠性评估方面,文献[8]基于导弹仪器设备的贮存可靠性和贮存使用过程中采取的技术准备措施,提出了一种以能执行任务率为判据的导弹贮存寿命评估方法。文献[9-10]构建了多类部件组成系统的贮存可靠度模型,研究使平均可靠度最大的检修策略。文献[11]针对贮存寿命和使用寿命均服从指数分布的部件,通过将贮存时间转化为使用时间,对贮存可靠性置信下限进行了估计。在综合考虑贮存延寿及保障费用优化方面,文献[12-13]建立了包含不同寿命分布组件的系统混合检测模型,并用仿真方法确定了长期运行的可用度和费用率。文献[14-17]对于定期检测与机会检测、随机检测结合的维修更换模型的费用进行了对比分析。文献[18]以固定贮存期内的费用率最低为目标,对检测周期以及更换周期进行了综合优化。文献[19]在分析部件瞬态贮存可用度变化规律基础上,研究了系统的平均贮存可用度,建立了贮存寿命的评估与优化模型。
目前,考虑装备子单元贮存方案对装备完好数量影响的文献较少,难以建立单元贮存数量、贮存时间和装备可用数量之间的关系,缺乏贮存方案的优化方法。本文以贮存期内装备完好数量为着眼点,分析常见寿命分布单元的贮存可靠度,建立初始贮存方案下的装备完好数量评估模型;以达标概率指标为约束条件,贮存单元购置费用为优化目标,建立单元初始贮存方案优化模型,给出相应的优化算法。为装备保障部门制定不同寿命分布单元贮存方案提供理论支撑。
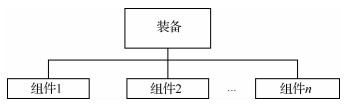
1 问题描述及模型假设 1.1 贮存过程描述装备通常具有多层级的结构特点,按照从低到高的次序,常见的层级划分有:元器件、零部件、组件、装备、分系统、系统等。本文将装备划分为2层,由高到低分为装备层和组件层。各组件之间的关系以可靠性连接关系进行描述,常见的连接关系有串联、并联、混联等。若按照是否关重件的标准对装备各组件可靠性结构进行划分,对于由一般数量规模关重件组成的装备系统,可简化为由多项关重组件串联而成。装备结构如图 1所示。
|
| 图 1 装备组织结构 Fig. 1 Framework of equipment |
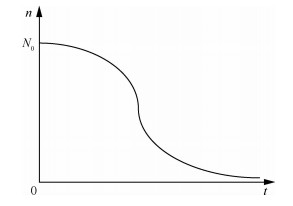
对于“长期贮存,一次使用”的装备而言,在贮存期内需对其进行检测维护,及时修复或更换出现故障或到寿组件以维持装备性能,保证贮存期内装备的完好数量。为了使得贮存期间的检修、修复工作顺利进行,对于分段贮存或整体贮存的装备系统,在装备交付的同时需配备一定数量的组件。装备组件在贮存过程中,受环境因素和维修管理措施的影响,会引起贮存组件失效或性能下降,导致不可用,组件完好的数量随着贮存时间的增长呈现逐渐下降的趋势,如图 2所示,图中:t为贮存时间;n为组件完好数量;N0为初始组件完好的数量。
|
| 图 2 组件可用数量随时间变化 Fig. 2 Variation of number of intact component with time |
一般情况下,新型装备技术密集,信息化、集约化程度高,在新型装备批量交付初期,装备保障部门难以配齐相应的维修设备和具有对应维修能力的技术人员。在装备保障现场,较难开展故障组件的维修和装备原位维修,对装备的维修仅具备换件维修能力。另外一方面,装备的重要组件通常为非货架产品,需要组织专门的生产线进行生产,订货周期通常较长。因此,在装备交付时,需建立组件的初始库存以满足贮存期内装备的故障维修。为了方便研究,本文在进行建模和优化时做如下假设:①贮存期内不考虑组件的再补给;②装备发生故障仅进行换件维修;③贮存期内的故障组件无法修复;④装备是否处于完好状态仅与各组件是否处于完好状态有关;⑤当组件到寿或故障后,必然出现故障,如有组件可换,故障装备可及时恢复完好;⑥在装备修复过程中,装备是不完好的。
在装备保障领域,战备完好率是装备保障部门关注的重要综合性指标,对于一定数量的装备而言,战备完好率的要求可以转换成装备完好数量上的要求。为了衡量贮存期内任意时刻提供某一具体数量可用装备的能力,本文引入达标概率这个指标。达标概率定义为贮存期t内,装备完好数量n大于等于某一规定数量M的概率,记为P(n≥M)。达标概率反映的是装备战备完好率达到某一水平的概率,衡量的是装备战备完好性水平。若将达标概率的门限值记为P0,P0为对组件初始贮存方案的达标概率指标要求,只有满足P(n≥M)≥P0的贮存方案才是合格的方案。
2 初始贮存方案评估模型装备组件从交付入库到其无法正常工作之间的时间间隔称为贮存寿命。贮存寿命呈现出一定的规律如服从指数分布、对数正态分布和威布尔分布等常见分布[20]。
2.1 常见寿命分布组件可靠度 2.1.1 指数型组件可靠度将贮存寿命T服从指数分布的组件称为指数型组件,记作T~Exp(μ),其中μ为平均贮存寿命,则该单元在贮存时间t的可靠度函数为
| $ R(t)=\mathrm{e}^{\frac{-t}{\mu}} $ | (1) |
将贮存寿命T服从对数正态分布的组件称为对数正态型组件,记作T~LN(μ, σ2),其中μ为对数均值,σ为对数标准差。该组件在贮存时间t的可靠度函数为
| $ R(t)=1-\frac{1}{\sigma \sqrt{2 \pi}} \int_{0}^{t} \frac{1}{x} \exp \left[-\frac{1}{2}\left(\frac{\ln x-\mu}{\sigma}\right)^{2}\right] \mathrm{d} x $ | (2) |
将贮存寿命T服从威布尔分布的组件称为威布尔型组件,记作T~W(α, b),其中尺度参数α>0,在工程上形状参数b≥1。该组件在贮存时间t的可靠度函数为
| $ R(t)=\mathrm{e}^{-\left(\frac{t}{\alpha}\right)^{b}} $ | (3) |
若组件i的初始贮存数量为si,该组件在贮存时间t内的任意时刻完好数量为n,则该组件完好的数量n≥M的达标概率为
| $ P_{i}\left(s_{i} | n \geqslant M\right)=1-\sum\limits_{m=0}^{M-1} \mathrm{C}_{s_{i}}^{m} R_{i}(t)^{m}\left(1-R_{i}(t)\right)^{s_{i}-m} $ | (4) |
式中:Ri(t)为组件i在t时刻的贮存可靠度函数;M为规定的最低完好数量,显然需si≥M。
对于由I类组件构成的装备,各组件之间为串联关系,若各组件的初始贮存方案为s=[s1, s2, …, si, …sI], 在t时间内的任意时刻,该类装备完好的数量为n,n≥M的达标概率为
| $ P(\boldsymbol{s} | n \geqslant M)=\prod\limits_{i=1}^{I} P_{i}\left(s_{i} | n_{i} \geqslant M\right) $ | (5) |
对于初始贮存方案优化问题,建立模型时以贮存时间t内的任意时刻,完好装备数量大于M的概率指标为约束条件,以寻求组件初始贮存方案的购置费用最低为优化目标。数学模型为
| $ \left\{\begin{array}{ll} \min & \sum\limits_{i} c_{i} s_{i} \\ \mathrm{s.t} & P(\boldsymbol{s} | n \geqslant M) \geqslant P_{0} \end{array}\right. $ | (6) |
式中:ci为单个第i项组件的购置费用。
本文以达标概率值为约束条件,运用边际优化方法求解上述模型,具体步骤如下:
步骤1 初始化所有组件的贮存数量,令各组件贮存的初始数量,即方案s各项元素为M。
步骤2 计算第i项组件的边际效益值:δ(i)={P(s+ones(i)|n≥M)-P(s|n≥M)}/ci 式中:ones(i)为一维数组,第i项元素为1,其他元素皆为0。
步骤3 将δ(i)最大值所对应的组件i配置数量加1, 由此得到新的组件初始贮存方案矩阵s。
步骤4 计算在新的贮存方案下,装备在贮存时间t内的任意时刻,装备完好数量n大于M的概率P,并与规定的概率P0比较,如果P≥P0,算法结束,此时s为最优配置结果;反之则转步骤2继续迭代运算。
边际优化算法相比其他优化算法操作简单、运算速度快、结果精度高,其最大优势在于算法迭代的整个过程中不丢失最优解,即能够保障整个费效曲线上的每个点都是最优解,便于决策人员对结果进行分析和调整[21]。该算法在以备件短缺数为约束条件的备件优化配置研究中得到了广泛的应用,并取得了良好的效果。
4 算法复杂度分析衡量算法是否具有较高的计算效率需要分析其算法复杂性。算法复杂性中,时间复杂度是衡量其计算效率的有效度量。针对3种可能的优化方法,算法复杂性分析如下:
1) 穷举法。即穷举所有可能的组件配置方案,选取所有可能方案中满足式(6)的最优方案。若各组件的配置数量上限为Nc,则配置方案的组合数量为NcJ,其中J表示组件的种类,在计算过程中,其时间复杂度T1=O(NcJ)。
2) 智能优化算法。若采用遗传算法为主程序生成组件配置方案。设嵌套法需迭代iter次,每代产生种群大小为num,则其时间复杂度T2=O(iter·num·(log2num+1)),其中,O(iter·num·log2num)为遗传算法本身的时间复杂度。
3) 本文算法。由第3节模型优化步骤可知,在算法迭代过程中,每次迭代均需遍历计算每类组件的边际效益值,其时间复杂度为O(J);而优化方法的迭代次数同样与组件种类密切相关,组件种类越多,迭代次数越多,迭代过程的时间复杂度为O(J),本文优化算法的时间复杂度为T3=O(J2)。
纵观3种算法的时间复杂度,当组件种类和数量规模较大时,有T1>T2>T3,而现有保障方案涉及组件种类和数量一般较多,上述不等式显然成立,可得本文算法计算效率较高。
5 算例分析假设某装备由6类组件组成,各组件的寿命分布类型及参数如表 1所示。
| 序号 | 寿命分布类型 | 参数1 | 参数2 | 寿命值 | 费用/万元 |
| 1 | 指数Exp(μ) | μ=13.1 | 13.1 | 55.7 | |
| 2 | 指数Exp(μ) | μ=9.5 | 9.5 | 30.8 | |
| 3 | 对数正态LN(μ, σ2) | μ=2.0 | σ=0.68 | 9.31 | 32.1 |
| 4 | 对数正态LN(μ, σ2) | μ=1.8 | σ=0.75 | 8.01 | 28.3 |
| 5 | 威布尔W(α, b) | α=8.0 | b=2.1 | 7.09 | 20.2 |
| 6 | 威布尔W(α, b) | α=11.1 | b=2.6 | 9.86 | 53.4 |
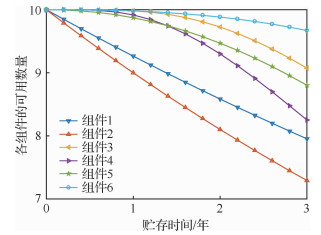
初始贮存期一般为1~3年,令贮存期为t=3年,在建立初始库存时,各组件的数量均为10,则在贮存期内,各组件的可用数量变化如图 3所示。由图 3可知,随着贮存时间的增长,各类组件的可用数量逐渐降低,不同类型的组件失效规律不同,组件2的可用数量下降幅度最高,组件6的可用数量下降幅度最低。装备可用数量与可用数量最低的组件保持一致。若在建立的初始库存中各组件的配置数量不加区分地同等看待,即各组件的配置数量相同,并不能保证装备的可用数量一定最大。在组件贮存过程中应结合其贮存失效规律合理配置组件的种类和数量,以使在组件采购费用最低的情况下装备可用数量最高。
|
| 图 3 不同组件完好数量随时间变化曲线 Fig. 3 Variation of number of different intact component with time |
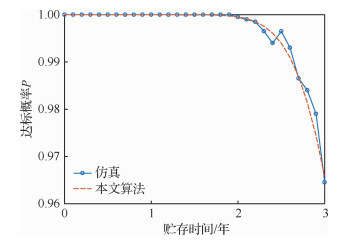
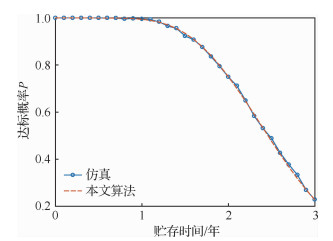
若装备由6类不同类型的组件组成,其分布类型和可靠性参数如表 1所示,组件初始贮存方案为[16, 18, 14, 12, 13, 15],在3年贮存期内的任意时刻,将各组件的可用数量大于或等于11的达标概率评估结果与模拟贮存过程进行多次仿真的结果进行对比,表 1中指数型、对数正态型及威布尔型3种不同类型的组件,分别取一型进行分析,如图 4~图 6所示。将整个贮存期内装备可用数量大于或等于11的达标概率的评估结果与模拟贮存过程进行多次仿真的结果进行比较,如图 7所示。

|
| 图 4 指数型组件1达标概率评估曲线 Fig. 4 Curves of evaluation for achieving standard probability of exponential component—Component 1 |
|
| 图 5 对数正态型组件3达标概率评估曲线 Fig. 5 Curves of evaluation for achieving standard probability of lognormal component—Component 3 |

|
| 图 6 威布尔型组件5达标概率评估曲线 Fig. 6 Curves of evaluation for achieving standard probability of Weibull component —Component 5 |
|
| 图 7 装备达标概率评估曲线 Fig. 7 Curves of evaluation for achieving standard probability of equipment |
将各图解析算法的计算结果与仿真结果进行对比可知,本文建立的模型能够较好地对各种不同寿命分布的组件及装备在给定贮存方案下,贮存期内任意时刻的达标概率进行评估,具有较高的精度,与仿真结果基本重合,解析结果真实可信。
对于各组件参数由表 1描述的装备,要求在贮存期t内的任意时刻,装备完好数n≥M的概率P(n≥M)不低于阈值P0。已知:t=3,M=11,P0=0.91,按照第3节边际优化的算法,计算满足要求的各组件最小贮存量。
表 2为贮存方案的优化过程,给出了每一步迭代计算的各组件的边际效益值和增加组件的编号。如在原始贮存方案[11, 11, 11, 11, 11, 11]下,组件1~6的边际效益值分别为7.1×10-7,1.7×10-6,5.6×10-7,1.2×10-6,1.2×10-6,1.2×10-7,如表 2所示,选取边际效益值最大的组件即组件2数量加1,得到贮存方案[11, 12, 11, 11, 11, 11],计算其达标概率是否满足指标要求,若不满足则继续迭代,计算各组件的边际效益值,将边际效益值最大的组件加1;若满足则停止迭代,输出对应的组件贮存方案,如此循环迭代,最终得到贮存方案[18, 20, 15, 17, 16, 13]即为满足指标要求的最优方案。按照该方案配置各组件的贮存数量,装备在3年的贮存期内,可用数量大于11的概率为0.916,大于指标要求,组件购置费用为3 598.6万元。
| 序号 | 组件1 | 组件2 | 组件3 | 组件4 | 组件5 | 组件6 | 增加组件的序号 | P(n≥M) | 费用/万元 | ||||||
| 贮存数量 | 边际效益值 | 贮存数量 | 边际效益值 | 贮存数量 | 边际效益值 | 贮存数量 | 边际效益值 | 贮存数量 | 边际效益值 | 贮存数量 | 边际效益值 | ||||
| 1 | 11 | 7.1×10-7 | 11 | 1.7×10-6 | 11 | 5.6×10-7 | 11 | 1.2×10-6 | 11 | 1.2×10-6 | 11 | 1.2×10-7 | 2 | 1.8×10-5 | 2 425.5 |
| 2 | 11 | 2.8×10-6 | 12 | 2.8×10-6 | 11 | 2.2×10-6 | 11 | 4.8×10-6 | 11 | 4.6×10-6 | 11 | 4.7×10-7 | 4 | 7.0×10-5 | 2 456.3 |
| 3 | 11 | 8.3×10-6 | 12 | 8.1×10-6 | 11 | 6.5×10-6 | 12 | 5.0×10-6 | 11 | 1.3×10-5 | 11 | 1.4×10-6 | 5 | 0.000 21 | 2 484.6 |
| 4 | 11 | 1.9×10-5 | 12 | 1.9×10-5 | 11 | 1.5×10-5 | 12 | 1.2×10-5 | 12 | 9.6×10-6 | 11 | 3.2×10-6 | 1 | 0.000 48 | 2 504.8 |
| 5 | 12 | 2.4×10-5 | 12 | 6.1×10-5 | 11 | 4.9×10-5 | 12 | 3.8×10-5 | 12 | 3.1×10-5 | 11 | 1.0×10-5 | 2 | 0.001 55 | 2 560.5 |
| 6 | 12 | 5.2×10-5 | 13 | 7.2×10-5 | 11 | 0.000 11 | 12 | 8.4×10-5 | 12 | 6.9×10-5 | 11 | 2.3×10-5 | 3 | 0.003 43 | 2 591.3 |
| 7 | 12 | 0.000 11 | 13 | 0.000 14 | 12 | 6.0×10-5 | 12 | 0.000 17 | 12 | 0.000 14 | 11 | 4.7×10-5 | 4 | 0.006 92 | 2 623.4 |
| 8 | 12 | 0.000 18 | 13 | 0.000 24 | 12 | 0.000 10 | 13 | 0.000 13 | 12 | 0.000 24 | 11 | 7.9×10-5 | 2 | 0.011 70 | 2 651.7 |
| 9 | 12 | 0.000 29 | 14 | 0.000 23 | 12 | 0.000 17 | 13 | 0.000 21 | 12 | 0.000 39 | 11 | 0.000 13 | 5 | 0.019 24 | 2 682.5 |
| 10 | 12 | 0.000 41 | 14 | 0.000 33 | 12 | 0.000 24 | 13 | 0.000 30 | 13 | 0.000 20 | 11 | 0.000 18 | 1 | 0.027 09 | 2 702.7 |
| 11 | 13 | 0.000 37 | 14 | 0.000 60 | 12 | 0.000 44 | 13 | 0.000 55 | 13 | 0.000 37 | 11 | 0.000 34 | 2 | 0.050 14 | 2 758.4 |
| 12 | 13 | 0.000 50 | 15 | 0.000 49 | 12 | 0.000 60 | 13 | 0.000 75 | 13 | 0.000 51 | 11 | 0.000 46 | 4 | 0.068 75 | 2 789.2 |
| 13 | 13 | 0.000 66 | 15 | 0.000 64 | 12 | 0.000 78 | 14 | 0.000 46 | 13 | 0.000 67 | 11 | 0.000 61 | 3 | 0.090 02 | 2 817.5 |
| 14 | 13 | 0.000 84 | 15 | 0.000 82 | 13 | 0.000 31 | 14 | 0.000 59 | 13 | 0.000 86 | 11 | 0.000 78 | 5 | 0.115 21 | 2 849.6 |
| 15 | 13 | 0.000 97 | 15 | 0.000 95 | 13 | 0.000 36 | 14 | 0.000 68 | 14 | 0.000 36 | 11 | 0.000 89 | 1 | 0.132 53 | 2 869.8 |
| 16 | 14 | 0.000 69 | 15 | 0.001 33 | 13 | 0.000 51 | 14 | 0.000 95 | 14 | 0.000 51 | 11 | 0.001 26 | 2 | 0.186 56 | 2 925.5 |
| 17 | 14 | 0.000 85 | 16 | 0.000 96 | 13 | 0.000 62 | 14 | 0.001 16 | 14 | 0.000 62 | 11 | 0.001 54 | 6 | 0.227 59 | 2 956.3 |
| 18 | 14 | 0.001 15 | 16 | 0.001 31 | 13 | 0.000 85 | 14 | 0.001 58 | 14 | 0.000 84 | 12 | 0.000 30 | 4 | 0.309 62 | 3 009.7 |
| 19 | 14 | 0.001 32 | 16 | 0.001 50 | 13 | 0.000 97 | 15 | 0.000 83 | 14 | 0.000 96 | 12 | 0.000 35 | 2 | 0.354 39 | 3 038 |
| 20 | 14 | 0.001 49 | 17 | 0.000 99 | 13 | 0.001 09 | 15 | 0.000 94 | 14 | 0.001 09 | 12 | 0.000 39 | 1 | 0.400 53 | 3 068.8 |
| 21 | 15 | 0.000 92 | 17 | 0.001 19 | 13 | 0.001 32 | 15 | 0.001 13 | 14 | 0.001 31 | 12 | 0.000 47 | 3 | 0.483 62 | 3 124.5 |
| 22 | 15 | 0.001 00 | 17 | 0.001 29 | 14 | 0.000 43 | 15 | 0.001 23 | 14 | 0.001 43 | 12 | 0.000 51 | 5 | 0.526 00 | 3 156.6 |
| 23 | 15 | 0.001 05 | 17 | 0.001 36 | 14 | 0.000 45 | 15 | 0.001 30 | 15 | 0.000 51 | 12 | 0.000 54 | 2 | 0.554 80 | 3 176.8 |
| 24 | 15 | 0.001 13 | 18 | 0.000 83 | 14 | 0.000 48 | 15 | 0.001 40 | 15 | 0.000 55 | 12 | 0.000 58 | 4 | 0.596 83 | 3 207.6 |
| 25 | 15 | 0.001 21 | 18 | 0.000 89 | 14 | 0.000 52 | 16 | 0.000 65 | 15 | 0.000 59 | 12 | 0.000 62 | 1 | 0.636 38 | 3 235.9 |
| 26 | 16 | 0.000 66 | 18 | 0.000 98 | 14 | 0.000 57 | 16 | 0.000 72 | 15 | 0.000 65 | 12 | 0.000 69 | 2 | 0.703 51 | 3 291.6 |
| 27 | 16 | 0.000 69 | 19 | 0.000 56 | 14 | 0.000 60 | 16 | 0.000 76 | 15 | 0.000 68 | 12 | 0.000 76 | 4 | 0.733 70 | 3 322.4 |
| 28 | 16 | 0.000 71 | 19 | 0.000 58 | 14 | 0.000 61 | 17 | 0.000 32 | 15 | 0.000 70 | 12 | 0.000 74 | 6 | 0.754 96 | 3 350.7 |
| 29 | 16 | 0.000 74 | 19 | 0.000 61 | 14 | 0.000 65 | 17 | 0.000 34 | 15 | 0.000 73 | 13 | 0.000 10 | 1 | 0.794 28 | 3 404.1 |
| 30 | 17 | 0.000 37 | 19 | 0.000 64 | 14 | 0.000 68 | 17 | 0.000 35 | 15 | 0.000 77 | 13 | 0.000 11 | 5 | 0.835 65 | 3 459.8 |
| 31 | 17 | 0.000 38 | 19 | 0.000 65 | 14 | 0.000 69 | 17 | 0.000 36 | 16 | 0.000 25 | 13 | 0.000 11 | 3 | 0.851 23 | 3 480 |
| 32 | 17 | 0.000 39 | 19 | 0.000 67 | 15 | 0.000 19 | 17 | 0.000 37 | 16 | 0.000 25 | 13 | 0.000 12 | 2 | 0.873 43 | 3 512.1 |
| 33 | 17 | 0.000 39 | 20 | 0.000 36 | 15 | 0.000 20 | 17 | 0.000 38 | 16 | 0.000 26 | 13 | 0.000 12 | 1 | 0.893 98 | 3 542.9 |
| 34 | 18 | 20 | 15 | 17 | 16 | 13 | 0.915 97 | 3 598.6 | |||||||
对比图 3表示的各可用组件数量随贮存时间的变化情况,组件可用数量下降幅度由高到低依次为组件2、组件1、组件4、组件5、组件3和组件6。相应地,若需要配置的组件数量满足可用装备数量大于某一固定值的要求,则需要配置的组件数量由高到低对应的组件编号依次为组件2、组件1、组件4、组件5、组件3和组件6。观察所得优化方案[18, 20, 15, 17, 16, 13],各组件的初始贮存数量符合这一规律,较为合理。
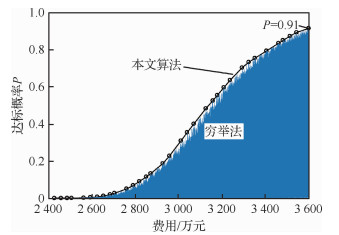
在该算例中,如果采用穷举法,待选方案数量至少为106个;采用本文算法,则最多只需33×5=165次计算即可得到满足要求的、效费比高的贮存方案。图 8中黑色曲线上的各数据点表示表 2中优化迭代过程每一步所得贮存方案的费用及其对应的达标概率,显示了各优化方案对应的达标概率和费用的变化过程,可用于回答“当达标概率指标要求P0确定后,至少需要多少经费采购组件”的问题。图 8蓝色曲线各数据点表示的是以穷举法产生的组件贮存方案对应的达标概率和购置费用,由该图可知,本文优化过程形成的曲线是采用穷举法形成曲线的外包络曲线。这意味着同等购置费用下,优化后的方案的达标率最高,即为性价比最高的方案。
|
| 图 8 穷举法及本文算法计算的贮存方案效费曲线对比 Fig. 8 Comparison of curves of effectiveness with cost for storage scheme of exhaustion method and algorithm of this paper |
分别采用穷举法、智能优化算法和本文算法求取符合达标概率指标要求的最优组件配置方案,求取结果和计算时间如表 3所示。由3种不同算法的计算结果可知,3种方法均能求得符合要求的最优方案,但本文算法的计算时间最少,这与第4节进行的算法复杂性分析的结果一致。当涉及组件种类较多,配置数量较大时,本文算法的优势将更加明显,具有更强的适用性。
| 方法 | 最优方案 | P(n≥M) | 费用/万元 | 运行时间/s |
| 穷举法 | [18, 20, 15, 17, 16, 13] | 0.916 0 | 3 598.6 | 1 154 |
| 智能优化算法 | [18, 20, 15, 17, 16, 13] | 0.916 0 | 3 598.6 | 293 |
| 本文算法 | [18, 20, 15, 17, 16, 13] | 0.916 0 | 3 598.6 | 0.119 |
1) 针对“长期贮存,一次使用”的装备,开展组件初始贮存方案评估及优化问题研究。分析了不同寿命分布贮存单元的可靠度模型,建立了贮存期内组件及装备完好数量评估模型;该模型能够在组件贮存方案确定之后,评估贮存期内各组件以及装备完好数量满足某一规定数值的概率。
2) 以装备数量达标概率指标为约束条件,组件购置费用为优化目标,建立了组件初始贮存方案优化模型,提出了基于边际效益值的方案优化算法。该优化算法能够在组件购置费用最低的情况下选出符合约束条件的方案,具有较高的计算效率,适合计算多种类、大批量的组件初始贮存方案。提出的模型和优化算法可扩展至2层以上的装备结构,为装备保障人员制定合理的装备组件贮存方案提供决策支持。
| [1] |
田智文, 刘文宝, 王敬贤. 宇航元器件长期贮存及寿命评价方法研究[J]. 质量与可靠性, 2015(3): 32-34. TIAN Z W, LIU W B, WANG J X. Study on long-term storage and life assessment method of aerospace components[J]. Quality and Reliability, 2015(3): 32-34. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [2] |
刘震宇, 马小兵, 赵宇. 非恒定温度场弹上性能退化型部件贮存可靠性评估方法[J]. 航空学报, 2012, 33(9): 1671-1678. LIU Z Y, MA X B, ZHAO Y. Storage reliability assessment for missile component with degradation failure mode in a temperature varying environment[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1671-1678. (in Chinese) |
| [3] | OKAN Y, BAYINDIER K, GOKHAN O O. Reliability assessment of solid-propellant rocket motors under storage and transportation loads[J]. Journal of Spacecraft and Rockets, 2017, 54(6): 1356-1366. |
| Click to display the text | |
| [4] |
罗巍, 张春华, 谭源源, 等. 系统贮存可靠度近似置信下限的Boots trap评估方法[J]. 宇航学报, 2009, 30(4): 1725-1730. LUO W, ZHANG C H, TAN Y Y, et al. Bootstrap estimate method of approximate confidence lower limits of system storage reliability[J]. Journal of Astronautics, 2009, 30(4): 1725-1730. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [5] | CHEN Y X, ZHANG Q, CAI Z Y, et al. Storage reliability assessment model based on competition failure of multi-components in missile[J]. Journal of Systems Engineering & Electronic, 2017, 28(3): 606-616. |
| Click to display the text | |
| [6] | LUO W, ZHANG C H, CHEN X, et al. Accelerated reliability demonstration under competing failure modes[J]. Reliability Engineering and System Safety, 2015, 136: 75-84. |
| Click to display the text | |
| [7] |
谭源源, 张春华, 陈循. 竞争失效场合步进应力加速试验统计分析[J]. 航空学报, 2011, 32(3): 429-437. TAN Y Y, ZHANG C H, CHEN X. Analysis of step stress accelerated testing with competing failure modes[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(3): 429-437. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [8] |
张仕念, 颜诗源, 张国彬, 等. 基于能执行任务率的导弹武器装备贮存寿命综合评估方法[J]. 系统工程理论与实践, 2015, 35(2): 513-520. ZHANG S N, YAN S Y, ZHANG G B, et al. Storage life synthesis evaluation method of guided missile weapon based on mission capable rate[J]. Systems Engineering Theory & Practice, 2015, 35(2): 513-520. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [9] | ITO K, NAKAGAWA T, NISHI K. Extended optimal inspection policies for a system in storage[J]. Mathematical and Computer Modeling, 1995, 22(10): 83-87. |
| Click to display the text | |
| [10] | ITO K, NAKAGAWA T. Optimal inspection policies for a storage system with degradation at periodic tests[J]. Mathematical and Computer Modeling, 2000, 31(10): 191-195. |
| Click to display the text | |
| [11] |
蔡静, 赵明. 指数型寿命分布的贮存-使用模型可靠性评估方法[J]. 济南大学学报:自然科学版, 2013, 27(2): 205-209. CAI J, ZHAO M. A reliability estimate method of storage-usage model based on exponential distribution[J]. Journal of University of Jinan (Sci. & Tech.), 2013, 27(2): 205-209. (in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [12] | SCARF P A, CAVALCANTE C A V. Hybrid block replacement and inspection policies for a multi-component system with heterogeneous component lives[J]. European Journal of Operational Research, 2010, 206(2): 384-394. |
| Click to display the text | |
| [13] | CAVALCANTE C A V, SCARF P A, DE ALMEIDA A T. A study of a two phase inspection policy for a preparedness system with a defective state and heterogeneous lifetime[J]. Reliability Engineering & System Safety, 2011, 96(6): 627-635. |
| Click to display the text | |
| [14] | LAGGOUNE R, CHATEAUNEUF A, AISSANI D. Impact of few failure data on the opportunistic replacement policy for multi-component systems[J]. Reliability Engineering & System Safety, 2010, 95(2): 108-119. |
| Click to display the text | |
| [15] | TAGHIPOUR S, BANJEVIC D. Optimum inspection interval for a system under periodic and opportunistic inspections[J]. IIE Transactions, 2012, 44(11): 932-948. |
| Click to display the text | |
| [16] | TAGHIPPOUR S, BANJEVIC D. Optimal inspection of a complex system subject to periodic and opportunistic inspections and preventive replacements[J]. European Journal of Operational Research, 2012, 220(3): 649-660. |
| Click to display the text | |
| [17] | NAKAGAWA T, MIZUTANI S, CHEN M. A summary of periodic and random inspection policies[J]. Reliability Engineering and System Safety, 2010, 95(8): 906-911. |
| Click to display the text | |
| [18] |
杨力, 马小兵. 维修-更换串联系统贮存可用度建模及费用分析[J]. 兵工学报, 2015, 36(3): 552-558. YANG L, MA X B. Storage availability modeling and cost analysis for a repair-replacement series system[J]. Acta Armamentarii, 2015, 36(3): 552-558. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [19] |
马小兵, 杨力. 贮存可用度约束下的可修系统寿命评估与优化[J]. 系统工程与电子技术, 2015, 37(3): 572-576. MA X B, YANG L. Life evaluation and optimization for a repairable system under the constraint of storage availability[J]. Systems Engineering and Electronics, 2015, 37(3): 572-576. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [20] |
甘茂治, 康建设, 高崎. 军用装备维修工程学[M]. 2版. 北京: 国防工业出版社, 2010: 42-47. GAN M Z, KANG J S, GAO Q. Military equipment maintenance engineering[M]. 2nd ed. Beijing: National Defense Industry Press, 2010: 42-47. (in Chinese) |
| [21] | SHERBROOKE C C. 装备备件最优库存建模:多级技术[M]. 2版. 北京: 电子工业出版社, 2008: 23-27. |
| [31] | SHERBROOKE C C. Optimal inventory modeling of systems multi-echelons[M]. Beijing: Publishing House of Electronics Industry, 2008: 23-27. |



