量子计算是基于量子力学原理的全新计算模型,利用量子叠加和量子纠缠等独特的量子效应进行信息处理,其概念最早由美国阿贡国家实验室的Benioff于20世纪80年代初提出。在1981年举办的第一届计算物理年会上,诺贝尔奖获得者Feynman勾勒出以量子现象实现计算的愿景,并指出利用量子计算机来求解特定问题是传统计算机所无法比拟的[1]。1985年Deutsch研究了量子图灵机和量子线路模型[2],使得量子计算开始具备数学基本型式。
量子计算是最重要的后摩尔计算技术之一。经过近40年的发展,量子计算领域已取得一些阶段性成果。例如,在量子算法方面产生了Deutsch-Jozsa算法[3]、Shor算法[4]、Grover算法[5]、Grover/Long算法[6-7]、HHL算法[8]等,使得量子计算在大数分解[3-4]、数据库搜索[5]、线性方程组求解[8]等领域展现出明显的优势;在量子计算机硬件系统方面,已研制出IBM Q[9]、光量子计算机(中国科学技术大学)[10]等原型系统。
量子计算被认为是一种可能对未来产生颠覆性影响的前沿技术[11]。加州理工学院理论物理学家John Preskill认为,如果单台量子计算机能够有效操纵50个左右量子比特,其能力就可以超过所有的经典计算机计算能力的总和,从而实现相对经典计算机的“霸权”。这种“量子霸权”[12]已成为各国科研机构和高科技公司竞相追逐的目标;同时,各国政府也适时推出针对量子计算的战略发展计划,以期占领未来量子计算技术的制高点。例如,美国通过了“国家量子计划法案”,要求实施为期10年的“国家量子计划”;英国宣布开展“国家量子技术”项目,并投入8 000万英镑支持量子技术研发和应用;欧盟启动了“量子技术旗舰”计划,预计投入10亿欧元,推动量子通信、量子模拟器、量子计算机等领域量子技术的发展,确立欧洲在量子技术和产业方面的领先优势[13]。
作为超大规模计算机的重要应用领域[14],空气动力学中的计算流体力学(CFD)、气动设计优化等数值模拟技术拥有无尽的计算资源需求,鉴于未来量子计算机在计算性能方面的巨大潜力,非常有必要评估量子计算技术给空气动力学带来的机遇和挑战。目前,已有部分学者开展此方面的研究,例如,Steijl和Barakos[15]研究了基于量子傅里叶变换的泊松方程并行求解,他们认为:尽管存在不可避免的噪声和不确定性,基于经典/量子硬件混合的计算方法可以得到有效的流场模拟结果。
本文首先介绍量子计算的基本原理,然后讨论量子计算机和量子算法/软件的研究进展,最后针对空气动力学数值模拟所涉及的若干关键数学问题,分析量子计算在空气动力学领域的应用前景。
1 量子计算的基本原理量子计算的基本单元是量子比特(Qubit)。每个量子比特都是两能级的量子系统,能够被可控地制备、操作和测量[16],如光子的两个偏振态、电子的两个自旋态等;而量子计算机可以被视为由n个量子比特所组成的集合,它的波函数属于一个2n维的复希尔伯特空间。
1.1 量子比特量子比特是量子计算的基本单位,与经典计算里的比特(bit)相对应,其状态通常由狄拉克符号来表示,任何量子比特都可以在二维复希尔伯特空间中描述。经典比特0和1可以用一对正交归一的量子态表示,即
| $ |0\rangle \equiv\left[\begin{array}{l} 0 \\ 1 \end{array}\right], \quad|1\rangle \equiv\left[\begin{array}{l} 1 \\ 0 \end{array}\right] $ | (1) |
根据叠加原理,量子比特的任意态都可以写成
| $ |\psi\rangle=\alpha|0\rangle+\beta|1\rangle $ | (2) |
式中:振幅α和β为复数且满足归一化条件,即
| $ \alpha^{2}+\beta^{2}=1 $ | (3) |
可见,量子比特属于由连续变量α和β所刻画的矢量空间。
N个量子比特能够存储2N个二进制数字。根据叠加原理,量子计算机可以同时对这些数字执行特定计算操作,对每一个叠加分量进行变换,并按一定的概率幅叠加起来给出结果。这种运行模式是量子计算机强大计算潜能的根本来源。
一次量子计算通常包含3个基本步骤,即制备输入态、基于酉变换操作输入态以及测量输出态[17]。假设待计算的函数为f(x),其量子计算过程如下:首先,根据输入值xi制备量子计算机的初态矢量|f(0)〉;然后,设计量子算法,通过酉算子操纵态矢量在复希尔伯特空间中旋转;最后,对终态矢量|f(t)〉实施量子测量操作,得到输出值f{xi}。
1.2 量子计算线路模型经典计算机能够通过布尔电路来描述[18]。针对量子计算,Deutsch[19]提出量子线路模型来描述量子图灵机。图灵奖获得者姚期智[20]曾证明,量子线路模型和量子图灵机模型是等价的,在特定情况下两者可以在多项式时间内相互模拟。
量子线路利用酉变换将多个量子比特的初始状态集合映射到某个终止状态。每个酉变换可被视为一个酉门,而该量子门又能够进一步分解为若干量子基础门。由于组成量子线路的每一个量子逻辑门都是一个酉矩阵,因此整个量子线路也是一个大的酉矩阵。在此以量子傅里叶变换(QFT)为例详细介绍量子线路图,如图 1所示,线路图从左到右运行,每条线代表一个量子比特的状态演化情况;酉门由线上带符号的盒子表示。
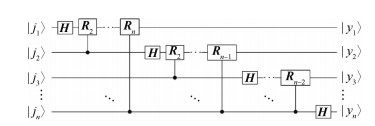
|
| 图 1 量子傅里叶变换线路图 Fig. 1 Circuit for QFT |
| $ y_{k} \equiv \frac{1}{\sqrt{N}} \sum\limits_{j=0}^{N-1} x_{j} \mathrm{e}^{\frac{2 \pi i j k}{N}} $ | (4) |
首先计算量子态
在图 1所示的量子线路中,H是Hadamard门,Rk表示幺正矩阵形式的量子门,即
| $ \boldsymbol{R}_{k} \equiv\left[\begin{array}{cc} 1 & 0 \\ 0 & \mathrm{e}^{2 \pi i / 2^{k}} \end{array}\right] $ | (5) |
第i个量子比特涉及一个H门和n-i个条件旋转门R。可以看出,量子线路模型能够直观地模拟量子信息的处理过程,可作为量子算法设计和量子计算机实现的指导性框架。
2 量子计算机研究进展自经典计算机诞生以来,其CPU性能基本按照摩尔定律[23]所预测的趋势在增长,相应的制造工艺也发展到14 nm(英特尔公司)甚至7 nm(三星公司)。业界普遍认为,7 nm是硅材料芯片的物理极限,而碳纳米管复合材料有望将现有晶体管制程缩减到1 nm[24]。当芯片上线条的宽度达到纳米量级时,量子效应会对材料的物理、化学性能产生影响,甚至使得现行工艺下的半导体器件不能正常工作。自Feynman提出量子计算机概念[1]以来,量子门、量子线路、电路集成等方面已取得重要进展[20, 25-27],并成功研制出多种量子计算机原型系统[9-10]。
2.1 量子计算机的几种物理实现方案量子计算机是基于量子力学原理实现的物理系统。著名理论物理学家Divincenzo提出了一套判据[28],用于判断特定系统能否实现量子计算的功能,包含如下要求:①构成系统的量子比特具有可扩展性;②能够有效初始化量子比特的状态;③能够可靠地实现一组普适逻辑门;④系统有足够长的相干时间,以实现编码和纠错过程;⑤能够对任意量子比特实施有效的测量;⑥可以实现计算量子比特和通信量子比特之间的转换。
郭光灿院士团队[29]综述了量子计算机的几种物理实现方案(包括离子阱[30-31]、超导[32]、冷原子[33]、光学[34]、核磁共振[35-36]、稀土、里德堡原子等),并指出目前基于上述方案所构建的系统都无法满足Divincenzo判据[28]的所有要求。在此简要介绍两种比较有前景的方案。
2.1.1 离子阱方案离子阱是最早采用的量子计算机研制方案,该方案将一串离子囚禁在线性阱中,用所囚禁离子的能级和振动模式作为量子比特。对于单量子比特,相关操作可通过激光作用在对应的离子上来实现;对于涉及两个离子的受控非门,该操作通过两束激光作用在两个离子上,并且在声子的协助下完成。该方案的主要障碍是可扩展性问题,即当达到约50个量子比特时的离子阱极限问题。
目前,基于离子阱方案研制量子计算机的单位有IonQ公司[30]和霍尼韦尔公司[37]等。其中,IonQ公司已研制出160个存储量子比特和79个离子阱比特的量子计算机;霍尼韦尔公司称其离子阱量子计算技术已达到“创纪录的高保真量子操作”,有望在2019年底开始创造营收。图 2显示了IonQ公司的量子计算机芯片[38]。
2.1.2 超导电路方案超导电路方案利用超导体中的约瑟夫森结来产生抗噪声的量子比特。借助现有微加工技术,该方案可以很好地解决系统的可扩展问题,是一种非常有前景的量子计算机研制方案。
目前,IBM、谷歌、Rigetti Computing、阿里巴巴等国际知名公司以及中国科学技术大学都采用了该方案。图 3显示了Rigetti Computing公司的超导处理器芯片[39]。
IBM公司已研制出首台独立量子计算机Q System One并提供了云计算平台;国内外很多学者已基于该平台开展量子计算方面的研究[40-42]。谷歌公司推出一款72个量子比特的计算机Bristlecone,而Rigetti Computing公司已启动128量子比特的芯片研制计划。另外,中国科学技术大学潘建伟院士团队已研制出24个超导量子比特处理器,并实现了Bose-Hubbard梯子模型多体量子系统的模拟[32]。
2.2 典型量子计算机原型系统 2.2.1 IBM Q系统早在2017年,IBM就推出一款17量子比特的量子计算原型系统(简称Q系统);2019年,IBM在国际消费电子展上又推出Q System One,并宣称它是专门为科学和商业用途设计的通用量子计算系统。该系统包含20个量子比特,采用模块化和紧凑式设计,具备如下特点:①量子硬件能够自动校准,提供高质量的量子比特;②可以提供独立的量子计算环境;③通过紧凑型高精度的电子元件控制量子比特;④采用混合计算模式,其中经典计算提供安全的云访问,量子模块支持量子算法。
基于Q系统,IBM推出了免费的量子计算云服务Quantum Experience。自2016年上线以来,该平台已经给各国科研人员提供了良好的量子算法研究环境,并催生出量子计算相关的许多成果。例如,Behera等[43]在Q系统上验证了两种延长量子中继器信息传输距离的途径(即纠缠交换和净化模式);Mandviwalla等[44]利用4量子比特实现了Grover算法;付向群等实现了t比特半经典量子傅里叶变换,相比经典算法可节省若干量子比特和门电路[41]。
2.2.2 中国科学技术大学多光子可编程量子计算原型机2017年,中国科学技术大学潘建伟院士团队联合浙江大学王浩华教授研究组,利用自主发展的综合性能国际最优的量子点单光子源,通过电控可编程的光量子线路,构建了针对多光子“玻色取样”任务的光量子计算原型机[45]。陆朝阳等发展了世界领先的多光子纠缠操控技术,成功运行了求解一个2×2线性方程组的量子线路,首次从原理上证明了HHL算法[8]的可行性[46];同时,他们在国际上首次实现量子机器学习算法[47-48],开创性地将量子计算应用于大数据分析和人工智能领域。
2.3 通用量子计算机研发情况目前国内外已经出现了多种量子计算机原型系统(如谷歌Bristlecone、IBM Q系统等),但这些系统都无法满足Divincenzo判据[28]包含的所有要求。现在,量子计算机所执行的任务经典计算机都能胜任;比较乐观的预计是,5年之后会在特定专业领域内出现完全超越经典计算机的专用量子计算机。
通用量子计算机的研制成功,必须以攻克众多关键技术[49]为前提,因此其研制成功可能在10年之后甚至更久。但是,在此之前会出现类似D-Wave(针对优化问题)的多种专用量子计算机。鉴于各国政府、高科技公司、资本市场对量子计算高度重视,量子计算机的研制进展非常顺利,无论是量子比特数还是其他量子性能指标都在不断刷新历史记录。
Tabuchi等[50]指出,要想实现中等规模(上万量子比特)的超导量子计算机,必须满足如下技术需求:①大规模量子比特的高效制备;②长时间保持集成线路中门电路的精度;③拥有室温下可扩展的控制和计算单元。Maslov等[38]认为,能够解决药物研制等实际问题的量子计算机将在未来10~20年内出现,为实现此目标,除持续发展量子计算机硬件技术外,还需要:①设计适应更多、更复杂计算任务的量子计算机体系结构;②研究将具体问题映射到量子计算机的算法和方法论;③联合领域专家共同界定适合量子计算机的应用问题;④优化量子计算机软件和硬件,提高具体应用软件的运行性能。
由美国国家科学院、工程院与医学院联合组建的专家委员会对量子计算的前景进行了评估,并撰写了252页的详实报告[49],认为未来10年内几乎不太可能建立起能够破解RSA2048的量子计算机。报告识别出如下需要解决的技术挑战:
1) 量子比特无法从根本上杜绝噪声。量子操作的微小误差或者耦合到物理系统的噪声最终都可能导致计算错误。
2) 量子计算需要鲁棒的纠错算法。尽管噪声无法避免,量子计算机可通过高效的量子误差纠正算法确保计算的正确性。
3) 量子计算无法实现大数据的高效输入。对于需要海量数据作为输入的应用,量子计算机暂时不具备针对大量初始数据的高效量子态制备方法。
4) 量子计算机需要全新的软件栈。为提高量子软件开发效率,需要重新研制集成开发环境等工具链。
5) 量子计算的中间态不能直接测量。量子状态无法拷贝,任何测量操作都会对被测量的量子系统产生扰动,甚至使其塌陷到经典比特。
关于通用量子计算机的前景,少数学者持有悲观态度,例如理论物理学泰斗Dyakonov[51], 他认为,当量子比特数N达到1 000时才能解决具体的问题;而这必然会导致描述量子计算机的连续变量达到2N(≈10300),这远远超过了宇宙中的总粒子数1080。因此,Dyakonov断言实际可用的通用量子计算机永远无法研制成功。关于量子计算机和经典计算机的关系,Steiger等[52]认为,量子计算机无法替代经典计算机,它更多地是作为一种类似GPU的加速部件存在,用于加速特定应用或者计算任务。
3 量子算法及软件研究进展Rigetti Computing公司的研究团队[53]指出,应该研制高效的量子计算软件以提高量子计算机的服务能力,具体包含3个方面:①发展“混合”软件,能够充分结合经典处理器和量子处理器的优势;②基于开源软件来开发量子计算应用;③倡导业界建立量子编程社区,逐步培育起量子软件生态。下面从量子算法、量子软件框架、量子计算云服务平台、量子机器学习等4个方面综述量子软件方面的研究进展。
3.1 量子算法量子算法是基于量子叠加性、纠缠性和状态变化等特点设计出的算法。第1个量子算法由Deutsch于1985年提出,主要用于解决Deutsch问题[2];Deutsch和Jozsa于1992年发展了Deutsch-Jozsa算法[3],解决了n量子比特的Deutsch问题,实现了针对经典算法的指数级加速。此后,又出现了几个著名的量子算法:量子傅里叶变换[21]算法、大数分解算法Shor[4]、无序数据库搜索算法Grover[5]及其变种Grover/Long[6-7]、线性系统求解算法HHL[8]等。
鉴于量子计算机与经典计算机的运行机理差异巨大[54],传统的算法设计技术已不再有效,因此量子算法设计非常具有挑战性。Shor建议[54]从计算复杂性理论的P问题中选取算法,并研究量子加速的可能性。邵长鹏等[55]研究了量子算法设计的5项技巧(量子相位估计、酉算子线性组合、量子线性求解器、Grover搜索以及量子行走)。现简要描述其中的前3项:
1) 量子相位估计[56]:首先将目标酉算子的特征值转存到量子态的概率幅,然后将概率幅中的相位提取到基态,最后输出相位估计。量子相位估计是目前量子算法设计中非常重要的技巧,已成为众多量子算法的关键子程序,如Shor算法[4]、量子线性求解器[8]、量子主成分分析[57]等。
2) 酉算子线性组合(LCU):对于N个非零复数αi和酉算子Ui,算子
3) 量子线性求解器:线性方程组求解是许多科学计算和工程应用领域的基础问题。自HHL算法[8]提出以来,国际上已发展了多种求解线性方程组的量子算法,如SVE[61]等。量子线性求解器可被广泛应用于科学计算[15]和量子机器学习领域[55]。
3.2 量子软件框架基于叠加、纠缠、干涉等量子特性,量子计算机具有超强的计算潜能,但必须借助量子软件才能真正展现出来。量子软件框架是研制量子软件的关键基础设施,是量子计算的一个重要研究领域[52, 62-67]。
吴楠等[62]对量子计算机软件层面的需求和架构进行了探索性研究,涉及量子指令集构建、量子编程语言设计准则等研究内容。Tulsi[63]设计出一种针对量子搜索算法的框架,封装了多种扩展版Grover算法,并允许灵活选择酉变换。刘树森等[67]研制出一款量子程序设计环境Q|SI〉,它包括支持量子while语言的编译器以及一套支持量子计算模拟、量子电路优化、量子程序分析和量子程序验证的工具集。Steiger等[52, 68]研制出一款开源量子软件框架ProjectQ;该框架定义了一种高级语言,能够针对各种后端(如IBM系列)芯片编译量子程序。
目前国内外软件公司已推出多款量子算法、量子程序设计方面的框架产品,如表 1所示。举例来说,HiQ[69]量子计算编程框架支持量子算法设计和量子软件开发,能够兼容开源框架ProjectQ[68],同时支持经典-量子混合算法的简易编程以及分块用户界面BlockUI。
另外,百度研究院量子计算研究所所长段润尧指出,百度提出了全栈式云架构下的多端量子计算平台架构,包含统一编程平台、分布式量子信息处理、量子硬件接口、量子网络和因特网、量子和后量子密码等5个方向。其中,统一编程平台主要研究和探索经典量子无缝架构的实践方法。
3.3 量子计算云服务平台量子云是以量子计算为核心的云服务,支撑量子算法设计以及量子程序编写等用户需求。目前,国内外已出现多个量子计算云服务平台[42]。
中国的云服务平台包括:①阿里云与中国科学院共同发布的量子计算云平台[75],包括量子计算系统架构及量子算法开发计算环境;②合肥本源量子计算科技有限责任公司部署的本源量子计算云服务平台[76],提供量子计算知识学习、量子程序模拟、真实量子芯片计算等服务;③华为公司发布的量子计算模拟器云服务平台HiQ[69],是一个量子计算研究和教育普及使能平台,包含常用的分布式模拟器(全振幅模拟云服务、最强单振幅模拟云服务、首个纠错电路模拟云服务)以及量子计算编程框架。
美国著名的量子计算云服务平台主要是IBM Q Experience[77],基于该平台,用户可以设计复杂的量子线路以及利用Qiskit开发量子软件。目前,国际上许多研究人员已基于该云服务开展了量子计算工作,并取得了阶段性成果[41, 43-44]。
3.4 量子机器学习技术图灵奖得主姚期智院士于2018年8月参加“墨论坛”时提出如下观点:未来=人工智能+量子计算。作为人工智能领域的研究热点,机器学习与量子计算的结合已被越来越多的研究机构和学者所关注。
Weinstein[78]研究了量子力学和数据挖掘之间的关系,利用动态量子聚类[79]技术,将聚类查找问题转换为量子力学中的问题,从而实现聚类的自我发现。Fischer等[80]结合数据挖掘和量子力学来预测晶体结构,使用机器学习方法来捕捉晶体结构的物理特性,其计算结果的精度由量子力学特性来保证。Biamonte等[81]系统阐述量子算法新成果在机器学习领域的应用前景;例如,HHL算法[8]可以用于加速卷积神经网络等机器学习方法,而量子主成分分析[82-83]可以用于模式识别的数据降维。相应地,黄一鸣等[84]发表综述性文章,按量子无监督聚类、量子有监督分类、量子降维、量子深度学习等4类算法,详细阐述量子机器学习算法的研究进展。
正如Biamonte[81]和黄一鸣[84]等指出,量子机器学习技术具有很好的前景,但同时也面临如下4个挑战性问题:①量子算法在读取输入数据方面没有优势,致使其运行时间可能被数据读取所主导;②从量子算法中获取完全解(以位串表示)时,需要学习的位数达到指数级,从而限制了某些量子机器学习算法的可用性;但是,该问题可以通过学习解状态的统计信息来避免;③目前量子机器学习算法所需要的量子比特数目尚未可知;④缺少验证量子机器学习算法与经典算法性能优劣的基准测试程序。对于量子数据,Biamonte等[81]认为量子机器学习算法将不存在上述前两条问题。
4 量子计算在空气动力学中的应用前景作为流体力学的重要分支,空气动力学对航空航天事业的发展和进步有重要影响[85]。风洞试验、数值模拟和飞行试验是空气动力学基础研究和应用研究的3大手段,其中数值模拟主要借助CFD方法来获取高精度的流场数值仿真结果。多年来数值模拟已积累了海量计算数据,如何据此解释流动现象和发现隐藏的模式,是空气动力学领域的一个研究热点[86]。同时,CFD技术在飞行器气动优化设计方面也得到了广泛应用[87]。
4.1 CFD与量子计算当今,科学和工程技术领域的许多问题都需要依靠计算机和计算方法来求解。科学计算已经成为科学研究的3种基本手段之一。在空气动力学领域,CFD对航空/航天飞行器的研制起着举足轻重的作用。CFD属于典型的计算/访存密集型科学计算领域。随着并行计算机性能的不断提升,CFD方法逐步从以面元法为主的工程算法,发展到势流方法、欧拉方法和雷诺平均Navier-Stokes(RANS)方法,再到大涡模拟(LES)和直接数值模拟(DES)等。由于计算资源的限制,目前普遍采用RANS方法来模拟复杂飞行器的湍流。据美国波音公司的Tinoco博士估计,民航客机的全机LES计算要等到2045年才能实现,而DNS模拟则要到2080年[14]。
量子计算机的飞速发展有希望解决CFD对计算性能的巨大需求。下面以线性方程组求解、插值、数值积分等常用的计算方法[88]为切入点,初步探讨基于量子计算进行CFD模拟的可行性。
4.1.1 线性方程组求解线性方程组是求解常微分方程、偏微分方程以及计算流体动力学问题中许多数值算法的基础,在科学和工程领域中起着至关重要的作用,其快速求解一直是科研人员致力解决的问题。
2009年,Harrow等提出了第1个关于线性系统求解的量子算法HHL[8],在特定条件下实现了对经典算法的指数级加速。人们正在以多种方式利用、实现和扩展该算法,以弥合量子计算算法和计算流体力学之间的巨大差距。潘建伟团队[89]成功运行了求解一个2×2线性系统的量子线路,首次从原理上验证了HHL算法的可行性;另外,杜江峰团队[90]在核磁共振量子芯片上实验验证了2×2阶线性系统的求解。Childs等[91]对HHL算法进行了优化,在对参数ε的依赖上实现了指数级加速,即达到了lg(1/ε)多项式时间。
针对稠密矩阵的线性系统Ax=b(A为谱范数有界的n×n稠密矩阵)求解,Wossnig等[92]提出了一种复杂度为
受绝热量子计算[93]的启发,Subasi等[94]提出了两个针对线性系统求解的量子算法,其计算复杂度为O(κ2lg(κ)/ε)和O(κlg(κ)/ε),在特定假设下能够达到指数级的量子加速;作者采用不同的设计思路,即基于哈密尔顿量来构建量子算法,展现出哈密尔顿量在设计新量子算法方面的前景。Wen等[95]在4量子比特的核磁共振系统上验证了该算法,成功求解了8×8线性系统。
4.1.2 插值操作插值是离散函数逼近的重要方法,主要通过有限数量点处的取值状况来估算函数在其他点处的近似值。鉴于插值操作在工程技术中的大量应用,量子插值算法已受到广泛关注[96-101]。
在纳米磁共振探测中,有限的采样次数限制了灵敏度和分辨率;对此,Ajoy等[97]提出了一种相干量子插值算法,能够显著提高量子感知的分辨率。针对量子图片处理中的缩放问题,Zhou等[98]提出了一种量子双线性插值算法,并基于受控非门、逆并行加法器、并行减法器、乘法器等设计了相应的量子线路;他们还研究了基于最近邻值的量子插值算法[101]。
关于多变量多项式插值,Chen等[100]研究了d自由度n变量多项式的量子插值算法,在复数域上可获得n+1加速比。在研究量子密码算法时,Diep和Giang[99]用该算法替换线性插值算法,实现了量子秘钥的分发。
4.1.3 数值积分数值积分是利用黎曼积分等数学定义,用数值逼近的方法近似计算定积分值,如气动力系数的计算等。国内外学者已针对量子积分算法开展了广泛研究[102-105],例如,在任意L2希尔伯特空间H,Gudder[102, 104]指出量子测量结果是天然可积的,并推导了量子积分公式;Krishnan等[105]则研究了Neumann边界条件下量子重力的路径积分问题。
4.1.4 典型量子算法:HHLHHL[8]是针对线性系统求解的第1个量子算法,在数据处理[106]、机器学习[81]、数值计算[107]等场景具有广泛的应用前景。其量子线路如图 4所示。
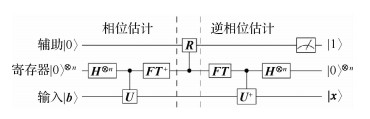
|
| 图 4 HHL量子算法线路图 Fig. 4 Quantum circuit for HHL quantum algorithm |
HHL算法的输入是n维向量b以及n×n的Hermitian矩阵
HHL算法包含相位估计、受控旋转和逆相位估计3个关键步骤,下面详细介绍其流程:
1) 针对寄存器R3准备
2) 将矩阵A作为相位估计中酉算子的一个组成部分,即U=eiAt。
3) 基于相位估计,在A的特征空间上分解|b〉,得到
4) 执行受控旋转操作R,寄存器R1由基态|0〉映射到|0〉和|1〉的叠加态上,即R|0〉=
5) 通过逆相位估计来计算|λi〉。测量寄存器R1;当结果为|1〉时,寄存器R3得到结果
需要注意的是,HHL算法只能得到真值
气动外形优化设计包括CFD数值模拟、优化搜索算法等内容[108]。4.1节介绍的线性方程组求解等量子算法能够显著加速CFD数值模拟的效率,从而减少气动外形优化设计的周期。量子优化搜索算法已出现大量的研究成果[109-111],为量子计算在气动外形优化设计领域的应用打下了坚实的理论基础。
4.2.1 量子优化搜索Yang等[112]提出一种基于量子个体的粒子群优化算法,能较好地优化离散问题。Boixo等[113]利用量子退火思路提出3种解决组合优化问题的策略,其中个别策略相对经典方法可获得多项式和指数级加速。经典遗传算法在个体选择步骤的复杂度为O(NlgN),其中N为种群个体的数量;对此,Malossini等[114]将经典算法中的适应性评估和个体选择两个步骤整合为一个步骤,并将个体选择部分的时间复杂度降到O(1)。
4.2.2 典型量子算法:量子退火在数学和应用领域,量子退火是一类新的量子优化算法。与基于热波动原理的模拟退火不同,量子退火主要通过模拟量子隧穿效应来实现对目标系统的优化。在设计量子退化算法时,通常将优化问题映射为一个量子系统,其中优化目标函数映射为施加在该量子系统上的一个势场,并引入一个幅度可控的动能项作为控制量子波动的穿透场。在这两个场的作用下,量子系统按照薛定谔方程描述的规律演化。杜卫林等[115]已详细综述了量子退火算法的研究进展,包括基于路径积分、格林函数等蒙特卡洛方法的量子算法。
基于横向场Ising模型,D-Wave公司致力于研制针对优化问题的专用量子计算机,其量子位已达到数千规模;例如,计划2020年投入运行的Advantage量子计算机(由美国洛斯阿拉莫斯国家实验室采购)将达到5 000量子位。此外,围绕D-Wave量子计算系统已取得许多量子优化方面的研究进展[116-118]。
4.3 数据处理与量子计算受理论不充分性等客观因素影响,空气动力学中仍存在许多人类难以解释的流动现象[85]。目前,研究人员已尝试借助人工智能方法对流体力学中的未知现象进行解释[119-121],量子机器学习领域出现了大量优秀算法[81-84],给数据处理带来了新的性能提升潜力。
4.4 应用前景分析目前国际上已出现一些针对CFD数值模拟量子算法研究的文献[15, 122-125]。Yepez[122]发展了一种针对黏性流体模拟的量子格子气模型,设计了一种量子计算网络来实现微观尺度的量子格子气传输方程。数值模拟结果表明,量子格子气模型服从碰撞时的细致平衡,是一种无条件稳定的流体动力模拟方法。另外,Yepez[123]还通过格子气系统的微观尺度特性来预测介观尺度的行为,并在工作站上实现了该量子格子气模型。数值模拟结果表明,在一维量子格子气系统中并未出现黏性阻尼现象。Scoville[124]也对格子气模型的量子算法进行了研究,并针对扩散方程进行了模拟。
Steijl和Barakos[15]使用格子涡方法求解泊松方程,其中离散傅里叶变换部分使用量子线路来实现。作者在经典并行计算机上模拟该量子线路,并分析了分布式存储模式下的数据交换情况。作者认为,基于经典/量子混合硬件途径能够实现流体的有效模拟。Frolov[125]综述了量子算法和量子计算机的研究进展,指出量子计算已逐步实现从纯科学到工程解决方案的转变,并讨论了量子计算机在数值天气预报领域的应用前景。
对于CFD计算和气动优化设计所涉及的基础数学方法,目前都有相关的量子算法出现。尽管可能存在通用算法到具体应用场景的适应性问题,但量子算法的优越性能已经充分展现出来。
5 结论量子计算可能对未来各行业领域产生颠覆性的影响,因此多国政府已推出相应的战略发展计划,科研机构和高科技公司都在竞相追逐“量子霸权”的目标。
一直以来,空气动力学中的CFD、气动优化设计等对计算资源都有巨大的需求。鉴于未来量子计算机在计算性能方面的超大潜力,本文探讨了量子计算技术给空气动力学带来的机遇和挑战。首先综述了量子计算机、量子算法的研究进展,然后介绍了量子计算在空气动力学相关基础方法上的进展情况,最后分析了量子计算在空气动力学领域的应用前景。
量子计算未来的研究方向将包括:完善和改进相关基础方法的量子算法,开展空气动力学领域的适应性研究和应用,并建立量子算法库;研制针对空气动力学领域的量子计算软件框架,建立行业量子软件的生态圈。
| [1] | FEYNMAN R P. Simulating physics with computers[J]. International Journal of Theoretical Physics, 1982, 21(6-7): 467-488. |
| Click to display the text | |
| [2] | DEUTSCH D. Quantum theory, the Church-Turing principle and the universal quantum computer[J]. Proceedings of the Royal Society A:Mathematical and Physical Sciences, 1985, 400(1818): 97-117. |
| Click to display the text | |
| [3] | DEUTSCH D, JOZSA R. Rapid solution of problems by quantum computation[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1992, 439(1907): 553-558. |
| Click to display the text | |
| [4] | SHOR P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]//Proceedings of the 35th Annual Symposium on Foundations of Computer Science, 1994: 124-134. |
| [5] | GROVER L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the 28th Annual ACM Symposium on the Theory of Computing. New York: ACM, 1996: 212-219. |
| [6] | LONG G L. Grover algorithm with zero theoretical failure rate[J]. Physical Review A, 2001, 64(2): 022307. |
| Click to display the text | |
| [7] | CASTAGNOLI G. Highlighting the mechanism of the quantum speedup by time-symmetric and relational quantum mechanics[J]. Foundations of Physics, 2016, 46(3): 360-381. |
| Click to display the text | |
| [8] | HARROW A, HASSIDIM A, LLOYD S. Quantum algorithm for linear systems of equations[J]. Physical Review Letters, 2009, 103(15): 150502. |
| Click to display the text | |
| [9] | IBM Q system[EB/OL].(2019-08-02)[2019-08-13]. http://www.research.ibm.com/ibm-q/system-one/. |
| [10] |
林落. 世界首台光量子计算机诞生[J]. 科学新闻, 2018(1): 23-24. LIN L. The first photon quantum computer[J]. Science News, 2018(1): 23-24. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [11] |
孙晓明. 量子计算若干前沿问题综述[J]. 中国科学:信息科学, 2016, 46(8): 982-1002. SUN X M. A survey on quantum computing[J]. Scientia Sinica Informationis, 2016, 46(8): 982-1002. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [12] | WU J, LIU Y, ZHANG B, et al. A benchmark test of boson sampling on Tianhe-2 supercomputer[J]. National Science Review, 2018, 5(5): 715-720. |
| Click to display the text | |
| [13] |
许文琪. 国外量子信息技术发展分析[J]. 国防科技工业, 2019(5): 46-48. XU W Q. Analysis on the development of foreign quantum information technology[J]. Defence Science&Technology Industry, 2019(5): 46-48. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [14] |
张来平, 邓小刚, 何磊, 等. E级计算给CFD带来的机遇与挑战[J]. 空气动力学学报, 2016, 34(4): 405-417. ZHANG L P, DENG X G, HE L, et al. The opportunity and grand challenges in computational fluid dynamics by exascale computing[J]. Acta Aerodynamica Sinica, 2016, 34(4): 405-417. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [15] | STEIJL R, BARAKOS G N. Parallel evaluation of quantum algorithms for computational fluid dynamics[J]. Computers and Fluids, 2018, 173: 22-28. |
| Click to display the text | |
| [16] | BENENTI G, CASATI G, STRINI G. Principles of quantum computation and information I[M]. Singapore: World Scientific Publishing Co. Pte. Ltd, 2004: 75-143. |
| [17] |
李明, 陈宗海.量子计算机——未来二十年的挑战[C]//2006年系统仿真及其应用学术交流会论文集.合肥: 中国科学技术大学出版社, 2006: 833-839. LI M, CHEN Z H. Quantum computers-The challenges in the next twenty years[C]//Proceedings of the 2006 System Simulation and Application. Hefei: China University of Science and Technology Press, 2006: 833-839(in Chinese). |
| [18] |
张焕国, 毛少武, 吴万青, 等. 量子计算复杂性理论综述[J]. 计算机学报, 2016, 39(12): 2403-2428. ZHANG H G, MAO S W, WU W Q, et al. Overview of quantum computation complexity theory[J]. Chinese Journal of Computers, 2016, 39(12): 2403-2428. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [19] | DEUTSCH D. Quantum computational networks[J]. Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences, 1989, 425(1868): 73-90. |
| Click to display the text | |
| [20] | YAO A C-C. Quantum circuit complexity[C]//Proceedings of the 34th Symposium on Foundations of Computer Science, 1993: 352-361. |
| [21] | COPPERSMITH D. An approximate fourier transform useful in quantum factoring: RC 19642[R]. New York: IBM Research Division, 1994. |
| [22] | MASHHADI S. General secret sharing based on quantum Fourier transform[J]. Quantum Information Processing, 2019, 18: 114. |
| Click to display the text | |
| [23] | MOORE G E. Progress in digital integrated electronics[J]. IEEE Solid-State Circuits Newsletter, 2006, 20(3): 36-37. |
| Click to display the text | |
| [24] | DESAI S B, MADHVAPATHY S R, SACHID A B, et al. MoS2 transistors with 1-nanometer gate lengths[J]. Science, 2016, 354(6308): 99-102. |
| Click to display the text | |
| [25] | SHENDE V V, PRASAD A K, MARKOV I L, et al. Synthesis of reversible logic circuits[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 22(6): 710-722. |
| Click to display the text | |
| [26] | YANG G, SONG X, HUNG W N N, et al. Bi-directional synthesis of 4-Bit rversible circuits[J]. Computer Journal, 2008, 51(2): 207-215. |
| Click to display the text | |
| [27] | AARONSON S, GOTTESMAN D. Improved simulation of stabilizer circuits[J]. Physical Review A, 2004, 70(5): 052328. |
| Click to display the text | |
| [28] | DIVINCENZO D P. The physical implementation of quantum computation[J]. Fortschritte Der Physik, 2010, 48(9-11): 771-783. |
| Click to display the text | |
| [29] |
韩永建, 李传锋, 郭光灿. 量子计算原理及研究进展[J]. 科技导报, 2017, 35(23): 70-75. HAN Y J, LI C F, GUO G C. The principle and development of quantum computation[J]. Science&Technology Review, 2017, 35(23): 70-75. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [30] | IonQ homepage[EB/OL].(2019-08-15)[2019-09-07]. https://ionq.com/. |
| [31] | CIRAC J I, ZOLLER P. Quantum computations with cold trapped ions[J]. Physical Review Letters, 1995, 74(20): 4091. |
| Click to display the text | |
| [32] | YE Y, GE Z Y, WU Y, et al. Propagation and localization of collective excitations on a 24-qubit superconducting processor[J]. Physical Review Letters, 2019, 123(5): 050502. |
| Click to display the text | |
| [33] | WU Z, ZHANG L, SUN W, et al. Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates[J]. Science, 2016, 354(6308): 83-88. |
| Click to display the text | |
| [34] | STEINBRECHER G R, OLSON J P, ENGLUND D, et al. Quantum optical neural networks[J]. NPJ Quantum Information, 2019, 5: 60. |
| Click to display the text | |
| [35] |
龙桂鲁, 肖丽. 核磁共振量子计算机与并行量子计算[J]. 物理与工程, 2003, 13(3): 12-14, 20. LONG G L, XIAO L. Nuclear magnetic resonance quantum computer and parallel quantum computing[J]. Physics and Engineering, 2003, 13(3): 12-14, 20. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [36] | GERSHENFELD N A, CHUANG I L. Bulk spin-resonance quantum computation[J]. Science, 1997, 275(5298): 350-356. |
| Click to display the text | |
| [37] | Honeywell quantum solutions[EB/OL].(2019-08-19)[2019-09-10]. https://www.honeywell.com/en-us/company/quantum. |
| [38] | MASLOV D, NAM Y, KIM J. An outlook for quantum computing[J]. Proceedings of the IEEE, 2019, 107(1): 5-10. |
| Click to display the text | |
| [39] | QPU developed by rigetti computing[EB/OL].(2019-07-14)[2019-09-10]. https://www.rigetti.com/qpu. |
| [40] | ALVAREZ-RODRIGUEZ U, SANZ M, LAMATA L, et al. Quantum artificial life in an ibm quantum computer[J]. Scientific Reports, 2018, 8: 14793. |
| Click to display the text | |
| [41] | FU X Q, BAO W S, HUANG H L, et al. Realization of t-bit semiclassical quantum Fourier transform on IBM's quantum cloud computer[J]. Chinese Physics B, 2019, 28(2): 020302. |
| Click to display the text | |
| [42] |
崔竞一, 刘翼鹏, 郭建胜. 基于IBM量子计算云服务的量子傅里叶变换实现[J]. 信息技术与网络安全, 2019, 38(4): 19-24. CUI J Y, LIU Y P, GUO J S. Implementation of quantum Fourier transform using IBM quantum computer on cloud[J]. Cryptography Technology and Application, 2019, 38(4): 19-24. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [43] | BEHERA B K, SETH S, DAS A, et al. Demonstration of entanglement purification and swapping protocol to design quantum repeater in IBM quantum computer[J]. Quantum Information Processing, 2019, 18(4): 125. |
| [44] | MANDVIWALLA A, OHSHIRO K, JI B. Implementing grover's algorithm on the ibm quantum computers[C]//Proceedings of IEEE International Conference on Big Data, 2018: 2531-2537. |
| [45] | WANG H H, HE Y, LI Y H, et al. High-efficiency multiphoton boson sampling[J]. Nature Photonics, 2017, 11: 361-365. |
| Click to display the text | |
| [46] | CAI X D, WEEDBROOK C, SU Z E, et al. Experimental quantum computing to solve systems of linear equations[J]. Physical Review Letters, 2013, 110(23): 230501. |
| Click to display the text | |
| [47] | CAI X D, WU D, SU Z E, et al. Entanglement-based machine learning on a quantum computer[J]. Physical Review Letters, 2015, 114(11): 110504. |
| Click to display the text | |
| [48] | ZHENG Y, SONG C, CHEN M C, et al. Solving systems of linear equations with a superconducting quantum processor[J]. Physical Review Letters, 2017, 118(21): 210504. |
| Click to display the text | |
| [49] | National Academies of Sciences, Engineering, and Medicine. Quantum computing:Progress and prospects[M]. Washington, D.C.: The National Academies Press, 2019: 1-252. |
| [50] | TABUCHI Y, TAMATE S, NAKAMURA Y. Toward scalable superconducting quantum computer implementation[J]. IEICE Transactions on Electronics, 2019, E102-C(3): 212-216. |
| Click to display the text | |
| [51] | DYAKONOV M I. When will we have a quantum computer[J]. Solid State Electronics, 2019, 155: 4-6. |
| Click to display the text | |
| [52] | STEIGER D S, HNER T, TROYER M. Advantages of a modular high-level quantum programming framework[J]. Microprocessors and Microsystems, 2019, 66: 81-89. |
| Click to display the text | |
| [53] | ZENG W, JOHNSON B, SMITH R, et al. First quantum computers need smart software[J]. Nature, 2017, 549(7671): 149-151. |
| Click to display the text | |
| [54] | SHOR P W. Why haven't more quantum algorithms been found?[J]. Journal of the ACM, 2003, 50(1): 87-90. |
| Click to display the text | |
| [55] | SHAO C P, LI Y, LI H B. Quantum algorithm design:Techniques and applications[J]. Journal of Systems Science&Complexity, 2019, 32: 375-452. |
| [56] | KITAEV A. Quantum measurements and the abelian stabilizer problem[J]. Hep Websearch Hep, 1995, 3: 1-22. |
| Click to display the text | |
| [57] | LLOYD S, REBENTROST P, MOHSENI M. Quantum principal component analysis[J]. Nature Physics, 2014, 10: 631-633. |
| Click to display the text | |
| [58] | LONG G L. General quantum interference principle and duality computer[J]. Communications in Theoretical Physics, 2006, 45: 825-844. |
| Click to display the text | |
| [59] | CHILDS A M, WIEBE N. Hamiltonian simulation using linear combinations of unitary operations[J]. Quantum Information and Computation, 2012, 12: 901-924. |
| Click to display the text | |
| [60] | GILY N A, ARUNACHALAM S, WIEBE N. Optimizing quantum optimization algorithms via faster quantum gradient computation[C]//Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, 2019: 1425-1444. |
| [61] | KERENIDIS I, PRAKASH A. Quantum recommendation system[C]//Proceedings of 8th Innovations in Theoretical Computer Science Conference, 2017: 49. |
| [62] | WU N, HU H, SONG F, et al. Quantum software framework:A tentative study[J]. Frontiers of Computer Science, 2013, 7(3): 341-349. |
| Click to display the text | |
| [63] | TULSI A. General framework for quantum search algorithms[J]. Physical Review A, 2012, 86: 042331. |
| Click to display the text | |
| [64] | GAO X, NIELSEN E, MULLER R P, et al. The QCAD framework for quantum device modeling[C]//Proceedings of 15th International Workshop on Computational Electronics, 2012. |
| [65] | JAVADIABHARI A, PATIL S, KUDROW D, et al. ScaffCC:Scalable compilation and analysis of quantum programs[J]. Parallel Computing, 2015, 45: 2-17. |
| Click to display the text | |
| [66] | AVILA A B D, REISER R H S, PILLA M L, et al. State-of-the-art quantum computing simulators: Features, optimizations, and improvements for D-GM[J]. Neurocomputing, 2019, https://doi.org/10.1016/j.neucom.2019.01.118[in press]. |
| [67] |
刘树森, 周立, 官极, 等. Q|SI〉:一个量子程序设计环境[J]. 中国科学:信息科学, 2017, 47(10): 1300-1315. LIU S S, ZHOU L, GUAN J, et al. Q|SI〉:A quantum programming environment[J]. Scientia Sinica Informationis, 2017, 47(10): 1300-1315. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [68] | STEIGER D S, HNER T, TROYER M. ProjectQ:An open source software framework for quantum computing[J]. Quantum, 2018, 2: 49. |
| Click to display the text | |
| [69] | Quantum computing environments HiQ[EB/OL].(2019-09-06)[2019-09-08]. https://www.huaweicloud.com/solution/hiq/index.html. |
| [70] | Qurator VSCode extension[EB/OL].(2019-07-15)[2019-08-30]. https://marketplace.visualstudio.com/items?itemName=Qurator.qurator-vscode. |
| [71] | Cirq[EB/OL].(2019-06-13)[2019-09-04]. https://github.com/quantumlib/cirq. |
| [72] | OpenFermion[EB/OL].(2019-08-14)[2019-09-05]. https://github.com/quantumlib/OpenFermion. |
| [73] | Quantum development kit[EB/OL].(2019-06-25)[2019-09-05]. https://www.microsoft.com/en-us/quantum/development-kit. |
| [74] | Qiskit[EB/OL].(2019-08-20)[2019-09-05]. https://qiskit.org/. |
| [75] | Quantum computing cloud[EB/OL].(2019-08-30)[2019-09-05]. http://quantumcomputer.ac.cn/. |
| [76] | Origion quantum computing cloud service platform[EB/OL].(2019-09-01)[2019-09-05]. http://www.qubitonline.cn/. |
| [77] | IBM Q experience[EB/OL].(2019-08-12)[2019-09-05]. https://www.research.ibm.com/ibm-q/technology/experience/. |
| [78] | WEINSTEIN M. Strange bedfellows:Quantum mechanics and data mining[J]. Nuclear Physics B Proceedings Supplements, 2010, 199: 74-84. |
| Click to display the text | |
| [79] | WEINSTEIN M, HORN D. Dynamic quantum clustering:A method for visual exploration of structures in data[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2009, 80(6): 066117. |
| Click to display the text | |
| [80] | FISCHER C C, TIBBETTS K J, DANE M, et al. Predicting crystal structure by merging data mining with quantum mechanics[J]. Nature Materials, 2006, 5(8): 641-646. |
| Click to display the text | |
| [81] | BIAMONTE J, WITTEK P, PANCOTTI N, et al. Quantum machine learning[J]. Nature, 2017, 549: 195-203. |
| Click to display the text | |
| [82] | LLOYD S, MOHSENI M, REBENTROST P. Quantum principal component analysis[J]. Nature Physics, 2014, 10: 631-633. |
| Click to display the text | |
| [83] |
阮越, 陈汉武, 刘志昊, 等. 量子主成分分析算法[J]. 计算机学报, 2014, 37(3): 666-676. RUAN Y, CHEN H W, LIU Z H, et al. Quantum principal component analysis algorithm[J]. Chinese Journal of Computers, 2014, 37(3): 666-676. (in Chinese) |
| Cited By in Cnki (50) | Click to display the text | |
| [84] |
黄一鸣, 雷航, 李晓瑜. 量子机器学习算法综述[J]. 计算机学报, 2018, 41(1): 145-163. HUANG Y M, LEI H, LI X Y. A survey on quantum machine learning[J]. Chinese Journal of Computers, 2018, 41(1): 145-163. (in Chinese) |
| Cited By in Cnki (15) | Click to display the text | |
| [85] |
张天姣, 钱炜祺, 周宇, 等. 人工智能与空气动力学结合的初步思考[J]. 航空工程进展, 2019, 10(1): 1-11. ZHANG T J, QIAN W Q, ZHOU Y, et al. Preliminary thoughts on the combination of artificial intelligence and aerodynamic[J]. Advances in Aeronautical Science and Engineering, 2019, 10(1): 1-11. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [86] | KAMATH C. Sapphire:Experiences in scientific data mining[J]. Journal of Physics Conference Series, 2008, 125(1): 012094. |
| Click to display the text | |
| [87] |
许瑞飞, 邓一菊, 钱瑞战. 气动优化设计及其对CFD的需求[J]. 航空科学技术, 2011(2): 50-52. XU R F, DENG Y J, QIAN R Z. Aerodynamic optimization design and its requirement to CFD[J]. Aeronautical Science&Technology, 2011(2): 50-52. (in Chinese) |
| Cited By in Cnki (9) | Click to display the text | |
| [88] |
孙文瑜, 杜其奎, 陈金如. 计算方法[M]. 北京: 科学出版社, 2007: 1-251. SUN W Y, DU Q K, CHEN J R. Computational methods[M]. Beijing: China Science Publishing, 2007: 1-251. (in Chinese) |
| [89] | CAI X D, WEEDBROOK C, SU Z E, et al. Experimental quantum computing to solve systems of linear equations[J]. Physical Review Letters, 2013, 110: 230501. |
| Click to display the text | |
| [90] | PAN J, CAO Y, YAO X, et al. Experimental realization of quantum algorithm for solving linear systems of equations[J]. Physical Review A, 2014, 89: 022313. |
| Click to display the text | |
| [91] | CHILDS A M, KOTHARI R, SOMMA R D. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision[J]. SIAM Journal on Computing, 2017, 46(6): 1920-1950. |
| Click to display the text | |
| [92] | WOSSNIG L, ZHAO Z, PRAKASH A. Quantum linear system algorithm for dense matrices[J]. Physical Review Letters, 2018, 120(5): 050502. |
| Click to display the text | |
| [93] | SATO S, KINJO M, NAKAJIMA K. An approach for quantum computing using adiabatic evolution algorithm[J]. Japanese Journal of Applied Physics, 2003, 42(11): 7169-7173. |
| Click to display the text | |
| [94] | SUBASI Y, SOMMA R D, ORSUCCI D. Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing[J]. Physical Review Letters, 2019, 122: 060504. |
| Click to display the text | |
| [95] | WEN J, KONG X, WEI S, et al. Experimental realization of quantum algorithms for a linear system inspired by adiabatic quantum computing[J]. Physical Review A, 2019, 99: 012320. |
| Click to display the text | |
| [96] | KANE D M, KUTIN S A. Quantum interpolation of polynomilas[J]. Quantum Information&Computation, 2011, 11(1-2): 95-103. |
| Click to display the text | |
| [97] | AJOY A, LIU Y X, SAHA K, et al. Quantum interpolation for high-resolution sensing[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(9): 2149-2153. |
| Click to display the text | |
| [98] | ZHOU R G, HU W, FAN P, et al. Quantum realization of the bilinear interpolation method for NEQR[J]. Scientific Reports, 2017, 7(1): 2511. |
| Click to display the text | |
| [99] | DIEP D N, GIANG D H. Quantum communication and quantum multivariate polynomial interpolation[J]. International Journal of Theoretical Physics, 2017, 56(9): 2797-2802. |
| Click to display the text | |
| [100] | CHEN J, CHILDS A M, HUNG S H. Quantum algorithm for multivariate polynomial interpolation[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2018, 474: 20170480. |
| Click to display the text | |
| [101] | ZHOU R, HU W, LUO G, et al. Quantum realization of the nearest neighbor value interpolation method for INEQR[J]. Quantum Information Processing, 2018, 17(7): 166. |
| Click to display the text | |
| [102] | GUDDER S. Examples of quantum integrals[J]. Reports on Mathematical Physics, 2010, 66(1): 21-40. |
| Click to display the text | |
| [103] | CHEN J, TANG Y. Quantum integral equations of volterra type in terms of discrete-time normal martingale[J]. Turkish Journal of Mathematics, 2019, 43: 1047-1060. |
| Click to display the text | |
| [104] | GUDDER S. Quantum measures and integrals[J]. Reports on Mathematical Physics, 2012, 69(1): 87-101. |
| Click to display the text | |
| [105] | KRISHNAN C, KUMAR K V P, RAJU A. An alternative path integral for quantum gravity[J]. Journal of High Energy Physics, 2016, 10: 043. |
| Click to display the text | |
| [106] | LLOYD S, GARNERONE S, ZANARDI P. Quantum algorithms for topological and geometric analysis of data[J]. Nature Communications, 2016, 7: 10138. |
| Click to display the text | |
| [107] | BERRY D W. Quantum algorithms for solving linear differential equations[J]. Journal of Physics A Mathematical&Theoretical, 2012, 47(10): 298-307. |
| Click to display the text | |
| [108] |
王丹, 白俊强, 黄江涛. FFD方法在气动优化设计中的应用[J]. 中国科学:物理学力学天文学, 2014, 44(3): 267-277. WANG D, BAI J Q, HUANG J T. The application of FFD method in aerodynamic optimization design[J]. Scientia Sinica Physica, Mechanica&Astronomica, 2014, 44(3): 267-277. (in Chinese) |
| Cited By in Cnki (21) | Click to display the text | |
| [109] | HOGG T, PORTNOV D. Quantum optimization[J]. Information Sciences, 2000, 128: 181-197. |
| Click to display the text | |
| [110] | ANGUITA D, RIDELLA S, RIVIECCIO F, et al. Quantum optimization for training support vector machines[J]. Neural Networks, 2003, 16: 763-770. |
| Click to display the text | |
| [111] | YAMAKAMI T. Quantum optimization problems[J]. Lecture Notes in Computer Science, 2002, 2509: 300-314. |
| Click to display the text | |
| [112] | YANG S, WANG M, JIAO L. A quantum particle swarm optimization[C]//Proceedings of the Congress on Evolutionary Computation, 2004: 320-324. |
| [113] | BOIXO S, ORTIZ G, SOMMA R. Fast quantum methods for optimization[J]. The European Physical Journal Special Topics, 2015, 224: 35-49. |
| Click to display the text | |
| [114] | MALOSSINI A, BLANZIERI E, CALARCO T. Quantum genetic optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(2): 231-341. |
| Click to display the text | |
| [115] |
杜卫林, 李斌, 田宇. 量子退火算法研究进展[J]. 计算机研究与发展, 2008, 45(9): 1501-1508. DU W L, LI B, TIAN Y. Quantum annealing algorithms:state of the art[J]. Journal of Computer Research and Development, 2008, 45(9): 1501-1508. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [116] | BERWALD J J. The mathematics of quantum-enabled applications on the D-wave quantum computer[J]. Notices of the American Mathematical Society, 2019, 66(6): 832-841. |
| Click to display the text | |
| [117] | KING A D, HOSKINSON E, LANTING T, et al. Degeneracy, degree, and heavy tails in quantum annealing[J]. Physical Review A, 2015, 93(2): 247-256. |
| Click to display the text | |
| [118] | D-wave publications[EB/OL].(2019-10-12)[2019-10-12].https://www.dwavesys.com/resources/publications?type=internal. |
| [119] | KUTZ J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1-4. |
| Click to display the text | |
| [120] | LIU Y, WANG Y, DENG L, et al. A novel in-situ compression method for CFD data based on generative adversarial network[J]. Journal of Visualization, 2019, 22(1): 95-108. |
| Click to display the text | |
| [121] | LIU Y, LU Y, WANG Y, et al. A CNN-based shock detection method in flow visualization[J]. Computers&Fluids, 2019, 184: 1-9. |
| Click to display the text | |
| [122] | YEPEZ J. Quantum computation of fluid dynamics[C]//Proceedings of the NASA International Conference on Quantum Computing and Quantum Communications. Berlin Heidelberg: Springer-Verlag, 1999: 34-60. |
| [123] | YEPEZ J. A quantum lattice-gas model for computational fluid dynamics[J]. Physical Review E, 2001, 63: 046702. |
| Click to display the text | |
| [124] | SCOVILLE J A. Type Ⅱ quantum computing algorithm for computational fluid dynamics[R]. Washington, D.C.: Air Force Institute of Technology, 2006. |
| [125] | FROLOV A V. Can a quantum computer be applied for numerical weather prediction?[J]. Russian Meteorology and Hydrology, 2017, 42(9): 545-553. |
| Click to display the text |





