目前,多智能体编队集成了单智能体的大量优势,并具有广泛的应用价值,其在军事领域的应用尤为突出。同时,多智能体编队在多约束情况下的协同控制、避障、信息融合以及容错一致性等关键技术被大量学者所关注和研究。其中,容错控制研究在解决实际问题过程中,具有非常重要的地位,也是当前研究的热点和难点。一致性理论在自主智能体的网络中,具有典型聚集行为,已经逐渐成为研究的热点问题[1-3],包括无人机协同编队飞行、网络、机器人编队、水下无人机编队等广泛的应用。内部交互系统是由离散的、一直变化的,并广泛分布在整个网络中的多种成分所构成。因此,容错一致性理论成为解决以上问题的方法。在典型的多智能体系统中,一般是由很多智能体组成一个协同系统,在该系统中,每个智能体仅在分布式结构状态下对其相邻的智能体共享其局部信息,进而以一种协同方式去实现全局普遍性行为。
因此,文献[4-5]采用代数图论对线性Vicsek模型进行了理论性的研究,得到实现多智能体一致性的充分条件是网络结构能够在有限的时间内频繁的连接。同时,还提出了一种有效的一致性结构用于解决复杂网络中多智能体的一致性和同步性问题。文献[6-7]均采用基于拓扑结构的智能体编队信息交换机制对编队进行控制,使得系统也能达到渐进一致稳定。文献[8-10]提出了一种分布式自适应一致性方法,用于克服智能体之间不同步的局限性,在一致性控制器设计中需要知道图论中拉普拉斯矩阵的特征值,这个特征值实际上是智能体系统的整体信息。文献[11]给出了二阶系统一致性理论在多智能体中的充分必要条件,充分证明了一致性方法的优势。文献[12]对国内外多智能体技术的应用进行了阐述,分析了多智能体一致性及控制的关键技术,并指出目前亟需解决容错一致性问题。对于多智能体编队系统的研究,当子系统的数目较少且通讯正常的情况下,可应用集中式控制方法解决多智能体协同编队运动。然而,对于一个多智能体系统而言,当有个别智能体逐渐老化或者出现故障时,在这种情况下,由于系统中单个智能体具有特定的作用,不能轻易取而代之。而且不同智能体出现老化或者故障的程度不同,可能导致增加修复的成本。因此,本文提出了分布式自适应下的容错控制研究,主要解决2个问题:①系统中单个智能体发生故障或者环境不确定,智能体仍能完成任务;②智能体系统发生故障时,设计分布式容错控制器及时补偿故障误差,使其快速恢复正常的工作状态。
在过去几年里,在对系统进行故障分析时,由于网络系统的复杂性和时实系统的安全需要,很多学者已做了大量研究去解决网络系统和执行机构中的故障问题。例如,文献[13]对延迟系统进行了故障估计研究,此后,复杂系统的故障诊断和检测有了一定的进展。文献[14]对一种广义非线性系统的执行器进行了容错控制研究。文献[15]研究了单一系统的容错控制服从于执行器饱和非线性扰动的影响。文献[16]对于一类非线性系统设计出了一种容错控制结构。文献[17]设计了一种容错控制适用于一类非线性样本数据系统。文献[18]将容错控制应用于实际工程中,解决了无人机的执行高负荷以及长航时旋翼疲劳断裂导致其失控甚至坠毁不能完成作战任务的问题,具有实际的应用价值。Yoo针对无人机编队中任意一架无人机的执行机构故障,在不确定外界环境条件下,设计了一种反步容错控制,有效地解决了无人机编队飞行中的容错控制问题[19]。文献[20-21]研究了四旋翼无人机在运动过程中执行机构容易发生故障影响飞行品质问题,提出了执行器故障下四旋翼无人机的容错控制估计方法,为后续研究提供了充足的理论支撑。魁北克大学Ghommam等[22]采用反步法,设计了基于局部相对信息的分布式控制器,实现了多无人机的有效跟踪,仿真实验验证了该算法的有效性。但是,作者并没有考虑系统的输入饱和因素,这不利于工程实践。文献[23]针对多个欧拉系统分布式编队牵制问题以及模型的不确定性,提出了一种输出反馈控制方法。然而,该成果未考虑避障情况和通讯时延的约束。综上所述,容错控制的发展非常迅速,并主要用于解决大量的实际应用问题。
尽管在现有文献中,一些有效的容错控制已经得到了发展,但在多智能体系统的研究中仍有一些问题亟待解决。总体上,多智能体系统已在生态系统、传感器网络以及机器人编队等方面得到了应用。然而,随着温度和设备年限的增加以及不可避免的能量损失等因素都能够引起故障的发生。因此,需要针对多智能体编队中个别单智能体出现故障问题,设计一种新的自适应一致性协议,解决以上问题。
为了解决多智能体容错控制一致性问题,相对于文献[19],本文的主要创新点和主要工作为:①在分布式一致性控制领域中,基于“领航者-跟随者”编队模型考虑多智能体中领航者模型的非线性和量化输入特性;②所设计的控制律不需要领航者的位置信息和速度信息以及任何自适应函数逼近器的信息补偿自身的故障所带来故障误差;③设计了一种离线情况下的自适应容错控制器,能够实现多智能体的横向距离误差减小70.58%,纵向距离误差减小87.09%,同时横向和纵向的动态收敛时间分别减小44.12%和25.85%。因此,所提出的控制方法能够对信号的扰动进行及时处理,并对故障后的编队系统进行实时补偿控制,达到快速编队运动的目的。
1 建立模型 1.1 图论一个加权无向图G= V, ε, A由非空顶点集V= {v1, v2, …, vN}和边缘集ε={eij=(vi, vj)}以及一个加权邻接矩阵A= aij N×N组成。其中,aij为非负元素,且aij>0,它是节点vi和vj之间的边,另外,当aij=0,表示节点vi和vj之间没有边。节点vi的邻边由Ni={vi∈V:(vi, vj)∈ε}指代。在图G中节点vi和vj之间的路径是一系列边vi1, vi2, vi2, vi3, …, (vil-1, vil)。如果图G是连通的,则图G中任何节点vi和vj,存在一条路径vi和vj(i, j=1, 2, …, N)[1]。
拉普拉斯矩阵L =[lij]∈RN×N定义为
| $ {l_{ij}} = \sum\limits_{j \ne i}^N {{a_{ij}}} \;\;\;\;{l_{ij}} = - {a_{ij}};i \ne j $ | (1) |
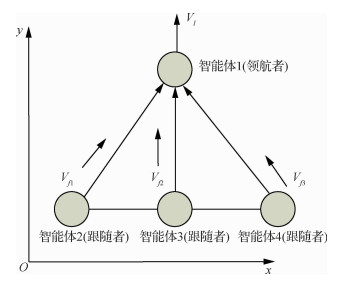
本文多智能体编队系统由4个智能体构成,其中智能体1作为领航者,其余智能体作为跟随者。同时,智能体1的速度方向作为编队前行方向,其余智能体紧跟其后。多智能体运动示意图,如图 1所示。
|
| 图 1 多智能体编队运动示意图 Fig. 1 Formation movement of multiple agents |
本文中,考虑了一组N(N=4)个具有相同特性的线性动力学智能体。第k个智能体的动态方程为
| $ \dot f\left( {{\mathit{\boldsymbol{x}}_k}\left( t \right)} \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_k}\left( t \right) + \mathit{\boldsymbol{Bu}}_k^{\rm{F}}\left( t \right) + g\left( {t,{\mathit{\boldsymbol{x}}_k}\left( t \right)} \right) $ | (2) |
式中:k=1, 2, …, N;xk∈Rn是状态变量,ukF∈Rm为输入量;A和B分别为常数矩阵;g(t, xk(t))表示第k个智能体的不确定性模型。
为了解决容错一致性问题,首先建立了故障模型。在本文中,考虑故障时的执行机构模型[22],其一致性控制协议为
| $ \mathit{\boldsymbol{u}}_k^{\rm{F}}\left( t \right) = {q_k}{\mathit{\boldsymbol{u}}_k}\left( t \right) $ | (3) |
式中:qk为未知执行器的故障因子,代表了第k个智能体的故障。
备注1 本文所设计的控制协议主要以执行机构故障为依据,协议中qk是智能体出现的故障因子,其大小反映故障大小的程度。每个智能体的故障因子均在两个常数范围之内,即
对于任意u∈R且ε>0[24],有
| $ 0 \le \left| u \right| - u\tanh \left( {\frac{u}{\varepsilon }} \right) \le k\varepsilon $ | (4) |
式中: k=0.2785。此外,对于Riccati方程,满足矩阵P正定,即
| $ \left( {\mathit{\boldsymbol{PA}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right) - \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{I}}_n} = {\bf{0}} $ | (5) |
式中:存在P正定且(A,B)是稳定的,同时他们之间的运算满足克罗内克积。In代表了N阶单位矩阵。1N∈RN指的是所有的列向量都为1。同时,令PB=Q。
令
| $ \begin{array}{l} \mathit{\boldsymbol{\dot z}} = \left( {\mathit{\boldsymbol{Q}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\mathit{\boldsymbol{\dot x}} = \left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{z}}\left( t \right) + \\ \;\;\;\;\;\left( {\mathit{\boldsymbol{M}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {\mathit{\boldsymbol{Q \boldsymbol{\varOmega} }}\left( t \right)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} + \\ \;\;\;\;\;\left( {\mathit{\boldsymbol{Q \boldsymbol{\varTheta} }} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{B}}} \right)f\left( {t,\mathit{\boldsymbol{x}}} \right) \end{array} $ | (6) |
式中:
为得到智能体的不确定模型,给出以下假设:
假设1 第k个智能体的不确定性:
| $ {\left[ {{g^1}\left( {t,{\mathit{\boldsymbol{x}}_k}(t)} \right),{g^2}\left( {t,{\mathit{\boldsymbol{x}}_k}(t)} \right), \cdots ,{g^m}\left( {t,{\mathit{\boldsymbol{x}}_k}(t)} \right)} \right]^{\rm{T}}} $ |
满足:
| $ \left\| {g\left( {t,{\mathit{\boldsymbol{x}}_k}(t)} \right)} \right\| \le {c_1}{\alpha _k} + {c_2}{\beta _k}\left\| {{\mathit{\boldsymbol{x}}_k}(t)} \right\| $ | (7) |
式中: αk和βk是未知常量,c1, c2∈ 0, 1是权重系数。
假设2 对于第k个智能体的故障因子qk存在2个已知的正常量
假设3 在智能体编队中,领航者和跟随者之间的通讯是通畅的。
2 控制器设计针对系统(2)中,领航者一旦出现故障,设计分布式自适应容错控制器能够有效快速地补偿故障影响,并完成预设的任务。其控制律为[25]
| $ {u_k} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\omega _k}\sum\limits_{j \in {N_k}} {{a_{kj}}} {\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right)^2} + {b_k}{u_{ak}} $ | (8) |
式中:bk为第k个智能体的权重系数,且当与邻近的智能体有信息交互,则bk=1,反之为零。
| $ \begin{array}{l} {u_{ak}} = - \tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2} \cdot } \right.\\ \;\;\;\;\;\left. {\mathit{\boldsymbol{\rho }}_B^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right].\\ \;\;\;\;\;\hat q_k^{ - 1}\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{x_k}} \right)} \right)\;\;\;\;\;l = 1,2, \cdots ,m \end{array} $ | (9) |
式中: ρBl∈Rn表示Riccati方程Q(PB=Q)矩阵的第l列,ωk∈R。uak用于补偿系统(5)中所提出的未知不确定扰动g(t, xk(t))对第k个智能体的影响。
备注2 式(8)中uak表示智能体故障补偿控制律。当领航者出现故障时,其模型的未知扰动项g(t, xk(t))为非线性函数,需要减小或消除这种未知扰动项,才能使系统快速达到稳定状态。
证明 令未知扰动项g(t, xk(t))=S1(非线性函数),控制项uk=S2(非线性函数)。
当多智能体中领航者出现故障时,自适应控制项uk必须满足以下关系:
| $ {u_k} = g\left( {t,{\mathit{\boldsymbol{x}}_k}\left( t \right)} \right) $ | (10) |
| $ {S_1} + {S_2} \cong 0 $ | (11) |
此时,所设计的控制协议能够减小或消除这种未知扰动。
备注3 控制协议中ωk表示第k个智能体的补偿控制增益。当第k个智能体发生故障时,通过测距传感器测量与之邻近的智能体之间的相对距离,进行实时智能体编队控制。
对于第k个智能体的一致协议增益更新率ωk为
| $ \begin{array}{l} {{\dot \omega }_k}\left( t \right) = - {d_{k1}}{\omega _k}\left( t \right) - {d_{k2}}{{\hat q}_k}{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)^2} \cdot \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} {{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|}^2}} \right) \end{array} $ | (12) |
式中: dk1、dk2为正常数。
式(12)中的参数
| $ \begin{array}{*{35}{l}} {{{\dot{\hat{q}}}}_{k}}=\text{Pro}{{\text{j}}_{\left[ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q}}}_{k}},{{{\bar{q}}}_{k}} \right]}}\left\{ {{{\hat{q}}}_{k}} \right\}= \\ \ \ \ \ \ \ \ \left\{ \begin{align} & 0\ \ {{\widehat{q}}_{k}}={{\underline{q}}_{k}}\And \ {{\overline{q}}_{k}}\le 0\ \ \ \\ & {{c}_{3}}{{\widehat{q}}_{kd}}\ \ \ 其他 \\ \end{align} \right. \\ \end{array} $ | (13) |
式中:
| $ \begin{array}{l} {{\hat q}_{kd}} = {\omega _k}\left( t \right){\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right|} \right)^2}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\\ \;\;\;\;\;\;\;{\left( {\sum\limits_{j \in {N_k}}^N {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)^2} - \\ \;\;\;\;\;\;\;\hat q_k^{ - 1}\sum\limits_{l = 1}^m {\left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2}} \right]\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + } \right.} \\ \;\;\;\;\;\;\;\left. {{c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{x_k}} \right)} \right)\tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat a}_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right] \end{array} $ | (14) |
其中:Proj{*}表示投影算子,参数
对于式(9)中第k个智能体的自适应更新参数
| $ \begin{array}{*{35}{l}} {{{\dot{\hat{\alpha }}}}_{k}}={{d}_{k2}}\left\{ \sum\limits_{l=1}^{m}{\left[ {{\left( \sum\limits_{j\in {{N}_{k}}}{{{a}_{kj}}}\left\| {{\mathrm{x}}_{k}}-{{\mathrm{x}}_{j}} \right\| \right)}^{2}} \right]\mathrm{ }\!\!\rho\!\!\text{ }_{\mathrm{B}}^{l}\cdot } \right. \\ \ \ \ \ \ \ \left. \left( 1-2\phi _{\mathrm{B}k}^{l}\left( t \right) \right) \right\}-{{d}_{k2}}{{{\hat{\alpha }}}_{k}}\left( t \right) \\ \end{array} $ | (15) |
| $ \begin{array}{l} {{\dot {\hat \beta} }_k} = {d_{k2}}\left[ {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2}} \mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l \cdot } \right.\\ \;\;\;\;\;\;\left. {\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l\left( t \right)} \right)} \right]{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right) - {d_{k1}}{{\hat \beta }_k}\left( t \right) \end{array} $ | (16) |
式中:
| $ \begin{array}{l} \phi _{\mathit{\boldsymbol{B}}k}^l\left( t \right) = \\ \;\;\;\;\;\;\;\min \left\{ {1 - sgn\left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2}\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l} \right],1} \right\} \end{array} $ | (17) |
式中:函数
1)
2)
该性质用于式(15)和式(16)参数的更新,为式(9)中自适应容错一致性控制器的设计提供理论支撑。在多智能体中,领航者出现故障后,所设计控制器能快速实现补偿,达到稳定状态的具体步骤为
步骤1 每个智能体的传感器用来感知和搜索邻近信息。
步骤2 每个智能体中的参数通常是更新的,这些参数根据式(15)和式(16)中的更新率来监测和调整。
步骤3 触发器能够使用这些参数去补偿式(9)中所控制的每一个智能体,最终使所有的智能体实现一致性的目的。
假设图G是连通的以及假设1和2成立,同时分布式自适应协议如式(9)所示,则对于一致性误差z,以及自适应参数
| $ \left\{ {z,{{\hat \alpha }_k},{{\hat \beta }_k},{{\hat \omega }_k},{{\hat q}_k}:W \le \sum\limits_{k = 1}^N {\frac{{{{\left( {{\alpha _k}} \right)}^2}}}{{2{d_{k1}}}}} + \sum\limits_{k = 1}^N {\frac{{{{\left( {{\beta _k}} \right)}^2}}}{{2{d_{k1}}}}} + \sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} + \sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar q}_k} - {{\underline q }_k}} \right)}^2}}}{{2{d_{k2}}}}} } \right\} $ | (18) |
构建李雅普诺夫函数,即
| $ \begin{array}{*{20}{c}} {V = \frac{1}{2}{\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{z}}(t) + \sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k1}}}}} + }\\ {\sum\limits_{k = 1}^N {\frac{{\tilde \alpha _k^2}}{{2{d_{k1}}}}} + \sum\limits_{k = 1}^N {\frac{{\tilde \beta _k^2}}{{2{d_{k2}}}}} + \sum\limits_{k = 1}^N {\frac{{\tilde q_k^2}}{{2{d_{k2}}}}} \ge 0} \end{array} $ | (19) |
式中:
对式(19)时间求导,有
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}})\mathit{\boldsymbol{\dot z}}(t) + \sum\limits_{k = 1}^N {\frac{{{{\left( {{{\dot \omega }_k}(t) + {{\dot {\bar \omega} }_k}} \right)}^2}}}{{{d_{k1}}}}} - \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\frac{{\tilde \alpha \dot {\tilde \alpha} }}{{{d_{k1}}}}} - \sum\limits_{k = 1}^N {\frac{{\mathit{\boldsymbol{\beta \dot {\tilde \beta} }}}}{{{d_{k2}}}}} - \sum\limits_{k = 1}^N {\frac{{\tilde q\dot {\tilde q}}}{{{d_{k2}}}}} \end{array} $ | (20) |
将式(6)代入式(20)可得
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}})\left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{z}}(t) + \left( {\mathit{\boldsymbol{M}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} \boldsymbol{\varOmega} }}(t)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} + \left( {\mathit{\boldsymbol{Q \boldsymbol{\varTheta} }} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{B}}} \right)f(t,\mathit{\boldsymbol{x}}) + \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\dot \omega }_k}(t) + {{\dot {\bar \omega} }_k}} \right)}^2}}}{{{d_{k1}}}}} - \sum\limits_{k = 1}^N {\frac{{\dot {\tilde \alpha} }}{{{d_{k1}}}}} - \sum\limits_{k = 1}^N {\frac{{\tilde \beta \dot {\tilde \beta} }}{{{d_{k2}}}}} - \sum\limits_{k = 1}^N {\frac{{\tilde q\dot {\tilde q}}}{{{d_{k2}}}}} \end{array} $ | (21) |
根据式(17)中ρBl和式(19)中
| $ \begin{array}{l} {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})f(t,\mathit{\boldsymbol{x}}) = \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {f_k^l\left( {{\mathit{\boldsymbol{x}}_k},t} \right)} \right) \le \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\mathit{\boldsymbol{\rho }}_B^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)\left( {{c_1}{\alpha _k} + {c_2}{\beta _k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) = {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\phi _\mathit{\boldsymbol{B}}}(t)} \right)G(t,\mathit{\boldsymbol{x}}) \end{array} $ | (22) |
由式(9)~式(22),可知:
| $ \begin{array}{l} {z^{\rm{T}}}(t)(\mathit{\boldsymbol{L \boldsymbol{\varTheta} }} \otimes \mathit{\boldsymbol{PB}}){u_{ak}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})f(t,\mathit{\boldsymbol{x}}) = {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L \boldsymbol{\varTheta} }} \otimes \mathit{\boldsymbol{PB}}){u_{ak}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}) \cdot \\ \;\;\;\;\;\;\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{B}}}(t)} \right) \times \hat G(t,\mathit{\boldsymbol{x}}) + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)( - \mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_B}(t)} \right)\hat G(t,\mathit{\boldsymbol{x}}) + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})f(t,\mathit{\boldsymbol{x}}) \le \\ \;\;\;\;\;\;{\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L \boldsymbol{\varTheta} }} \otimes \mathit{\boldsymbol{PB}}){u_{ak}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{B}}}(t)} \right)\hat G(t,\mathit{\boldsymbol{x}}) - {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{B}}}(t)} \right) \cdot \\ \;\;\;\;\;\;(\hat G(t,\mathit{\boldsymbol{x}}) - G(t,\mathit{\boldsymbol{x}})) = \sum\limits_{k = 1}^N {{\theta _k}} \sum\limits_{l = 1}^m {\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {u_{\omega k}^l} \right)} - \sum\limits_{k = 1}^n {{\theta _k}} \sum\limits_{l = 1}^n {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} \mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + } \right.\\ \;\;\;\;\;\;\;\left. {{c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)\left\{ { - \tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right]} \right\} + \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)\left\{ { - \tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^L\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right]} \right\} + \\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^L\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)( - \mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}) \cdot \\ \;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_B}(t)} \right)(\hat G(t,\mathit{\boldsymbol{x}}) - G(t,\mathit{\boldsymbol{x}})) \end{array} $ | (23) |
式中:
当
| $ \begin{array}{l} \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \cdot \\ \;\;\;\;\;\left\{ { - \tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2} \cdot } \right.} \right.\\ \;\;\;\;\;\left. {\left. {\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right]} \right\} + \\ \;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\mathit{\boldsymbol{\rho }}_B^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) = \\ \;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {\left\| {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l} \right\|} } \cdot \\ \;\;\;\;\;\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) - \\ \;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \cdot \\ \;\;\;\;\;\left( { - \tanh \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2} \cdot } \right.} \right.\\ \;\;\;\;\;\left. {\left. {\mathit{\boldsymbol{\rho }}_B^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right]} \right) \le \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m \varepsilon } (t)k \end{array} $ | (24) |
式(24)中不等式源于克罗内积性质,即用
当
| $ \begin{array}{l} \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) - \\ \;\;\;\;\;\;\tanh {\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} {z_k} - {z_j}} \right)^2} \cdot \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \le 0 \end{array} $ | (25) |
| $ \begin{array}{l} \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)} } \cdot \\ \;\;\;\;\;\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \le 0 \end{array} $ | (26) |
根据不等式(24)~(26),可得
| $ \begin{array}{l} \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \cdot \\ \;\;\;\;\;\;\left[ { - \tanh {{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2} \cdot } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right] + \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}} } \cdot \\ \;\;\;\;\;\;\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)\left( {{c_1}{{\hat \alpha }_k} + {c_2}{{\hat \beta }_k}{\mu _k}\left( {t,{\mathit{\boldsymbol{x}}_k}} \right)} \right) \le \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m \varepsilon } (t)k \end{array} $ | (27) |
考虑式(23)中
| $ \begin{array}{l} {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)\left( {\mathit{\boldsymbol{L \boldsymbol{\varTheta} \boldsymbol{\varOmega} }}(t)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} + \sum\limits_{k = 1}^N {\frac{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right){{\dot \omega }_k}}}{{{d_{k2}}}}} = {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)\left( {\mathit{\boldsymbol{L \boldsymbol{\varTheta} \boldsymbol{\varOmega} }}(t)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} - \sum\limits_{k = 1}^N {\left( {{\omega _k}(t) + } \right.} \\ \;\;\;\;\;\;\;\left. {{{\bar \omega }_k}} \right){{\hat q}_k}\left\{ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left[ {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left( {{z_k} - {z_j}} \right)} \right]} \right\} + \sum\limits_{k = 1}^N {\left( {{q_k}{\omega _k}(t)} \right)} \left\{ {{{\left[ {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left( {\left| {{z_k} - {z_j}} \right|} \right)} \right]}^2} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left( {\left| {{z_k} - {z_j}} \right|} \right)} \right)} \right\} - \sum\limits_{k = 1}^N {\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right){{\hat q}_k} \cdot \left\{ {{{\left[ {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left( {\left| {{z_k} - {z_j}} \right|} \right)} \right]}^2} \cdot } \right.} \\ \;\;\;\;\;\;\left. {\;\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left[ {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left( {\left| {{z_k} - {z_j}} \right|} \right)} \right]} \right\} + \left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} + \left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;\;\left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} = \sum\limits_{k = 1}^N {\left( { - \left( {{{\hat q}_k} - {q_k}} \right){\omega _k}(t)} \right)} \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\sum\limits_{j \in {N_k}}^N {{a_{kj}}\left| {{z_k} - {z_j}} \right|} } \right] + \\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^N {\left( { - {{\hat q}_k}{{\bar \omega }_k}} \right)} \left[ {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right)}^2}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\sum\limits_{j \in {N_k}}^N {{a_{kj}}} \left| {{z_k} - {z_j}} \right|} \right] + \left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} + \\ \;\;\;\;\;\;\;\left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - \left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} \end{array} $ | (28) |
结合不等式(23)和(27),代入式(13)中的更新律,可以得到
| $ \sum\limits_{k = 1}^N {\left( {{{\hat q}_k} - {q_k}} \right)} \left( { - {{\hat q}_k}} \right) + \sum\limits_{k = 1}^N {\frac{{\left( {{{\hat q}_k} - {q_k}} \right)}}{{{d_{k2}}}}} \le 0 $ | (29) |
进一步,可得
| $ \begin{array}{l} {\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\left( {\mathit{\boldsymbol{L \boldsymbol{\varTheta} \boldsymbol{\varOmega} }}(t)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} + \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\frac{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right){{\dot \omega }_k}}}{{{d_{k2}}}}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}(t)(\mathit{\boldsymbol{L \boldsymbol{\varTheta} }} \otimes \mathit{\boldsymbol{PB}}) \le \\ \;\;\;\;\;\;{u_{ak}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}}} \right)f(t,\mathit{\boldsymbol{x}}) + \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\frac{{{{\tilde q}_k}{{\dot {\tilde q}}_k}}}{{{d_{k2}}}}} \le \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m \varepsilon } (t)k + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{z}}^{\rm{T}}}(t)( - \mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{PB}})\left( {{\mathit{\boldsymbol{I}}_{mN}} - 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{B}}}(t)} \right) \cdot \\ \;\;\;\;\;\;\;(\hat G(t,\mathit{\boldsymbol{x}}) - G(t,\mathit{\boldsymbol{x}})) + \\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^N {\left( { - {{\hat q}_k}{{\bar \omega }_k}} \right)} \times \left( {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {\sum\limits_{j \in {N_k}}^N {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right) + \\ \;\;\;\;\;\;\;\left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} + \\ \;\;\;\;\;\;\;\;\left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - \left( { - {d_{k2}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} \end{array} $ | (30) |
将参数
| $ \begin{array}{l} \sum\limits_{k = 1}^N {\frac{{{{\tilde \alpha }_k}{{\dot {\tilde \alpha} }_k}}}{{{d_{k2}}}}} = \sum\limits_{k = 1}^N {\frac{{\left( {{{\hat \alpha }_k}(t) - {\alpha _k}} \right)\left( { - {k_{\alpha k}}} \right){{\hat \alpha }_k}(t)}}{{{d_{k2}}}} \cdot } \\ \;\;\;\;\;\;\left[ {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2}} \mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)} \right] = \\ \;\;\;\;\;\;\left( { - {k_{\alpha k}}} \right)\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \alpha }_k}(t) - {\alpha _k}} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;{k_{\alpha k}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \alpha }_k}(t)} \right)}^2}}}{{2{d_{k2}}}}} + {k_{\alpha k}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{\alpha _k}} \right)}^2}}}{{2{d_{k2}}}}} + \\ \;\;\;\;\;\;\sum\limits_{k = 1}^N {\left( {{{\hat \alpha }_k}(t) - {\alpha _k}} \right)} \left[ {\sum\limits_{l = 1}^m {{{\left( {\sum\limits_{j \in {N_k}} {{a_{kj}}} \left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right)}^2} \cdot } } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{\rho }}_\mathit{\boldsymbol{B}}^l\left( {1 - 2\phi _{\mathit{\boldsymbol{B}}k}^l(t)} \right)} \right] \end{array} $ | (31) |
通过选择足够大的ω满足2ωλi≥1(i=2, 3, …, N), 同时根据式(5),可以得到
| $ \begin{array}{l} \frac{1}{2}\left[ {\left( {\mathit{\boldsymbol{PA}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right) - 2\omega {\lambda _i}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right] \le \\ \frac{1}{2}\left[ {\left( {\mathit{\boldsymbol{PA}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right] = - \frac{1}{2}{\mathit{\boldsymbol{I}}_n} \end{array} $ | (32) |
令ζ=1/λmax(P),同时选择kαk=ζ,kβk=ζ,其可以进一步简化为
| $ \begin{array}{l} \dot V \le - \zeta V - \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^m \varepsilon } (t)k - {d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;{d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - {d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;\zeta \left[ {\sum\limits_{k = 1}^N {\frac{{{{\left( {{\omega _k}(t) + {{\bar \omega }_k}} \right)}^2}}}{{2{d_{k2}}}}} + \sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \alpha }_k}} \right)}^2}}}{{2{d_{k2}}}}} + } \right.\\ \;\;\;\;\;\;\left. {\sum\limits_{k = 1}^N {\frac{{{{\left( {{\beta _k}} \right)}^2}}}{{2{d_{k2}}}}} + \sum\limits_{k = 1}^N {\frac{{\tilde \theta _k^2}}{{2{d_{k2}}}}} } \right] - \\ \;\;\;\;\;\;{d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \alpha }_k}(t) - {\alpha _k}} \right)}^2}}}{{2{d_{k2}}}}} - {d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \alpha }_k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;{d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{\alpha _k}} \right)}^2}}}{{2{d_{k2}}}}} - {d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \beta }_k}(t) - {\beta _k}} \right)}^2}}}{{2{d_{k2}}}}} - \\ \;\;\;\;\;\;{d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{{\hat \beta }_k}(t)} \right)}^2}}}{{2{d_{k2}}}}} - {d_{k2}}\sum\limits_{k = 1}^N {\frac{{{{\left( {{\beta _k}} \right)}^2}}}{{2{d_{k2}}}}} \end{array} $ | (33) |
根据所设置的参数,可得
根据式(6)误差动力学,当多智能体中领航者出现故障时,有
证明 由式(3)可知,智能体故障模型控制协议如下:
| $ u_k^{\rm{F}}(t) = {m_k}{q_k}{u_k}(t) $ | (34) |
式中:mk为正常数。
假设故障因子qk=a(a为常数),则误差动力学模型,可进一步化简为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot z}} = \left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{z}}(t) + \left( {\mathit{\boldsymbol{M \boldsymbol{\varTheta} \boldsymbol{\varOmega} }}(t)\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{z}} + }\\ {(\mathit{\boldsymbol{M \boldsymbol{\varTheta} }} \otimes \mathit{\boldsymbol{B}}){u_{ak}} + (M \otimes \mathit{\boldsymbol{B}})f(t,\mathit{\boldsymbol{x}})} \end{array} $ | (35) |
当多智能体经过时间t,达到既定的队形并保持,则误差z等于零,即z=0。因此,式(35)可简化为
| $ \mathit{\boldsymbol{\dot z}} = {\bf{0}} $ | (36) |
可得,
在本文中,多智能体编队由4个智能体构成,他们具有相同的特性。为了验证所设计分布式自适应容错方法在领航者出现故障的情况下多智能体编队运动的有效性和稳定性,本文基于系统模型(2)进行数值仿真。同时将文献[19]和本文所提出的方法进行对比分析,进一步验证所提方法的优势所在。根据图 1,本文考虑具有4个节点的多智能体系统,同时模型(2)系统矩阵A∈R4×4,B∈R4×2。
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 2.9}&{0.3}&{0.4}&{1.2}\\ { - 0.1}&{ - 0.2}&{0.6}&{1.5}\\ {1.2}&{2.1}&{ - 2.8}&{3.4}\\ 1&{ - 2}&{ - 2.5}&{ - 2.5} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ { - 1}&{0.5}\\ { - 0.1}&{0.2} \end{array}} \right] $ |
根据图论,可得多智能体编队系统的拉普拉斯矩阵L,即
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {2.168}&{ - 1.037}&0&{ - 0.266}\\ { - 1.037}&{1.037}&0&0\\ 0&0&{1.651}&0\\ { - 0.266}&0&0&{0.613} \end{array}} \right] $ | (37) |
采用MATLAB解式(5),可得矩阵P,即
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.1584}&{0.0213}&{0.0021}&{0.1254}\\ {0.0254}&{0.7852}&{0.0079}&{0.2351}\\ {0.0010}&{0.2321}&{0.2136}&{ - 0.3985}\\ {0.1236}&{0.2531}&{ - 0.2154}&{0.4021} \end{array}} \right] $ | (38) |
考虑多智能体编队系统出现故障,即
| $ g\left( {{\mathit{\boldsymbol{x}}_i}(t),t} \right) = {\left[ {\begin{array}{*{20}{l}} {{\alpha _{li}} + {\beta _{fi}}\sin (t){x_{i1}}}\\ {{\alpha _{li}} + {\beta _{fi}}\cos (t){x_{i2}}} \end{array}} \right]^{\rm{T}}} $ | (39) |
式中:αli表示领航者的故障系数,(αl1, αl2, αl3, αl4)= 0.214,0,0,0,0,βfi表示跟随者的故障系数,(αf1, αf2, αf3, αf4)=(0.3452, 0.5474, 0.3214, 0)。同时,考虑多智能体模型容错参数估计,即
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar q}} = {\left[ {\begin{array}{*{20}{c}} {0.2548}&{1.3265}&{1.3321}&{1.3362} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{\underline q}} = {\left[ {\begin{array}{*{20}{l}} {0.532}&1&{0.8654}&{0.8562}&{0.7948} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (40) |
其他初始值为
| $ \mathit{\boldsymbol{\alpha }} = {\left[ {\begin{array}{*{20}{c}} {0.3215}&{0.8021}&{0.0265}&{0.5231} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\beta }} = {\left[ {\begin{array}{*{20}{c}} {0.4168}&{0.3654}&{0.2920}&{0.4321} \end{array}} \right]^{\rm{T}}} $ |
| $ k = 1,2,3,4,\zeta = 1/{\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right) = 1.0811 $ |
| $ {\mathit{\boldsymbol{x}}_1}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {1.5211}&{0.3254}&{1.5211}&{1.8521} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{x}}_2}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {0.3254}&{1.5214}&{1.5218}&{2.2144} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{x}}_3}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {1.5214}&{0.3214}&{1.3254}&{2.9514} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{x}}_4}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {2.6254}&{0.2364}&{1.4215}&{3.2143} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\hat \alpha }} = {\left[ {\begin{array}{*{20}{c}} {0.2125}&{1.0214}&{0.0265}&{0.5231} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\hat \beta }} = {\left[ {\begin{array}{*{20}{c}} {0.7452}&{1.8865}&{1.9652}&{0.7321} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\omega }}\left( 0 \right) = {\left[ {\begin{array}{*{20}{c}} {0.36214}&{0.8562}&{0.3421}&{1.2154} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\hat q}}\left( 0 \right) = {\left[ {\begin{array}{*{20}{l}} {1.0521}&{1.3247}&{0.8542}&{0.9635} \end{array}} \right]^{\rm{T}}} $ |
基于以上的假设和初始条件,对所提出方法在多智能体编队的运动收敛性进行分析。其仿真结果如图 2~图 4所示。
|
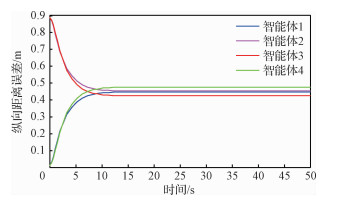
| 图 2 纵向距离误差曲线 Fig. 2 Curves of longitudinal distance error |
|
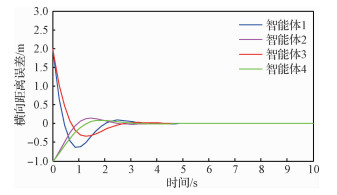
| 图 3 横向距离误差曲线 Fig. 3 Curves of lateral distance error |
|
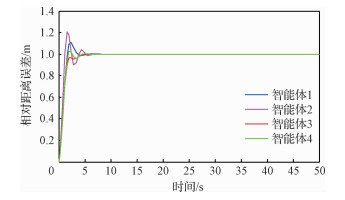
| 图 4 “领航-跟随”相对距离误差曲线 Fig. 4 Curves of relative distance error for "leader-follower" |
图 2给出了多智能体纵向距离误差曲线图。由图可知,随着时间变化,该曲线呈现出一种智能体2和3缓慢下降,智能体1和4缓慢上升,之后均趋于稳定状态。0~10 s,智能体2和3在前,智能体1和4在后,并追赶智能体2和3。在领航者出现故障后,自适应算法启动,智能体2和3减速,智能体2和4加速,使得他们与期望位置的误差逐渐减小至稳定状态;10 s后,多智能体编队系统按照“领航者-跟随者”编队模式运动。
图 3给出了多智能体横向距离误差曲线图。由图可知,随着时间变化,该曲线呈现一种智能体1和3快速下降,智能体2和4缓慢上升,且智能体2和4小幅振荡,之后均趋于稳态。在1 s时,智能体1和3的横向距离误差已达到最小,此时智能体2和4基本趋于零,这是由于智能体1在0.9 s时出现故障,此时自适应容错算法立刻启动,该曲线缓慢上升并迅速趋于稳定;在3 s之后,4个智能体横向距离误差收敛于零,保持预设的队形运动。
图 4给出了“领航者-跟随者”智能体编队系统的相对距离误差曲线图。由图可知,随着时间的变化,该曲线呈现一种先快速上升,然后小幅振荡直至趋于稳态的趋势。在0.9 s之前,曲线呈现一种快速上升,这是由于跟随者以不同的速度追踪领航者,智能体间的距离增大;在领航者出现故障后,该曲线呈现波动趋势,这是由于在0.9 s之后智能体处于从即将到达预设的队形到期望的队形之间的微调整阶段,即领航者需保持速度,而跟随者需减速;在5 s之后,曲线趋于稳定状态,并4个智能体的速度和相对位置保持一致。
4.2 鲁棒性分析为了进一步验证所提出自适应控制方法的鲁棒性,本节采用相同参数进行仿真研究。由于多智能体编队在平面内运动,本节针对所设计的分布式自适应容错方法在横向和纵向因领航者出现故障补偿后的跟随者的追踪距离误差进行对比分析,如图 5~图 7所示。
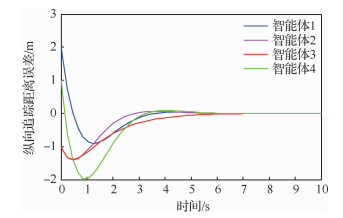
|
| 图 5 智能体纵向追踪距离误差收敛图 Fig. 5 Convergence diagram of longitudinal tracking distance error of agent |

|
| 图 6 “领航-跟随”编队偏航角指令曲线 Fig. 6 Command curves of yaw angle of "leader- follower" formation |

|
| 图 7 多智能体偏航角速率曲线 Fig. 7 Curves of multi-agent yaw angle rate |
图 5给出了智能体纵向追踪距离误差曲线图。由图可知,随着时间的变化,该曲线呈现一种先快速下降,而后缓慢上升,直到稳定状态。在0.9 s之前,该曲线呈现快速下降趋势,这是由于他们的初始位置和速度均不相等,在集结过程中,他们之间的纵向距离逐渐缩小,且智能体4的速度减小最大;在1~3.5 s,曲线呈现缓慢上升,这是由于领航者出现故障,自适应算法启动后,智能体达到预设的队形之前处于微调整阶段,而且跟随者几乎收敛于领航者的飞行轨迹。在6 s之后,多智能体之间的相对位置和速度保持一致同时确保避障。
图 6给出了“领航者-跟随者”编队系统的偏航角指令曲线。由图可知,随着时间的变化,该曲线呈现先快速上升,后小幅振荡直至稳定状态。在多智能体编队系统运动过程中,因领航者出现故障,为了补偿或者消除这种故障影响,所提出的分布式自适应容错控制算法可以确保在故障情况下,正常编队运动。在0.9~3 s之前,领航者在前,跟随者在其后,跟随者追踪领航者过程中,速度方向指向领航者,此时偏航角增大。智能体1的偏航角达到1.4°,即将达到预设队形,此时需减小偏航角防止发生碰撞;在4~10 s,4个智能体处于即将达到预设队形微调整阶段,此时领航者减小,保持一个常值,其余跟随者微调其偏航角保持预设队形运动;在12 s之后,4个智能体处于稳定状态。
图 7给出了多智能体偏航角速率曲线图。随着时间的变化,该曲线呈现一种快速上升后,趋于稳定状态。在集结预设编队之前,智能体编队系统缩小之间的相对距离;在即将达到预设队形时进行微调整,然后保持速度和相对位置的一致性稳定运动。由图 7可知,4个智能体的偏航角速率的变化量分别是0.43、0.11、0、0.10 (°)/s,稳态所需时间分别为5、4.2、4.21、2.5 s。易得,在0.9 s,智能体1为领航者出现故障,此时所设计的容错控制算法启动,使其在2 s调整至正常运动状态,直至6 s后保持一致协同编队运动。
从以上分析可知,多智能体编队系统中领航者出现故障时,所提出的分布式自适应容错控制方法能够补偿故障带来的损失,保持系统正常运行。而且,该方法动态响应快,追踪误差效果好。
4.3 可行性分析为了进一步验证所提出方法的可行性和优势性,本节采用相同的系统模型,初始条件以及相关参数,将所提出的方法和文献[19]在横向距离误差和纵向距离误差以及达到稳定所需的收敛时间进行对比分析,仿真结果如图 8和图 9所示。

|
| 图 8 横向距离误差对比 Fig. 8 Comparison of lateral distance errors |

|
| 图 9 纵向距离误差对比 Fig. 9 Comparison of longitudinal distance errors |
图 8给出了多智能体横向距离误差对比曲线图。由图可知,随着时间变化,文献[19]中的方法的横向距离误差曲线呈现一种先迅速上升,后缓慢下降直至趋于稳态,而本文所提出的方法的横向距离误差曲线呈现一种迅速上升后趋于稳态。同时,文献[19]和本文方法的横向距离误差分别为0.17、0.05 m;相应的达到平衡状态所需时间分别为3.4、1.9 s,由此可知本文所提的控制方法,稳态误差小,动态响应快,有利于容错补偿控制。
图 9给出了多智能体纵向距离误差对比曲线图。文献[19]所提方法的纵向距离误差曲线,随着时间变化,呈现一种快速上升,然后缓慢下降,之后又小幅震荡,直至缓慢达到稳定状态,而本文所提出的控制方法的纵向距离误差曲线呈现缓慢上升后迅速达到稳定状态。文献[19]和本文方法纵向距离误差分别为0.31和0.04 m,相对应达到稳态的时间分别为32.5和24.1 s,显然易知,本文所提出的控制方法,不但可以使领航者受损的多智能体编队系统恢复正常的运动状态,而且能够快速达到预定的队形,同时保持队形不变。
根据文献[19]和本文所提出的方法对应的横、纵向距离误差以及相对应收敛时间,将其汇总,如表 1所示。
由表 1可知,本文所提出的方法不仅在横向距离误差小,响应时间短,而且在纵向距离误差更小,响应时间更短,对于多智能编队系统的容错补偿更有利。
基于一致性理论,本文提出一种分布式自适应容错控制方法,该方法采用李雅普诺夫稳定性理论对其进行了证明,并通过数值仿真实验验证了该方法的收敛性和鲁棒性。主要结论如下:
1) 本文故障形式有一定的限制,即
2) 如果多智能体故障发生在集结预设队形之后,通过本文相关理论推导,易知多智能系统是稳定的,即使发生故障,所提出的方法也不能实现容错控制。因此,本文所研究的被控对象有相应的约束条件。
3) 本文是以多智能体最小研究单元作为被控对象,即4个智能体,并采用所提出的方法进行容错控制。同时所提出的方法适用于数目小于10的多智能体编队。
然而,本文仅考虑多智能体从不同起点以不同速度出发到集结预设队形过程中容错控制,每个智能体视为质点处理,未考虑测距传感器的精确等,下一步工作将在缩比模型上进行试验以验证所设计的控制方法的可控性和有效性。
| [1] |
成浩浩, 齐晓慧, 杨森, 等. 一种基于一致性的四旋翼无人机编队避障方法[J]. 飞行力学, 2019, 37(2): 51-55. CHENG H H, QI X H, YANG S, et al. A method for obstacle avoidance of consistency based quadrotor UAV formation[J]. Flight Dynamics, 2019, 37(2): 51-55. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [2] |
易文, 雷斌. 基于一致性的无人机编队飞行几何构型控制[J]. 武汉科技大学学报, 2019, 42(2): 150-155. YI W, LEI B. Consensus-based control method for geometrical configuration of UAVs formation flight[J]. Journal of Wuhan University of Science and Technology, 2019, 42(2): 150-155. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [3] | LIU X, ZHANG K, XIE W C. Consensus seeking in multi-agent systems via hybrid protocols with impulse delays[J]. Nonlinear Analysis:Hybrid Systems, 2017, 25: 90-98. |
| Click to display the text | |
| [4] | JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001. |
| Click to display the text | |
| [5] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. |
| Click to display the text | |
| [6] |
乔琳, 邓彦松, 田晓亮. 基于一致性理论的多机器鱼编队控制[J]. 兵工自动化, 2011, 30(12): 70-74. QIAO L, DENG Y S, TIAN X L. Formation control of multiple robot fish based on consensus theory[J]. Ordnance Industry Automation, 2011, 30(12): 70-74. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [7] |
王冶.多智能体编队控制方法研究[D].哈尔滨: 哈尔滨工业大学, 2012. WANG Y. Research on formation control methods for multi-agent[D]. Harbin: Harbin Institute of Technology, 2012 (in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [8] |
王超瑞.基于信息一致性理论的无人机编队控制算法研究[D].哈尔滨: 哈尔滨工业大学, 2017. WANG C R. UAV formation control algorithm based on information consistency theory[D]. Harbin: Harbin Institute of Technology, 2017 (in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [9] |
吴亚霄.基于一致性理论的多导弹协同制导研究[D].哈尔滨: 哈尔滨工业大学, 2017. WU Y X. Research on cooperative guidance for multi-missile based on consensus protocols[D]. Harbin: Harbin Institute of Technology, 2017 (in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [10] |
郝然, 艾芊, 朱宇超. 基于多智能体一致性的能源互联网协同优化控制[J]. 电力系统自动化, 2017, 41(15): 10-17. HAO R, AI Q, ZHU Y C. Cooperative optical control of energy internet based on multi-agent consistency[J]. Automation of Electric Power Systems, 2017, 41(15): 10-17. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [11] | XU S, HO D W C, LI L. A distributed event-triggered scheme for discrete-time multi-agent consensus with communication delays[J]. IET Control Theory & Applications, 2014, 8(10): 830-837. |
| Click to display the text | |
| [12] |
李杨, 徐峰, 谢光强, 等. 多智能体技术发展及其应用综述[J]. 计算机工程与应用, 2018, 54(9): 13-21. LI Y, XU F, XIE G Q, et al. Survey of development and application of multi-agent technology[J]. Computer Engineering and Applications, 2018, 54(9): 13-21. (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [13] | GAO Z, DING S X. State and disturbance estimator for time-delay systems with application to fault estimation and signal compensation[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5541-5551. |
| Click to display the text | |
| [14] | GAO Z, DING S X. Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems[J]. Automatica, 2007, 43(5): 912-920. |
| Click to display the text | |
| [15] | ZUO Z, HO D W C, WANG Y. Fault tolerant control for singular systems with actuator saturation and nonlinear perturbation[J]. Automatica, 2010, 46(3): 569-576. |
| Click to display the text | |
| [16] | JIANG B, STAROSWIECKI M, COCQUEMPOT V. Fault accommodation for nonlinear dynamic systems[J]. IEEE Transactions on Automatic Control, 2006, 51(9): 1578-1583. |
| Click to display the text | |
| [17] | MAO Z, JIANG B, SHI P. Fault-tolerant control for a class of nonlinear sampled-data systems via a Euler approximate observer[J]. Automatica, 2010, 46(11): 1852-1859. |
| Click to display the text | |
| [18] |
邢小军, 陈潇然, 黄龙亮, 等. 面向执行机构故障的四旋翼无人机主动容错飞行控制方法研究[J]. 西北工业大学学报, 2018, 36(4): 748-753. XING X J, CHEN X R, HUANG L L, et al. Study on active fault tolerant flight control systems for quadrotor UAV with actuator failures[J]. Journal of Northwestern Polytechnical University, 2018, 36(4): 748-753. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [19] | YOO S J. Distributed low-complexity fault-tolerant consensus tracking of switched uncertain nonlinear pure-feedback multi-agent systems under asynchronous switching[J]. Nonlinear Analysis Hybrid Systems, 2019, 32: 239-253. |
| Click to display the text | |
| [20] |
陈胜强.执行器故障下的四旋翼无人机容错控制方法研究[D].长春: 长春工业大学, 2018. CHEN S Q. Research on the fault tolerant control method of the quad-rotor under the actuator faults[D]. Changchun: Changchun University of Technology, 2018 (in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [21] |
张平.执行器故障下四旋翼无人机容错控制研究[D].燕山: 燕山大学, 2018. ZHANG P. Research on actuator fault-tolerant control of quad-rotor UAV[D]. Yanshan: Yanshan University, 2018 (in Chinese). |
| [22] | GHOMMAM J, LUQUE-VEGA L F, CASTILLO-TOLEDO B, et al. Three-dimensional distributed tracking control for multiple quadrotor helicopters[J]. Journal of the Franklin Institute, 2016, 353(10): 2344-2372. |
| Click to display the text | |
| [23] | LI D, ZHANG W, HE W, et al. Two-layer distributed formation-containment control of multiple Euler-Lagrange systems by output feedback[J]. IEEE Transactions on Cybernetics, 2018, 49(2): 675-687. |
| Click to display the text | |
| [24] | ZHANG X, WANG F, ZHANG L. Finite time controller design of nonlinear quantized systems with nonstrict feedback form[J]. International Journal of Control, Automation and Systems, 2019, 17(1): 225-233. |
| Click to display the text | |
| [25] | CHEN S, HO D W C, LI L, et al. Fault-tolerant consensus of multi-agent system with distributed adaptive protocol[J]. IEEE Transactions on Cybernetics, 2014, 45(10): 2142-2155. |
| Click to display the text |



