在工程复杂外形的CFD模拟过程中,存在着多种来源的不确定性输入,包括计算网格、湍流模型和数值格式等[1-2],这使得最终的模拟结果也有不可忽视的不确定性。在工程外形的性能评估和优化设计、CFD与试验数据的相互确认等过程中,需要考虑CFD结果的不确定性,这样才能更为准确地评价设计外形能否满足性能需求,优化过程是否有效可靠。因此CFD结果的不确定性量化研究受到越来越广泛和持续的关注。
蒙特卡洛(Monte Carlo,MC)方法[3]构造简单、易于实现,是一种被广泛使用的不确定性量化方法。但是MC方法收敛速度慢,计算开销巨大,需要大量的采样点计算才能得到精度满足要求的结果,因此限制了其在多变量不确定性量化问题中的应用。多项式混沌(Polynomial Chaos,PC)方法[4-6]是一种更加高效的不确定性量化方法。Wiener[7]在研究湍流问题中随机变量的谱空间展开时提出了各向同性混沌理论,这也被认为是PC方法的起源。Ghanem和Spanos[8]在分析固体力学中的不确定性问题时将该方法应用到有限元计算中。Xiu和Karniadakis[9]将适合高斯随机过程的Hermite PC推广到Wiener-Askey PC,适用于满足更一般概率密度分布的随机过程。基于PC方法的不确定性量化已经有了很多成功的应用[10-16]。
PC展开的项数随着输入变量的维数和展开阶数的增加呈几何级数式急剧增加,导致“维数灾难”现象产生,这限制了PC在多变量不确定性量化问题中的应用。近些年来,各国学者们尝试了更加高效的方法,包括自适应方法[17-19]、稀疏重构方法[20-21]和减基法[22-23]等,以此来降低随机空间的维数。计算表明这些方法与完整的PC方法相比确实能够在相对较小的计算成本下产生精度大体相当的结果。本文主要研究了稀疏多项式混沌方法。在包含多输入变量的随机问题中,经常会遇到目标响应的展开是稀疏的情况[24-25],展开中占主导的通常是独立的输入变量和变量之间的低阶交叉项,某些自由度的量值可能非常小,完全可以舍去,这也是稀疏多项式混沌方法能够成功应用的前提。Blatman和Sudret[20]使用稀疏效应准则,提出了一种双曲算法来截断PC展开。后来信号处理领域的稀疏感知算法被用来重构稀疏的PC展开[26-32]。该算法的效率取决于PC展开的稀疏性或者说是展开式中自由度的衰减程度。
本文发展了非嵌入式的稀疏多项式混沌方法,提出了一种截断误差设定方法,并在湍流模型系数不确定性传播和炭化材料烧蚀热响应模拟不确定性分析中开展了应用研究。文章首先介绍了基于1范数最小的稀疏重构算法,然后对两个算例进行了分析研究,最后给出了研究结论。
1 稀疏PC展开PC方法将整个数值模拟过程看作是一个随机过程,根据随机输入参数的概率密度分布,选择对应的正交基函数序列,然后将该随机过程的输出在基函数空间中展开。通过嵌入式或者非嵌入式方法,确定PC展开式中的自由度,从而得到输出的各种统计信息,包括平均值、方差以及每个输入变量的全局敏感性等。
假定随机的输入变量ξ,满足某种概率密度分布f(ξ)。对于任意的随机输出变量y,可以在输入变量ξ的正交基函数序列构成的谱空间中展开,即
| $y=\sum\limits_{j=0}^{p} \alpha_{j} \psi_{j}(\xi) $ | (1) |
式中:αj为待求的展开式自由度;ψj为确定的随机变量的基函数。
在回归法中,通过确定性的CFD计算得到采样点{ξ1, ξ2, …, ξN}对应的响应值为{y1, y2, …, yN}。通常情况下,采样点的数目大于PC展开中自由度的个数,因此形成了一个关于自由度的超定方程组:Ψα=Y,其中Ψ是测量矩阵,Ψij=ψj(ξi),α是自由度组成的向量,Y是响应值组成的向量。PC方法更详细的介绍可以参考文献[6]。
压缩感知(Compressed Sensing,CS)方法是图像和信号处理领域兴起的新方法,能够高效地重构稀疏信号,需要的采样点数目小于自由度的个数。CS通过选择有限个对系统输出影响较大的基函数,实现由不完全的观测样本准确或者近似准确地还原稀疏信号。如果PC展开是稀疏的,即自由度非零的个数是有限的,可以通过求解P0优化问题得到完整的展开,即
| $\hat \alpha = \arg \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_0}\quad {\rm{s}}.{\rm{t}}.\quad \mathit{\boldsymbol{ \boldsymbol{\varPsi} \alpha }} = \mathit{\boldsymbol{Y}} $ | (2) |
式中:0范数表示α中非零元素的个数。然而P0优化问题中的目标函数是非凸函数,这是一个NP-hard问题,在实际中很难求解[33]。为此将P0优化问题转化为凸松弛的P1优化问题,即
| $\hat \alpha = \arg \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}\quad {\rm{s}}.{\rm{t}}.\quad \mathit{\boldsymbol{ \boldsymbol{\varPsi} \alpha }} = \mathit{\boldsymbol{Y}} $ | (3) |
结果表明基于1范数最小的算法能够有效地处理拥有有限个非零自由度的PC展开问题。
在实际应用中,考虑到测量噪声的情况下,不要求约束Ψα=Y精确满足。因此得到了有噪声信号的P1优化问题:
| $\hat \alpha = {\mathop{\rm argmin}\nolimits} {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}\quad {\rm{s}}{\rm{.t}}{\rm{.}}\quad {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} \alpha - Y}}} \right\|_2} \le \varepsilon $ | (4) |
在求解过程中,需要指定截断误差ε。ε的设定对于稀疏PC重构的精度十分关键。如果ε设置得过大,则重构的PC不够准确;如果ε设置得过小,则重构的PC有可能出现过拟合现象。ε的设定可以认为是模型评估和选择问题。本文通过机器学习中常用的交叉验证方法得到较优的截断误差设定。具体做法为:首先给定有限个初选的截断误差,分别求解有噪声信号的P1优化问题,得到每个截断误差对应的留一法(Leave-One-Out,LOO)误差。最终选择最小的LOO误差对应的截断误差为优化问题的设定值。LOO误差是在机器学习领域广泛使用的误差估计。将N个样本分为N-1个学习样本和1个验证样本,通过学习样本建立PC展开,在验证样本上评估该展开的泛化误差。在PC法中,LOO误差表达式为
| $E_{\mathrm{LOO}}=\frac{1}{N} \sum\limits_{i=1}^{N}\left(\frac{y_{i}-y_{\mathrm{PC}}\left(\xi_{i}\right)}{1-h_{i}}\right)^{2} $ | (5) |
式中:yPC是指得到的PC展开;hi是矩阵Ψ(ΨTΨ)-1ΨT的第i个对角元素。
大体上有两类算法来解决上述优化问题:线性规划算法和贪婪算法。两种方法的优劣本文不作深入研究, 这里使用贪婪算法中的正交匹配追踪算法[33]。该算法通过计算残差向量和每个基函数向量的相关性来得到与当前残差最相关的基函数,然后通过求解最小二乘问题得到响应的展开。
算法的输入是测量矩阵Ψ、观测向量Y、截断误差ε。定义迭代次数指标k,残差向量r,特征索引集$\mathcal{I}$,具体实施过程为
初始化:k=0, r(0)=Y, $\mathcal{I}=\varnothing$
如果:||r(k)||≥ε
1) 定义残差向量与每个基函数向量的内积,即
| $\lambda_{j}=\frac{\left|\left\langle\Psi_{a_{j}}, r^{(k)}\right\rangle\right|}{\left\|\Psi_{a_{j}}\right\|_{2}} $ |
并找到与当前残差最相关的特征:λ=argmaxjλj。
2) 更新迭代次数指标和特征索引集:
| $k \leftarrow k+1\\ \mathcal{I} \leftarrow \mathcal{I} \cup \lambda $ |
3) 使用$\mathcal{I}$中的特征基函数通过最小二乘法得到PC展开的自由度,并更新残差:
| $\begin{array}{l} {\alpha ^{(k)}} = {{\mathop{\rm argmax}\nolimits} _{\alpha }}\left\| {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\cal I}}\mathit{\boldsymbol{\alpha }}} \right\|\\ {\mathit{\boldsymbol{r}}^{(k)}} = \mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\cal I}}{\alpha ^{(k)}} \end{array} $ |
循环过程1)~3),直至||r(k)|| < ε。
2 不确定性量化分析本文选择两个算例来验证稀疏多项式混沌方法和其中的截断误差设定策略,分别研究了湍流模型系数的不确定性对RAE2822翼型跨声速绕流模拟的影响和材料物性参数的不确定性对烧蚀热响应预测的影响。
2.1 SA模型系数的不确定性对跨声速翼型模拟的影响第1个算例是Spalart-Allmaras(SA)模型系数的不确定性对跨声速翼型模拟的影响。在该算例中,假定模型系数不再为常数,而是在一定区间内变化的随机变量。关注重点是不确定性的传播研究,即模拟结果的统计特性分析。
计算外形是RAE2822翼型[34],本文的计算状态是:马赫数Ma=0.729,雷诺数Rec=6.5×106,迎角α=2.31°,计算使用的程序是课题组自行发展的MFlow[34],使用的网格和算法可以参考文献[35]。
计算使用SA一方程模型[36],假定流动为全湍流,忽略了原始模型中的转捩项(Trip Term)。因此模型中有9个常数,分别为:cb1、σ、cb2、κ、cw2、cw3、cv1、ct3、ct4。本文假定每个参数在各自的支撑集内为均匀分布,具体参数的取值范围与文献[34]保持一致。
文献[37]通过完整PC展开得到了系统输出的响应。这里提到的完整PC展开是指使用完全多项式展开,需要的样本点数目为
| $N=n_{p}(p+1)=n_{p} \cdot \frac{(n+p) !}{n ! p !} $ | (6) |
式中:n为输入随机变量的维数;p为混沌多项式的阶数;np定义为过采样率。该算例中,假定展开多项式为2阶,过采样率np=2,因此完整PC展开需要的样本点数目为N=110。
为了演示有噪声信号的P1优化问题中截断误差ε的设定过程,图 1给出了采样点N=50时,截断误差设定值和升力系数LOO误差的关系。计算中设定ε从10-8逐渐增加到10-3,在此过程中LOO误差先减小后增加。选取最小的LOO误差对应的截断误差作为优化问题的设定值。在本文中分别尝试了N=20,30,40,50,表 1给出了不同采样点下的截断误差设定值。

|
| 图 1 LOO误差与截断误差设定值的关系(N=50) Fig. 1 LOO error variation with truncation error settings (N=50) |
| 采样点N | 截断误差设定值 | LOO误差 |
| 20 | 1.000×10-7 | 3.925 6×10-13 |
| 30 | 4.650×10-6 | 1.666 9×10-10 |
| 40 | 1.298×10-5 | 2.052 3×10-9 |
| 50 | 9.322×10-5 | 4.173 2×10-9 |
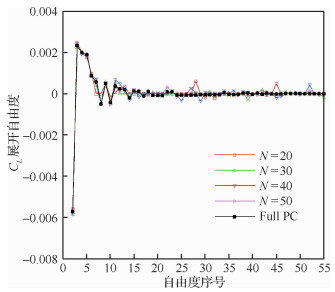
确定好不同采样点下优化问题的截断误差后,可以得到关注变量的稀疏PC展开。图 2给出了不同采样点下得到的升力系数CL展开自由度,这里分别按自由度幅值大小排序。完整PC展开并不代表真正的精确解,只是作为精度较高的结果对比参考。首先从完整PC展开(图中Full PC曲线)的结果可以看到,升力系数的PC展开存在明显的稀疏特性,都只有少数若干项的自由度量值较大,其他展开项的自由度可以忽略不计。从图可以看出,当样本点数目分别为N=20,30,40,50时,本文发展的稀疏PC展开能够比较准确地还原量级较大的若干个自由度,捕捉到输出的主要特征。
|
| 图 2 不同采样点下升力系数PC展开的自由度 Fig. 2 Freedoms of lift coefficient obtained with PC under different samples |
稀疏PC展开的精度可以进一步通过预测值和CFD计算值对比验证,表 2给出了模型参数为标准取值时预测值和计算值的对比。不同采样点下的预测值都跟CFD计算非常接近,说明稀疏PC展开也能够准确预测系统输出的响应。
| 方法 | CL | CD | |
| PC展开 | N=20 | 0.693 19 | 0.013 135 |
| N=30 | 0.693 16 | 0.013 152 | |
| N=40 | 0.692 95 | 0.013 133 | |
| N=50 | 0.693 14 | 0.013 126 | |
| 完整PC | 0.693 16 | 0.013 130 | |
| CFD | 0.693 37 | 0.013 137 |
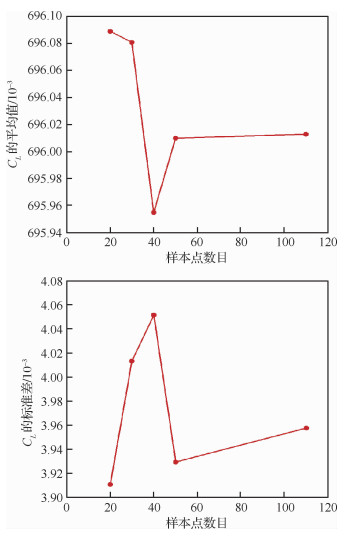
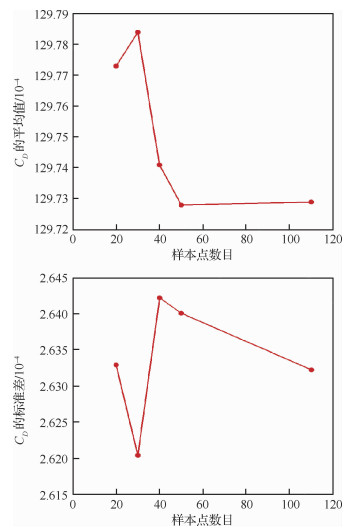
在不确定性量化中,比较关注的是输出的平均值和标准差等统计信息。图 3和图 4给出了不同采样点下,升、阻力系数的统计信息,其中N=110代表完整PC展开的结果。从图可以看出,升、阻力系数的平均值随着样本点数目的增加变化不大,标准差的变化稍大,但仍在可以接受的范围内。
|
| 图 3 升力系数的平均值和标准差 Fig. 3 Mean value and standard deviation of lift coefficients |
|
| 图 4 阻力系数的平均值和标准差 Fig. 4 Mean value and standard deviation of drag coefficients |
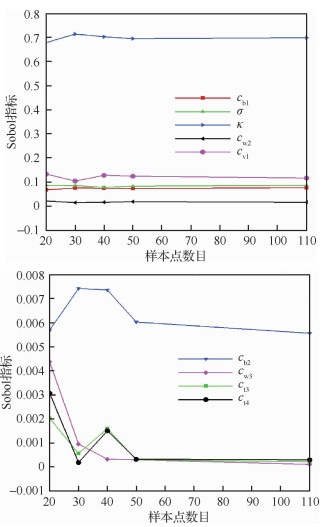
在不确定性量化分析中,另一个关注的是每个随机输入变量对输出变化的贡献度。本文使用Sobol指标[38-39]来分析每个输入变量对输出方差的贡献大小。图 5给出了9个输入变量在升力系数分析中的Sobol指标。从图中可以明显看出,稀疏PC相对于完整的PC,也能够比较准确地预测每个输入变量的贡献大小。随着样本点数目的增加,预测的Sobol指标变化不大,充分证明了稀疏PC展开的精度。cb1、σ、κ、cw2、cv1这5个参数对于升力系数的不确定性影响都相对较大,κ是其中贡献最大的参数,ct3、ct4、cb2、cw3这4个参数的贡献可以忽略不计。
|
| 图 5 升力系数预测中各输入变量的Sobol指标 Fig. 5 Sobol indices for input parameters in lift coefficient prediction |
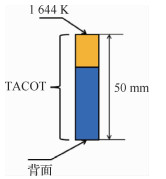
第2个算例选取了一维烧蚀热响应算例,以此来考核稀疏PC方法的适应性和精度。此处选取4th Abaltion Workshop官方网站提供的标准算例[40]进行分析,计算条件如图 6所示。
|
| 图 6 测试算例的计算条件 Fig. 6 Calculation condition of test case |
计算使用的控制方程包括组分的热解过程、动量方程、质量守恒方程和能量方程,数值方法可以参考文献[41]。分析中选择材料25 mm厚度位置的温度值作为目标变量,材料物性参数为输入不确定性参数,进行不确定性传播分析。
本算例所使用的材料为TACOT,是为方便数据对比而提供的一种假想材料,材料物性参数的不确定性也非本文的重点研究对象。因此此处对材料参数的不确定性,在参考以往相关工作的基础上,采取如表 3所示的假设值。
| 输入参数 | 编号 | 不确定性 |
| 原始材料导热率 | x1 | ±10%W/(m·K) |
| 炭化材料导热率 | x2 | ±20%W/(m·K) |
| 原始材料比热 | x3 | ±5%J/(kg·K) |
| 炭化材料比热 | x4 | ±10%J/(kg·K) |
| 原始材料密度 | x5 | ±6%kg/m3 |
| 原始材料生成焓 | x6 | ±15%J/kg |
| 热解气体焓 | x7 | ±15%J/kg |
| 渗透率 | x8 | ±10%m2 |
| 孔隙率 | x9 | ±8% |
本文使用拉丁超立方抽样方法,在输入参数构成的9维随机空间里抽样获得30个样本点,通过稀疏PC方法构建了目标变量与随机输入参数的响应关系,借此来分析目标变量的统计特性。同时为了验证稀疏PC方法的精度,使用蒙特卡洛采样方法采样500次,其统计结果作为参考值来进行对比分析。需要指出的是,蒙特卡洛方法非常依赖于样本空间的大小,这里使用500个样本进行直接统计分析可能会有偏差,因此也同时使用这些样本点进行完整PC展开来进行统计分析。
表 4给出了稀疏PC方法(N=30)、完整PC方法(N=500)和蒙特卡洛方法(N=500)预测的目标变量的均值和标准差。3种方法得到的统计量均相差不大,说明稀疏PC方法能够较为准确地刻画目标变量的统计特性。
| 预测方法 | 均值/K | 标准差/K |
| 稀疏PC方法 | 355.517 3 | 8.712 5 |
| 完整PC方法 | 356.008 0 | 9.015 7 |
| 蒙特卡洛方法 | 355.285 8 | 8.612 3 |
9个物性参数中,究竟哪一些参数对于目标变量预测影响较大,需要进行敏感度分析。这里分别使用稀疏PC和完整PC得到每个输入参数的Sobol指标,如表 5所示,以此来衡量对输出方差的贡献大小。两种方法得到的敏感性大小基本一致,x1和x5是最重要的两个参数,其次是x2和x3,剩余的5个参数的贡献很小。
| 变量编号 | Sobol指标 | |
| 稀疏PC | 完整PC | |
| x1 | 0.359 0 | 0.409 0 |
| x2 | 0.158 2 | 0.155 9 |
| x3 | 0.117 4 | 0.152 1 |
| x4 | 0.010 9 | 0.007 5 |
| x5 | 0.412 7 | 0.341 6 |
| x6 | 0 | 0.002 1 |
| x7 | 0.028 5 | 0.020 7 |
| x8 | 0 | 0.002 4 |
| x9 | 0 | 0.001 2 |
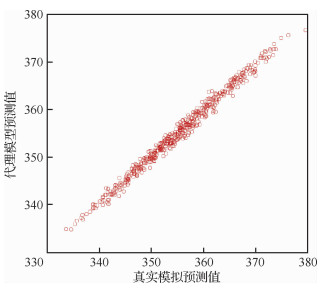
为了验证稀疏PC方法的精度,进一步地在500个样本点上进行评估,如图 7所示。其中横坐标为通过CFD模拟得到的目标变量,纵坐标为通过稀疏PC方法预测的目标值,两者呈现出很好的线性关系。定义R2为决定系数来评估预测的准确度:
|
| 图 7 目标变量CFD模拟与PC预测的比较 Fig. 7 Comparison of CFD simulation and PC prediction for quantity of interest |
| ${R^2} = 1 - \frac{{\sum\nolimits_{i = 0}^{{n_{{\rm{sample }}}} - 1} {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\nolimits_{i = 0}^{{n_{{\rm{sample }}}} - 1} {{{\left( {{y_i} - \bar y} \right)}^2}} }} $ | (7) |
式中:yi是通过确定的CFD计算得到的系统响应;y是响应的平均值;ŷi是根据模型得到的预测值;nsample是验证样本点的数目。在本算例中R2=0.987 4,说明发展的稀疏PC方法能够很好地预测新样本点的目标变量。
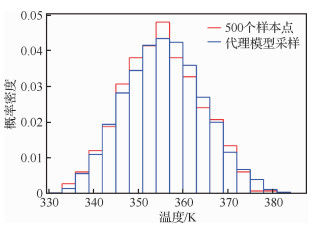
为进一步分析该问题的不确定性传播规律,对目标变量的概率密度函数进行了研究,结果如图 8所示。其中蓝色分布是通过对目标变量的稀疏PC展开进行重采样得到的。可以看出稀疏PC方法得到的目标变量概率密度分布与500个采样点基本一致,都呈现出近似的高斯分布形态。
|
| 图 8 目标变量的概率密度估计 Fig. 8 Probability density estimation for quantity of interest |
为了解决多变量不确定性量化问题中的“维数灾难”问题,本文发展了基于1范数最小的稀疏PC方法。该方法可以识别出若干个对系统输出影响较大的基函数,从而得到近似的输出响应。实施过程中通过交叉验证方法确定有噪声信号的P1规划问题的截断误差,使用正交匹配追踪算法求解该规划问题。
通过SA模型系数的不确定性对RAE2822翼型跨声速绕流模拟的影响和材料物性参数的不确定性对炭化材料烧蚀热响应影响这两个算例,证实了发展的稀疏PC方法能够准确预测系统输出。对于输出的统计信息,包括均值、标准差和敏感性指标,稀疏PC都能够取得和完整PC基本一致的结果。
稀疏PC方法证实能够在样本点数目小于自由度的不利条件下预测输出的响应,为解决工程中多变量的不确定性量化问题提供了很好的解决方案。不过需要指出的是,稀疏PC方法适用的前提是输出的PC展开存在稀疏特性。对于一个未知的复杂系统,如何使用稀疏性判断准则预判系统的稀疏性需要进一步研究讨论。对于某些各展开项自由度都有着不可忽视贡献的问题,稀疏PC方法不再适用,需要发展其他更加高效的算法。
| [1] |
王晓东, 康顺. 多项式混沌方法在随机方腔流动模拟中的应用[J]. 中国科学:技术科学, 2011, 41(6): 790-798. WANG X D, KANG S. Application of polynomial chaos on numerical simulation of stochastic cavity flow[J]. Sci China Tech Sci, 2011, 41(6): 790-798. (in Chinese) |
| Cited By in Cnki (20) | Click to display the text | |
| [2] |
刘智益, 王晓东, 康顺. 多元多项式混沌法在随机方腔流动模拟中的应用[J]. 工程热物理学报, 2012, 33(3): 419-422. LIU Z Y, WANG X D, KANG S. Application of multidimensional polynomial chaos on numerical simulations of stochastic cavity flow[J]. Journal of Engineering Thermophysics, 2012, 33(3): 419-422. (in Chinese) |
| Cited By in Cnki (9) | Click to display the text | |
| [3] | FISHMAN G. Monte Carlo:Concepts, algorithms and applications[M]. New York: Springer, 1996. |
| [4] | GHANEM R, SPANOS P. Stochastic finite elements:A spectral approach[M]. New York: Springer, 1938. |
| [5] | XIU D, KARNIADAKIS G. The Wiener-Askey polynomial chaos for stochastic differential equations[J]. SIAM Journal of Science Computer, 2002, 24(2): 619-644. |
| Click to display the text | |
| [6] | NAJM H N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 2009, 41: 35-52. |
| Click to display the text | |
| [7] | WIENER N. The homogeneous chaos[J]. American Journal of Mathematics, 1938, 60: 897-936. |
| Click to display the text | |
| [8] | GHANEM R G, SPANOS P D. Stochastic finite elements: A spectral approach[M]. Revised edition. New York: Dover Publications, 2003. |
| [9] | XIU D, KARNIADAKIS G E. Modeling uncertainty in flow simulations via generalized polynomial chaos[J]. Journal of Computational Physics, 2003, 187: 137-167. |
| Click to display the text | |
| [10] | LE MAITRE O P, KNIO O, HABIB N N, et al. A stochastic projection method for fluid flow I. Basic formulation[J]. Journal of Computational Physics, 2001, 173: 481-511. |
| Click to display the text | |
| [11] | LACOR C, SMIRNOV S. Uncertainty propagation in the solution of compressible Navier-Stokes equations using polynomial chaos decomposition[C]//NATO RTO AVF-147 Symposium on Computational Uncertainty in Military Vehide Design, 2007. |
| [12] |
王晓东, 康顺. 多项式混沌法求解随机Burgers方程[J]. 工程热物理学报, 2010, 31(6): 393-398. WANG X D, KANG S. Solving sochastic Burgers equation using polynomial chaos decomposition[J]. Journal of Engineering Thermophysics, 2010, 31(6): 393-398. (in Chinese) |
| Cited By in Cnki (22) | Click to display the text | |
| [13] | ELDRED M S. Recent advances in non-intrusive polynomial chaos and stochastic collocation methods for uncertainty analysis and design: AIAA-2009-2274[R]. Reston, VA: AIAA, 2009. |
| [14] | HOSDER S, WALTERS R W, BALCH M. Point-collocation nonintrusive polynomial chaos method for stochastic computational fluid dynamics[J]. AIAA Journal, 2010, 48(12): 2721-2730. |
| Click to display the text | |
| [15] |
张伟, 王小永, 于剑, 等. 来流导致的高超声速气动热不确定性量化分析[J]. 北京航空航天大学学报, 2018, 44(5): 1102-1109. ZHANG W, WANG X Y, YU J, et al. Uncertainty quantification analysis in hypersonic aerothermodynamics due to freestream[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(5): 1102-1109. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] |
刘全, 王瑞利, 林忠, 等. 爆轰计算JWL状态方程参数不确定性研究[J]. 爆炸与冲击, 2013, 33(6): 647-654. LIU Q, WANG R L, LIN Z, et al. Uncertainty quantification for JWL EOS parameters in explosive numerical simulation[J]. Explosion and Shock Waves, 2013, 33(6): 647-654. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] | LUCOR D, KARNIADAKIS G E. Adaptive generalized polynomial chaos for nonlinear random oscillators[J]. SIAM Journal on Scientific Computing, 2004, 26(2): 720-735. |
| Click to display the text | |
| [18] | WAN X, KARNIADAKIS G E. An adaptive multi-element generalized polynomial chaos method for stochastic differential equations[J]. Journal of Computational Physicss, 2005, 209(2): 617-642. |
| Click to display the text | |
| [19] | BLATMAN G, SUDRET B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis[J]. Probability Engineering Mechanics, 2010, 25(2): 183-97. |
| Click to display the text | |
| [20] | BLATMAN G, SUDRET B. Adaptive sparse polynomial chaos expansion based on least angle regression[J]. Journal of Computational Physics, 2011, 230(6): 2345-2367. |
| Click to display the text | |
| [21] | BLATMAN G, SUDRET B. Efficient computation of global sensitivity indices using sparse polynomial chaos expansions[J]. Reliability Engineering & System Safety, 2010, 95(11): 1216-1229. |
| Click to display the text | |
| [22] | NAIR P B, KEANE A J. Stochastic reduced basis methods[J]. AIAA Journal, 2002, 40(8): 1653-1664. |
| Click to display the text | |
| [23] | RAISEE M, KUMAR D, LACOR C. A non-intrusive model reduction approach for polynomial chaos expansion using proper orthogonal decomposition[J]. International Journal for Numerical Methods in Engineering, 2015, 103(4): 293-312. |
| Click to display the text | |
| [24] | TODOR R A, SCHWAB C. Convergence rates for sparse chaos approximations of elliptic problems with stochastic coefficients[J]. IMA Journal of Numerical Analysis, 2007, 27(2): 232. |
| Click to display the text | |
| [25] | BIERI M, SCHWAB C. Sparse high order FEM for elliptic spdes[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(1314): 1149-1170. |
| Click to display the text | |
| [26] | DOOSTAN A, OWHADI H. A non-adapted sparse approximation of PDEs with stochastic inputs[J]. Journal of Computational Physics, 2011, 230(8): 3015-3034. |
| Click to display the text | |
| [27] | MATHELIN L, GALLIVAN K. A compressed sensing approach for partial differential equations with random input data[J]. Communications in Computational Physics, 2012, 12(4): 919-954. |
| Click to display the text | |
| [28] | YANG X, KARNIADAKIS G E. Reweighted 1 minimization method for stochastic elliptic differential equations[J]. Journal of Computational Physics, 2013, 248: 87-108. |
| Click to display the text | |
| [29] | PENG J, HAMPTON J, DOOSTAN A. A weighted 1-minimization approach for sparse polynomial chaos expansions[J]. Journal of Computational Physics, 2014, 267: 92-111. |
| Click to display the text | |
| [30] | SARGSYAN K, SAFTA C, NAJM H N, et al. Dimensionality reduction for complex models via bayesian compressive sensing[J]. International Journal of Uncertainty Quantify, 2014, 4(1): 63-93. |
| Click to display the text | |
| [31] | HAMPTON J, DOOSTAN A. Compressive sampling of polynomial chaos expansions:Convergence analysis and sampling strategies[J]. Journal of Computational Physics, 2015, 280: 363-386. |
| Click to display the text | |
| [32] | JAKEMAN J D, ELDRED M S, SARGSYAN K. Enhancing 1-minimization estimates of polynomial chaos expansions using basis selection[J]. Journal of Computational Physics, 2015, 289: 18-34. |
| Click to display the text | |
| [33] | SAEED S, MEHRDAD R, MICHEL J C, et al. Efficient uncertainty quantification of stochastic CFD problems using sparse polynomial chaos and compressed sensing[J]. Computers and Fluids, 2017, 157: 296-321. |
| Click to display the text | |
| [34] | CHEN J T, ZHANG Y B, ZHOU N C, et al. Numerical investigations of the high-lift configuration with Mflow solver[J]. Journal of Aircraft, 2015, 52(4): 1051-1062. |
| Click to display the text | |
| [35] | COOK P H, MCDONALD M A, FIRMIN M C P. Aerofoil RAE2822 pressure distributions, and boundary layer and wake measurements, experimental data base for computer program assessment: AGARD-1979-0138[R]. Paris: AGARD, 1979. |
| [36] | SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flowst: AIAA-1992-0439[R]. Reston, VA: AIAA, 1992. |
| [37] |
赵辉, 胡星志, 张健, 等. 湍流模型系数的不确定度对翼型绕流模拟的影响[J]. 航空学报, 2019, 40(6): 122581. ZHAO H, HU X Z, ZHANG J, et al. Effects of the uncertainty in turbulence model closure coefficients on the simulation of flow over airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(6): 122581. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [38] | SOBOL I. Sensitivity estimates for nonlinear mathematical models[J]. Mathematical Modeling and Computational, Experiment, 1993(1): 407-414. |
| [39] |
胡军, 张树道. 基于多项式混沌的全局敏感度分析[J]. 计算物理, 2016, 33(1): 1-13. HU J, ZHANG S D. Global sensitivity analysis based on polynomial chaos[J]. Chinese Journal of Computational Phsics, 2016, 33(1): 1-13. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [40] | LACHAUD J, LAUB B. Ablation workshop test case[C]//4th Ablation Workshop, 2011: 1-3. |
| [41] |
刘骁, 国义军. 碳化材料三维烧蚀热响应有限元计算研究[J]. 宇航学报, 2016, 37(9): 1150-1156. LIU X, GUO Y J. Numerical simulation research on three-dimensional ablative thermal response of charring ablators[J]. Journal of Astronautics, 2016, 37(9): 1150-1156. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text |



