2. 中国科学院 力学研究所 高温气体动力学重点实验室, 北京 100190;
3. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000;
4. 中国科学院大学 工程科学学院, 北京 100049
2. State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
3. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China;
4. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
激波/湍流边界层干扰区内流动参数变化剧烈,涉及了湍流非平衡效应、可压缩效应、边界层分离和再附、激波/激波干扰、分离激波的非定常振荡等多种复杂流动现象,流动机理极其复杂。Zheltovodov[1]将激波-湍流边界层干扰的特殊物理现象归纳总结为以下6大类:①分离激波非定常运动对边界层内湍流的放大机制;②非定常激波对外流湍流的放大机制;③膨胀波对湍流的抑制作用;④再附区边界层特征;⑤ Taylor-Görtler涡的形成;⑥分离区内湍流的层流化。
经过半个多世纪的深入探索,国内外学者在激波与湍流边界层的相互作用机制方面已取得长足的进展,例如快速畸变近似[2]、初始分离准则[3]、干扰模式与相似律[4]、分离激波的低频振荡及其形成机制[5-6]等。当前,风洞试验以及高精度数值模拟研究主要针对压缩拐角和入射激波/平板两类简单构型。在风洞试验方面,自20世纪50年代以来,研究人员采用热线、激光风速仪、三维粒子成像测速技术、纳米粒子平面激光散射技术等先进测量手段准确获得了干扰区内高分辨率瞬态结构及脉动信息。研究结果表明,强干扰下激波的非定常运动是造成快速畸变理论分析结果严重偏离试验数据的重要因素[7];在激波作用后的下游湍流边界内质量通量脉动强度显著增强,湍流剪切应力的变化要明显强于雷诺应力其他分量[8]。近些年,Humble和Scarano[9]通过试验获得了激波干扰问题中的三维瞬态流场结构,发现上游拟序结构对激波低频振荡特性影响显著。与此同时,在直接数值模拟(Direct Numerical Simulation,DNS)研究方面,国内外也都取得了较大的突破。美国Martin等[10-13]对马赫数Ma=2.9、雷诺数Reθ=2 300下激波与湍流边界层的相互作用进行了一系列直接数值模拟研究,其计算问题为24°压缩拐角和12°入射激波/平板干扰,计算结果也得到了Bookey等[14]低雷诺数试验结果的验证和确认。在国内,文献[15-18]基于其DNS数据,系统开展了拐角角度、壁温、拐角导圆、可压缩性以及转捩等因素对分离泡、边界层演化特性以及激波振荡特性的影响规律和作用机制。
超声速膨胀角是流体力学基础问题之一,普遍存在于各类高速飞行器的内外表面,尤其是在超燃冲压发动机进气道中。工程实践表明,气流在进气道唇口附近急剧压缩后形成较强的入射激波,与前体压缩面以及后部的膨胀区边界层将产生相互干扰作用。情况恶劣时,将会严重影响进气道工作性能,甚至导致发动机不启动。与以往传统的激波/湍流边界层干扰问题不同的是,此时,膨胀角内存在较强的顺压梯度和膨胀波系,这会对激波运动及湍流脉动特性均带来显著影响,进而膨胀区内相互干扰也将呈现不同的演化机制。因此,深入开展膨胀角激波/湍流边界层干扰区内复杂流动现象的机理研究,将有助于进一步加深对该问题的理解和认识,具有重要的工程优化设计和应用背景。
早期研究主要以风洞试验为主,计算模型也多采用入射激波与平板/膨胀角构型。Chew[19]对Ma∞=1.8、2.5下的6°膨胀角入射激波/湍流边界层干扰问题进行了试验研究,发现当入射激波再入点位于膨胀角角点附近(约3~4倍边界层厚度范围内)时,膨胀效应对上游流动的影响较为明显。Chung和Lu[20]分析研究了Ma∞=8下入射激波再入点位置对膨胀区内物面压力平均量及脉动量的影响规律,但由于入射激波强度较弱,干扰区内并没有发生流动分离现象。随后,White和Ault[21]进一步研究发现在强激波干扰下膨胀效应将会导致干扰区内分离泡尺度的减小。最近,Sathianarayanan和Verma[22]试验研究了考虑侧壁效应的入射激波与膨胀角湍流边界层相互作用,着重探究了入射激波强度、膨胀角角度以及入射点位置等因素对分离区三维形态的影响机制。相较于风洞试验,国内外在膨胀角激波/湍流边界层干扰的高精度数值模拟研究方面,相关工作还较为少见。Konopka等[23]采用大涡模拟对Ma∞=1.76的入射激波/膨胀角湍流边界层干扰问题进行了初步研究,激波入射点位于膨胀角的下游,重点关注了激波干扰对膨胀区内湍流统计特性的影响规律。
本文采用直接数值模拟方法对超声速膨胀角入射激波与湍流边界层相互作用问题进行系统研究。着重探讨强激波干扰下入射激波入射点位置的改变对干扰区内复杂流动结构的影响规律,如分离泡、物面压力脉动特性及激波非定常运动、湍流边界层统计特征等。采用本征正交分解方法,分析比较不同入射位置下膨胀区内动力学过程的差异。为了便于比较和验证结果,来流参数的选取与Bookey等[14]的试验和Priebe等[13]的DNS相近。
1 计算参数控制方程为曲线坐标系(ξ, η, ζ)下三维可压缩无量纲Navier-Stokes方程组,流场变量和长度变量分别采用无穷远处来流参数和单位毫米进行无量纲化,具体形式为
| $ \begin{array}{l} \partial_{t} \boldsymbol{U}+\partial_{\varepsilon}\left(\boldsymbol{F}+\boldsymbol{F}_{\mathrm{v}}\right)+\partial_{\eta}\left(\boldsymbol{G}+\boldsymbol{G}_{\mathrm{v}}\right)+ \\ \partial_{\zeta }\left(\boldsymbol{H}+\boldsymbol{H}_{\mathrm{v}}\right)=\boldsymbol{0} \end{array} $ | (1) |
式中:U=J-1[ρ, ρu, ρv, ρw, ρE]为守恒变量; F和Fv分别为ξ方向上的无黏和黏性通量; (G, Gv)和(H, Hv)分别对应于η和ζ方向; J为坐标系转换时的雅可比矩阵。各项的具体表达式参见文献[10]。
采用高精度有限差分解算器OpenCFD-SC进行DNS计算。在本文作者前期研究中[15-18, 24],采用该软件对大量压缩拐角和入射激波/平板湍流边界层干扰问题进行了直接数值模拟研究,DNS结果可靠性和准确性都得到了充分的验证与确认。DNS计算时,我们采用了Martin等[25]优化构造的WENO_SYMBO_LMT格式以及Steger-Warming流通量分裂方法计算无黏通量。该数值格式在激波/湍流边界层干扰问题中具有较好的鲁棒性和计算精度,可以保证在精确捕捉湍流边界层内不同尺度流动结构的同时,又能较好地抑制强激波间断处的数值振荡。另外,采用八阶中心差分格式对黏性项进行计算,时间离散采用的是三阶精度的Runge-Kutta方法。
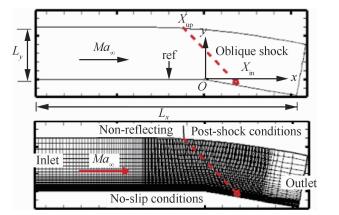
如图 1所示,计算模型为入射激波与平板/膨胀角湍流边界层的相互作用问题。气流方向为从左往右,坐标系原点取为膨胀角角点处,膨胀角为10°,入射激波的激波角为30°。Xin和Xup分别对应为入射激波在物面上的名义入射点和在上边界的入射点位置。通过改变计算域上边界中Xup的流向位置使得入射激波打在膨胀角壁面上不同的流向位置Xin。计算域流向长度为Lx=470 mm,流向跨度为-363 mm < x < 107 mm,其中平板区和膨胀区长度分别为363 mm和107 mm。法向高度为Ly=60 mm,展向宽度为Lz=14 mm。边界条件的设置具体如下。首先,计算域入口处(Inlet)取为相同来流下的层流解。为了消除扰动波反射对计算结果的影响,在计算域的出口处(Outlet)使用了超声速出口无反射边界条件及缓冲区。物面边界为无滑移和等温壁,展向取为周期性边界条件。在计算域的上边界,入射点Xup的左侧取为无反射自由来流边界(Non-reflecting),而在入射点Xup右侧的流动参数取为按照Rankine-Hugoniot关系式给出的波后值。此外,膨胀角上游的充分发展湍流边界层则是通过采用文献[26]中的壁面吹吸方法生成。在计算域层流入口下游的平板壁面(-335 mm < x < -315 mm)添加多频正弦波扰动促使流动发生转捩,随后在平板下游x=-60 mm处获得充分发展的湍流边界层,采用的扰动幅值和频率均与文献[16-18]相同。
|
| 图 1 计算域及网格示意图 Fig. 1 Illustration of computational domain and grid |
具体来流条件如下:来流马赫数为Ma∞=2.9,基于单位长度的来流雷诺数为Re∞=5 581.4 mm-1,来流静温为T∞=108.1 K,壁面温度取为Tw=307 K。计算的DNS工况分别为Case1~Case4,其中Case1为无膨胀情况下入射激波/平板湍流边界层干扰,Case2~Case4为膨胀角入射激波/湍流边界层干扰,其壁面上名义入射点位置Xin分别对应为膨胀角点上游、角点处以及角点下游3种工况。为了更好地揭示膨胀效应的影响,这里通过调整Xup将Case1和Case3的壁面入射点位置Xin均取为0,Case2和Case4的入射点Xin则分别取在角点上下游约δ的位置处(δ对应为上游参考点ref处的湍流边界层厚度,见图 1)。各工况中其他DNS参数设置均完全相同。
如表 1所示,各DNS工况的网格点数均为3 200×200×140(流向Nx×法向Ny×展向Nz),计算网格采用代数解析方法生成。为了精确捕捉流动信息,流向网格点在膨胀角激波与湍流边界层干扰区内均匀密集分布,法向网格在近壁区采用了双曲正切函数的加密处理,以保证在整个边界层内有120个网格点,展向网格点均匀分布。以x=-60 mm处壁面量为参考(见图 1中参考点ref),膨胀角干扰区内流向和展向网格尺度分别为Δx+=5.0和Δz+=7.1, 壁面及边界层外缘的法向网格尺度分别Δyw+=0.7和Δye+=11.2,与Priebe等[13]的DNS较为接近。表 2还分别给出了上游参考点ref处湍流边界层的边界层厚度δ、位移厚度δ*、动量厚度θ、形状因子H和物面摩阻系数Cf。可以看到,本文结果与DNS数据[13]及试验结果[14]较为接近。
| Case | Lx×Ly×Lz/mm3 | Nx×Ny×Nz | Δx+×(Δyw+, Δye+)×Δz+ | Xup/mm | Xin/mm | Expansion angle/(°) |
| Case1 | 470×60×14 | 3 200×200×140 | 5.0×(0.7, 11.2)×7.1 | -104.00 | 0 | |
| Case2 | 470×60×14 | 3 200×200×140 | 5.0×(0.7, 11.2)×7.1 | -112.00 | -7.60 | 10 |
| Case3 | 470×60×14 | 3 200×200×140 | 5.0×(0.7, 11.2)×7.1 | -104.00 | 0 | 10 |
| Case4 | 470×60×14 | 3 200×200×140 | 5.0×(0.7, 11.2)×7.1 | -96.00 | 6.15 | 10 |
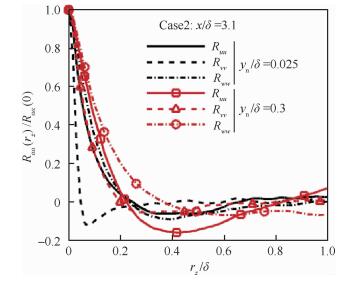
首先,为了验证本文DNS计算展向宽度的合理性,图 2给出了膨胀角干扰区内速度展向关联函数Rαα(rz)在边界层内不同法向位置处的分布情况,这里rz为展向间距,Ruu、Rvv和Rww分别为流向、法向和展向速度关联函数,具体表达式参见文献[26], yn为物面法向距离。可以看到,3个方向上脉动速度的关联函数在展向距离rz大于半个计算宽度时,均衰减到0附近,这表明本文DNS计算的展向宽度是合理的,能够有效捕捉干扰区大尺度结构。需要特别说明的是,本文将在后续结果分析和讨论中,通过与DNS结果[13]以及试验数据[14]的比对,进一步验证和确认本文计算结果的可靠性。
|
| 图 2 两点展向相关函数分布 Fig. 2 Distribution of two-point correlation as afunction of spanwise spacing |
DNS计算时,在经过两个无量纲时间(Lx/U∞)后流场达到统计定常状态,随后对瞬态场进行统计采样。总无量纲采样时间跨度约为500δ/U∞,物面压力脉动信号的采样间隔为0.06δ/U∞,共获得400个三维瞬态流场样本。如无特别说明,本文所指的平均定义为时间和展向平均。
2 流场结构图 3给出了膨胀角干扰区瞬态密度梯度场,这里粉色曲线代表Ma∞=1的瞬态等值线,图中Xsep为平均分离点位置。为了更好地显示流场结构,采用文献[10]中定义的流场变量NS:

|
| 图 3 瞬态密度梯度场 Fig. 3 Instantaneous gradient of density |
| $ {\rm{NS}} = 0.8{{\rm{e}}^{ - 10\left( {|\nabla \rho | - |\nabla \rho {|_{\min }}} \right)/\left( {|\nabla \rho {|_{\max }} - |\nabla \rho {|_{\min }}} \right)}} $ | (2) |
式中:Δρ为密度梯度。可以看到,膨胀干扰区内流场结构与激波/平板湍流边界层干扰区较为类似:在边界层外缘可以清楚地看到入射激波(IS)以及反射激波(RS),同时在干扰区下游仍存在较弱压缩波系。此外,在激波干扰作用下,边界层内Ma∞=1的瞬态等值线逐渐远离物面,这主要是干扰区内均出现了流动分离现象所致。膨胀效应对流场结构的影响主要体现在干扰区下游的再附边界层。如图 3(a)和图 3(c)所示,相较于激波/平板干扰工况,膨胀区内马赫数等值线的法向位置更为靠近物面,这也表明此时再附边界层外层出现了流动加速现象。另外,从定性分布规律来看,入射激波流向位置改变对膨胀角内流场结构特征的影响不大。
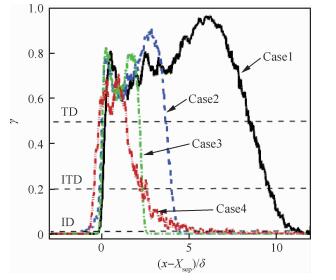
Simpson[27]依据瞬态分离的统计概率将边界层分离划分为以下3类:初始分离(Incipient Detachment, ID)、间歇性瞬变分离(Intermittent Transitory Detachment, ITD)以及瞬变分离(Transitory Detachment, TD)。前两者分别对应回流的统计概率为1%和20%,后者则为50%,对应为平均意义上的流动分离。图 4给出了膨胀角内物面上流动分离的统计概率(γ)分布情况。这里的流动分离定义为Us/yn < 0,其中Us为沿物面的流向速度。为了便于比较,流向坐标采用分离点坐标Xsep和上游湍流边界层厚度δ进行归一化。整体来看,Case1~Case4工况物面流动分离统计概率的分布规律基本类似,均以双峰结构为主,呈现V字型分布。从定量分布来看,所有工况下峰值概率均超过0.5,这说明膨胀角内流动存在平均意义上的流动分离。可以看到,膨胀角上游区域的统计概率分布较为一致,而下游区域内流动分离特征则变化显著,特别是Case4工况,物面上存在较大范围的初始分离。
|
| 图 4 物面上流动分离的统计概率分布 Fig. 4 Statistical probability distribution of flowseparation at wall |
为了更好地定量化描述膨胀效应对干扰区内分离泡流向尺度的影响,图 5给出各工况下物面平均摩阻系数Cf的流向分布。如图所示,本文Case1结果与Priebe等[13]DNS结果吻合良好,这也进一步证实计算结果的可靠性。以摩阻分布曲线过零点的流向位置来确定分离区长度。可以看到,随着激波入射点位置往下游移动,分离区流向长度急剧减小,Case4时分离区长度为1.45δ,约为Case1工况的17%。此外,Case2和Case3分离区摩阻分布还出现急剧升高随后急剧下降的突跃,Fang等[28]DNS结果也存在类似现象,该现象主要是由于膨胀角角点的曲面不连续而导致的。然而,Case4工况下则无局部极值出现,造成这种差异的原因很可能是:Case4时角点位于分离区内,流动变化较为缓慢,对曲面变化的影响不敏感。另外,Case2~Case4工况膨胀角下游的摩阻分布较为吻合,均明显高于Case1工况。此外,图 6还给出了分离泡高度h沿流向的分布情况。这里采用Us=0的平均等值线来表征分离泡高度。可以看到,分离泡形态呈现两边低中间高的山峰型,入射点流向位置的改变对分离泡的高度影响显著,特别是当入射激波点位于角点及其下游区域时(Case3和Case4),分离泡高度约为无膨胀角工况的1/10。该现象很可能是由于入射激波位置靠近膨胀角,此时角区膨胀波降低了入射激波强度[29],使得干扰区内物面压力流向梯度急剧减小的缘故。

|
| 图 5 物面平均摩阻系数分布 Fig. 5 Distribution of mean wall skin-frictioncoefficients |

|
| 图 6 分离泡高度沿流向分布 Fig. 6 Streamwise variations of separation bubble height |
干扰区物面压力及其脉动特征一直以来都是激波与湍流边界层相互作用问题的研究重点及热点。深入分析膨胀效应对物面压力脉动的影响机制,将有助于理解膨胀角分离激波的非定常运动规律及其物理机制,特别是不同入射位置下膨胀效应对分离激波低频振荡运动的影响规律。本节将通过与激波/平板湍流边界层干扰结果的比对分析,进一步深入揭示膨胀效应对物面压力脉动强度、概率密度函数、时空关联特性以及功率谱密度等方面的影响。
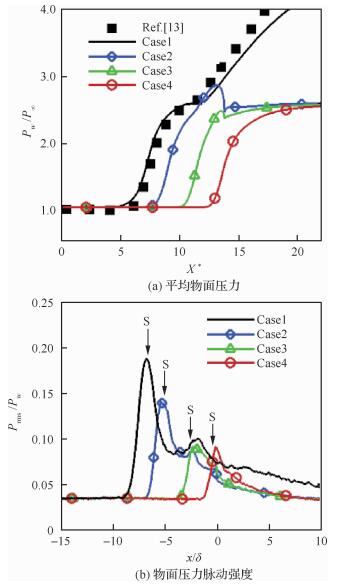
图 7分别给出了各工况干扰区内平均物面压力Pw/P∞及脉动强度Prms/Pw的分布情况, 这里下标w和∞分别代表物面和无穷远来流,下标rms为脉动均方根。图中符号S表示分离区起始点的位置。需要说明的是,为了便于比较,将流向坐标进行了平移及归一化,使得Case1计算结果中压力升高点与Priebe等[13]的DNS结果相互重合,如图 7(a)中横坐标X*所示。可以看到,两者在干扰区内分布规律非常吻合,这也充分证实了本文DNS数据的准确性。从Case2~Case4的分布规律来看,膨胀效应使得干扰区下游物面压力降低,总压差减小,但入射激波流向位置的改变对膨胀区内总压差没有实质影响,不同工况下压力分布曲线在膨胀角下游吻合良好。流向位置变化对分离区内物面压力流向分布规律的影响则更为直接。Case4时压力的变化则相对较为缓慢,这主要是此时膨胀角角点的强膨胀波系对入射激波存在较强抑制作用,如图 3(d)所示。从图 7(b)中还可以看到,物面压力脉动强度的极值点主要出现在分离激波点S处,这主要是由于分离激波的存在。同时,随着入射激波位置往下游移动,脉动峰值也逐步下降,这与Chung和Lu[20]的试验结果是一致的。
|
| 图 7 平均物面压力及脉动强度分布 Fig. 7 Distribution of mean and fluctuation intensityof wall pressure |
图 8分别给出了分离点及膨胀角再附区物面压力脉动的概率密度函数(Probability Density Function, PDF),这里采用当地脉动压力均方根σp对脉动量进行归一化处理。与高斯分布的比较结果表明,各工况下分离点压力脉动的PDF分布均呈现非对称特征,大概率事件出现在-1 < p′ /σp< 0的区域,如图 8(a)所示。本文计算结果与Loginov[30]及Pasquariello[31]等的高雷诺数大涡模拟结果较为类似,但在0 < p′/σp < 1的范围内没有出现明显的局部峰值,这很可能是由于本文来流雷诺数Reθ较低。可以看到,图 8(b)中下游膨胀区内压力脉动PDF近似对称分布,不同工况PDF曲线分布规律均基本类似。总体来看,膨胀效应对干扰区内物面脉动压力PDF的影响可以忽略不计。

|
| 图 8 物面压力脉动概率密度函数 Fig. 8 Probability density function of fluctuatingwall pressure |
为了更好地考察膨胀效应对物面压力脉动p′时空关联特性的影响规律,这里采用流向时空关联系数R(Δξ, Δζ, Δt),具体定义为[32]
| $ \frac{R(\Delta \xi, \Delta \zeta, \Delta t)=}{\frac{p^{\prime}\left(x_{0}, z_{0}, t\right)}{p^{\prime 2}\left(x_{0}, z_{0}, t\right)^{1 / 2}} \frac{p^{\prime}\left(x_{0}+\Delta \xi, z_{0}+\Delta \zeta, t+\Delta t\right)}{p^{\prime 2}\left(x_{0}+\Delta \xi, z_{0}+\Delta \zeta, t+\Delta t\right)^{1 / 2}}} $ | (3) |
式中:(x0, z0)为参考点坐标;Δξ、Δζ和Δt分别为流向间距、展向间距和延迟时间。在本文中沿展向中心线从-60 mm < x < 60 mm的范围内均匀布置了200个压力测点,并对脉动压力信号进行了高频采样。
图 9分别给出了分离点和下游膨胀区内物面压力的自相关系数R(0, 0, Δt)。可以看到,分离点和下游膨胀区自相关系数分布的差异较为明显。在图 9(a)中,Case1~Case4分离点自相关系数要明显高于其上游湍流边界层(TBL),而且随着延迟时间的增大,其自相关系数仍维持在较高的量值,特别是Case1。Muck等[33]研究表明,分离激波大尺度振荡运动产生的强间歇性是该现象的主要诱导因素。从本文计算结果来看,Case2~Case4分离点的自相关系数分布仍基本符合这一规律,但是其量值急剧下降,峰值系数对应的延迟时间也相对减小。这表明膨胀效应使得分离激波的非定常运动间歇性减弱和时间尺度减小。另外,在膨胀区x/δ=4.64处,从图 9(b)中仍可以看到自相关系数随着延迟时间呈现急剧下降的趋势,压力脉动时间尺度也呈现进一步减小趋势,特别是在ΔtU∞/δ>1.0时,脉动压力自相关性非常弱。入射点流向位置的改变对下游再附边界层物面压力自相关系数分布规律的影响可以忽略不计。

|
| 图 9 物面压力脉动自相关 Fig. 9 Autocorrelation of wall pressure fluctuations |
本文还进一步给出膨胀效应对物面压力脉动流向时空关联系数的影响规律。图 10首先给出了上游湍流边界层内物面压力脉动的流向互相关,这里参考点(x0, z0)取为(-60 mm, 7 mm)。如图 10(a)所示,随着流向间距Δξ的增大,互相关系数的极值逐渐减小,延迟时间逐渐增大。通常,脉动压力的对流速度可由压力测点流向距离Δξ除以互相关曲线峰值对应的延迟时间τopt求得。本文由此计算得到的对流速度Uc约为0.6U∞~0.8U∞,这与Willmarth和Wooldridge[34]的试验结果较为接近。图 10(b)还给出了无量纲流向间距Δξuτ/(Ucδ)与互相关系数极值的关系。这里的无量纲间距表征了两个不同时间尺度的比值:Δξ/Uc和δ/uτ,其中前者对应大尺度涡特征对流时间,而后者则是含能涡时间尺度。可以看到,本文计算结果与试验结果[33, 35-37]吻合较好。

|
| 图 10 上游湍流边界层物面压力脉动流向时空关联 Fig. 10 Time-space correlations of fluctuatingwall pressure in upstream turbulentboundary layer |
图 11和图 12还分别给出了分离区以及下游膨胀区的流向时空关联。相较于上游湍流边界层,分离区及膨胀区流向互相关曲线分布规律主要有以下两个方面值得重点关注。一方面,从图 11(a)中可以清楚看到,分离点物面压力脉动的时空关联曲线在负延迟时间区域仍存在较强关联性。以往研究结果表明[31],造成这一现象的物理机制与分离激波非定常运动密切相关。可以看到,随着激波入射点位置往下游移动,负延迟时间区域内的相关性急剧下降,这表明膨胀效应对分离激波的非定常运动特性影响显著。可以看到,特别在Case3和Case4工况,此时关联曲线与上游湍流边界层的差别较小。

|
| 图 11 分离区内物面压力脉动时空关联系数 Fig. 11 Time-space correlation coefficients of fluctua-ting wall pressure in separation region |

|
| 图 12 下游膨胀区内物面压力脉动时空关联系数 Fig. 12 Time-space correlation coefficients of fluctua-ting wall pressure in downstream expansionregion |
另一方面,无论是在分离区还是膨胀区,在正延迟时间区域内,相关曲线均存在明显的局部峰值。在分离区内,膨胀效应对关联系数峰值大小的影响较为显著,而延迟时间位置的变化则相对较小。如图 11(a)和图 11(b)所示,局部峰值对应的延迟时间ΔtU∞/δ主要位于0.46~0.78的范围内,由此估算的对流速度Uc约为(0.41~ 0.69)U∞,略小于上游湍流边界层。Muck等[33]在压缩拐角分离泡也发现类似流动现象。在图 12中还可以看到,膨胀区内关联曲线峰值及其延迟时间的分布则相对较为集中,峰值大小出现在0.5~0.6范围内,延迟时间ΔtU∞/δ约为0.35,由此估算得到的对流速度约为0.91U∞,这说明膨胀区内物面压力波的传播存在一个加速过程,分离区与膨胀区内对流速度的差异很可能是由于湍流大尺度结构在分离区与膨胀区内不同的演化机制。在分离区内,尽管物面压力测点位于分离泡底部,但其传播特性主要由剪切层外部大尺度结构所决定。上游边界层内的大尺度结构在穿过分离激波后,其对流速度将相对降低;而在膨胀区内,外层的大尺度结构又经历一个急剧的加速膨胀过程,导致物面压力波的传播速度将增大。
为了定量化描述膨胀效应对分离激波非定常运动特性的影响规律,图 13还给出了物面压力脉动加权功率谱密度云图(Weighted Power Spectral Density, WPSD),图中符号S和R分别代表平均分离点和再附点的流向位置,黑色实线代表膨胀角角点位置(EC)。加权功率谱密度具体定义为[31]

|
| 图 13 物面压力脉动加权功率谱密度云图 Fig. 13 Weighted power spectral density map of fluctuating wall pressure |
| $ \mathrm{WPSD}=f \mathit{\Psi}(f) / \mathit{\Psi}(f) \mathrm{d} f $ | (4) |
式中:f为频率;Ψ(f)为功率谱密度。
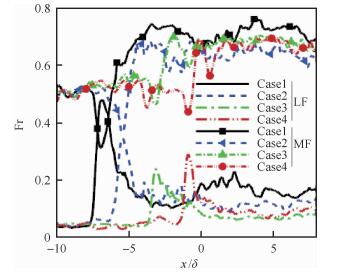
如图 13(a)所示,对于入射激波/平板湍流边界层干扰问题,上游湍流边界层物面脉动压力的峰值频率约为fδ/U∞=1,而在分离点附近,由于分离激波的大尺度流向低频振荡,物面脉动压力的低频能量急剧增加,峰值频率出现在fδ/U∞=0.01附近,随后在下游再附边界层内,峰值频率又恢复到较上游略低的高频区。本文Case1的计算结果与DNS结果[13]以及风洞试验[14]均较为一致。从图 13(b)~图 13(d)中可以清楚看到,膨胀角分离点附近脉动压力加权功率谱密度的低频能量呈现急剧降低的趋势,在fδ/U∞ < 0.1频段内Case2~Case4工况均无明显能量峰值,这表明膨胀效应极大地抑制了分离激波的大尺度低频振荡。在定量比较方面,图 14还分别给出各频段能量在总脉动能量的占比(Fr)沿流向的分布情况,其中选取的低频段(LF)为fδ/U∞ < 0.1,而中频段(MF)为0.1 < fδ/U∞ < 1.0,其他频率则为高频段。可以看到,Case1分离点低频、中频和高频能量占比分别约为0.5、0.3和0.2,低频能量明显占优。而Case2~Case4时,各工况的低频能量占比分别约为0.35、0.25和0.3,此时中高频能量明显占优。研究结果表明,膨胀角内分离激波的低频振荡运动被极大地抑制了。
|
| 图 14 物面压力脉动各频段占比分布 Fig. 14 Frequency-band percentage of fluctuatingwall pressure |
本节将讨论入射激波位置对膨胀区湍流边界层统计特性的影响规律,如平均速度剖面、雷诺应力及其各向异性张量不变量和湍动能输运机制等。结果均取自于x/δ=4.64处,上标+表示采用当地壁面量进行的无量纲化。
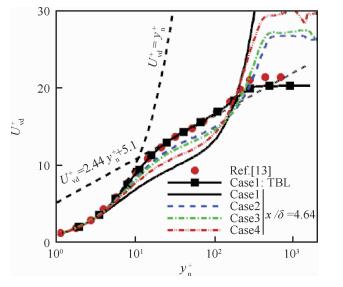
图 15给出各工况van-Driest转换后的平均速度剖面Uvd+。在上游可压缩湍流边界层内(TBL),本文计算得到的平均速度剖面在黏性底层呈现线性分布规律Uvd+=yn+,在对数率区30 < yn+ < 100符合对数律Uvd+=2.44yn++5.1,且与DNS结果[13]吻合良好。从Case2~Case4分布规律来看,膨胀效应对平均速度剖面的影响主要体现在对数区以及尾迹率区,黏性底层的变化可以忽略不计。如图所示,在对数率区,速度剖面已不再符合对数律,且入射激波位置的下游移动使得扰动边界层速度剖面更为远离对数律,更接近于Case1的结果。尾迹区的演化规律也呈现类似趋势。
|
| 图 15 平均速度剖面分布 Fig. 15 Distribution of mean velocity profile |
图 16(a)和图 16(b)分别给出了湍流边界层雷诺正应力τ11和切应力τ12的分布情况。从量值大小来看,由于激波对湍流的增强作用,雷诺应力呈现显著升高的趋势。相较于上游TBL,Case1雷诺正应力和切应力分别增大了约4倍和10倍。以往研究表明[38],强膨胀效应对湍流脉动具有抑制作用,会使得湍流边界层出现层流化的趋势。可以看到,Case2~Case4雷诺应力变化规律也进一步证实了该结论。此时,膨胀区内各分量量值急剧减小,与上游TBL已较为接近,但两者在分布规律方面仍存在着较大差异。如图所示,膨胀区内峰值雷诺应力出现在边界层外层区域yn/δ>0.3,而上游充分发展湍流边界层则集中在0.01 < yn/δ < 0.1的内层区域。

|
| 图 16 雷诺应力分量及结构参数 Fig. 16 Reynolds stress components and structureparameter |
为了进一步定量评估内外层雷诺应力演化机制的差异,图 16(c)还给出了结构参数-τ12/τii在边界层内分布情况。Klebanoff[39]和Grilli等[40]研究发现,结构参数在边界层0.1 < yn/δ < 0.8内基本维持不变,Reθ在697~2 788范围时,其量值范围约为0.14~0.16,如图 16(c)中方框所示。本文上游湍流边界层的计算结果也符合该分布规律。膨胀区内湍流边界层结构参数的分布有以下两个显著特征:首先,其量值明显小于TBL和平板再附边界层,特别是外层区域,这说明边界层仍处于强非平衡态;其次,膨胀效应对内外层结构呈现相反的作用机制,入射激波位置往下游移动使得内层结构参数(-τ12/τii)升高而外层降低。
图 17给出了膨胀区内湍流边界层雷诺应力各向异性张量不变量的分布情况, 图中横坐标为第3不变量IIIb,纵坐标为第2不变量IIb,定义为[40]

|
| 图 17 雷诺应力各向异性张量不变量 Fig. 17 Invariants of Reynolds stress anisotropy tensor |
| $ \left\{\begin{array}{l} b_{i j}=\widetilde{u^{\prime \prime} u^{\prime \prime}} / 2 K-1 / 3 \delta_{i j} \\ I I_{b}=b_{i j} b_{j i} \\ I I I_{b}=b_{i j} b_{j k} b_{k i} \end{array}\right. $ | (5) |
式中:上标~代表Favre平均;K代表湍动能。
与以往研究结果[40]一致:在上游可压缩TBL内,靠近壁面的区域,流动以两组元湍流为主,随后在近壁区则逐步逼近一组元湍流,而边界层外缘流动表征为各向同性状态。对于Case1,平板下游再附边界层内湍流状态在靠近壁面区域呈现两组元轴对称,近壁区内湍流则沿着轴对称压缩特征线变化,并在边界层外缘附近趋近于轴对称压缩状态,如图 17第2个图(放大图)所示,这与以往压缩拐角激波/湍流边界层干扰再附区的研究结果[40]是一致的。从Case3与Case1的结果比较来看(两者激波入射位置完全相同),膨胀效应使得下游再附边界层近壁区内湍流沿着两组元特征线逐步趋近一组元湍流状态,而边界层外缘呈现逼近各向同性状态的态势,这表明膨胀效应加速了下游再附边界层的恢复过程。从Case2和Case4的分布规律来看,激波入射流向位置的改变对近壁区内湍流状态的影响更为明显,而外层的变化则相对要小得多。可以看到,当入射激波位于膨胀角下游,近壁区湍流呈现远离一组元湍流的态势,与入射激波位于角区上游的演化规律完全相反,这很可能是此时恢复区较短的缘故。
可压缩湍动能的输运方程为[41]
| $ \frac{\partial \bar{\rho} K}{\partial t}=C+T+P+V++\mathit{\Pi}+\mathit{\varepsilon}+M $ | (6) |
式中:C为对流项;T为湍流输运项;P为生成项;V为黏性扩散项;П为压力膨胀项;ε为黏性耗散项;M为可压缩质量通量项。各项具体表达式可参见文献[41]。以往研究表明[41],湍动能输运机制中起主要作用的是生成项P、输运项T、扩散项V和耗散项ε。本节将重点研究膨胀效应对湍动能输运方程各项的影响规律。
首先,给出了上游TBL湍动能输运方程各项的分布情况,如图 18所示。为了便于比较验证,图中还给出了Schlatter和Örlü[42]的不可压缩DNS结果。这里的各项均采用当地ρwuτ4/νw进行归一化处理,其中ρw和νw分别为壁面密度以及动力学黏性系数。可以看到,本文计算结果与DNS结果[42]吻合良好。如图所示,在近壁区,湍流扩散项V和黏性耗散ε起主导作用,而在其他大部分区域内湍流的输运则是由湍流生成项P和黏性耗散ε共同决定。另外,湍流输运项的作用主要是将外层湍动能输运到壁面耗散掉。

|
| 图 18 上游湍流边界层湍动能输运方程各项分布 Fig. 18 Budget of turbulent kinetic energy in upstreamturbulent boundary layer |
图 19分别给出了膨胀区内湍动能输运方程各项的分布情况。总体来看,Case2~Case4膨胀区边界层近壁区和外层区域的湍动能输运机制均与上游湍流边界层较为类似,膨胀效应的影响主要是体现在各项具体量值。为了反映真实量值的变化规律,这里各项均采用无穷远处来流进行归一化。值得特别关注的是图 19(a)中的生成项。如图中黑色曲线所示,此时生成项在Case1的再附边界层内呈现双峰结构,外层峰值要明显高于内层峰值,这主要是由于此时再附边界层仍未恢复到平衡态,分离区剪切层产生的外层大尺度结构仍占主导。可以看到,膨胀效应使得内层生成项峰值升高,而外层生成项峰值降低。随着入射激波位置往下游移动,这一演化趋势有所缓解。从图 19(b)~图 19(d)中还可以清楚看到,膨胀效应显著降低了近壁区黏性耗散项、湍流输运项和湍流扩散项,特别是在内层yn/δ < 0.01的范围,但入射点流向位置改变对各项分布规律的影响可以忽略不计。

|
| 图 19 膨胀区湍动能输运方程各项分布(x/δ=4.64) Fig. 19 Budget of turbulent kinetic energy in expansion region(x/δ=4.64) |
这里采用本征正交分解方法探究膨胀角入射激波与湍流边界层干扰的非定常动力学过程。通过本征正交分解(Proper Orthogonal Decomposition, POD)方法可以对复杂高维度的流场进行低阶近似,提取出非定常演化历程中能量占优的特征模态。这里将着重分析入射激波在不同流向位置时膨胀效应对干扰区流场内非定常运动历程的影响机制。具体的POD分析方法介绍可参见文献[43]。
与Mustafa等[44]的研究相似,这里POD分析主要针对400个展向平均流向速度脉动场进行操作。假设非定常流向速度场Us(x, y, t),POD分析可以确定一族正交基函数Φj(x, y),j=1, 2, …,具体分解过程为[43]
| $ U_\text{s}(x, y, t)=\left\langle U_\text{s}(x, y, t)\right\rangle+\sum\limits_{j=1}^{N_\text{t}} a_{j}(t) \mathit{\Phi}_{j}(x, y) $ | (7) |
式中:〈Us(x, y, t)〉为时空平均场;aj(t)为第j个模态随时间变化的模态系数;Nt为模态总数。
图 20给出了各模态能量分布。为了验证POD分析结果的收敛性,图中还给出了Case1工况Nt=600的结果。可以看到,模态总数Nt分别取400和600时,能量分布曲线基本重合。因此,后续的POD分析都基于Nt=400的样本空间进行。从图 20(a)中整体分布趋势来看,随着模态阶数增大,模态能量急剧降低。值得注意的是,Case1高阶模态能量衰减符合j-11/9律,该研究结果与Mustafa等[44]在压缩拐角中的发现相吻合。同时还可以看到,Case2~Case4工况在膨胀效应作用下其高阶模态能量的衰减律与j-11/9律存在着较为明显的差异。此外,随着入射激波位置往下游移动,第1阶模态单调下降,第2阶模态能量变化较小,而高阶模态能量(j>10)则呈现较为明显的升高趋势。对于第1阶模态,其对总能量的贡献最大,下文也称为主能量模态。从图 20(b)中还可以清楚看到,相较于Case1、Case2~Case4工况模态累积能量曲线的梯度存在逐步升高的趋势,这说明高阶模态能量在总能量中的占比逐渐增强。以100~400阶模态为例,Case1时其能量占比约为8%,而Case4时其能量贡献增大到了约26%。

|
| 图 20 POD模态能量分布 Fig. 20 Energy distributions of POD modes |
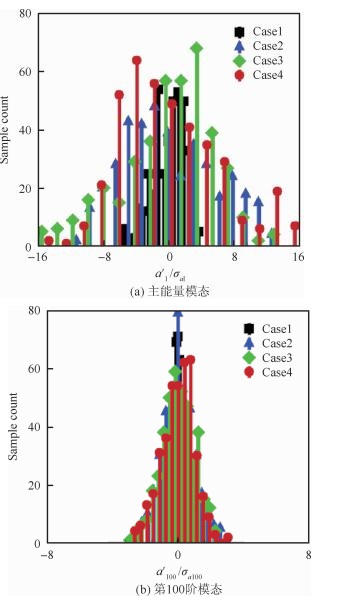
为了进一步考察主能量模态和高阶模态的差异,图 21分别给出了主能量模态和第100阶模态系数的频率分布直方图。可以看到,各工况主能量模态和高阶模态系数aj(t)均近似为对称分布,但两者的波动范围差异显著。可见,高阶模态系数的归一化脉动a′j(t)/σaj主要集中在[-2, 2]范围内,这里σaj为模态系数的均方根,而低阶模态系数在[-16, 16]的范围内仍存在一定的出现概率,这说明低阶模态的波动性要明显强于高阶模态。
|
| 图 21 POD模态系数aj(t)频数分布直方图 Fig. 21 Histogram of frequency distribution of time-varying coefficient aj(t) of POD modes |
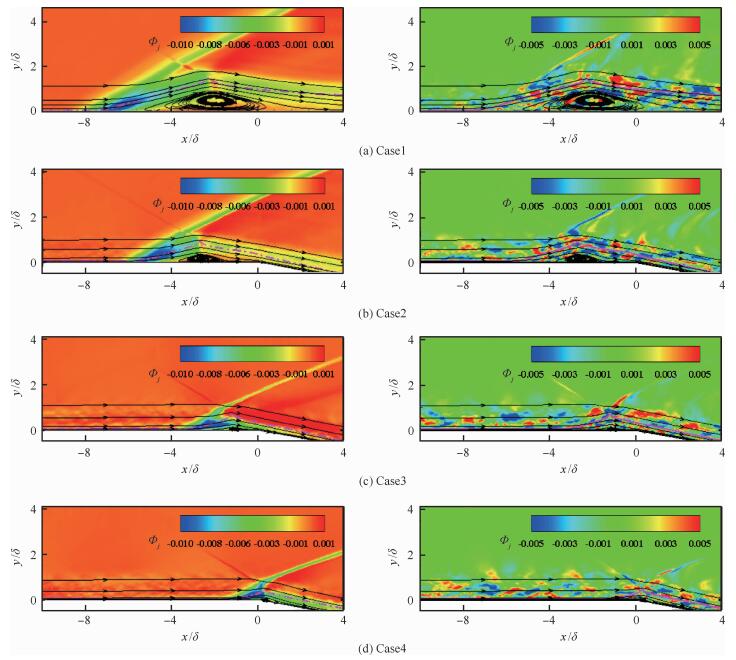
图 22分别给出了各工况下主能量模态和第100阶模态的空间结构分布。为了便于比较说明,图中黑色曲线和粉色点画线分别代表平均流线和声速线。如图所示,各工况下主能量模态空间结构特征与高阶模态完全不同,前者主要集中在分离激波附近及分离区内,特别是在分离泡剪切层角部、分离泡内及其下游再附区域。而高阶模态结构则表征为正负交替的小尺度结构, 这与湍流边界层内小尺度的高频脉动结构密切相关。可以看到,随着入射激波位置往下游移动,主能量模态及高阶模态结构的分布规律基本一致,只是特征结构分布区域有所减小。
|
| 图 22 POD模态1(左)和100(右)空间分布 Fig. 22 Spatial distributions of POD modes 1 (left) and 100 (right) |
此外,为了观察主能量模态和高阶模态动力学性质的差异,图 23分别基于POD主能量模态和高阶模态对膨胀角内非定常流场进行了低阶重构。这里定义如下变量Ms[45]:

|
| 图 23 基于POD主能量模态低价重构得到的分离泡流量随时间变化 Fig. 23 Time series of separation bubble flux basedon low-order reconstructions using the firstPOD mode |
| $ \left\{\begin{array}{l} M_\text{s}(x, t)=\int_{0}^{\infty} U_\text{s}^{\mathrm{re}}(x, y, t) \mathrm{d} y \\ U_\text{s}^{\mathrm{re}}(x, y, t)=\left\{\begin{array}{ll} 0 & U_{s}^{\mathrm{re}}>0 \\ -U_\text{s}^{\mathrm{re}} & U_\text{s}^{\mathrm{re}} \leqslant 0 \end{array}\right. \end{array}\right. $ | (8) |
式中:Usre为基于POD模态低阶重构得到的瞬时流向速度场。通过研究该变量的瞬时变化特征,可以直观地定量显示干扰区内分离泡的非定常运动历程。
图 23(a)给出了基于POD主能量模态重构得到M′s(xp, t)随时间的变化情况,这里瞬态脉动量M′s(xp, t)=Ms(xp, t)-〈Ms(xp, t)〉,〈·〉代表时间平均。图中各工况xp均取为分离泡的最大法向高度对应的流向位置(如图 6所示)。从量值大小来看,图 23(a)中Case1工况瞬态脉动量M′s(xp, t)要明显大于Case2~Case4,前者约为Case4工况的20倍,这说明膨胀效应作用下分离泡的瞬时脉动急剧衰减。与此同时,为了更好地比较分离泡的时间演化历程,图 23(b)采用最大值Max(M′s)对分离泡瞬时脉动进行了归一化处理。值得关注的是,尽管Case2~Case4工况下分离泡瞬时脉动急剧衰减,但其时间演化历程仍与Case1工况较为相似,均表征为低频膨胀/收缩过程,无量纲时间跨度约为100。尽管主能量模态系数aj(t)的频谱以宽频特征为主,但Case1~Case4工况的POD主能量模态占优频率均集中在低频区,因而各工况动力学过程较为接近,均以低频特征为主。以往研究均表明[12, 45-46],分离泡的膨胀/收缩运动是分离激波低频振荡的主要形成机制之一。然而,尽管此时Case2~Case4工况中分离泡脉动仍存在明显的低频膨胀/收缩过程,但是从图 13和图 14中物面压力脉动功率谱密度和各频段占比来看,在膨胀效应作用下分离激波的大尺度低频振荡被极大地抑制了。结果表明,此时Case2~Case4主能量模态主导的分离泡膨胀/收缩运动对分离激波非定常运动的影响较小。这很可能是由于主能量模态的能量贡献急剧减小,Case1时其能量占比约为60%,而Case4时急剧下降到了10%。另外,分离泡的流向尺度以及法向高度的急剧减小也是另一个重要影响因素。
图 24给出了基于POD第100阶模态重构得到M′s(xp, t)随时间的变化情况。各工况下分离泡瞬时脉动曲线较为类似。可以明显看到,此时高阶模态主导的分离泡非定常运动与主能量模态不同之处主要体现在以下两个方面。一方面,分离泡瞬态脉动量值要远小于前者,这主要是由于高阶模态对应为湍流边界层内的小尺度高频结构,其脉动能量远小于主能量模态;另一方面,从时间历程来看,分离泡脉动以高频振荡为主,这是高阶模态系数占优频率主要集中在高频区的缘故。

|
| 图 24 基于POD高阶模态低价重构得到的分离泡流量随时间变化 Fig. 24 Time series of separation bubble flux basedon low-order reconstructions using high-orderPOD mode |
本文采用直接数值模拟方法研究了来流马赫数2.9、30°激波角的入射激波与膨胀角湍流边界层相互作用问题,详细分析了入射激波分别位于膨胀角上游、膨胀角角点和膨胀角下游3种工况下膨胀角干扰区内复杂流动现象的一些基本问题,如分离泡、物面压力脉动及激波的非定常运动特性,膨胀区湍流边界层统计特性和相干结构动力过程等,得到以下结论:
1) 入射激波位置的改变对膨胀角分离泡影响显著。随着入射激波位置往下游移动,分离泡长度及高度急剧减小,特别是入射激波位于膨胀角角点和下游区域时,分离泡长度和高度分别约为无膨胀角工况的17%和10%。
2) 随着入射激波位置往下游移动,物面压力脉动急剧衰减,而概率密度函数的变化则可相对忽略不计。时空关联分析表明,分离泡内物面压力脉动对流速度均有所降低,而下游膨胀区对流速度将相对增大。研究发现,膨胀效应极大地抑制了分离激波的低频振荡运动。
3) 膨胀区再附湍流边界层仍处于非平衡态。统计结果表明,膨胀效应对平均速度剖面对数区和尾迹区影响显著。入射激波位置的改变将使得边界层内层结构参数升高而外层降低,同时近壁区内湍流呈现远离一组元湍流的态势。湍动能输运机制与无膨胀角工况基本类似,差异主要体现在输运方程各项的量值。
4) 速度场本征正交分解结果表明,膨胀角主能量模态的能量占比急剧降低,高阶模态能量占比逐渐增强。前者空间结构主要集中在分离激波以及剪切层根部附近,对应为分离泡的低频膨胀/收缩过程;而后者则以小尺度正负交替脉动结构为主,表征为分离泡高频脉动。入射激波位置的改变对膨胀区内动力学过程影响主要体现在分离泡脉动强度。
致谢
感谢国家超级计算天津中心、国家超级计算长沙中心、国家超级计算广州中心以及中国科学院网络中心超级计算中心提供计算机时。
| [1] | ZHELTOVODOV A A. Some advances in research of shock wave turbulent boundary layer interactions: AIAA-2006-0496[R]. Reston, VA: AIAA, 2006. |
| [2] | SELIG M S, ANDREOPOULOS J, MUCK K C, et al. Turbulence structure in a shock wave/turbulent boundary layer interaction[J]. AIAA Journal, 1989, 27(7): 862-869. |
| Click to display the text | |
| [3] | SETTLES G S, BOGDONOFF S M, VAS I E. Incipient separation of a supersonic turbulent boundary layer at high Reynolds number[J]. AIAA Journal, 1976, 14(1): 50-56. |
| Click to display the text | |
| [4] | ZHELTOVODOV A A, SCHULEIN E, HORSTMAN C. Development of separation in the region where a shock interacts with a turbulent boundary layer perturbed by rarefaction waves[J]. Journal of Applied Mechanics and Technical Physics, 1993, 34(3): 346-354. |
| Click to display the text | |
| [5] | CLEMENS N T, NARAYANASWAMY V. Low frequency unsteadiness of shock wave turbulent boundary layer interactions[J]. Annual Review of Fluid Mechanics, 2014, 46: 469-492. |
| Click to display the text | |
| [6] | GAITONDE D V. Progress in shock wave/boundary layer interactions[J]. Progress in Aerospace Sciences, 2015, 72: 80-99. |
| Click to display the text | |
| [7] | SMITS A J, MUCK K C. Experimental study of three shock wave/turbulent boundary layer interactions[J]. Journal of Fluid Mechanics, 1987, 182: 291-314. |
| Click to display the text | |
| [8] | ARDONCEAU P L. The structure of turbulence in a supersonic shock wave/boundary layer interaction[J]. AIAA Journal, 1984, 22(9): 1254-1262. |
| Click to display the text | |
| [9] | HUMBLE R A, SCARANO F. Unsteady aspects of an incident shock wave turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2009, 635: 47-74. |
| Click to display the text | |
| [10] | WU M, MARTIN M P. Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp[J]. AIAA Journal, 2007, 45(4): 879-889. |
| Click to display the text | |
| [11] | WU M, MARTIN M P. Analysis of shock motion in shock wave and turbulent boundary layer interaction using direct numerical simulation data[J]. Journal of Fluid Mechanics, 2008, 594: 71-83. |
| Click to display the text | |
| [12] | PRIEBE S, WU M, MARTIN M P. Low-frequency unsteadiness in shock wave turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2012, 699: 1-49. |
| Click to display the text | |
| [13] | PRIEBE S, WU M, MARTIN M P. Direct numerical simulation of a reflected shock wave turbulent boundary layer interaction[J]. AIAA Journal, 2009, 47(5): 1173-1185. |
| Click to display the text | |
| [14] | BOOKEY P B, WYCKHAM C, SMITS A J. Experimental investigations of Mach 3 shock wave turbulent boundary layer interaction: AIAA-2005-4899[R]. Reston, VA: AIAA, 2005. |
| [15] | LI X L, FU D X, MA Y W, et al. Direct numerical simulation of shock/turbulent boundary layer interaction in a supersonic compression ramp[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(9): 1651-1658. |
| Click to display the text | |
| [16] | TONG F L, YU C P, TANG Z G, et al. Numerical studies of shock wave interactions with a supersonic turbulent boundary layer in compression corner:Turning angle effects[J]. Computers and Fluids, 2017, 149: 56-69. |
| Click to display the text | |
| [17] | TONG F L, TANG Z G, YU C P, et al. Numerical analysis of shock wave and supersonic turbulent boundary interaction between adiabatic and cold walls[J]. Journal of Turbulence, 2017, 18(6): 569-588. |
| Click to display the text | |
| [18] | TONG F L, LI X L, DUAN Y H, et al. Direct numerical simulation of supersonic turbulent boundary layer subjected to a curved compression ramp[J]. Physics of Fluids, 2017, 29: 125101. |
| Click to display the text | |
| [19] | CHEW Y T. Shock wave and boundary layer interaction in the presence of an expansion corner[J]. Aeronautical Quarterly, 1979, 30: 506-527. |
| Click to display the text | |
| [20] | CHUNG K M, LU F K. Hypersonic turbulent expansion-corner flow with shock impingement[J]. Journal of Propulsion and Power, 1995, 11(3): 441-447. |
| Click to display the text | |
| [21] | WHITE M E, AULT D A. Expansion corner effects on hypersonic shock wave/turbulent boundary-layer interactions[J]. Journal of Propulsion and Power, 1996, 12(6): 1169-1173. |
| Click to display the text | |
| [22] | SATHIANARAYANAN A, VERMA S B. Experimental investigation of an incident shock-induced interaction near an expansion corner[J]. AIAA Journal, 2017, 54(3): 769-773. |
| Click to display the text | |
| [23] | KONOPKA M, MEINKE M, SCHRODER W. Large-eddy simulation of relaminarization in supersonic flow: AIAA-2012-2978[R]. Reston, VA: AIAA, 2012. |
| [24] |
童福林, 周桂宇, 周浩, 等. 激波/湍流边界层干扰物面剪切应力统计特性[J]. 航空学报, 2019, 40(5): 122504. TONG F L, ZHOU G Y, ZHOU H, et al. Statistical characteristics of wall shear stress in shock wave and turbulent boundary layer interactions[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(5): 122504. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [25] | MARTIN M P, TAYLOR E M, WU M. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence[J]. Journal of Computational Physics, 2006, 220: 270-289. |
| Click to display the text | |
| [26] | PIROZZOLI S, GRASSO F. Direct numerical simulation of impinging shock wave turbulent boundary layer interaction at M=2.25[J]. Physics of Fluids, 2006, 18: 065-113. |
| [27] | SIMPSON R L. Turbulent boundary-layer seperation[J]. Annual Review of Fluid Mechanics, 1989, 21: 205-234. |
| Click to display the text | |
| [28] | FANG J, YAO Y F, ZHELTOVODOV A A, et al. Direct numerical simulation of supersonic turbulent flows around a tandem expansion-compression corner[J]. Physics of Fluids, 2015, 27: 125104. |
| Click to display the text | |
| [29] |
史爱明, DOWELL E H. 斜激波总压损失率极小值理论解及物理意义[J]. 航空学报, 2018, 39(12): 122517. SHI A M, DOWELL E H. Theoretical solutions and physical significances for minimum ratio of total pressure loss by oblique shock[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 122517. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [30] | LOGINOV M S, ADAMS N A, ZHELTOVODOV A A. Large eddy simulation of shock wave/turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2006, 565: 135-169. |
| Click to display the text | |
| [31] | PASQUARIELLO V, HICKEL S, ADAMS N A. Unsteady effects of strong shock wave/boundary layer interaction at high Reynolds number[J]. Journal of Fluid Mechanics, 2017, 823: 617-657. |
| Click to display the text | |
| [32] | BERNARDINI M, PIROZZOLI S. Wall pressure fluctuations beneath supersonic turbulent boundary layers[J]. Physics of Fluids, 2011, 23: 085102. |
| Click to display the text | |
| [33] | MUCK K C, ANDREOPOULOS J, DUSSAUGE J P. Unsteady nature of shock wave/turbulent boundary layer interaction[J]. AIAA Journal, 1988, 26(2): 179-187. |
| Click to display the text | |
| [34] | WILLMARTH W W, WOOLDRIDGE C E. Measurements of the fluctuating pressure at the wall beneath a thick turbulent boundary layer[J]. Journal of Fluid Mechanics, 1962, 14: 187-210. |
| Click to display the text | |
| [35] | SCHEWE G. On the structure and resolution of wall pressure fluctuations associated with turbulent boundary layer flow[J]. Journal of Fluid Mechanics, 1983, 134: 311-328. |
| Click to display the text | |
| [36] | TAN D K M, TRAN T T, BOGDONOFF S M. Wall pressure fluctuations in a three-dimensional shock wave/turbulent boundary layer interaction[J]. AIAA Journal, 1987, 25(1): 14-21. |
| Click to display the text | |
| [37] | MAESTRELLO L. Radiation from and panel response to a supersonic turbulent boundary layer: DOC. D1-82-0719[R]. Seattle: Boeing Scientific Research Laboratories, 1968. |
| [38] | ARNETTE S A, SAMIMY M, ELLIOTT G S. The effects of expansion on the turbulence structure of compressible boundary layers[J]. Journal of Fluid Mechanics, 1998, 367: 67-105. |
| Click to display the text | |
| [39] | KLEBANOFF P S. Characteristics of turbulence in a boundary layer with zero pressure gradient: NACA Report 1247[R]. Washington, D.C.: NASA, 1955. |
| [40] | GRILLI M, HICKEL S, ADAMS N A. Large-eddy simulation of a supersonic turbulent boundary layer over a compression-expansion ramp[J]. International Journal of Heat and Fluid Flow, 2013, 42: 79-93. |
| Click to display the text | |
| [41] | PIROZZOLI S, BERNARDINI M. Direct numerical simulation database for impinging shock wave/turbulent boundary layer interaction[J]. AIAA Journal, 2011, 49(6): 1307-1312. |
| Click to display the text | |
| [42] | SCHLATTER P, ORLU R. Assessment of direct numerical simulation data of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2010, 659: 116-126. |
| Click to display the text | |
| [43] | TAIRA K, BRUNTON S L, DAWSON S T, et al. Modal analysis of fluid flows:An overview[J]. AIAA Journal, 2017, 55(12): 1-29. |
| Click to display the text | |
| [44] | MUSTAFA M A, PARZIALE N J, SMITH M S, et al. Amplification and structure of streamwise velocity fluctuations in compression corner shock wave/turbulent boundary layer interactions[J]. Journal of Fluid Mechanics, 2019, 863: 1091-1122. |
| Click to display the text | |
| [45] |
童福林, 李新亮, 段焰辉. 超声速压缩拐角激波/边界层干扰动力学模态分解[J]. 航空学报, 2017, 38(12): 121376. TONG F L, LI X L, DUAN Y H. Dynamic mode decomposition of shock wave and supersonic boundary layer interactions in a compression ramp[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(12): 121376. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [46] | GRILLI M, SCHMID P J, HICKEL S, et al. Analysis of unsteady behavior in shock wave turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2012, 700: 16-28. |
| Click to display the text |



