由于空间任务的日益频繁和深入，各国都相继开展或实施了在轨服务技术研究。具体研究任务形式有:对报废航天器的离轨操作，对失效航天器的在轨维修，对燃料耗尽航天器的在轨加注等等。总之，航天器的在轨服务成为目前航天技术必须面对和亟需解决的一个关键课题^[1]。

为了对目标航天器进行在轨服务，通常服务航天器首先需要捕获目标航天器。在捕获前服务航天器需要能够与目标航天器同步运动，以便对接; 捕获后两者的组合体可能需要稳定或者重定向等^[2]，这些都需要控制航天器姿态和角速度能够跟踪上一个预定的参考轨迹。但是，由于燃料的消耗、航天器构型的变换或模块的转移以及对目标的捕获组成双星复合系统等，都会造成系统的惯性特性(质量、质心、转动惯量矩阵)等发生较大变化，并且这个变化通常事先是未知的^[3]。因此，本文研究惯性参数未知的航天器姿态跟踪控制具有重大的实际意义。

针对被控对象中含有参数不确定的模型，自适应控制由于不需要被控对象的先验信息而得到了广泛的研究^[4]。传统的自适应控制方法是基于等价确定性(Certainty Equivalence, CE)^[3-5]原则而设计的。但是由于CE方法中参数估计更新律是通过Lyapunov函数导数中干扰项的精确抵消而来的，导致其更新律中不含有自身的负反馈项。参数估计误差和跟踪误差的直接耦合，造成了系统闭环性能的下降。

针对该问题，Astolfi等^[6-7]开创性提出了一种非等价确定性(Non-Certainty Equivalence, Non-CE)理论:浸入与不变(Immersion and Invariance, I&I)理论。通过在参数估计中增加一项关于状态的修正项，从而间接将未知参数引入到参数估计动态当中。通过合理设计，可以把参数估计误差动态与其自身直接建立起联系，这在CE方法中是做不到的。但是，由于理论上，获得修正项的具体形式需要求解一个偏微分方程(Partial Differential Equation, PDE)。对于一阶系统，方程的解析解总是存在并很容易通过积分求解; 但对于高阶系统，方程有解析解需要满足比较严格的条件，在实际情形中一般不满足，通常被称为“可积分性障碍(Integrability Obstacle)”，这使得其应用受到极大的限制^[8-11]。

针对该障碍，Seo和Akella^[8-9]提出了一种基于滤波方法(Filter-based)的控制器，通过巧妙构造一个指数收敛的增广滤波系统，然后通过增广滤波状态设计修正项和控制器，使得整个闭环系统具有I&I理论的特点，从而间接地避免了求解PDE。虽然该方法给I&I控制器设计提供了一种新的思路，但是缺点是低通滤波器降低了系统的带宽; 并且对增广系统滤波，会导致闭环系统的阶数急剧增加，大大加重了计算负担。

Karagiannis等^[11-12]开创性地将动态放缩法(Dynamic Scaling)运用到I&I控制器设计当中，该方法考虑参数回归矩阵不满足可积条件，通过引入状态滤波器，按照一定方式替换掉回归矩阵中的积分变量使得其可积并得到其近似解，然后运用动态放缩技术将近似解和真解之间误差部分消除。由于动态放缩法相比于Seo和Akella^[8-9]提出的增广滤波法，只需对被积状态设计滤波器，因此明显地降低了闭环系统的阶数，优势比较突出，吸引了一大批研究者的关注^[13-18]，极大推进了I&I理论的发展。但是，基于动态放缩法的控制器设计过程中，动态放缩因子为单调递增函数，尽管能够证明有界，但是事先并不知会增大到多大; 而控制器和滤波器动态反馈增益系数与放缩因子的平方呈线性关系，这些因素会导致控制器反馈增益很大，可能会出现不希望的瞬态特性。

Yang等^[17]首次将动态放缩法的I&I理论运用到航天器的姿态控制模型中。针对参数回归矩阵不可积的困难，通过添加一个补偿矩阵使其可积，然后利用构造的角速度滤波器或者参考角速度信号来抵消补偿矩阵的影响，并用动态放缩技术将其影响消除。并且针对动态放缩因子单调递增所带来“高增益”控制现象，通过使用“三标量动态(three scalar dynamics)”方法构造一个动态调节系数，使递减的调节系数中和放缩因子的增长。虽然该文章也提出了基于动态放缩法I&I控制器，但是需要额外设计标量动态，并且需要事先知道惯性矩阵的最小特征值的下界，这给实际应用带来了困难。

Wen等^[18]同样将动态放缩法和I&I方法应用在姿态跟踪模型上，采用的是文献[11]中的回归矩阵改造技巧，但是创新地提出了修正缩放因子和附加调节系数动态，使得控制器中不需要惯量矩阵最小特征值，也能约束缩放因子在一个事先确定的上界内。但是该方法只是将反馈增益与缩放因子从平方线性关系修正到呈线性关系，仍需要调节系数来中和缩放因子的增长。

目前国内相关的研究^[19-23]只是将I&I理论结合一些backstepping或者滑模控制方法应用到一些较简单的实际模型中。所考虑的模型都是可以拆分成一维的子系统的级联形式，此时的PDE可以直接通过积分求解，不存在不可解的问题。而本文中姿态控制、机械臂等强耦合非线性多维系统并不能直接利用I&I方法进行设计，因为其PDE并不能直接积分求解，国内文献在这方面并没有深入研究。

本文针对航天器姿态跟踪控制模型，采用I&I理论，提出了一种新的参数回归矩阵改造方式，解决了“可积分性障碍”。通过引入全新的缩放因子形式，利用动态放缩技术证明了矩阵改造带来的误差不影响闭环系统的稳定性，并且设计的姿态跟踪自适应控制器不需要缩放因子信息，也不需要惯量矩阵的最小特征值信息，有效地减小了闭环系统复杂度和闭环系统阶数，并且保证了跟踪误差的渐近收敛。

本文结构如下:第1节对本文所研究的问题进行了详细描述; 第2节对本文提出的矩阵改造方法进行了介绍，并依据该方法给出了一种新的I&I姿态跟踪控制律; 且第2节用Lyapunov方法证明了所设计控制器的稳定性; 第3节通过数值仿真，将本文设计的控制器与CE方法的控制器和Filter-based方法的控制器进行了对比分析，表明了本文设计方法的有效性和优越性; 最后，在第4节中对相关研究内容作了简单总结。

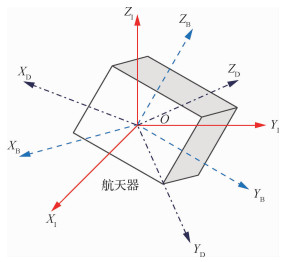
1 问题描述 1.1 坐标系定义

航天器姿态跟踪问题中，通常会涉及到3个坐标系:惯性坐标系F_I、本体坐标系F_B和期望坐标系F_D。由于姿态控制只考虑本体坐标系的相对方位，而不考虑其质心的位置，所以以上3个坐标系均以航天器质心O为原点。其中，惯性坐标系作为基准坐标系，本体坐标系和期望坐标系的姿态均是相对于惯性坐标系而言; 本体坐标系与航天器固连，其坐标轴的方位也就代表了航天器的方位; 期望坐标系是一个引入的假想坐标系，坐标轴的相对方位由要跟踪的期望方位确定。坐标系的示意图如图 1所示。姿态跟踪的任务就是控制航天器，使其固连的本体坐标系与期望坐标系重合。

1.2 动力学模型

本文采用全局无奇异的四元数来描述刚体的姿态动力学方程

$ \mathit{\boldsymbol{\dot q}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{q}}_{\rm{v}}^{\rm{T}}}\\ {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{\rm{v}}^ \times } \end{array}} \right]\mathit{\boldsymbol{\omega }} $	（1）

$ \mathit{\boldsymbol{J\dot \omega }} = - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{u}} $	（2）

式中:q=[q₀ q_v^T]^T=[q₀ q₁ q₂ q₃]^T∈R⁴为航天器本体系F_B相对惯性系F_I的姿态四元数，且有‖q‖²=q₀²+q_v^Tq_v=1;I₃为3阶单位矩阵; ω=[ω₁ ω₂ ω₃]^T∈R³为航天器相对于惯性系F_I的角速度，且在本体系F_B中表达; u∈R³为本体坐标系中表达的作用在航天器上的力矩，表示系统的控制输入; J为表达在本体坐标系中的惯量矩阵，因此是一个常量矩阵; 叉乘算子v^×作用在矢量v=[v₁ v₂ v₃]^T上，得到以下反对称矩阵:

$ {\mathit{\boldsymbol{v}}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {v_3}}&{{v_2}}\\ {{v_3}}&0&{ - {v_1}}\\ { - {v_2}}&{{v_1}}&0 \end{array}} \right] $

满足对任意的矢量v、w∈R，v^×w=v×w; 并且存在性质‖v^×‖=‖v‖，其中，‖·‖表示相应向量或矩阵的2-范数。

由四元数q得到的从F_I到F_B的坐标变换矩阵为

$ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{I}}_3} - 2{q_0}\mathit{\boldsymbol{q}}_{\rm{v}}^ \times + 2\mathit{\boldsymbol{q}}_{\rm{v}}^ \times \mathit{\boldsymbol{q}}_{\rm{v}}^ \times $	（3）

假设，被跟踪的期望姿态四元数和期望角速度轨迹为q_d=[q_d0 q_dv^T]^T和ω_d，ω_d为光滑函数，且其一阶和二阶导数均有界; 由q_d定义的从F_I到F_D的坐标变换矩阵为R_d。那么可以得到四元数跟踪误差为

$ {\mathit{\boldsymbol{q}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {{q_{{\rm{e}}0}}}\\ {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{q_{{\rm{do}}}}{q_0} + \mathit{\boldsymbol{q}}_{{\rm{dv}}}^{\rm{T}}{\mathit{\boldsymbol{q}}_{\rm{v}}}}\\ {{q_{{\rm{d0}}}}{\mathit{\boldsymbol{q}}_{\rm{v}}} - {q_0}{\mathit{\boldsymbol{q}}_{{\rm{dv}}}} - \mathit{\boldsymbol{q}}_{{\rm{dv}}}^ \times {\mathit{\boldsymbol{q}}_{\rm{v}}}} \end{array}} \right] $

（4）

从F_D到F_B的坐标变换矩阵为

$ {\mathit{\boldsymbol{R}}_{\rm{e}}} = {\mathit{\boldsymbol{I}}_3} - 2{q_{{\rm{e}}0}}\mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times + 2\mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times \mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times $	（5）

角速度跟踪误差为

$ {\mathit{\boldsymbol{\omega }}_{\rm{e}}} = \mathit{\boldsymbol{\omega }} - {\mathit{\boldsymbol{R}}_{\rm{e}}}{\mathit{\boldsymbol{\omega }}_{\rm{d}}} = \mathit{\boldsymbol{\omega }} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $	（6）

式中:Ω=R_eω_d为ω_d在本体坐标系中表达的期望角速度。

这里不加推导地给出航天器姿态跟踪的动力学模型为^[17-18]

$ {{\dot q}_{{\rm{e}}0}} = - \frac{1}{2}\mathit{\boldsymbol{q}}_{{\rm{ev}}}^{\rm{T}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} $	（7）

$ {{\mathit{\boldsymbol{\dot q}}}_{{\rm{ev}}}} = \frac{1}{2}\left( {{q_{{\rm{e}}0}}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times } \right){\mathit{\boldsymbol{\omega }}_{\rm{e}}} $	（8）

$ \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}} $	（9）

式中:${\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}} = {\mathit{\boldsymbol{R}}_{\rm{e}}}{\mathit{\boldsymbol{\dot \omega }}_{\rm{d}}}$。本文接下来的设计问题可以描述为:假设航天器姿态信号和角速度信号都能精确测量，设计控制器u，使得航天器能够准确跟踪上期望的姿态四元数q_d(t)和角速度ω_d(t)，即满足t→∞时，q_ev(t), ω_e(t)→0。

1.3 参数线性化

由于J为实对称常量矩阵，可以写为

$ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}&{{J_{13}}}\\ {{J_{12}}}&{{J_{22}}}&{{J_{23}}}\\ {{J_{13}}}&{{J_{23}}}&{{J_{33}}} \end{array}} \right] $

J包含6个未知参数，可以设未知参数向量为

$ \mathit{\boldsymbol{\theta }} = {\left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}&{{J_{13}}}&{{J_{22}}}&{{J_{23}}}&{{J_{33}}} \end{array}} \right]^{\rm{T}}} $

为了方便后面控制器的设计，将式(9)改造为

$ {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - {k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{J}}^{ - 1}}\left( {\mathit{\boldsymbol{W\theta }} + \mathit{\boldsymbol{u}}} \right) $	（10）

式中:k_q>0和k_ω>0分别为姿态误差反馈增益系数和角速度误差反馈增益系数，为待定常数; 根据线性参数化性质:

$ \mathit{\boldsymbol{W\theta }} = - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}} + \mathit{\boldsymbol{J}}\left( {{k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} + {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right) $

（11）

式中:W=W(ω, q_ev, Ω, Ω_d)∈R^3×6为参数回归矩阵。

2 基于动态放缩法的I&I控制器设计

考虑如下形式的控制器设计:

$ \mathit{\boldsymbol{u}} = - \mathit{\boldsymbol{W\hat \theta }} $	（12）

式中:$\mathit{\boldsymbol{\hat \theta }}$为对未知参数θ的估计。系统(10)可以进一步改写为

$ {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - {k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} - {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{W\tilde \theta }} $	（13）

式中:$\mathit{\boldsymbol{\tilde \theta }} = \mathit{\boldsymbol{\hat \theta }} - \mathit{\boldsymbol{\theta }}$为参数估计误差。

基于浸入与不变的思想，接下来需要设计合适的参数估计器，使得闭环系统最终收敛到流形面$M = \left\{ {\mathit{\boldsymbol{\widehat \theta }}, \mathit{\boldsymbol{\theta }} \in {{\bf{R}}^6}|\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} = \mathit{\boldsymbol{W}}(\mathit{\boldsymbol{\widehat \theta }} - \mathit{\boldsymbol{\theta }}) = {\bf{0}}} \right\}$上。

2.1 参数估计

根据I&I方法，参数估计一般由2项组成，因此考虑如下的参数估计形式:

$ \mathit{\boldsymbol{\hat \theta }} = \mathit{\boldsymbol{\alpha }} + \mathit{\boldsymbol{\beta }}\left( {\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{\varphi }}} \right) $	（14）

式中:β(ω, φ)为修正项。其中φ={φ_i}(i=1, 2, 3, …)为修正项β中除角速度ω以外的完全已知信号(φ_i和$\mathit{\boldsymbol{\dot \varphi }}$_i均已知)。若令

$ \mathit{\boldsymbol{\dot \alpha }} = \frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial \mathit{\boldsymbol{\omega }}}}\left( {{k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} + {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} - \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}} \right) - \sum\limits_i {\frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial {\mathit{\boldsymbol{\varphi }}_i}}}{{\mathit{\boldsymbol{\dot \varphi }}}_i}} $

（15）

那么对${\mathit{\boldsymbol{\widetilde \theta }}}$求导，并考虑θ为常数，可得

$ \mathit{\boldsymbol{\dot {\tilde \theta} }} = \mathit{\boldsymbol{\dot \alpha }} + \frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial \mathit{\boldsymbol{\omega }}}}\left( {{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} + \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}} \right) + \sum\limits_i {\frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial {\mathit{\boldsymbol{\varphi }}_i}}}{{\mathit{\boldsymbol{\dot \varphi }}}_i}} = - \frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial \mathit{\boldsymbol{\omega }}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{W\tilde \theta }} $

（16）

为了保证闭环系统最终收敛到流形面M上，需要求解一个偏微分方程，从而得出修正项β的具体形式

$ \frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial \mathit{\boldsymbol{\omega }}}} = \gamma {\mathit{\boldsymbol{W}}^{\rm{T}}} $	（17）

但是，式(17)有解的条件是W^T∈R^6×3为雅克比矩阵，即

$ \begin{array}{l} \mathit{\boldsymbol{\beta }} = \gamma \int\limits_\mathit{\boldsymbol{\omega }} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{w}}_1^{\rm{T}}}&{\mathit{\boldsymbol{w}}_2^{\rm{T}}}&{\mathit{\boldsymbol{w}}_3^{\rm{T}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{d}}{\omega _1}}\\ {{\rm{d}}{\omega _2}}\\ {{\rm{d}}{\omega _3}} \end{array}} \right]} = \\ \;\;\;\;\;\gamma \int\limits_\mathit{\boldsymbol{\omega }} {\mathit{\boldsymbol{w}}_1^{\rm{T}}{\rm{d}}{\omega _1} + \mathit{\boldsymbol{w}}_2^{\rm{T}}{\rm{d}}{\omega _2} + \mathit{\boldsymbol{w}}_3^{\rm{T}}{\rm{d}}{\omega _3}} \end{array} $

（18）

式中: w_i^T(i=1, 2, 3)为矩阵W^T的第i列。根据数学知识，式(18)能够积分得到解析解，需要满足积分与路径(状态ω轨迹)无关的条件，即需要满足w₁^Tdω₁+w₂^Tdω₂+w₃^Tdω₃是某个函数的全微分，其判定条件是

$ \frac{{\partial \mathit{\boldsymbol{w}}_1^{\rm{T}}}}{{\partial {\omega _2}}} = \frac{{\partial \mathit{\boldsymbol{w}}_2^{\rm{T}}}}{{\partial {\omega _1}}},\frac{{\partial \mathit{\boldsymbol{w}}_1^{\rm{T}}}}{{\partial {\omega _3}}} = \frac{{\mathit{\boldsymbol{w}}_3^{\rm{T}}}}{{\partial {\omega _1}}},\frac{{\partial \mathit{\boldsymbol{w}}_2^{\rm{T}}}}{{\partial {\omega _3}}} = \frac{{\partial \mathit{\boldsymbol{w}}_3^{\rm{T}}}}{{\partial {\omega _2}}} $

（19）

式(19)是一个很强的限制条件，在强耦合非线性系统中，参数回归矩阵一般不满足该条件。在本文航天器姿态跟踪模型中，由式(11)得到的参数回归矩阵W^T由于叉乘矩阵ω^×的存在，使得W^T不满足式该条件，也即式(17)不可解。因此，按照传统I&I控制器设计方法在这里遇到了极大的阻碍。

观察式(11)并将其分解为

$ \begin{array}{l} \mathit{\boldsymbol{W\theta }} = \mathit{\boldsymbol{J}}\left( {{k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}}} \right) + {k_\mathit{\boldsymbol{\omega }}}\mathit{\boldsymbol{J\omega }} + \\ \;\;\;\;\;\;\;\left( { - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right) = \\ \;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{W}}_1} + {\mathit{\boldsymbol{W}}_2} + {\mathit{\boldsymbol{W}}_3}} \right)\mathit{\boldsymbol{\theta }} \end{array} $

（20）

对于Jx=M(x)θ，可得其参数回归矩阵形式为

$ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}&0&0&0\\ 0&{{x_1}}&0&{{x_2}}&{{x_3}}&0\\ 0&0&{{x_1}}&0&{{x_2}}&{{x_3}} \end{array}} \right] $	（21）

式中:x=[x₁ x₂ x₃]^T。对比观察式(17)和式(18)，可知

$ {\mathit{\boldsymbol{W}}_1} = \mathit{\boldsymbol{M}}\left( {{k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}}} \right),{\mathit{\boldsymbol{W}}_2} = {k_\mathit{\boldsymbol{\omega }}}\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{\omega }} \right) $

（22）

可以验证条件(19)发现，回归矩阵W₁^T和W₂^T满足可积条件(19)，并且若令

$ {\mathit{\boldsymbol{\beta }}_1} = \mathit{\boldsymbol{W}}_1^{\rm{T}}\mathit{\boldsymbol{\omega }} $	（23）

$ {\mathit{\boldsymbol{\beta }}_2} = {k_\mathit{\boldsymbol{\omega }}}{\left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\omega _1^2}&{{\omega _1}{\omega _2}}&{{\omega _1}{\omega _3}}&{\frac{1}{2}\omega _2^2}&{{\omega _2}{\omega _3}}&{\frac{1}{2}\omega _3^2} \end{array}} \right]^{\rm{T}}} $	（24）

则有$\frac{{\partial {\mathit{\boldsymbol{\beta }}_1}}}{{\partial \mathit{\boldsymbol{\omega }}}} = \mathit{\boldsymbol{W}}_1^{\rm{T}}和\frac{{\partial {\mathit{\boldsymbol{\beta }}_2}}}{{\partial \mathit{\boldsymbol{\omega }}}} = \mathit{\boldsymbol{W}}_2^{\rm{T}}$。对于－ω^×Jω+Jω^×Ω=W₃θ可得其回归矩阵W₃为

$ \begin{array}{l} {\mathit{\boldsymbol{W}}_3} = \left( {\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right) = \left[ {\begin{array}{*{20}{c}} 0&{{\omega _1}{\omega _3}}&{ - {\omega _1}{\omega _2}}&{{\omega _2}{\omega _3}}&{\omega _3^2 - \omega _2^2}&{ - {\omega _2}{\omega _3}}\\ { - {\omega _1}{\omega _3}}&{ - {\omega _2}{\omega _3}}&{\omega _1^2 - \omega _3^2}&0&{{\omega _1}{\omega _2}}&{{\omega _1}{\omega _3}}\\ {{\omega _1}{\omega _2}}&{\omega _2^2 - \omega _1^2}&{{\omega _2}{\omega _3}}&{ - {\omega _1}{\omega _2}}&{ - {\omega _1}{\omega _3}}&0 \end{array}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\omega _2}{\mathit{\Omega }_3} - {\omega _3}{\mathit{\Omega }_2}}&{{\omega _3}{\mathit{\Omega }_1} - {\omega _1}{\mathit{\Omega }_3}}&{{\omega _1}{\mathit{\Omega }_2} - {\omega _2}{\mathit{\Omega }_1}}&0&0&0\\ 0&{{\omega _2}{\mathit{\Omega }_3} - {\omega _3}{\mathit{\Omega }_2}}&0&{{\omega _3}{\mathit{\Omega }_1} - {\omega _1}{\mathit{\Omega }_3}}&{{\omega _1}{\mathit{\Omega }_2} - {\omega _2}{\mathit{\Omega }_1}}&0\\ 0&0&{{\omega _2}{\mathit{\Omega }_3} - {\omega _3}{\mathit{\Omega }_2}}&0&{{\omega _3}{\mathit{\Omega }_1} - {\omega _1}{\mathit{\Omega }_3}}&{{\omega _1}{\mathit{\Omega }_2} - {\omega _2}{\mathit{\Omega }_1}} \end{array}} \right] \end{array} $

（25）

可以证明，W₃^T不满足条件(19)，也就是不存在矢量β₃使得$\frac{{\partial {\mathit{\boldsymbol{\beta }}_3}}}{{\partial \mathit{\boldsymbol{\omega }}}} = \mathit{\boldsymbol{W}}_3^{\rm{T}}(\mathit{\boldsymbol{\omega }}, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }})$成立。此时若令

$ {\mathit{\boldsymbol{\beta }}_3} = \mathit{\boldsymbol{W}}_3^{\rm{T}}\left( {\mathit{\boldsymbol{\hat \omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)\mathit{\boldsymbol{\omega }} $	（26）

式中:$\mathit{\boldsymbol{\hat \omega }}$为经过以下滤波器生成

$ \mathit{\boldsymbol{\dot {\hat \omega} }} = - {k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} - {k_{\rm{f}}}\left( {\mathit{\boldsymbol{\hat \omega }} - \mathit{\boldsymbol{\omega }}} \right) $	（27）

式中:k_f为滤波器反馈增益，是一个待定的变量。那么，可以将修正项β(ω, φ)设计为

$ \mathit{\boldsymbol{\beta }}\left( {\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{\varphi }}} \right) = \gamma \left( {{\mathit{\boldsymbol{\beta }}_1} + {\mathit{\boldsymbol{\beta }}_2} + {\mathit{\boldsymbol{\beta }}_3}} \right) $	（28）

并且有

$ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{\beta }}}}{{\partial \mathit{\boldsymbol{\omega }}}} = \gamma {\left( {{\mathit{\boldsymbol{W}}_1} + {\mathit{\boldsymbol{W}}_2} + {\mathit{\boldsymbol{W}}_3}\left( {\mathit{\boldsymbol{\hat \omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)} \right)^{\rm{T}}} = \\ \;\;\;\;\gamma {\left( {\mathit{\boldsymbol{W}} - {\mathit{\boldsymbol{W}}_3}\left( {\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right) + {\mathit{\boldsymbol{W}}_3}\left( {\mathit{\boldsymbol{\hat \omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)} \right)^{\rm{T}}} = \gamma {\left( {\mathit{\boldsymbol{W}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} \right)^{\rm{T}}} \end{array} $

（29）

式中:γ>0为一个由设计者确定的调节系数，为常数; 并且Δ=${\mathit{\boldsymbol{W}}_3}(\mathit{\boldsymbol{\hat \omega }}, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}) - {\mathit{\boldsymbol{W}}_3}(\mathit{\boldsymbol{\omega }}, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }})$为矩阵改造带来的误差影响。现在，可以确定信号φ应包含如下信号

$ \mathit{\boldsymbol{\varphi }} = \left\{ {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }},{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}},\mathit{\boldsymbol{\hat \omega }}} \right\} $

为了后续叙述的简洁性和严谨性，首先给出L₂和L_∞范数的定义。

定义  对于定义在时间域[0 ∞)上的函数f(t)=f₁(t) f₁(t) … f_n(t)^T∈Rⁿ，若其2-范数满足:

$ {\left\| {\mathit{\boldsymbol{f}}\left( t \right)} \right\|_2} = \sqrt {\int_0^\infty {{\mathit{\boldsymbol{f}}^{\rm{T}}}\left( \tau \right)\mathit{\boldsymbol{f}}\left( \tau \right){\rm{d}}\tau } } < \infty $

则称f(t)是平方可积的，或称f(t)∈L₂; 若其∞-范数满足:

$ {\left\| {\mathit{\boldsymbol{f}}\left( t \right)} \right\|_\infty } = \mathop {\sup }\limits_t \left| {{f_i}\left( t \right)} \right| < \infty $

则称f(t)是有界的，或称f(t)∈L_∞。

接下来，根据以上内容，可以得出以下定理。

定理1  对于航天器系统(7)~系统(9)，在惯量矩阵完全未知的条件下，若控制器(12)中参数估计由式(15)和式(28)组成; 需要的反馈增益分别为

$ {k_\mathit{\boldsymbol{q}}} = 1 + {\delta _\mathit{\boldsymbol{q}}},{k_\mathit{\boldsymbol{\omega }}} = 1.5 + {\delta _\mathit{\boldsymbol{\omega }}} $	（30）

$ {k_{\rm{f}}} = 1 + {\delta _{\rm{d}}} + {\delta _{\rm{f}}} $	（31）

式中:δ_q, δ_ω, δ_f>0为任意正常数; δ_d为一个动态增益，其动态为

$ {{\dot \delta }_{\rm{d}}} = \lambda {\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} = \lambda {\left\| {\mathit{\boldsymbol{\hat \omega }} - \mathit{\boldsymbol{\omega }}} \right\|^2} $	（32）

式中:$\mathit{\boldsymbol{\tilde \omega }} = \mathit{\boldsymbol{\hat \omega }} - \mathit{\boldsymbol{\omega }}$为滤波误差; λ为调节系数。

则在控制器(12)的作用下，可以保证闭环系统渐近稳定，即有${\mathit{\boldsymbol{q}}_{{\rm{ev}}}}, {\mathit{\boldsymbol{\omega }}_{\rm{e}}}, \mathit{\boldsymbol{\tilde \omega }}, \mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} \in {L_2} \cap {L_\infty }和\mathit{\boldsymbol{\widetilde \theta }} \in {L_\infty }$。

证明  参见以下分析过程。

2.2 动态放缩法

为了方便以下的稳定性证明，定义如下的缩放参数估计误差:

$ \mathit{\boldsymbol{z}} = \frac{{\mathit{\boldsymbol{\tilde \theta }}}}{R} $	（33）

式中:R为缩放因子，由辅助缩放因子r确定，其定义式为

$ R = \frac{{\sqrt {{j_{\rm{m}}}} }}{{\exp \left( {\frac{{1 + C}}{2}} \right)}}\exp \left( {\sqrt {\ln f\left( r \right) + C} } \right) $	（34）

式中:j_m为惯量矩阵J的最小特征值; f(r)为上界缩放为1的某一饱和函数，例如双曲正切函数、反正切函数、sigmoid函数等。辅助缩放因子r的动态为

$ \dot r = \frac{\gamma }{{{j_{\rm{m}}}}} \cdot \frac{{f\left( r \right)\sqrt {\ln f\left( r \right) + C} }}{{{f^\prime }\left( r \right)}}{\left\| \Delta \right\|^2} $	（35）

注意到，若选取r(0)>0，不管f(r)是双曲正切函数、反正切函数，还是sigmoid函数，都能保证f(r)>0和f′(r)>0;并且根据f(r)的有界性，存在某一合适常数C，可以保证lnf(r)+C>0。因此，式(35)总是有意义的。

通过式(32)和式(33)，可得以下2个性质:

$ \frac{{\dot R}}{R} = \frac{{{f^\prime }\left( r \right)\dot r}}{{2f\left( r \right)\sqrt {\ln f\left( r \right) + C} }} = \frac{\gamma }{{2{j_{\rm{m}}}}}{\left\| \Delta \right\|^2} $	（36）

$ \begin{array}{l} {R^2} \le {\left[ {\frac{{\sqrt {{j_{\rm{m}}}} }}{{\exp \left( {\frac{{1 + C}}{2}} \right)}}\exp \left( {\frac{1}{2} + \frac{{\ln f\left( r \right) + C}}{2}} \right)} \right]^2} = \\ \;\;\;\;{j_{\rm{m}}}f\left( r \right) \end{array} $	（37）

对式(31)求导，并利用式(27)和式(34)可得

$ \mathit{\boldsymbol{\dot z}} = \frac{{\mathit{\boldsymbol{\dot {\tilde \theta} }}}}{R} - \frac{{\dot R}}{R}\mathit{\boldsymbol{z}} = - \gamma {\left( {\mathit{\boldsymbol{W}} + \Delta } \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - \frac{\gamma }{{2{j_{\rm{m}}}}}{\left\| \Delta \right\|^2}\mathit{\boldsymbol{z}} $	（38）

若选择以缩放参数估计误差z为变量的Lyapunov函数为

$ {V_\mathit{\boldsymbol{z}}} = \frac{1}{{2\gamma }}{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}} $	（39）

对式(39)求导，结合式(38)和杨不等式，得到

$ \begin{array}{l} {{\dot V}_\mathit{\boldsymbol{z}}} = - {\mathit{\boldsymbol{z}}^{\rm{T}}}{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - {\mathit{\boldsymbol{z}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - \\ \;\;\;\;\;\;\;\frac{1}{{2{j_{\rm{m}}}}}{\mathit{\boldsymbol{z}}^{\rm{T}}}{\left\| \Delta \right\|^2}\mathit{\boldsymbol{z}} \le {j_{\rm{m}}}{\left\| {{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}}} \right\|^2} - \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{z}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - \frac{1}{{2{j_{\rm{m}}}}}{\left\| {\Delta \mathit{\boldsymbol{z}}} \right\|^2} \le - \frac{{{j_{\rm{m}}}}}{2}{\left\| {{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}}} \right\|^2} \end{array} $

（40）

2.3 闭环系统稳定性分析

首先考虑以下Lyapunov函数:

$ {V_{\mathit{\boldsymbol{\tilde \omega }}}} = \frac{1}{2}{{\mathit{\boldsymbol{\tilde \omega }}}^{\rm{T}}}\mathit{\boldsymbol{\tilde \omega }} $	（41）

$ \begin{array}{l} {V_{\rm{e}}} = \left( {{k_\mathit{\boldsymbol{q}}} + {k_\mathit{\boldsymbol{\omega }}}} \right)\left[ {{{\left( {1 - {q_{{\rm{e0}}}}} \right)}^2} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^{\rm{T}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right] + \\ \;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\omega }}_{\rm{e}}^{\rm{T}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^{\rm{T}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} \end{array} $

（42）

注意到，式(30)自动满足k_q+k_ω>0.5，从而式(42)的正定性得到保证。

分别对式(38)和式(39)求导得到

$ {{\dot V}_{\mathit{\boldsymbol{\tilde \omega }}}} = {{\mathit{\boldsymbol{\tilde \omega }}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\tilde \omega} }} = R{{\mathit{\boldsymbol{\tilde \omega }}}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - {k_{\rm{f}}}{\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} $	（43）

$ \begin{array}{l} {{\dot V}_{\rm{e}}} = \left( {{k_\mathit{\boldsymbol{q}}} + {k_\mathit{\boldsymbol{\omega }}}} \right)\mathit{\boldsymbol{q}}_{{\rm{ev}}}^{\rm{T}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + \mathit{\boldsymbol{\omega }}_{\rm{e}}^{\rm{T}}\left( { - {k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\omega }{\mathit{\boldsymbol{\omega }}_{\rm{e}}} - } \right.\\ \;\;\;\;\;\left. {R{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}}} \right) + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^{\rm{T}}\left( { - {k_q}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} - } \right.\\ \;\;\;\;\;\left. {R{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}}} \right) + \mathit{\boldsymbol{\omega }}_{\rm{e}}^{\rm{T}}\left( {\frac{1}{2}\left( {{q_{{\rm{e0}}}}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times } \right){\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right) \le \\ \;\;\;\;\; - {k_\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - {k_\mathit{\boldsymbol{\omega }}}{\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - R{\left( {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} + {\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right)^{\rm{T}}} \cdot \\ \;\;\;\;\;{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} + \frac{{\left\| {{q_{{\rm{e0}}}}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times } \right\|}}{2}{\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} \le \\ \;\;\;\;\; - {k_\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - \left( {{k_\mathit{\boldsymbol{\omega }}} - \frac{1}{2}} \right){\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - \\ \;\;\;\;\;R{\left( {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} + {\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} \end{array} $

（44）

式(44)利用到了性质$\left\| {{q_{{\rm{e}}0}}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{{\rm{ev}}}^ \times } \right\| = \left\| {{\mathit{\boldsymbol{q}}_{\rm{e}}}} \right\| = 1$。

定义如下Lyapunov函数:

$ {V_{\rm{c}}} = {V_\mathit{\boldsymbol{z}}} + {V_{\mathit{\boldsymbol{\tilde \omega }}}} + {V_{\rm{e}}} $	（45）

对式(45)求导，并结合式(30)、式(31)、式(38)、式(43)和式(44)得到

$ \begin{array}{l} {{\dot V}_{\rm{c}}} \le - \frac{{{j_{\rm{m}}}}}{2}{\left\| {{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}}} \right\|^2} + R{{\mathit{\boldsymbol{\tilde \omega }}}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} - {k_{\rm{f}}}{\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} - \\ \;\;\;\;\;\;{k_\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - \left( {{k_\mathit{\boldsymbol{\omega }}} - \frac{1}{2}} \right){\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - \\ \;\;\;\;\;R{\left( {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} + {\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Wz}} \le \\ \;\;\;\;\; - \left( {{k_\mathit{\boldsymbol{q}}} - \frac{{{R^2}}}{{{j_{\rm{m}}}}}} \right){\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - \left( {{k_\mathit{\boldsymbol{\omega }}} - \frac{1}{2} - \frac{{{R^2}}}{{{j_{\rm{m}}}}}} \right) \cdot \\ \;\;\;\;\;{\left\| {{\omega _{\rm{e}}}} \right\|^2} - \left( {{k_{\rm{f}}} - \frac{{{R^2}}}{{{j_{\rm{m}}}}} - {\delta _{\rm{d}}}} \right){\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} \le \\ \;\;\;\;\; - {\delta _\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - {\delta _\mathit{\boldsymbol{\omega }}}{\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - \left( {{\delta _{\rm{f}}} + {\delta _{\rm{d}}}} \right){\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} \le 0 \end{array} $

（46）

因为V_z和V_c非增且有下界0，即存在极限。并且从式(40)和式(46)可知，V_z∈L_∞，V_c∈L_∞，从而有$\mathit{\boldsymbol{z}}, \mathit{\boldsymbol{\tilde \omega }}, {q_{{\rm{e}}0}}, {\mathit{\boldsymbol{q}}_{{\rm{ev}}}}, {\mathit{\boldsymbol{\omega }}_{\rm{e}}} \in {L_\infty }$。根据参考轨迹的有界性，即可得到$\mathit{\boldsymbol{\hat \omega }}, \mathit{\boldsymbol{\omega }} \in {L_\infty }$。继续分析前，先给出以下结论:对全局有界的x∈R³连续可微的矩阵函数W₃^T(x, Ω)，根据中值定理可知，存在一个正数L使得

$ \begin{array}{l} {\left\| {\mathit{\boldsymbol{W}}_2^{\rm{T}}\left( {\mathit{\boldsymbol{\hat \omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right) - \mathit{\boldsymbol{W}}_2^{\rm{T}}\left( {\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)} \right\|^2} = \\ \;\;\;\;\;\;\left\| {L\left( {\mathit{\boldsymbol{\hat \omega }},\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)} \right\|{\left\| {\mathit{\boldsymbol{\hat \omega }} - \mathit{\boldsymbol{\omega }}} \right\|^2} \le L{\left\| {\mathit{\boldsymbol{\hat \omega }} - \mathit{\boldsymbol{\omega }}} \right\|^2} \end{array} $

（47）

成立。这里, L($\mathit{\boldsymbol{\hat \omega }}$, ω, Ω)是某一有界矩阵函数，范数上界为某一未知常数L。

接着定义如下Lyapunov函数:

$ {V_{\rm{f}}} = \frac{1}{{2\lambda }}{\left( {{\delta _{\rm{d}}} - L} \right)^2} $	（48）

$ {V_{\rm{R}}} = \frac{1}{\gamma }{R^2} $	（49）

对以上Lyapunov函数求导，可得

$ {{\dot V}_{\rm{f}}} = \left( {{\delta _{\rm{d}}} - L} \right){\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} $	（50）

$ \begin{array}{l} {{\dot V}_{\rm{R}}} = \frac{2}{\gamma }R\dot R = \frac{2}{\gamma } \cdot \frac{{\dot R}}{R}{R^2} = \\ \;\;\;f\left( r \right){\left\| \Delta \right\|^2} \le {\left\| \Delta \right\|^2} \le L{\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} \end{array} $	（51）

最后定义总的Lyapunov函数为

$ V = {V_{\rm{c}}} + {V_{\rm{f}}} + {V_{\rm{R}}} $	（52）

根据式(46)、式(50)和式(51)的结果，对式(52)求导得

$ \begin{array}{l} \dot V \le - {\delta _\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - {\delta _\mathit{\boldsymbol{\omega }}}{\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - \left( {{\delta _{\rm{f}}} + {\delta _{\rm{d}}}} \right){\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} + \\ \;\;\;\;\;L{\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} + \left( {{\delta _{\rm{d}}} - L} \right){\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} \le \\ \;\;\;\;\; - {\delta _\mathit{\boldsymbol{q}}}{\left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\|^2} - {\delta _\mathit{\boldsymbol{\omega }}}{\left\| {{\mathit{\boldsymbol{\omega }}_{\rm{e}}}} \right\|^2} - {\delta _{\rm{f}}}{\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|^2} \le 0 \end{array} $

（53）

从而有$\boldsymbol{z}, \tilde{\boldsymbol{\omega}}, R, q_{\mathrm{e} 0}, \boldsymbol{q}_{\mathrm{ev}}, \boldsymbol{\omega}_{\mathrm{e}} \in L_{\infty}, \boldsymbol{\tilde { \theta }}=R z$∈L_∞; 可以进一步对式(40)、式(46)和式(53)求导，其导数也是包含以上有界信号，不会产生新的信号，得到${\ddot V_\mathit{\boldsymbol{z}}} \in {L_\infty }、\;\ddot V \in {L_\infty }$，从而根据Barbalat引理得到$\mathop {\lim }\limits_{t \to \infty } {\dot V_\mathit{\boldsymbol{z}}} = 0、\;\mathop {\lim }\limits_{t \to \infty } \dot V = 0$，因此有$\mathit{\boldsymbol{\tilde \omega }}、{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}、{\mathit{\boldsymbol{\omega }}_{\rm{e}}} \in {L_2} \cap {L_\infty }, {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} \in {L_2}$。

综上证明过程，证明了闭环系统最终会收敛到流形面$\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }}{\rm{ = }}{\bf{0}}$上，并且保证了参数估计误差$\mathit{\boldsymbol{\widetilde \theta }}$有界，滤波器输出渐近收敛到角速度ω，跟踪误差q_ev, ω_e渐近收敛，从而完成了控制器的设计和稳定性证明过程。

经过以上分析过程，有以下几点改进和创新值得说明一下:

注1  通过稳定性可以证明，闭环系统可以保证W$\mathit{\boldsymbol{\tilde \theta }}$趋近于零，但是只能保证参数估计$\mathit{\boldsymbol{\hat \theta }}$有界，并不能保证其收敛到真值θ，除非可以保证参数回归矩阵W满秩且满足持续激励(Persistent Excitation，PE)条件。不过，观察式(13)，可以保证闭环系统最终会收敛到理想系统

$ {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - {k_\mathit{\boldsymbol{q}}}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}} - {k_\mathit{\boldsymbol{\omega }}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}} $	（54）

这在CE控制方法中是保证不了的，也是I&I控制方法相对于CE方法的一大改进。

注2  本文通过设计一种新颖的缩放因子式(34)，使得其满足性质式(37)。而通过饱和函数f(r)的引入，使得控制器增益中不再含有r²或者r，这在文献[12-18]中是做不到的。并且注意到，根据饱和函数f(r)的有界性，控制器中不再需要缩放因子R和r的信息，缩放因子的引入只是为了稳定性的证明，这是对已有基于动态放缩法I&I控制器的一大突破。

注3  从式(48)发现，通过在滤波器增益式(31)k_f中添加动态项式(32) δ_d，使得增益式(31)中不再需要Lipschitz常数L，从而避免了复杂的矩阵推导来确定L的过程，例如文献[17-18]中的推导过程。

3 数值仿真

对所设计的自适应跟踪控制器进行仿真，验证本文所提出设计方案的有效性和优越性。仿真中，惯量矩阵J取为

$ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {20}&{1.2}&{0.9}\\ {1.2}&{17}&{1.4}\\ {0.9}&{1.4}&{15} \end{array}} \right]\;{\rm{kg}} \cdot {{\rm{m}}^2} $

被跟踪的期望角速度轨迹设定为

$ \begin{array}{l} {\mathit{\boldsymbol{\omega }}_{\rm{d}}}\left( t \right) = \left[ {0.3\left( {1 - {{\rm{e}}^{ - 0.01{t^2}}}} \right)\cos t + t{{\rm{e}}^{ - 0.01{t^2}}}\left( {0.08{\rm{ \mathsf{ π} }} + } \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {0.006\sin t} \right)} \right] \cdot {\left[ {\begin{array}{*{20}{l}} 1&1&1 \end{array}} \right]^{\rm{T}}}{\rm{rad}}/{\rm{s}} \end{array} $

初始条件设定为

$ \mathit{\boldsymbol{q}}\left( 0 \right) = {\left[ {\begin{array}{*{20}{l}} {0.5}&{0.5}&{0.5}&{0.5} \end{array}} \right]^{\rm{T}}} $

$ {\mathit{\boldsymbol{q}}_{\rm{d}}}\left( 0 \right) = {\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \end{array}} \right]^{\rm{T}}} $

$ \mathit{\boldsymbol{\omega }}\left( 0 \right) = {\left[ {\begin{array}{*{20}{l}} {1.5}&{ - 2}&1 \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{\hat \omega }}\left( 0 \right) = \mathit{\boldsymbol{\omega }}\left( 0 \right) $

$ {\delta _{\rm{d}}}\left( 0 \right) = \left\| {\mathit{\boldsymbol{\hat \omega }}\left( 0 \right) - \mathit{\boldsymbol{\omega }}\left( 0 \right)} \right\| = 0 $

$ \mathit{\boldsymbol{\hat \theta }}\left( 0 \right) = \mathit{\boldsymbol{\alpha }}\left( 0 \right) + \mathit{\boldsymbol{\beta }}\left( 0 \right) = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0 \end{array}} \right]^{\rm{T}}} $

被跟踪的期望姿态可以根据初始姿态和期望角速度得出。控制器的常数参数设定为:k_p=10, k_d=20, δ_f=0.5。

3.1 调节系数γ、λ的影响

在控制器中，调节系数γ的作用是调节闭环系统向流形面$M = \left\{ {\mathit{\boldsymbol{\widehat \theta }}, \mathit{\boldsymbol{\theta }} \in {{\bf{R}}^6}|\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} = {\bf{0}}} \right\}$的收敛速度，调节系数λ是调整滤波器$\mathit{\boldsymbol{\hat \omega }}$向ω的收敛速度。为了更好地验证控制方案的有效性和观察调节系数对闭环控制性能的影响，仿真采用的3组调节系数γ、λ分别为:γ=λ=15, 20, 30。

得到的仿真曲线如图 2所示。

通过仿真结果表明，本文所设计的控制器在保证闭环系统信号有界的同时，也实现了惯量矩阵未知的条件下跟踪误差的渐近收敛。从图 2(a)~图 2(d)来看，在一定范围内增大调节系数值可以加快闭环误差的渐近收敛速度，并且调节系数增大到一定程度，闭环系统收敛速度不再增大; 图 2(d)表明，增大调节增益，并没有引起所需控制力矩的明显增大; 从图 2(e)和图 2(f)来看，更大的γ、λ值，导致参数估计误差更小，但也是有界收敛，参数估计并没有收敛到其真值; 但是可以保证闭环系统渐近收敛到流形面$\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} = {\bf{0}}$上。值得一提的是，观察图 2(g)，更大的调节增益γ、λ，动态增益δ_d反而变得更小; 再观察δ_d动态式(32)，δ_d的增长速度跟λ和$\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|$²均成正比，因此可以发现，该条件下，$\left\| {\mathit{\boldsymbol{\tilde \omega }}} \right\|$²的快速减小比λ的增大对δ_d的影响更大。

总之，本组仿真算例证明了本文所提出的跟踪控制器的有效性，并且增大调节增益γ、λ值能够一定程度加快闭环跟踪误差的收敛。但是，需要指出的是，尽管γ、λ值能够使得闭环系统更快地收敛，但是实际应用中并不是γ, λ值越大越好。这是因为本文的控制器和仿真均是基于姿态和角速度能够实时精确测量的假设，而实际情况中可能存在测量噪声、高频干扰以及未建模动态的影响，更大的γ, λ值将增大系统的带宽，使其更容易受到这些影响。所以，在实际应用中，应该综合闭环系统的快速性和鲁棒性，对γ, λ值进行合理的选定。

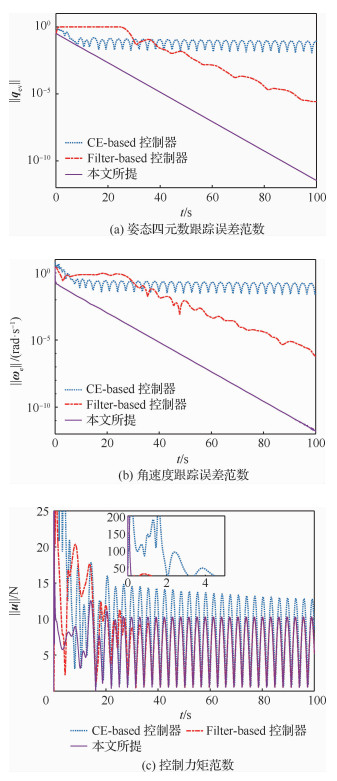
3.2 控制器性能的比较

为了验证本文所设计控制器的优越性，该组仿真将比较CE-based控制器^[5]、Filter-based控制器^[8]和本文提出的控制器的跟踪性能。为了保证对比的公平性，首先通过调节各控制器的反馈增益，保证3种控制器在理想情况下(惯量矩阵已知)跟踪误差的渐近收敛速度一致，然后，设定惯量矩阵未知，通过数值仿真，得到的跟踪性能曲线如图 3所示。

从图 3(a)和图 3(b)可以看到，本文提出的控制器相比于CE-based和Filter-based控制器有更快的收敛速度和更高的跟踪精度。从图 3(c)发现，初始过渡阶段，CE-based控制器和Filter-based控制器所需的控制量非常大，并且有着非常严重的瞬态，在稳态阶段，Filter-based控制器所需的控制量和本文提出的已经基本趋于相同了，但是CE-based控制器所需的控制量更大，这也可以从图 3(a)和图 3(b)可以看出，CE-based控制器的稳态时闭环跟踪误差比较大，并存在一定的振荡，这会额外消耗一定的控制量。

造成这样的原因主要有:首先，从控制器设计原理上，本文所提控制器和Filter-based控制器都是基于非等价确定性原则(Non-CE-based)设计的，相对于CE-based控制器在原理上就具有优越性，因为CE-based控制器只是单纯地将Lyapunov函数中关于参数不确定项抵消掉，并且只要参数估计没有收敛到真值，闭环系统就会一直存在一个外干扰附加到理想系统上; 其次本文提出的控制器中滤波系数k_f中的动态增益在系统运行过程中使得系统等效控制增益变大，加快了闭环系统向理想系统(流形面上的等效系统)的收敛。并且Filter-based控制器将状态、回归矩阵和控制量均进行一阶低通滤波构造出一个指数收敛的増广状态，这严重增大了闭环系统的阶数和复杂性，在计算上造成很大负担并且引入了很多的舍入误差，并且指数收敛増广状态的初值必须根据其他状态初值来设置使其为零，不然不就会有一个指数收敛的外干扰附加在理想系统上，因此本文所提控制器相对于Filter-based控制器更加简洁和高效。

综上，对于跟踪精度要求高和燃料有限且宝贵的航天在轨服务任务来说，本文所提出的控制器相对于CE-based控制器和Filter-based控制器有着不可比拟的优势。

3.3 控制器鲁棒性验证

在工程应用中，系统中会不可避免地存在一些干扰，例如外界干扰、测量误差等。为了验证本文设计控制器的鲁棒性，在原有的系统模型(9)中加入有界外干扰:

$ \begin{array}{l} \mathit{\boldsymbol{d}} = \\ {\left[ {\begin{array}{*{20}{c}} {0.15\sin t}&{ - 0.05\cos \left( {t + \frac{{\rm{ \mathsf{ π} }}}{4}} \right)}&{0.1\sin \left( {t - \frac{{\rm{ \mathsf{ π} }}}{6}} \right)} \end{array}} \right]^{\rm{T}}} \end{array} $

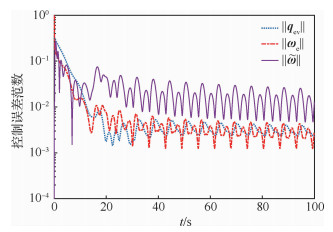
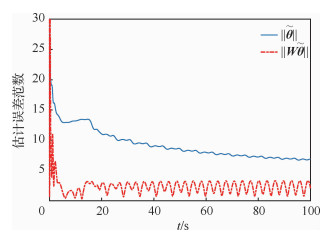
调节系数参数设置为γ=λ=20。其他控制参数和初值设置与3.1节中相同。通过数值仿真，得到的闭环性能曲线如图 4~图 6所示。

从图 4可知，当存在有界干扰作用在闭环系统控制通道时，所设计的控制器仍能保证闭环系统的稳定，但是此时跟踪误差不再渐近收敛于零，而是收敛在零附近的一个很小邻域内; 对比图 5和图 2(d)发现，存在有界干扰需要的控制力矩比不存在干扰时略大，但是变化趋势基本相同; 从图 6可以发现，此时闭环系统不再渐近收敛于流形面$\mathit{\boldsymbol{W}}\mathit{\boldsymbol{\widetilde \theta }} = {\bf{0}}$上，但是仍能保证参数估计误差的有界收敛。

总之，通过该组仿真可以看出，本文设计的控制器存在有界外干扰时，仍能保证闭环系统的有界收敛，只是之前的渐近稳定品质已经丧失了，但仍可将跟踪误差控制在零附近的一个很小邻域内，表明控制器具有一定的鲁棒性。

4 结论

本文针对惯性参数不确定情况下航天器的姿态跟踪，基于浸入与不变方法设计了一种自适应控制器。首先分析了浸入与不变理论应用在航天器姿态跟踪动力学模型，存在偏微分方程不存在解析解的问题; 然后针对该问题，本文提出了一种矩阵改造方法，使得参数回归矩阵满足可积条件，并通过引入一种全新的缩放因子，采用动态放缩法证明了矩阵改造前后的误差对闭环系统的影响可以消除; 最后根据本文提出的矩阵改造方案设计出了一种新的I&I姿态自适应跟踪控制器，保证了跟踪误差的渐近收敛。文章的创新之处在于采用全新的缩放因子，使得控制器执行过程中不需缩放因子信息，也不需要惯量矩阵的先验信息; 并且在滤波器反馈增益中加入动态自适应增益项，使得不需要去确定矩阵范数上界，总之本文设计控制器相比于已有的基于动态放缩法的I&I控制器具有更简单的形式和更低的闭环系统阶数。文章最后通过数值仿真验证和对比得出了本文设计控制器的有效性和优越性。总之，本文的设计思想和方法对参数不确定的自适应控制器设计具有一定的指导和借鉴意义。