2. 西北工业大学 航天学院, 西安 710072
2. School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
随着未来战场环境的愈加复杂和反导武器系统智能化程度的提高,单枚导弹对拦截器的有效突防变得越来越困难,且技术实现上也变得越来越复杂。研究者们开始意识到可以采用带防御器的多导弹协同制导技术实现我方导弹的突防与反拦截,因为这种技术在提高高价值飞行器的突防概率的同时,还可以扩大对拦截器的拦截范围[1]。本文考虑我方突防器作为引诱角色,携带并配合两枚防御器协同反拦截敌方拦截器的情形。在后续的研究中可知这种协同方式是一种显式的协同[2],它更加深入地考虑了弹间的内在联系,所以研究这种协同方式具有重要的现实意义。
就现有的文献来看,可将协同制导方式划分为两大类:显式的协同和隐式的协同[2]。隐式的协同,本质上是多对一制导中的每个个体,根据提前设定好的协调参数,执行一对一交战方案,共同打击一个目标的联合行为。例如,Jeon等[3]提出的碰撞时间控制制导律(Impact-Time-Control Guidance, ITCG)制导律,对每一枚导弹预先指定了一个共同的到达时间,所有的导弹依据这个共同时间同时到达目标。相对应的显式的协同,能够在制导的过程中考虑并实时协调个体之间的内在关系,调节整个团队的某些性能指标,降低个体之间差异性,协同完成作战任务。
在多导弹协同反拦截技术中比较典型的是三体(突防器-防御器-拦截器)协同制导问题,三体协同制导指的是突防器针对来袭拦截器发射一枚防御导弹,对拦截器进行反拦截以保护自己。最早研究三体协同制导的是Boyell[4-5],给出了三体问题的运动学结论,推导出了常定方位碰撞过程的闭式关系。近几年Ratnoo和Shima、Yamasaki和Balakrishnan率先研究了三体制导问题。Ratnoo和Shima[6]提出了一种防御器利用指令视线角(Command-to-LOS,CLOS)方法的制导律,考虑了各种攻击几何和攻击者机动的情况。后来,他们在文献[7]中又分析了采用比例导引(PN)制导律和纯追击制导的攻击导弹对抗采用PN和CLOS策略的防御器的情形,给出了不同情况下的边界条件。Yamasaki和Balakrishnan[8-9]基于最优控制理论和速度误差反馈,研究了修正的CLOS制导的问题,但是这种方法会造成比较平直的弹道。上述的研究都没有考虑突防器与防御器的配合,协同程度较低,是一种隐式的协同制导方式。考虑到实际战场环境中需要实时地对拦截器的运动状态进行探测和估计,Shaferman和Shima[10]提出了一种多模自适应协同制导律,将探测估计问题加入到了三体制导中。文中突防器作为引诱角色配合防御器执行躲避机动,使得防御器能以较小的能量消耗拦截敌方拦截器。
考虑到制导过程需在有限时间内完成,描述末制导过程的模型只有在有限时间间隔内才有意义,国内的许多学者开始用有限时间理论[11-12]来设计制导律。在目标对拦截器执行引诱机动的情况下,Guo等[11]研究了有限时间约束下的三体拦截制导情形。提出了线性系统输入输出有限时间稳定(IO-FTS)方法,同时提出了有限时间有界约束下的线性系统IO-FTS的充分条件。在Guo等[11]的基础上,张帅等[12]提出了一种带拦截角约束的FTCG协同制导方法。引入度量矩阵反映系统有限时间输入输出的稳定性,基于微分矩阵不等式设计了状态反馈控制器,能确保有闭环系统限时间输入输出稳定。后来,张帅等在文献[12]的基础上,又研究了突防器与两个防御器相配合并施加一个预置拦截角的反拦截情形[13],但是文献[13]是分离设置两个防御器的拦截角的。此外,上述文献中利用有限时间理论所设计的制导律都不能得出控制器的解析解。
针对突防器与防御器在制导过程中需要实时协同,设计合适的控制器成为必不可少的部分。最常用的方法是采用最优控制理论[14-15]和微分对策理论[16]来设计控制器,这样设计出的控制器能够得出控制输入的解析解。Shima[14]在考虑单侧最优控制问题的基础上,针对攻击导弹采用PN、扩展比例导引(APN)和最优控制制导律(OGL)这3种情况首先给出了突防器与防御器协同制导策略,此外又给出了攻击导弹没有被防御器拦截时的最优一对一目标规避策略。在文献[14]的基础上,Prokopov和Shima[15]考虑了针对3种不同协同方式的线性二次协同制导策略。结果表明,突防器-防御器的性能依赖于协同的方案,验证了突防器配合防御器机动的协同方式是最好的。文献[16]利用微分对策理论提出了一种双侧最优协同制导律,考虑了突防器-防御器组与拦截器的博弈对抗情形。文中针对任意阶线性动力学问题,采用末端投影变换的方法降低了问题的阶数,简化了推导的过程。利用线性二次微分对策公式分析了在连续域和离散域上的任意阶线性动力学问题。Kumar和Shima[17]提出了一种非线性的协同防御制导律,与之前提出的线性化的方法不同,非线性方法确保了制导策略即使在大的航向角误差的情况下也是有效的。Weiss等[18]基于所需攻击者攻击的最大化脱靶量和目标规避的最小控制提出了两种制导算法。此外,在考虑不依赖导弹间实时通信的情况下,文献[19]采用集中式“领弹-从弹”协同制导架构,设计了从弹的3种末制导律,实现了无导引头下对目标的精确打击。
从已有的国内文献来看,大多数集中在对相同角色的多导弹飞行器协同制导研究中,对不同角色的多导弹的协同制导研究较少。现有的多导弹协同反拦截技术大多考虑突防器和单枚防御器的协同制导情形,要使得突防器协同两枚或多枚防御器对拦截器实现较好的拦截效果还需要深入的研究。此外,还需将诸如引诱[10-15]或探测[19-23]等不同的角色加入到多导弹协同制导中以实现更加深度的协同。因此,本文考虑了在制导末端施加相对拦截角的带有引诱角色的显式协同反拦截方案,该方案实现了突防器与两枚防御器的深度协同。
综上,本文在文献[13, 23]的基础上,基于最优控制理论,针对突防器发射两枚防御器协同反拦截来袭拦截器并施加一个相对拦截角的情形,提出了一种带引诱角色的显式协同制导律。相比于文献[23]提出的隐式协同,本文在制导律设计中,考虑了突防器与两防御器的协同。相比于文献[13],通过建立性能指标,求解了突防器和两防御器三者最优控制输入的解析解。本文设计的制导律能够保证两防御器都能成功拦截拦截器,且能在拦截末端施加预置的相对拦截角。同时,所设计的制导律在不同的发射条件下具有较好的稳定性。
1 问题描述本文考虑一个突防器、2个防御器与一个拦截器交战的情形。在XI-OI-YI惯性坐标系下建立动力学与运动学模型。下标D1和D2分别表示防御器1和防御器2。a、v、q、r和γ分别表示法向加速度、速度、视线角、相对距离和航向角,下标E和P分别表示突防器和拦截器。防御器1和拦截器之间的终端拦截角为γD1+γP,防御器1和拦截器之间的终端拦截角为γD2+γP。当2个防御器同时到达时,它们之间的夹角为γD1-γD2。图 1为突防器、防御器1、防御器2和拦截器之间的运动模型。
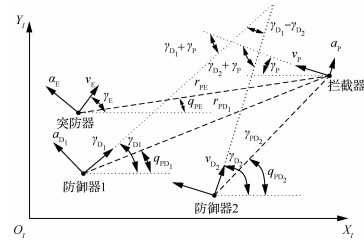
|
| 图 1 多导弹协同拦截交战 Fig. 1 Multi-missile cooperative interception engagement |
从图 1中可以得知在制导末端施加的拦截角是2个防御器之间的相对拦截角。本文的模型是建立在以下的假设下:
假设1 突防器、防御器1、防御器2和拦截器的模型建立在二维平面质点运动空间下。
假设2 假设突防器、防御器1、防御器2和拦截器的速度恒定,在碰撞三角形成立的条件下,他们的相对运动速度恒定。
假设3 假设拦截器采用带有修正项比例导引对突防器进行拦截。
1.1 动力学与运动学模型突防器与拦截器交战过程可以表示为与突防器相关的极坐标(r, q)的形式,即
| $ {{\dot r}_{{\rm{PE}}}} = {v_{{\rm{PE}}}} = - {v_{\rm{E}}}\cos \left( {{\gamma _{\rm{E}}} - {q_{{\rm{PE}}}}} \right) - {v_{\rm{P}}}\cos \left( {{\gamma _{\rm{P}}} + {q_{{\rm{PE}}}}} \right) $ | (1) |
| $ {{\dot q}_{{\rm{PE}}}} = \frac{{{v_{\rm{E}}}\sin \left( {{\gamma _{\rm{E}}} - {q_{{\rm{PE}}}}} \right) - {v_{\rm{P}}}\sin \left( {{\gamma _{\rm{P}}} + {q_{{\rm{PE}}}}} \right)}}{{{r_{{\rm{PE}}}}}} $ | (2) |
式中:
对式(2)两边分别对时间进行求导,可得
| $ {{\ddot q}_{{\rm{PE}}}} = - 2\frac{{{{\dot r}_{{\rm{PE}}}}}}{{{r_{{\rm{PE}}}}}}{{\dot q}_{{\rm{PE}}}} + \frac{{a_{\rm{E}}^\prime - a_{\rm{P}}^\prime }}{{{r_{{\rm{PE}}}}}} $ | (3) |
式中:
相似地,可以得到防御器与拦截器之间的极坐标形式,即
| $ \begin{array}{l} {{\dot r}_{{\rm{P}}{{\rm{D}}_1}}} = {v_{{\rm{P}}{{\rm{D}}_1}}} = - {v_{{{\rm{D}}_1}}}\cos \left( {{\gamma _{{{\rm{D}}_1}}} - {q_{{\rm{P}}{{\rm{D}}_1}}}} \right) - \\ \;\;\;\;\;{v_{\rm{P}}}\cos \left( {{\gamma _{\rm{P}}} + {q_{{\rm{P}}{{\rm{D}}_1}}}} \right) \end{array} $ | (4) |
| $ {{\dot q}_{{\rm{P}}{{\rm{D}}_1}}} = \frac{{{v_{{{\rm{D}}_1}}}\sin \left( {{\gamma _{{{\rm{D}}_1}}} - {q_{{\rm{PE}}}}} \right) - {v_{\rm{P}}}\sin \left( {{\gamma _{\rm{P}}} + {q_{{\rm{P}}{{\rm{D}}_1}}}} \right)}}{{{r_{{\rm{P}}{{\rm{D}}_1}}}}} $ | (5) |
| $ \begin{array}{l} {{\dot r}_{{\rm{P}}{{\rm{D}}_2}}} = {v_{{\rm{P}}{{\rm{D}}_2}}} = - {v_{{D_2}}}\cos \left( {{\gamma _{{{\rm{D}}_2}}} - {q_{{\rm{P}}{{\rm{D}}_2}}}} \right) - \\ \;\;\;\;\;{v_{\rm{P}}}\cos \left( {{\gamma _{\rm{P}}} + {q_{{\rm{P}}{{\rm{D}}_2}}}} \right) \end{array} $ | (6) |
| $ {{\dot q}_{{\rm{P}}{{\rm{D}}_2}}} = \frac{{{v_{{{\rm{D}}_2}}}\sin \left( {{\gamma _{{{\rm{D}}_2}}} - {q_{{\rm{PE}}}}} \right) - {v_{\rm{P}}}\sin \left( {{\gamma _{\rm{P}}} + {q_{{\rm{P}}{{\rm{D}}_2}}}} \right)}}{{{r_{{\rm{P}}{{\rm{D}}_2}}}}} $ | (7) |
对式(5)和式(7)两边分别对时间进行求导,可得
| $ {{\ddot q}_{{\rm{P}}{{\rm{D}}_1}}} = - 2\frac{{{{\dot r}_{{\rm{P}}{{\rm{D}}_1}}}}}{{{r_{{\rm{P}}{{\rm{D}}_1}}}}}{{\dot q}_{{\rm{P}}{{\rm{D}}_1}}} + \frac{{a_{{{\rm{D}}_1}}^\prime - a_{\rm{P}}^\prime }}{{{r_{{\rm{P}}{{\rm{D}}_1}}}}} $ | (8) |
| $ {{\ddot q}_{{\rm{P}}{{\rm{D}}_2}}} = - 2\frac{{{{\dot r}_{{\rm{P}}{{\rm{D}}_2}}}}}{{{r_{{\rm{P}}{{\rm{D}}_2}}}}}{{\dot q}_{{\rm{P}}{{\rm{D}}_2}}} + \frac{{a_{{{\rm{D}}_2}}^\prime - a_{\rm{P}}^\prime }}{{{r_{{\rm{P}}{{\rm{D}}_2}}}}} $ | (9) |
式中:a′Di为aDi在视线上的分量。
各飞行器的法向加速度ai与航向角速率i之间的关系为
| $ {{\dot \gamma }_i} = \frac{{{a_i}}}{{{v_i}}}\;\;\;i \in \left\{ {{\rm{E}},{{\rm{D}}_1},{{\rm{D}}_2},{\rm{P}}} \right\} $ | (10) |
假设在整个制导过程中,4个飞行器都具有一阶线性动力学特性,则
| $ {{\dot a}_i} = \frac{{{a_{i{\rm{c}}}} - {a_i}}}{{{\tau _i}}}\;\;\;\;i \in \left\{ {{\rm{E}},{{\rm{D}}_1},{{\rm{D}}_2},{\rm{P}}} \right\} $ | (11) |
式中:aic为飞行器的指令加速度;τi为飞行器的过载响应时间常数。
根据假设3,可以得出拦截器制导律,其指令加速度为
| $ {a_{{\rm{PC}}}} = N{V_{{\rm{PE}}}}{{\dot q}_{{\rm{PE}}}} + \frac{K}{2}a_{\rm{E}}^\prime \;\;\;\left| {{a_{{\rm{PC}}}}} \right| \le {a_{{\rm{Pmax}}}} $ | (12) |
式中:N、K和aPmax分别为拦截器制导过程中的导航参数、修正系数和过载限制。
在交战的后期会形成3个碰撞三角形,它们分别是突防器与拦截器、防御器1和拦截器及防御器2与拦截器之间的。根据假设2,一旦碰撞三角形形成,就可以针对非线性运动方程作线性化处理。此时,各视线的法向加速度可表示为
| $ a_{\rm{E}}^\prime = {a_{\rm{E}}}\cos \left( {{\gamma _{{{\rm{E}}_0}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right) $ | (13) |
| $ a_{\rm{P}}^\prime = {a_{\rm{P}}}\cos \left( {{\gamma _{{{\rm{E}}_0}}} + {q_{{\rm{P}}{{\rm{E}}_0}}}} \right) $ | (14) |
| $ a_{{{\rm{D}}_i}}^\prime = {a_{{\rm{D}}i}}\cos \left( {{\gamma _{{{\rm{D}}_{i0}}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right) $ | (15) |
突防器与拦截器之间的初始相对距离为rPE0。相似地,防御器1与拦截器之间的初始相对距离为rPD10,防御器2与拦截器之间的初始相对距离为rPD20。在线性化的假设下,它们之间的相对速度是一个常值,且拦截时间是固定的,满足:
| $ {t_{{\rm{fPE}}}} = \frac{{ - {r_{{\rm{P}}{{\rm{E}}_0}}}}}{{{{\dot r}_{{\rm{PE}}}}}} = \frac{{ - {r_{{\rm{P}}{{\rm{E}}_0}}}}}{{{v_{{\rm{PE}}}}}} $ | (16) |
| $ {t_{{\rm{fP}}{{\rm{D}}_1}}} = \frac{{ - {r_{{\rm{P}}{{\rm{D}}_{10}}}}}}{{{{\dot r}_{{\rm{P}}{{\rm{D}}_1}}}}} = \frac{{ - {r_{{\rm{P}}{{\rm{D}}_{10}}}}}}{{{v_{{\rm{P}}{{\rm{D}}_1}}}}} $ | (17) |
| $ {t_{{\rm{fP}}{{\rm{D}}_2}}} = \frac{{ - {r_{{\rm{PD}}{2_0}}}}}{{{{\dot r}_{{\rm{PD}}2}}}} = \frac{{ - {r_{{\rm{PD}}{2_0}}}}}{{{v_{{\rm{PD}}2}}}} $ | (18) |
显然,确保突防器与防御器1和防御器2成功协同的必要条件是
通过以上的分析,结合式(3)、式(8)~式(12),可以设定系统的状态变量为
| $ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {{{\dot q}_{{\rm{PE}}}}}&{{{\dot q}_{{\rm{P}}{{\rm{D}}_1}}}}&{{{\dot q}_{{\rm{P}}{{\rm{D}}_2}}}}&{{a_{\rm{P}}}}&{{a_{\rm{E}}}}&{{a_{{{\rm{D}}_1}}}}&{{a_{{{\rm{D}}_2}}}}&{{x_{{\gamma _1}}}}&{{x_{{\gamma _2}}}} \end{array}} \right]^{\rm{T}}} $ | (19) |
式中:xγ1和xγ2分别为防御器1和拦截器与防御器2和拦截器之间的终端拦截角γD1+γP和γD2+γP。本文中将控制2个防御器在制导末端形成预置的相对拦截角。
1.2 突防器配合防御器协同交战突防器配合防御器1和防御器2协同交战的方式是一种显式的协同。在这种情况下,突防器能配合防御器1和防御器2协同机动,提高拦截性能,由式(2)、式(5)、式(7)、式(10)和式(11)可以得到状态方程:
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}(t)\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{B}}(t)\mathit{\boldsymbol{u}}(t) $ | (20) |
| $ \begin{array}{l} \mathit{\boldsymbol{A}}(t) = \\ \;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\frac{{ - 2}}{{{t_{{\rm{fPE}}}} - t}}}&0&0&{\frac{{ - \cos \left( {{\gamma _{{{\rm{E}}_0}}} + {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{PE}}}}\left( {{t_{{\rm{fPE}}}} - t} \right)}}}&{\frac{{\cos \left( {{\gamma _{{{\rm{E}}_0}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{PE}}}}\left( {{t_{{\rm{fPE}}}} - t} \right)}}}&0&0&0&0\\ 0&{\frac{{ - 2}}{{{t_{{\rm{fP}}{{\rm{D}}_1}}} - t}}}&0&{\frac{{ - \cos \left( {{\gamma _{{{\rm{E}}_0}}} + {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{P}}{{\rm{D}}_1}}}\left( {{t_{{\rm{fP}}{{\rm{D}}_1}}} - t} \right)}}}&0&{\frac{{\cos \left( {{\gamma _{{{\rm{D}}_{10}}}} - {q_{{\rm{P}}{{\rm{D}}_{10}}}}} \right)}}{{{v_{{\rm{P}}{{\rm{D}}_1}}}\left( {{t_{{\rm{fP}}{{\rm{D}}_1}}} - t} \right)}}}&0&0&0\\ 0&0&{\frac{{ - 2}}{{{t_{{\rm{fP}}{{\rm{D}}_2}}} - t}}}&{\frac{{ - \cos \left( {{\gamma _{{{\rm{E}}_0}}} + {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{P}}{{\rm{D}}_2}}}\left( {{t_{{\rm{fP}}{{\rm{D}}_2}}} - t} \right)}}}&0&0&{\frac{{\cos \left( {{\gamma _{{{\rm{D}}_{20}}}} - {q_{{\rm{P}}{{\rm{D}}_{20}}}}} \right)}}{{{v_{{\rm{P}}{{\rm{D}}_1}}}\left( {{t_{{\rm{fP}}{{\rm{D}}_1}}} - t} \right)}}}&0&0\\ {\frac{{N{v_{{\rm{PE}}}}}}{{{\tau _{\rm{P}}}}}}&0&0&{\frac{{ - 1}}{{{\tau _{\rm{P}}}}}}&{\frac{{K\cos \left( {{\gamma _{{{\rm{E}}_0}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{2{\tau _{\rm{P}}}}}}&0&0&0&0\\ 0&0&0&0&{\frac{{ - 1}}{{{\tau _{\rm{E}}}}}}&0&0&0&0\\ 0&0&0&0&0&{\frac{{ - 1}}{{{\tau _{{{\rm{D}}_1}}}}}}&0&0&0\\ 0&0&0&0&0&0&{\frac{{ - 1}}{{{\tau _{{{\rm{D}}_2}}}}}}&0&0\\ 0&0&0&{\frac{1}{{{v_{\rm{P}}}}}}&0&{\frac{1}{{{v_{{{\rm{D}}_1}}}}}}&0&0&0\\ 0&0&0&{\frac{1}{{{v_{\rm{P}}}}}}&0&0&{\frac{1}{{{v_{{{\rm{D}}_2}}}}}}&0&0 \end{array}} \right] \end{array} $ | (21) |
式中:u(t)=[uE uD1 uD2]T,且满足:
uDi≤uDmax,uDmax为防御器的过载限制。由突防器、防御器1和防御器2的加速度指令组成,即
相应的B(t)可以表示为
| $ \mathit{\boldsymbol{B}}\left( t \right) = {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{\frac{1}{{{\tau _{\rm{E}}}}}}&0&0&0&0\\ 0&0&0&0&0&{\frac{1}{{{\tau _{{D_1}}}}}}&0&0&0\\ 0&0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_2}}}}}}&0&0 \end{array}} \right]^{\rm{T}}} $ | (22) |
式中:可设
| $ {\mathit{\boldsymbol{B}}_E} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&{\frac{1}{{{\tau _{\rm{E}}}}}}&0&0&0&0 \end{array}} \right]^{\rm{T}}} $ | (23) |
| $ {\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_1}}}}}}&0&0&0 \end{array}} \right]^{\rm{T}}} $ | (24) |
| $ {\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_2}}}}}}&0&0 \end{array}} \right]^{\rm{T}}} $ | (25) |
突防器不配合防御器1和防御器2协同交战的方式总体来看是一种隐式的协同。在这种情况下,突防器只负责执行自己的任务,不配合两个防御器进行机动,防御器1和防御器2两者之间进行显式的协同,可以得到状态方程
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{\tilde A}}(t)\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{B}}(t)\mathit{\boldsymbol{u}}(t) + \mathit{\boldsymbol{G}}(t)w(t) $ | (26) |
式中:u(t)=[uD1uD2]T,由防御器1和防御器2的加速度指令组成,即uD1=aD1C,uD2=aD2C;而突防器的加速度作为状态方程的外部输入,由w(t)表示,即w(t)=aEC;G(t)为相应的外部输入传递矩阵。
此时,相应的B(t)和G(t)可以表示为
| $ \mathit{\boldsymbol{B}}\left( t \right) = {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_1}}}}}}&0&0&0\\ 0&0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_2}}}}}}&0&0 \end{array}} \right]^{\rm{T}}} $ | (27) |
| $ \mathit{\boldsymbol{G}}\left( t \right) = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&{\frac{1}{{{\tau _{\rm{E}}}}}}&0&0&0&0 \end{array}} \right]^{\rm{T}}} $ | (28) |
其中定义
| $ {\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_1}}}}}}&0&0&0 \end{array}} \right]^{\rm{T}}} $ | (29) |
| $ {\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0&{\frac{1}{{{\tau _{{{\rm{D}}_2}}}}}}&0&0 \end{array}} \right]^{\rm{T}}} $ | (30) |
本文设计的制导律要满足在突防器显式协同的情况下,防御器1和2可实现对拦截器的有效拦截,使得拦截脱靶量和能量消耗尽量最小,且在拦截终端施加一个相对拦截角。
可将拦截器进入制导盲区时刻的零效脱靶量作为末端拦截时刻的脱靶量,即
| $ Z{\rm{E}}{{\rm{M}}_{{{\rm{D}}_i}}} = \frac{{{{\dot q}_{{\rm{P}}{{\rm{D}}_i}}}\left( {{t_{\rm{f}}}} \right)D_{{{\rm{D}}_i}}^2}}{{{v_{{\rm{P}}{{\rm{D}}_i}}}}} $ | (31) |
式中:tf为防御器进入末端制导的时刻;DDi为防御器进入制导盲区的值。由式(31)可知,末端拦截脱靶量与末端视线角速率
注1 综合考虑拦截脱靶量、终端拦截角和能量消耗3个方面,本文采用最优控制理论设计制导律。需要设立包含上述3个方面在内的目标函数,依据目标函数求解突防器与防御器1和防御器2协同的最优控制输入,满足制导律设计的要求。
2.1 目标函数在本文中考虑一种特殊情况,防御器1和防御器2的拦截时间一致,即tfn=tfPD1=tfPD2。
注2 在制导过程中,要求以最小的机动控制要求,在拦截时达到最小的拦截脱靶量,且施加一个设定好的终端拦截角γD1-γD2,因此可以得到目标函数为
| $ \begin{array}{*{20}{c}} {J = \frac{1}{2}{\alpha _1}\dot q_{{\rm{P}}{{\rm{D}}_1}}^2\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \frac{1}{2}{\alpha _2}\dot q_{{\rm{P}}{{\rm{D}}_2}}^2\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \frac{\beta }{2}\left[ {{x_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.}\\ {\left. {{x_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]2 + \frac{1}{2}\int_0^{{t_{{{\rm{f}}_{\rm{n}}}}}} {\left( {u_{{{\rm{D}}_1}}^2 + u_{{{\rm{D}}_2}}^2 + u_{\rm{E}}^2} \right){\rm{d}}t} } \end{array} $ | (32) |
权重系数α1、α2和β是非负的,xγi=γT+γi。当αi→∞时,可以对拦截器产生完美的拦截。相似地,当β→∞时,可以在2个防御器之间产生完美的拦截角。
2.2 模型降阶注3 为了降低求解问题的阶数,得到控制输入的解析解,在此引入终端投影法对模型进行降阶处理,引入新的状态变量Z(t)。
| $ Z(t) = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{x}}(t) $ | (33) |
式中:Φ(tfn, t)为与式(21)相关的状态转移矩阵;D为常值向量,用来分离状态变量x(t)中的元素。
因为
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right) = - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{A}} $ | (34) |
结合式(34)和新的状态变量Z(t)对时间的导数,得到
| $ \begin{array}{l} \dot Z(t) = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{\rm{n}}},t} \right)\mathit{\boldsymbol{\dot x}}(t)\\ \;\;\;\;\;\;\; = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{Bu}}\left( t \right) \end{array} $ | (35) |
式(35)表明Z·(t)是状态独立的,只与所设计的控制器相关。
当D=Dq1=[010000000]时,可分离防御器1的视线角速率信息。
当D=Dq2=[010000000]时,可分离防御器2的视线角速率信息。
当D=Dγ1=[000000010]时,可分离防御器1的航向角信息。
当D=Dγ2=[000000001]时,可分离防御器2的航向角信息。
将Dq1、Dq2、Dγ1和Dγ2代入式(33)中,得
| $ {Z_{{q_i}}}(t) = {\mathit{\boldsymbol{D}}_{{q_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{x}}(t) $ | (36) |
| $ {Z_{{\gamma _i}}}(t) = {\mathit{\boldsymbol{D}}_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right)\mathit{\boldsymbol{x}}(t) $ | (37) |
式中:i={1, 2};Zqi(t)记为零效脱靶量;Zγi(t)记为零效航向角度。
使用终端投影法降阶得到新的变量,式(32)的目标函数可表示为
| $ \begin{array}{*{20}{c}} {J = \frac{1}{2}{\alpha _1}Z_{{q_1}}^2\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \frac{1}{2}{\alpha _2}Z_{{q_2}}^2\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \frac{\beta }{2}\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.}\\ {\left. {{Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]2 + \frac{1}{2}\int_0^{{t_{{{\rm{f}}_{\rm{n}}}}}} {\left( {u_{{{\rm{D}}_1}}^2 + u_{{{\rm{D}}_2}}^2 + u_{\rm{E}}^2} \right){\rm{d}}t} } \end{array} $ | (38) |
式中:新的状态变量Zq1(tfn)、Zq2(tfn)、Zγ1(tfn)和Zγ2(tfn)分别表示式(32)中的
在突防器配合防御器1和防御器2协同交战的情况下,所设计的制导律为显式的制导律。
u(t)=[uE uD1 uD2]T,故式(35)可写为
| $ \dot Z(t) = {{\tilde B}_{\rm{E}}}(t){u_{\rm{E}}} + {{\tilde B}_{{{\rm{D}}_1}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_2}}}(t){u_{{{\rm{D}}_2}}} $ | (39) |
式中:
| $ \begin{array}{l} {{\tilde B}_{\rm{E}}}(t) = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right){\mathit{\boldsymbol{B}}_{\rm{E}}};{{\tilde B}_{{{\rm{D}}_1}}}(t) = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right){\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}};\\ {{\tilde B}_{{{\rm{D}}_2}}}(t) = \mathit{\boldsymbol{D \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{\rm{n}}}}},t} \right){\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}}。\end{array} $ |
将Dq1、Dq2、Dγ1、Dγ2、
| $ \begin{array}{l} {{\dot Z}_{{q_i}}}(t) = {\mathit{\boldsymbol{D}}_{{q_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{\rm{E}}}{u_{\rm{E}}} + {\mathit{\boldsymbol{D}}_{{q_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}}{u_{{{\rm{D}}_1}}} + {\mathit{\boldsymbol{D}}_{{q_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}}{u_{{{\rm{D}}_2}}}\\ \;\;\;\;\;\;\;\;\; = {{\tilde B}_{{{\rm{E}}_{{q_i}}}}}(t){u_{\rm{E}}} + {{\tilde B}_{{{\rm{D}}_{1{q_i}}}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_{2{q_i}}}}}(t){u_{{{\rm{D}}_2}}} \end{array} $ | (40) |
| $ \begin{array}{l} {{\dot Z}_{{\gamma _i}}}(t) = {\mathit{\boldsymbol{D}}_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_E}{u_E} + {\mathit{\boldsymbol{D}}_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{D_1}}}{u_{{D_1}}} + {\mathit{\boldsymbol{D}}_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{D_2}}}{u_{{D_2}}}\\ \;\;\;\;\;\;\;\;\; = {{\tilde B}_{{{\rm{E}}_{{\gamma _i}}}}}(t){u_{\rm{E}}} + {{\tilde B}_{{{\rm{D}}_{1{\gamma _i}}}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _i}}}}}(t){u_{{{\rm{D}}_2}}} \end{array} $ | (41) |
目标函数的Hamiltonian函数为
| $ \begin{array}{l} H = \frac{1}{2}\left( {u_{{{\rm{D}}_1}}^2 + u_{{{\rm{D}}_2}}^2 + u_{\rm{E}}^2} \right) + {\lambda _{{Z_1}}}{{\dot Z}_{{q_1}}}(t) + \\ \;\;\;\;{\lambda _{{Z_2}}}{{\dot Z}_{{q_2}}}(t) + {\lambda _{{Z_{{\gamma _1}}}}}{{\dot Z}_{{\gamma _1}}}(t) + {\lambda _{{Z_{{\gamma _2}}}}}{{\dot Z}_{{\gamma _2}}}(t) \end{array} $ | (42) |
由横截条件得
| $ {\lambda _{{Z_1}}} = {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) $ | (43) |
| $ {\lambda _{{Z_2}}} = {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) $ | (44) |
| $ {\lambda _{{Z_{{\gamma _1}}}}} = \beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] = \beta \Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) $ | (45) |
| $ {\lambda _{{z_{{\gamma _2}}}}} = - \beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] = - \beta \Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) $ | (46) |
式(45)和式(46)中的ΔZγ(tfn)表示防御器1和防御器2在拦截时的拦截角误差。
由控制方程得
| $ \begin{array}{l} \frac{{\partial H}}{{\partial {u_{\rm{E}}}}} = 0 \Rightarrow \\ {u_{\rm{E}}} = - {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{E}}_{{q_1}}}}} - {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{E}}_{{q_2}}}}} + \\ \;\;\;\;\;\;\beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]\left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}} - {{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}}} \right) \end{array} $ | (47) |
| $ \begin{array}{l} \frac{{\partial H}}{{\partial {u_{{{\rm{D}}_1}}}}} = 0 \Rightarrow \\ {u_{{{\rm{D}}_1}}} = - {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} - {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + \\ \;\;\;\;\beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]\left( {{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} - {{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}} \right) \end{array} $ | (48) |
| $ \begin{array}{l} \frac{{\partial H}}{{\partial {u_{{{\rm{D}}_2}}}}} = 0 \Rightarrow \\ {u_{{{\rm{D}}_2}}} = - {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{2{q_1}}}}} - {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{2{q_2}}}}} + \\ \;\;\;\;\;\beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]\left( {{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}} - {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}} \right) \end{array} $ | (49) |
将式(47)~式(49)分别代入式(40)和式(41)可得
| $ \begin{array}{l} {{\dot Z}_{{q_1}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{E}}_{{q_1}}}}}{{\tilde B}_{{{\rm{E}}_{{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{1{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {\alpha _2}\left( {{{\tilde B}_{{{\rm{E}}_{{q_2}}}}}{{\tilde B}_{{{\rm{E}}_{{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{1{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}}{{\tilde B}_{{{\rm{E}}_{{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \\ \;\;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}}{{\tilde B}_{{{\rm{E}}_{{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (50) |
| $ \begin{array}{l} {{\dot Z}_{{q_2}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{E}}_{{q_1}}}}}{{\tilde B}_{{{\rm{E}}_{{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_1}_{{q_1}}}}{{\tilde B}_{{{\rm{D}}_1}_{{q_2}}}} + {{\tilde B}_{{{\rm{D}}_2}_{{q_1}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {\alpha _2}\left( {{{\tilde B}_{{{\rm{E}}_{{q_1}}}}}{{\tilde B}_{{{\rm{E}}_{{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_1}_{{q_2}}}}{{\tilde B}_{{{\rm{D}}_1}_{{q_2}}}} + {{\tilde B}_{{{\rm{D}}_2}_{{q_2}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}}{{\tilde B}_{{{\rm{E}}_{{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_1}_{{\gamma _1}}}}{{\tilde B}_{{{\rm{D}}_1}_{{q_2}}}} + {{\tilde B}_{{{\rm{D}}_2}_{{\gamma _2}}}}{{\tilde B}_{{{\rm{D}}_2}_{{q_2}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}}{{\tilde B}_{{{\rm{E}}_{{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_1}_{{\gamma _1}}}}{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\tilde B}_{{{\rm{D}}_2}_{{\gamma _1}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (51) |
| $ \begin{array}{l} {{\dot Z}_{{\gamma _1}}}\left( t \right) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{E}}_{{q_1}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{q_1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{q_1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {\alpha _2}\left( {{{\tilde B}_{{{\rm{E}}_{{q_2}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{q_2}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \\ \;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (52) |
| $ \begin{array}{l} {{\dot Z}_{{\gamma _2}}}\left( t \right) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{E}}_{{q_1}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{q_1}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{q_1}}}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \\ \;\;\;\;\;\;\;\;{\alpha _2}\left( {{{\tilde B}_{{{\rm{E}}_{{q_2}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{q_2}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{q_2}}}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \\ \;\;\;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}}{{\tilde B}_{{{\rm{E}}_{{\gamma _1}}}}} + {{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}} \right) \cdot \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (53) |
对式(53)两边从t到tfn积分,并整理可得齐次线性方程组Zi(t)=L(t)Zi(tfn),即
| $ \left[ {\begin{array}{*{20}{c}} {{Z_{{q_1}}}(t)}\\ {{Z_{{q_2}}}(t)}\\ {\Delta {Z_\gamma }(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_{{q_1}1}}}&{{l_{{q_1}2}}}&{{l_{{q_1}3}}}\\ {{l_{{q_2}1}}}&{{l_{{q_2}2}}}&{{l_{{q_2}3}}}\\ {{l_{\gamma 1}}}&{{l_{\gamma 2}}}&{{l_{\gamma 3}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)}\\ {{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)}\\ {\Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)} \end{array}} \right] $ | (54) |
式中:L(t)为积分后整理得到系数矩阵。
求解式(54)可得
| $ \begin{array}{l} {Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = \frac{{{l_{{q_2}2}}{l_{{\gamma _3}}} - {l_{{q_2}3}}{l_{\gamma 2}}}}{N}{Z_{{q_1}}}(t) - \\ \;\;\;\;\frac{{{l_{{q_1}2}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{\gamma 2}}}}{N}{Z_{{q_2}}}(t) + \frac{{{l_{{q_1}2}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}2}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (55) |
| $ \begin{array}{l} {Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = - \frac{{{l_{{q_2}1}}{l_{\gamma 3}} - {l_{{q_2}3}}{l_{\eta 1}}}}{N}{Z_{{q_1}}}(t) + \\ \;\;\;\;\frac{{{l_{{q_1}1}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{\gamma 1}}}}{N}{Z_{{q_2}}}(t) - \frac{{{l_{{q_1}1}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}1}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (56) |
| $ \begin{array}{l} \Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = \frac{{{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_2}2}}{l_{\gamma 1}}}}{N}{Z_{{q_1}}}(t) - \\ \;\;\;\;\;\;\frac{{{l_{{q_1}1}}{l_{\gamma 2}} - {l_{{q_1}2}}{l_{\gamma 1}}}}{N}{Z_{{q_2}}}(t) + \frac{{{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (57) |
式中:
| $ \begin{array}{l} N = {l_{{q_1}1}}{l_{{q_2}2}}{l_{\gamma 3}} - {l_{{q_1}1}}{l_{{q_2}3}}{l_{\gamma 2}} - {l_{{q_1}2}}{l_{{q_2}1}}{l_{\gamma 3}} + {l_{{q_1}2}}{l_{{q_2}3}}{l_{\gamma 1}} + \\ \;\;\;{l_{{q_1}2}}{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_1}3}}{l_{{q_2}2}}{l_{\gamma 1}} \end{array} $ |
将式(55)~式(57)分别代入到式(47)~式(49)中,得
| $ {u_i} = \frac{{{N_{i1}}}}{N}{Z_{{q_1}}}(t) + \frac{{{N_{i2}}}}{N}{Z_{{q_2}}}(t) + \frac{{{N_{i3}}}}{N}\Delta {Z_\gamma }(t) $ | (58) |
式中:i∈{E, D1, D2},导航增益参数如下:
| $ \left\{ \begin{array}{l} {N_{i1}} = - {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_2}2}}{l_{\gamma 3}} - {l_{{q_2}3}}{l_{\gamma 2}}} \right) + {\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_2}1}}{l_{\gamma 3}} - } \right.\\ \;\;\;\;\left. {{l_{{q_2}3}}{l_{\gamma 1}}} \right) + \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - {{\tilde B}_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_2}2}}{l_{\gamma 1}}} \right)\\ {N_{i2}} = {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_1}2}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{{\gamma _2}}}} \right) - {\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_1}1}}{l_{{\gamma _3}}} - } \right.\\ \;\;\;\;\left. {{l_{{q_1}3}}{l_{\gamma 1}}} \right) + \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - {{\tilde B}_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}} \right)\\ {N_{i3}} = - {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_1}2}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}2}}} \right) + {\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_1}1}}{l_{{q_2}3}} - } \right.\\ \;\;\;\;\left. {{l_{{q_1}3}}{l_{{q_2}1}}} \right) + \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - {{\tilde B}_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}} \right) \end{array} \right. $ |
Zq1(t)和Zq2(t)分别为防御器1和防御器2的零效脱靶量;ΔZγ(t)为防御器1和防御器2相对于拦截器的零效航向角误差。
3.2 隐式的制导律在突防器不配合防御器1和防御器2协同交战的情况下,所设计的制导律为隐式的制导律。在设计制导律时,考虑突防器针对拦截器做最优躲避bang-bang机动[14]。根据突防器与拦截器的相对运动学,得到两者之间的状态方程。
| $ \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_{\rm{E}}}(t){\mathit{\boldsymbol{x}}_{\rm{E}}}(t) + {\mathit{\boldsymbol{B}}_{\rm{E}}}(t){u_{\rm{E}}}(t) $ | (59) |
式中:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{\rm{E}}}(t) = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} {\frac{{ - 2}}{{{t_{{\rm{fPE}}}} - t}}}&{\frac{{ - \cos \left( {{\gamma _{{{\rm{E}}_0}}} + {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{PE}}}}\left( {{t_{{\rm{fPE}}}} - t} \right)}}}&{\frac{{\cos \left( {{\gamma _{{{\rm{E}}_0}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{{v_{{\rm{PE}}}}\left( {{t_{{\rm{fPE}}}} - t} \right)}}}\\ {\frac{{N{v_{{\rm{PE}}}}}}{{{\tau _{\rm{P}}}}}}&{\frac{{ - 1}}{{{\tau _{\rm{P}}}}}}&{\frac{{K\cos \left( {{\gamma _{{{\rm{E}}_0}}} - {q_{{\rm{P}}{{\rm{E}}_0}}}} \right)}}{{2{\tau _{\rm{P}}}}}}\\ 0&0&{\frac{{ - 1}}{{{\tau _{\rm{E}}}}}} \end{array}} \right] \end{array} $ |
| $ {u_{\rm{E}}} = {u_{{\rm{Emax}}}}{\rm sign}\left( {{s_{{\rm{PE}}}}} \right){\rm sign}\left( {{Z_{{\rm{PE}}}}(t)} \right) $ | (60) |
式中:uEmax为突防器的最大指令加速度;
| $ {s_{{\rm{PE}}}} = {\mathit{\boldsymbol{D}}_E}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{{\rm{PE}}}}}},t} \right){\mathit{\boldsymbol{B}}_{\rm{E}}};{Z_{{\rm{PE}}}}(t) = {\mathit{\boldsymbol{D}}_{\rm{E}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_{{{\rm{f}}_{{\rm{PE}}}}}},t} \right){\mathit{\boldsymbol{x}}_{\rm{E}}}。$ |
因为u(t)=[uD1uD2]T,式(35)可写为
| $ \dot Z(t) = {{\tilde B}_{{{\rm{D}}_1}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_2}}}(t){u_{{{\rm{D}}_2}}} $ | (61) |
式中:
将Dq1、Dq2、Dγ1、Dγ2、
| $ \begin{array}{*{20}{c}} {{{\dot Z}_{{{\rm{q}}_i}}}(t) = {\mathit{\boldsymbol{D}}_{{q_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}}{u_{{{\rm{D}}_1}}} + {D_{{{\rm{q}}_i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}}{u_{{{\rm{D}}_2}}} = }\\ {{{\tilde B}_{{{\rm{D}}_{{1_{{q_i}}}}}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_{2{q_i}}}}}(t){u_{{{\rm{D}}_2}}}} \end{array} $ | (62) |
| $ \begin{array}{*{20}{c}} {{{\dot Z}_{{\gamma _i}}}(t) = {\mathit{\boldsymbol{D}}_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_1}}}{u_{{{\rm{D}}_1}}} + {D_{{\gamma _i}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_{{{\rm{D}}_2}}}{u_{{{\rm{D}}_2}}} = }\\ {{{\tilde B}_{{D_{1{\gamma _i}}}}}(t){u_{{{\rm{D}}_1}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _i}}}}}(t){u_{{{\rm{D}}_2}}}} \end{array} $ | (63) |
目标函数的Hamiltonian函数为
| $ \begin{array}{l} H = \frac{1}{2}\left( {u_{{{\rm{D}}_1}}^2 + u_{{{\rm{D}}_2}}^2} \right) + {\lambda _{{Z_1}}}{{\dot Z}_{{q_1}}}(t) + {\lambda _{{Z_2}}}{{\dot Z}_{{q_2}}}(t) + \\ \;\;\;\;\;{\lambda _{{Z_{{\gamma _1}}}}}{{\dot Z}_{{\gamma _1}}}(t) + {\lambda _{{Z_{{\gamma _2}}}}}{{\dot Z}_{{\gamma _2}}}(t) \end{array} $ | (64) |
横截条件与显式下情形相同,由控制方程得
| $ \begin{array}{l} \frac{{\partial H}}{{\partial {u_{{{\rm{D}}_1}}}}} = 0 \Rightarrow \\ {u_{{{\rm{D}}_1}}} = - {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} - {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{{1_{{q_2}}}}}}} + \\ \;\;\;\;\;\;\beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]\left( {{{\tilde B}_{{{\rm{D}}_{1{\gamma _2}}}}} - {{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}} \right) \end{array} $ | (65) |
| $ \begin{array}{l} \frac{{\partial H}}{{\partial {u_{{{\rm{D}}_2}}}}} = 0 \Rightarrow \\ {u_{{{\rm{D}}_2}}} = - {\alpha _1}{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_{2{q_1}}}}} - {\alpha _2}{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right){{\tilde B}_{{{\rm{D}}_2}_{{q_2}}}} + \\ \;\;\;\;\;\beta \left[ {{Z_{{\gamma _1}}}\left( {{t_{\rm{n}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right]\left( {{{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}} - {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}} \right) \end{array} $ | (66) |
将式(65)和式(66)分别代入式(62)和式(63)可得
| $ \begin{array}{l} {{\dot Z}_{{q_1}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \\ \;\;\;\;\;\;{\alpha _2}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right)\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.\\ \;\;\;\;\;\;\left. {{Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \beta \left( {{{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}} \right) \cdot \\ \;\;\;\;\;\;\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (67) |
| $ \begin{array}{l} {{\dot Z}_{{q_2}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \\ \;\;\;\;\;\;{\alpha _2}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _2}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right)\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.\\ \;\;\;\;\;\;\left. {{Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \beta \left( {{{\tilde B}_{{{\rm{D}}_{1{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}} + {{\tilde B}_{{{\rm{D}}_{2{\gamma _1}}}}}{{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}} \right) \cdot \\ \;\;\;\;\;\;\left[ {{Z_{{\gamma _1}}}\left( {{t_{{f_n}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (68) |
| $ \begin{array}{l} {{\dot Z}_{{\gamma _1}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}}{{\tilde B}_{{{\rm{D}}_1}_{{\gamma _1}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}{{\tilde B}_{{{\rm{D}}_2}_{{\gamma _1}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \\ \;\;\;\;\;{\alpha _2}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_2}_{{\gamma _1}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}} + {{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}} \right)\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.\\ \;\;\;\;\;\left. {{Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}} \right) \cdot \\ \;\;\;\;\;\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (68) |
| $ \begin{array}{l} {{\dot Z}_{{\gamma _2}}}(t) = - {\alpha _1}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_1}}}}}{{\tilde B}_{{{\rm{D}}_1}_{{\gamma _2}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_1}}}}}{{\tilde B}_{{{\rm{D}}_2}_{{\gamma _2}}}}} \right){Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \\ \;\;\;\;\;{\alpha _2}\left( {{{\tilde B}_{{{\rm{D}}_{1{q_2}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}} + {{\tilde B}_{{{\rm{D}}_{2{q_2}}}}}{{\tilde B}_{{{\rm{D}}_2}_{{\gamma _2}}}}} \right){Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) + \\ \;\;\;\;\;\beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _2}}}}}}}{{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _2}}}}}}}} \right)\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - } \right.\\ \;\;\;\;\;\left. {{Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] - \beta \left( {{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{1_{{\gamma _2}}}}}}} + {{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _1}}}}}}}{{\tilde B}_{{{\rm{D}}_{{2_{{\gamma _2}}}}}}}} \right) \cdot \\ \;\;\;\;\;\left[ {{Z_{{\gamma _1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - {Z_{{\gamma _2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) - \Delta } \right] \end{array} $ | (70) |
对式(70)两边从t到tfn积分,并整理可得齐次线性方程组
| $ \left[ {\begin{array}{*{20}{c}} {{Z_{{q_1}}}(t)}\\ {{Z_{{q_2}}}(t)}\\ {\Delta {Z_\gamma }(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_{{q_1}1}}}&{{l_{{q_1}2}}}&{{l_{{q_1}3}}}\\ {{l_{{q_2}1}}}&{{l_{{q_2}2}}}&{{l_{{q_2}3}}}\\ {{l_{\gamma 1}}}&{{l_{\gamma 2}}}&{{l_{\gamma 3}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)}\\ {{Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)}\\ {\Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right)} \end{array}} \right] $ | (71) |
式中:L(t)为积分后整理得到的系数矩阵。
求解式(71)可得
| $ \begin{array}{l} {Z_{{q_1}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = \frac{{{l_{{q_2}2}}{l_{\gamma 3}} - {l_{{q_2}3}}{l_{\gamma 2}}}}{N}{Z_{{q_1}}}(t) - \\ \;\;\;\;\;\frac{{{l_{{q_1}2}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{\gamma 2}}}}{N}{Z_{{q_2}}}(t) + \frac{{{l_{{q_1}2}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}2}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (72) |
| $ \begin{array}{l} {Z_{{q_2}}}\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = - \frac{{{l_{{q_2}1}}{l_{\gamma 3}} - {l_{{q_2}3}}{l_{\gamma 1}}}}{N}{Z_{{q_1}}}(t) + \\ \;\;\;\;\;\frac{{{l_{{q_1}1}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{\gamma 1}}}}{N}{Z_{{q_2}}}(t) - \frac{{{l_{{q_1}1}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}1}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (73) |
| $ \begin{array}{l} \Delta {Z_\gamma }\left( {{t_{{{\rm{f}}_{\rm{n}}}}}} \right) = \frac{{{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_2}2}}{l_{\gamma 1}}}}{N}{Z_{{q_1}}}(t) - \\ \;\;\;\;\frac{{{l_{{q_1}1}}{l_{\gamma 2}} - {l_{{q_1}2}}{l_{\gamma 1}}}}{N}{Z_{{q_2}}}(t) + \frac{{{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}}}{N}\Delta {Z_\gamma }(t) \end{array} $ | (74) |
式中:
| $ \begin{array}{l} N = {l_{{q_1}1}}{l_{{q_2}2}}{l_{{\gamma _3}}} - {l_{{q_1}1}}{l_{{q_2}3}}{l_{\gamma 2}} - {l_{{q_1}2}}{l_{{q_2}1}}{l_{\gamma 3}} + \\ \;\;\;\;{l_{{q_1}2}}{l_{{q_2}3}}{l_{\gamma 1}} + {l_{{q_1}2}}{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_1}3}}{l_{{q_2}2}}{l_{\gamma 1}}。\end{array} $ |
将式(72)~式(74)分别代入到式(65)和式(66)中,得
| $ {u_i} = \frac{{{N_{i1}}}}{N}{Z_{{{\rm{q}}_{\rm{1}}}}}(t) + \frac{{{N_{i2}}}}{N}{Z_{{{\rm{q}}_{\rm{2}}}}}(t) + \frac{{{N_{i3}}}}{N}\Delta {Z_\gamma }(t) $ | (75) |
式中:i∈{D1, D2}; 导航增益参数如下:
| $ \left\{ \begin{array}{l} {N_{i1}} = - {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_2}2}}{l_{\gamma 3}} - {l_{{q_2}3}}{l_{\gamma 2}}} \right) + {\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_2}1}}{l_{\gamma 3}} - } \right.\\ \;\;\;\;\left. {{l_{{q_2}3}}{l_{\gamma 1}}} \right) + \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - {B_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_2}1}}{l_{\gamma 2}} - {l_{{q_2}2}}{l_{\gamma 1}}} \right)\\ {N_{i2}} = {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_1}2}}{l_{\gamma 3}} - {l_{{q_1}3}}{l_{\gamma 2}}} \right) + {\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_1}1}}{l_{\gamma 3}} - } \right.\\ \;\;\;\;\left. {{l_{{q_1}3}}{l_{\gamma 1}}} \right) - \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - {B_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}} \right)\\ {N_{i3}} = - {\alpha _1}{{\tilde B}_{{i_{{q_1}}}}}\left( {{l_{{q_1}2}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}2}}} \right) + \\ \;\;\;\;{\alpha _2}{{\tilde B}_{{i_{{q_2}}}}}\left( {{l_{{q_1}1}}{l_{{q_2}3}} - {l_{{q_1}3}}{l_{{q_2}1}}} \right) + \beta \left( {{{\tilde B}_{{i_{{\gamma _2}}}}} - } \right.\\ \;\;\;\;\left. {{{\tilde B}_{{i_{{\gamma _1}}}}}} \right)\left( {{l_{{q_1}1}}{l_{{q_2}2}} - {l_{{q_1}2}}{l_{{q_2}1}}} \right) \end{array} \right. $ |
在本节中,将分析第3节设计的突防器、防御器1和防御器2三者协同的最优制导律(显式的协同)的性能,并与突防器不与两个防御器协同的最优制导律(隐式的协同)进行比较。
在仿真中,拦截器采用APN制导律对突防器进行拦截,突防器发射两枚防御器对拦截器进行反拦截,所以突防器、防御器1和防御器2的初始发射位置相等。由先前的假设可知,防御器1和防御器2的拦截时间相等,所以它们的速度相等。此外,根据文献[23],当相对拦截角在30°与65°之间时,两防御器之间能产生较好的拦截性能,所以本文设定相对拦截角30°。为具体的仿真参数可参照表 1。
| 参数 | 初始值 |
| 初始相对距离rPE0/m | 16 000 |
| 初始相对距离rPD10/m, rPD20/m | 16 000 |
| 突防器的速度vE | 300 |
| 防御器的速度vD1/(m·s-1), vD2/(m·s-1) | 500 |
| 拦截器的速度vP | 500 |
| 防御器的过载限制uDmax/(m·s-2) | 150 |
| 拦截器的过载限制aPmax/(m·s-2) | 100 |
| 突防器的响应时间τE/s | 0.1 |
| 防御器的响应时间τD1/s, τD2/s | 0.1 |
| 拦截器的响应时间τP/s | 0.1 |
| 导航参数N | 3 |
| 修正系数K | 3 |
| 初始状态变量x0 | |
| 相对拦截角Δ/(°) | 30 |
| 权重系数α1, α2 | 10 000 000 000 |
| 权重系数β | 30 000 |
图 2为突防器、防御器1和防御器2三者协同下的拦截交战图。可知,在拦截器对突防器进行拦截时,突防器发射两枚防御器对拦截器进行反拦截的同时,执行引诱机动,协助两枚防御器在坐标点(12 950 m, 4 543 m)成功实现对拦截器的反拦截,并在拦截末端形成一个预置的30°的拦截角。
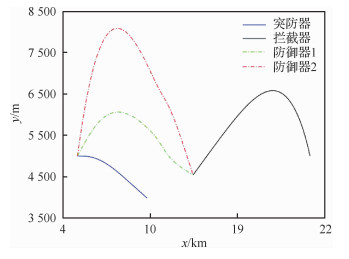
|
| 图 2 显式的协同:多导弹协同拦截交战 Fig. 2 Multi-missile cooperative interception engagement in explicit cooperation |
图 3为突防器、防御器1和防御器2的加速度曲线变化图。可知,在三者的相互协同下,突防器的最大需用加速度为12.91 m/s2,2个防御器的加速度都达到了过载限制150 m/s2。当敌方拦截器的加速度不受限制时,其最大需用加速度为108.1 m/s2,显然,此种情形拦截器的作战效费比较大。此外,在突防器的协同下,防御器1和防御器2的加速度变化基本相同。这说明,突防器的协同机动过程可以使得防御器1和防御器2都能同时达到一个较好的制导效果。此外,图中显示在将要达到拦截点附近时,它们的加速度趋近于0,此时三者均作匀速运动。

|
| 图 3 显式的协同:加速度的变化 Fig. 3 Variation of acceleration in explicit cooperation |
图 4为防御器1和防御器2的能量消耗随时间变化图,在10~12 s之间因为加速度变化剧烈,所以消耗的能量增加较快,在12 s以后基本稳定下来。在最终时刻防御器1的能量消耗略大于防御器2的能量消耗。
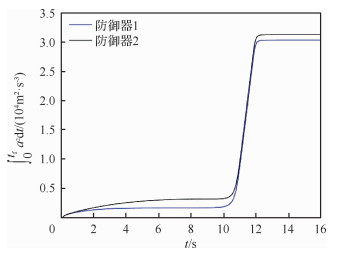
|
| 图 4 显示的协同:能量消耗的变化 Fig. 4 Variation of energy consumptions in explicit cooperation |
图 5为突防器、防御器1和防御器2的视线角速率变化图。可知,防御器1和防御器2的视线角速率最终都能稳定地收敛到0附近,结合式(31)可知防御器1和防御器2能以较小的脱靶量拦截拦截器。
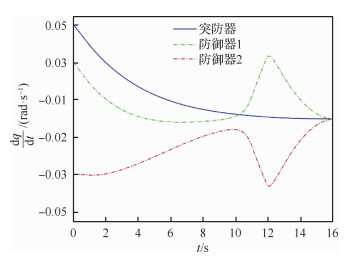
|
| 图 5 显式的协同:视线角速率的变化 Fig. 5 Variation of LOS angle rotation rates in explicit cooperation |
图 6为防御器1和防御器2之间的相对拦截角变化图。可知,防御器1和防御器2在制导过程中不断调整它们之间的夹角,并在拦截终端达到设定的预置相对拦截角。图中的最终相对拦截角为29.84°,与设定的30°存在0.06°的偏差。

|
| 图 6 显示的协同:相对拦截角的变化 Fig. 6 Variation of relative interception angles in explicit cooperation |
图 7以防御器1为例,视线角速率随其过载限制的变化图。可知,随着防御器过载限制的减小,视线角速率在逐渐减小。根据式(31),视线角速率与脱靶量成正比关系,这说明过大的过载限制会降低防御器的制导性能。同样地,较大的拦截器过载限制会降低其对突防器的拦截性能。

|
| 图 7 显式的协同:视线角速率随防御器过载限制的变化 Fig. 7 Variation of LOS angle rotation rates with overload limit on defender in explicit cooperation |
通过对3.2节中设计的隐式协同制导律进行仿真验证得到:
图 8为突防器不配合防御器1和防御器2协同的拦截交战图,防御器1和防御器2仅知道突防器未来的机动,无法与突防器进行实时的协同,且它们两者协同施加一个预置的拦截角。

|
| 图 8 隐式的协同:多导弹协同拦截交战 Fig. 8 Multi-missile cooperative interception engagement in implicit cooperation |
图 9为突防器、防御器1和防御器2的加速度变化曲线,突防器执行最大指令加速度为50 m/s2的bang-bang最优躲避机动,此时,防御器1和防御器2的加速度均达到了过载限制值,相比于显示的协同,在突防器实行躲避机动的情况下它们的加速度变化比较剧烈,且三者对机动的要求较高。当敌方拦截器的加速度不受限制时,其最大需用加速度为147 m/s2,相比于隐式的协同,显式的协同提高了敌方拦截器的作战效费比。
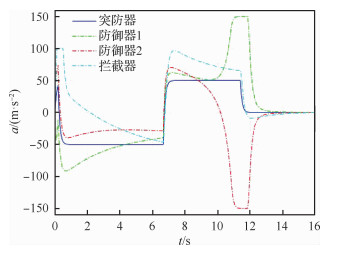
|
| 图 9 隐式的协同:加速度的变化 Fig. 9 Variation of accelerations in implicit cooperation |
图 10显示了在突防器执行最大指令加速度为50 m/s2的bang-bang最优躲避机动情况下的防御器1和防御器2的能量消耗图。由图中可知,隐式协同下的两个防御器的能量消耗远远大于显示协同下的对应的防御器的能量消耗。且在隐式协同下两防御器的能量消耗相差较大,在12 s之前的制导过程中,两者的能量消耗一直在快速增加。显然,显式的协同可以大大节约防御器1和防御器2的能量消耗。

|
| 图 10 隐式的协同:能量消耗的变化 Fig. 10 Variation of energy consumptions in implicit cooperation |

|
| 图 11 隐式的协同:视线角速率的变化 Fig. 11 Variation of LOS angle rotation rates in implicit cooperation |
这表明,所设计的最优制导律在突防器配合机动的情况下,能够有效地减少三者所需的加速度和能量消耗。
图 11显示了在隐式协同的情况下,防御器1和防御器2的视线角速率最终能够收敛到0附近。能够以较小的脱靶量拦截拦截器。图 12显示了在隐式的协同下,防御器1和防御器2能在拦截末端达到预置的相对拦截角。
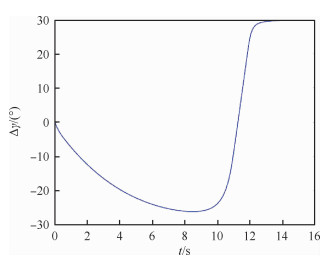
|
| 图 12 隐式的协同:相对拦截角的变化 Fig. 12 Variation of relative interception angles in implicit cooperation |
当面对不同的作战任务时,防御器也会面临不同的战场发射环境,所以设计的制导律在确保制导精度的稳定性上显得尤为重要。基于所设计的显式的最优制导律,本节分析了在不同初始发射条件下的制导性能。当防御器从突防器上发射出去之后,不同的发射环境将最终影响初始的视线角速率。
在设置相对拦截角为30°的情况下,仿真中研究了5种不同的初始发射条件(初始视线角速率)对制导性能的影响。2个防御器的初始发射参数见表 2。
| 情况 | 初值 |
初值 |
| 1 | 0.01 | -0.01 |
| 2 | 0.02 | -0.02 |
| 3 | 0.03 | -0.03 |
| 4 | 0.04 | -0.04 |
| 5 | 0.05 | -0.05 |
图 13和图 14分别为防御器1和防御器2在5种不同初始值情况下的视线角速率变化图。由图可知,在5种不同初始值情况下,防御器1和防御器2的视线角速率最终都能收敛到0附近。
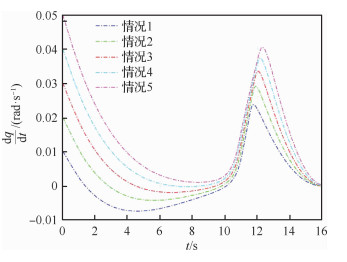
|
| 图 13 防御器1的视线角速率变化 Fig. 13 Variation of LOS angle rotation rates for Defender 1 |
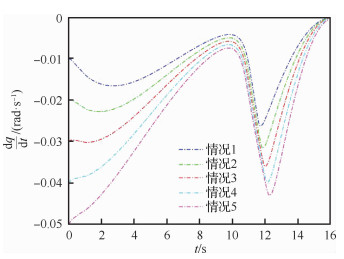
|
| 图 14 防御器2的视线角速率变化 Fig. 14 Variation of LOS angle rotation rates for Defender 1 |
图 15为在5种不同初始值情况下的相对拦截角的变化图。可知,在5种不同的初始值情况下,防御器1和防御器2最终都能在制导末端施加预置的30°的相对拦截角。
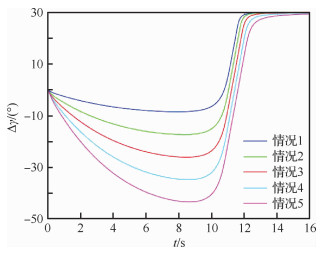
|
| 图 15 相对拦截角的变化 Fig. 15 Variation of relative interception angles |
上述仿真验证了所提制导律的有效性,同时也表明了在不同的发射条件下,所提制导律能保持较好的稳定性。
5 结论1) 针对我方飞行器发射两枚防御器有效拦截对方拦截器的突防问题,提出了一种带引诱角色的显式协同制导律,并将其与隐式的协同制导律进行比较,仿真结果表明显式的协同优于隐式的协同。
2) 所设计的制导律将脱靶量、能量消耗和施加末端相对拦截角考虑在目标函数的建立中,利用最优控制理论求得了不同策略下的控制输入。
3) 本文没有考虑制导过程中的探测估计问题,探测效果影响着制导的效果和精度,未来有必要将探测角色加入到协同制导律的设计中,实现探测制导一体化设计。
| [1] |
姚郁, 郑天宇, 贺风华, 等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报, 2015, 36(8): 2696-2716. YAO Y, ZHENG T Y, HE F H, et al. Several hot issues and challenges in terminal guidance of flight vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2696-2716. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [2] | SHAFERMAN V, SHIMA T. Cooperative optimal guidance laws for imposing a relative intercept angle[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1395-1408. |
| Click to display the text | |
| [3] | JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266. |
| Click to display the text | |
| [4] | BOYELL L R. Defending a moving target against missile or torpedo attack[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(4): 522-526. |
| Click to display the text | |
| [5] | BOYELL L R. Counterweapon aiming for defense of a moving target[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, 16(3): 402-408. |
| Click to display the text | |
| [6] | RATNOO A, SHIMA T. Line-of-sight interceptor guidance for defending an aircraft[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 522-532. |
| Click to display the text | |
| [7] | RATNOO A, SHIMA T. Guidance strategies against defended aerial targets[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1059-1068. |
| Click to display the text | |
| [8] | YAMASAKI T, BALAKRISHNAN S N, TAKANO H. Modified command to line-of-sight intercept guidance for aircraft defense[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 898-902. |
| Click to display the text | |
| [9] | YAMASAKI T, BALAKRISHNAN S N. Intercept guidance for cooperative aircraft defense against a guided missile[J]. IFAC Proceedings Volumes, 2010, 43(15): 118-123. |
| Click to display the text | |
| [10] | SHAFERMAN V, SHIMA T. Cooperative multiple model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control, and Dynamics, 2010, 6(33): 1801-1813. |
| Click to display the text | |
| [11] | GUO Y, XIAO X H, HE F H, et al. Triangle interception scenario:A finite-time guidance approach[J]. International Journal of Aerospace Engineering, 2016, 2016(1): 1-12. |
| Click to display the text | |
| [12] |
张帅, 郭杨, 王仕成. 带有引诱角色的有限时间协同制导方法[J]. 宇航学报, 2018, 39(3): 308-317. ZHANG S, GUO Y, WANG S C. Finite time cooperative guidance method with a lure role[J]. Journal of Astronautics, 2018, 39(3): 308-317. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [13] | ZHANG S, GUO Y, WANG S C. Cooperative intercept guidance of multiple aircraft with a lure role included[J]. International Journal of Aerospace Engineering, 2018, 2018: 1-15. |
| Click to display the text | |
| [14] | SHIMA T. Optimal cooperative pursuit and evasion strategies against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 414-425. |
| Click to display the text | |
| [15] | PROKOPOV O, SHIMA T. Linear quadratic optimal cooperative strategies for active aircraft protection[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 753-764. |
| Click to display the text | |
| [16] | PERELMAN A, SHIMA T, RUSNAK I. Cooperative differential game strategies for active aircraft protection from a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 761-773. |
| Click to display the text | |
| [17] | KUMAR S R, SHIMA T. Cooperative nonlinear guidance strategies for aircraft defense[J]. Journal of Guidance, Control, and Dynamics, 2016, 40(1): 1-15. |
| Click to display the text | |
| [18] | WEISS M, SHIMA T, CASTANEDA D, et al. Combined and cooperative minimum-effort guidance algorithms in an active aircraft defense scenario[J]. Journal of Guidance, Control, and Dynamics, 2017, 1-14. |
| Click to display the text | |
| [19] |
赵建博, 杨树兴, 熊芬芬. 无导引头也无惯导导弹的协同制导[J]. 航空学报, 2019, 40(10): 323191. ZHAO J B, YANG S X, XIONG F F. Cooperative guidance for seeker less missile without inertial navigation system[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(10): 323191. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [20] | SHAFERMAN V, OSHMAN Y. Cooperative interception in a multi-missile engagement[C]//AIAA Guidance, Navigation, & Control Conference. Reston, VA: AIAA, 2009. |
| [21] | LIU Y F, QI N M, SHAN J J. Cooperative interception with double-line-of sight-measuring[C]//AIAA Guidance, Navigation, & Control Conference.Reston, VA: AIAA, 2013. |
| [22] | CHEN T, XU S. Approach guidance with double-line-of-sight measuring navigation constraint for autonomous rendezvous[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 678-687. |
| Click to display the text | |
| [23] | FONOD R, SHIMA T. Estimation enhancement by cooperatively imposing relative intercept angles[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(7): 1711-1725. |
| Click to display the text |



