2. 航空动力装备振动及控制教育部重点实验室, 沈阳 110819;
3. 上海航空材料结构检测股份有限公司, 上海 201210
2. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Shenyang 110819;
3. Shanghai Aeronautical Material and Structures Testing Co., LTD, Shanghai 201210, China
早在19世纪,人们就已经认识到了材料的疲劳问题,Wöhler在1860年就绘制出了最早的S-N(应力-寿命)曲线[1]。此后,对疲劳问题的研究逐步深入。目前,在常规疲劳问题的研究方面已经形成了较为完善的理论体系。但是,振动疲劳的研究则起步较晚,直到1958年,美国学者Crandall将振动与疲劳问题结合起来[2],从此人们才真正开始关注到振动疲劳问题。1963年,Crandall和Mark将振动疲劳定义为结构在振动激励下产生的响应所造成的可以累加损伤的强度破坏[3]。
在疲劳寿命预测问题上,工程中常用的求解方式主要有2种,即时域分析和频域分析。日常对各种物理量的认知普遍是从时域角度出发的,表述时以时间作为横坐标,体现出了物理量在一定时间范围内的变化情况;而频域方法表达的则是物理量与频率之间的关系。相比之下,简单的、规律性的变化用时域求解方式较为直观、准确,而当面对一些复杂的或随机的载荷时,频域求解方式则能更加清晰明了地表达载荷特征,且求解速度更快。
在振动疲劳寿命预测理论模型方面,Bendat和Piersol于1966年率先提出了使用功率谱密度直接计算疲劳损伤的方法,其计算方法基于窄带随机过程的特点,使用功率谱密度函数估计随机应力的幅值分布,进而计算出结构的疲劳损伤[4];但是Bendat的研究是在窄带随机过程的基础上进行的,而实际工程中的随机振动普遍是以宽带分布的形式存在的,若直接使用则会出现较大误差。Wirsching等在Bendat的研究基础上进行了修正,提出了新的计算模型[5-6]。此外,Chaudhury和Dover也基于Bendat所提出的计算模型进行了修正[7]。1985年,Dirlik使用了计算机模拟的方式对宽带随机过程的幅值分布进行了拟合,总结出了一个适用于宽带分布的经验公式[8],该公式对于带宽的敏感性低,在实际使用时具有比其他模型更高的精度,因此应用较为广泛。Benasciutti和Tovo同样在其研究中提出了一个适用于宽带随机过程的幅值分布模型,并且也具有较高的拟合精度[9]。
1 随机振动疲劳理论 1.1 随机过程随机过程可分为平稳过程与非平稳过程,生活中常见的一般为平稳随机过程,该条件下反映随机过程x(t)在t1时刻自身前后相关性的自相关函数Rx不随时间变化[10],即
| $ {R_x}\left( {{t_1},{t_1} + \tau } \right) = {R_x}(\tau ) = E\left[ {x(t)x(t + \tau )} \right] $ | (1) |
式中:E为期望;t为时间;τ为时间间隔。
自相关函数在时域内描述了随机过程的统计特征,而在频域内描述随机过程用的则是功率谱密度函数(Power Spectral Density,PSD),二者组成一个傅里叶变换对[11-12]:
| $ {S_x}(\omega ) = \int\limits_{ - \infty }^{ + \infty } {{R_x}(\tau ){{\rm{e}}^{ - {\rm{i}}\omega \tau }}{\rm{d}}\tau } $ | (2) |
| $ {R_x}(\tau ) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int\limits_{ - \infty }^{ + \infty } {{R_x}(\omega ){{\rm{e}}^{{\rm{i}}\omega \tau }}{\rm{d}}\omega } $ | (3) |
式中:Sx(ω)为功率谱密度函数;ω为圆频率。
值得注意的是,功率谱的定义区间为正负2个实数域,称作双边功率谱,而现实中不存在负频率,因此定义单边功率谱密度Gx(ω)为
| $ {G_x}(\omega ) = \left\{ {\begin{array}{*{20}{l}} {2{S_x}(\omega )}&{\omega \ge 0}\\ 0&{\omega < 0} \end{array}} \right. $ | (4) |
此外,除了可以通过自相关函数定义随机信号的功率谱密度外,还可以通过滤波法与快速傅里叶变换法来定义功率谱密度,公式分别为
| $ {G_{滤波法}}(f) = \mathop {\lim }\limits_{t \to \infty } \mathop {\lim }\limits_{b \to 0} \frac{1}{{bt}}\int\limits_0^t {{y^2}(f,t,b){\rm{d}}t} $ | (5) |
| $ {G_{傅里叶}}(f) = \mathop {\lim }\limits_{t \to \infty } \frac{2}{t}E\left[ {{{\left| {{\rm{fft}}\left( {f,t} \right)} \right|}^2}} \right] $ | (6) |
式中:y(f, t, b)为滤波后中心频率为f、时间长度为t、带宽为b的信号的幅值;fft为对信号进行快速傅里叶变换。
快速傅里叶变换法即为将时间长度趋于无限的随机信号通过傅里叶变换完成从时域到频域的转换。
基于信号的功率谱密度,定义平稳随机过程的谱矩mi为
| $ {m_i} = \int\limits_0^{ + \infty } {{f^i}G\left( f \right){\rm{d}}f} \;\;\;i = 0,1,2, \cdots $ | (7) |
其各阶谱矩在时域内的意义为[13]
| $ {m_0} = E\left[ {{x^2}(t)} \right] $ | (8) |
| $ {m_2} = E\left[ {{{\dot x}^2}(t)} \right] $ | (9) |
| $ {m_4} = E\left[ {{{\ddot x}^2}(t)} \right] $ | (10) |
式中:x为时域信号幅值;
定义了谱矩之后,可用各阶谱矩来表达随机过程的一些特征,如随机过程的均方根值σRMS :
| $ {\sigma _{{\rm{RMS}}}} = m_0^{\frac{1}{2}} = \sqrt {\int\limits_0^{ + \infty } {G\left( \omega \right){\rm{d}}\omega } } $ | (11) |
随机过程的均方根值是均方值的开根,均方值代表了功率谱密度曲线与横轴包围的面积,面积越大,说明随机谱的能量越大,因此随机振动的均方值和均方根值在某种意义上表明了随机振动的强弱,二者越大说明振动越强。
引入不规则因子γ来描述随机过程的不规则性,其公式为
| $ \gamma = \frac{{{m_2}}}{{\sqrt {{m_0}{m_4}} }} $ | (12) |
不规则因子的取值范围为[0, 1],当其取值趋近于1时,即意味着在时域历程中几乎每次正向穿越零水平后都会对应出现一个波峰,也就意味着此时随机过程为窄带随机过程,当γ=1时,随机过程则变成了简单的简谐波;相反地,当不规则因子趋近于0时,随机过程也随之趋近于宽带过程,当γ=0时,随机过程为白噪声。
另外,带宽系数ε也可以衡量随机过程为宽带还是窄带过程:
| $ \varepsilon = \sqrt {1 - \frac{{m_2^2}}{{{m_0}{m_4}}}} = \sqrt {1 - {\gamma ^2}} $ | (13) |
与不规则因子相反,当带宽系数趋近于1时,随机过程趋近于宽带过程,反之则趋近于窄带过程。
反映单位时间内峰值次数的峰值期望率Vp[14]为
| $ {V_{\rm{p}}} = \sqrt {\frac{{{m_4}}}{{{m_2}}}} $ | (14) |
反映单位时间内正向穿越均值的正斜率穿越期望值V+为
| $ {V_ + } = \sqrt {\frac{{{m_2}}}{{{m_0}}}} $ | (15) |
频域疲劳寿命预测,广泛应用于解决结构承受随机载荷时的疲劳问题。经典疲劳理论是建立在应力或应变的时域分析基础之上的,主要思路为对零部件工作状态中的危险点进行应力应变时间历程的求解,结合Miner准则与响应历程中的循环次数来计算累积损伤量,从而推算出预估的疲劳寿命;而频域疲劳分析方法的基本思想则是从载荷的功率谱密度等统计特征出发,通过传递函数求解出零部件危险点的响应应力应变的统计特征,并根据这些统计特征估算出各水平的应力在单位时间内的期望循环次数的概率密度函数,然后使用Miner准则从统计学角度求出疲劳损伤的期望值,最终完成疲劳寿命的预测。时域方法能够清晰明了地反映出结构的寿命周期中的受载过程,可将加载顺序等频域方法无法考虑到的因素考虑进来,寿命预测更为精准,但疲劳分析时域方法的计算量非常大,计算起来难度较大;而频域分析方法的切入点则是载荷的统计学特征,该方法无法准确地描述应力应变历程,只能通过统计学的方式计算疲劳损伤,因此准确性上要低于时域方法,但其优势在于计算量小,求解速度快,更加适合工程应用。
根据Miner准则可知,应力应变每循环一次都会造成一定损伤,不同大小的应力应变将造成不同程度的损伤,当累积损伤量到达一定值时,零件将会发生疲劳失效[15]。S-N曲线中某应力幅S对应的疲劳循环次数为N(S),该水平应力在某时段内实际的循环次数为n(S),规定零件总损伤量为1时发生疲劳失效,则这一时段内该水平应力造成的损伤量D为[16-19]
| $ D = \frac{{n(S)}}{{N(S)}} $ | (16) |
式中:N(S)可以由材料疲劳曲线的表达式获得,工程上常用的疲劳曲线幂函数公式为
| $ {S^m}N = C $ | (17) |
其中:m与C均为材料常数;N为疲劳寿命对应循环数。
若某工况下应力为连续分布,则时间t内幅值在(S, S+ΔS)的应力循环次数可以记为
| $ n(S) = vtp(S)\Delta S $ | (18) |
式中:v为单位时间内所有应力雨流幅值循环次数;p(S)代表幅值为S的应力分布密度;ΔS为应力区间。因此,连续分布的应力幅造成的疲劳损伤为
| $ D = vt\int {\frac{{p(S)}}{{N(S)}}{\rm{d}}S} $ | (19) |
则用时间表示的零件的疲劳寿命tL为
| $ {t_{\rm{L}}} = \frac{1}{{v\int {\frac{{p(S)}}{{N(S)}}{\rm{d}}S} }} = \frac{C}{{v\int {{S^m}} p(S){\rm{d}}S}} $ | (20) |
由此可见,要想在频域范围内合理预测零部件的疲劳寿命,需要了解响应应力的幅值分布情况,即式(20)中的p(S),而这正是频域疲劳方法的重难点所在,目前的研究中最为常用的是Dirlik应力幅值分布模型。
Dirlik使用蒙特卡洛方法在计算机中建立了时域模拟信号,对大量不同不规则因子的PSD曲线进行了模拟仿真,总结出了一套经验公式。Dirlik将幅值范围概率密度函数假设为了一个指数分布与2个瑞利分布的和,公式为
| $ p(S) = \frac{{\frac{{{D_1}}}{Q}{{\rm{e}}^{\frac{{ - Z}}{Q}}} + \frac{{{D_2}Z}}{{{R^2}}}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2{R^2}}}}} + {D_3}Z{{\rm{e}}^{\frac{{ - {Z^2}}}{2}}}}}{{2\sqrt {{m_0}} }} $ | (21) |
式中:
| $ Z = \frac{S}{{2\sqrt {{m_0}} }};{D_1} = \frac{{2\left( {{X_m} - {\gamma ^2}} \right)}}{{1 + {\gamma ^2}}} $ |
| $ {D_2} = \frac{{1 - \gamma - {D_1} + D_1^2}}{{1 - R}};{D_3} = 1 - {D_1} - {D_2} $ |
| $ R = \frac{{\gamma - {X_m} - D_1^2}}{{1 - \gamma - {D_1} + D_1^2}};{X_m} = \frac{{{m_1}}}{{{m_0}}}\sqrt {\frac{{{m_2}}}{{{m_4}}}} $ |
| $ Q = \frac{{1.25\left( {\gamma - {D_3} - {D_2}R} \right)}}{{{D_1}}} $ |
Dirlik法是频域疲劳寿命预测研究中使用最广泛的方法,对于大部分宽带随机过程都有很好的适应性,因此工程中一般采用该模型进行随机振动疲劳寿命预测。虽然其只是经验公式,没有理论支撑,但在绝大多数情况下,都有比其他模型更好的计算精度[12-14, 16-20]。
以目前的研究与应用来看,多数研究人员将频域幅值分布模型直接应用在了单一S-N曲线表达式所描述的应力分布区间内,但使用基于Dirlik等模型的频域方法时,计算出的应力幅分布区间宽泛,而且会有大量的小幅值应力出现。对于一些常用的碳钢、合金钢、高强钢等材料,其S-N曲线在双对数坐标系下会出现明显的拐点,如果用单一的S-N曲线表达式来描述其疲劳性能将导致一部分应力幅值对应的损伤出现一定的误差,降低了寿命预测模型的准确度。因此在使用频域幅值分布模型时,可以采用分段计算疲劳损伤的方法,这样将得到更加精确的计算结果。
在考虑超高周疲劳的影响时,大部分材料的S-N曲线将呈现出三段甚至更多段的形式[21],此时如果使用单一幂函数拟合的S-N曲线将会存在明显的精度问题,显然也应该分开计算疲劳损伤。本文仅以两段式S-N曲线进行说明。
使用双对数坐标系下的2条直线来拟合S-N曲线,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{S^{{m_{\rm{a}}}}}N = {C_{\rm{a}}}}&{0 < S \le {S_0}}\\ {{S^{{m_{\rm{b}}}}}N = {C_{\rm{b}}}}&{S > {S_0}} \end{array}} \right. $ | (22) |
式中:下标a、b用以区分两段表达式参数; S0为两段表达式的分隔点。
此时零件的疲劳损伤表达式为
| $ D = vt\left( {\int\limits_0^{{S_0}} {\frac{{{S^{{m_{\rm{a}}}}}p(S)}}{{{C_{\rm{a}}}}}{\rm{d}}S} + \int\limits_{{S_0}}^\infty {\frac{{{S^{{m_{\rm{b}}}}}p(S)}}{{{C_{\rm{b}}}}}{\rm{d}}S} } \right) $ | (23) |
对应的疲劳寿命为
| $ {t_{\rm{L}}} = \frac{1}{{v\left( {\int\limits_0^{{S_0}} {\frac{{{S^{{m_{\rm{a}}}}}p(S)}}{{{C_{\rm{a}}}}}{\rm{d}}S} + \int\limits_{{S_0}}^\infty {\frac{{{S^{{m_{\rm{b}}}}}p(S)}}{{{C_{\rm{b}}}}}{\rm{d}}S} } \right)}} $ | (24) |
在机械装备产品的研发过程中,可靠性试验是不可或缺的一环。在产品前期的设计研发阶段中,一般需要对产品的可靠性及寿命进行预估,并在之后通过可靠性试验的方式对其进行验证。通常来讲,机械产品的疲劳寿命普遍较高,如果将其按照正常的工作应力水平进行寿命试验,需要很长的时间,因此可以在试验时适当提高激励水平,使结构工作在比正常工况更加严酷的环境中,达到更早地出现失效的目的,以此节省大量的试验时间。在试验结束后通过等效关系便可推算出正常应力水平下的工作寿命,这一试验方法即加速寿命试验。
2.1 基于Dirlik模型的加速等效关系除使用随机响应分析直接求解结构的响应功率谱密度外,工程上也会使用结构的传递函数来得出危险点的应力功率谱密度。在合理范围内,当外载荷的施加形式、位置、方向没有变化时,结构的传递函数只取决于结构本身,而与载荷大小无关。某点的响应应力PSD与在某特定位置处施加的激励PSD之间的关系为[20]
| $ {G_{\rm{b}}}(f) = {W_{\rm{a}}}(f)H_{{\rm{ba}}}^2(f) $ | (25) |
式中:Gb(f)为结构上b点的响应应力功率谱密度函数;Wa(f)为施加在结构a处的激励功率谱密度函数,其形式不限,可以为集中力、基础运动等;Hba(f)则为结构在a点处承受激励时b点的频响函数,即传递函数。
由式(25)可知,在一定合理范围内,当结构所受的激励增大时,危险点处的响应也随之线性增大。当激励点处的激励PSD的幅值W′a(f)变为原有幅值的k倍时,危险点b处的响应应力PSD即G′(f)将同样变为原有的k倍,而根据式(7)中的谱矩定义,各阶谱矩的变化情况为
| $ m_i^\prime = \int\limits_0^{ + \infty } {{f^i}{G^\prime }(f){\rm{d}}f = km_i^\prime } $ | (26) |
随机过程其他参数的变化情况为
| $ \sigma _{{\rm{RMS}}}^\prime = {\left( {k{m_0}} \right)^{\frac{1}{2}}} = \sqrt k {\sigma _{{\rm{RMS}}}} $ | (27) |
| $ {\gamma ^\prime } = \frac{{k{m_2}}}{{\sqrt {k{m_0}k{m_4}} }} = \gamma $ | (28) |
| $ {\varepsilon ^\prime } = \sqrt {1 - \frac{{{k^2}m_2^2}}{{k{m_0}k{m_4}}}} = \varepsilon $ | (29) |
| $ V_{\rm{P}}^\prime = \sqrt {\frac{{k{m_4}}}{{k{m_2}}}} = {V_{\rm{P}}} $ | (30) |
| $ V_ + ^\prime = \sqrt {\frac{{k{m_2}}}{{k{m_0}}}} = {V_ + } $ | (31) |
式中:上标′表示变化后的变量。对于Dirlik模型来说,当响应应力PSD的幅值G′b(f)为原有幅值的k倍时,模型中各参数的变化情况为
| $ {Z^\prime } = \frac{S}{{2\sqrt {k{m_0}} }} = \frac{Z}{{\sqrt k }};D_1^\prime = \frac{{2\left( {{X_m} - {\gamma ^2}} \right)}}{{1 + {\gamma ^2}}} = {D_1} $ |
| $ D_2^\prime = \frac{{1 - \gamma - {D_1} + D_1^2}}{{1 - R}} = {D_2} $ |
| $ D_3^\prime = 1 - {D_1} - {D_2} = {D_3} $ |
| $ {Q^\prime } = \frac{{1.25\left( {\gamma - {D_3} - {D_2}R} \right)}}{{{D_1}}} = Q $ |
| $ {R^\prime } = \frac{{\gamma - {X_m} - D_1^2}}{{1 - \gamma - {D_1} + D_1^2}} = R;X_m^\prime = \frac{{{m_1}}}{{{m_0}}}\sqrt {\frac{{{m_2}}}{{{m_4}}}} = {X_m} $ |
则此时应力幅值的概率密度函数为
| $ {p^\prime }(S) = \frac{{\frac{{{D_1}}}{Q}{{\rm{e}}^{\frac{{ - Z}}{{\sqrt {kQ} }}}} + \frac{{{D_2}Z}}{{{R^2}\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k{R^2}}}}} + \frac{{{D_3}Z}}{{\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k}}}}}}{{2\sqrt {k{m_0}} }} $ | (32) |
单位时间内的疲劳损伤为
| $ \begin{array}{*{20}{c}} {{D^\prime } = \frac{{{V_{\rm{P}}}}}{{{C_{\rm{a}}}}}\int\limits_0^{{S_0}} {{S^{{m_{\rm{a}}}}}\frac{{\frac{{{D_1}}}{Q}{{\rm{e}}^{\frac{{ - Z}}{{\sqrt {kQ} }}}} + \frac{{{D_2}Z}}{{{R^2}\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k{R^2}}}}} + \frac{{{D_3}Z}}{{\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k}}}}}}{{2\sqrt {km} }}{\rm{d}}S} + }\\ {\frac{{{V_{\rm{P}}}}}{{{C_{\rm{b}}}}}\int\limits_{{S_0}}^0 {{S^{{m_{\rm{b}}}}}\frac{{\frac{{{D_1}}}{Q}{{\rm{e}}^{\frac{{ - Z}}{{\sqrt {kQ} }}}} + \frac{{{D_2}Z}}{{{R^2}\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k{R^2}}}}} + \frac{{{D_3}Z}}{{\sqrt k }}{{\rm{e}}^{\frac{{ - {Z^2}}}{{2k}}}}}}{{2\sqrt {k{m_0}} }}{\rm{d}}S} } \end{array} $ | (33) |
可推导出使用不完全gamma函数表达的基于Dirlik模型的损伤比例j损伤表达式为
| $ {j_{损伤}} = \frac{{{D^\prime }}}{D} = \frac{1}{{\sqrt k }} \cdot \frac{{{A_1} + {A_2} + {A_3} + {B_1} + {B_2} + {B_3}}}{{{G_1} + {G_2} + {G_3} + {H_1} + {H_2} + {H_3}}} $ | (34) |
因此寿命之间的比例关系j寿命为
| $ {j_{寿命}} = \sqrt k \frac{{{G_1} + {G_2} + {G_3} + {H_1} + {H_2} + {H_3}}}{{{A_1} + {A_2} + {A_3} + {B_1} + {B_2} + {B_3}}} $ | (35) |
其中:
| $ {A_1} = \frac{{{D_1}{{\left( {4{m_0}k} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}{Q^{{m_{\rm{a}}}}}}}{{{C_{\rm{a}}}}}\gamma \left( {{m_{\rm{a}}} + 1,\frac{{{S_0}}}{{2Q\sqrt {{m_0}k} }}} \right) $ |
| $ {A_2} = \frac{{{8^{\frac{{{m_{\rm{a}}}}}{2} + 1}}{D_2}{{\left( {{m_0}k} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}{R^{{m_{\rm{a}}}}}}}{{{C_{\rm{a}}}}}\gamma \left( {\frac{{{m_{\rm{a}}}}}{2} + 1,\frac{{S_0^2}}{{8k{R^2}{m_0}}}} \right) $ |
| $ {A_3} = \frac{{{8^{\frac{{{m_{\rm{a}}}}}{2} + 1}}{D_3}{{\left( {{m_0}k} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}}}{{{C_{\rm{a}}}}}\gamma \left( {\frac{{{m_{\rm{a}}}}}{2} + 1,\frac{{S_0^2}}{{8k{m_0}}}} \right) $ |
| $ {B_1} = \frac{{{D_1}{{\left( {4{m_0}k} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}{Q^{{m_{\rm{b}}}}}}}{{{C_{\rm{b}}}}}\mathit{\Gamma }\left( {{m_{\rm{b}}} + 1,\frac{{{S_0}}}{{2Q\sqrt {{m_0}k} }}} \right) $ |
| $ \begin{array}{*{20}{c}} {{B_2} = \frac{{{8^{\frac{{{m_{\rm{b}}}}}{2} + 1}}{D_2}{{\left( {{m_{\rm{0}}}k} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}{R^{{m_{\rm{b}}}}}}}{{{C_{\rm{b}}}}} \cdot }\\ {\mathit{\Gamma }\left( {\frac{{{m_{\rm{b}}}}}{2} + 1,\frac{{S_0^2}}{{8k{R^2}{m_0}}}} \right)} \end{array} $ |
| $ {B_3} = \frac{{{8^{\frac{{{m_{\rm{b}}}}}{2} + 1}}{D_3}{{\left( {{m_{\rm{0}}}k} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}}}{{{C_{\rm{b}}}}}\mathit{\Gamma }\left( {\frac{{{m_{\rm{b}}}}}{2} + 1,\frac{{S_0^2}}{{8k{m_0}}}} \right) $ |
| $ {G_1} = \frac{{{D_1}{{\left( {4{m_0}} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}{Q^{{m_{\rm{a}}}}}}}{{{C_{\rm{a}}}}}\gamma \left( {{m_{\rm{a}}} + 1,\frac{{{S_0}}}{{2Q\sqrt {{m_0}} }}} \right) $ |
| $ {G_2} = \frac{{{8^{\frac{{{m_{\rm{a}}}}}{2} + 1}}{D_2}{{\left( {{m_0}} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}{R^{{m_{\rm{a}}}}}}}{{{C_{\rm{a}}}}}\gamma \left( {\frac{{{m_{\rm{a}}}}}{2} + 1,\frac{{S_0^2}}{{8{R^2}{m_0}}}} \right) $ |
| $ {G_3} = \frac{{{8^{\frac{{{m_{\rm{a}}}}}{2} + 1}}{D_3}{{\left( {{m_0}} \right)}^{\frac{{{m_{\rm{a}}} + 1}}{2}}}}}{{{C_{\rm{a}}}}}\gamma \left( {\frac{{{m_{\rm{a}}}}}{2} + 1,\frac{{S_0^2}}{{8{m_0}}}} \right) $ |
| $ {H_1} = \frac{{{D_1}{{\left( {4{m_0}} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}{Q^{{m_{\rm{b}}}}}}}{{{C_{\rm{b}}}}}\mathit{\Gamma }\left( {{m_{\rm{b}}} + 1,\frac{{{S_0}}}{{2Q\sqrt {{m_0}} }}} \right) $ |
| $ {H_2} = \frac{{{8^{\frac{{{m_{\rm{b}}}}}{2} + 1}}{D_2}{{\left( {{m_0}} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}{R^{{m_{\rm{b}}}}}}}{{{C_{\rm{b}}}}}\mathit{\Gamma }\left( {\frac{{{m_{\rm{b}}}}}{2} + 1,\frac{{S_0^2}}{{8{R^2}{m_0}}}} \right) $ |
| $ {H_3} = \frac{{{8^{\frac{{{m_{\rm{b}}}}}{2} + 1}}{D_3}{{\left( {{m_0}} \right)}^{\frac{{{m_{\rm{b}}} + 1}}{2}}}}}{{{C_{\rm{b}}}}}\mathit{\Gamma }\left( {\frac{{{m_{\rm{b}}}}}{2} + 1,\frac{{S_0^2}}{{8{m_0}}}} \right) $ |
式中:Γ(·)为上不完全伽马函数;γ为下不完全伽马函数。
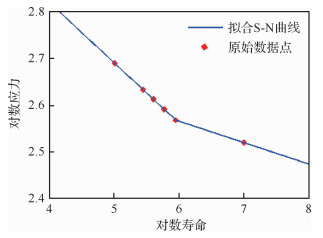
2.2 算例某吊挂结构局部如图 1所示,查询机械工程材料数据手册得知,该结构所用材料的S-N曲线散点数据如表 1所示[22],可以看出该材料的S-N曲线在疲劳极限附近出现了明显的拐点,如果用一条直线对其进行拟合则效果较差。忽略各修正系数的影响,使用双对数坐标系下的两条直线对材料的疲劳特性拟合情况如图 2所示。

|
| 图 1 某吊挂结构局部模型 Fig. 1 Local model for a suspension structure |
|
| 图 2 S-N曲线拟合结果 Fig. 2 Result of S-N curve fitting |
图 2中所对应的两拟合线的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{S^{7.7118}}N = 5.701 \times {{10}^{25}}}&{S > 370.0076}\\ {{S^{21.6914}}N = 4.5564 \times {{10}^{61}}}&{0 < S \le 370.0076} \end{array}} \right. $ |
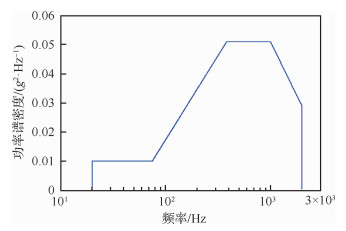
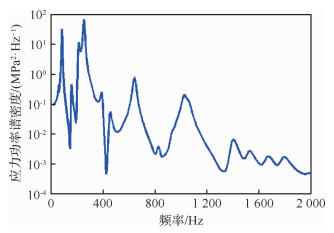
对该结构给定如图 3所示的y方向宽带随机加速度载荷,该载荷与GJB150A中所给出的喷气式飞机外挂设备振动载荷相一致[23]。使用有限元分析得到危险点的位置如图 1所示,其响应Mises应力功率谱密度如图 4所示。
|
| 图 3 输入加速度功率谱密度 Fig. 3 Inputted acceleration power spectral density |
|
| 图 4 危险点响应应力功率谱密度 Fig. 4 Power spectral density of stress response at dangerous point |
由图 4曲线可以看出,该结构的响应应力PSD有多个尖峰,属于宽带随机过程,使用Dirlik模型可以较好地拟合出应力幅值的分布。基于该模型,使用式(24)求解出该结构危险点的疲劳寿命为5.468×107 s。
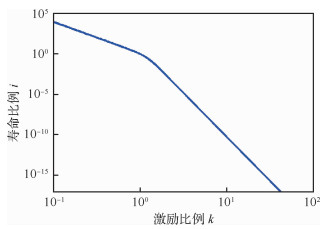
将该点的响应PSD数据与材料疲劳性能数据代入式(35)中,使用MATLAB绘制出激励与寿命放大倍数之间的加速关系如图 5所示,其中横坐标表示激励PSD的放大倍数,纵坐标表示寿命的放大倍数。从图中可以看出,曲线大体呈两段直线走向。
|
| 图 5 激励与损伤的等效关系 Fig. 5 Equivalent relationship between excitation and damage |
不难理解这一规律,当施加在结构上的随机载荷由小变大时,也就意味着有更多的大幅值应力出现,即落入图 2所示S-N曲线左段的应力幅占比越来越大,因此在激励比例增加时,寿命将以更快的比例衰减,也可以说,图 5中的右半段直线对应了所使用的S-N曲线高应力部分,左半段则对应了低应力部分;而如果使用一条直线对S-N曲线进行表征,则这一等效关系也将变为一条直线,即激励与寿命呈对数线性关系,此种情况下与他人现有的研究结论保持一致[20]。Clevenson和Steiner曾经对一批2024-T4铝合金试件进行了多次随机振动疲劳试验,研究各种载荷参数对寿命的影响,针对2个不同形状的PSD,在一定范围内改变一组试样所受载荷大小,得到了不同均方根值下的寿命如表 2[24]所示,将数据绘制在双对数坐标系内如图 6所示。

|
| 图 6 加速试验结果 Fig. 6 Results of accelerated test |
图 6中,2条折线分别是根据2个PSD在各级载荷水平下的对数寿命均值点连线所得,曲线1与数据1对应中表 2中载荷均方根1列的数据,曲线2与数据2对应表 2中载荷均方根2列的数据。可以注意到2组数据均呈现出较明显的线性特征;同时,在2条折线的左上方均呈现出了一种向下弯折的趋向,同图 5中的曲线特征保持一致,从而证明了该方法的正确性。
| 载荷均方根1/MPa | 寿命1/s | 载荷均方根2/MPa | 寿命2/s |
| 24.5 | 93 360 | 24.6 | 65 580 |
| 32.7 | 61 860, 32 340 | 30.8 | 51 660 |
| 44.2 | 11 400, 5 490, 9 660 | 42.2 | 8 850 |
| 63.2 | 1 440, 1 200, 1 410 | 54.4 | 1 332, 1 320, 1 530 |
| 93.1 | 259.8, 225, 198 | 77.2 | 334.8, 319.8, 295.8, 183.6 |
| 124.8 | 64.98 | 110.5 | 44.7, 42, 40.02 |
| 129.2 | 30.54 | 152.6 | 11.58, 6.48 |
| 151.7 | 90 | ||
| 158.0 | 7.98, 6.4 |
另外,一般加速试验需要提高应力水平来缩短试验时间,即对应图中k>1的部分,可以看出,这一段曲线既有后续呈现线性的部分,也有两段曲线的过渡部分,因此针对零部件结构上这一点的加速关系不能用简单的对数线性来表达。需要注意的是,假设该算例中其他条件均不变,增大原有载荷PSD的幅值,则须将曲线整体向左移,此时k>1的部分可按照对数线性近似处理;反之,需要将曲线向右平移,此时k>1的部分同时包含了曲线中两段呈直线的部分,这样则不能简化处理。
由讨论可以看出,在进行基于频域疲劳模型的加速试验时,加速关系不仅仅取决于材料性能,还与零部件所承受的载荷有关,如果按照一般的对数线性关系来计算的话,可能会出现较大的误差。
3 结论1) 针对随机振动中小应力循环占比较大的情况,将Dirlik雨流幅值分布模型应用到了双对数坐标系下的2段直线所表征的S-N曲线上,该求解思路使得频域方法更加适用于随机振动疲劳问题,且该方法还可以拓展到多段直线所表征的S-N曲线的情况中。
2) 基于所提出的多段式S-N曲线的求解思路,以2段的情况为例,推导了使用Dirlik模型为基础的振动疲劳频域求解方法支撑下的加速应力等效关系式,总结出了加速寿命换算方法,为振动疲劳的加速试验提供了理论支持。
3) 算例表明,在使用双对数坐标系下的2条直线对S-N曲线进行表达时,所推导出的应力与损伤放大倍数的等效关系近似为2段对数直线关系,并借助相关文献中的试验数据对方法进行了验证。
| [1] | WÖHLER A. Versuche zur Ermittlung der auf die Eisenbahnwagenachsen einwirkenden Kräfte und die Widerstandsfähigkeit der Wagen-Achsen[J]. Zeitschrift fär Bauwesen, 1860, 10(1860): 583-614. |
| [2] | CRANDALL S H. Random vibration[M]. New York: Technology Press of MIT and John Wiley and Sons, 1958. |
| [3] | CRANDALL S H, MARK W D. Random vibration in mechanical systems[M]. New York: Academic Press, 1963. |
| [4] | BENDAT J S, PIERSOL A G. Measurement and analysis of random data[M]. New York: John Wiley&Sons, 1966. |
| [5] | WIRSCHING P H, LIGHT M C. Fatigue under wide band random stresses[J]. Journal of the Structural Division, 1980, 106(7): 1593-1607. |
| Click to display the text | |
| [6] | WIRSCHING P H, SHEHATA A M. Fatigue under wide band random stresses using the rain-flow method[J]. Journal of Engineering Materials and Technology, 1977, 99(3): 205-211. |
| Click to display the text | |
| [7] | CHAUDHURY G K, DOVER W D. Fatigue analysis of offshore platforms subject to sea wave loadings[J]. International Journal of Fatigue, 1985, 7(1): 13-19. |
| Click to display the text | |
| [8] | DIRLIK T. Application of computers in fatigue analysis[D]. Coventry: University of Warwick, 1985. |
| [9] | BENASCIUTTI D, TOVO R. Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes[J]. Probabilistic Engineering Mechanics, 2006, 21(4): 287-299. |
| Click to display the text | |
| [10] |
何选森. 随机过程[M]. 北京: 人民邮电出版社, 2009: 70-74. HE X S. Stochastic processes[M]. Beijing: Posts and Telecommunications Press, 2009: 70-74. (in Chinese) |
| [11] |
陆大. 随机过程及其应用[M]. 北京: 清华大学出版社, 2012: 101-112. LU D J. Stochastic processes and their application[M]. Beijing: Tsinghua University Press, 2012: 101-112. (in Chinese) |
| [12] |
周凌波.航空典型结构件的随机振动疲劳寿命分析[D].南京: 南京航空航天大学, 2014. ZHOU L B. Random vibration fatigue life analysis of aircraft typical structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014(in Chinese). |
| [13] |
黄义科.基于频域的多轴随机振动疲劳寿命预测[D].成都: 西南交通大学, 2015. HUANG Y K. Prediction of multiaxial random vibration fatigue life based on frequency domain[D]. Chengdu: Southwest Jiaotong University, 2015(in Chinese). |
| [14] |
宋宇.多轴随机载荷下疲劳寿命预测方法的研究[D].沈阳: 东北大学, 2012. SONG Y. The multiaxial fatigue life estimation of metal structures under random loading[D]. Shenyang: Northeastern University, 2012(in Chinese). |
| [15] |
谭秀峰, 谢里阳, 马洪义, 等. 基于对数正态分布的多部位疲劳结构的疲劳寿命预测方法[J]. 航空学报, 2017, 38(2): 220376. TAN X F, XIE L Y, MA H Y, et al. Fatigue life prediction method for multi-site fatigue structure with lognormal fatigue life[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 220376. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [16] |
胡磊.一种随机振动疲劳寿命分析技术研究[D].南京: 南京航空航天大学, 2012. HU L. Research on a kind of random vibration fatigue life analysis technique[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). |
| [17] |
管鹏.铁道车辆设备随机振动疲劳寿命分析[D].成都: 西南交通大学, 2012. GUAN P. Fatigue life analysis of random vibration for rolling stock equipment[D]. Chengdu: Southwest Jiaotong University, 2012(in Chinese). |
| [18] |
贺光宗, 陈怀海, 贺旭东. 一种多轴向随机激励下结构疲劳寿命分析方法[J]. 振动与冲击, 2015, 34(7): 59-63. HE G Z, CHEN H H, HE X D. Vibration fatigue life prediction method for structures under multi-axial random excitations[J]. Journal of Vibration and Shock, 2015, 34(7): 59-63. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [19] |
王明珠, 姚卫星. 随机振动载荷下缺口件疲劳寿命分析的频域法[J]. 南京航空航天大学学报, 2008, 40(4): 489-492. WANG M Z, YAO W X. Frequency domain method for fatigue life analysis on notched specimens under random vibration loading[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2008, 40(4): 489-492. (in Chinese) |
| Cited By in Cnki (31) | Click to display the text | |
| [20] |
张方, 周凌波, 姜金辉, 等. 基于频域法的随机振动疲劳加速试验设计[J]. 振动·测试与诊断, 2016, 36(4): 659-664, 807-808. ZHANG F, ZHOU L B, JIANG J H. Random vibration fatigue accelerated test design based on frequency domain methods[J]. Journal of Vibration, Measurement and Diagnosis, 2016, 36(4): 659-664, 807-808. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [21] |
洪友士, 孙成奇, 刘小龙. 合金材料超高周疲劳的机理与模型综述[J]. 力学进展, 2018, 48(1): 1-65. HONG Y S, SUN C Q, LIU X L. A review on mechanisms and models for very-high-cycle fatigue of metallic materials[J]. Advances in Mechanics, 2018, 48(1): 1-65. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [22] |
机械工程材料性能数据手册编委会. 机械工程材料性能数据手册[M]. 北京: 机械工业出版社, 1995: 197. Editorial Committee of Mechanical Engineering Materials Performance Data Manual. Mechanical engineering materials performance data manual[M]. Beijing: China Machine Press, 1995: 197. (in Chinese) |
| [23] |
施荣明, 朱广荣, 吴枫, 等.军用装备实验室环境试验方法第16部分振动试验: GJB 150.16A-2009[S]. 2009 SHI R M, ZHU G R, WU F, et al. Laboratory environment test methods for military materiel-Part 16: Vibration test: GJB 150.16A-2009[S]. 2009(in Chinese). |
| [24] | CLEVENSON S A, STEINER R. Fatigue life under random loading for several power spectral shapes: NASA-TR-266[R]. Washington, D.C.: NASA, 1967. |



