多输入多输出(Multi-Input-Multi-Output, MIMO)随机振动试验,因其可以更好地模拟试验对象的真实工作状态,是一种重要的振动环境试验手段, 广泛运用于航空航天领域[1-7]。MIMO随机振动试验,要求控制点的响应谱与参考谱间误差满足容差要求,该控制目标一般都是通过频域方法实现的,采用时域化方法的很少。Cui等[6]提出使用一种基于Markov参数的时域方法,用于改善多输入多输出随机振动控制过程中出现的病态问题。此外,时域控制方法更适用于控制非高斯信号[8]的情况。
逆系统方法是一类将系统响应作为输入得到驱动信号的时域方法,它起源于载荷识别领域。Kammer和Steltzner在一系列文章[9-10]中提出并发展的逆结构滤波器(Inverse Structural Filter, ISF)是逆系统方法的一种典型代表。Allen和Carne[11-12]针对ISF在小阻尼结构中经常出现的不稳定现象,根据工程经验提出了延迟多步ISF方法,但并未给出理论解释。逆系统方法也可以用于振动试验中驱动信号的生成。陈怀海等[8]基于ISF方法尝试使用逆系统方法进行随机振动试验的信号生成,并进行了悬臂梁仿真。Zheng等[13-14]对系统的时域转移矩阵求逆构造逆系统,但忽略了由奇异值截断对驱动信号质量的影响。
本文从时域有限差分模型入手,推导系统的逆多步预测系统,并利用该逆系统进行驱动信号生成;最后经仿真算例与振动台试验验证了该方法的可行性。
1 逆多步预测系统传统逆系统方法直接对原系统的状态空间模型求逆[9, 10, 15],但得到的逆模型往往是不稳定的[12];此外,实际试验系统的状态空间模型难以直接由理论推导得到,需通过ERA (Eigensystem Realization Algorithm)等手段识别[16-17],这增加了驱动生成过程的复杂度,因而限制了这些时域化方法在MIMO随机振动试验中的应用。本文从系统的多步预测模型出发,得到更为稳定的逆多步预测模型,用于MIMO随机振动试验驱动信号的生成。
多步预测模型由系统的有限差分模型推导得到。有限差分模型将振动系统描述为当前时刻的输出与有限个过去时刻的输入与输出的线性组合关系。对于一个ni输入no输出的振动系统,其在k时刻的驱动与响应关系依有限差分模型可写为
| $ \begin{array}{l} \mathit{\boldsymbol{y}}\left( k \right) = - \sum\limits_{i = 1}^p {\mathit{\boldsymbol{\alpha }}_i^{\left( 0 \right)}} {B^i}\mathit{\boldsymbol{y}}\left( k \right) + \sum\limits_{i = 1}^p {\mathit{\boldsymbol{\beta }}_i^{\left( 0 \right)}} {B^i}\mathit{\boldsymbol{u}}\left( k \right) + \\ \;\;\;\;\;\;\mathit{\boldsymbol{\beta }}_0^{\left( 0 \right)}\mathit{\boldsymbol{u}}\left( k \right) \end{array} $ | (1) |
式中:u(·)∈Rni×1和y(·)∈Rno×1分别为驱动与响应向量;对应系数矩阵βi(0)∈Rno×ni,αi(0)∈Rno×no(i=0, 1, …, p),p为有限差分模型的阶数;B(·)为后移算子,其定义为By(k)=y(k-1),并有逆运算B-1y(k)=y(k+1)。对式(1)进行一系列的平移和代入计算[18],可以得到k+j时刻的输出:
| $ \begin{array}{l} \mathit{\boldsymbol{y}}\left( {k + j} \right) = - \sum\limits_{i = 1}^p {\mathit{\boldsymbol{\alpha }}_i^{\left( j \right)}} {B^i}\mathit{\boldsymbol{y}}\left( k \right) + \sum\limits_{i = 1}^p {\mathit{\boldsymbol{\beta }}_i^{\left( j \right)}} {B^i}\mathit{\boldsymbol{u}}\left( k \right) + \\ \;\;\;\;\;\;\;\sum\limits_{i = 0}^j {\mathit{\boldsymbol{\beta }}_i^{\left( 0 \right)}} {B^i}\mathit{\boldsymbol{u}}\left( {k + j} \right) \end{array} $ | (2) |
其系数矩阵为(令αp+1(j-1)=0, βp+1(j-1)=0)
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\alpha }}_k^{\left( j \right)} = \mathit{\boldsymbol{\alpha }}_{k + 1}^{\left( {j - 1} \right)} - \mathit{\boldsymbol{\alpha }}_1^{\left( {j - 1} \right)}\mathit{\boldsymbol{\alpha }}_k^{\left( 0 \right)}\quad k = 1,2, \cdots ,p\\ \mathit{\boldsymbol{\beta }}_k^{\left( j \right)} = \mathit{\boldsymbol{\beta }}_{k + 1}^{\left( {j - 1} \right)} - \mathit{\boldsymbol{\alpha }}_1^{\left( {j - 1} \right)}\mathit{\boldsymbol{\beta }}_k^{\left( 0 \right)}\quad k = 0,1, \cdots ,p \end{array} \right. $ | (3) |
取j=1, 2, …, q-1 (q为多步预测模型预测响应步数),即预测系统从k到k+q-1时刻的响应,由式(1)~式(3)可以得到系统的多步预测模型为
| $ {\mathit{\boldsymbol{y}}_q}\left( k \right) = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{u}}_q}\left( k \right) + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{u}}_p}\left( {k - p} \right) \to \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{y}}_p}\left( {k - p} \right) $ | (4) |
式中:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{y}}_q}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{B^0}}&{{B^{ - 1}}}& \cdots &{{B^{1 - q}}} \end{array}} \right]^{\rm{T}}}\mathit{\boldsymbol{y}}\left( k \right)\\ {\mathit{\boldsymbol{u}}_q}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{B^0}}&{{B^{ - 1}}}& \cdots &{{B^{1 - q}}} \end{array}} \right]^{\rm{T}}}\mathit{\boldsymbol{u}}\left( k \right) \end{array} \right. $ | (5) |
将式(5)中q与p、k与k-p进行替换即可类似地写出up(k-p)和yp(k-p)的表达式,式(4)中的系数矩阵为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\beta }}_0^{\left( 0 \right)}}&{\bf{0}}& \cdots &{\bf{0}}\\ {\mathit{\boldsymbol{\beta }}_0^{\left( 1 \right)}}&{\mathit{\boldsymbol{\beta }}_0^{\left( 0 \right)}}& \cdots &{\bf{0}}\\ \vdots & \vdots &{}& \vdots \\ {\mathit{\boldsymbol{\beta }}_0^{\left( {q - 1} \right)}}&{\mathit{\boldsymbol{\beta }}_0^{\left( {q - 2} \right)}}& \cdots &{\mathit{\boldsymbol{\beta }}_0^{\left( 0 \right)}} \end{array}} \right] $ | (6) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha }}_p^{\left( 0 \right)}}&{\mathit{\boldsymbol{\alpha }}_{p - 1}^{\left( 0 \right)}}& \cdots &{\mathit{\boldsymbol{\alpha }}_1^{\left( 0 \right)}}\\ {\mathit{\boldsymbol{\alpha }}_p^{\left( 1 \right)}}&{\mathit{\boldsymbol{\alpha }}_{p - 1}^{\left( 1 \right)}}& \cdots &{\mathit{\boldsymbol{\alpha }}_1^{\left( 1 \right)}}\\ \vdots & \vdots &{}& \vdots \\ {\mathit{\boldsymbol{\alpha }}_p^{\left( {q - 1} \right)}}&{\mathit{\boldsymbol{\alpha }}_{p - 1}^{\left( {q - 1} \right)}}& \cdots &{\mathit{\boldsymbol{\alpha }}_1^{\left( {q - 1} \right)}} \end{array}} \right] $ | (7) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\beta }}_p^{\left( 0 \right)}}&{\mathit{\boldsymbol{\beta }}_{p - 1}^{\left( 0 \right)}}& \cdots &{\mathit{\boldsymbol{\beta }}_1^{\left( 0 \right)}}\\ {\mathit{\boldsymbol{\beta }}_p^{\left( 1 \right)}}&{\mathit{\boldsymbol{\beta }}_{p - 1}^{\left( 1 \right)}}& \cdots &{\mathit{\boldsymbol{\beta }}_1^{\left( 1 \right)}}\\ \vdots & \vdots &{}& \vdots \\ {\mathit{\boldsymbol{\beta }}_p^{\left( {q - 1} \right)}}&{\mathit{\boldsymbol{\beta }}_{p - 1}^{\left( {q - 1} \right)}}& \cdots &{\mathit{\boldsymbol{\beta }}_1^{\left( {q - 1} \right)}} \end{array}} \right] $ | (8) |
在多步预测模型式(4)中,初始的参数αi(0)和βi(0)可从试验数据中识别,再利用式(3)得到从1到q-1之间的αi(j)和βi(j),最后根据式(6)~式(8)计算系数矩阵T、A和B。
如果T矩阵可逆,可以得到多步预测模型的逆为
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_q}\left( k \right) = {\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{u}}_q}\left( k \right) = \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{T}}^{ - 1}}{\mathit{\boldsymbol{y}}_q}\left( k \right) + {\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{y}}_p}\left( {k - p} \right) - {\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{u}}_p}\left( {k - p} \right) \end{array} $ | (9) |
然而实际系统的T矩阵往往接近奇异,这时可以利用截断奇异值(Truncated Singular Value Decomposition, TSVD)法求逆,以获得稳定的结果[19-20]。由于截断奇异值法只选择前r阶奇异值,得到的伪逆矩阵T+满足:
| $ {\mathit{\boldsymbol{T}}^ + }\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_r}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right] $ | (10) |
式中:Ir为r×r维单位矩阵。
由于这样生成的驱动信号在尾段存在不可信的成分,可以仅生成l个时刻的驱动,即选择T+矩阵的前lni行(lni < r)构成T矩阵,并用T替换式(9)中的T-1,将得到
| $ {\mathit{\boldsymbol{u}}_l}\left( k \right) = \mathit{\boldsymbol{\bar T}}{\mathit{\boldsymbol{y}}_q}\left( k \right) + \mathit{\boldsymbol{\bar B}}{\mathit{\boldsymbol{y}}_p}\left( {k - p} \right) - \mathit{\boldsymbol{\bar A}}{\mathit{\boldsymbol{u}}_p}\left( {k - p} \right) $ | (11) |
式中:
| $ {\mathit{\boldsymbol{u}}_l}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{B^0}}&{{B^{ - 1}}}& \cdots &{{B^{1 - l}}} \end{array}} \right]^{\rm{T}}}\mathit{\boldsymbol{u}}\left( k \right) $ | (12) |
| $ \begin{array}{l} \mathit{\boldsymbol{\bar T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{\mathit{l}{\mathit{n}_i}}}}&{\bf{0}} \end{array}} \right]\mathit{\boldsymbol{T}}_r^ + \\ \mathit{\boldsymbol{\bar B}} = \mathit{\boldsymbol{\bar TA}},\mathit{\boldsymbol{\bar A}} = \mathit{\boldsymbol{\bar TB}} \end{array} $ | (13) |
系数矩阵T、A和B的维数分别为lni×qno、lni×pni和lni×pno。式(11)与式(4)中多步预测模型具有相同的形式,因此后文将式(11)称为逆多步预测模型。容易看出,逆多步预测模型为非因果系统,这是因为当前的激励会影响系统未来的响应,因此当前激励需通过未来的响应确定。
在试验中,获得逆多步预测模型具体的步骤包括:①对系统进行白噪声激励,估计系统差分模型参数;②通过式(3)和式(6)~式(8)的计算,得到系统的多步预测模型;③对T矩阵依截断奇异值法求逆,并根据式(11)~式(13)计算得到逆多步预测模型。
2 随机振动试验算法将第1节推导得到的逆多步预测模型与矩阵幂次算法[2]结合,构成一种MIMO随机振动控制试验算法。
逆多步预测模型将目标响应作为输入,计算得到随机振动试验的驱动信号。这里的目标响应即参考信号,是根据用户设置的参考谱生成的时域信号。MIMO随机振动试验中,一般给出参考谱的功率谱密度,乘以频率分辨率即转换为参考功率谱R。
生成参考信号的过程包含伪随机信号生成与时域随机化2部分。在生成伪随机信号前,先应得到其频谱
| $ \mathit{\boldsymbol{Y}}\left( f \right) = \mathit{\boldsymbol{L}}\left( f \right)\mathit{\boldsymbol{P}}\left( f \right) $ | (14) |
式中:下三角矩阵L满足R=LLT,是对参考功率谱矩阵R进行Cholesky分解的结果;对角阵P包含随机相位信息;对Y进行逆傅里叶变换
| $ \mathit{\boldsymbol{y}}\left( t \right) = {{\cal F}^{ - 1}}\left( {\mathit{\boldsymbol{Y}}\left( f \right)} \right) $ | (15) |
对伪随机信号进行时域随机化[2],即可得到任意帧长度的真随机信号。使用该真随机信号作为参考信号,由逆多步预测模型生成驱动信号。
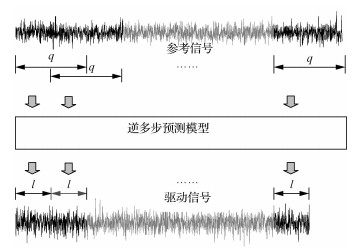
从式(11)可以看出,逆多步预测模型中输入的参考信号的长度大于输出的驱动信号的长度。因此,在生成驱动信号的过程中,参考信号是重叠使用的,如图 1所示, 图中,l为逆多步预测模型生成激励步数。
|
| 图 1 逆多步预测模型驱动信号生成过程 Fig. 1 Drive signal generation using inverse multi-step prediction model |
之后,通过矩阵幂次算法对参考信号进行调整,再将修正后的参考信号代入逆多步预测模型,实现对驱动信号的更新。矩阵幂次算法可以有效的防止Smallwood差分算法[21]可能导致的发散问题,提高了算法的稳定性。传统的矩阵幂次算法直接对驱动信号进行更新[2],而本文中它被用于对参考信号的调整。
矩阵幂次算法以矩阵乘法形式对式(14)中的下三角矩阵L进行迭代更新,第n+1次迭代表示如下:
| $ {\mathit{\boldsymbol{L}}_{n + 1}} = {{\bf{\Delta }}^\varepsilon }{\mathit{\boldsymbol{L}}_n}\;\;\;\;n = 0,1,2, \cdots $ | (16) |
式中:ε∈(0, 1)为压缩因子,防止控制结果的不稳定。误差矩阵Δ的计算公式为
| $ {\bf{\Delta }} = {\mathit{\boldsymbol{L}}_0}\mathit{\boldsymbol{L}}_y^{ - 1} $ | (17) |
式中: L0为由参考谱Cholesky分解得到的下三角阵; Ly则由响应谱分解得到。本文提出的完整的控制流程如图 2所示。

|
| 图 2 基于逆多步预测模型的矩阵幂次控制 Fig. 2 Matrix power control based on inverse multi-step prediction model |
本文以悬臂梁作为仿真对象,进行双输入双输出随机振动试验控制试验。悬臂梁的几何参数与材料属性见表 1,激励与响应点的配置如图 3所示。
| 参数 | 数值 |
| 密度/(kg·m-3) | 7 850 |
| 弹性模量/MPa | 720 |
| 长度/mm | 1 000 |
| 截面宽度/mm | 50 |
| 截面高度/mm | 15 |

|
| 图 3 两输入两输出振动试验悬臂梁 Fig. 3 A cantilever beam for double input double output vibration test |
参考航空航天振动试验标准要求,随机振动控制试验的频率范围取20~2 000 Hz,参考谱中自谱密度各段的幅值与斜率如图 4所示,Oct表示倍频程,响应点间相关系数取0.6,相位差取30°。

|
| 图 4 参考谱的自功率谱密度 Fig. 4 Auto spectra density of reference spectra |
使用白噪声对试验件进行激励,得到系统的逆多步预测模型。之后,进行控制试验模拟,使用初始生成的驱动信号进行激励,所得响应自谱结果如图 5所示,响应点间的相关系数与相位角分别如图 6(a)与图 6(b)所示。从图中可以看出,对于该仿真系统,逆多步预测模型能够很容易的生成满足控制要求的驱动信号。

|
| 图 5 响应点1与响应点2的自谱 Fig. 5 Auto spectra at response 1 and 2 |

|
| 图 6 响应点间相关系数和相位差 Fig. 6 Correlation coefficient and phase between two response points |
为进一步验证该MIMO振动控制试验方法,在三轴振动台上进行试验,试验系统的构成如图 7所示。考虑到工程中部件级试验时多对振动台面的加速度进行控制,所安装的试件对这种控制过程的影响可忽略,因此本试验仅对振动台面的加速度进行控制。

|
| 图 7 MIMO随机振动试验系统的构成 Fig. 7 Configuration of MIMO random vibration test system |
试验频率范围为20~2 000 Hz,自谱密度如图 8所示,各轴向间相关系数均取0.6,X-Y、Y-Z轴向间相位差取30°,X-Z轴向间取60°。

|
| 图 8 三轴振动试验参考谱的自功率谱密度 Fig. 8 Auto spectra density of reference spectra for 3-axes vibration test |
首先采用白噪声激励,依第1节中所述步骤,估计得到系统的逆多步预测模型参数,并据此生成初始驱动信号。在实物试验中,如果逆多步预测模型生成异常驱动信号,可能会对试验系统产生损害。因此,可预生成一段较长的驱动信号,在该信号无幅值超标等情况时,才可以进行试验。
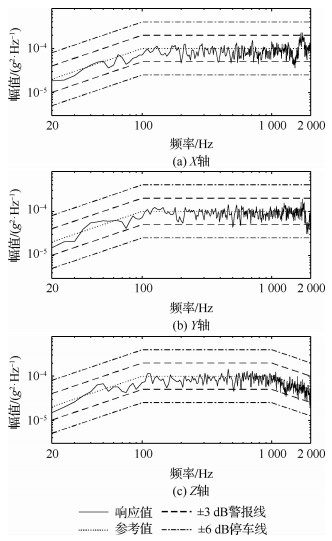
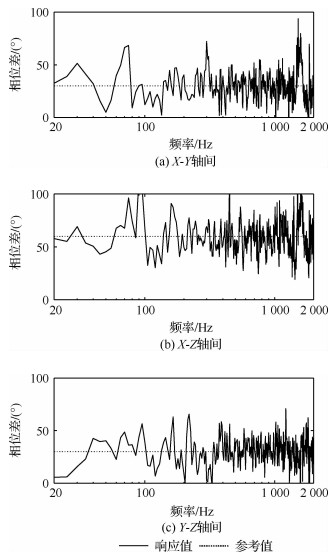
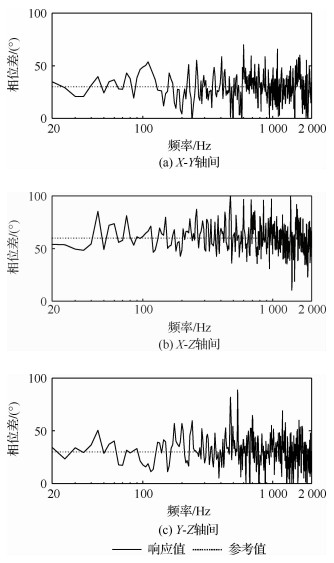
控制前的自谱、相关系数与相位差分别如图 9、图 10和图 11所示。从控制前的响应结果中可以看出,由于噪声等干扰因素影响,初次生成的驱动信号一般无法满足试验要求。经过控制算法的三次迭代修正后,如图 12所示,振动台3个轴向的自谱密度均已满足±3 dB的容差要求,同时各轴向间的相关系数(见图 13)与相位差(见图 14)也取得了理想的控制效果。
|
| 图 9 控制前的自谱 Fig. 9 Auto spectra before control |

|
| 图 10 控制前的相关系数 Fig. 10 Correlation coefficient before control |
|
| 图 11 控制前的相位差 Fig. 11 Phase before control |

|
| 图 12 三次迭代后的自谱 Fig. 12 Auto spectra after 3 iterations |

|
| 图 13 三次迭代后的相关系数 Fig. 13 Correlation coefficient after 3 iterations |
|
| 图 14 三次迭代后的相位差 Fig. 14 Phase after 3 iterations |
图 15中比较了本文提出的逆多步预测模型法与传统的矩阵幂次方法,自谱的总体均方根值误差随迭代过程的变化。在同样的试验条件下,逆多步预测模型法同样取得了良好的迭代效率,并继承了矩阵幂次方法不会产生负值问题的优点。但由于逆多步预测模型法,直接在时域由参考信号生成驱动信号,采用的参考信号可以更灵活。

|
| 图 15 迭代过程 Fig. 15 Iteration process |
本文给出一种了MIMO逆多步预测模型,利用该逆模型进行驱动信号生成,并结合矩阵幂次算法,构成了一种MIMO随机振动试验控制方法。
仿真算例的结果表明,由逆多步预测模型生成的驱动信号可以一次使响应满足试验要求;但在振动台的实际试验中,由于噪声等干扰因素影响,初次生成的驱动信号不能立即满足试验要求,但通过控制算法调整,可将响应控制在容差范围内。仿真算例与振动台试验验证了本文方法的有效性和可行性。
| [1] |
邹学锋, 郭定文, 潘凯, 等. 综合载荷环境下高超声速飞行器结构多场联合强度试验技术[J]. 航空学报, 2018, 39(12): 222326. ZOU X F, GUO D W, PAN K, et al. Test technique for multi-load combined strength of hypersonic vehicle structure under complex loading environment[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 222326. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [2] | CUI X, CHEN H, HE X, et al. Matrix power control algorithm for multi-input multi-output random vibration test[J]. Chinese Journal of Aeronautics, 2011, 24(6): 741-748. |
| Click to display the text | |
| [3] | CUI S, CHEN H, HE X, et al. Multi-input multi-output random vibration control using Tikhonov filter[J]. Chinese Journal of Aeronautics, 2016, 29(6): 1649-1663. |
| Click to display the text | |
| [4] |
张步云, 汪若尘, 曾发林. MIMO随机加正弦振动试验J-阻抗复合控制算法[J]. 振动.测试与诊断, 2017, 37(6): 1089-1093, 1274. ZHANG B Y, WANG R C, ZENG F L. J-impedance compound control algorithm for MIMO random plus sinusoidal vibration test[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(6): 1089-1093, 1274. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [5] | ZHENG R, CHEN H, HE X. Control method for multi-input multi-output non-Gaussian random vibration test with cross spectra consideration[J]. Chinese Journal of Aeronautics, 2017, 30(6): 1895-1906. |
| Click to display the text | |
| [6] | CUI S, CHEN H, HE X. Time-domain approach for multi-exciter random environment test[J]. Journal of Sound and Vibration, 2017, 398: 52-69. |
| Click to display the text | |
| [7] | CUI S, CHEN H, HE X, et al. Control algorithm update for multi-input multi-output random environment test[J]. Mechanical Systems and Signal Processing, 2018, 111: 643-662. |
| Click to display the text | |
| [8] |
陈怀海, 王鹏宇, 孙建勇. 基于逆系统方法的多输入多输出非高斯驱动信号生成[J]. 航空学报, 2016, 37(5): 1544-1551. CHEN H H, WANG P Y, SUN J Y. Generation of multi-input multi-output non-Gaussian driving signal based on inverse system method[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1544-1551. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [9] | KAMMER D C. Input force reconstruction using a time domain technique[J]. Journal of Vibration and Acoustics, 1998, 120(4): 868-874. |
| Click to display the text | |
| [10] | STELTZNER A D, KAMMER D C. Input force estimation using an inverse structural filter[C]//Proceedings of the 17th International Modal Analysis Conference. Kissimmee, Florida: Society for Experimental Mechanics, 1999: 954-960. |
| [11] | ALLEN M, CARNE T. Comparison of Inverse Structural Filter (ISF) and Sum of Weighted Accelerations Time (SWAT) domain force identification methods[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2006. |
| [12] | ALLEN M S, CARNE T G. Delayed, multi-step inverse structural filter for robust force identification[J]. Mechanical Systems and Signal Processing, 2008, 22(5): 1036-1054. |
| Click to display the text | |
| [13] | ZHENG R, CHEN H, HE X, et al. Probability distributions control for multi-input multi-output stationary non-Gaussian random vibration test[J]. Journal of Vibration and Control, 2017, 24(21): 5201-5210. |
| Click to display the text | |
| [14] | ZHENG R, CHEN H, HE X. Control method for multiple-input multiple-output non-gaussian random vibration test[J]. Packaging Technology and Science, 2017, 30(7): 331-345. |
| Click to display the text | |
| [15] |
廖林雨.结构振动的逆系统预测控制[D].武汉: 华中科技大学, 2011: 9-17. LIAO L Y. Inverse system predictive control of structural vibration[D]. Wuhan: Huazhong University of Science and Technology, 2011: 9-17(in Chinese). |
| [16] |
朱锐, 杭晓晨, 姜东, 等. 基于奇异值分解的ERA改进算法及模态定阶[J]. 振动.测试与诊断, 2018, 38(1): 115-122. ZHU R, HANG X C, JIANG D, et al. Improved ERA algorithm and modal order determination based on SVD[J]. Journal of Vibration, Measurement and Diagnosis, 2018, 38(1): 115-122. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] |
蒲黔辉, 洪彧, 王高新, 等. 快速特征系统实现算法用于环境激励下的结构模态参数识别[J]. 振动与冲击, 2018, 37(6): 55-60. PU Q H, HONG Y, WANG G X, et al. Fast eigensystem realization algorithm based structural modal parameters identification for ambient tests[J]. Journal of Vibration and Shock, 2018, 37(6): 55-60. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [18] | JUANG J N, PHAN M. Identification and control of mechanical systems[M]. Cambridge: Cambridge University Press, 2001: 256-272. |
| [19] | HANSEN P C. The truncated SVD as a method for regularization[J]. Bit Numerical Mathematics, 1987, 27(4): 534-553. |
| Click to display the text | |
| [20] |
吴太旗, 邓凯亮, 黄谟涛, 等. 一种改进的不适定问题奇异值分解法[J]. 武汉大学学报(信息科学版), 2011, 36(08): 900-903, 880. WU T Q, DENG K L, HUANG M T, et al. An improved singular values decomposition method for ill-posed problem[J]. Geomatics and Information Science of Wuhan University, 2011, 36(08): 900-903, 880. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [21] | SMALLWOOD D O, PAEZ T L. A frequency domain method for the generation of partially coherent normal stationary time domain signals[J]. Shock and Vibration, 1991, 1(1): 45-53. |
| Click to display the text |



