2. 中国人民解放军95791部队, 酒泉 735018
2. China PLA 95791 Unit, Jiuquan 735018, China
在可压缩非定常流动中,激波的产生、传播及其与几何边界的相互干扰,往往支配着整个流动的特性。在计算流体力学(CFD)领域中,一些学者采用激波捕捉(Shock-Capturing, S-C)法研究激波与湍流/声波的干扰时,发现激波处产生的非物理波动会显著降低下游流场的精度,即无论格式的设计精度有多高,激波下游的流场难以恢复到应有的格式精度[1-2]。
本质上讲,这些缺陷的根源在于激波捕捉格式的基本构造,即捕捉的激波等强间断往往会跨越若干网格点,而这些节点上的参数仅仅是由人为引进而来的,丝毫不能反映真实间断内部的流动结构[3]。因此近年来有很多学者在认识到捕捉法的先天不足后,坚信只有类似激波装配(Shock-Fitting, S-F)的算法才能从根本上解决这些问题[2, 4-5]。
传统激波装配法主要基于结构网格框架,取得了一系列卓有成效的研究成果[6-8]。然而,考虑到其深受网格拓扑限制、算法逻辑比较复杂及程序移植性差等缺点,因此近年来激波装配法的研究热点逐渐转移到较为灵活的非结构网格算法框架。经过十几年的发展,基于非结构网格的激波装配法已成功应用于一些超/高超声速、二/三维定常流动问题[9-11],然而将其拓展到复杂的非定常流动中仍然困难重重,目前仅有一些探索性的尝试。
2016年,Bonfiglioli等成功将其基于非结构网格和格点型有限体积法的装配算法[9]拓展到非定常计算并模拟了激波与涡的相互作用[12],随后又进一步模拟了运动激波正规反射问题[13];刘君等模拟了运动激波与氦气柱的相互作用,采用装配方法对气柱界面进行装配,而运动激波仍用捕捉法进行模拟[14];随后,邹东阳等对等截面通道内的运动激波进行装配,与理论值比较考察了算法的计算精度[15];此外,作者所在团队采用边界装配策略对超高速弹丸发射时头部大范围运动的强激波进行处理,拓展了装配法在此类问题中的应用[16]。然而,从以上研究来看,装配的激波只在直壁面上运动,而对于激波在弯曲壁面上的传播并未涉及;在整个计算中,装配的激波阵面大多不能自发地实现大变形,如拉伸、缩短和弯曲,往往需要人为调整改变装配激波点的分布;且当激波运动致使流场网格质量变差时,经常需要人为重新替换网格,算法的自动化程度比较低,计算代价比较大;最重要的一点,由于缺少成熟有效的基于非结构网格的运动激波探测(Shock Detection)算法,目前尚不能自动处理激波发生拓扑变化这类情况[12],如激波的正规反射向马赫反射演化、激波的新生与弱化等。
针对上述前3个问题,本文在近年来发展的自适应间断装配求解器(Adaptive Discontinuity Fitting solver,ADFs)[17]的基础上进行了若干算法改进,实现了装配激波点在曲壁面上的运动;通过自动调整间断节点的分布,保证了激波阵面在演化中不失真;局部自动网格重构策略的实现大大减少了人为干预,显著提高了算法的计算效率;此外,结合数值算例,提出了一种针对激波干扰点运动的装配策略。仿真结果表明了算法的合理性和有效性。
1 自适应间断装配求解器本节首先对激波捕捉算法和以此为基础发展而来的ADFs进行简单介绍,然后重点说明针对非定常问题的一些改进。
1.1 激波捕捉算法考虑网格运动变形,控制方程采用任意拉格朗日-欧拉(Arbitrary Lagrange-Euler,ALE)法描述的二维可压缩非定常Euler方程的积分形式:
| $ \left\{ \begin{matrix} \frac{\partial }{\partial t}\iiint\limits_{V}{\mathit{\boldsymbol{Q}}\text{d}\sigma \text{+}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S \left( {{\mathit{\boldsymbol{F}}_c}}-\mathit{\boldsymbol{Q}}\cdot {{\mathit{\boldsymbol{x}}}_{\text{c}}} \right)\cdot \mathit{\boldsymbol{n}}\text{d}\psi =\mathrm{0} } \\ \mathit{\boldsymbol{Q}}={{\left[ \rho , \rho {{u}_{i}}, \rho E \right]}^{\text{T}}} \\ {{\mathit{\boldsymbol{F}}_c}}={{\left[ \rho {{u}_{i}}, \rho {{u}_{i}}{{u}_{j}}+p{{\delta }_{ij}}, \left( \rho E+p \right){{u}_{i}} \right]}^{\text{T}}} \\ E=\frac{P}{\rho \left( \gamma -1 \right)}+\frac{1}{2}{{u}_{i}}{{u}_{i}} \\ \end{matrix} \right. $ | (1) |
式中:Q为守恒变量;Fc为对流项通量;xc为网格运动速度;n为控制体表面外法向单位向量;V和S分别表示控制体和控制体表面;dσ和dψ分别表示体积微元和面积微元;ρ为密度;ui为速度;E为单位质量流体总能;p为压强;δij为Kronecker函数;考虑量热完全气体,比热比γ=1.4。
数值计算采用格心型有限体积法,流场变量仅存储在网格单元中心。不特别说明,本文均采用AUSM+(Advection Upstream Splitting Method+)格式计算面元对流通量,采用显式4步Runge-Kutta格式进行时间推进,以此保证在光滑流场中时空离散上均具有二阶精度。
非结构动网格技术方面,本文利用改进后的弹簧近似法[18],避免网格在变形运动中出现失效单元,保持较好的网格质量,且不会造成求解器计算效率的大幅度降低。此外,当流场边界因出现大变形、大位移而导致网格质量急剧下降时,往往需要进行网格重构。这又涉及到新/旧网格间的流场信息传递,为了尽量减小插值引起的空间精度下降和非物理振荡,本文采用基于单元相交的混合网格精确守恒插值方法[19]。同时,为了防止因网格运动引入非物理解,还需要根据“离散几何守恒率”对计算方法进行修正。由于篇幅所限,相关算法这里不再详述,可参考文献[18]。
1.2 自适应间断装配算法 1.2.1 标记间断位置在使用激波装配法时,首先都需要给定拟装配的初始间断位置。一般来说,对于定常流动,只需给定大概位置,不要求十分准确,随着流场收敛间断最终便会移动到准确的位置[17];然而,对于间断处于不断运动的非定常流动,初始间断位置的标记比较重要,若偏差过大可能会严重影响后续流场的演化。
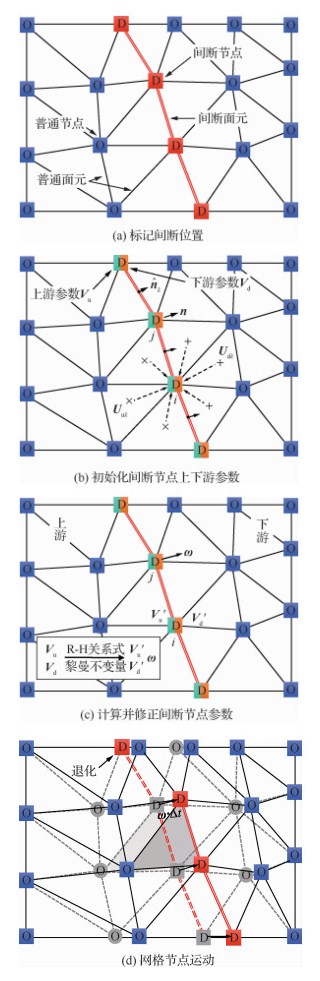
如图 1(a)所示,ADFs通过指定网格节点的属性(间断或普通)来标记间断的位置,间断阵面由一系列间断面元组成,而间断面元同时也作为流场网格单元的边界;每个间断阵面上的间断节点均存储两组流场数据,分别对应间断两侧的状态。特别地,对于由m条间断汇聚的干扰点,则该点将存储2m组流场参数,分别对应m条间断的两侧。
|
| 图 1 自适应间断求解器的关键步骤 Fig. 1 Key procedures of ADFs |
对于格心型有限体积法,已知t时刻的流场数据仅存储于所有网格单元中心。考虑到ADFs的装配计算是建立在网格节点上的,因此采用反距离加权(Inverse Distance Weighted)法,如图 1(b)所示,由间断两侧贡献单元的格心值(Uu和Ud)插值得到所有间断节点两侧参数(Vu和Vd),即
| $ {\mathit{\boldsymbol{V}}_{u, i}} = \frac{{\sum\limits_{k = 1}^{{N_1}} {{\alpha _{ik}}{\mathit{\boldsymbol{U}}_{{\rm{u}}k}}} }}{{\sum\limits_{k = 1}^{{N_1}} {{\alpha _{ik}}} }}, {\mathit{\boldsymbol{V}}_{d, i}} = \frac{{\sum\limits_{k = 1}^{{N_2}} {{\alpha _{ik}}{\mathit{\boldsymbol{U}}_{{\rm{d}}k}}} }}{{\sum\limits_{k = 1}^{{N_2}} {{\alpha _{ik}}} }} $ | (2) |
式中:N1、N2分别表示与间断节点i相邻的上下游区域贡献单元的总个数,考虑到超声速流动影响范围的有限性,此处需引入判断准则[17]用于剔除非贡献的邻居单元;用αik=Rikh表示贡献单元k对间断节点i的作用权系数,通常取h=-2,Rik为贡献单元k的中心到节点i的距离。由于本文仅对激波进行装配,因此全文用下标u和d分别指代激波的上游和下游。
此外,间断节点j的法向构造如下:
| $ {{\mathit{\boldsymbol{n}}}_{j}}=\frac{\sum\limits_{k=1}^{{{N}_{3}}}{\alpha _{jk}^{'}{{\widehat{\mathit{\boldsymbol{n}}}}_{k}}}}{\sum\limits_{k=1}^{{{N}_{3}}}{\alpha _{jk}^{'}}} $ | (3) |
式中: N3表示同一个间断阵面上与间断节点j相邻的贡献间断面元的总个数;
1.2.2节得到的间断节点两侧参数并不满足描述间断的跳跃关系式,如Rankine-Hugoniot(R-H)关系式。对激波来讲,在激波坐标系下,由于上游流动是超声速的,即下游流动信息理论上不会污染上游参数,因此上游流动参数Vu无需修正。沿着间断节点法向n,一共有4个参数需要计算,即修正后的激波下游流动参数V′d=[ρ′d, u′d, p′d]和激波节点的运动速度ω=ω·n。R-H关系式和下游特征相容关系式分别为
| $ \left\{ \begin{matrix} \rho {{'}_{\text{d}}}\left( u_{\text{d}}^{'}-\omega \right)={{\rho }_{\text{u}}}\left( {{u}_{\text{u}}}-\omega \right) \\ \rho {{'}_{\text{d}}}{{\left( u_{\text{d}}^{\text{ }\!\!'\!\!\text{ }}-\omega \right)}^{2}}+p_{\text{d}}^{'}={{\rho }_{\text{u}}}{{\left( {{u}_{\text{u}}}-\omega \right)}^{2}}+{{p}_{\text{u}}} \\ \begin{align} & \frac{\gamma }{\gamma -1}\cdot \frac{p_{\text{d}}^{'}}{\rho _{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}+\frac{{{\left( u_{\text{d}}^{\text{ }\!\!'\!\!\text{ }}-\omega \right)}^{2}}}{2}= \\ & \frac{\gamma }{\gamma -1}\cdot \frac{{{p}_{\text{u}}}}{{{\rho }_{\text{u}}}}+\frac{{{\left( {{u}_{u}}-\omega \right)}^{2}}}{2} \\ \end{align} \\ \end{matrix} \right. $ | (4) |
| $ \frac{2}{\gamma -1}\sqrt{\gamma p_{\text{d}}^{'}/\rho _{\text{d}}^{'}}-u_{\text{d}}^{\text{ }\!\!'\!\!\text{ }}=\frac{2}{\gamma -1}\sqrt{\gamma {{p}_{\text{d}}}/{{\rho }_{\text{d}}}}-{{u}_{\text{d}}} $ | (5) |
联立式(4)和式(5)即可求得V′d和ω。
此外,在求得激波节点运动速度后,便可以计算出间断节点在激波坐标系下的上游相对马赫数为
| $ Ma_{\text{u}}^{\text{ref}}=\frac{{{u}_{\text{u}}}-\omega }{\sqrt{\gamma {{p}_{\text{u}}}/{{\rho }_{\text{u}}}}} $ | (6) |
考虑到数值误差,规定Mauref < 1.01的间断节点退化成普通节点不进行装配,相应的间断面元也退化为普通面元,在一定程度上实现了装配计算和捕捉计算的灵活调用[17]。
1.2.4 网格节点运动在确定了每个间断节点运动速度矢量ω后,便可以求得间断节点j在下一时刻的位置坐标Xjt+Δt为
| $ \mathit{\boldsymbol{X}}_j^{t + \Delta t} = \mathit{\boldsymbol{X}}_j^t + {\mathit{\boldsymbol{\omega }}_j}\Delta t $ | (7) |
如图 1(d)所示,通过弹簧近似法便可求得流场其余所有普通节点在新时刻的位置,从而更新得到新的流场网格。值得注意的是,对于定常流动,最终ω将趋于0,即间断位置收敛,流场网格将不发生变形。
1.2.5 流场更新基于新的流场网格,采用1.1节所述的激波捕捉求解器进行流场更新,获得t+Δt时刻各个网格单元的格心值,为此需要计算各个面元的对流通量。对于普通面元,仍可以采用各种空间离散方法进行通量分解计算,无需任何修正;而对于间断面元,其通量可以根据上游参数直接写出:
| $ \mathit{\boldsymbol{F}}_j^D = {\left[ {\begin{array}{*{20}{c}} \phi \\ {\phi {u_i} + p{A_i}}\\ {\phi E{\rm{ + }}p\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{A}}} \end{array}} \right]_{{\rm{u, }}j}} $ | (8) |
式中:
最后,通过时间推进算法便可得到t+Δt时刻的流场,重复1.2.1节~1.2.5节的步骤进行下一时间步的装配计算直到计算终止。
1.3 非定常激波装配的一些改进非定常激波相比定常激波的一个显著特点是其阵面的位置或形状会随时间发生变化,因此算法需要具备有效模拟激波形状或长度发生剧烈变化的能力。本节针对运动激波传播特性,对ADFs进行相应的改进,使其能准确高效地模拟激波运动问题。
1.3.1 间断节点沿壁面运动采用ADFs模拟管道中的运动激波时,需要对沿壁面运动的间断节点进行特殊处理。根据壁面的弯曲特性,一般可以将其分为直壁面和曲壁面两大类,对两者的处理有明显区别。
对于直壁面,如图 1(d)所示,间断节点可以沿壁面方向自由滑动,不需要跨越任何壁面网格节点;而间断附近的壁面节点根据非结构动网格技术调整位置,同样沿壁面滑动,不会破坏直壁面的形状。
对于曲壁面,处理要复杂一点,由于其是由一系列非共线的小直线段(壁面网格面元)离散的,为了保证贴体特性,曲壁面上的网格节点在计算中通常固定不动,因此间断节点必然会跨越壁面网格节点。针对弯曲方向的不同,曲壁面又可分为凸曲壁和凹曲壁,两者的处理方式略有差异,下面简要介绍。
如图 2所示,用i、j、k、m、n表示各个网格节点。在t时刻,间断节点i沿面元mk向壁面节点k滑动,根据间断节点沿壁面运动速度ωt, i,若计算有ωt, iΔt>lik,其中lik为节点i、k之间的距离,则说明下一时刻间断节点i将跨越节点k。

|
| 图 2 间断节点沿曲壁面的运动 Fig. 2 Movements of discontinuity nodes along curved wall |
在确定t+Δt时刻新的壁面间断节点位置时,首先根据式(7)计算出间断节点i的虚拟推进位置k′;对于凹曲壁(见图 2(a2)),新间断节点取直线jk′与面元in的交点;对于凸曲壁(见图 2(b2)),过点k′作面元in的垂线,新间断节点取垂足。
实际上,从动网格角度考虑,该过程相当于间断节点i移动到了壁面网格节点处并退化成普通节点,而对应壁面网格节点k移动到新的壁面间断位置并转化成间断节点。从间断角度考虑,相当于间断节点跨越了运动方向上邻近的曲壁面网格节点。值得注意的是,在跨越前后,由节点i、j、k组成的三角形网格单元①从激波上游移动到了激波下游,因此需要对其格心参数重新进行赋值,直接由间断节点下游激波参数插值即可得到。
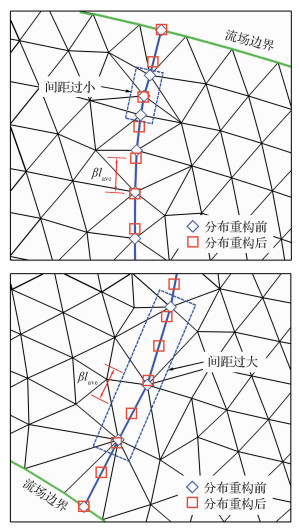
1.3.2 间断节点分布的自动重构对于定常间断装配,由于间断移动变形有限,通常间断节点能维持较好的分布;在前期的一些装配计算中,若有必要调整间断节点分布时,通常要人为重新划分网格[17],费时费力。而间断在移动过程中往往会不断变长或缩短,从而造成相邻间断节点的间距过大或过小,使得间断阵面附近的网格质量迅速下降,如图 3所示。当这种情况发生时,需要沿间断阵面重新调整间断节点分布,使其间距近似等于周边网格单元的尺寸。对于二维问题,具体步骤如下:
|
| 图 3 间断节点分布重构前后的网格 Fig. 3 Grids before and after redistribution of discontinuity nodes |
步骤1 判断间断节点是否满足分布重构条件关系式:
| $ {l_k}/{l_{{\rm{ave}}}} < {\delta _{\min }}或{l_k}/{l_{{\rm{ave}}}} > {\delta _{\max }} $ | (9) |
式中: lk为第k个旧间断面元的长度;lave为间断邻近网格单元的平均尺度;δmin和δmax分别为预设的最小间距和最大间距系数,通常取0.3和1.7。
步骤2 对需要分布重构的各组间断散点进行排序并曲线拟合。考虑到每条间断阵面的始点和终点在重构前后的位置固定,本文采用多次Bézier曲线拟合法[20]得到各条间断拟合曲线。
步骤3 将拟合曲线按照尺寸βlave进行平均分割获得各个均分点。为了更好地描述曲线的弯曲程度,用β来控制均分点的疏密程度,对较为平直的曲线,β通常取1.2;而对于比较弯曲的曲线,β通常取0.7。
步骤4 将均分点映射到旧间断面元上从而得到分布重构后的间断节点。注意,如果不进行映射,直接采用均分点作为新间断节点,会在一定程度上损失位置精度,当进行多次分布重构后位置误差积累可能造成间断位置形状出现显著偏差。
步骤5 基于新的间断节点,重新划分间断附近网格,通过插值算法获得新网格单元格心的流场参数。
该方法不仅用于间断节点的分布重构,同样,当间断节点在直壁面上滑动时,若干壁面网格节点难免会过近或过远,此时便需进行壁面网格节点的分布重构。
1.3.3 流场网格的局部自动重构对于定常激波装配,由于间断阵面的变形幅度较小,一般只需进行几次网格重构即可,可以输出网格并导入专业CFD网格生成软件(如Pointwise)人工生成网格,然后再读入网格完成重构过程。而对于运动激波装配,由于网格变形比较剧烈,需要频繁重构网格,若再进行人工手动重构将付出极大的计算代价,严重影响计算效率,因此需要高效的自动网格生成策略。
本文成功将Shewchuk研发并开源的二维Delaunay三角形网格生成程序“Triangle”[21]嵌入到ADFs中,实现了流场网格的自动重构。下面以一道右行激波在平直管道中运动为例,通过展示若干关键时刻的流场网格,来具体说明该重构策略的特性:
1) 采用局部网格变形/重构策略能显著提高计算效率,同时重构单元数量的缩减很大程度上可以减小流场信息插值引入的误差。如图 4(a)所示,以间断位置作为起点向两侧搜寻网格,标记距离间断最近的n层网格单元作为可变形单元且可以重构,其他网格静止且不参与重构,即流场可分为“动网格区”(图 4阴影区)和“静网格区”。当激波在直壁面上运动时,n通常取10;而在曲壁面上运动时,由于网格重构较为频繁,动网格区可以取小一点,如n=3。

|
| 图 4 间断附近局部网格自动重构(n=5) Fig. 4 Automatically local re-meshing around discontinuity front(n=5) |
2) 当激波运动使得网格质量较差时(如图 4(b)),需要进行网格重构。考虑到计算初始网格通常用专业网格生成软件划分,网格质量可以控制得比较好(如大部分为正三角形),因此ADFs在网格重构时利用了初始网格信息。如图 4(c)所示,提取位于重构区内的初始网格点,作为网格生成“控制点”供Triangle程序调用生成Delaunay三角形网格。注意,为了保证网格质量,距离间断过近(约一个网格尺寸内)的初始网格点不作为控制点。这样,经控制生成的大部分网格单元的尺寸和形状与初始高质量网格保持一致(对比图 4(a)与图 4(c)),一定程度上减弱了网格重构对流场网格分布和拓扑的影响。
3) 每次完成网格重构后,由于旧网格变形区已经不太适合新的间断位置,因此需要重新标记动网格区和静网格区,如图 4(d)所示,即计算过程中流场网格重构区是动态变化的,随间断移动需要动态调整。
2 验证算例本节通过3个二维算例对若干改进的准确性、可行性和可靠性做了验证,体现了该非定常激波装配算法在处理运动激波的潜力。值得强调的是,以下所有装配算例整个计算完全自动进行,没有经过任何人为干预。
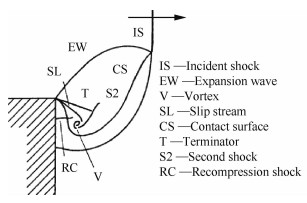
2.1 激波绕射90°拐角平面运动激波绕射尖锐拐角是一类相当常见的气动问题,许多学者从试验和数值的角度出发,对90°拐角的激波绕射问题做了大量研究[22-24]。根据入射运动激波的强弱,该问题主要分为两类,即激波下游的流场是超声速或亚声速。图 5给出了强激波绕射下该流场的若干主要波系结构,流场在演化中具有明显的自相似性和准定常特性。
本节考虑一道平直入射激波(运动激波马赫数Mas =2.4)绕射90°拐角的情况,初始流场参数详见表 1,流场计算区域如图 6所示,初始激波位于拐角前0.5L处,网格尺度Δ=0.25L,全场初始共有28 762个均匀分布的三角形网格单元。本算例中的时间均为无量纲量,计算中只对入射强激波进行装配,流场演化产生的新激波仍然用捕捉法计算。
| 参数 | 入射激波马赫数Mas | 激波下游流场马赫数 | 激波上、下游压强比 | 激波上、下游密度比 |
| 数值 | 2.4 | 1.157 | 6.553 | 3.212 |

|
| 图 6 不同时刻下绕射激波的装配阵面 Fig. 6 Fitted fronts of diffracted shock waves at various moments |
图 6直观地给出了一系列装配得到的运动激波阵面,无量纲间隔时间dt =0.05。可以看出当入射强激波绕过壁面拐角后,激波会逐渐向垂直壁面弯曲,这是由于拐角附近的流场在膨胀波干扰下,激波强度减弱,激波运动速度降低;此外,通过观察可以发现,相比流场上方未受干扰的入射激波,弯向垂直壁面的激波间距明显减小,经推算此处的激波马赫数约降为1.36。
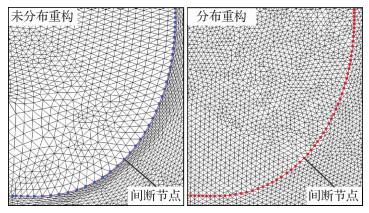
由于该算例的激波阵面在传播过程发生了剧烈地弯曲和伸长,因此需要频繁进行间断节点的分布重构。从某一时刻流场出发,考察了一段时间后是否进行间断节点分布重构的流场网格,结果对比如图 7所示。其中,左图未进行间断节点重构,且采用传统的全局网格变形策略,可以发现局部间断面元被过度拉长或挤短,不能较好地描述间断曲率;同时激波下游网格尺度将逐渐增大,会降低此处复杂流场的解析精度。相反,算法改进后,经过若干次网格重构,间断阵面及其附近的网格尺度和邻近网格始终保证接近,且间断的形状更加光滑合理,充分反映了1.3节改进策略的必要性和有效性。
|
| 图 7 算法改进前后的装配激波附近流场网格对比 Fig. 7 Comparison of flow field grids near fitted shock wave before and after algorithm improvement |
为了定性说明装配结果的准确性,基于相同网格尺度用激波捕捉法重新计算了该问题。图 8给出了2个无量纲时刻流场密度等值线的对比(ρ0为初始入射激波上游密度),由于捕捉激波本质上存在的数值误差,捕捉法计算的密度等值线(白色实线)会出现两条不合理的波带,严重降低了流场等值线的光滑性;而装配计算的等值线(黑色实线)光滑合理,没有出现误差带,整体看来装配法的流场结果更加准确可信。

|
| 图 8 不同时刻流场密度云图对比 Fig. 8 Comparison of flow field density contours at various moments |
图 9对比了装配法和捕捉法计算终止时刻流场压强云图(p0为初始入射激波上游压强),可以看到两者的激波位置和大部分区域的等值线符合得较好。进一步提取x=1.6L直线上的数据,定量比较两者压强分布,如图 10所示,装配法避免了捕捉法处理激波产生的虚假数值过渡区,而在膨胀波区两者吻合很好。以上说明了对于非定常流场,装配法即使经历了多次网格重构和流场信息插值,仍能保持较高的计算精度。

|
| 图 9 t=0.8时刻流场压强云图对比 Fig. 9 Comparison of flow field pressure contours at t=0.8 |

|
| 图 10 x=1.6L处压强分布对比 Fig. 10 Comparison of pressure distributions at x=1.6L |
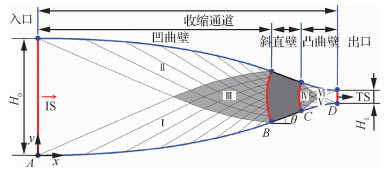
本节模拟二维激波管内激波增强问题。计算模型如图 11所示,通过设计特定的上下壁面收缩型线[25],初始平面运动激波依次经过光滑的凹形曲线段、斜直线段和光滑的凸形曲线段,先后受到壁面产生的“激波-压缩”和“激波-膨胀”扰动,形状不断发生改变,最终在收缩段出口恢复为增强的平面激波,且激波波面上没有明显扰动。
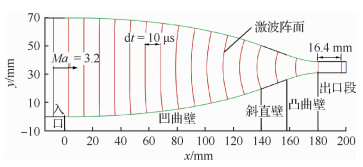
该激波管收缩段入口高度H0 =70 mm,出口高度H1 =8 mm,汇集角θ =20°;收缩段总长179.4 mm,其中凹曲壁、斜直壁和凸曲壁的水平长度分别为139.8、18.1、21.5 mm。仿真计算时,初始入射激波(Mas =3.2)位于收缩段入口前方8 mm处,激波上游为静止空气,且上游压强p0和密度ρ0分别为6 kPa和0.072 855 kg/m3。采用激波装配法计算时,全场网格尺寸ΔLSF =1 mm,一共有25 082个均匀分布的三角形网格单元。
在整个过程中,激波一共运动了170 μs。图 12依次给出了间隔10 μs装配的激波阵面。可以清晰直观地看到,平面激波在进入收缩段后开始逐渐自底部向中心弯曲,在斜直壁段时曲率保持不变,当传播到凸曲壁时,激波阵面曲率逐渐减小,最终在出口位置再次转变为平面激波。从收缩段入口运动到出口,激波长度明显缩小,采用1.3.2节所述的间断节点自动分布重构技术,激波阵面上的间断节点从初始71个逐渐减少到12个。根据160~170 μs时段中激波的水平运动16.4 mm,近似求出收缩段出口位置的激波马赫数为4.83,与试验纹影[25]推算出的激波马赫数4.80吻合得非常好,相对偏差仅有0.6%。
|
| 图 12 激波管内不同时刻装配激波阵面 Fig. 12 Fitted shock wave fronts at various moments in shock tube |
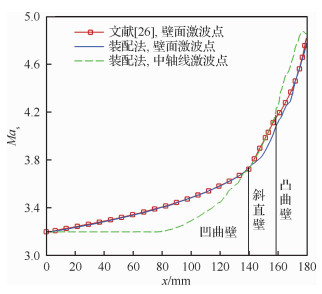
文献[26]理论分析了激波运动到不同水平位置的强度,即运动激波马赫数Mas,考虑到装配法需要计算出间断节点的运动速度,进而很方便地推导出激波运动马赫数,因此本文就该数值进行对比,结果如图 13所示。可以看出,在凹曲壁段,装配结果和理论预测符合得很好,而在斜直壁段和凸曲壁段,二者略有差别,有待进一步校核;中轴线附近的激波强度在x < 80 mm段基本没变化,受到压缩波作用之后迅速增强,且在斜直壁段与理论预测出的壁面激波强度较为吻合,同样,在靠近出口处,受膨胀波的影响强度有所下降。总之,采用激波装配法可以很容易得到激波在传播过程中的强度变化,而激波捕捉法很难直接得到,这也是装配法的一个优势所在。
|
| 图 13 激波在不同水平位置的强度对比 Fig. 13 Comparison of shock wave intensity at various horizontal locations |
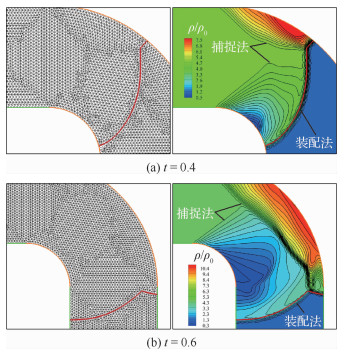
图 14依次对比了激波捕捉法和装配法模拟的密度ρ、压强p和熵S=p/ργ的云图,图中S0为初始入射激波上游熵值。捕捉法的流场网格尺度ΔLSC=ΔLSF/5,全场共有626 128个三角形网格单元,即网格单元总量约是装配法的25倍。对比密度和压强云图可以发现,捕捉法得到的等值线在x=30,130 mm左右存在明显的振荡,而装配法得到的等值线光滑合理没有波动;从熵云图可以大致看出造成捕捉法出现非物理波动的原因,捕捉得到的激波下游会出现一条逐渐远离激波的熵带,一定程度污染了下游流场,这可能是由捕捉激波从本质上产生的数值误差造成的,文献[12, 15]在计算静止激波与涡的相互作用中也同样发现这种现象,此处有待进一步探讨。相比之下,装配法由于精确处理了激波,即使用很少的网格也能得到较好的流场。

|
| 图 14 t=165 μs时刻装配法和捕捉法模拟的流场对比 Fig. 14 Comparison of flow fields simulated by S-F and S-C at t=165 μs |
爆震发动机中经常会出现激波在弯曲管道中的传播现象,其典型波系结构如图 15试验阴影图[27]所示。本节采用激波装配法模拟激波在“L”形弯管内的传播、加速过程,进一步考核本方法的可靠性。
计算模型由直管段和“L”形弯管段组成,如图 16所示,内径均为L,且弯管段的内壁面曲率半径r=0.5 L。初始入射激波马赫数Mas=4.0,下游与上游的压强比和密度比分别为18.5、4.571;且初始入射激波上游为静止空气,下游气流马赫数为1.553。全场网格尺度Δ=0.03L,初始共有11 654个均匀分布的三角形网格单元。本算例中的时间均为无量纲量。

|
| 图 16 计算区域、初始条件和网格 Fig. 16 Computational domain, initial condition and meshes |
图 17给出了间隔dt =0.04装配的激波阵面,入射激波于t=0.22时刻到达弯曲段入口,此时激波阵面仍是平整的,激波进入弯曲管道后同时受到内壁面的膨胀干扰及外壁面的压缩干扰,使得靠近内壁面的激波逐渐减弱并发生弯曲以保持传播方向与管道轴线一致,而靠近外壁面的激波受到压缩波的作用而逐渐增强最终形成马赫反射结构。图中可以清晰地看到马赫杆随着激波的传播逐渐变长,即三波点逐渐向内壁面移动;且从间距可以看出马赫杆的强度更高,运动速度更快。

|
| 图 17 不同时刻下L形弯管内装配的激波阵面 Fig. 17 Fitted shock wave fronts at various moments in L-shaped tube |
非定常流动中三波点等间断相交点运动速度的求解一直以来是个难题,目前尚未有完善的理论模型,因此运动相交点的处理是装配法的一个研究重点。图 18给出了某时刻间断节点运动示意,其中三波点的运动速度没有修正,造成邻近的间断面元斜率出现异常,随着时间推进,三波点位置会迅速发散引起计算失败。

|
| 图 18 未修正的三波点运动 Fig. 18 Motion of triple point before correction |
本文提出一种“预估位移,推算速度”的策略间接完成运动三波点的装配,下面结合图 19介绍其关键步骤:
|
| 图 19 三波点运动速度计算模型 Fig. 19 Calculation model of triple point motion speed |
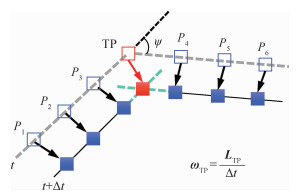
步骤1 辨识三波点(TP)。分析可知三波点一般位于几个不同斜率激波线的交汇处,如图 19所示,求解每个间断节点左右两个相邻间断线元的夹角ψ,若ψ高于某阈值ψthr,则标记该节点为三波点。数值试验表明ψthr通常取15°即可。
步骤2 求解相交点新时刻位置。首先根据1.2.3节求得的间断节点运动速度,分别计算三波点TP左邻居间断节点(P1~P3)和右邻居间断节点(P4~P6)在t+Δt时刻的位置(图 19蓝色实心方块),然后分别拟合出两条直线(图 19黑色实线),可以认为这两条直线与新时刻三波点附近的激波线斜率近似一致,最后求解这两条直线的相交点(图 19红色实心方块)作为新时刻三波点的位置。
步骤3 计算三波点速度。由旧三波点到新三波点的位移矢量为LTP,则三波点的运动速度矢量ωTP=LTP/Δt。
值得注意的是,虽然此处针对的是三波点结构,但其他间断相交点的运动也可以类似处理,这里不再详述。
为了校核本算例三波点位置计算的准确性,图 20对比了任意两个时刻捕捉法和装配法的结果,可见装配的入射激波、马赫杆和三波点位置和捕捉结果基本吻合。此外,对比图 20和图 16的流场网格,可见装配激波走过的区域,经1.3.3节所述的网格重构策略,流场网格可以恢复到初始高质量网格,很好地减弱了装配阵面对流场网格的影响。
|
| 图 20 不同时刻流场密度云图及网格对比 Fig. 20 Comparison of flow field density contours and meshes at various moments |
本文面向非定常流动中激波传播问题,对最近发展的自适应间断装配求解器ADFs进行了若干改进,主要结论如下:
1) 当激波在曲壁面上运动时,运动间断节点可以在固定壁面网格节点的前提下实现装配。
2) 针对激波产生大变形、大位移运动问题,通过间断节点分布的自动重构保证激波阵面不失真,同时采用局部网格自动重构策略确保了网格的高质量,并提高了程序计算效率。
3) 对于激波相交点的运动,设计了一种根据位移推算速度的方法进行装配,数值算例表明该方法行之有效。
总之,采用激波装配法处理激波传播问题,相比激波捕捉方法可以获得流场间断更加直观清晰的图谱,有利于进一步深入认识激波的演化过程。本文仅对单个运动激波进行装配,流场演化中的新生激波仍用捕捉法进行处理,而激波装配法的目标是显式地自动模拟这些间断拓扑变化问题,因此将激波辨识技术融合到激波装配法中将是下一步工作的重点。
致谢
中国科学技术大学的杨基明老师在激波增强管壁型线几何模型方面给予了协助和宝贵的指导,在此致以衷心的感谢!
| [1] | CASPER J, CARPENTER M H. Computational considerations for the simulation of shock-induced sound[J]. SIAM Journal on Scientific Computing, 1998, 19(3): 813-828. |
| Click to display the text | |
| [2] | ARORA M, ROE P L. On postshock oscillations due to shock capturing schemes in unsteady flows[J]. Journal of Computational Physics, 1997, 130(1): 25-40. |
| Click to display the text | |
| [3] | ZAIDE D, ROE P L. Shock capturing anomalies and the jump conditions in one dimension: AIAA-2011-3686[R]. Reston, VA: AIAA, 2011. |
| [4] | PIROZZOLI S. Numerical methods for high-speed flows[J]. Annual Review of Fluid Mechanics, 2011, 43: 163-194. |
| Click to display the text | |
| [5] | JOHNSEN E, LARSSON J, BHAGATWALA A V, et al. Assessment of high-resolution methods for numerical simulations of compressible turbulence with shock waves[J]. Journal of Computational Physics, 2010, 229(4): 1213-1237. |
| Click to display the text | |
| [6] | MORETTI G. Computation of flows with shocks[J]. Annual Review of Fluid Mechanics, 1987, 19(1): 313-337. |
| Click to display the text | |
| [7] | NASUTI F, ONOFRI M. Analysis of unsteady supersonic viscous flows by a shock-fitting technique[J]. AIAA Journal, 1996, 34(7): 1428-1434. |
| Click to display the text | |
| [8] | SALAS M D. A shock-fitting primer[M]. Boca Raton, FL: CRC Press, 2009: 115-124. |
| [9] | PACIORRI R, BONFIGLIOLI A. A shock-fitting technique for 2D unstructured grids[J]. Computers & Fluids, 2009, 38(3): 715-726. |
| Click to display the text | |
| [10] | BONFIGLIOLI A, GROTTADAUREA M, PACIORRI R, et al. An unstructured, three-dimensional, shock-fitting solver for hypersonic flows[J]. Computers & Fluids, 2013, 73: 162-174. |
| Click to display the text | |
| [11] | ZOU D Y, XU C G, DONG H B, et al. A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes[J]. Journal of Computational Physics, 2017, 345: 866-882. |
| Click to display the text | |
| [12] | BONFIGLIOLI A, PACIORRI R, CAMPOLI L. Unsteady shock-fitting for unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2016, 81(4): 245-261. |
| Click to display the text | |
| [13] | BONFIGLIOLI A, PACIORRI R, CAMPOLI L, et al. Development of an unsteady shock-fitting technique for unstructured grids[C]//30th International Symposium on Shock Waves 2. Berlin: Springer, 2017: 1501-1504. |
| [14] |
刘君, 邹东阳, 董海波. 基于非结构变形网格的间断装配法原理[J]. 气体物理, 2017, 2(1): 13-20. LIU J, ZOU D Y, DONG H B. Principle of new discontinuity fitting technique based on unstructured moving grid[J]. Physics of Gases, 2017, 2(1): 13-20. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [15] |
邹东阳, 刘君, 邹丽. 可压缩流动激波装配在格心型有限体积法中的应用[J]. 航空学报, 2017, 38(11): 121363. ZOU D Y, LIU J, ZOU L. Applications of shock-fitting technique for compressible flow in cell-centered finite volume methods[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(11): 121363. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] |
常思源, 邹东阳, 刘君. 自适应间断装配法模拟弹道靶中超高速弹丸发射[J]. 实验流体力学, 2019, 33(2): 23-29. CHANG S Y, ZOU D Y, LIU J. Simulating hypersonic projectile launching process in the ballistic range by adaptive discontinuity fitting solver technique[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(2): 23-29. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] | CHANG S Y, BAI X Z, ZOU D Y, et al. An adaptive discontinuity fitting technique on unstructured dynamic grids[J]. Shock Waves, 2019, 29: 1103-1115. |
| Click to display the text | |
| [18] |
刘君, 徐春光, 白晓征. 有限体积法和非结构动网格[M]. 北京: 科学出版社, 2016: 42-163. LIU J, XU C G, BAI X Z. Finite volume methods and unstructured dynamic grids technique[M]. Beijing: Science Press, 2016: 42-163. (in Chinese) |
| [19] |
徐春光, 董海波, 刘君. 基于单元相交的混合网格精确守恒插值方法[J]. 爆炸与冲击, 2016, 36(3): 305-312. XU C G, DONG H B, LIU J. An accurate conservative interpolation method for the mixed grid based on the intersection of grid cells[J]. Explosion and Shock Waves, 2016, 36(3): 305-312. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [20] | BÉZIER P. Numerical control:Mathematics and applications[M]. London: Wiley, 1972. |
| [21] | SHEWCHUK J R. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator[C]//Workshop on Applied Computational Geometry. Berlin: Springer, 1996: 203-222. |
| [22] | KLEINE H, RITZERFELD E, GRÖNIG H. Shock wave diffraction-New aspects of an old problem[M]//Shock waves@Marseille Ⅳ. Berlin: Springer, 1995: 117-122. |
| [23] | HILLIER R. Computation of shock wave diffraction at a ninety degrees convex edge[J]. Shock Waves, 1991, 1(2): 89-98. |
| Click to display the text | |
| [24] | RIPLEY R C, LIEN F S, YOVANOVICH M M. Numerical simulation of shock diffraction on unstructured meshes[J]. Computers & Fluids, 2006, 35(10): 1420-1431. |
| Click to display the text | |
| [25] |
詹东文, 杨剑挺, 杨基明, 等. 一种形状可控的激波增强管道型线设计新方法[J]. 航空学报, 2016, 37(8): 2408-2416. ZHAN D W, YANG J T, YANG J M, et al. A new method of wall profile design for shape-controllable shock wave enhancement[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2408-2416. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [26] |
詹东文.一种激波增强管壁型线设计方法[D].合肥: 中国科学技术大学, 2018: 48. ZHAN D W. An investigation of the channel profile design for shock wave enhancement[D]. Hefei: University of Science and Technology of China, 2018: 48(in Chinese). |
| [27] |
袁雪强.弯曲爆震管中爆震传播特性及弯曲管道射流起爆机理研究[D].长沙: 国防科技大学, 2015: 29-30. YUAN X Q. Characteristics of detonation wave propagation and detonation initiation via hot jet in bend tubes[D]. Changsha: National University of Defense Technology, 2015: 29-30(in Chinese). |