螺旋桨在飞行器中有着广泛的应用,为提高飞行器巡航效率,应设计合适且高效的螺旋桨。关于螺旋桨的设计方法,国内外学者已有大量研究。Larrabee[1]提出了最小诱导损失螺旋桨的设计方法。Angelo等[2]提出了根据给定工作状态和桨叶剖面翼型,快速设计桨叶弦长和扭转角分布的高效率螺旋桨设计方法。项松等[3-4]在设计时对桨叶截面弦长进行限制,改进了Angelo设计方法获得的弦长可能过大的缺点,并对设计的螺旋桨进行了风洞试验。翟若岱[5]应用项松等改进的方法,对临近空间太阳能飞机的螺旋桨进行了多点设计。
为进一步提高螺旋桨的效率,众多学者引入优化设计的思想,对螺旋桨桨叶的弦长及扭转角分布进行优化。许建华等[6]以求解雷诺平均Navier-Stokes方程为螺旋桨气动性能计算方法,以剖面翼型压力分布为目标,对螺旋桨平面形状进行反设计。梁撑刚等[7]将Betz条件和遗传算法相结合,对无人机螺旋桨桨叶弦长及扭转角分布进行优化。焦俊等[8]对高空飞艇螺旋桨进行了弦长和扭转角优化设计,并进行车载试验。刘芳等[9]采用Xfoil对翼型性能快速求解,首先进行螺旋桨翼型优化,之后对螺旋桨扭转角分布和弦长分布进行优化,得到高空低雷诺数高效螺旋桨。而Kwon等[10]提出一种螺旋桨多层次优化设计方法:首先对螺旋桨弦长和扭转角进行优化,得到初始构型; 接着对桨叶不同站位的翼型进行优化设计,以提高效率; 翼型优化后,再优化弦长和扭转角,使得效率进一步提高。
此外,Morgado等[11]基于JBLADE软件,分别采用最大L/D及L3/2/D进行螺旋桨设计,结果表明采用最大L3/2/D设计处的螺旋桨能够产生更多的升力,且效率更高,其中:L为升力,D为阻力。Yonezawa等[12]针对火星飞行器,对低雷诺数螺旋桨进行设计,并讨论了螺旋桨半径、桨叶个数及前进比对设计结果的影响。
上述螺旋桨设计方法均基于叶素动量理论及涡流理论,不能真实且准确地体现如径向流动、桨叶桨根及桨尖效应等。而对于太阳能无人机等飞行器应用的螺旋桨,其主要面临低雷诺数的问题,低雷诺数下桨叶叶素气动力计算的准确性及桨叶真实三维状态与设计间的差异,均会对设计的准确性产生较大的影响。一方面会导致螺旋桨真实拉力偏离设计拉力; 另一方面,设计状态下虽然能够保证螺旋桨效率达到最高,但在真实情况下螺旋桨的高效率并不能够保证。而若采用CFD求解对螺旋桨进行优化设计,由于单次螺旋桨数值模拟求解便需一定的计算时间,导致设计周期过长。
为解决上述问题,本文在设计过程中耦合数值模拟求解,并以CFD计算结果为参考进行桨叶气动力反解,以此进行修正与再设计,建立一种螺旋桨快速设计方法,在保证拉力要求下,提高螺旋桨效率。
1 传统螺旋桨设计方法传统螺旋桨设计方法基于最小能量损失[13]。图 1展示了螺旋桨桨叶叶素受力分析,其中,α为叶素实际迎角,β为干涉角,φ0为几何入流角,φ为实际入流角,W为合速度,W1为诱导合速度,Va1为轴向诱导速度,Vt1为环向诱导速度,V′为诱导螺距。这里假设合速度W与诱导合速度W1垂直。

|
| 图 1 螺旋桨叶素受力分析 Fig. 1 Force analysis of propeller blade element |
给定设计高度H、来流速度V0、密度ρ、设计拉力T及设计转速Ω,通过设计得到各叶素合适的翼型、弦长b及实际迎角α。设计过程如下:
1) 确定桨叶数NB,螺旋桨半径R,将桨叶划分为N个截面,并确定各截面翼型。
2) 根据设计拉力T及设计状态求解诱导螺距V′。
最小能量损失下诱导螺距V′沿桨叶为定值[13]。根据涡流理论可知,桨盘径向r处环向诱导速度与当地环量的关系为
| $ \mathit{\Gamma }\left( r \right) = \frac{{4{\rm{ \mathsf{ π} }}r}}{{{N_{\rm{B}}}}}{V_{{\rm{t1}}}} $ | (1) |
宽度为dr的叶素产生的拉力dT为
| $ {\rm{d}}T = \rho \mathit{\Gamma }\left( r \right)\left( {\mathit{\Omega }r - {V_{{\rm{t}}1}}} \right){\rm{d}}r $ | (2) |
由式(1)、式(2)和图 1的几何关系可得
| $ {\rm{d}}T = \frac{{4{\rm{ \mathsf{ π} }}r\rho }}{{{N_{\rm{B}}}}}\left( {{V_0} + V'{{\cos }^2}\varphi } \right)V'{\cos ^2}\varphi {\rm{d}}r $ | (3) |
则总拉力T为
| $ T = \int_{{R_{\min }}}^{{R_{\max }}} f \frac{{4{\rm{ \mathsf{ π} }}r\rho }}{{{N_{\rm{B}}}}}\left( {{V_0} + V'{{\cos }^2}\varphi } \right)V'{\cos ^2}\varphi {\rm{d}}r $ | (4) |
其中:f为Prandtl修正因子,即
| $ f = \frac{2}{{\rm{ \mathsf{ π} }}}\arccos \exp \left[ { - \frac{{{N_{\rm{B}}}\left( {R - r} \right)}}{{2r\tan \varphi }}} \right] $ | (5) |
故可根据设计状态及设计拉力,采用Newton迭代求解式(4)得到诱导螺距V′,从而确定各个截面的受力几何关系,进而得到考虑修正的螺旋桨最佳环量分布:
| $ \mathit{\Gamma }\left( r \right) = f\frac{{4{\rm{ \mathsf{ π} }}r}}{{{N_{\rm{B}}}}}V'\cos \varphi \sin \varphi $ | (6) |
3) 求解r处截面的弦长b及扭转角θ。
根据库塔-茹科夫斯基定理,叶素升力与当地环量关系为
| $ {\rm{d}}L = \rho \mathit{\Gamma }\left( r \right)W{\rm{d}}r $ | (7) |
而升力又可表示为
| $ {\rm{d}}L = \frac{1}{2}\rho {W^2}{C_L}b{\rm{d}}r $ | (8) |
联立式(7)和式(8)可得
| $ \mathit{\Gamma }\left( r \right) = \frac{1}{2}W{C_L}b $ | (9) |
式中:CL为升力系数。
叶素工作在最大升阻比下,螺旋桨的效率最高。而根据当地弦长b,可得到对应的雷诺数Re与马赫数Ma,进而求得叶素截面翼型最大升阻比对应的迎角α及气动力。根据式(9)迭代求解得到弦长b。对应截面的扭转角为
| $ \theta = \alpha + \varphi $ | (10) |
限制弦长范围取为0.02R~0.3R,采用“黄金分割法”求取最接近最佳环量分布的弦长。弦长超过最大限制,则考虑增加桨叶数目。
4) 重复求解,得到所有截面几何信息。
5) 对弦长b及扭转角θ分布进行光顺处理。
采用四阶贝塞尔样条曲线对弦长b及扭转角θ分布进行拟合:
| $ \begin{array}{l} p = {\left( {1 - t} \right)^4}{p_0} + 4{\left( {1 - t} \right)^3}t{p_1} + \\ \;\;\;\;\;\;6{\left( {1 - t} \right)^2}{t^2}{p_2} + 4(1 - t){t^3}{p_3} + {t^4}{p_4} \end{array} $ | (11) |
式中:t取值范围为0~1。
沿桨叶径向进行积分,可得设计下的螺旋桨总拉力T、扭矩M及效率η分别为
| $ {\rm{d}}T = \frac{1}{2}\rho {W^2}b\left( {{C_L}\cos \varphi - {C_D}\sin \varphi } \right){\rm{d}}r $ | (12) |
| $ {\rm{d}}F = \frac{1}{2}\rho {W^2}b\left( {{C_L}\sin \varphi + {C_D}\cos \varphi } \right){\rm{d}}r $ | (13) |
| $ T = \int_{{R_{\min }}}^{{R_{\max }}} {{N_{\rm{B}}}} {\rm{d}}T $ | (14) |
| $ M = \int_{{R_{\min }}}^{{R_{\max }}} {{N_{\rm{B}}}} r{\rm{d}}F $ | (15) |
| $ \eta = \frac{{T{V_0}}}{{\mathit{\Omega }M}} $ | (16) |
式中:CD为阻力系数。
2 数值模拟方法验证对于螺旋桨气动力的求解,相比于动量叶素理论的快速求解方法,CFD方法基于真实模型计算更加接近真实物理状态,已发展出如多重参考系法、滑移网格及嵌套网格模拟等多种方法。其中多重参考系(Multiple Reference Frames,MRF)法作为一种准定常方法,计算效率高,在螺旋桨数值模拟中应用广泛[14-16]。
这里以某型太阳能无人机螺旋桨为例,对其分别进行地面试验与数值模拟。该型螺旋桨桨叶半径R=0.203 2 m,桨叶数NB=2。地面试验在无来流状态下进行,通过改变转速测量螺旋桨拉力及扭矩的变化。
数值模拟基于MRF法,采用SA湍流模型,通过混合网格技术进行网格生成。其中旋转域采用四面体非结构网格,网格量为260万,外流域生成结构网格,网格量为50万。局部网格如图 2所示。
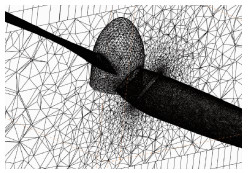
|
| 图 2 局部网格示意图 Fig. 2 Schematic diagram of local mesh |
拉力和扭矩测量结果(EXP)与数值模拟结果(CFD)对比如图 3和图 4所示。可以看出,在较小拉力下,数值模拟结果与试验测试结果符合较好,验证了数值模拟方法的可行性,且相比于叶素动量理论,拉力的计算更加准确。

|
| 图 3 拉力对比 Fig. 3 Comparison of thrust |

|
| 图 4 扭矩对比 Fig. 4 Comparison of torque |
对某型太阳能无人机的螺旋桨进行设计,设计高度H=3 km,来流速度V0=13 m/s,拉力T=10 N,桨盘半径R=0.27 m。取螺旋桨转速Ω=2 700 r/min,桨叶数NB=2,桨叶采用Clark Y翼型。
3.2 设计结果设计得到的螺旋桨弦长、扭转角分布及三维几何图形如图 5所示。主要对0.2R以上的桨叶进行设计,而桨毂至0.2R处做过渡处理。

|
| 图 5 螺旋桨设计结果 Fig. 5 Design results of propeller |
采用上述螺旋桨方法对设计得到的螺旋桨进行计算,设计结果与CFD计算结果如表 1所示,可以看出实际的螺旋桨拉力及效率均小于设计结果,不能满足设计要求。
| 方法 | 拉力/N | 扭矩/(N·m) | 效率/% |
| 设计 | 9.871 | 0.610 | 74.402 |
| CFD | 8.793 | 0.576 | 70.188 |
设计结果与真实情况间的差异最终体现在桨叶各叶素截面的气动力之上,若能够得到较为准确的叶素截面气动力,那么一方面设计的拉力较为准确,另一方面设计更接近最小能量损失,可提高螺旋桨效率。因此,本文提出耦合CFD求解的螺旋桨快速设计方法,该方法的主要思想便是:采用CFD数值模拟对设计进行修正,根据CFD的计算结果反解桨叶截面气动力,之后根据新的气动力重新设计新的螺旋桨。
4.1 给定叶素气动力的螺旋桨设计桨叶各截面采用相同的翼型进行设计时,传统螺旋桨设计方法得到的沿径向各叶素截面最大升阻比对应的气动力如图 6所示。除在桨尖和桨根处存在一定的变化外,沿径向最大升阻比对应的迎角与升力系数变化不大,而桨尖和桨根处本身的环量偏小,对螺旋桨气动力的贡献较低。因此,设计时可视各叶素截面最大升阻比对应的气动力相同,采用固定的迎角α、升力系数CL及阻力系数CD进行设计。
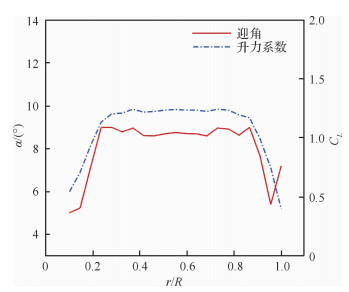
|
| 图 6 迎角及升力系数径向分布 Fig. 6 Radial distribution of angle of attack and lift coefficient |
用固定的迎角、升力系数及阻力系数进行设计时,主要步骤同传统设计方法。首先根据设计拉力T及设计状态求解诱导螺距V′。而在求解r处截面的弦长b及扭转角θ时,由于升力系数CL确定,那么根据式(9)可直接求解弦长,不必进行迭代求解。剩余设计步骤与传统设计方法一致。
4.2 根据CFD结果反解桨叶素气动力假设各叶素截面最大升阻比对应的气动力相同,对于给定设计状态及桨叶几何的螺旋桨,可根据CFD计算得到的拉力及扭矩结果,反解最大升阻比对应的气动力。步骤如下:
1) 将桨叶划分为N个截面,根据设计拉力T及设计状态求解诱导螺距V′,具体步骤同传统设计方法。
2) 求解最大升阻比对应的迎角α。
根据诱导螺距V′,计算得到第i个截面的实际入流角φi,进而根据式(10)求得迎角αi,故取最大升阻比对应的迎角α为
| $ \alpha = \frac{1}{N}\sum\limits_{i = 1}^N {{\alpha _i}} $ | (17) |
3) 已知螺旋桨总拉力T、扭矩M,根据式(12)、式(13),求得满足要求的升力系数CL及阻力系数CD。
4.3 耦合CFD修正的螺旋桨设计方法基于以上方法及分析,提出一种耦合CFD修正的螺旋桨快速设计方法,主要步骤如下:
1) 根据给定的设计状态,采用传统螺旋桨设计方法,计算得到初始螺旋桨几何形状(弦长及扭转角分布)。
2) 由于设计采用的叶素气动力与真实情况存在差异,为保证螺旋桨效率最高,需找到真实情况叶素截面最大升阻比对应的迎角。因此,在初始几何外形的基础上,将桨叶的扭转角整体调整“±θ0”,生成n个螺旋桨外形。接着,采用CFD分别计算其拉力及扭矩,并反解其对应的桨叶叶素气动力。选取升阻比最大的气动力数据。
3) 根据选定的数据,通过给定截面气动力的螺旋桨设计方法,设计新的螺旋桨。
设计流程如图 7所示。
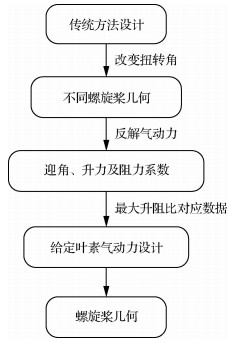
|
| 图 7 螺旋桨快速设计流程 Fig. 7 Rapid design process of propeller |
在图 5所示传统方法求得的螺旋桨基础上,通过整体偏转扭转角,得到5个新的构型,对其分别进行CFD求解,并反解气动力,结果如表 2所示。
| 扭转角/(°) | CFD结果 | 反解得到的气动力 | |||||
| 拉力/N | 扭矩/(N·m) | 迎角/(°) | 升力系数 | 升阻系数 | 升阻比 | ||
| 0 | 8.793 | 0.576 | 8.402 | 1.032 | 0.057 2 | 18.042 | |
| -1 | 8.396 | 0.539 | 7.521 | 0.983 | 0.050 0 | 19.660 | |
| -2 | 7.925 | 0.500 | 6.663 | 0.926 | 0.044 8 | 20.670 | |
| -3 | 7.412 | 0.463 | 5.819 | 0.864 | 0.041 2 | 20.971 | |
| -4 | 6.840 | 0.423 | 4.994 | 0.796 | 0.038 0 | 20.947 | |
选取升阻比最大的数据,迎角α=5.819°,升力系数CL=0.864,阻力系数CD=0.041 2,采用给定叶素气动力的设计方法重新设计。设计结果如图 8所示。
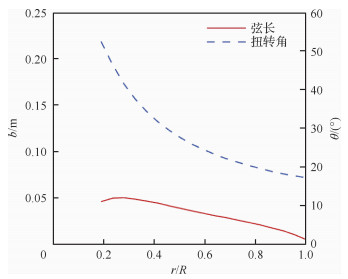
|
| 图 8 新设计方法所得弦长与扭转角分布 Fig. 8 Distribution of chord length and twist angle from new design method |
采用CFD方法计算其气动力,并与传统设计结果进行对比,如表 3所示。在设计点处,本文提出的设计方法,一方面能够较好地满足拉力要求,另一方面相比于传统设计方法,设计得到的螺旋桨效率提高2.75%。在非设计点,大前进比(λ)下设计得到的螺旋桨拉力及效率略小于传统方法设计结果,而前进比小于0.6时,螺旋桨的拉力及效率均优于传统方法设计结果,如图 9所示。验证了设计方法的可行性。
| 设计方法 | 拉力/N | 扭矩/(N·m) | 效率/% |
| 传统方法 | 8.793 | 0.576 | 70.188 |
| 新方法 | 9.756 | 0.622 | 72.116 |

|
| 图 9 传统和新设计方法螺旋桨性能对比 Fig. 9 Comparison of propeller performances between origin and new design methods |
为进一步提高螺旋桨效率,在前文提出方法的基础上,对螺旋桨翼型进行优化。
5.1 优化方法采用“代理优化”[17]方法对螺旋桨翼型进行优化。文中采用的代理优化方法基于“Kriging代理模型”[18],子优化方法采用“遗传算法+乘子法”。遗传算法采用拟二进制交叉、多项式变异、最佳保留策略及联赛选择; 乘子法采用Rockfellar推广的乘子法; 并在优化过程中采用“最小代理模型预测准则[17](Minimum of Prediction, MSP)+改善期望准则[19](Expected Improvement, EI)”两种加点法则更新代理模型。
文献[20]研究表明:Xfoil在低雷诺数下求解精度虽不及采用高级湍流模型的CFD方法,但其本身具有一定的精度。且对于翼型的优化,更关注其相比于原翼型的改进趋势,因此对翼型采用Xfoil快速求解,这也能够节省大量设计时间。而翼型采用“CST参数化方法”[21]。
5.2 优化目标及约束对于上文采用耦合CFD修正设计得到的螺旋桨,选取0.2R、0.5R及0.8R这3个桨叶截面,优化迎角α=5.819°状态下的翼型气动力,对应的雷诺数分别取为50 000、70 000、90 000。
优化目标:平均阻力最小,即Min C′D,且
| $ C_D^\prime = \left( {{C_{D1}} + {C_{D2}} + {C_{D3}}} \right)/3 $ | (18) |
式中:CD1对应第1个状态的阻力系数。这里对阻力进行优化的原因是,低雷诺数下阻力的变化更加剧烈,优化的空间更大。
约束条件:平均升力不减小,C′L≥C′L0,下标0代表基础翼型; 翼型面积不减小,A≥A0; 翼型最大厚度不减小,t≥t0。
5.3 翼型优化结果优化过程收敛曲线如图 10所示。优化前后翼型对比如表 4和图 11所示。优化后的翼型最大厚度和面积略有增加,后缘弯度增大。从图 11中可以看出,优化后翼型前缘上表面的低压降低,后缘下表面的高压增大,因此阻力的降低随之带来翼型升力的提高,这也是采用“升力不减小”而非“升力不变”约束进行翼型优化的原因,图中:Cp为压力系数。

|
| 图 10 优化收敛曲线 Fig. 10 Optimizing convergence curve |
| 翼型 | 平均升力系数 | 平均阻力系数 | 升阻比 |
| 基础翼型 | 0.943 | 0.026 6 | 35.451 |
| 优化翼型 | 0.974 | 0.023 4 | 41.624 |

|
| 图 11 优化前后翼型压力分布对比(Re=50 000) Fig. 11 Comparison of pressure distributions around airfoil before and after optimization (Re=50 000) |
考虑翼型优化的螺旋桨快速设计流程如图 12所示,优化前后翼型外形对比如图 13所示。得到优化翼型后,在耦合CFD修正的设计结果上替代基础翼型,生成新的螺旋桨并进行计算。因为对翼型优化时只限制升力的下限,故会存在升力系数变化的情况,此时得到的拉力则会偏离设计拉力。并且新的翼型应用在桨上后,其叶素截面最大升阻比对应的迎角也无法保证与基础翼型一致。因此,需再次通过改变桨叶扭转角生成不同螺旋桨,根据CFD计算结果进行反解气动力及再设计,从而得到满足设计要求的高效螺旋桨。
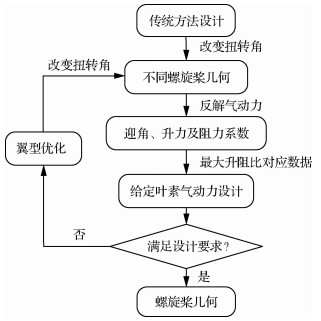
|
| 图 12 考虑翼型优化的螺旋桨快速设计流程 Fig. 12 Propeller rapid design process considering airfoil optimization |

|
| 图 13 优化前后翼型外形对比 Fig. 13 Comparison of airfoil shapes before and after optimization |
反解得到叶素截面最大升阻比对应的最佳气动力特性包括:α=4.565°,CL=0.835,CD=0.036 4。再采用该气动力重新设计,得到如图 14所示结果。

|
| 图 14 优化翼型前后设计结果对比 Fig. 14 Comparison of design results before and after airfoil optimization |
表 5及图 15展示了3种设计方法得到的螺旋桨性能对比。考虑翼型优化的设计方法,能够在满足拉力要求的同时,进一步提高螺旋桨效率。在设计点处,相比于传统方法,效率提高3.95%。
| 设计方法 | 拉力/N | 扭矩/(N·m) | 效率/% |
| 传统方法 | 8.793 | 0.576 | 70.188 |
| 新方法 | 9.756 | 0.622 | 72.116 |
| 新方法+优化翼型 | 9.743 | 0.614 | 72.958 |

|
| 图 15 不同设计方法螺旋桨性能对比 Fig. 15 Comparison of propeller performances among different design methods |
本文根据CFD计算对螺旋桨的设计进行修正,提出一种能够较好满足设计拉力要求的高效螺旋桨设计方法,得到的结论如下:
1) 传统螺旋桨设计方法存在一定缺陷。首先,设计得到的螺旋桨其真实的拉力与目标拉力存在一定偏差; 其次,不能保证真实情况下桨叶叶素截面的升阻比最大,因此不能保证设计螺旋桨的高效率。
2) 将设计与实际情况叶素气动力的差异,以及真实情况下如展向流动、桨叶桨根及桨尖处的三维效应带来的影响,归结于螺旋桨桨叶气动力的改变。提出了根据给定气动力进行螺旋桨设计的方法。假设桨叶叶素截面最大升阻比对应的气动力沿径向不变,通过整体改变螺旋桨扭转角,生成多个螺旋桨构型,再通过CFD计算及反解气动力,可得到升阻比最大的气动力数据。根据该数据进行螺旋桨的再设计,可得到高效率的螺旋桨。
3) 经过实例的对比分析,文中所建耦合CFD求解的螺旋桨设计方法,一方面能够较好地满足设计拉力要求,另一方面相比于传统设计方法,设计得到的螺旋桨效率提高了2.75%。而采用代理优化的方法对螺旋桨翼型进行优化后,相比于传统设计方法螺旋桨的效率可进一步提高3.95%。此外,该方法只需进行少量的CFD计算即可,计算量远小于直接采用数值模拟优化螺旋桨弦长及扭转角分布的方法。
| [1] | LARRABEE E E. Practical design of minimum induced loss propellers[C]//Wichita: Business Aircraft Meeting and Exposition, 1979. |
| [2] | ANGELO S D, BERARDI F, MINISCI E. Aerodynamic performances of propellers with parametric considerations on the optimal design[J]. The Aeronautical Journal, 2002, 106: 1-34. |
| Click to display the text | |
| [3] |
项松, 王吉, 张利国, 等. 一种高效率螺旋桨设计方法[J]. 航空动力学报, 2015, 30(1): 136-141. XIANG S, WANG J, ZHANG L G, et al. A design method for high efficiency propeller[J]. Journal of Aerospace Power, 2015, 30(1): 136-141. (in Chinese) |
| Cited By in Cnki (7) | Click to display the text | |
| [4] |
项松, 佟刚, 吴江, 等. 某型三叶螺旋桨的设计及性能试验[J]. 航空动力学报, 2016, 31(8): 1793-1798. XIANG S, TONG G, WU J, et al. Design and performance test of a kind of three-blade propeller[J]. Journal of Aerospace Power, 2016, 31(8): 1793-1798. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [5] |
翟若岱.太阳能飞机高效率螺旋桨设计关键技术研究[D].沈阳: 沈阳航空航天大学, 2017. ZHAI R D. Research on key technology of high efficiency propeller design for solar powered aircraft[D]. Shenyang: Shenyang Aerospace University, 2017(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [6] |
许建华, 宋文萍, 刘俊.基于NS方程的螺旋桨气动反设计与优化设计方法研究[C]//第十五届全国计算流体力学会议, 2012: 727-731. XU J H, SONG W P, LIU J. Investigation of inverse design and optimization design method for propellers based on Navier-Stokes equations[C]//The 15th National Conference on Computational Fluid Dynamics, 2012: 727-731(in Chinese). |
| [7] |
梁撑刚, 郁新华, 龚军锋. 一种无人机螺旋桨的快速优化设计方法[J]. 航空计算技术, 2017, 47(2): 76-79. LIANG C G, YU X H, GONG J F. A quick approach to optimum design of UAV propeller[J]. Aeronautical Computing Technique, 2017, 47(2): 76-79. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [8] |
焦俊, 宋笔锋, 张玉刚, 等. 高空飞艇螺旋桨优化设计与气动性能车载试验[J]. 航空动力学报, 2017, 23(1): 196-202. JIAO J, SONG B F, ZHANG Y G, et al. Optimal design and truck-mounted testing of aerodynamic performance for the propeller of high altitude airship[J]. Journal of Aerospace Power, 2017, 23(1): 196-202. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [9] |
刘芳, 杜绵银, 岳良明, 等.高空低雷诺数高效螺旋桨设计[C]//第三届中国航空科学技术大会论文集, 2017: 15-21. LIU F, DU M Y, YUE L M, et al. High efficiency propeller design at low-Reynolds number and high-altitude[C]//The 3rd China Aeronautical Science and Technology Conference, 2017: 15-21(in Chinese). |
| [10] | KWON H, YI S, KIM T, et al. Aerodynamic performances of propellers with parametric considerations on the optimal design[C]//31st AIAA Applied Aerodynamics Conference. Reston, VA: AIAA, 2013. |
| [11] | MORGADO J, ABDOLLAHZADEH M, SILVESTRE M A R, et al. High altitude propeller design and analysis[J]. Aerospace Science and Technology, 2015, 45: 398-407. |
| Click to display the text | |
| [12] | YONEZAWA K, ABE K, SUNADA S, et al. Propeller design and loss mechanisms in low-Reynolds-number flows[J]. Journal of Propulsion and Power, 2016, 32(6): 1378-1385. |
| Click to display the text | |
| [13] |
刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006. LIU P Q. Theory and application of airscrew[M]. Beijing: Beihang University Press, 2006. (in Chinese) |
| [14] |
程晓亮, 李杰. 螺旋桨滑流对机翼气动特性影响的方法研究[J]. 科学技术与工程, 2011, 11(14): 3229-3235. CHENG X L, LI J. Unsteady computational method for the propeller/wing interaction[J]. Science Technology and Engineering, 2011, 11(14): 3229-3235. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [15] |
王红波, 祝小平, 周洲, 等. 太阳能无人机螺旋桨滑流气动特性分析[J]. 西北工业大学学报, 2015, 33(6): 910-920. WANG H B, ZHU X P, ZHOU Z, et al. Aerodynamic investigation on propeller slipstream flows for solar powered airplanes[J]. Journal of Northwestern Polytechnical University, 2015, 33(6): 910-920. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [16] |
王科雷, 祝小平, 周洲, 等. 低雷诺数分布式螺旋桨滑流气动影响[J]. 航空学报, 2016, 37(9): 2669-2678. WANG K L, ZHU X P, ZHOU Z, et al. Distributed electric propulsion slipstream aerodynamic effects at low Reynolds number[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2669-2678. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [17] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [18] | SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science, 1989, 4(4): 409-423. |
| Click to display the text | |
| [19] | JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. |
| Click to display the text | |
| [20] | MORGADO J, VIZINHO R, SILVESTRE M A R, et al. XFOIL vs CFD performance predictions for high lift low Reynolds number airfoils[J]. Aerospace Science and Technology, 2016, 52: 207-214. |
| Click to display the text | |
| [21] | KULFAN B M. Universal parametric geometry representation method[J]. Journal of Aircraft, 2008, 45(1): 142-158. |
| Click to display the text |



