全局灵敏度分析可以从输入变量的整个分布范围来衡量输入变量的不确定性对工程设计中所感兴趣的输出性能统计特征的贡献程度[1-2],通常在可靠性分析中,更关注结构是否失效以及输入变量对于结构失效概率的影响程度。为了衡量输入变量对于结构失效概率的影响并对输入变量的重要性进行排序,Cui等[3]提出了可靠性全局灵敏度指标。可靠性全局灵敏度指标定义为某一输入变量固定时,结构的无条件失效概率与条件失效概率的差异在输入变量的整个分布范围内的平均值,该指标反映了输入变量固定时对失效概率的平均影响。与可靠性局部灵敏度指标[4-5]不同,可靠性全局灵敏度指标可以从输入变量的整个不确定性范围来衡量其对于失效概率的平均影响。
本文提出了利用贝叶斯公式转换以及元重要抽样算法[6-7]结合自适应Kriging代理的可靠性全局灵敏度,并组织了求解可靠性全局灵敏度指标的高效算法。基于贝叶斯公式可以将可靠性全局灵敏度指标的原始定义等价表示为输入变量的无条件概率密度函数(Probability Density Fanction, PDF)与条件概率密度函数之间的差异与失效概率的乘积形式,从而避免条件失效概率的求解[8-9]。基于此等价形式,只需要一组样本,便可以得到各输入变量的可靠性全局灵敏度指标。利用贝叶斯算法进行可靠性全局灵敏度分析的研究已有很多,Wang等[8]利用贝叶斯公式,将可靠性全局灵敏度指标的定义式进行了等价转换,并采用蒙特卡罗法来计算可靠性全局灵敏度指标。该方法适用范围虽广,但在计算工程实际中的小失效概率问题时计算量过于庞大。Wang等[9]则结合重要抽样方法来计算可靠性全局灵敏度指标的贝叶斯等价形式。该方法只需一组样本便可以计算得到所有输入变量的可靠性全局灵敏度指标,且计算量独立于输入变量的维数,明显地提高了计算的效率。但是重要抽样方法[10-11]需要构造重要抽样密度函数,一般来说需要将重要抽样密度函数的中心放在设计点处,这就使得该方法依赖于其他方法来寻找设计点,并且重要抽样方法对于多设计点的情况和多失效域的情况并不适用。Yun等[12]基于可靠性全局灵敏度指标的贝叶斯公式转换后的等价形式,利用子集模拟方法[13-16]结合重要抽样的方法进行可靠性全局灵敏度的计算。该方法在利用子集模拟结合重要抽样的方法计算得到无条件失效概率的同时,通过重复利用子集模拟重要抽样方法抽取的样本,并利用Metropolis-Hastings(M-H)[17]准则来实现失效样本的转换,进而估计各输入变量的失效条件概率密度函数。该方法同样只需要一组样本便可计算得到可靠性全局灵敏度指标,且对于小失效概率问题是有效可行的。但该方法抽样过程中所结合的重要抽样方法仍然依赖于设计点的选取,因而该方法依旧很难适用于多设计点和多失效域的情况。
对于实际工程中普遍存在大量复杂的功能函数,自适应Kriging(Adaptive Kriging, AK)代理模型法是处理这类问题的高效算法[18]。可靠性分析中涉及到的自适应Kriging算法有自适应Kriging代理模型结合Monte Carlo模拟(Monte Carlo Simulation, MCS)法(AK-MCS) [19]、自适应Kriging代理模型结合重要抽样(Important Sampling, IS)法(AK-IS) [20]以及元重要抽样算法(Meta-IS)[6-7]等。AK-MCS算法将自适应Kriging代理模型与Monte Carlo模拟法相结合,其首先由输入变量的联合概率密度函数产生MCS备选样本池,然后利用学习函数在备选样本池中逐步挑选对失效面拟合贡献较大的点来更新Kriging模型,最终能够确保Kriging模型能在一定的置信水平下识别样本池内样本的功能函数值的正负号,从而较准确地求得失效概率。但对于工程上常见的小失效概率问题,AK-MCS算法的样本池容量庞大,进而使得代理过程十分耗时。将重要抽样法与自适应Kriging过程相结合形成的AK-IS算法可以大大降低备选样本池的规模,从而提高自适应学习的效率,减少自适应学习过程所消耗的时间。但是对于多设计点及多失效域问题,基于一次二阶矩法构造重要抽样密度函数的AK-IS算法将失效,因而对于多设计点及多失效域的问题需要另寻解决途径。元模型重要抽样算法(Meta-IS)通过元模型构造重要抽样密度函数,进而来抽取重要抽样样本点。该方法在降低AK-MCS样本池规模的同时避免了设计点的求解,适用于多设计点和多失效域问题的可靠性分析。然而,Meta-IS算法在抽取重要抽样样本后仍需要求解重要抽样样本点处真实的功能函数值来估计失效概率,所以该算法仍有较大的计算量。如果在元重要抽样的基础上嵌入自适应Kriging模型,形成Meta-IS-AK算法,则有可能极大程度地提高失效概率求解的效率,本文将采用这种思路求解失效概率,并在此基础上组织可靠性全局灵敏度的算法。
利用可靠性全局灵敏指标的贝叶斯转换形式,只要能求得无条件失效概率和失效域条件下输入变量的概率密度函数即可直接求得可靠性全局灵敏度,而求解无条件失效概率的数字模拟法可以同时完成失效概率的计算以及失效域条件下输入变量概率密度函数的求解,为此本文将Meta-IS与自适应Kriging模型结合起来,以便完成可靠性全局灵敏度的高效求解。本文所组织的Meta-IS-AK算法主要分3步来执行。第1步是由元重要抽样的迭代策略得到逐步逼近最优重要抽样函数的样本点,在迭代收敛后便可以得到第1步的Kriging模型以及相应的重要抽样样本点。第2步是基于重要抽样样本构建自适应Kriging模型,该步的Kriging模型是在第1步得到的Kriging模型的基础上逐步更新得到的,其目的是为了构建能够对第1步中重要抽样样本点失效与否做出准确预测的Kriging模型,从而高效地求解出无条件失效概率。然而Meta-IS-AK算法抽取的失效域内的样本点的密度函数为最优重要抽样密度函数,因而无法直接用于估计输入变量失效域内的条件概率密度函数,为此第3步则对失效域内服从于重要抽样密度函数的样本点进行转换,该转换将利用Metropolis-Hastings准则由重要抽样密度函数的失效样本点来得到原概率密度函数在失效域内的样本点,进而求得各个输入变量在失效域中的条件概率密度函数。
本文主要由以下几部分组成。第1节简要地回顾了已有的利用贝叶斯公式转换的可靠性全局灵敏度的形式,第2节详细介绍了本文所提的计算可靠性全局灵敏度的高效算法。第3节分别给出了数值与工程算例,验证了所提算法的高效性,第4节则得出结论。
1 基于贝叶斯公式的可靠性全局灵敏度指标的转换形式记功能函数为Y=g(X), 对于具有联合概率密度函数fX(x)的n维随机输入变量X=[X1 X2 … Xn],F={X:g(X)≤0}为其失效域,失效概率Pf=P{g(X)≤0}。记输入变量Xi取其实现值时的条件失效概率为Pf|Xi不确定性的消除会对失效概率造成影响,而这种影响可由Pf和Pf|Xi的平均差异来度量。将Xi的可靠性全局灵敏度指标记为δXiPf,其定义为[21-22]
| $ \begin{array}{l} {\rm{ \mathit{ δ} }}_{{X_i}}^{{P_{\rm{f}}}} = {E_{{X_i}}}{\left( {{P_{\rm{f}}} - {P_{{\rm{f}}|{X_i}}}} \right)^2} = \\ \;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {{{\left( {{P_{\rm{f}}} - {P_{\rm{f}}}|{X_i}} \right)}^2}} {f_{{X_i}}}\left( {{x_i}} \right){\rm{d}}{x_i} \end{array} $ | (1) |
利用贝叶斯公式,可将条件失效概率Pf|Xi进行如下转换[8-9, 12, 23-24]:
| $ {P_{{\rm{f}}|{X_i}}} = \frac{{{f_{{X_i}}}\left( {{x_i}\left| F \right.} \right)}}{{{f_{{X_i}}}\left( {{x_i}} \right)}}{P_{\rm{f}}} $ | (2) |
将式(2)代入到式(1)中,即可得到基于贝叶斯公式的可靠性全局灵敏度指标表达式:
| $ \begin{array}{l} {\rm{ \mathit{ δ} }}_{{X_i}}^{{P_{\rm{f}}}} = {E_{{X_i}}}{\left( {{P_{\rm{f}}} - {P_{{\rm{f}}|{X_i}}}} \right)^2} = \\ \;\;\;\;\;\;\;{E_{{X_i}}}{\left( {{P_{\rm{f}}} - \frac{{{f_{{X_i}}}\left( {{x_i}|F} \right)}}{{{f_{{X_i}}}\left( {{x_i}} \right)}}{P_{\rm{f}}}} \right)^2} = \\ \;\;\;\;\;\;\;P_{\rm{f}}^2{E_{{X_i}}}{\left( {\frac{{{f_{{X_i}}}\left( {{x_i}} \right) - {f_{{X_i}}}\left( {{x_i}|F} \right)}}{{{f_{{X_i}}}\left( {{x_i}} \right)}}} \right)^2} \end{array} $ | (3) |
由式(3)可知,通过将Pf|Xi利用贝叶斯公式进行等价转化,输入变量Xi(i=1, 2, …, n)的可靠性全局灵敏度指标δXiPf由无条件失效概率Pf与条件失效概率Pf|Xi平均差异的求解,转换为无条件失效概率Pf与失效条件概率密度函数fXi(xi|F)的求解。式(3)中所有输入变量的条件概率密度函数fXi(xi|F)都可以利用求解Pf时失效域F内的失效样本来同时得到,减少了传统方法中条件失效概率Pf|Xi的计算量。
2 求解可靠性全局灵敏度指标的高效算法由式(3)可知,求解δXiPf的关键是估计失效概率Pf与失效条件概率密度fXi(xi|F),本节将基于元模型重要抽样法来构造可靠性全局灵敏度指标δXiPf的高效算法。
2.1 失效概率Pf的估计由第1节的内容可知,为了求得可靠性全局灵敏度,必须要同时求得失效概率Pf以及失效域条件下输入变量的概率密度函数fXi(xi|F)。文献[6]的Meta-IS算法采用Kriging元模型gK1(x)来近似构造功能函数g(x),并在此基础上构造准最优重要抽样密度函数hqoptX(x)。根据hXqopt(x)抽取得到重要抽样样本点xih(i=1, 2, …, Ncorr)之后(Ncorr表示重要抽样样本点的数量),文献[6]的Meta-IS算法需要计算重要抽样样本点xih(i=1, 2, …, Ncorr)处真实的功能函数值,才能由式(4)求得修正因子αcorr的估计值
| $ {{\hat \alpha }_{{\rm{corr}}}} = \frac{1}{{{N_{{\rm{corr}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{corr}}}}} {\frac{{{I_F}\left( {\mathit{\boldsymbol{x}}_i^h} \right)}}{{\pi \left( {\mathit{\boldsymbol{x}}_i^h} \right)}}} $ | (4) |
式中:IF(·)为失效域指示函数,若重要抽样样本点xih(i=1, 2, …, Ncorr)落入失效域,则IF(xih)=1,否则IF(xih)=0;π(·)为概率密度分类函数,π(xih)表示当前Kriging模型gK1(x)在重要抽样样本点xih(i=1, 2, …, Ncorr)处预测值gK1(xih)≤0的概率。扩展失效概率Pfε由概率分类函数π(x)的数学期望来表达,详细求解过程见文献[6]。
显然,依照式(4)去求解修正因子αcorr需要再调用Ncorr次功能函数,计算量较大。本文则基于近似构造最优重要抽样密度函数的Kriging代理模型gK1(x),在重要抽样样本池Sh={x1h, x2h, …,xNcorrh}内更新gK1(x),使得训练收敛后的代理模型(记为gK2(x))能够正确识别Sh中每个样本点处的功能函数的取值符号,从而准确地预测IFxih(i=1, 2, …, Ncorr)的取值。这种在gK1(x)的基础上重构g(x)的代理模型gK2(x),并使得gK2(x)能够正确识别g(x)在重要抽样样本点xih(i=1, 2, …, Ncorr)处的取值符号的过程可以通过U学习函数轻松实现,并且由于重构gK2(x)所需的功能函数调用次数远小于Ncorr,因此该思路的计算效率将远高于文献[6]的效率。本文求解失效概率的步骤可归纳为
步骤1 以gK1(x)作为gK2(x)的初始模型,即令gK2(x)=gK1(x)。
步骤2 判别gK2(x)的收敛性。由当前Kriging模型gK2(x)计算xih(i=1, 2, …, Ncorr)的U学习函数值u(xih)=
步骤3 计算g(xu),将(xu, g(xu))添加到训练集T中,形成更新的训练集T={T∪(xu, g(xu))}。
步骤4 由T更新gK2(x),并返回步骤2。
步骤5 以收敛的gK2(x)预测Sh中样本点xih(i=1, 2, …, Ncorr)处的IF(xih)的估计值
| $ {{\hat I}_F}\left( {\mathit{\boldsymbol{x}}_i^h} \right) = \left\{ {\begin{array}{*{20}{l}} 0&{{g_{{K_2}}}\left( {\mathit{\boldsymbol{x}}_i^h} \right) > 0}\\ 1&{{g_{{K_2}}}\left( {\mathit{\boldsymbol{x}}_i^h} \right) \le 0} \end{array}} \right. $ | (5) |
| $ {{\hat \alpha }_{{\rm{corr}}}} = \frac{1}{{{N_{{\rm{corr}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{corr}}}}} {\frac{{{I_F}\left( {\mathit{\boldsymbol{x}}_i^h} \right)}}{{{\rm{ \mathit{ π} }}\left( {\mathit{\boldsymbol{x}}_i^h} \right)}}} $ | (6) |
| $ {{\hat P}_{\rm{f}}} = {{\hat P}_{{{\rm{f}}_\varepsilon }}}{{\hat \alpha }_{{\rm{corr}}}} $ | (7) |
为了利用第1节的方法求解可靠性全局灵敏度δXiPf,在2.1节求得失效概率的同时,还必须求得失效域F条件下Xi的概率密度函数fXi(xi|F)。显然fXi(xi|F)的求解必须要有失效域中Xi的分布信息。由2.1节可知,重构gK2(x)可以得到hXqopt(x)的失效域样本,将hXqopt(x)的失效样本记为xFih(i=1, 2, …, NF)(NF为失效样本的个数),则这些失效样本需要转换成fX(x)的失效样本后,才能用于估计fXi(xi|F)。Metropolis-Hastings准则提供了将hXqopt(x)的失效样本转化成fX(x)失效样本的方法,并且这种转换不需要调用功能函数,其转换的过程可归纳为
步骤1 根据Metropolis-Hastings准则[17],取马尔科夫链的初始点z1=xFih。
步骤2 计算下列比值r, 并由r确定下一个马尔可夫链样本
| $ \begin{array}{*{20}{c}} {r\left( {{\mathit{\boldsymbol{z}}_i}, {\mathit{\boldsymbol{z}}_{i + 1}}} \right) = \frac{{{f_\mathit{\boldsymbol{X}}}\left( {\mathit{\boldsymbol{x}}_{{\rm{F}}\left( {i + 1} \right)}^h} \right){h_\mathit{\boldsymbol{X}}}\left( {{\mathit{\boldsymbol{z}}_i}} \right)}}{{{f_\mathit{\boldsymbol{X}}}\left( {{\mathit{\boldsymbol{z}}_i}} \right){h_\mathit{\boldsymbol{X}}}\left( {\mathit{\boldsymbol{x}}_{{\rm{F}}\left( {i + 1} \right)}^h} \right)}}}\\ {i = 1, 2, \cdots , {N_{\rm{F}}} - 1} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{i + 1}} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}_{{\rm{F}}\left( {i + 1} \right)}^h}&{\min \left( {1, r} \right) > u}\\ {{\mathit{\boldsymbol{z}}_i}}&{\min (1, r) \le u} \end{array}} \right.}\\ {i = 1, 2, \cdots , {N_{\rm{F}}} - 1} \end{array} $ | (9) |
式中:u为[0, 1]区间上服从均匀分布的随机数。
步骤3 重复步骤2直到元重要抽样密度hXqopt(x)的失效样本点xFih(i=1, 2, …, NF)全部转化为fX(x)的失效样本zi(i=1, 2, …, NF)。
步骤4 zi(i=1, 2, …, NF)即为近似服从于原始失效条件概率密度函数fX(x|F)的样本xFif=zi(i=1, 2, …, NF),基于xFif就可以采用已有的概率密度函数逼近方法求得fXi(xi|F)。
联合2.1节求得的失效概率估计值
由上述求解可靠性全局灵敏度的过程可知,本文所组织的算法具有以下优点:①通过将元重要抽样与可靠性全局灵敏度的贝叶斯算法相结合,使得求解可靠性全局灵敏度指标的计算量独立于输入变量的维度,且避免了基于传统重要抽样的可靠性全局灵敏度的贝叶斯算法不适用于多设计点多失效域情况的问题。基于等价的贝叶斯形式,可靠性全局灵敏度完全转化成了输出样本的分类问题,进而也使得利用嵌入式代理模型结合数字模拟的方法去求解δXiPf成为可能。②所提方法在元模型重要抽样的基础上进一步在重要抽样样本池中重构功能函数的代理模型,重构所得到的代理模型能够准确地对元重要抽样样本进行分类,提高了失效概率计算的效率。③利用Metropolis-Hastings准则,将准重要抽样密度函数的失效样本转化成原概率密度函数的失效样本,由于转化过程无需调用功能函数,因而提高了可靠性全局灵敏度指标求解的计算效率。综上所述,本文所组织的可靠性全局灵敏度算法是适用于多设计点多失效域问题的一种高效算法。
2.3 Meta-IS-AK算法求解可靠性全局灵敏度指标流程图由2.1和2.2节的内容可给出Meta-IS-AK算法求解可靠性全局灵敏度的流程如图 1所示。

|
| 图 1 Meta-IS-AK算法求解δXiPf的流程图 Fig. 1 Flowchart of estimating δXiPf with Meta-IS-AK algorithm |
为了验证所提算法在求解可靠性全局灵敏度的效率和精度,本节给出了3个算例,分别采用准Monte Carlo算法(QMC)、AK-MCS算法、Meta-IS算法及Meta-IS-AK算法求解可靠性全局灵敏度指标。其中QMC算法结果将作为参照解。
3.1 不连续多失效域算例考虑一个多失效域的算例,其功能函数为
| $ g\left( {{X_1}, {X_2}} \right) = 10 - \sum\limits_{i = 1}^2 {\left[ {X_i^2 - 5\cos \left( {2{\rm{ \mathit{ π} }}{X_i}} \right)} \right]} $ | (10) |
式中:X1与X2都是服从标准正态分布的随机变量。算例3.1的失效边界如图 2所示。从图 2可以看出,该数值算例的失效边界很复杂,属于多失效域的情况。文献[6]提出了失效概率计算的Meta-IS方法,该方法无法直接应用于可靠性全局灵敏度的求解。本文将文献[6]的方法进行了扩展,将其与可靠性全局灵敏度的贝叶斯算法相结合,使得其可以应用于计算可靠性全局灵敏度,本文在算例部分将基于文献[6]发展的算法记作Meta-IS算法。用QMC算法、AK-MCS算法、Meta-IS算法以及Meta-IS-AK算法求得的可靠性全局灵敏度指标如表 1所示。为了进一步说明所提算法计算结果的稳健性,δXiPf估计值的标准差(记为SDi)也在表 1计算结果的上标位置给出,SDi由s次独立的估计值的标准差计算得到,其定义为

|
| 图 2 算例3.1失效边界 Fig. 2 Failure boundary of Example 3.name-style="western" |
| 算法 | X1/10-3 | X2/10-3 | Ncall |
| QMC | 14.5[0.30] | 14.5[0.46] | 1×105 |
| AK-MCS | 14.2[0.23] | 14.1[0.35] | 440 |
| Meta-IS | 14.2[0.41] | 14.0[0.65] | 42+5 000 |
| Meta-IS-AK | 14.2[0.43] | 13.9[0.65] | 42+254 |
| 注:数据右上标为可靠性全局灵敏度指标估计值的标准差, Ncall为功能函数的调用次数。 | |||
| $ {\rm{S}}{{\rm{D}}_i} = \sqrt {\frac{1}{s}\sum\limits_{j = 1}^s {{{\left( {{\rm{ \mathit{\hat δ} }}_{X_i^{\rm{f}}}^{\left( j \right)} - {\rm{ \mathit{\bar δ} }}_{X_i^{\rm{f}}}^{{P_{\rm{f}}}}} \right)}^2}} } $ | (11) |
式中:s为独立计算的次数,本文算例中取s=50;δXiPf为s次独立计算δXiPf的平均值;
Meta-IS-AK算法求解δXiPf时功能函数的调用次数由2部分组成,第1部分是元重要抽样法中构建Kriging模型gK1(x)过程中功能函数的调用次数,第2部分是重要抽样样本结合自适应Kriging算法构建Kriging模型gK2(x)时功能函数的调用次数。由表 1中结果可以看出,Meta-IS-AK算法与QMC算法计算得到的可靠性全局灵敏度指标的结果基本一致,且功能函数的调用次数远远低于QMC算法,相比于AK-MCS算法计算效率也进一步提高。与基于文献[6]发展的Meta-IS算法相比,本文所提的可靠性全局灵敏度求解的Meta-IS-AK算法避免了逐一求解重要抽样样本点处的真实功能函数值,因而计算效率也进一步提高。对于该模型而言,输入变量X1与X2对失效概率的影响基本相等。以上结果说明本文所提的可靠性全局灵敏度分析的Meta-IS-AK算法能够较好地应用于不连续的多失效域情况,体现了该算法较强的适用性。
3.2 钢架结构算例对于一钢架结构,有4个失效模式:
| $ \left\{ \begin{array}{l} {g_1} = 2{M_1} + 2{M_2} - 4.5S\\ {g_2} = 2{M_1} + {M_2} + {M_3} - 4.5S\\ {g_3} = {M_1} + {M_2} + 2{M_3} - 4.5S\\ {g_4} = {M_1} + 2{M_2} + {M_3} - 4.5S \end{array} \right. $ | (12) |
因为是串联系统,所以系统的功能函数g为g=min{g1, g2, g3, g4}。在各个失效模式的功能函数中,Mi(i=1, 2, 3)与S是独立的,均值和标准差分别为: μMi=2(i=1, 2, 3), μS=1, σMi=2(i=1, 2, 3), σS=0.25。各输入变量所对应的可靠性全局灵敏度指标的计算结果如表 2所示。
| 算法 | M1/10-5 | M2/10-5 | M3/10-5 | S/10-5 | Ncall |
| QMC | 1.24[0.5] | 0.57[0.4] | 1.26[0.5] | 143.0[2.6] | 1×106 |
| AK-MCS | 1.26[0.5] | 0.62[0.4] | 1.31[0.5] | 142.5[2.0] | 725 |
| Meta-IS | 1.36[0.3] | 0.65[0.3] | 1.37[0.4] | 140.9[2.4] | 36+2 000 |
| Meta-IS-AK | 1.32[0.3] | 0.60[0.1] | 1.36[0.3] | 140.2[1.9] | 36+297 |
由表 2中结果可以看出,Meta-IS-AK算法得到的计算结果与QMC算法计算所得结果基本一致,且模型的调用次数低于QMC算法与AK-MCS算法以及Meta-IS算法。这说明Meta-IS-AK算法能够很好地适用于多个失效模式的情况。对于此算例,输入变量的重要性排序为S>M3>M1>M2。此外,输入变量S对失效概率的影响较其他输入变量的影响大很多。因此在进行可靠性设计时通过调整输入变量S的不确定性可以更有效地满足可靠性要求。此外,M2对失效概率影响的灵敏度指标较其他的输入变量小很多,因此可以忽略M2的不确定性对于失效概率的影响,可以通过将M2固定在均值处来简化失效概率的求解模型。
3.3 简化的翼盒结构算例(多设计点算例)图 3(a)是简化翼盒模型的示意图。这种翼盒结构由64个杆和42个板组成。64个杆根据它们的方向分为3组,x、y和z方向上杆的长度分别是2L、L和3L。所有杆的截面积均为A,所有板的厚度均为TH,E和P分别是所有板和杆的弹性模量和外部载荷。泊松比为0.3。假设输入变量是独立的正态变量,其分布参数如表 3所示。

|
| 图 3 翼盒结构 Fig. 3 Wing box structure |
| 变量 | 分布 | 均值 | 变异系数 |
| A/m2 | 正态 | 1×10-4 | 0.1 |
| L/m | 正态 | 0.2 | 0.1 |
| E/Pa | 正态 | 7.1×1010 | 0.12 |
| P/N | 正态 | 1 500 | 0.1 |
| TH/m | 正态 | 2.5×10-3 | 0.15 |
由于翼盒结构承担了来自机翼的大部分垂直方向的载荷,其自由端的位移可能相对较大。大的位移可能会引起杆的变形并导致杆或板的破坏,这在飞行过程中是不允许的。因此计算翼盒结构的位移是很有必要的,且位移的计算可以通过有限元分析完成。图 3(b)显示了在ANSYS 14.0中构建的翼盒结构的有限元模型,其中输入变量固定在它们的均值处,此外,翼盒的变形如图 3(c)所示。
本文中,该翼盒的隐式功能函数是根据翼盒的最大位移Dmax不超过临界值构造的(这里临界值等于0.01),其表达式为
| $ g\left( \mathit{\boldsymbol{X}} \right) = 0.01 - \left| {{D_{\max }}} \right| $ | (13) |
式中:Dmax=D(L, A, E, P, TH),是关于输入变量的隐式函数,由有限元分析确定。算例3.3的可靠性全局灵敏度计算结果如图 4所示,计算结果的标准差如表 4所示。
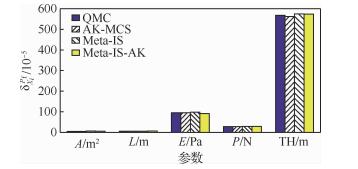
|
| 图 4 算例3.3可靠性全局灵敏度指标的计算结果 Fig. 4 Results of reliability global sensitivity indexfor Example 3. |
| 变量 | SDi/10-5 | |||
| QMC | AK-MCS | Meta-IS | Meta-IS-AK | |
| A/m2 | 0.27 | 0.20 | 0.17 | 0.18 |
| L/m | 0.26 | 0.11 | 0.14 | 0.11 |
| E/Pa | 5.36 | 3.87 | 5.04 | 5.05 |
| P/N | 0.35 | 0.42 | 0.33 | 0.32 |
| TH/m | 8.17 | 8.85 | 6.37 | 6.30 |
| Ncall | 5×105 | 120 | 33+5 000 | 33+59 |
由表 4中的结果可以看出,Meta-IS-AK算法得到的计算结果精度较高且模型的调用次数低于QMC算法与AK-MCS算法以及Meta-IS算法,这说明了Meta-IS-AK算法能够很好地适用于隐式功能函数的情况。对于算例3.3,输入变量的的不确定性对于失效概率影响的重要性排序为TH>E>P>L>A。从图 4的结果可以看出,输入变量TH对失效概率的影响较其他输入变量的影响大很多,因此在进行可靠性设计时调整输入变量TH的不确定性可以更有效地满足可靠性要求。从图 4的结果还可以看出,L和A的不确定性对于失效概率的影响较其他的输入变量小很多,因此忽略L和A的不确定性对于失效概率的影响可以简化失效概率的求解模型。
4 结论1) 可靠性全局灵敏度指标可以有效地衡量输入变量对于结构失效概率的影响。为了高效地计算可靠性全局灵敏度指标,本文提出了可靠性全局灵敏度指标计算的Meta-IS-AK算法。
2) Meta-IS-AK算法在计算可靠性全局灵敏度指标时充分利用了可靠性全局灵敏度指标贝叶斯算法的维度独立性,也使得该指标的求解转化为输出样本的分类问题,这就使可靠性全局灵敏度指标可以通过嵌入式代理模型结合数字模拟法来求解。相比于传统的重要抽样函数,元重要抽样法构造的准最优抽样密度函数能够很好地适用于多设计点和多失效域的情况。在此基础上构造重构的功能函数的代理模型能够准确地对准重要抽样密度函数抽取的样本进行分类,进一步地提高了失效概率的计算效率。M-H准则无需额外调用功能函数便可以将准重要抽样密度函数的失效样本转化成原概率密度函数的失效样本,大大提高了求解输入变量的失效条件概率密度函数的效率。
3) 所提方法能够很好地适用于多设计点和多失效域的情况,也适用于隐函数问题的可靠性灵敏度分析。所提方法的计算效率远远高于QMC算法,同时较AK-MCS算法以及Meta-IS算法也有提高。所给算例充分验证了以上结论。
| [1] |
刘付超, 魏鹏飞, 周长聪, 等. 含旋转铰间隙平面运动机构可靠性灵敏度分析[J]. 航空学报, 2018, 39(11): 422133. LIU F C, WEI P F, ZHOU C C, et al. Time-independent reliability and sensitivity analysis for planar motion mechanisms with revolution joint clearances[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(11): 422133. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [2] |
冯凯旋, 吕震宙, 蒋献. 基于偏导数的全局灵敏度指标的高效求解方法[J]. 航空学报, 2018, 39(3): 221699. FENG K X, LYU Z Z, JIANG X. Efficient algorithm for estimating derivative-based global sensitivity index[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(3): 221699. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [3] | CUI L J, LV Z Z, ZHAO X P. Moment-independent importance measure of basic random variable and its probability density evolution solution[J]. Science China Technological Science, 2010, 53(4): 1138-1145. |
| Click to display the text | |
| [4] | KARAMCHANDANI A, COMELL C A. Sensitivity estimation within first and second-order reliability methods[J]. Structural Safety, 1992, 11: 95-107. |
| Click to display the text | |
| [5] | MELCHERS R E, AHAMMED M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability[J]. Computers and Structures, 2004, 82: 55-61. |
| Click to display the text | |
| [6] | DUBOURG V, SUDRET B, DEHEEGER F. Metamodel-based importance sampling for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2013, 33: 47-57. |
| Click to display the text | |
| [7] | CADINI F, GIOLETTAL A, ZIO E. An improvement of a meta model-based importance sampling algorithm for estimating small failure probabilities[C]//International Conference on Vulnerability and Risk Analysis and Management, 2014: 2104-2114. |
| [8] | WANG Y P, XIAO S N, LV Z Z. An efficient global reliability sensitivity analysis algorithm based on classification of model output and subset simulation[J]. Structural Safety, 2018, 74: 49-57. |
| Click to display the text | |
| [9] | WANG Y P, XIAO S N, LV Z Z. A new efficient simulation method based on Bayes' theorem and importance sampling Markov chain simulation to estimate the failure-probability-based global sensitivity measure[J]. Aerospace Science and Technology, 2018, 79: 364-372. |
| Click to display the text | |
| [10] | MELCHERS R E. Importance sampling in structural system[J]. Structural Safety, 1989, 6: 3-10. |
| Click to display the text | |
| [11] | HARBITZ A. An efficient sampling method for probability of failure calculation[J]. Structural Safety, 1986, 3: 109-115. |
| Click to display the text | |
| [12] | YUN W Y, LV Z Z, JIANG X. An efficient global reliability sensitivity analysis algorithm based on classification of model output and subset simulation[J]. Structural Safety, 2018, 74: 49-57. |
| Click to display the text | |
| [13] | AU S K, BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263-277. |
| Click to display the text | |
| [14] | PAPAIOANNOU I, BETZ W, ZWIRGLMAIER K, et al. MCMC algorithms for subset simulation[J]. Probabilistic Engineering Mechanics, 2015, 41: 89-103. |
| Click to display the text | |
| [15] | ZUEY K M. Subset simulation method for rare event estimation:An introduction[J]. Encyclopedia of Earthquake Engieering, 2014, 3671-3691. |
| [16] | SONG S F, LV Z Z, QIAO H W. Subset simulation for structural reliability sensitivity analysis[J]. Reliability Engineering System Safety, 2009, 94(2): 658-665. |
| Click to display the text | |
| [17] | AU S K. Probabilistic failure analysis by importance sampling Markov chain simulation[J]. Journal of Engineering Mechanics, 2004, 130: 303-311. |
| Click to display the text | |
| [18] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| Cited By in Cnki (110) | Click to display the text | |
| [19] | ECHARD B, GAYTON N, LEMAIRE M. An active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33: 145-154. |
| Click to display the text | |
| [20] | ECHARD B, GAYTON N, LEMAIRE M, et al. A combined importance sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models[J]. Reliability Engineering and System Safety, 2013, 111: 232-240. |
| Click to display the text | |
| [21] | LI L Y, LV Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38: 40-47. |
| Click to display the text | |
| [22] | WEI P F, LV Z Z, HAO W R. Efficient sampling methods for global reliability sensitivity analysis[J]. Computer Physics Communications, 2012, 183: 1728-1743. |
| Click to display the text | |
| [23] | LING C Y, LV Z Z, FENG K X, et al. Efficient numerical simulation methods for estimating fuzzy failure probability based importance measure indices[J]. Structural and Multidisciplinary Optimization, 2019, 59: 577-593. |
| Click to display the text | |
| [24] | XIAO S N, LV Z Z. Structural reliability sensitivity analysis based on classification of model output[J]. Aerospace Science and Technology, 2017, 71: 52-61. |
| Click to display the text |



