感受性问题是研究高超声速边界层转捩过程的关键,精确刻画相对来流参数10-4量级的声波、熵波和涡波扰动经过激波的变化特性对现有的数值模拟是个挑战。实际上准确模拟激波一直是计算流体力学(CFD)的重要研究内容,早期以激波装配法为主[1],自Harten[2]提出TVD格式以来,在超声速流动应用领域激波捕捉法一枝独秀,取得了ENO[3]、WENO[4-9]、CNS[10],WCNS[11]等一系列标志性成果。捕捉法假设激波为空间连续函数,计算必然得到数值解表示的过渡区。这个过渡区对于Euler方程来说不存在,对于Navier-Stokes方程来说常常比理论值大几个数量级(激波厚度仅为几个分子自由程),因此捕捉法面对感受性问题显得力不从心。几乎所有高精度捕捉格式需要构建或选择限制器,通过降阶来实现计算稳定,Zhong等[12-14]使用五阶WENO格式模拟包含有激波的流场,数值结果表明精度很难超过一阶,为此,他们研究感受性时选择了激波装配法。
装配法把激波当作间断处理,将R-H关系式直接嵌入流场内部。从Euler方程出发模拟相当于精确解;对于Navier-Stokes方程来说,激波厚度与飞行器尺度或网格尺度相比小几个数量级,可以忽略,当作间断处理不影响激波上下游参数的精确性。这种理论优势为发展全场一致高精度算法提供了可能。近年来Zhong等[12-14]采用激波装配法研究高超声速边界层转捩的感受性问题的工作受到国内湍流研究专家周恒院士的关注。周恒和张涵信[15]指出“对于复杂激波系,用激波装配法研究扰动通过激波经历的变化是不现实的”。因此,将激波装配法应用于高超声速边界层转捩的感受性问题研究,首先需要解决复杂几何拓扑结构的网格描述问题。
文献[16]回顾了装配法发展历史和综述了最新进展,本文作者刘君等受邀介绍课题组提出的捕捉/装配混合算法(Mixed Capturing and Fitting Solver,MCFS),体现了非结构动网格技术在解决复杂几何拓扑结构激波装配方面的优势。但非结构网格有限体积法很难超过二阶精度,用于感受性模拟精度较低,目前高精度格式主要应用于有限差分法。嵌入激波等间断后流场空间被分割为多个相邻区域,原则上可以应用基于结构网格的多块拼接网格技术,但激波相交点等局部区域网格正交性较差且结构网格变形易于扭结,全部采用结构网格描述较为困难。本文的目的是发展基于非结构网格的有限差分法,解决局部复杂几何形状区域的网格拼接和激波边界附近的网格变形难题。
近年来相关学者采用无网格算法的思想,在非结构网格基础上利用点云拟合局部基函数来构造相应的广义有限差分法(Generalized Finite Difference,GFD)[17-26]。这类方法在连接局部相邻点的时候不需要建立局部的贴体坐标系,而本文的算法是基于曲线贴体坐标下的控制方程,本质上是目前常用的有限差分法的推广,二者构造思路差异明显。关于GFD的研究进展可以参考国内任玉新团队的研究[27],他们在这一领域的研究成果得到了同行认可。
1 离散等价方程及其离散准则在前期结构网格的研究中,通过理论推导得出贴体坐标系下带有源项的离散等价方程是有限差分法控制方程的结论,并且提出相应的离散准则[28-29],这些研究成果是本文研究非结构网格有限差分法的基础,下面进行简单介绍。
考虑笛卡尔坐标系(t, x, y, z)下三维守恒型Euler方程:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial z}} = 0 $ | (1) |
从(t, x, y, z)变换到计算空间(τ, ξ, η, ζ)上,得到含源项的形式:
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\hat H}}}}{{\partial \zeta }} = \\ \;\;\;\;\;\;\;{I_t}\mathit{\boldsymbol{U}} + {I_x}\mathit{\boldsymbol{F}} + {I_y}\mathit{\boldsymbol{G}} + {I_z}\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{S}} \end{array} $ | (2) |
式中:
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ E \end{array}} \right], \;\;\;\;\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {\rho uw}\\ {\left( {E + p} \right)u} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\rho v}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {\rho vw}\\ {\left( {E + p} \right)v} \end{array}} \right], \;\;\;\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\rho w}\\ {\rho uw}\\ {\rho vw}\\ {\rho {w^2} + p}\\ {\left( {E + p} \right)xw} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\hat U}} = \frac{1}{J}\left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ E \end{array}} \right], \;\;\;\mathit{\boldsymbol{\hat F}} = \frac{1}{J}\left[ {\begin{array}{*{20}{c}} {\rho U}\\ {\rho uU + p{\xi _x}}\\ {\rho vU + p{\xi _y}}\\ {\rho wU + p{\xi _z}}\\ {\left( {E + p} \right)U - p{\xi _t}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\hat G}} = \frac{1}{J}\left[ {\begin{array}{*{20}{c}} {\rho V}\\ {\rho uV + p{\eta _x}}\\ {\rho vV + p{\eta _y}}\\ {\rho wV + p{\eta _z}}\\ {\left( {E + p} \right)V - p{\eta _t}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\hat H}} = \frac{1}{J}\left[ {\begin{array}{*{20}{c}} {\rho {W_t}}\\ {\rho uW + p{\zeta _x}}\\ {\rho vW + p{\zeta _y}}\\ {\rho wW + p{\zeta _z}}\\ {\left( {E + p} \right)W - p{\zeta _t}} \end{array}} \right] $ |
E为单位体积流体总能量,即
| $ E = \frac{p}{{\left( {\gamma - 1} \right)\rho }} + \frac{1}{2}\left( {{u^2} + {v^2} + {w^2}} \right) $ |
U、V、W称为逆变速度,即
| $ \left\{ \begin{array}{l} U = {\xi _x}u + {\xi _y}v + {\xi _z}w + {\xi _t}\\ V = {\eta _x}u + {\eta _y}v + {\eta _z}w + {\eta _t}\\ W = {\zeta _x}u + {\zeta _y}v + {\zeta _z}w + {\zeta _t} \end{array} \right. $ |
| $ \begin{array}{l} {I_t} = \frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) + \frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _t}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _t}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _t}}}{J}} \right) = \\ \;\;\;\;\;\;\frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) + \frac{{\partial {{\hat \xi }_t}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_t}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_t}}}{{\partial \zeta }} \end{array} $ |
| $ {I_x} = \frac{{\partial {{\hat \xi }_x}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_x}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_x}}}{{\partial \zeta }} $ |
| $ {I_y} = \frac{{\partial {{\hat \xi }_y}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_y}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_y}}}{{\partial \zeta }} $ |
| $ {I_z} = \frac{{\partial {{\hat \xi }_z}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_z}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_z}}}{{\partial \zeta }} $ |
在坐标变换函数空间导数连续条件下S=0,因此CFD经典教科书给出方程形式:
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\hat H}}}}{{\partial \zeta }} = {\bf{0}} $ | (3) |
实际应用中网格常采用软件生成,
根据离散等价方程的理论推导过程,分析了源项的产生机理,提出了在S≠0条件下离散方程的相容性准则:源项中
考虑本文验证算例是空间二维的,介绍离散算子时采用如下形式更为合适:
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \eta }} = {I_t}\mathit{\boldsymbol{U}} + {I_x}\mathit{\boldsymbol{F}} + {I_y}\mathit{\boldsymbol{G}} = \mathit{\boldsymbol{S}} $ | (4) |
首先,考虑It=0的静止网格,源项中只有空间离散问题。引入符号
| $ \mathit{\boldsymbol{\hat F}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\hat G}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}}{{\partial \xi }}} \right)^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPi} }}}}{{\partial \eta }}} \right)^{\rm{T}}} $ |
采用统一算子δ1离散左右两侧,考虑到通量和变换系数呈线性函数,可得离散形式为
| $ {\delta ^1}\mathit{\boldsymbol{F}} = {\delta ^1}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right)^{\rm{T}}} + \left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right) \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}} $ |
| $ {\delta ^1}\mathit{\boldsymbol{\hat G}} = {\delta ^1}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}}} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPi} }}} \right)^{\rm{T}}} + \left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right) \cdot {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right)^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {\left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPi} }}} \right)^{\rm{T}}} $ |
代入方程(4)得到半离散形式为
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} + \left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right) \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}} + \left( {{\delta ^1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right) \cdot {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}} = {\bf{0}} $ | (5) |
构建双曲型方程算法时,常用通量分裂格式体现扰动沿特征线传播的特性,如AUSM、HLLC、Roe、Vanleer等。由于通量分裂格式中变换系数不一定保持线性关系,很多分裂格式出现(Φ0++Φ0-)·
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} + {\delta ^1}\left( {\mathit{\boldsymbol{\tilde F}}} \right) + {\delta ^1}\left( {\mathit{\boldsymbol{\tilde G}}} \right) = {\bf{0}} $ | (6) |
如果把方程(6)中换成当地系数,就是经典CFD教科书方程(3)的算子形式, 即
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} = - {\delta ^1}\left( {\mathit{\boldsymbol{\tilde F}}} \right) - {\delta ^1}\left( {\mathit{\boldsymbol{\tilde G}}} \right) = {\bf{RHS}} $ | (7) |
通量
对于刚性运动网格,变换行列式J没有变化,由于通量分裂格式包含有
对于变形网格,时间方向导数中离散时要考虑J的变化,按照以上离散准则,如果左侧时间导数采用一阶显式格式,源项中J的导数也要匹配:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial \tau }} = \frac{{\mathit{\boldsymbol{\hat U}}_v^{r + 1} - \mathit{\boldsymbol{\hat U}}_v^n}}{{\Delta \tau }} = \frac{1}{{\Delta \tau }}\left[ {\left( {\frac{\mathit{\boldsymbol{U}}}{J}} \right)_{ij}^{n + 1} - \left( {\frac{\mathit{\boldsymbol{U}}}{J}} \right)_{ij}^n} \right]}\\ {\mathit{\boldsymbol{U}}_{ij}^n\frac{\partial }{{\partial \tau }}{{\left( {\frac{1}{J}} \right)}_{ij}} = \frac{{\mathit{\boldsymbol{U}}_{ij}^n}}{{\Delta \tau }}\left[ {\left( {\frac{1}{J}} \right)_{ij}^{n + 1} - \left( {\frac{1}{J}} \right)_{ij}^n} \right]} \end{array}} \right. $ |
按照CFD领域习惯,RHS表示空间离散格式计算结果,时间一阶显式格式写为
| $ \mathit{\boldsymbol{U}}_{ij}^{n + 1} = \mathit{\boldsymbol{U}}_{ij}^n + \Delta \tau \cdot J_{ij}^{n + 1} \cdot {\bf{RHS}} $ | (8) |
结构网格应用到激波装配法时遇到分区边界运动会引起网格变形问题,在研究几何守恒律的过程中提出以上离散等价方程及其离散准则[28-29],注意到构造出的有限差分格式表达式中仅用到当地几何参数,利用该特点可以建立基于非结构网格的有限差分法和激波装配法。
2 非结构网格有限差分法与GFD思路不同,本文基于离散等价方程,在离散点0上建立局部贴体坐标系,通过关联相邻连线计算
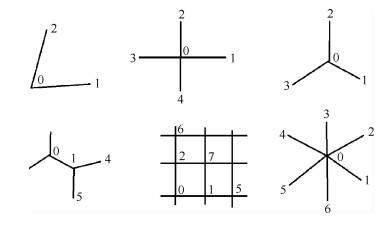
在二维情况下,如果从离散点出发只有2条网格线,对亚声速流动无法应用一阶迎风格式;如果从离散点出发有4条网格线,采用一阶迎风格式离散正合适;如果从离散点出发有4条以上网格线,选择正交性较好的4条线采用一阶迎风格式离散也没有问题。目前还没看到将3条线作为局部曲线坐标的离散算法,这是本文研究重点。
尽管从物理空间(t, x, y)到计算空间(τ, ξ, η)的映射需要点对点的对应关系,但是,变换函数在方程(4)中体现为导数,数值方法计算这些导数只需要相对位置,如图 1所示,1-0-2或1-0-3连成的曲线平移不影响其斜率,因此,把1-0-2映射成计算空间的ξ、把1-0-3映射成η,网格节点位置确定以后,采用中心格式计算如下变换系数的导数不会出现数学奇性:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \xi }_x} = {J^{ - 1}}{\xi _x} = {y_\eta }}\\ {{{\hat \xi }_y} = {J^{ - 1}}{\xi _y} = - {x_\eta }} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \eta }_x} = {J^{ - 1}}{\eta _x} = - {y_\xi }}\\ {{{\hat \eta }_y} = {J^{ - 1}}{\eta _y} = {x_\xi }} \end{array}} \right. $ |
| $ J = \left| {\frac{{\partial \left( {x, y} \right)}}{{\partial \left( {\xi , \eta } \right)}}} \right| = {x_\xi }{y_\eta } - {x_\eta }{y_\xi } $ |

|
| 图 1 三相邻节点的坐标变换对应关系 Fig. 1 Coordinate transformation relationship ofthree adjacent nodes |
代入方程(4)的离散格式计算得到0点计算空间的数值解,记为Û1。在数值实验中发现Û1分布不均匀,明显受到线段方向影响。超声速流场内扰动不会传播到马赫锥外,线段方向和当地速度之间夹角对于迎风格式中正负通量分裂非常重要,在Û1计算中1-0线段用了2次,所起的作用和其他2条不同,定性认为这是导致不均匀的主要原因。为消除线段权重,进行3次计算,除了1-0线段,还选择2-0线段和3-0线段进行双映射,重新计算坐标变换系数及其对应的数值解,并分别记为Û2和Û3,初步假设3条线段权重相等,最后转换到物理空间后0点数值解为
| $ {\mathit{\boldsymbol{U}}_0} = \frac{1}{3}\left( {\frac{{{{\mathit{\boldsymbol{\hat U}}}_1}}}{{{J_1}}} + \frac{{{{\mathit{\boldsymbol{\hat U}}}_2}}}{{{J_2}}} + \frac{{{{\mathit{\boldsymbol{\hat U}}}_3}}}{{{J_3}}}} \right) $ | (9) |
如图 2所示,原则上采用沿着3条网格线方向拓展模板节点来应用高精度格式,从第1点分支到第4、5点,可以构造二阶迎风格式,但此策略又出现选择组合,影响计算效率,无应用价值。计算空间多维的有限差分法格式大多由一维格式直接推广而来,图 2中包含5、6、7点的图形是二维结构网格,构造二阶迎风格式只能沿网格线延展,模板中有第5、6点,没有包含距离更近的第7点,越是高精度格式这种舍近求远的现象更严重,定性分析这是不合理的。本文提出的非结构有限差分法解决了3条网格线基础上构造一阶迎风格式的问题,正在探索如图 2最后一个图所示的在6条网格线基础上构造二阶迎风格式。
|
| 图 2 不同相邻节点数的节点连接关系 Fig. 2 Node connection relationship of differentadjacent nodes number |
本文发展非结构网格有限差分法是为了提高激波装配法的实用性,未来的应用方向主要考虑超声速流动,因此选择如下存在理论解的斜激波和激波相交问题来验证本文算法。
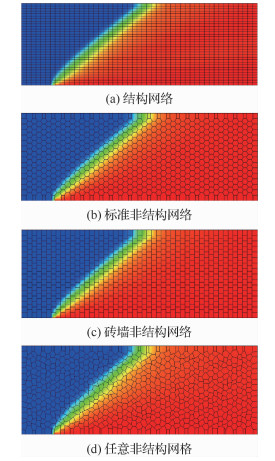
3.1 捕捉法首先计算激波角β=40°的斜激波。图 3(a)是在笛卡尔坐标系下的直角结构网格上数值模拟得到的结果,称之为结构网格算例,作为非结构网格计算结果的标准;图 3(b)中每条线长度相等、夹角相等,构成各向同性的六边形,称之为标准非结构网格;图 3(c)中线段长度相等、夹角不同,其中两条网格线夹角为180°,称之为砖墙非结构网格,考查夹角各向异性影响;图 3(d)网格是在标准非结构网格基础上引入随机误差产生,考查网格质量的影响,称之为任意非结构网格。以上4种网格的节点数均为1 650。图 3中还给出一阶迎风格式计算得到的密度云图,非结构网格有限差分格式能够分辨出流场内激波结构,与结构网格的结果基本相符。
|
| 图 3 斜激波:4种网格密度云图 Fig. 3 Oblique shock wave: density contours offour types of mesh |
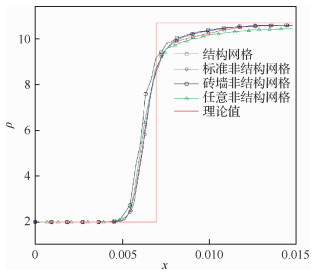
在固定高度y沿着x方向采用Tecplot软件提取的密度ρ分布曲线和理论值如图 4所示,从图中定量比较看,不同非结构网格计算的激波位置和结构网格结果一致,过渡区宽度也较为接近,表明精度接近常规的结构网格有限差分。
|
| 图 4 斜激波:密度随x变化曲线 Fig. 4 Oblique shock wave: curves of densitychange along with x |
各算例的收敛曲线如图 5所示,单调下降,没有出现异常波动,表明从离散等价方程出发的非结构网格离散格式是可以得到收敛解的, 图中t为无量纲时间。

|
| 图 5 斜激波:残差收敛曲线 Fig. 5 Oblique shock wave: convergence curves |
为进一步考查3条网格线的非结构网格有限差分法的算法对网格的适应性和收敛性,选择含有激波相互干扰结构的流场作为数值模拟算例。如图 6所示,两道入射激波激波角为β1=41°和β2=30°,相交以后形成两道激波和一条接触间断,流场分为5个区域,其中,Ⅰ、Ⅲ和Ⅴ区采用正交性较好的伞形网格,可以看出,存在网格线相交的奇性点和网格疏密分布不合理这两个突出的问题,Ⅱ和Ⅳ区采用平行四边形网格,在激波相交和小夹角情况下难以满足正交性要求。因此,很难生成高质量的结构网格。

|
| 图 6 异侧激波相交流场结构网格空间离散 Fig. 6 Flow field spatial discrete of opposite sideshock wave intersection with structural mesh |
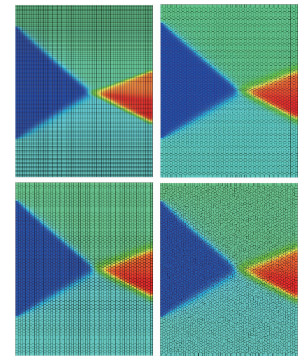
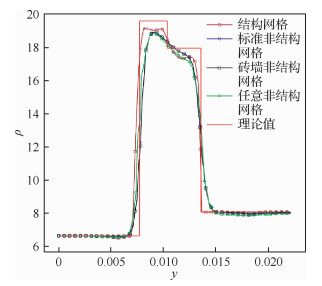
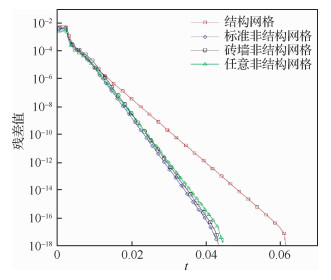
同样采用前面4种形状的网格进行数值模拟计算,网格分布和流场密度云图如图 7所示。图 8为固定位置x处沿着y方向的密度分布及其理论值曲线。从图中可以看出,在不同形状的非结构网格上计算得到的激波位置和过渡区宽度基本一致,仅在下游强激波一侧和常规结构网格有差异,在其他区域非常接近。图 9是各算例的收敛曲线。
|
| 图 7 激波相交:激波捕捉法中4种网格密度云图 Fig. 7 Shock wave intersection: density contoursof four types of mesh |
|
| 图 8 激波相交:密度随y变化曲线 Fig. 8 Shock wave intersection: curves of densitychange along with y |
|
| 图 9 激波相交:残差收敛曲线 Fig. 9 Shock wave intersection: residual convergencecurves |
以上两个算例验证了本文算法的有效性。下面通过装配法展示应用前景。
3.2 装配法按照GFD格式,在考虑网格点运动情况时,模板函数增加了时间变量,处理起来较为困难,本文从离散等价方程出发建立的相容性准则对时间和空间均可使用。在下面计算中按照方程(8)处理变形网格引起的几何守恒律问题。
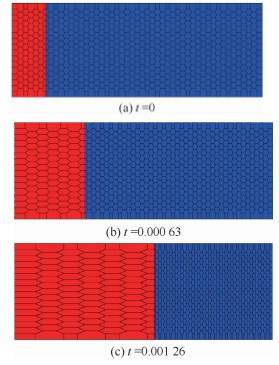
模拟马赫数Mas=3.0的非定常激波在静止大气中运动,初始时刻、无量纲时间t=0.000 63和t=0.001 26的流场如图 10所示,在此基础上将激波后流场换成β=40°的斜激波波后参数,保持下边界的流动参数不变,计算从初始正激波收敛到斜激波的过程,初始时刻、无量纲时间t=0.001 09和充分收敛时间t=0.16的流场如图 11所示。以上两个算例,尽管网格不规则,但是激波阵面保持平稳,运动速度和波后流场参数没有波动,而且和理论值完全相同,这一结果表明本文算法满足几何守恒律,在装配激波引起的网格变形过程中不会产生误差。
|
| 图 10 运动正激波算例 Fig. 10 Moving normal shock wave sample |

|
| 图 11 斜激波算例 Fig. 11 Oblique shock wave sample |
采用激波装配法数值模拟前面的非对称激波相交问题装配法,计算结果如图 12所示,和理论解完全相符。为了考查算法的网格敏感性,针对入射激波角相等(β=40°)的对称流动,在网格中加入随机扰动,计算结果如图 13所示,即使上下网格不对称,计算得到的流场也非常对称,很好地体现出装配法精确刻画激波所产生的效果。

|
| 图 12 非对称激波相交密度云图 Fig. 12 Density contours for asymmetric shock waveintersection |

|
| 图 13 对称激波相交密度云图 Fig. 13 Density contours of symmetric shock waveintersection |
早期的边界激波装配法(Boundary Shock-Fitting Method, BSFM)把激波作为计算区域的边界采用动网格技术进行跟踪,这种算法适合于位置大致确定的钝体扰流的脱体激波。为了模拟复杂内部激波结构和在计算过程中激波发生大变形的情况,Moretti[16]提出了在固定背景网格基础上的浮动激波装配法(Floating Shock-Fitting Method,FSFM),这种算法类似于嵌入边界法(Immersed Boundary Method, IBM),背景网格常用笛卡尔网格,也可以用非结构网格[1, 16]。为了解决多点模板WENO格式应用难题,Zhong等对浮动激波装配法进行改进,提出激波阵面追踪法[12-14](Front-Tracking Shock-Fitting Method, FTSFM),其原理如图 14所示,首先判断激波面和网格的交点Si±k,再将这些点拟合得到激波面曲线,在此基础上建立曲线坐标系采用单侧WENO模板离散激波上下游,例如,x方向激波上游低压区Si处的格式模板涉及A~E点,时间推进到下一时刻(图中虚线),需要重新判断激波位置。

|
| 图 14 激波阵面追踪法 Fig. 14 Front-tracking shock fitting method |
下面通过和Zhong等的激波装配法比较,来说明本文方法的特点:
1) Zhong等的方法基于结构网格,将激波限定在两个网格点之间,两个流动参数只能准确描述一种间断,原则上不能分辨和装配前面算例中激波相交点处存在多个流动参数的情况,在目前也没有看到这种方法在类似问题中应用。本文算法采用非结构网格,不限制网格点连接的线段,理论上可以描述任意Riemann结构,在处理激波相交等复杂几何方面更有优势。
2) 本文算法的格式也是从曲线坐标体系下方程出发离散,沿着激波切向拓展模板,如图 15(a)中黑线所示,沿着激波法向拓展单侧模板,如图 15(b)中绿线所示,和Zhong等的激波阵面追踪法一样,也可以应用高精度格式。本文算法在每个网格点上计算量较大,但由于采用动网格装配跟踪间断,计算中不需要每一步辨识和拟合激波,比Zhong等的方法更适合于并行计算。因此,二者的计算效率还有待于针对具体应用问题的比较。

|
| 图 15 本文算法高精度模板和拼接网格计算 Fig. 15 High order template and stitching meshcomputing of the algorithms in this paper |
3) 直线激波的上下游参数为常数,一阶格式也能计算得到精确解,换言之,对于激波附近的流场,装配法一阶格式的计算结果也比捕捉法任何格式的精度高。激波变弯曲来自于切向参数的非均匀,激波两侧流动参数的法向导数小于切向导数。如图 14所示,Zhong的方法引入当地坐标系的目的是准确表达R-H关系式,WENO格式模板A~E点连成的网格线与激波并没有正交,因此,在格式离散过程中无法区分激波切向和法向。本文基于非结构网格的算法可以保证网格与激波的正交性,这样计算中不同方向采用不同格式,有助于提高计算精度。
根据以上分析,定性分析本文算法在超声速边界层转捩过程的感受性问题研究中的应用策略:
1) 对于头部脱体激波,在现有结构网格基础上先用捕捉法计算,然后采用流场结构辨识算法确定激波大致位置,局部区域采用本文的非结构网格进行激波装配,激波切向直接采用高精度格式、法向可以从一阶格式逐步过渡到高精度格式。
2) 激波前后法向速度间断、切向速度不变,利用这个特性在模拟飞行环境下自由来流扰动时,可以根据声波、熵波和涡波的传播特点进行方向分解,然后精确地施加在激波上游。
3) 对于激波相交等几何拓扑复杂的流场,局部用本文方法来解决相交点的多值问题和激波两侧的网格正交性问题,其他区域采用常规的结构网格有限差分法。
除了高超声速的感受性研究的应用前景,本文算法还有其他用处。如图 15(b)所示,对应用多块拼接网格和加密网格常遇到的相邻区域网格节点不对应的情况,目前的算法只能作为特殊边界处理。前面的砖墙非结构网格已演示,本文算法可以采用与内点统一的计算格式。
5 结束语本文研究是在周恒院士的文章[15]启发下开展的,基于离散等价方程及其离散准则提出一种新的非结构网格有限差分格式构造算法。从算例演示来看,能够解决激波装配法遇到复杂波系时引起的几何拓扑难题,通过对节点引入扰动,证明了本方法的稳定性和对畸形网格处理的有效性,基本上实现了预期目标,为开展高超声速边界层转捩过程的感受性研究打下基础。
| [1] | MORETTI G. Thirty-six years of shock fitting[J]. Computers & Fluids, 2002, 31: 719-723. |
| Click to display the text | |
| [2] | HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49(3): 357-393. |
| Click to display the text | |
| [3] | HARTEN A, ENGQUIST B, OSHER S, et al. Uniformly high order accurate essentially non-oscillatory schemes Ⅲ[M]. Berlin Heidelber: Springer, 1987: 231-303. |
| [4] | SHI J, HU C, SHU C W. A technique of treating negative weights in WENO schemes[J]. Journal of Computational Physics, 2002, 175(1): 108-127. |
| Click to display the text | |
| [5] | LEVY D, PUPPO G, RUSSO G. On the behavior of the total variation in CWENO methods for conservation laws[J]. Applied Numerical Mathematics, 2000, 33(1): 407-414. |
| Click to display the text | |
| [6] | QIU J, SHU C W. On the construction, comparison, and local characteristic decomposition for high-order central WENO schemes[J]. Journal of Computational Physics, 2002, 183(1): 187-209. |
| Click to display the text | |
| [7] | WANG Z J, CHEN R F. Optimized weighted essentially nonoscillatory schemes for linear waves with discontinuity[J]. Journal of Computational Physics, 2001, 174(1): 381-404. |
| Click to display the text | |
| [8] |
宗文刚, 邓小刚, 张涵信. 双重加权实质无波动激波捕捉格式[J]. 空气动力学学报, 2003, 21(2): 218-225. ZONG W G, DENG X G, ZHANG H X. Double weighted essentially non-oscillatory shock-capturing schemes[J]. Acta Aerodynamica Sinica, 2003, 21(2): 218-225. (in Chinese) |
| Cited By in Cnki (25) | Click to display the text | |
| [9] |
沈孟育, 李海东, 刘秋生. 用解析离散法构造WENO-FCT格式[J]. 空气动力学学报, 1998, 16(1): 56-63. SHEN M Y, LI H D, LIU Q S. Analytic discrete WENO-FCT scheme[J]. Acta Aerodynamica Sinica, 1998, 16(1): 56-63. (in Chinese) |
| Cited By in Cnki (16) | Click to display the text | |
| [10] | DENG X G, MAEKAWA H. Compact high-order accurate nonlinear schemes[J]. Journal of Computational Physics, 1997, 130: 77-91. |
| Click to display the text | |
| [11] | DENG X G, MAO M. Weighted compact high-order nonlinear schemes for the Euler equations[C]//Computational Fluid Dynamics Conference, 2006. |
| [12] | ZHONG X L. High-order finite-difference schemes for numerical simulation of hypersonic boundary-layer transition[J]. Journal of Computational Physics, 1998, 144(2): 662-709. |
| Click to display the text | |
| [13] | PRADEEP S R, ZHONG X L. High-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions[J]. Journal of Computational Physics, 2010, 229(19): 6744-6780. |
| Click to display the text | |
| [14] | ZHONG X L, WANG X W. Direct numerical simulation on the receptivity, instability, andtransition of hypersonic boundary layers[J]. Annual Review of Fluid Mechanics, 2012, 44(1): 527-561. |
| Click to display the text | |
| [15] |
周恒, 张涵信. 有关近空间高超声速飞行器边界层转捩和湍流的两个问题[J]. 空气动力学学报, 2017, 35(2): 151-155. ZHOU H, ZHANG H X. Two problems in the transition and turbulence for near space hypersonic flying vehicles[J]. Acta Aerodynamica Sinica, 2017, 35(2): 151-155. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] | MARCELLO O, RENATO P. Shock-fitting:Classical technique, recent developments, and memoirs of Gino Moretti[M]. Springer, 2017. |
| [17] | CHUNG K C. A generalized finite-difference method for heat transfer problems of irregular geometries[J]. Numerical Heat Transfer, 1981, 4: 345-357. |
| Click to display the text | |
| [18] | BATINA J T. A gridless Euler/Navier-Stokes solution algorithm for complex-aircraft applications: AIAA-1993-0333[R]. Reston, VA: AIAA, 1993. |
| [19] | RAINALD L, CARLOS S, EUGENIO O, et al. A finite point method for compressible flow[J]. International Journal for Numerical Methods in Engineering, 2002, 53: 1765-1779. |
| Click to display the text | |
| [20] | SRIDAR D, BALAKRISHNAN N. An upwind finite difference scheme for meshless solvers[J]. Journal of Computational Physics, 2003, 189: 1-29. |
| Click to display the text | |
| [21] | DING H, SHU C, YEO K S. Development of least-square-based two-dimensional finite difference schemes and their application to simulate natural convection in a cavity[J]. Computers & Fluids, 2004, 33: 137-154. |
| Click to display the text | |
| [22] | SHU C, DING H, CHEN H Q, et al. An upwind local RBF-DQ method for simulation of inviscid compressible flows[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194: 2001-2017. |
| Click to display the text | |
| [23] | TOTA P, WANG Z J. Meshfree Euler solver using local radial basis functions for inviscid compressible flows: AIAA-2007-4581[R]. Reston, VA: AIAA, 2007. |
| [24] | KATZ A, JAMENSON A. A comparison of various meshless schemes within a unified algorithm: AIAA-2009-0596[R]. Reston, VA: AIAA, 2009. |
| [25] | SU X R, YAMAMOTO S, NAKAHASHI K. Analysis of a meshless solver for high Reynolds number flow[J]. Journal of Computational Physics, 2013, 72: 505-527. |
| Click to display the text | |
| [26] | SUNDAR D S, YEO K S. A high order meshless method with compact support[J]. Journal of Computational Physics, 2014, 272: 70-87. |
| Click to display the text | |
| [27] | XUE L L, YU X R, W L. Construction of the high order accurate generalized finite difference schemes for inviscid compressible flows[J]. Computers & Fluids, 2019, 25(2): 481-507. |
| [28] |
刘君, 韩芳, 夏冰. 有限差分法中几何守恒律的机理及算法[J]. 空气动力学学报, 2018, 36(6): 918-926. LIU J, HAN F, XIA B. Mechanism and algorithm for geometric conservation law in finite difference method[J]. Acta Aerodynamica Sinica, 2018, 36(6): 918-926. (in Chinese) |
| Cited By in Cnki | |
| [29] |
刘君, 韩芳. 有限差分法中的贴体坐标变换[J]. 气体物理, 2019(5): 18-29. LIU J, HAN F. Body-fitted coordinate transformation for finite difference method[J]. Physics of Gases, 2019(5): 18-29. (in Chinese) |
| Cited By in Cnki |



