在民用航空飞行活动中,航空器的监视主要通过陆基一次雷达、二次雷达及广播式自动相关监视系统实现[1]。受监视地面站部署位置的限制,传统的陆基监视系统无法实现陆地偏远地区、海洋及地球南北两极的航空器监视覆盖,据统计目前地球表面近71%的空域没有实现监视覆盖[2]。2014年MH370航班失联事件以后,为解决全球范围内航空器的可靠持续监视问题,国际民航组织(ICAO)提出了星基监视的概念[3-4],通过将ADS-B接收机部署于低轨道卫星中,并利用多颗低轨道卫星形成覆盖全球的星基ADS-B系统。与传统的陆基监视系统相比,星基ADS-B系统具有覆盖范围广、不受地理环境限制、可满足航空器持续监视等多方面的优势[5]。然而,星基ADS-B系统存在严重的共信道干扰,共信道干扰导致ADS-B消息产生冲突,最终导致星基ADS-B系统获取的航空器位置报告更新间隔的增大,这将限制星基ADS-B系统在航空器监视领域的应用[6]。因此定量给出共信道干扰对星基ADS-B系统监视性能的影响及规律具有重要的意义。
围绕着星基ADS-B系统国内外研究现状如下,在星基ADS-B监视技术可行性方面,为验证星基ADS-B监视技术的可行性,文献[7-10]研制了星基ADS-B试验设备,并发射低轨道试验卫星,实现了ADS-B信号的接收,验证了星基ADS-B监视技术的可行性。
在星基ADS-B系统方案方面,Aireon公司提出了基于“铱星”的星基监视方案[11],该方案通过在“铱星”中搭载ADS-B接收机,从而形成一个覆盖全球的星基ADS-B系统,文献[12]基于“铱星”开展了航空器的监视实验;此外,美国Globalstar公司提出了ADS-B链路增强方案[13]。
在ADS-B系统安全方面,为提高系统的安全性,文献[14]提出一种ADS-B消息的广播认证方法;文献[15]提出了一种基于到达时间差/到达时间和的ADS-B系统防欺骗方法;文献[16]基于深度学习seq2seq模型,提出ADS-B系统异常数据检测方法。
在星基ADS-B系统监视性能评估方面,为研究共信道干扰对星基ADS-B系统监视性能的影响,文献[17]提出了星基ADS-B共信道干扰模型,并仿真研究了共信道干扰对星基ADS-B航空器位置报告更新间隔的影响;此外文献[18-19]也通过仿真方法开展了相似的研究;仿真方法的优点是构建模型与实际系统较接近,然而该方法难以定量给出共信道干扰对位置报告更新间隔的影响;文献[20]基于简化共信道干扰模型,分析给出了星基ADS-B接收机的监视容量计算方法,但该研究存在以下不足,首先,该文献使用的共信道干扰模型较简单,没有考虑A/C模式及S模式信号对ADS-B信号干扰的影响;其次没有考虑星间链路丢帧率及星地链路误码率对位置报告更新间隔的影响。
针对文献[17-20]存在问题和不足,本文提出了共信道干扰环境下星基ADS-B系统的监视容量的计算方法。首先给出星基ADS-B系统模型,然后分析给出各类消息到达速率及概率、消息正确接收概率、位置消息更新间隔、位置报告更新间隔的计算公式,以此为基础得到了95%位置报告的更新间隔及星基ADS-B系统监视容量的计算公式,最后通过仿真验证了理论结果的正确性。本文存在两个方面创新:①定量给出共信道干扰对星基ADS-B系统95%位置报告更新间隔的影响;②定量给出了星基ADS-B系统监视容量的计算方法。
1 星基ADS-B系统及模型 1.1 星基ADS-B系统图 1为星基ADS-B系统的示意图。星基ADS-B系统由机载ADS-B发射机、星基ADS-B接收机、星基ADS-B地面站及ADS-B应用子系统组成。在航空器飞行过程中,机载ADS-B发射机从导航系统获取航空器的状态信息,并周期性产生ADS-B消息(Message),最后ADS-B消息经脉冲位置调制(PPM)后上变频到1 090 MHz,并以随机突发的方式广播发射;位于低轨道卫星的星基ADS-B接收机正确解调ADS-B消息后,通过星间链路和星地链路将消息传输至星基ADS-B地面站;最后,星基ADS-B地面站完成位置消息的解码,并将航空器位置信息及其他相关信息一起封装到ASTERIX CAT 021报告(Report),并通过地面网络分发给ADS-B应用子系统。

|
| 图 1 星基ADS-B系统示意图 Fig. 1 Satellite-based ADS-B system |
由于1 090 MHz频率被多个航空器监视系统共享使用,因此1 090 MHz频率存在多种类型的射频信号,例如A/C模式应答信号、S模式应答信号及ADS-B信号等。对于星基ADS-B接收机而言,A/C模式应答信号、S模式应答信号及ADS-B信号构成了共信道干扰。
参考文献[17]给出的ADS-B接收机共信道干扰模型,假设星基ADS-B接收机覆盖空域内航空器总数为N,则装载A/C模式应答机的航空器数量为NA=γAN,其中γA为装载A/C模式应答机航空器数占总航空器数的比例;装载S模式应答机的航空器数为NS=γSN,其中γS为装载S模式应答机航空器数占总航空器数的比例,且γA+γS=1;装载ADS-B发射机的航空器数为NB=γBNS,其中γB为装载ADS-B发射机航空器数占S模式航空器数的比例。最后,假设各个航空器发送消息是统计独立的,且各类发射机以随机突发方式发射消息,因此覆盖空域内所有发射机与星基ADS-B接收机一起构成了ALOHA系统[6, 19]。
2 星基ADS-B系统监视性能分析首先给出各类消息到达星基ADS-B接收机的速率及概率,随后分析给出ADS-B消息正确接收概率及位置消息的更新间隔,进一步给出星基ADS-B地面站输入位置消息的更新间隔及输出位置报告的更新间隔,最后给出星基ADS-B系统的监视容量。
2.1 消息到达速率与概率星基ADS-B接收机覆盖空域内,ADS-B消息到达星基ADS-B接收机的速率λB为
| $ {\lambda _{\rm{B}}} = {N_{\rm{B}}}{v_{\rm{B}}}{\alpha _{\rm{B}}} $ | (1) |
式中:λB的单位为消息数/s;vB为航空器发送ADS-B消息的速率;αB为ADS-B消息由航空器顶部天线发出的比例。
同理,S模式消息到达星基ADS-B接收机的速率λS为
| $ {\lambda _{\rm{S}}} = {N_{\rm{S}}}{v_{\rm{S}}}{\alpha _{\rm{S}}} $ | (2) |
式中:λS单位为消息数/s;vS为航空器发送S模式消息的速率;αS为S模式消息从航空器顶部天线发出的比例。
A/C模式消息到达星基ADS-B接收机的速率λA为
| $ {\lambda _{\rm{A}}} = {N_{\rm{A}}}{v_{\rm{A}}}{\alpha _{\rm{A}}} $ | (3) |
式中:λA的单位为消息数/s;vA为单架航空器发送A/C模式消息的速率,单位为消息数/(s·架);αA为A/C模式消息由航空器顶部天线发出的比例。
假设单位时间内各类消息到达星基ADS-B接收机的数量服从泊松分布[6, 18-19],对于ADS-B消息,时间间隔t内有k个ADS-B消息到达星基ADS-B接收机的概率为[21]
| $ {P_{\rm{B}}}(k,t) = \frac{{{{\left( {{\lambda _{\rm{B}}}t} \right)}^k}}}{{k!}}{{\rm{e}}^{ - {\lambda _{\rm{B}}}t}} $ | (4) |
对于S模式消息,时间间隔t内有k个S模式消息到达星基ADS-B接收机的概率为
| $ {P_{\rm{S}}}(k,t) = \frac{{{{\left( {{\lambda _S}t} \right)}^k}}}{{k!}}{{\rm{e}}^{ - {\lambda _{\rm{S}}}t}} $ | (5) |
对于A/C模式消息,时间间隔t内有k个A/C模式消息到达星基ADS-B接收机的概率为
| $ {P_{\rm{A}}}(k,t) = \frac{{{{\left( {{\lambda _{\rm{A}}}t} \right)}^k}}}{{k!}}{{\rm{e}}^{ - {\lambda _{\rm{A}}}t}} $ | (6) |
为便于计算ADS-B消息正确接收概率,引入A代表ADS-B消息被正确接收的事件,B0代表ADS-B消息与其他消息不冲突的事件,B1代表ADS-B消息与其他一个消息冲突的事件,B2代表ADS-B消息与其他2个消息冲突的事件,B3代表ADS-B消息与其他3个消息冲突的事件,B4代表ADS-B消息与其他4个及以上消息冲突的事件,由于Bi∩Bj=Ø(i≠j; i, j=0, 1, 2, 3, 4),且
| $ {P_{\rm{u}}} = P(A) = \sum\limits_{i = 0}^4 P \left( {A|{B_i}} \right)P\left( {{B_i}} \right) $ | (7) |
式中:P(A|Bi)为ADS-B消息与其他i个消息冲突情况下,ADS-B消息被正确接收的概率,P(Bi)为ADS-B消息与其他i个消息冲突的概率。利用附录A的推导知道
| $ P\left( {A|{B_i}} \right)P\left( {{B_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}}}&{i = 0}\\ {0.89{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right){{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}}}&{i = 1}\\ {0.64{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}\frac{{{{\left[ {{\lambda _{\rm{A}}} \cdot \left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^2}}}{2}{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}}}&{i = 2}\\ {0.52{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}\frac{{{{\left[ {{\lambda _{\rm{A}}} \cdot \left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^3}}}{6}{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}}}&{i = 3}\\ 0&{i{\rm{ }} = {\rm{ }}4} \end{array}} \right. $ | (8) |
式中:Pe, u为航空器-卫星链路的误码率;n为ADS-B消息包含码元的数目;τB、τS与τA分别代表ADS-B消息、S模式消息与A/C模式消息的长度。
将式(8)代入式(7)得到
| $ \begin{array}{l} {P_{\rm{u}}} = {\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)^n}\left\{ {1 + 0.89{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right) + } \right.\\ \;\;\;\;\left. {\frac{{0.64}}{2}{{\left[ {{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^2} + \frac{{0.52}}{6}{{\left[ {{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^3}} \right\} \cdot \\ \;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (9) |
文献[18, 22]表明,航空器从底部天线发射信号经过地球表面反射到达星基ADS-B接收机的信号强度低于接收机的接收灵敏度,因此仅需考虑航空器从顶部天线发射的信号,此时参数αA=0,则式(9)最终化简为
| $ \begin{array}{l} {P_{\rm{u}}} = {\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)^n}{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \approx \\ \;\;\;\;\;\;\;\left( {1 - n{P_{{\rm{e}},{\rm{u}}}}} \right){{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} = \\ \;\;\;\;\;\;\;\left( {1 - n{P_{{\rm{e}},{\rm{u}}}}} \right) \cdot \\ \;\;\;\;\;\;\;{{\rm{e}}^{ - \left[ {{\gamma _{\rm{B}}}{\gamma _{\rm{S}}}{v_{\rm{B}}}{\alpha _{\rm{B}}}2{\tau _{\rm{B}}} + {\gamma _{\rm{S}}}{v_{\rm{S}}}{\alpha _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\gamma _{\rm{A}}}{v_{\rm{A}}}{\alpha _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]N}} \end{array} $ | (10) |
式(10)表明:在相关参数给定情况下,星基ADS-B消息正确接收概率决定于星基ADS-B接收机覆盖空域内航空器的数量N及航空器-卫星链路的误码率Pe, u。
2.3 星基ADS-B接收机位置消息的更新间隔机载ADS-B发射机发射的ADS-B消息包括:位置消息、速度消息、标识消息及状态消息等,其中位置消息包含航空器的经纬度信息,利用位置消息可实现航空器的监视,位置消息的更新间隔对航空器监视性能有重要影响,下面分析给出星基ADS-B接收机位置消息的更新间隔。
为便于分析,假设某航空器从顶部天线发出的初始位置消息的发送时刻为t0,随后从顶部天线发出的第I个位置消息的发送时刻t0+
将星基ADS-B接收机连续两次正确接收该航空器位置消息的时间间隔定义为星基ADS-B接收机位置消息的更新间隔,记为ΔT,ΔT取值为一个随机变量,其可能的取值及相应概率为[20]
| $ \Delta T = \left\{ {\begin{array}{*{20}{l}} {{T_1}}&{\;\;\;\;\;{P_{\rm{u}}}}\\ {{T_1} + {T_2}}&{\left( {1 - {P_{\rm{u}}}} \right){P_{\rm{u}}}}\\ {\; \vdots }&{}\\ {\sum\limits_{i = 1}^I {{T_i}} }&{{{\left( {1 - {P_{\rm{u}}}} \right)}^{I - 1}}{P_{\rm{u}}}}\\ {\; \vdots }&{} \end{array}} \right. $ | (11) |
式中:Pu为星基ADS-B接收机正确接收消息的概率,由式(10)给出;表达式右侧条件项代表相应概率。
2.4 星基ADS-B地面站输入位置消息的更新间隔星基ADS-B接收机输出的消息经过h跳(h=1, 2, …, H)星间链路的传输,然后再通过星-地链路传输到星基ADS-B地面站。假设单跳星间链路传输迟延为τ,单跳星间链路的丢帧率为Pf,考察星间链路传输的最不利情况,星基ADS-B接收机输出的消息需要经过H跳链路传输,此时星间链路总传输延迟为tISL(H)=Hτ,星间链路总丢帧率[23]为
| $ {P_{\rm{f}}}\left( H \right) = 1 - {\left( {1 - {P_{\rm{f}}}} \right)^H} \approx H{P_{\rm{f}}} $ | (12) |
另外,假设星-地链路传输迟延为td(在问题考察期间内,参数td可视为常量),星-地链路的误码率记为Pe, d,则星-地链路传输的消息被ADS-B地面站正确接收的概率为
| $ {P_{\rm{d}}} = {\left( {1 - {P_{{\rm{e}},{\rm{d}}}}} \right)^n} \approx 1 - n{P_{{\rm{e}},{\rm{d}}}} $ | (13) |
假设ADS-B接收机t0+tu时刻发送的位置消息已被ADS-B地面站在t0+tu+tISL(H)+td时刻正确接收,由于星间链路存在丢帧及星-地链路传输存在差错,因此ADS-B地面站随后正确接收位置消息的时刻可能为t0+
| $ \Delta {T_{{\rm{In}}}} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{T_1}}&{\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}}}\\ {{T_1} + {T_2}}&{{P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \left[ {1 - {P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}\\ {{T_1} + {T_2} + {T_3}}&{{P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot {{\left[ {1 - {P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^2}}\\ {\; \vdots }&{}\\ {\sum\limits_{i = 1}^I {{T_i}} }&{{P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot {{\left[ {1 - {P_{\rm{u}}}\left( {1 - H \cdot {P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{I - 1}}} \end{array}\\ \; \vdots \end{array} \right. $ | (14) |
假设航空器从顶部天线发出位置消息的发送间隔{Ti, i=1, 2, …}已给定,则地面站输入位置消息更新间隔的条件均值为
| $ \begin{array}{*{20}{c}} {E\left[ {\Delta {T_{{\rm{In}}}}|{T_i},i = 1,2, \cdots } \right] = {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot }\\ {\sum\limits_{i = 1}^\infty {\left\{ {{{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}\sum\limits_{j = 1}^i {{T_j}} } \right\}} } \end{array} $ | (15) |
考虑到{Ti, i=1, 2, …}是统计独立的,航空器平均每秒发出2个ADS-B位置消息,且从顶部和底部天线交替发送[24-25],则E[Ti]=Tpos=1 s,Tpos代表航空器从顶部天线发送位置消息的平均发送周期。进一步对式(15)中的{Ti, i=1, 2, …}进行统计平均可得到地面站输入位置消息更新间隔的均值为
| $ \begin{array}{l} \Delta {{\bar T}_{{\rm{ln}}}} = {E_{{T_i}}}\left\{ {E\left[ {\Delta {T_{{\rm{ln}}}}|{T_i},i = 1,2, \cdots } \right]} \right\} = \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\sum\limits_{i = 1}^\infty {\left\{ {{{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}i{T_{{\rm{pos}}}}} \right\}} \end{array} $ | (16) |
利用附录B的推导,ΔTIn化简为
| $ \Delta {{\bar T}_{{\rm{In}}}} = \frac{{{T_{{\rm{pos}}}}}}{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}} $ | (17) |
由式(17)可得到星基ADS-B地面站输入位置消息的平均到达速率为
| $ {{\bar \lambda }_{{\rm{In}}}} = \frac{1}{{\Delta {{\bar T}_{{\rm{In}}}}}} = \frac{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}}{{{T_{{\rm{pos}}}}}} $ | (18) |
考虑到星基ADS-B地面站输入的位置消息数是服从泊松分布的随机变量,因此位置消息的更新间隔服从1/λIn的指数分布[26],其概率密度函数表示为
| $ f(t) = {{\bar \lambda }_{{\rm{ln}}}}{{\rm{e}}^{ - {{\bar \lambda }_{{\rm{ln}}}t}}}\;\;\;\;t > 0 $ | (19) |
星基ADS-B地面站的主要任务是接收ADS-B消息,并根据位置消息完成航空器经纬度坐标的解码,最后将航空器经纬度坐标信息及其他信息一起封装到ASTERIX CAT021格式的报告(report)中,并分发给ADS-B应用子系统。为保证ADS-B系统输出航空器监视信息的时效性,ICAO对ADS-B系统的输出位置报告的更新间隔有明确的要求。影响星基ADS-B地面站输出位置报告更新间隔的因素有两个方面:星基ADS-B地面站的工作模式及位置消息的解码方法。
由ADS-B地面站技术规范[27]知:ADS-B地面站将ADS-B消息封装为CAT021报告时,通常采用数据驱动模式(Data Driven Mode),即星基ADS-B地面站收到位置消息,并成功解算出航空器经纬度坐标后,就输出一个CAT021格式的报告,由于该报告包含有航空器的经纬度坐标,因此该报告也称为位置报告(Position Report)。参考技术规范[24],ADS-B地面站有两种位置消息的解码方法:全球CPR解码与本地CPR解码。如果星基ADS-B地面站预先知晓航空器参考点的经纬度坐标(注:航空器参考点的经纬度坐标可通过全球CPR解码方法获得),则该航空器随后位置消息的解码可采用本地CPR方法进行,此时星基ADS-B地面站每收到航空器的一个位置消息,就可成功解码出航空器的一个经纬度坐标。
综合以上两个方面因素,并进一步假设星基ADS-B地面站解码及封装CAT021报告的时延为恒定值,则可认为星基ADS-B地面站输出位置报告的更新间隔ΔTOutput与输入位置消息的更新间隔ΔTIn是完全一致,即
| $ \Delta {T_{{\rm{Output }}}} = \Delta {T_{{\rm{In}}}} $ | (20) |
此外,星基ADS-B地面站输出位置报告更新间隔的概率密度函数与式(19)具有相同的形式。
2.6 95%位置报告的更新间隔为保证ADS-B系统所提供监视信息的时效性,ICAO相关技术规范对ADS-B地面站输出位置报告的更新间隔有严格的要求,例如在无雷达覆盖航路区域,空中交通管制系统要求位置报告的更新间隔以95%概率小于8 s[28-29],因此下面针对式(20)定义给出星基ADS-B地面站95%位置报告的更新间隔ΔT95%:
| $ P\left( {\Delta {T_{{\rm{Output }}}} \le \Delta {T_{95\% }}} \right) = 95\% $ | (21) |
假设95%位置报告更新间隔ΔT95%取值为
| $ J = \frac{{\ln 0.05}}{{\ln \left( {1 - {P_{\rm{u}}}{P_{\rm{d}}}} \right)}} $ | (22) |
考虑到ΔT95%=
| $ \Delta {T_{95\% }} = E\left[ {\sum\limits_{j = 1}^J {{T_j}} } \right] = JE\left[ {{T_i}} \right] = J{T_{{\rm{pos}}}} $ | (23) |
将式(10)、式(13)及式(22)代入式(23),可得到
| $ \Delta {T_{95\% }} = \frac{{\ln \;0.05}}{{\ln \left[ {1 - {{\rm{e}}^{ - \left[ {{\gamma _{\rm{B}}}{\gamma _{\rm{S}}}{v_{\rm{B}}}{\alpha _{\rm{B}}}2{\tau _{\rm{B}}} + {\gamma _{\rm{S}}}{v_{\rm{S}}}{\alpha _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\gamma _{\rm{A}}}{v_{\rm{A}}}{\alpha _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]N}}{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{{\left( {1 - {P_{{\rm{e}},{\rm{d}}}}} \right)}^n}} \right]}} \cdot {T_{{\rm{pos}}}} $ | (24) |
参考共信道干扰模型[17]及技术规范[24],相关参数取值如下:vA=60消息数/s, vS=6消息数/s, vB=6.2消息数/s, τA=21 μs, τS=64 μs, τB=120 μs, γA=0.1, γS=0.9,γB=0.3,αA=0,αS=0.5,αB=0.5,n=112, Tpos=1 s,式(24)最终化简为
| $ \begin{array}{l} \Delta {T_{95\% }} \approx \\ \frac{{\ln \;0.05}}{{\ln \left[ {1 - {{\rm{e}}^{ - 697.68 \times {{10}^{ - 6}} \times N}}\left( {1 - 112{P_{{\rm{e}},{\rm{u}}}}} \right)\left( {1 - 112{P_{{\rm{e}},{\rm{d}}}}} \right)} \right]}} \end{array} $ | (25) |
式(25)表明:星基ADS-B地面站输出95%位置报告的更新间隔由星基ADS-B接收机覆盖空域内航空器数量N,航空器-卫星链路误码率Pe, u及星-地链路误码率Pe, d联合确定。
此外,利用星基ADS-B地面站输出位置报告更新间隔的概率密度函数也可以计算得到95%位置报告的更新间隔ΔT95%
| $ \Delta {T_{95\% }} \approx - \frac{{\ln 0.05}}{{{P_{\rm{u}}}{P_{\rm{d}}}}}{T_{{\rm{pos}}}} $ | (26) |
式(23)的近似结果与式(26)完全一致。
2.7 星基ADS-B接收机监视容量及系统监视容量对式(24)进行变换,可得到航空器数量N与95%位置报告更新间隔ΔT95%的关系为
| $ \begin{array}{l} N = \\ \frac{{\ln \left[ {{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{{\left( {1 - {P_{{\rm{e}},{\rm{d}}}}} \right)}^n}} \right] - \ln \left( {1 - {{0.05}^{\frac{{{T_{{\rm{pos}}}}}}{{\Delta {T_{95\% }}}}}}} \right)}}{{{\gamma _{\rm{B}}}{\gamma _{\rm{S}}}{v_{\rm{B}}}{\alpha _{\rm{B}}}2{\tau _{\rm{B}}} + {\gamma _{\rm{S}}}{v_{\rm{S}}}{\alpha _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\gamma _{\rm{A}}}{v_{\rm{A}}}{\alpha _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)}} \end{array} $ | (27) |
如果ADS-B应用子系统要求的95%位置报告更新间隔ΔT95%取值为ΔTreq,则星基ADS-B接收机可提供满足ADS-B应用子系统服务要求的航空器的数量定义为星基ADS-B接收机的监视容量。根据以上定义,星基ADS-B接收机的监视容量为
| $ \begin{array}{l} {C_{\rm{s}}} = \\ \frac{{\ln \left[ {{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{{\left( {1 - {P_{{\rm{e}},{\rm{d}}}}} \right)}^n}} \right] - \ln \left( {1 - {{0.05}^{\frac{{{T_{{\rm{pos}}}}}}{{\Delta {T_{{\rm{req}}}}}}}}} \right)}}{{{\gamma _{\rm{B}}}{\gamma _{\rm{S}}}{v_{\rm{B}}}{\alpha _{\rm{B}}}2{\tau _{\rm{B}}} + {\gamma _{\rm{S}}}{v_{\rm{S}}}{\alpha _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\gamma _{\rm{A}}}{v_{\rm{A}}}{\alpha _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)}} \end{array} $ | (28) |
参考共信道干扰模型及相关参数取值,式(28)最终化简为
| $ \begin{array}{l} {C_{\rm{s}}} \approx 1433 \times \\ \;\;\;\;\;\left\{ {\ln \left[ {\left( {1 - 112{P_{{\rm{e}},{\rm{u}}}}} \right)\left( {1 - 112{P_{{\rm{e}},{\rm{d}}}}} \right)} \right]} \right. - \\ \;\;\;\;\;\left. {\ln \left( {1 - {{0.05}^{1/\Delta {T_{{\rm{req}}}}}}} \right)} \right\} \end{array} $ | (29) |
式(29)表明:星基ADS-B接收机的监视容量由ADS-B应用子系统所要求的95%位置报告更新间隔ΔTreq、航空器-卫星链路误码率Pe, u及星-地链路误码率Pe, d联合决定。
假设星基ADS-B系统的所有卫星均使用单通道ADS-B接收机,则根据式(29)可得到星基ADS-B系统的监视容量为
| $ C = {M_{\rm{s}}}{C_{\rm{s}}} $ | (30) |
式中:Ms为星基ADS-B系统的卫星数量。式(29)与式(30)相比,星基ADS-B接收机的监视容量使用更灵活,因此以下仅使用星基ADS-B接收机的监视容量。
3 仿真结果 3.1 仿真环境及仿真参数设置为验证理论分析结果的正确性,基于空间网络仿真系统(Space Network Simulation, SNS)构建星基ADS-B仿真系统。SNS系统是北京航空航天大学CNS/ATM实验室研制的一套离散时间仿真系统,与目前主流网络仿真软件相比,该仿真系统具有开发灵活、代码可重用性、可移植性高等特点[30]。所构建的星基ADS-B仿真系统包括航空器节点、卫星节点、星基ADS-B地面站节点组成。仿真系统的主要技术参数如表 1所示。
图 2为星基ADS-B接收机消息正确接收概率与航空器数量的关系曲线,其中,横坐标代表航空器数量,纵坐标代表星基ADS-B接收机消息正确接收概率。
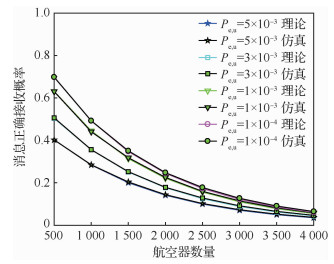
|
| 图 2 消息正确接收概率与航空器数量的关系曲线(Pe, d=1×10-4) Fig. 2 Correct reception probability of message versus aircraft counts(Pe, d=1×10-4) |
曲线比较表明:①仿真结果与理论结果完全一致,验证理论公式(10)的正确性;②航空器-卫星链路误码率对星基ADS-B接收机消息正确接收概率影响较大,当链路误码率为5×10-3时,航空器数量为500架时,消息正确接收概率约为0.402,当链路误码率降低至1×10-4时,消息正确接收概率则提升至0.698;③航空器数量对消息正确接收概率影响较大,随着航空器数量的增加,消息正确接收概率迅速降低,当航空器数量超过3 500架,消息正确接收概率低于0.1。
3.3 95%位置报告更新间隔图 3(a)为位置报告更新间隔的直方图和概率密度函数(Probability Density Function,PDF)曲线。其中,直方图是根据星基ADS-B地面站输出位置报告更新间隔数据统计得到;实线是根据式(19)绘制的理论概率密度曲线;虚线是基于星基ADS-B地面站输出位置报告更新间隔数据估计得到的概率密度曲线。曲线比较表明:理论结果与仿真结果完全一致,验证了式(19)的正确性。
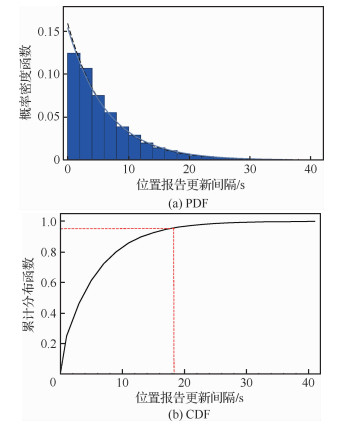
|
| 图 3 位置报告更新间隔的概率密度函数及累积分布函数曲线(Pe, u=1×10-3,Pe, d=1×10-4,N=2 500) Fig. 3 PDF and CDF of position report update interval(Pe, u=1×10-3, Pe, d=1×10-4, N=2 500) |
图 3(b)为位置报告更新间隔累积分布函数(Cumulative Distribution Function, CDF)曲线。从图 3(b)可观察到95%位置报告更新间隔近似取值为18.3 s,该结果与式(25)理论计算的结果一致,验证了理论结果的正确性。
图 4为星基ADS-B系统的95%位置报告更新间隔与航空器数量关系曲线,其中,横坐标代表航空器数量,纵坐标代表 95%位置报告更新间隔。

|
| 图 4 95%位置报告更新间隔与航空器数量的关系曲线(Pe, d=1×10-4) Fig. 4 95% update interval of position report versus aircraft counts(Pe, d=1×10-4) |
曲线比较表明:①仿真结果与理论结果一致,验证了理论公式(24)的正确性;②航空器-卫星链路误码率对95%位置报告更新间隔的影响较大,链路误码率为1×10-3时,4 000架航空器的95%位置报告更新间隔为53.7 s,而当链路误码率增加为5×10-3时,4 000架航空器的95%位置报告更新间隔提高到85.03 s;③航空器数量对95%位置报告更新间隔影响较大,随着航空器数量增加,95%位置报告更新间隔增大,航空器-卫星链路误码率为5×10-3,航空器数量为2 000架时,95%位置报告更新间隔为19.9 s;而当航空器增加到3 500架时,95%位置报告更新间隔显著提高到59.54 s。
图 5给出了95%位置报告更新间隔ΔT95%与N和Pe, d的关系曲面,其中,X轴代表航空器数量,Y轴代表星-地链路误码率,Z轴代表 95%位置报告更新间隔。

|
| 图 5 95%位置报告更新间隔ΔT95%与N和Pe, d的关系图(Pe, u=1×10-3) Fig. 5 95% update interval of position report versus aircraft counts and SER of satellite-earth link (Pe, u=1×10-3) |
由图 5可看出:①当星-地链路误码率给定情况下,95%位置报告更新间隔随航空器数量的增加而显著增大;②当航空器数量给定情况下,星-地链路误码率对95%位置报告更新间隔影响不大;总之,两个影响因素相比,航空器的数量对95%位置报告更新间隔的影响更明显。
图 6给出了95%位置报告更新间隔ΔT95%与N和Pe, u的关系曲面,其中,X轴代表航空器数量,Y轴代表航空器-卫星链路误码率,Z轴代表 95%位置报告更新间隔。

|
| 图 6 95%位置报告更新间隔ΔT95%与N和Pe, u的关系图(Pe, d=1×10-4) Fig. 6 95% update interval of position report versus aircraft counts and SER of aircraft-satellite link (Pe, d=1×10-4) |
由图 6可看出:①当航空器-卫星链路误码率给定情况下,95%位置报告更新间隔随航空器数量的增加而显著增大;②当航空器数量给定情况下,95%位置报告更新间隔随航空器-卫星链路误码率的增大而显著增大;③两种影响因素中,航空器数量及航空器-卫星链路误码率对95%位置报告更新间隔均有明显影响。
3.4 星基ADS-B接收机的监视容量图 7给出了星基ADS-B接收机监视容量与要求的位置报告更新间隔的关系曲线,其中,横坐标代表要求的位置报告更新间隔,纵坐标代表星基ADS-B接收机的监视容量。曲线比较表明:①仿真结果与理论结果完全一致,验证了理论公式(28)的正确性;②航空器-卫星链路误码率对监视容量的影响显著,当误码率为5×10-3时,要求的位置报告更新间隔为8 s时,监视容量为847架,当误码率下降至1×10-4时,监视容量则提高到1 635架;③监视容量与要求的位置报告更新间隔呈现近似线性关系,要求的位置报告更新间隔每减小1 s,监视容量减少138架左右。
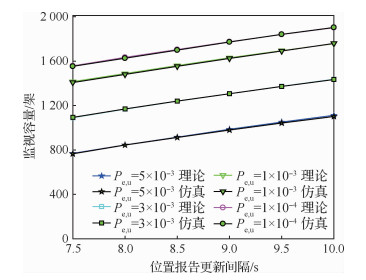
|
| 图 7 星基ADS-B接收机监视容量与位置报告更新间隔的关系曲线(Pe, d=1×10-4) Fig. 7 Surveillance capacity of satellite receiver versus update interval of position report (Pe, d=1× 10-4) |
图 8给出了监视容量Cs与Pe, u和Pe, d的关系曲面,其中,X轴代表航空器-卫星链路误码率,Y轴代表星-地链路误码率,Z轴代表监视容量。

|
| 图 8 监视容量C与Pe, u和Pe, d的关系图(ΔTreq=8 s) Fig. 8 Surveillance capacity versus SER of aircraft-satellite link and SER of satellite-earth link (ΔTreq=8 s) |
由图 8可看出:①当给定航空器-卫星链路误码率时,监视容量随星-地链路误码率的增大几乎保持不变;②当星-地链路误码率给定时,监视容量随航空器-卫星链路误码率的增大而显著减小;③相对于星-地链路误码率,航空器-卫星链路误码率对监视容量的影响程度更明显。
表 2给出了要求的位置报告更新间隔为ΔTreq=8 s,Pe, d=1×10-4时,不同航空器-卫星链路误码率情况下,星基ADS-B接收机的监视容量。
| 误码率(Pe, u) | 5×10-3 | 3×10-3 | 1×10-3 | 1×10-4 |
| 监视容量/架 | 847 | 1 169 | 1 491 | 1 635 |
由表 2可观测到:误码率为Pe, u=1×10-4时,星基ADS-B接收机可为1 635架航空器提供监视服务,误码率为Pe, u=1×10-3时,监视容量为1 491架,当链路误码率为Pe, u=5×10-3时,监视容量为847架。
4 结论为澄清星基ADS-B系统共信道干扰对系统监视性能的影响,提出了星基ADS-B系统监视容量的计算方法。研究结论如下:
1) 星基ADS-B系统的监视容量由ADS-B应用子系统所要求的95%位置报告更新间隔、航空器-卫星链路误码率、星-地链路误码率及卫星数量联合决定。
2) 当ADS-B应用子系统所要求的95%位置报告更新间隔给定后,降低航空器-卫星链路误码率可提高星基ADS-B系统的监视容量。
附录A:式(8)的推导假设航空器-卫星链路的误码率为Pe, u,ADS-B消息包含码元的数目为n,则ADS-B消息与其他消息不冲突情况下,ADS-B消息被正确接收的概率为
| $ P\left( {A|{B_0}} \right) = {\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)^n} $ | (A1) |
下面分析给出ADS-B消息与其他消息不冲突事件B0的概率P(B0),为便于分析,将ADS-B消息与其他ADS-B消息不冲突的事件记为B01,将ADS-B消息与S模式消息不冲突的事件记为B02,将ADS-B消息与A/C模式消息不冲突的事件记为B03,另外ADS-B消息、S模式消息与A/C模式消息的长度分别记为τB、τS与τA。假设某时刻一个ADS-B消息已到达星基ADS-B接收机,如果该时刻前τB和后τB的2τB时间内无其他ADS-B消息到达,则意味着该ADS-B消息与其他ADS-B消息不冲突,其概率为
| $ P\left( {{B_{01}}} \right) = {P_{\rm{B}}}\left( {0,2{\tau _{\rm{B}}}} \right) = {{\rm{e}}^{ - {\lambda _{\rm{B}}}2{\tau _{\rm{B}}}}} $ | (A2) |
同理,ADS-B消息与S模式消息不冲突的概率为
| $ P\left( {{B_{02}}} \right) = {P_{\rm{S}}}\left( {0,{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) = {{\rm{e}}^{ - {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right)}} $ | (A3) |
ADS-B消息与A/C模式消息不冲突的概率为
| $ P\left( {{B_{03}}} \right) = {P_{\rm{A}}}\left( {0,{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right) = {{\rm{e}}^{ - {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)}} $ | (A4) |
根据式(A2)、式(A3)与式(A4)可进一步得到ADS-B消息与其他消息都不冲突的概率为
| $ \begin{array}{l} P\left( {{B_0}} \right) = P\left( {{B_{01}} \cap {B_{02}} \cap {B_{03}}} \right) = \\ \;\;\;\;\;\;\;P\left( {{B_{01}}} \right)P\left( {{B_{02}}} \right)P\left( {{B_{03}}} \right) = \\ \;\;\;\;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (A5) |
综合式(A1)与式(A5)可得到ADS-B消息与其他消息不冲突且ADS-B消息被正确接收的概率为
| $ \begin{array}{l} P\left( {A|{B_0}} \right)P\left( {{B_0}} \right) = {\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)^n} \cdot \\ \;\;\;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (A6) |
下面计算ADS-B消息与其他一个消息冲突且ADS-B消息被正确接收概率P(A|B1)P(B1),根据概率乘法公式得
| $ P\left( {A|{B_1}} \right)P\left( {{B_1}} \right) = P\left( {{B_1}|A} \right)P(A) $ | (A7) |
为便于计算,进一步引入B11代表ADS-B消息与一个ADS-B消息冲突的事件,B12代表ADS-B消息与一个S模式消息冲突的事件,B13代表ADS-B消息与一个A/C模式消息冲突的事件,则B1=B11∪B12∪B13,且B11、B12与B13为两两互不相容的事件,将B1代入式(A7)后得
| $ \begin{array}{l} P\left( {A|{B_1}} \right)P\left( {{B_1}} \right) = \\ \;\;\;\;\;\;P\left( {{B_{11}} \cup {B_{12}} \cup {B_{13}}|A} \right)P(A) \end{array} $ | (A8) |
随后利用条件概率的可列可加性及概率乘法公式,式(A8)化简为
| $ \begin{array}{l} P\left( {A|{B_1}} \right)P\left( {{B_1}} \right) = \left[ {P\left( {{B_{11}}|A} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {P\left( {{B_{12}}|A} \right) + P\left( {{B_{13}}|A} \right)} \right]P(A) = \\ \;\;\;\;\;\;\;P\left( {A|{B_{11}}} \right)P\left( {{B_{11}}} \right) + P\left( {A|{B_{12}}} \right)P\left( {{B_{12}}} \right) + \\ \;\;\;\;\;\;\;P\left( {A|{B_{13}}} \right)P\left( {{B_{13}}} \right) \end{array} $ | (A9) |
根据ADS-B相关技术规范[24]及文献[17, 32],知道P(A|B11)=P(A|B12)=0,P(A|B13)=0.89(1-Pe, u)n,下面分析事件B13的概率。
假设某时刻一个ADS-B消息已到达星基ADS-B接收机,则该时刻前τA和后τB的(τA+τB)时间内仅有一个A/C模式消息到达,且该时刻前τB和后τB的2τB时间内无ADS-B消息到达,该时刻前τS和后τB的(τS+τB)时间内无S模式消息到达的概率为
| $ \begin{array}{l} P\left( {{B_{13}}} \right) = {P_{\rm{A}}}\left( {1,{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right){P_{\rm{B}}}\left( {0,2{\tau _{\rm{B}}}} \right) \cdot \\ \;\;\;\;\;\;{P_{\rm{S}}}\left( {0,{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) = {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right) \cdot \\ \;\;\;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (A10) |
结合式(A10)及相关计算的结果,式(A9)化简为
| $ \begin{array}{*{20}{c}} {P\left( {A|{B_1}} \right)P\left( {{B_1}} \right) = 0.89{{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)}^n}{\lambda _{\rm{A}}} \cdot }\\ {\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right){{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}}} \end{array} $ | (A11) |
采用相同的方法,ADS-B消息与其他2个消息冲突且ADS-B消息被正确接收的概率为
| $ \begin{array}{l} P\left( {A|{B_2}} \right)P\left( {{B_2}} \right) = \\ \;\;\;\;\;0.64{\left( {1 - {P_{{\rm{e}}.{\rm{u}}}}} \right)^n}\frac{{{{\left[ {{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^2}}}{2}\\ \;\;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (A12) |
ADS-B消息与其他3个消息冲突且ADS-B消息被正确接收的概率为
| $ \begin{array}{l} P\left( {A|{B_3}} \right)P\left( {{B_3}} \right) = \\ \;\;\;\;\;\;0.52{\left( {1 - {P_{{\rm{e}},{\rm{u}}}}} \right)^n} \cdot \frac{{{{\left[ {{\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}^3}}}{6} \cdot \\ \;\;\;\;\;\;{{\rm{e}}^{ - \left[ {{\lambda _{\rm{B}}}2{\tau _{\rm{B}}} + {\lambda _{\rm{S}}}\left( {{\tau _{\rm{S}}} + {\tau _{\rm{B}}}} \right) + {\lambda _{\rm{A}}}\left( {{\tau _{\rm{A}}} + {\tau _{\rm{B}}}} \right)} \right]}} \end{array} $ | (A13) |
ADS-B消息与其他4个及以上消息冲突且ADS-B消息被正确接收的概率为
| $ P\left( {A|{B_4}} \right)P\left( {{B_4}} \right) = 0 $ | (A14) |
| $ \begin{array}{l} \Delta {{\bar T}_{{\rm{ln}}}} = {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\;\sum\limits_{i = 1}^\infty {\left\{ {{{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}i{T_{{\rm{pos}}}}} \right\}} = \\ \;\;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\;\sum\limits_{i = 1}^I {\left\{ {{{\left[ {1 - {P_u}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}i{T_{{\rm{pos}}}}} \right\}} + \\ \;\;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\sum\limits_{i = I + 1}^\infty {\left\{ {{{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}i{T_{{\rm{pos}}}}} \right\}} \end{array} $ | (B1) |
当I充分大时,Pu(1-HPf)Pd·
| $ \begin{array}{l} \Delta {{\bar T}_{{\rm{ln}}}} \approx {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\;\sum\limits_{i = 1}^I {\left\{ {{{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]}^{i - 1}}i{T_{{\rm{pos}}}}} \right\}} = \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}{T_{{\rm{pos}}}} + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right] \cdot 2{T_{{\rm{pos}}}} + \cdots + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^{{\rm{I}} - 1}}I{T_{{\rm{pos}}}} \end{array} $ | (B2) |
式(B2)两边同乘因子[1-Pu(1-HPf)Pd]得到
| $ \begin{array}{l} \left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]\Delta {{\bar T}_{{\rm{In}}}} = \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]{T_{{\rm{pos}}}} + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^2}2{T_{{\rm{pos}}}} + \cdots + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^{I - 1}}(I - 1){T_{{\rm{pos}}}} + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^I}I{T_{{\rm{pos}}}} \end{array} $ | (B3) |
式(B2)与式(B3)错位相减后得到
| $ \begin{array}{l} {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}\Delta {{\bar T}_{{\rm{In}}}} = \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}{T_{{\rm{pos}}}} + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]{T_{{\rm{pos}}}} + \cdots + \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^{I - 1}}{T_{{\rm{pos}}}} - \\ \;\;\;\;\;{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^I}I{T_{{\rm{pos}}}} \end{array} $ | (B4) |
对式(B4)进行整理后表示
| $ \begin{array}{l} \Delta {{\bar T}_{{\rm{ln}}}} = \frac{{1 - {\Delta _1}\Delta _2^I}}{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}} \cdot {T_{{\rm{pos}}}} = \\ \;\;\;\;\;\;\;\;\;\frac{{{T_{{\rm{pos}}}}}}{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}} - \\ \;\;\;\;\;\;\;\;\;\frac{{{\Delta _1}\Delta _2^I}}{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}} \cdot {T_{{\rm{pos}}}} \end{array} $ | (B5) |
式中:Δ1=1+IPu(1-H·Pf)Pd; Δ2=1-Pu(1-H·Pf)Pd。
当I→∞时,输入位置消息更新间隔的均值简化为
| $ \Delta {{\bar T}_{{\rm{ln}}}} = \frac{{{T_{{\rm{pos}}}}}}{{{P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}}} $ | (B6) |
| $ \begin{array}{l} P\left( {\Delta {T_{{\rm{output}}}} \le \Delta {T_{95\% }}} \right) = P\left( {\Delta {T_{{\rm{ln}}}} \le \Delta {T_{95\% }}} \right) = \\ \;\;\;\;\;\;P\left( {\Delta {T_{{\rm{In}}}} \le \sum\limits_{j = 1}^J {{T_j}} } \right) = {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} + \\ \;\;\;\;\;\; \cdots + {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}} \cdot \\ \;\;\;\;\;\;{\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^{J - 1}} = \\ \;\;\;\;\;\;1 - {\left[ {1 - {P_{\rm{u}}}\left( {1 - H{P_{\rm{f}}}} \right){P_{\rm{d}}}} \right]^J} = \\ \;\;\;\;\;\;1 - {\left( {1 - {P_{\rm{u}}}{P_{\rm{d}}} + {P_{\rm{u}}}H{P_{\rm{f}}}{P_{\rm{d}}}} \right)^j} \end{array} $ | (C1) |
式中:由于Pf=10-3[23],考虑PuHPfPd远小于1-PuPd,因此1-PuPd+Pu·HPfPd≈1-PuPd。式(C1)化简为
| $ P\left( {\Delta {T_{{\rm{ln}}}} \le \Delta {T_{95\% }}} \right) \approx 1 - {\left( {1 - {P_{\rm{u}}}{P_{\rm{d}}}} \right)^j} $ | (C2) |
进一步考虑到
| $ P\left( {\Delta {T_{{\rm{Output }}}} \le \Delta {T_{95\% }}} \right) = 0.95 $ | (C3) |
式(C3)整理后得到
| $ J = \frac{{\ln 0.05}}{{\ln \left( {1 - {P_{\rm{u}}}{P_{\rm{d}}}} \right)}} $ | (C4) |
| [1] |
张军. 空域监视技术的新进展及应用[J]. 航空学报, 2011, 32(1): 1-14. ZHANG J. New development and application of airsp-ace surveillance technology[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 1-14. (in Chinese) |
| Cited By in Cnki (34) | Click to display the text | |
| [2] | BLOMENHOFER H, PAWLITZKI A, ROSENTHAL P, et al. Space-based automatic dependent surveillance broadcast (ADS-B) payload for in-orbit demonstration[C]//Advanced Satellite Multimedia Systems Conference. Washington, D.C.: IEEE Computer Society, 2012: 160-165. |
| [3] | ICAO. 38th Session of the Assembly: The concept of satellite-based reception of ADS-B[R].Montreal: ICAO, 2013. |
| [4] | ITU.[ADS-B]-Reception of automatic dependent surveillance broadcast via satellite and compatibility studies with incumbent systems in the frequency band 1088.7-1091.3 MHz: Annex 12 to Working Party 5B[R]. Budapest: International Telecommunication Union, 2015. |
| [5] | Flight Safety Foundation. Benefits analysis of space-based ADS-B[R]. Alexandria: Flight Safety Foundation, 2016. |
| [6] | ORLANDO V A, HARMAN W H. GPS-squitter capacity analysis: Project Report ATC-214[R]. Massachusetts: Linc-oln Laboratory, 1994. |
| [7] | FRANCIS R, VINCENT R, NOEL JM, et al. The flying laboratory for the observation of ADS-B signals[J]. International Journal of Navigation and Observation, 2011, 1-5. |
| Click to display the text | |
| [8] | DELOVSKI T, WERNER K, RAWLIK T, et al. ADS-B over satellite-the world's first ADS-B receiver in space[C]//Small Satellites Systems and Services Symposium. Berlin: DLR, 2014: 1-16. |
| [9] | ALMINDE L, KAAS K, BISGAARD M, et al. GOMX-1 flight experience and air traffic monitoring results[C]//28th Annual AIAA/USU Conference on Small Satellites. Reston, VA: AIAA, 2014: 1-7. |
| [10] |
陈利虎, 陈小前, 赵勇. 星载ADS-B接收系统及其应用[J]. 卫星应用, 2016(3): 34-40. CHEN L H, CHEN X Q, ZHAO Y. Satellite-based ADS-B receiving system and application[J]. Satellite Application, 2016(3): 34-40. (in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [11] | MARK R. Aireon launch begins new era for satellite-based aircraft surveillance[EB/OL]. (2017-01-18)[2019-05-16]. US: Flying Magazine, 2017. Available from: https://www.flyi-ngmag.com/aireon-launch-begins-new-era-for-satellite-based-aircraft-surveillance. |
| [12] | MICHAEL A G, JOHN D, BEN H, et al. A compilation of measured ADS-B performance characteristic from aireon's on-orbit test program[C]//Enhanced Solutions for Aircraft and Vehicle Surveillance (ESAVS) Applications Conference, 2018. |
| [13] | DIEGO M. Globalstar's space-based ADS-B[EB/OL]. (2014-09-19)[2019-05-16]. Virginia: Globalstar, 2014.Available from: https://www.globalstar.com/en/index.php?cid=6300. |
| [14] | YANG H M, HUANG R S, WANG X F, et al. EBAA:An efficient broadcast authentication scheme for ADS-B communication based on IBS-MR[J]. Chinese Journal of Aeronautics, 2014, 27(3): 688-696. |
| Click to display the text | |
| [15] |
颜可壹, 吕泽均, 时宏伟, 等. 基于TDOA/TSOA的ADS-B系统防欺骗技术[J]. 计算机应用研究, 2015, 32(8): 2272-2275. YAN K Y, LV Z J, SHI H W, et al. ADS-B system anti cheat technology based on TDOA/TSOA[J]. Application Research of Computers, 2015, 32(8): 2272-2275. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] |
丁建立, 邹云开, 王静, 等. 基于深度学习的ADS-B异常数据检测模型[J]. 航空学报, 2019, 40(12): 323220. DING J L, ZOU Y K, WANG J, et al. ADS-B anomaly data detection model based on deep learning[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(12): 323220. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [17] | GARCIA M A, STAFFORD J, MINNIX J, et al. Aireon space based ADS-B performance model[C]//Integrated Communication, Navigation, and Surveillance Conference. Washington, D.C: IEEE Computer Society, 2015: C2-1-C2-10. |
| [18] | PRYT R V D, VINCENT R. A Simulation of signal col-lisions over the north atlantic for a spaceborne ADS-B receiver using aloha protocol[J]. Positioning, 2015, 6(3): 23-31. |
| Click to display the text | |
| [19] | MARTIN J P, GARCIA C E, FOLONIER M F, et al. Satellite ADS-B message collision simulation[C]//Telecommunications and TIC, 2015: 1-6. |
| [20] |
刘海涛, 王松林, 秦定本, 等. 星基ADS-B接收机监视容量分析[J]. 航空学报, 2018, 39(5): 182-189. LIU H T, WANG S L, QING D B, et al. Performance analysis of surveillance capacity of satellite-based ADS-B receiver[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 182-189. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [21] | ABRAMSON N. THE ALOHA SYSTEM: another alternative for computer communications[C]//Fall Joint Computer Conference. New York: ACM, 1970: 281-285. |
| [22] | PRYT R V D, VINCENT R. A simulation of the reception of automatic dependent surveillance-broadcast signals in low earth orbit[J]. International Journal of Navigation and Observation, 2015(56): 1-11. |
| Click to display the text | |
| [23] |
顾明, 张涛, 李林. 星间网络可靠传输重传机制分[J]. 空间控制技术与应用, 2013, 39(6): 49-52. GU M, ZHANG T, LI L. Retransmission mechanism analysis of reliable transmission in satellite network[J]. Aerospace Control and Application, 2013, 39(6): 49-52. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [24] | RTCA. Minimum operational performance standards for 1090 MHz extended squitter automatic dependent surveillance-broadcast (ADS-B) and traffic information services-broadcast (TIS-B): DO-260B[S]. Washington, D.C.: Radio Technical Commission for Aeronautics, 2009. |
| [25] | RTCA. Minimum operational performance standards for air traffic control radar beacon system/mode select (A/C/Mode S) airborne equipment: DO-181D[S]. Washington, D.C.: Radio Technical Commission for Aeronautics, 2008. |
| [26] |
SHELDON M R.应用随机过程: 概率模型导论[M].11版.龚光鲁, 译.北京: 人民邮电出版社, 2016. SHELDON M R. Introduction to probability models[M]. 11th ed. GONG L G, translated. Beijing: Posts & Telecom Press, 2016(in Chinese). |
| [27] | EUROCAE. Technical specification for a 1090 MHz extended squitter ADS-B ground system: ED-129B[S].Malakoff: The European Organisation for Civil Aviation Equipment, 2016. |
| [28] | EUROCONTROL. Preliminary safety case for enhanced air traffic services in non-radar areas using ADS-B surveillance[S]. Belgium: European Organisation for the Safety of Air Navigation, 2008. |
| [29] | Aireon. It's just ADS-B[EB/OL]. (2015-03)[2019-06-18]. USA: Aireon, 2015. Available from: https://aireon.com/resou-rces/its-just-ads-b/. |
| [30] |
郭欣, 张军, 张涛. 移动卫星网络仿真验证系统研究[J]. 遥测遥控, 2010, 31(1): 41-47, 60. GUO X, ZHANG J, ZHANG T. Mobile satellite network simulation and verification system[J]. Journal of Telemetry, Tracking and Command, 2010, 31(1): 41-47, 60. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [31] |
尹艳平, 刘波, 赵宝康, 等. 星地链路建模与分析[J]. 小型微型计算机系统, 2012, 33(10): 2213-2218. YIN Y P, LIU B, ZHAO B K, et al. Modeling and analysis of satellite-ground link[J]. Journal of Chinese Computer Systems, 2012, 33(10): 2213-2218. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [32] | ITU. Reception of automatic dependent surveillance broadcast via satellite and compatibility studies with incumbent systems in the frequency band 1087.7-1092.3 MHz[R]. Budapest: International Telecommunication Union, 2017. |



