模块级故障诊断属于航空装备三级维修体系中的中继级维修范畴,是提升航空保障能力的关键环节。航空电子设备各模块间交联关系复杂[1-3],难以对各故障建立严格的数学模型,这对故障诊断带来了极大的挑战[4-5]。
基于数据驱动的方法为解决上述问题提供了良好的思路。其中,深度学习与基于核方法的学习算法在航空电子部件的故障诊断中得到了最广泛的关注。前者主要适用于故障样本充足、计算资源丰富的情况,因此应用范围较为狭小,在电路元件级诊断中较为常见,文献[6-7]用深度置信网络(DBN)自动提取模拟电路的抽象故障特征,极大地提高了诊断正确率;考虑到神经网络训练时间长以及固有的人为经验依赖性,文献[8]结合数据压缩和自编码技术,提出了一种基于改进人工神经网络的航天器电信号分类方法。后者在小样本条件下尤为适用[9],在文献[10-11]中,支持向量机(SVM)与核极限学习机(KELM)分别被运用于电子系统的故障诊断,展现了较强的统计学习能力。此外,从诊断方法的角度看,为使航空电子设备的诊断结论更加可靠,将多个分类器的结果进行信息融合是另一个重要的研究方向[12];从诊断对象的角度看,作为航空电子设备在服役中后期的主要故障类型,间歇故障的诊断正受到越来越多的关注,将成为复杂电子设备故障诊断的新方向[13];从诊断的基础看,当前航空电子设备很少考虑故障诊断的测试需求,直接导致特征参数获取困难,因此,测试性设计技术也依然是研究的重点[14]。
实际应用中,航空电子部件的样本规模一般很小[11],因此,基于核方法的学习算法更有前景。在该类方法中,核函数及其参数的选取将严重制约方法的性能[15-16]。大量研究表明,多核学习(Multiple Kernel Learning, MKL)可增强决策函数的可解释性,且比单核模型具备更优的性能[17-18]。文献[19-20]分别在模拟电路、局域网的故障诊断中尝试运用MKL,在多种复杂故障情形下验证了MKL对提升诊断精度的有效性。文献[21]提出了一种更有效的MKL方法,称作SimpleMKL,通过简单的子梯度下降方法求解MKL问题,提高了MKL的实用性。但在MKL的框架里,基核权重被不加判别地应用于整个输入空间,忽视了基核在不同样本上可用性的差异。针对该问题,局部算法被引入到MKL中,称之为局部多核学习(Localized MKL,LMKL)。
近年来,国内外学者对LMKL进行了广泛的研究,大致可分为两类。一类为每一个样本学习一组独立的基核权重,称之为面向样本的LMKL(Sample-based Localized MKL,S-LMKL)模型[22-23]。针对S-LMKL中局部权重的优化形式二次非凸的问题,文献[24]中Gnen和Alpaydin通过一系列参数化的门模型(Gating Model)去局部地拟合核参数;文献[25]则着重研究了SVM分类框架下,对基核权重施加不同的范数约束对LMKL的影响。另一类是由Yang等[26]最初提出的基于分组的LMKL(Group-based Localized MKL,G-LMKL)模型,该方法首先根据样本相似性进行聚类,再为每个聚类学习一组基核权重,继承了S-LMKL的局部特征自适应表达能力,还有效约减了计算量,避免了过拟合。基于文献[26]的思想,文献[27]将聚类过程嵌入LMKL的训练中,提出了基于动态聚类的G-LMKL模型;文献[11]则引入近邻传播聚类来挖掘局部特征信息,由于事先不需指定聚类数目,使得G-LMKL对于不同规模的样本均具有较好的实用性。
G-LMKL克服了S-LMKL面临的主要风险,并且可以通过控制聚类数量来控制计算复杂性,更具灵活性。然而,G-LMKL中简单的“硬聚类”并不足以有效描述样本间的多样性,在同一聚类的内部基核的可用性显然也存在差异。出于这样的考虑,针对航空电子设备故障样本的采集困难性、分布复杂性以及本身固有的不确定性,提出一种小样本条件下融合隶属度信息的局部多核超限学习机模型(Fuzzy Clustering Localized Multi-Kernel Extreme Learning Machine,FC-LMKELM),其主要贡献在于:
1) 不同于现有的基于SVM的G-LMKL,受2015年提出的多核超限学习机(MK-ELM)[28]和文献[11]启发,本文将G-LMKL与ELM结合,从理论上给出了G-LMK-ELM的形式化表达。
2) 不同于已有的基于“硬聚类”的G-LMKL,基于模糊C均值聚类结果,本文的核权重将由样本落入各聚类的概率以及为每个聚类分配的核权重共同决定。在继承一般G-LMKL算法局部特征自适应能力和计算复杂性约减能力的同时,还进一步挖掘类内多样性,有利于提高诊断精度。
3) 针对局部权重优化形式的二次非凸问题,通过剖析G-LMK-ELM的初始优化问题及其对偶优化问题之间的关系,搭建了面向初始-对偶混合优化问题的参数三阶段交替更新策略。
1 问题描述对于一个多故障模式诊断问题,设训练集和测试集分别为
设原始数据集可聚类为G个不同的“群组”,
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{\beta }},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\gamma }}} \;\;\;\;\frac{1}{2}\sum\limits_{q = 1}^r {\left\| {{\mathit{\boldsymbol{\beta }}_q}} \right\|_{\rm{F}}^2} + \frac{C}{2}\sum\limits_{i = 1}^n {\left\| {{\mathit{\boldsymbol{\xi }}_i}} \right\|_2^2} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\sum\limits_{q = 1}^r {\gamma _q^{c\left( {{\mathit{\boldsymbol{x}}_i}} \right)}{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\beta }}_q}} = \mathit{\boldsymbol{y}}_i^{\rm{T}} - \mathit{\boldsymbol{\xi }}_i^{\rm{T}},i = 1,2, \cdots ,n \end{array} $ | (1) |
式中:
在该问题的Lagrange函数中分别对βq和ξi求偏导,并令结果等于0,可以进一步获得其对偶优化形式,即
| $ \begin{array}{l} \mathop {\max }\limits_\alpha \mathop {\min }\limits_x - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_j}} } \sum\limits_{q = 1}^r {\gamma _q^{c\left( {{\mathit{\boldsymbol{x}}_i}} \right)}\gamma _q^{c\left( {{\mathit{\boldsymbol{x}}_j}} \right)}{k_q}\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{2C}}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_i}} + \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{y}}_i}} \end{array} $ | (2) |
式中:αi为Lagrange乘子,对应于ELM的模型参数,并且有αi=[αi1, αi2, …, αim]T,α=[α1, α2, …, αn]T。
求解上述对偶优化问题,得到以下决策函数
| $ f\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \sum\limits_{j = 1}^n {\mathit{\boldsymbol{\alpha }}_j^{\rm{T}}} \sum\limits_{q = 1}^r {\gamma _q^{c\left( {{\mathit{\boldsymbol{x}}_i}} \right)}\gamma _q^{c\left( {{\mathit{\boldsymbol{x}}_j}} \right)}{k_q}\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)} $ | (3) |
尽管G-LMK-ELM在继承LMKL局部特征自适应能力的同时,兼顾了模型的泛化性能,但两个关键问题制约着式(2)所示优化问题的求解:① “粗暴”的硬聚类无法解释群组内部的基核可用性的差异,只依赖于群组的局部核权重会带来诊断准确性下降的风险;②式(2)对
本节运用模糊C均值聚类方法(FCM)[29]对数据集进行模糊划分,进而达到挖掘样本局部分布特征的目的。不同于硬聚类方法,模糊C均值聚类可以获取每个故障样本对于各个聚类的隶属度,将该隶属度信息作为先验知识融入G-LMK-ELM的局部核权重的优化中,有利于增强诊断模型的解释性,提高其诊断精度。
在FCM中,对样本的模糊划分可以表示成一个隶属度矩阵U=[uij](1≤i≤n, 1≤j≤C),且U满足:
| $ \begin{array}{l} \sum\limits_{j = 1}^G {{\mu _{ij}}} = 1\;\;\;\;{\mu _{ij}} \in \left[ {0,1} \right]\\ \;\;\;\;\;\;0 < \sum\limits_{i = 1}^n {{\mu _{ij}}} < n,1 \le i \le n,1 \le j \le G \end{array} $ | (4) |
式中:μij为第i个数据关于第j个聚类的隶属度,uij越大,则第i个数据落入第j个聚类的概率越大。FCM算法的具体实施流程描述如下:
步骤1 输入训练数据集{xi}i=1n、糊聚类数目G、权重指数w、最大迭代次数maxT,初始化隶属度矩阵U,阈值ε,当前迭代次数t=1。
步骤2 更新聚类中心
| $ {\mathit{\boldsymbol{c}}_i} = \frac{{\sum\limits_{j = 1}^n {\mu _{ij}^w{\mathit{\boldsymbol{x}}_j}} }}{{\sum\limits_{j = 1}^n {\mu _{ij}^w} }} $ |
步骤3 更新隶属度矩阵
| $ {\mu _{ij}}\left( t \right) = {\left( {\sum\limits_{g = 1}^G {{{\left( {\frac{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{c}}_j}} \right\|}}{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{c}}_g}} \right\|}}} \right)}^{2/\left( {w - 1} \right)}}} } \right)^{ - 1}} $ |
步骤4 若
根据2.1节的聚类结果,将隶属度矩阵U中元素记为pxg(g=1, 2, …, G),表示样本x落入聚类g的概率。将关于群组的局部权重记为γ=
| $ \begin{array}{l} \mathop {\min }\limits_{\beta ,\xi ,\gamma } \;\;\;\;\frac{1}{2}\sum\limits_{q = 1}^r {\left\| {{\mathit{\boldsymbol{\beta }}_q}} \right\|_{\rm{F}}^2} + \frac{C}{2}\sum\limits_{i = 1}^n {\left\| {{\mathit{\boldsymbol{\xi }}_i}} \right\|_2^2} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\sum\limits_{q = 1}^r {\sum\limits_{g = 1}^G {\gamma _q^gp_{{\mathit{\boldsymbol{x}}_i}}^g{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\beta }}_q}} } = \mathit{\boldsymbol{y}}_i^{\rm{T}} - \mathit{\boldsymbol{\xi }}_i^{\rm{T}},i = 1,2, \cdots ,n \end{array} $ | (5) |
不同于G-LMKL和S-LMKL,在FC-LMKL中,每个样本的核权重既与群组权重γ=
| $ \begin{array}{l} \mathop {\max }\limits_\mathit{\boldsymbol{\alpha }} \mathop {\min }\limits_\mathit{\boldsymbol{\gamma }} \left[ { - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_j}} } \sum\limits_{g = 1}^G {\sum\limits_{g' = 1}^G {\sum\limits_{q = 1}^r {p_{{\mathit{\boldsymbol{x}}_i}}^g\gamma _q^g{k_q}} } } \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)p_{{\mathit{\boldsymbol{x}}_j}}^{g'}\gamma _q^{g'} - \frac{1}{{2C}}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_i}} + \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{y}}_i}} } \right] \end{array} $ | (6) |
式(5)和式(6)对应的基于隶属度信息的FC-LMKL-ELM优化问题可以等效为式(7)所示的初始-对偶混合优化问题
| $ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{\gamma }} \mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \mathop {\max }\limits_\mathit{\boldsymbol{\alpha }} \;\;\;\;\frac{1}{2}\sum\limits_{q = 1}^r {\left\| {{\mathit{\boldsymbol{\beta }}_q}} \right\|_{\rm{F}}^2} + \frac{1}{{2C}}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_i}} - \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\left( {\sum\limits_{g = 1}^G {\sum\limits_{q = 1}^r {\gamma _q^g} } p_{{\mathit{\boldsymbol{x}}_i}}^G{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\beta }}_q} - \mathit{\boldsymbol{y}}_i^{\rm{T}}} \right){\mathit{\boldsymbol{\alpha }}_i}} \end{array} $ | (7) |
证明:
步骤1 由表达式(5)到表达式(7)
初始优化问题(5)对应的Lagrange函数为
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\gamma }}} \right) = \frac{1}{2}\sum\limits_{q = 1}^r {\left\| {{\mathit{\boldsymbol{\beta }}_q}} \right\|_{\rm{F}}^2} + \frac{C}{2}\sum\limits_{i = 1}^n {\left\| {{\mathit{\boldsymbol{\xi }}_i}} \right\|_{\rm{2}}^2} - \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\left( {\sum\limits_{g = 1}^G {\sum\limits_{q = 1}^r {\gamma _q^g} } p_{{\mathit{\boldsymbol{x}}_i}}^g{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\beta }}_q} - \mathit{\boldsymbol{y}}_i^{\rm{T}} + \mathit{\boldsymbol{\xi }}_i^{\rm{T}}} \right){\mathit{\boldsymbol{\alpha }}_i}} \end{array} $ |
在Lagrange函数中对ξi求偏导,并令结果等于0,有
| $ \frac{{\partial L\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\gamma }}} \right)}}{{\partial {\mathit{\boldsymbol{\xi }}_i}}} = C\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\xi }}_i}} - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\alpha }}_i}} = 0 \Rightarrow {\mathit{\boldsymbol{\xi }}_i} = \frac{1}{C}{\mathit{\boldsymbol{\alpha }}_i} $ |
将该结果代入Lagrange函数中,得到式(7)。
步骤2 由表达式(7)到表达式(6)
将表达式(7)重新写为
| $ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{\gamma }} \mathop {\max }\limits_\mathit{\boldsymbol{\alpha }} \mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \;\;\;\;\;\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{y}}_i}} - \frac{1}{{2C}}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\alpha }}_i^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_i}} + \\ \;\;\;\;\;\;\sum\limits_{q = 1}^r {\sum\limits_{k = 1}^m {\left( {\frac{1}{2}\left\| {\mathit{\boldsymbol{\beta }}_q^k} \right\|_2^2 - \sum\limits_{i = 1}^n {\sum\limits_{g = 1}^g {{\alpha _{ik}}} } \gamma _q^gp_{{\mathit{\boldsymbol{x}}_i}}^g{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right)\mathit{\boldsymbol{\beta }}_q^k} \right)} } \end{array} $ | (8) |
式中:βqk为矩阵
| $ \mathit{\boldsymbol{\beta }}_q^k = \sum\limits_{i = 1}^n {\sum\limits_{g = 1}^G {{\alpha _{ik}}} } \gamma _q^gp_{{x_i}}^g{\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right) $ | (9) |
将式(9)代入式(7)中,整理后可式(6)。
证毕。
2.3 FC-LMKELM的模型优化为了求解融合隶属度的FC-LMKELM模型,针对式(7)定义的优化问题,提出一种3阶段的参数交替优化策略。
1) 固定γ,优化α
为了表示的简洁性,对于Lagrange乘子
| $ J\left( {\mathit{\boldsymbol{\alpha '}}} \right) = {{\mathit{\boldsymbol{\alpha '}}}^{\rm{T}}}\mathit{\boldsymbol{y'}} - \frac{1}{2}{{\mathit{\boldsymbol{\alpha '}}}^{\rm{T}}}\mathit{\boldsymbol{K'\alpha '}} - \frac{1}{{2C}}{{\mathit{\boldsymbol{\alpha '}}}^{\rm{T}}}\mathit{\boldsymbol{\alpha '}} $ | (10) |
式中:
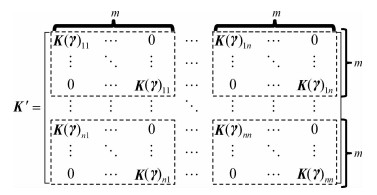
|
| 图 1 增广矩阵K′ Fig. 1 Augmentation matrix K′ |
对式(10)的α′求偏导,并令结果等于0,可得
| $ \mathit{\boldsymbol{\alpha '}} = {\left( {\mathit{\boldsymbol{K'}} + \mathit{\boldsymbol{I''}}/C} \right)^{ - 1}}\mathit{\boldsymbol{y'}} $ | (11) |
式中:I″为一个mn阶的单位矩阵。通过反矩阵向量化操作可得
2) 给定α、γ,计算βq和fq(xi)
根据式(9)所示的βqk,容易得到
| $ {\mathit{\boldsymbol{\beta }}_q} = \sum\limits_{i = 1}^n {\sum\limits_{g = 1}^G {\gamma _q^g} } p_{{\mathit{\boldsymbol{x}}_i}}^g\phi _q^T\left( {{\mathit{\boldsymbol{x}}_i}} \right)\mathit{\boldsymbol{\alpha }}_i^{\rm{T}} $ | (12) |
不妨用fq(·)表示第q个基核导出的子分类器的输出函数,则样本xi基于fq(·)的输出向量为
| $ {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = {\phi _q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\beta }}_q} = \sum\limits_{j = 1}^n {\sum\limits_{g = 1}^G {\gamma _q^g} } p_{{\mathit{\boldsymbol{x}}_j}}^g{k_q}\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\boldsymbol{\alpha }}_j^{\rm{T}} $ | (13) |
3) 固定α、fq(xi),更新γ
只考虑式(7)中与γ相关的项目,且注意到
| $ \mathop {\min }\limits_\mathit{\boldsymbol{\gamma }} - \frac{1}{2}\sum\limits_{q = 1}^r {\sum\limits_{i = 1}^n {\sum\limits_{g = 1}^G {\gamma _q^g} } } p_{{\mathit{\boldsymbol{x}}_i}}^g{f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i} $ | (14) |
在式(14)中对γqg施加不同约束,可得以下两种不同的局部权重更新方式。
1) l1-范数约束
此时,式(14)在
2) lp-范数约束
式(14)在lp-范数约束下的Lagrange函数表示为
| $ \begin{array}{l} L = - \frac{1}{2}\sum\limits_{g = 1}^G {\sum\limits_{q = 1}^r {\gamma _q^g} } \sum\limits_{i = 1}^n {{p_{\mathit{\boldsymbol{x}}_i^g}}} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i} + \\ \;\;\;\;\;{\lambda _g}\left( {\sum\limits_{q = 1}^r {{{\left[ {\gamma _q^g} \right]}^p}} - 1} \right) \end{array} $ | (15) |
在式(15)中对γqg求偏导并令结果等于0,有
| $ \sum\limits_{i = 1}^n {p_{{\mathit{\boldsymbol{x}}_i}}^g} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i} = 2p{\lambda _i}{\left[ {\gamma _q^g} \right]^{p - 1}} $ | (16) |
联合lp-范数约束条件和式(16),可得
| $ \gamma _q^g = \frac{{{{\left( {\sum\limits_{i = 1}^n {{p_{\mathit{\boldsymbol{x}}_i^g}}} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i}} \right)}^{1/\left( {p - 1} \right)}}}}{{{{\left( {\sum\limits_{q = 1}^r {{{\left[ {\sum\limits_{i = 1}^n {{p_{\mathit{\boldsymbol{x}}_i^g}}} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i}} \right]}^2}} } \right)}^{1/2}}}} $ | (17) |
特别地,当p=2时,有
| $ \gamma _q^g = \frac{{\sum\limits_{i = 1}^n {{p_{\mathit{\boldsymbol{x}}_i^g}}} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i}}}{{{{\left( {\sum\limits_{q = 1}^r {\left[ {\sum\limits_{i = 1}^n {{p_{\mathit{\boldsymbol{x}}_i^g}}} {f_q}\left( {{\mathit{\boldsymbol{x}}_i}} \right){\mathit{\boldsymbol{\alpha }}_i}} \right]} } \right)}^{1/2}}}} $ | (18) |
基于2.3节3阶段交替优化后的α*=[α1, α2, …, αn]T和
| $ f\left( z \right) = \sum\limits_{j = 1}^n {\sum\limits_{q = 1}^r {\sum\limits_{g' = 1}^G {\sum\limits_{g = 1}^G {\gamma _q^g} } } } p_\mathit{\boldsymbol{z}}^g\gamma _q^{g'}{p_{x_q^{g'}}}{k_q}\left( {\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\boldsymbol{\alpha }}_j^{*{\rm{T}}} $ | (19) |
决策模型的图形解释如图 2所示。
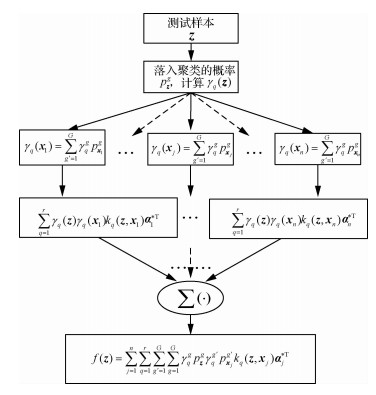
|
| 图 2 FC-LMKELM的决策模型 Fig. 2 Decision-making model of FC-LMKELM |
在融合隶属度的FC-LMKELM模型中,不妨设测试样本的模型输出
| $ label\left( \mathit{\boldsymbol{z}} \right) = \arg \mathop {\max }\limits_{l \in \left\{ {1,2, \cdots ,m} \right\}} {f^{\left( l \right)}}\left( \mathit{\boldsymbol{z}} \right) $ | (20) |
融合隶属度的FC-MKELM模型整体框架总结如图 3所示。
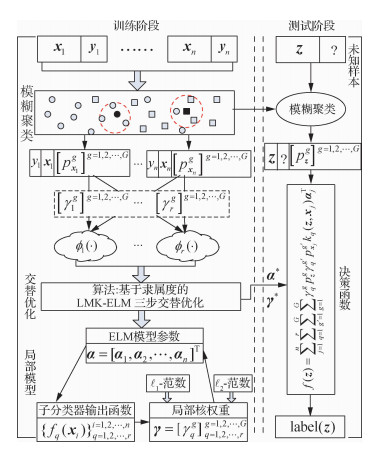
|
| 图 3 FC-MKELM模型的流程图 Fig. 3 Flowchart of FC-MKELM model |
为方便表示,不妨将采用l1-范数和l2-范数约束时的FC-LMKELM分别记为l1-FC-LMKELM和l2-FC-LMKELM。根据图 4将所提方法的实施流程总结如下:
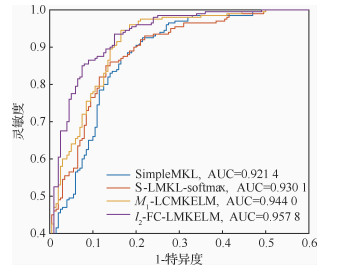
|
| 图 4 4种方法的ROC曲线 Fig. 4 ROC curves of 4 methods |
步骤1 确定训练数据集DTr=[(xi, yi)]i=1n、基核[kq(·, ·)]q=1r、模糊聚类数目G、最大迭代次数maxT以及ELM正则化因子C。
步骤2 通过FCM算法对训练样本进行聚类划分,获得隶属度矩阵U(即获取
步骤3 基于
步骤4 通过式(13)计算fq(xi)。
步骤5 若采用l1-范数约束,通过解式(14)在l1-范数约束下的线性规划问题获得
步骤6 若
步骤7 计算测试样本x′i到聚类中心vg(g=1, 2, …, G)的隶属度获取
步骤8 基于
本节将以SimpleMKL[21](基于MKL),LCMKELM[11](基于G-LMKL)和LMKL[24](基于S-LMKL)作为比较算法,设计两个实验来验证FC-LMKELM的性能优势。其中,因选通函数不同,LMKL分别记作S-LMKL-softmax和S-LMKL-sigmoid,与文献[11]一致,LCMKELM分别记作M1-LCMKELM和M2-LCMKELM;根据范数约束的不同,将所提方法分别记为l1-FC-LMKELM和l2-FC-LMKELM。在训练之前,对所有的非高斯核矩阵
所有算法均在MATLAB 2018a上运行,实验电脑配置为:Windows 7操作系统,Inter Core i7-4770 CPU,3.4 GHz主频和8 GB RAM。
4.1 方法有效性验证本节通过人造数据集Gauss4证明FC-LMKELM的有效性。由于Gauss4具有明显的类内局部结构,因此常用其进行局部算法的性能验证[11, 24]。该数据集包含2种类别,每个类别服从2个不同的高斯分布,每个分布产生300个样本,共1200个样本。与文献[11, 24]一致,每种分布的先验概率、均值、协方差为
| $ {\rho _{11}} = 0.25,{\rho _{12}} = 0.25,{\rho _{21}} = 0.25,{\rho _{22}} = 0.25 $ |
| $ {\mathit{\boldsymbol{\mu }}_{11}} = \left[ {\begin{array}{*{20}{l}} { - 3.0}\\ { + 1.0} \end{array}} \right],{\mathit{\boldsymbol{\mu }}_{12}} = \left[ {\begin{array}{*{20}{l}} { + 1.0}\\ { + 1.0} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{\mu }}_{21}} = \left[ {\begin{array}{*{20}{c}} { - 1.0}\\ { - 2.2} \end{array}} \right],{\mathit{\boldsymbol{\mu }}_{22}} = \left[ {\begin{array}{*{20}{l}} { + 3.0}\\ { - 2.2} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{11}} = \left[ {\begin{array}{*{20}{c}} {0.8}&0\\ 0&{2.0} \end{array}} \right],{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{12}} = \left[ {\begin{array}{*{20}{c}} {0.8}&0\\ 0&{2.0} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{21}} = \left[ {\begin{array}{*{20}{c}} {0.8}&0\\ 0&{4.0} \end{array}} \right],{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{22}} = \left[ {\begin{array}{*{20}{c}} {0.8}&0\\ 0&{4.0} \end{array}} \right] $ |
实验共进行20次,每次随机选择600个样本用于训练,400个样本用于测试,设置所提方法的聚类数量为4。将所提方法与SimpleMKL[21]、M1-LCMKELM[11]、M2-LCMKELM[11]、S-LMKL-softmax[24]、S-LMKL-sigmoid[24]比较。参考文献[11, 24]中的配置,上述所有方法均以线性核、参数是2的多项式核、参数是1的高斯核作为基核;F1分数是统计学中衡量二分类模型精确度的重要指标[30],本节将之与分类准确率以及文献[31]中的G-mean作为评价分类性能的3大指标,其值以“均值±标准差”的形式记录于表 1中。
| 方法 | 准确率 | F1 | G-mean |
| SimpleMKL | 0.8569±0.0135 | 0.8621±0.0118 | 0.8588±0.0122 |
| S-LMKL-softmax | 0.8605±0.0182 | 0.8610±0.0176 | 0.8601±0.0175 |
| S-LMKL-sigmoid | 0.8591±0.0134 | 0.8596±0.0137 | 0.8586±0.0130 |
| M1-LCMKELM | 0.8662±0.0090 | 0.8660±0.0091 | 0.8656±0.0086 |
| M2-LCMKELM | 0.8694±0.0079 | 0.8693±0.0084 | 0.8689±0.0079 |
| l1-FC-LMKELM | 0.8729±0.0098 | 0.8782±0.0101 | 0.8751±0.0097 |
| l2-FC-LMKELM | 0.8804±0.0095 | 0.8811±0.0099 | 0.8819±0.0103 |
由表 1可知,与其他方法相比,在l1-范数和l2-范数约束下,FC-LMKELM可以实现最优的分类性能。其原因在于:
1) SimpleMKL没有考虑样本的局部特征信息,因此在所有方法中,其分类性能最差。
2) 与2种常见的S-LMKL方法相比,LCMKELM和FC-LMKELM将基核权重拟合到样本所属聚类而非每个样本上,一定程度上抑制了过学习问题,分类精度得以提升;与2种基于硬聚类的LCMKELM方法相比,隶属度信息的融入使FC-LMKELM得以有效描述聚类内部样本间的多样性,因此,即便与诊断性能更佳的M2-LCMKELM相比,在不同范数约束下,诊断精度也分别提升了0.35%和1.10%。
为更直观地展现FC-LMKELM相较于其他方法的优势,选取l2-FC-LMKELM、SimpleMKL、S-LMKL-softmax与M1-LCMKELM的受试者工作特征曲线(ROC)绘制于图 4中。由图 4可知,l2-FC-LMKELM的曲线下方面积(AUC)依次大于M1-LCMKELM、S-LMKL-softmax和SimpleMKL,这进一步验证了所提方法的性能。
为说明聚类数量对算法精度的影响,随机选择600个样本用于训练,400个样本用于测试,设置不同的聚类数量后,其测试结果如表 2所示。
| 聚类数量 | l1-FC-LMKELM | l2-FC-LMKELM |
| 1 | 0.86 | 0.8625 |
| 2 | 0.8675 | 0.8775 |
| 4 | 0.885 | 0.8925 |
| 8 | 0.885 | 0.89 |
| 16 | 0.8725 | 0.885 |
| 32 | 0.8625 | 0.87 |
| 64 | 0.8575 | 0.8625 |
| 128 | 0.8825 | 0.8925 |
| 256 | 0.885 | 0.895 |
| 600 | 0.865 | 0.8725 |
由表 2可知:当聚类数量为1时,诊断精度处于较低水平;随着聚类数量增加,模型诊断精度出现不同程度的提高,但最佳的聚类数量与输入空间的局部结构有关,并无明确的规律可循,当聚类数量取值不当时,测试精度甚至会出现下降;当聚类数量增加到训练样本数量时,本文方法演变为S-LMKL-ELM,泛化性能有所降低。
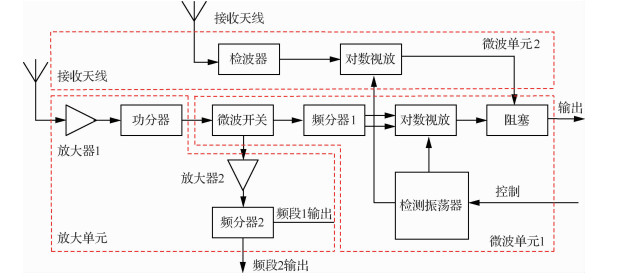
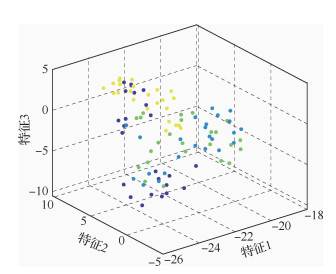
4.2 某型机前端接收机故障诊断实例某型机前端接收机组成如图 5所示,本节以其为例,验证FC-LMKELM的有效性。自动测试系统(ATS)对其进行12项测试:5个频点的灵敏度、动态范围,以及两项射频增益。用F0、F1、F2、F3分别表示正常模式、放大单元故障、微波单元1故障和微波单元2故障。ATS对每种模式采集48组样本,共得到192组样本,将之均分后形成训练集和测试集。基于厂家维护保养手册中的测量方法,利用ATS的标准信号源、功率计和频谱仪对每种模式采集48组样本,共获得特征数为12、样本数为192的原始数据集,对该数据集按特征进行Z-score标准化预处理,然后将之均分为训练集和测试集。运用t分布随机邻域嵌入(t-SNE)算法[32]将训练集的96个样本降维到三维空间中,如图 6所示。显然,不同故障模式的样本间重叠严重,同一故障模式的样本分布也并不集中,这对分类算法性能提出了较高的要求。
|
| 图 5 前端接收机 Fig. 5 Front-end receiver |
|
| 图 6 训练集的三维可视化图 Fig. 6 3-D visualization of training set |
基于该训练集,以线性核、参数为2的多项式核、参数分别为[2,10,20,30,40,50]的高斯核作为基核(共8个),运用FC-LMKELM进行诊断。首先对训练样本进行模糊C均值聚类,经试验,当聚类数为4时可达到最佳性能,其隶属度矩阵如表 3所示。
| 样本序号 | 中心1 | 中心2 | 中心3 | 中心4 |
| 1 | 0.4067 | 0.2923 | 0.1239 | 0.1771 |
| 2 | 0.4216 | 0.2083 | 0.1834 | 0.1867 |
| 3 | 0.3916 | 0.2334 | 0.1869 | 0.1881 |
| 4 | 0.4238 | 0.2567 | 0.1733 | 0.1462 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 96 | 0.0823 | 0.1339 | 0.2088 | 0.5750 |
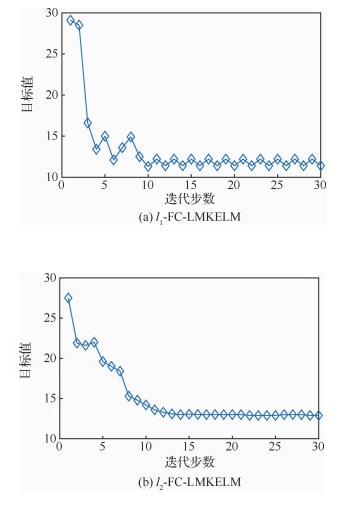
基于表 3所示的隶属度信息,按照第3节中的步骤3~步骤6执行迭代更新过程,在不同的范数约束下,FC-LMKELM的学习曲线如图 7所示。
|
| 图 7 FC-LMKELM的学习曲线 Fig. 7 Learning curves of FC-LMKELM |
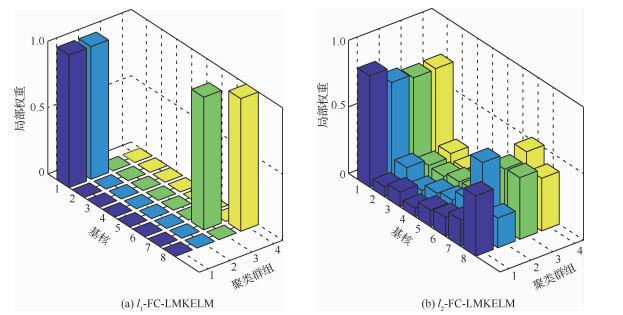
模型收敛后
|
| 图 8 FC-LMKELM的局部权重分布 Fig. 8 Localized weight distribution of FC-LMKELM |
图 9以混淆矩阵的形式直观地展示了FC-LMKELM与SimpleMKL、S-LMKL-softmax、S-LMKL-sigmoid、M2-LCMKELM的诊断效果。
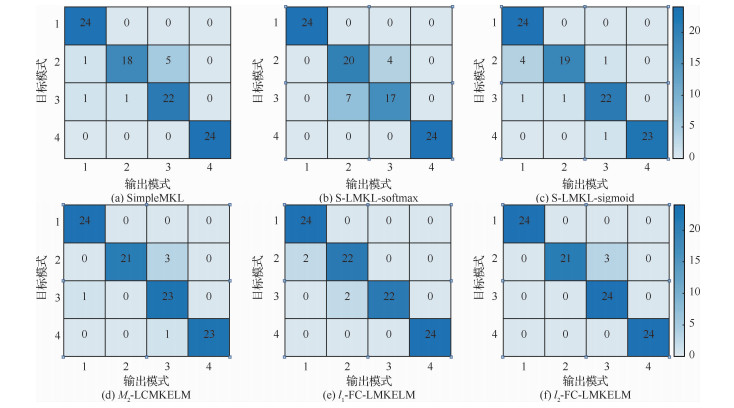
|
| 图 9 不同方法的混淆矩阵 Fig. 9 Confusion matrices of different methods |
| 方法 | 漏警率/% | 虚警率/% | 训练准确率/% | 测试准确率/% |
| SimpleMKL | 2.7778 | 0 | 96.8750 | 91.6667 |
| S-LMKL-softmax | 0 | 0 | 100 | 88.8417 |
| S-LMKL-sigmoid | 6.9444 | 0 | 100 | 91.6667 |
| M2-LCMKELM | 1.3889 | 0 | 100 | 94.7916 |
| l1-FC-LMKELM | 2.7778 | 0 | 100 | 95.8333 |
| l2-FC-LMKELM | 0 | 0 | 100 | 96.8750 |
1) FC-LMKELM在避免漏警与抑制虚警方面表现优异,尤其是l2-FC-LMKELM,实现了0漏警,0虚警。
2) 两种S-LMKL方法的测试诊断精度远远低于训练诊断精度,显然发生了严重的过拟合,其原因在于为每一个样本点学习独立的基核权重导致了算法泛化性能严重下降。与之相对的是M2-LCMKELM,通过“硬聚类”的方式将局部权重关联至所属聚类而非各个样本上,既关注了局部特征又防止了过学习,泛化性能得以提升。
3) 由于融合了各个样本对群组的隶属度信息,相比于M2-LCMKELM,这种“软聚类”的方式使FC-LMKELM的泛化性能得到了进一步的提升;l2-FC-LMKELM的诊断准确性比l1-FC-LMKELM高,原因在于后者的基核权重具有稀疏性(见图 8),可能带来有用信息的损失。相比其他4种非“软聚类”方法,在测试精度方面,l1-FC-LMKELM分别提升了4.16%、6.99%、4.16%和1.04%;l2-FC-LMKELM则分别提升了5.20%、8.03%、5.20%和2.08%。
从另一个角度看,本节以文献[28]中给出的适用于多分类问题的F1的推广形式微观F1(Micro-F1)、宏观F1(Macro-F1)以及G-mean作为诊断方法的精确性评价指标,基于图 9的直观结果将这3大指标统计于表 5中,从中可知FC-LMKELM仍然表现最佳。
| 方法 | Micro-F1 | Macro-F1 | G-mean |
| SimpleMKL | 0.9167 | 0.9150 | 0.9106 |
| S-LMKL-softamx | 0.8854 | 0.8850 | 0.8765 |
| S-LMKL-sigmoid | 0.9167 | 0.9162 | 0.9132 |
| M2-LCMKELM | 0.9479 | 0. 9484 | 0.9468 |
| l1-FC-LMKELM | 0.9583 | 0.9583 | 0.9574 |
| l2-FC-LMKELM | 0.9688 | 0.9686 | 0.9672 |
最后,为了探究所提方法的时效性,重复10次实验,表 6以“均值±标准差”的形式统计了各方法的时间开销。
| 方法 | 训练时间/s | 测试时间/s |
| SimpleMKL | 0.1326±0.0112 | 0.0085±0.0015 |
| S-LMKL-softamx | 0.2235±0.0125 | 0.0072±0.0011 |
| S-LMKL-sigmoid | 0.3652±0.0292 | 0.0076±0.0021 |
| M2-LCMKELM | 0.4065±0.0523 | 0.0081±0.0019 |
| l1-FC-LMKELM | 1.8579±0.0868 | 0.0083±0.0013 |
| l2-FC-LMKELM | 0.5136±0.0326 | 0.0079±0.0009 |
由表 6可知:①在训练时间上,尽管FC-LMKELM要略长于其他方法,尤其在l1-范数约束下,每次迭代中加入的解线性规划过程更多地延长了训练时间,但需要注意的是,正如图 7所示,只需极少的迭代步数FC-LMKELM就能快速收敛,因此训练时间开销实际上是可控的;②在测试时间上,FC-LMKELM与其他方法基本相同,均可实现实时输出;③作为线下诊断方法,以少量时间开销来换取更多的精确性上的提高是值得的;此外,航空电子部件的诊断多数情况下在小样本条件下进行,时间花费不会过多,因此FC-LMKELM是有效的。
5 结论面向航空电子部件模块级故障诊断问题,提出一种融合隶属度信息的FC-LMKELM诊断方法。以某型机前端接收机的ATS测试数据为例,验证了所提方法的有效性,可以得到以下结论:
1) 在诊断精度方面,相比于MKL方法和3种非“软聚类”的LMKL方法,FC-LMKELM能够有效避免漏警、抑制虚警并提升诊断精确度。对于某型机前端接收机,l1-FC-LMKELM和l2-FC-LMKELM比其他方法的平均值分别提高了4.09%和5.13%。
2) 在时间开销方面,相比于MKL方法和3种非“软聚类”的LMKL方法,FC-LMKELM训练时间稍长,但较少的迭代次数确保了时间开销的可控性;在测试时间上各方法基本在同一水平。
3) 聚类数量对所提方法的性能有很大的影响,并且没有明确的规律可循,需要依据具体的数据进行验证后确定。在训练过程中融入聚类数量自适应变化的“软聚类”方法是下一步的研究方向。
| [1] |
孙伟超, 李文海, 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J]. 北京航空航天大学学报, 2015, 41(10): 1902-1909. SUN W C, LI W H, LI W F. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902-1909. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [2] | KNÜPPEL T, BLANKE M, ØSTERGAARD J. Fault diagnosis for electrical distribution systems using structural analysis[J]. International Journal of Robust and Nonlinear Control, 2014, 24: 1446-1465. |
| Click to display the text | |
| [3] | JAMIL T, MOHAMMED I. Simulation of VICTOR algorithm for fault diagnosis of digital circuits[J]. International Journal of Computer Theory and Engineering, 2015, 7(2): 103-107. |
| Click to display the text | |
| [4] | DAI X W, GAO Z W. From model, signal to knowledge:A data-driven perspective of fault detection and diagnosis[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2226-2238. |
| Click to display the text | |
| [5] | GAO Z W, CECATI C, DING S X. A survey of fault diagnosis and fault tolerant techniques-Part Ⅰ:Fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757-3767. |
| Click to display the text | |
| [6] | LIU Z B, JIA Z, VONG C M, et al. Capturing high-discriminative fault features for electronics-rich analog system via deep learning[J]. IEEE Transactions on Industrial Informatics, 2017, 13(3): 1213-1226. |
| Click to display the text | |
| [7] |
赵光权, 葛强强, 刘小勇, 等. 基于DBN的故障特征提取及诊断方法研究[J]. 仪器仪表学报, 2016, 37(9): 1946-1953. ZHAO G Q, GE Q Q, LIU X Y, et al. Fault feature extraction and diagnosis based on deep belief network[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1946-1953. (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [8] |
李可, 王全鑫, 宋世民, 等. 基于改进人工神经网络的航天器电信号分类方法[J]. 北京航空航天大学学报, 2016, 42(3): 596-601. LI K, WANG Q X, SONG S M, et al. Spacecraft electrical signal classification method based onimproved artificial neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(3): 596-601. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [9] | ZHANG M J, CHAI K, HUANG J, et al. Combined improved EEMD with SVM in the bearing low dimensional small sample fault diagnosis[J]. Applied Mechanics & Materials, 2013, 427: 354-357. |
| [10] | GUO Y, MA J, XIAO F, et al. SVM with optimized parameters and its application to electronic system fault diagnosis[C]//Prognostics and Health Management. Piscataway, NJ: IEEE Press, 2012: 1-6. |
| [11] |
张伟, 许爱强, 平殿发, 等. 基于近邻传播聚类的航空电子部件LMK诊断模型[J]. 北京航空航天大学学报, 2018, 44(8): 1693-1704. ZHANG W, XU A Q, PING D F, et al. Localized multi-kernel diagnosis model for avionics based on affinity propagation clustering[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(8): 1693-1704. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [12] |
闫涛, 赵文俊, 胡秀洁, 等. 基于信息融合技术的航空电子设备故障诊断研究[J]. 电子科技大学学报, 2015, 44(3): 392-396. YAN T, ZHAO W J, HU X J, et al. Fault diagnosis of avionic devices based on information fusion technology[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(3): 392-396. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [13] |
吕克洪, 程先哲, 李华康, 等. 电子设备故障预测与健康管理技术发展新动态[J]. 航空学报, 2019, 40(11): 323285. LYU K H, CHENG X Z, LI H K, et al. New developments of prognostic and health management technology for electronic equipment[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(11): 323285. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [14] |
刘艳芳, 吕江花, 马世龙, 等. 航电系统并行检测过程与检测设备解耦方法[J]. 航空学报, 2019, 40(8): 322818. LIU Y F, LYU J H, MA S L, et al. Decoupling method for test process and test devices in parallel testing of avionics systems[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(8): 322818. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [15] |
邴其春, 龚勃文, 杨兆升, 等. 一种组合核相关向量机的短时交通流局域预测方法[J]. 哈尔滨工业大学学报, 2017, 49(3): 144-149. BING Q C, GONG B W, YANG Z S, et al. A short-term traffic flow local prediction method of combined kernel function relevance vector machines[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 144-149. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [16] |
李军, 李大超. 基于优化核极限学习机的风电功率时间序列预测[J]. 物理学报, 2016, 65(13): 39-48. LI J, LI D C. Wind power time series prediction using optimized kernel extreme learning machine method[J]. Acta Physica Sinica, 2016, 65(13): 39-48. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [17] | FENG J, JIAO L C, SUN T, et al. Multiple kernel learning based on discriminative kernel clustering for hyperspectral band selection[J]. IEEE Transactions on Geosciences and Remote Sensing, 2016, 54(11): 6516-6530. |
| Click to display the text | |
| [18] | GÖNEN M, ALPAYDIN E. Multiple kernel learning algorithms[J]. Journal of Machine Learning Research, 2011, 12: 2211-2268. |
| Click to display the text | |
| [19] | ZHANG C L, HE Y G, YUAN L F, et al. A novel approach for diagnosis of analog circuit fault by using GMKL-SVM and PSO[J]. Journal of Electronic Testing, 2016, 32: 531-540. |
| Click to display the text | |
| [20] | LI Y X, REN C Q, BO J Y, et al. The application of GMKL algorithm to fault diagnosis of local area network[J]. Journal of Networks, 2014, 9(3): 747-753. |
| Click to display the text | |
| [21] | RAKOTOMAMONJY A, BACH F R, CANU S, et al. SimpleMKL[J]. Journal of Machine Learning Research, 2008, 9: 2491-2521. |
| Click to display the text | |
| [22] | LIU X W, WANG L, ZHANG J, et al. Sample-adaptive multiple kernel learning[C]//28th AAAI Conference on Artificial Intelligence, 2014: 1975-1981. |
| [23] | HAN Y N, YANG K D, MA Y L, et al. Localized multiple kernel learning via sample-wise alternating optimization[J]. IEEE Transactions on Cybernetics, 2014, 44(1): 137-147. |
| Click to display the text | |
| [24] | GÖNEN M, ALPAYDIN E. Localized algorithms for multiple kernel learning[J]. Pattern Recognition, 2013, 46: 795-807. |
| Click to display the text | |
| [25] | HAN Y N, YANG K D, YANG Y X, et al. On the impact of regularization variation on localized multiple Kernel learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(6): 2625-2630. |
| Click to display the text | |
| [26] | YANG J J, LI Y N, TIAN Y H, et al. Group-sensitive multiple kernel learning for object recognition[J]. IEEE Transactions on Image Processing, 2012, 21(5): 2838-2852. |
| Click to display the text | |
| [27] | HAN Y N, YANG K D, YANG Y X, et al. Localized multiple Kernel learning with dynamical clustering and matrix regularization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(2): 486-499. |
| [28] | LIU X W, WANG L, HUANG G B, et al. Multiple kernel extreme learning machine[J]. Neurocomputing, 2015, 149: 253-264. |
| Click to display the text | |
| [29] | BEZDEK J C, EHRLICH R, FULL W. FCM:The fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2-3): 191-203. |
| Click to display the text | |
| [30] | SOKOLOVA M, LAPALME G. A systematic analysis of performance measures for classification tasks[J]. Information Processing and Management, 2009, 45(4): 427-437. |
| Click to display the text | |
| [31] | PHOUNGPHOL P, ZHANG Y Q, ZHAO Y C. Robust multiclass classification for learning from imbalanced biomedical data[J]. Tsinghua Science and Technology, 2012, 17(6): 619-628. |
| Click to display the text | |
| [32] | MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(11): 2579-2605. |



