2. 中国电子科技集团公司 数据链技术重点实验室, 西安 710077
2. Key Laboratory of Data Link Technology, CETC, Xi'an 710077, China
舰艇编队防空作战指利用舰艇编队以及我方作战资源对来袭的空中威胁进行有效拦截的一种作战方式。水面舰艇编队是由多艘水面舰艇构成的多功能作战系统,水面舰艇编队的作战效能作为水面舰艇编队完成各种任务的度量,舰艇编队防空作战通过指控中心对战场信息的收集、融合以及指令的发布来实现编队各作战单元的协同来应对空中来袭威胁。对舰艇编队防空作战系统效能评估并非对单舰、单装备的效能评估,体系效能评估的方法也能够适用于舰艇编队防空作战系统。
随着信息技术发展以及仿真作战系统的日益完善,对作为完成各种任务度量的作战效能进行评估也越来越复杂。作战效能评估是一个既需要综合集成定性与定量信息,又需要综合主观信息与客观信息的复杂问题,不仅仅要考察依据当前作战装备能够达到的作战效能值,而且要能够评估出哪些因素对效能指标有影响以及多大影响。
传统的作战系统效能评估主要采用基于专家、直觉、知识和逻辑的方法,如层次分析法[1]、云模型[2]等,评估过程主观性较强,对于影响作战效能的关键因素及其各个因素之间的关系分析不够深入。敏感性分析作为一种基于数据的效能分析方法,往往用来研究模型输出结果受输入因素变化的影响程度及模型本身受输入因素影响程度。该方法优点是无需深入了解模型的内在作用机理,比较适合高维度非线性复杂的实兵对抗演习下的作战效能分析[3-7]。
但是在利用敏感性分析方法对系统作战效能进行评估时,对于仿真数据的数量以及形式要求较高。这对于不能产生新数据以及不能快速产生新数据的作战系统,如何利用已有数据生成新的符合要求的数据,利用敏感性分析方法完成系统效能分析是一个非常值得研究的问题。通常采用插值或拟合等方法来产生新的数据,由于体系作战中呈现出空间多维化、时间实时化、对象多元化、样式多样化等特点,导致这些方法存在着很大的不确定性,难以稳定地得到有效的结果。
本文针对系统敏感性分析方法中存在的对于仿真数据的数量以及形式要求较高的问题,将深度学习的相关知识引入进来,构建了基于深度信念网络(Deep Belief Network, DBN)的拟合模型。该模型在系统作战效能敏感性分析的研究中,能够有效地重构作战模型,利用其产生新数据,可以解决已有数据不符合敏感性分析要求的问题,进而对作战系统优化提供相应的支撑,提高了系统敏感性分析的有效性。
1 基于Sobol指数法的全局敏感性Sobol敏感性分析法[8-10]是最具有代表性的全局敏感性分析方法,它基于模型分解思想,可以分别得到参数1、2次及更高次的敏感度。它的核心思想是方差分解,把模型分解为单个参数及参数之间相互组合的函数,通过计算单个输入参数或输入参数集的方差对总输出方差的影响来分析参数的重要性以及各个参数之间的交互效应。
具体的确定敏感性指标对应的主效应指数和交互效应指数步骤如下:
1) 利用Sobol序列对输入的作战性能指标进行抽样,得到抽样矩阵(N×2n维),将矩阵前n列设置为矩阵A,后n列设置为矩阵B :
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1n}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{x_{N1}}}&{{x_{N2}}}& \cdots &{{x_{Nn}}} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {x_{11}^\prime }&{x_{12}^\prime }& \cdots &{x_{1n}^\prime }\\ {x_{21}^\prime }&{x_{22}^\prime }& \cdots &{x_{2n}^\prime }\\ \vdots & \vdots & \vdots & \vdots \\ {x_{N1}^\prime }&{x_{N2}^\prime }& \cdots &{x_{Nn}^\prime } \end{array}} \right] $ |
式中:n为作战性能指标的数量;N为作战性能指标的抽样数量;xij、x′ij均为第j个作战性能指标的第i个采样值。
将矩阵B的第i列换成矩阵A第i列,所得的矩阵记为Mi,将矩阵A的第i列换成矩阵B的第i列,所得的矩阵记为M-i,同理可定义Mi, j,M-i, -j。记YA,YB和YM分别为相应的输入矩阵值对应的输出值的列向量。
2) 基于输出列向量计算相应的估计量。
| $ \begin{array}{l} V\left( \mathit{\boldsymbol{Y}} \right) = \frac{1}{N}\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{A}}^{\rm{T}}\left( {{\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{A}}} - {\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{B}}}} \right) = \frac{1}{N}\sum\limits_{r = 1}^N {{F^2}} \left( {{x_{{r_1}}},{x_{{r_2}}}, \cdots ,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{x_{{r_n}}}} \right) - f_0^2 \end{array} $ | (1) |
| $ V\left( {E\left( {\mathit{\boldsymbol{Y}}|{\mathit{\boldsymbol{X}}_i}} \right)} \right) = \frac{1}{N}\mathit{\boldsymbol{Y}}_A^{\rm{T}}\left( {{\mathit{\boldsymbol{Y}}_{{\mathit{\boldsymbol{M}}_{\rm{i}}}}} - {\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{B}}}} \right) $ | (2) |
并记:
| $ \begin{array}{l} f_0^2 = \frac{1}{N}\mathit{\boldsymbol{Y}}_A^{\rm{T}}{\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{B}}} = \frac{1}{N}\sum\limits_{r = 1}^N {F\left( {{x_{{r_1}}},{x_{{r_2}}}, \cdots ,{x_{{r_n}}}} \right)} \cdot \\ \;\;\;\;\;\;F\left( {{{x'}_{{r_1}}},{{x'}_{{r_2}}}, \cdots ,{{x'}_{{r_n}}}} \right) \end{array} $ |
| $ \begin{array}{l} {U_i} = \frac{1}{N}\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{A}}^{\rm{T}}{\mathit{\boldsymbol{Y}}_{{\mathit{\boldsymbol{M}}_i}}} = \frac{1}{N}\sum\limits_{r = 1}^N {F\left( {{x_{{r_1}}},{x_{{r_2}}}, \cdots ,{x_{{r_n}}}} \right)} \cdot \\ \;\;\;\;\;\;F\left( {{{x'}_{{r_1}}},{{x'}_{{r_2}}}, \cdots ,{{x'}_{{r_{\left( {i - 1} \right)}}}},{x_{{r_i}}},{{x'}_{{r_{\left( {i + 1} \right)}}}}, \cdots ,{{x'}_{{r_n}}}} \right) \end{array} $ |
| $ \begin{array}{l} {U_{ - i}} = \frac{1}{N}\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{A}}^{\rm{T}}{\mathit{\boldsymbol{Y}}_{{\mathit{\boldsymbol{M}}_{ - i}}}} = \frac{1}{N}\sum\limits_{r = 1}^N {F\left( {{x_{{r_1}}},{x_{{r_2}}}, \cdots ,{x_{{r_n}}}} \right)} \cdot \\ \;\;\;\;\;\;F\left( {{x_{{r_1}}},{x_{{r_2}}}, \cdots ,{x_{{r_{\left( {i - 1} \right)}}}},{{x'}_{{r_i}}},{x_{{r_{\left( {i + 1} \right)}}}}, \cdots ,{x_{{r_n}}}} \right) \end{array} $ |
式中:f02为矩阵A和B均值的估计;V(Y)为系统响应的方差估计;Ui为矩阵A和Mi均值的估计;U-i为矩阵A和M-i均值的估计。
3) 计算敏感性指标对应的主效应指数和二阶交互效应指数。
输入变量Xi的主效应指数SXi的估计为
| $ {S_{{\mathit{\boldsymbol{X}}_i}}} = \frac{{{U_i} - f_0^2}}{{V\left( \mathit{\boldsymbol{Y}} \right)}} $ |
输入变量Xi和Xj的二阶交互效应指数SXiXj的估计为
| $ {S_{{\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{X}}_j}}} = \frac{{{U_{ij}} - f_0^2}}{{V\left( \mathit{\boldsymbol{Y}} \right)}} - {S_{{\mathit{\boldsymbol{X}}_i}}} - {S_{{\mathit{\boldsymbol{X}}_j}}} $ |
至此,在Sobol指数法的基础上,便可以开展相关参数对所确定效能的全局敏感性分析。
2 舰艇编队防空作战效能分析指标体系舰艇编队防空作战体系的效能指标可以由体系内组成系统的效能指标组合得到,而系统的效能指标又和组成舰艇编队的各类武器装备的性能指标存在很紧密的关系。接下来对构成舰艇编队的指标体系进行分析[11-13]。
系统作战效能指标是指舰艇编队各个不同的系统完成相关子任务程度的度量。主要包括舰艇编队预警探测系统的发现目标概率、可靠性概率等,指挥控制系统的指挥时效性、指挥稳定性等,以及武器打击系统的导弹杀伤目标概率、系统生存概率等。舰艇编队作战系统的作战效能指标往往和多个性能指标存在一定的联系,比如信息探测系统的发现目标概率就和预警雷达的探测范围、虚警概率、工作模式等性能指标有关。
系统性能指标是系统装备物理部件的固有特性,由装备的固有性质所决定,是系统功能特质的量化描述,从本质上反映了系统的作战能力。它主要包括功能实现的程度,功能维持的持久度,以及功能适用的范围,功能的实现条件等等。本文中主要指构成舰艇编队防空作战系统的各项子系统用于表征装备性能的指标,比如导弹数量、杀伤半径、雷达探测精度、雷达探测范围、信息处理速度、信息处理精度等。
构建作战指标体系是后续舰艇编队防空作战效能分析的基础。由以上分析可知,舰艇编队防空作战体系的性能指标、系统作战效能指标以及体系作战效能指标众多,对其进行完全的构造以及分析工作量极大。本文主要是利用该系统产生分析数据进而验证对其效能评估方法的有效性,因此主要从对来袭目标的拦截角度选择对来袭目标的拦截概率作为体系作战效能指标,分析其与性能指标的关系,如图 1所示。

|
| 图 1 与拦截概率相关的系统性能指标与效能指标 Fig. 1 System performance indicators and effectiveness indicators related to interception probability |
对于编队防空作战效能分析,分析结果的精确程度与指标体系的构建有着紧密的联系,指标选择得越详细、准确,对于作战系统的描绘就越深入,最终分析的结果就会更加精确。但是指标选择过多,会增加计算量,浪费不必要的资源。参考已有研究,指标体系的构建应该满足以下要求[14-16]:
1) 简洁性:为了减少分析的复杂程度,尽可能去除不必要的指标来评估整个系统。
2) 客观性:所选择的指标应尽量保持客观,可以通过实验等方法得到具体的值,不能主观性太强。
3) 完整性:选择的指标对于评估的各个方面都有所涉及,可以衡量待评估的所有内容。
4) 独立性:所选择的指标不能重复,尽量互不干扰。
舰艇编队作战效能指标重点考虑表 1中16个性能指标,将其作为系统的输入因素,其他因素取值固定。舰艇编队防空作战模型的输出因素选择对来袭目标的拦截概率。输出因素值可以通过舰艇编队作战模型的输入因素确定后利用仿真得到。
拦截概率为
| $ {P_{{\rm{lj}}}} = {P_{{\rm{fx}}}}{P_{{\rm{sxx}}}}{P_{{\rm{ss}}}} $ | (3) |
式中:Pss为武器杀伤目标概率;Pfx为预警探测系统发现目标概率,表达式为
| $ {P_{{\rm{fx}}}} = \int\limits_{{R_{\min }}}^{{R_{\max }}} {{P_{\rm{d}}}{\rm{d}}R/\left( {{R_{\max }} - {R_{\min }}} \right)} $ | (4) |
| 系统 | 参数 | 输入参数含义 |
| 信息探测类 | x1 = P | 发射脉冲功率 |
| x2 = G | 天线增益 | |
| x3 = λ | 雷达工作波长 | |
| x4 = σ | 目标的有效散射截面积 | |
| x5 = L | 损失系数 | |
| x6 = Fn | 雷达接收机噪声系数 | |
| x7 = nEi(n) | 积累效率 | |
| x8 = δR | 天气常数 | |
| x9 = Rmax | 雷达最大探测距离 | |
| x10 = Rmin | 雷达最小探测距离 | |
| 指挥控制类 | x11 = tbg | 发现敌情到指挥部收到情报的时间 |
| x12 = txd | 收到敌情报告到战斗任务下达完毕时间 | |
| x13 = tzb | 兵力收到战斗任务到完成准备的时间 | |
| 打击武器类 | x14 = Rhs | 导弹的毁伤半径 |
| x15 = σ | 导弹的射击误差 | |
| x16 = n1 | 导弹射击枚数 |
式中:Rmax为雷达能够发现到目标的最远距离;Rmin为雷达可以发现目标的最近距离,即雷达的可探测最小距离。来袭目标的发现概率为雷达对的探测概率Pd在Rmin到Rmax上的平均值;Psxx为舰艇编队指挥控制系统时效性概率:
| $ {P_{{\rm{sxx}}}}\left( t \right) = {{\rm{e}}^{ - \gamma {t_{{\rm{sxx}}}}}} $ | (5) |
舰艇编队指控系统需要调整的时间称为指挥时效性时间tsxx,即编队完成应对措施的时间。系统丧失指挥时效性能力的强度为γ。
| $ {P_{{\rm{ss}}}} = 1 - {\left( {1 - {P_{\rm{m}}}} \right)^n} $ | (6) |
式中:Pm为导弹对目标的命中概率;n为用来打击目标的导弹数目。
3 基于深度信念网络的效能拟合模型基于Sobol指数法的效能分析模型对于数据的完整性要求比较高,有时无法直接利用已有数据直接对作战系统进行效能评估。本文将深度学习知识应用于已有的仿真数据中,构建了基于深度信念网络的效能拟合模型,完善了效能分析模型所需要的数据。
深度信念网络[17-19]可以更加抽象地学习高层特征,并且适用于高维复杂的海量数据,这节主要基于DBN在抽取数据特征方面的优秀能力构建效能拟合模型。对于已有的历史仿真数据,利用无监督训练方法对拟合模型进行预训练,旨在对系统输入性能指标因素与系统输出效能指标之间的复杂非线性关系进行分层表征,以更好地逼近复杂现实情况。然后采用反向传播算法对预训练阶段得到的初始网络参数进行全局微调,避免了简单网络收敛缓慢和容易陷入局部最优的缺点。下面主要对效能拟合模型的网络结构,构建方法等进行分析。
3.1 效能拟合模型网络结构利用已有的仿真数据,构建基于深度信念网络的效能拟合模型。模型的输出主要是体系效能指标的值,输入数据则为影响最终体系效能指标值的各个关键性能指标值。每一种影响因素都可以再次进行划分形成输入向量x,其与输出向量y构成一个训练样本。本文提出的基于深度信念网络的效能拟合模型结构如图 2所示。
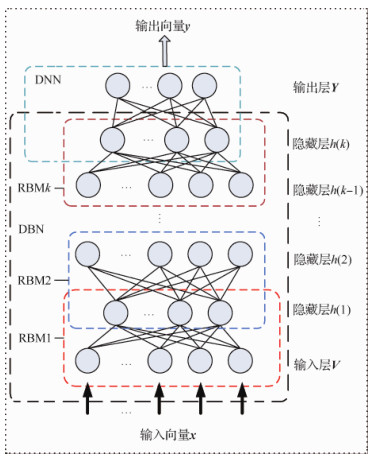
|
| 图 2 基于DBN的效能拟合模型 Fig. 2 DBN-based effectiveness fitting model |
其由一个若干层受限玻尔兹曼机组成的DBN结构和一层全连接的神经网络组成,DBN最后一层受限玻尔兹曼机的隐藏层与全连接的BP神经网络构成深度神经网络(DNN),作为网络的回归层。将DBN最后一层隐含层的输出特征向量作为神经网络的输入向量,DBN的预训练过程可以看作是整个神经网络参数初始化的过程。
3.2 效能拟合模型的预训练及调优深度信念网络是由多个受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)组成,第1层RBM的隐含层作为第2个RBM的显层,这样逐层叠加之后,就形成DBN结构。可以应用RBM的训练方法对其逐层训练,具体训练过程如下:先对受限玻尔兹曼机按逐层贪婪的方法进行逐层无监督预训练,再利用反向传播算法进行有监督调优。
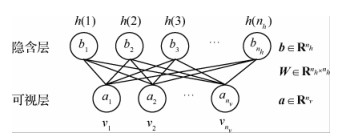
|
| 图 3 受限玻尔兹曼机的网络结构 Fig. 3 Restricted Boltzmann machine network structure |
DBN的训练过程[24]如下:先对受限玻尔兹曼机按逐层贪婪的方法进行逐层无监督预训练,再利用反向传播算法进行有监督调优。
对网络进行无监督预训练时,主要是利用训练RBM的方法对DBN进行逐层训练。DBN从下至上每相近两层可以视为一个RBM,然后利用对比散度算法对RBM进行训练并得到相应的参数。前一个RBM的输出参数作为下一个RBM的输入参数,直到最后一个RBM训练完成,便可以得到整个网络的参数。训练具体过程如图 4所示。

|
| 图 4 深度信念网络的逐层训练过程 Fig. 4 Layer-by-layer training process of deep belief network |
首先把输入向量V和第一个隐藏层h(1)作为受限玻尔兹曼机,利用对比散度算法训练出当前玻尔兹曼机中的参数,包括向量V与隐含层之间的权重以及各个节点的偏置等。获得当前受限玻尔兹曼机参数之后,参数不再改变;然后将当前隐含层h(1)作为可视层,与隐含层h(2)作为新的受限玻尔兹曼机,训练当前的受限玻尔兹曼机并获得参数;同理,将当前的隐含层h(2)作为可视层,与隐含层h(3)组成受限玻尔兹曼机,再次训练,依次逐层计算,直至最后。
预训练过程主要是通过逐层训练的方式来对DBN进行训练,训练后得到的参数只能保证该层结构对输入的特征提取达到最优,但是随着训练层数的增加,训练过程中前一层训练误差会逐渐传递到下一层,导致最后整个网络的误差较大。所以为保证整体结果的最优性,接下来需要对网络的权值进一步优化。
通常将DBN视为深层神经网络,把上一步训练得出的参数作为整个网络的初始参数,选择一定的准则来对参数进行调整。本文采用最小均方误差准则来确定参数优化方向,此时可将参数调整问题转变为均方误差最小化求优问题,即求解参数的均方误差的极小值。对于极值问题,可以利用梯度下降法来求解。然后使用反向传播的方法对这个网络的整体权值进行有监督的学习。反向传播算法将权重误差视作以权重向量中的每个元素为变量的高维函数,通过不断调整权重,来寻找训练误差的最小值,并且按照误差函数梯度下降的方向来更新权值。从而使得网络性能更优。这个过程被称为有监督的调优。具体步骤如下:
1) 采用最小均方误差准则来衡量参数的更新效果,当代价函数最小时表示参数更新完成。其中代价函数定义为
| $ E = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over Y} }_i}\left( {{W^{\left( 1 \right)}},{b^{\left( 1 \right)}}} \right) - {Y_i}} \right)}^2}} $ | (7) |
式中:E为平均平方误差;
2) 采用反向传播算法,求解网络各层梯度值,并利用求解的梯度值来更新网络的权重和偏置参数,更新过程为
| $ \left( {{W^{\left( 1 \right)}},{b^{\left( 1 \right)}}} \right) \leftarrow \left\{ {\left( {{W^{\left( 1 \right)}},{b^{\left( 1 \right)}}} \right) - \varepsilon \cdot \frac{{\partial E}}{{\partial \left( {{W^{\left( 1 \right)}},{b^{\left( 1 \right)}}} \right)}}} \right\} $ | (8) |
式中:ε为学习效率。
3) 通过上述权值更新规则,逐渐调整权重,以使误差函数值达到最小,从而得出最优的权重组合。
4 作战效能分析仿真实验 4.1 实验环境本文的舰艇编队防空作战效能评估模型是利用C++编程语言在VC++6.0编译环境下完成的。基于深度信念网络的效能拟合模型及其对比实验的仿真分析是利用MATLAB 2015b完成。
4.2 效能拟合模型搭建及分析首先重点对效能拟合模型的网络隐藏层的层数、每一层的神经元数量等结构参数进行实验,分析不同的结构参数对于效能拟合模型的影响。然后与其他方法进行对比,验证了本文提出方法的有效性。
设计实验,对指标进行随机抽样产生16 000组方案,通过舰艇编队作战模型仿真得到相应的输出因素值。这16 000组包含输入因素及输出因素值的数据构成了实验数据。实验中,主要从误差的角度选择效能拟合模型的评价指标,选择的指标主要为平均绝对百分比误差(MAPE)和平方根均方误差(RMSE),y1为拟合值,y2为实际值。
| $ {\rm{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{y_1} - {y_2}}}{{{y_2}}}} \right|} $ | (9) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left| {{y_1} - {y_2}} \right|}^2}} } $ | (10) |
对于基于深度信念网络的效能拟合模型,本文首先主要对隐藏层层数、每个隐藏层的神经元数量这两个参数的选取进行重点分析。
为了获取最佳的模型结构,首先设置第1层隐藏单元的数量,根据评价指标优劣找到最佳数量后固定;然后增加一层隐藏层,确定新一层隐藏节点的最佳数量;以此类推,直到预测精度不再提高为止。
表 2给出了选择不同隐藏层数目及每层不同节点时模型的评价指标值,隐藏层数有1~4层4种选择,每层的节点数有6种选择,分别为5、10、20、30、40、50。训练数据为16 000组实验数据,将其分成14 000组训练数据以及2 000组测试数据,对模型进行训练并计算评价指标的值。为了减小随机抽取实验样本的误差,每次按照一定的数据量抽取10次,分别对模型进行训练,然后分别计算评价指标的值,最后取平均值。结果如表 2所示。
| 隐含层数 | 隐层单元数 | 平均绝对百分误差/% | 均方根误差/% | 时间/s |
| 1 (GRBM) |
10 | 4.9776 | 3.651 | 10.38 |
| 20 | 3.79 | 2.636 | 10.97 | |
| 30 | 3.878 | 2.645 | 11.30 | |
| 40 | 3.851 | 2.656 | 11.71 | |
| 2 (1GRBM, 1BRBM) |
10 | 3.727 | 3.670 | 26.17 |
| 20 | 2.953 | 2.618 | 26.84 | |
| 30 | 2.207 | 3.587 | 27.75 | |
| 40 | 2.208 | 3.581 | 28.64 | |
| 3 (1GRBM, 2BRBM) |
10 | 1.923 | 2.061 | 34.55 |
| 20 | 1.519 | 1.988 | 35.50 | |
| 30 | 1.117 | 1.260 | 36.99 | |
| 40 | 1.366 | 1.436 | 36.89 |
分析以上结果可以得到以下结论:
1) 随着隐含层数以及节点数的增加,利用该模型得到的拟合数据的精度在一定范围内会有所提升,训练网络所用时间也在增长。当模型特别复杂时,可能会存在过拟合、训练参数需要不断动态调整等问题,导致拟合效果反而不太好。所以在构建模型时也需要考虑模型复杂度、训练难度以及训练时间等因素。
2) 当网络结构包含两个隐含层时,拟合数据的RMSE相对较大,表示结果具有较大的波动性,可能与受限玻尔兹曼机种类的更改有关。
3) 对于本文选择的数据集,效能拟合模型选择3个隐含层结构,并且第1个隐含层选择20个节点、第2个隐含层选择30个节点、第3个隐含层选择30个节点时模型的拟合效果比较好,此时模型为5层结构。
4.2.2 不完备数据下拟合模型有效性前面对模型参数结构对效能拟合模型建模效果进行了分析,接下来通过效能评估结果来分析对比完备数据和效能拟合模型2种方式下的差异,说明效能拟合模型的有效性。
对16个输入因素每个采样1 000次,得到的矩阵,共有138 000组实验方案,依次按照采样值改变各个输入参数的取值,其他参数选择初始值固定,通过性能指标与效能指标之间的映射关系进行计算,得到舰艇编队作战体系效能指标——拦截概率。
利用效能拟合模型进行敏感性分析时,首先从完备数据条件中选择500组实验方案,利用数据按照前面介绍的方法来训练效能拟合模型,并选择其中效果最好的模型作为最终的效能拟合模型。再选择1 000组实验方案,训练拟合模型,与完备数据条件下拦截概率进行对比。结果如图 5所示。
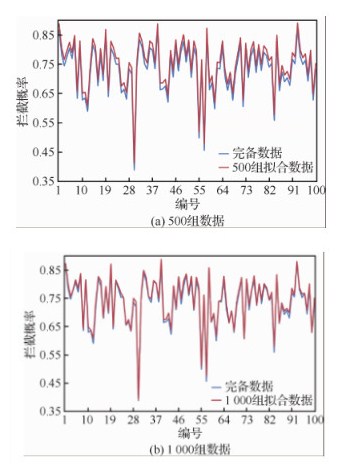
|
| 图 5 500和1 000组数据训练模型输出拦截概率 Fig. 5 Output interception probability of 500 and 1 000 data training models |
由此可见,通过拟合模型拦截概率来分析对比完备数据和效能拟合模型2种方式下的差异,随着训练数据量的提高,不完备数据下的拟合精度随之提升,可以说明拟合模型的有效性。
4.2.3 敏感性分析效果对比在不完备数据条件下,选用1 000组实验方案,利用效能拟合模型得到方案对应的效能值,计算输入变量的主效应指数以及输入变量和的二阶交互效应指数。
在完备数据条件下,通过舰艇编队作战模型仿真直接得到方案对应的效能值,计算输入变量的主效应指数以及输入变量和的二阶交互效应指数。
1) 对于主效应指数,2种方式得到的输入变量的主效应指数对比如表 3和图 6所示。
| 指标 | SXi | S′Xi |
| x1 | 0.001 841 | 0.007 09 |
| x2 | 0.122 358 | 0.155 81 |
| x3 | 0.000 139 | 0.008 62 |
| x4 | 0.000 063 | 0.001 96 |
| x5 | 0.075 703 | 0.088 95 |
| x6 | 0.010 333 | 0.040 24 |
| x7 | 0.000 112 | 0.002 48 |
| x8 | 0.004 047 | 0.005 79 |
| x9 | 0.133 080 | 0.145 97 |
| x10 | 0.030 291 | 0.051 37 |
| x11 | 0.007 314 | 0.018 50 |
| x12 | 0.111 860 | 0.159 60 |
| x13 | 0.065 481 | 0.069 25 |
| x14 | 0.115 553 | 0.129 66 |
| x15 | 0.101 984 | 0.083 29 |
| x16 | 0.006 978 | 0.040 48 |
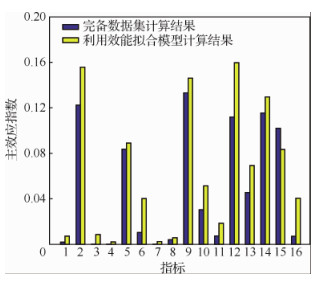
|
| 图 6 2种方式下各个指标的主效应指数值对比 Fig. 6 Comparison of main effect index values of each index under two modes |
两种方式计算的各个指标主效应指数值排序如表 4所示。
| 方式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 完备 | x9 | x2 | x14 | x12 | x15 | x5 | x13 | x10 | x6 | x11 | x16 | x8 | x1 | x3 | x7 | x4 |
| 拟合 | x12 | x2 | x9 | x14 | x5 | x15 | x13 | x10 | x16 | x6 | x11 | x3 | x1 | x7 | x4 | x4 |
由以上结果对比可知,利用效能拟合模型得到的敏感性分析主效应指数结果与完备数据条件下的敏感性分析主效应指数结果相比,各个指标的主效应指数值大小上存在有一定的差距。但是在排序上,主效应指数值最大的前4个指标是一样的,最小的后5个指标也是相同的,两个结果的整体排序相差不大。仍然可以得到对作战效能影响较大的指标为雷达最大探测距离(x9)、雷达天线增益(x2)、导弹的毁伤半径(x14)、指控系统收到敌情报告到战斗任务下达完毕的时间(x12)、导弹的射击误差(x15)以及损失系数(x5)。
2) 对于二阶交互效应指数,两种方式下每一个指标与其他指标的交互效应值见图 7~图 9。
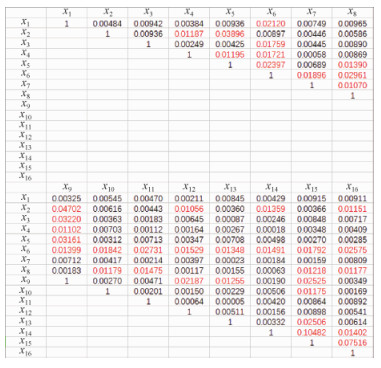
|
| 图 7 不完备数据条件下的全局敏感性分析结果 Fig. 7 Global sensitivity analysis results under incomplete data conditions |
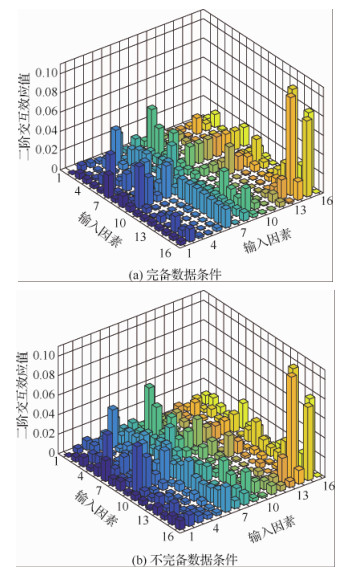
|
| 图 8 不同条件下指标间的交互作用值 Fig. 8 Interaction value of indicators under different conditions |
|
| 图 9 交互效应值对应的指标组合及排序对比 Fig. 9 Combination and ranking comparison of indicators corresponding to interactive effect values |
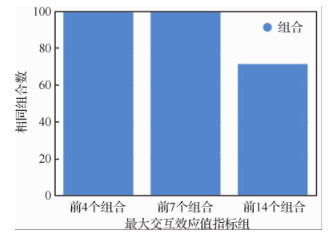
在实际的应用中,对于作战系统的效能分析会更加关注哪些指标间的交互关系对效能值影响更大,而交互作用较小的指标间的关系往往可以忽略。因此接下来对2种方式计算的全局敏感性分析结果较大的交互效应值进行比较,由大到小取前14个交互效应指数值对应的指标组合,排序对比如表 5和图 9所示。
| 方式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 完备 | x14/x15 | x15/x16 | x2/x9 | x2/x5 | x5/x9 | x6/x8 | x3/x9 | x9/x12 | x9/x15 | x1/x6 | x5/x6 | x4/x6 | x6/x12 | x6/x11 |
| 拟合 | x14/x15 | x15/x16 | x2/x9 | x2/x5 | x3/x9 | x5/x9 | x6/x8 | x6/x11 | x9/x15 | x13/x15 | x5/x6 | x9/x12 | x1/x6 | x6/x7 |
由以上结果对比可知,利用效能拟合模型得到的二阶交互效应指数值与完备数据条件下的得到的二阶交互效应指数值相比,尽管具体数值不完全一致,但是14个最大的交互效应值对应的指标组合排序很接近。其中,最大的4个交互效应值对应的指标组合及其排序是完全一致的;最大的7个交互效应值对应的指标组合是完全一致的;最大的14个交互效应值对应的指标组合中有10组是相同的。效能拟合模型在不完备数据条件下可以得到有一定参考价值的结论并且与完备条件下敏感性分析结果相近,进而证明了本文提出的方法的有效性。
5 结论1) 建立了基于Sobol指数法的效能分析模型。通过Sobol指数法来分析多个输入因素的同时改变对系统效能的影响,便可以确定影响系统效能的主要因素,为系统优化提供相应的支撑。
2) 提出了基于深度信念网络的效能拟合模型。利用深度信念网络的学习能力,对数据进行特征提取,深入探索输入与输出的复杂关系,构建了效能拟合模型。模型通过预训练及网络调优,实现了模拟作战系统产生数据的功能,进而得到足够数据来完成作战系统的效能分析。
3) 针对舰艇编队防空作战效能分析分别给出了不同的仿真案例。对于效能拟合模型,探究了不同数据量对于所提出的效能拟合模型拟合数据效果的影响,并与其他方法进行了对比,验证了提出的方法的有效性;对于数据量不足的作战系统,将所提出的效能拟合模型应用于其中得到完备数据,然后进行效能分析得到相应结果,并与完备数据条件下的效能分析结果进行对比。验证了本文提出的效能拟合模型对于不完全数据下的舰艇编队作战系统敏感性分析的有效性。
| [1] |
李国伟, 王付明, 王南星. 基于模糊AHP法的网络空间联合反恐作战指挥体系效能评估[J]. 兵器装备工程学报, 2016, 37(4): 111-113, 117. LI G W, WANG F M, WANG N X. Joint terrorism combat command system effectiveness evaluation based on fuzzy AHP in cyberspace[J]. Journal of Ordnance Equipment Engineering, 2016, 37(4): 111-113, 117. (in Chinese) |
| Cited By in Cnki (10) | Click to display the text | |
| [2] |
雷志良, 秦开兵, 许明, 等. 基于AHP-云模型的雷达对抗装备组网作战效能评估[J]. 舰船电子对抗, 2014, 37(6): 77-82. LEI Z L, QIN K B, XU M, et al. Efficiency evaluation of radar countermeasure equipment joint netting operation based on AHP-Cloud model[J]. Shipboard Electronic Countermeasure, 2014, 37(6): 77-82. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [3] |
周经伦, 傅攀峰, 罗鹏程. 基于方差的全局敏感性方法在空战效能分析中的运用[J]. 现代防御技术, 2007(6): 22-27. ZHOU J L, FU P F, LUO P C. Variance based global sensitivity analysis method using in air combat effectiveness analysis[J]. Modern Defence Technology, 2007(6): 22-27. (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [4] |
谢瑞煜, 赵建军, 蒋涛. 基于蒙特卡洛法的武器系统标定误差分析[J]. 兵器装备工程学报, 2019, 40(1): 130-134, 158. XIE R Y, ZHAO J J, JIANG T. Error analysis of weapon system calibration based on Monte Carlo method[J]. Journal of Ordnance Equipment Engineering, 2019, 40(1): 130-134, 158. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [5] |
姚裕盛, 徐开俊. 基于BP神经网络的飞行训练品质评估[J]. 航空学报, 2017, 38(S1): 24-32. YAO Y S, XU K J. Quality assessment of flight training based on BP neural network[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(S1): 24-32. (in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [6] |
郭媛媛, 孙有朝, 李龙彪. 基于蒙特卡罗方法的民用飞机故障风险评估方法[J]. 航空学报, 2017, 38(10): 155-163. GUO Y Y, SUN Y C, LI L B. Failure risk assessment method of civil aircraft based on Monte Carlo method[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 155-163. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [7] |
周智超. 面向武器装备系统效能的敏感性分析[J]. 火力与指挥控制, 2013, 38(2): 98-102. ZHOU Z C. Sensitivity analysis of oriented to system effectiveness of weapons and equipment[J]. Fire Control and Command Control, 2013, 38(2): 98-102. (in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [8] |
衡德正, 陈伟, 胡轶敏, 等. 基于Sobol序列的装配公差分析[J]. 机械设计与制造, 2016(12): 227-230. HENG D Z, CHEN W, HU Y M, et al. Assembly tolerance analysis based on the Sobol sequence[J]. Machinery Design & Manufacture, 2016(12): 227-230. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [9] | JOE S, KUO F Y. Constructing Sobol sequences with better two-dimensional projections[J]. SIAM Journal on Scientific Computer, 2008, 30(5): 2635-2654. |
| Click to display the text | |
| [10] | BRATLEY P, FOX B L. Algorithm 659:Implementing Sobol's quasirandom sequence generator[J]. ACM Transactions on Mathematical Software, 1988, 14(1): 88-100. |
| Click to display the text | |
| [11] |
陈国生, 马良, 张明. 舰艇编队协同防空作战效能评估[J]. 舰船科学技术, 2011, 33(2): 105-107. CHEN G S, MA L, ZHANG M. Effect evaluation of coordinated-air defense of warships[J]. Ship Science and Technology, 2011, 33(2): 105-107. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [12] | SONGLEI N, YAN J. Research on coordination air-defense decision-making optimum model of naval ship formation[J]. Computer Engineering & Applications, 2013, 49(6): 257-261. |
| Click to display the text | |
| [13] |
罗鹏程, 周经伦, 金光, 等. 武器装备体系作战效能与作战能力评估分析方法[M]. 北京: 国防工业出版社, 2014. LUO P C, ZHOU J L, JIN G, et al. Analysis on assessment methods for combat capability of weapon SoS[M]. Beijing: National Defense Industry Press, 2014. (in Chinese) |
| [14] |
罗亚民, 宋贵宝. 海军导弹装备采办综合绩效评价体系构建[J]. 兵器装备工程学报, 2018(2): 146-152. LUO Y M, SONG G B. Construction of comprehensive performance evaluation system for navy missile equipment acquisition[J]. Journal of Ordnance Equipment Engineering, 2018(2): 146-152. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [15] |
苏建刚.武器装备效能评估指标体系研究[A].北京: 中国自动化学会, 2017: 4. SU J G. Research on effectiveness evaluation index system of weapon equipment[A]. Beijing: Chinese Association of Automation, 2017: 4(in Chinese). |
| [16] |
周静杨.舰艇编队分布式协同防空建模与仿真[D].西安: 西北工业大学, 2016. ZHOU J Y. Modeling and simulation of distributed cooperative air defense for warship fleet[D]. Xi'an: Northwestern Polytechnical University, 2016(in Chinese). |
| [17] |
张晓海, 操新文, 耿松涛, 等. 基于深度学习的军事辅助决策智能化研究[J]. 兵器装备工程学报, 2018, 39(10): 162-167. ZHANG X H, CAO X W, GENG S T, et al. Research on intelligence of military auxiliary decision-Making system based on deep learning[J]. Journal of Ordnance Equipment Engineering, 2018, 39(10): 162-167. (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [18] | JABARDI M H, AL-FATLAWI A H, LING S. Jabardi diagnosis system for parkinson's disease using speech characteristics of patients and deep belief network[J]. CAAI Transaction on Intelligence Technology, 2017, 2(9): 246-253. |
| [19] | HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2014, 18(7): 1527-1554. |
| Click to display the text | |
| [20] | FISCHER A, IGEL C. Training restricted boltzmann machines:An introduction[J]. Pattern Recognition, 2014, 47: 25-39. |
| Click to display the text | |
| [21] | HOCHREITER S, MOZER M C. Monaural speech separation by support vector machines:Bridging the divide between supervised and unsupervised learning methods[M]. Blind Speech Separation. Berlin: Springer, 2008: 18. |
| [22] | HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2014, 18(7): 1527-1554. |
| Click to display the text | |
| [23] | SUTSKEVER I, TIELEMAN T. On the convergence properties of contrastive divergence[J]. Journal of Machine Learing Research, 2010, 9(4): 789-795. |
| Click to display the text | |
| [24] |
陈春利, 金炜东. 一种改进的DNN算法在雷达信号分选中的应用[J]. 计算机应用研究, 2019(4): 1-5. CHEN C L, JIN W D. Application of improved DNN algorithm in radar signal sorting[J]. Application Research of Computers, 2019(4): 1-5. (in Chinese) |
| Cited By in Cnki (2) | Click to display the text |



