结构振动普遍存在于航空、航天、船舶等工程领域^[1]中。过大的振动会导致结构的高周疲劳甚至失效，而增加阻尼是降低振动的有效方式。虽然对新型阻尼器的研究长盛不衰(如压电分支阻尼技术^[2-5])，但基于摩擦耗能原理的干摩擦阻尼器由于具有结构简单、可靠性高、减振效果明显且受温度影响较小等优点，仍是最常用且最受关注的阻尼技术之一^[6-8]。在现役航空发动机中，就有多种形式的干摩擦阻尼器，如叶冠、叶片凸肩、缘板阻尼器、阻尼环等^[9-12]。随着未来飞行器对更高的推重比的追求，将进一步大量采用薄壁结构，这必然会导致更为突出的结构振动问题^[9]。然而针对适用于一般薄壁结构的干摩擦阻尼器的研究尚不多见。

设计干摩擦阻尼器的关键技术之一是发展含接触环节的非线性动力学模型及其求解方法。如果主要关注的是一类干摩擦系统的普适动力学行为，则常用集总参数模型，即将结构用少数几个质量和弹簧的组合表征。研究人员已经用这类模型探索了叶根阻尼器^[13]、缘板阻尼器^[14-16]、针对齿轮扭振的单个^[17]和多个^[18]阻尼环。集中参数模型的自由度很少，数值问题不突出，因此适合用于机理性研究或算法的合理有效性研究^[19-20]。

如果主要关注的是具体的干摩擦阻尼器及其对所施加结构的减振效果(尤其是针对多个高阶模态时)，则应考虑使用高保真有限元模型。例如，张大义等^[21]基于实体有限元模型建立了缘板阻尼结构的设计流程和优化方法，并给出了结构设计合理性的评估参数。Petrov和Ewins^[22]利用高保真有限元模型分析了带冠叶片的强迫响应，并对屋顶形阻尼器(Cottage Roof Dampers, CRDs)与分离式阻尼器(Split Dampers, SDs)的减振性能进行了比较^[23]，并说明相比于CRDS，SDs对质量参数的变化不敏感。Charleux等^[24]将榫接叶盘结构强迫响应的试验与仿真结果进行对比，说明了利用高保真模型来预测带接触系统的振动特性是可行、可信的。高保真模型的自由度数一般较大，使得直接进行时域积分变得非常耗时，这就需要发展减缩模型和高效的频域求解算法。目前常用动力凝缩和子结构方法减缩线性自由度的规模^[25-26]。对于非线性自由度，可以在谐波平衡的框架内利用周期对称性对叶盘等循环周期结构上的接触点数目进行减缩^[27]；或对于一般结构，Krack等^[28-29]还发展了非线性模态减缩技术，用以计算失谐榫接叶盘的强迫响应。目前最常用的频域求解方法是谐波平衡法，即通过傅里叶变换将对非线性常微分方程的求解转换为对非线性代数方程组的求解。即使针对集总参数模型，其计算效率远高于时间积分法^[30](CPU时间只是后者的约1%), 但随着自由度数的增加，谐波平衡法也面临多个数值问题，其中的一个主要问题是用数值差分求雅克比矩阵的误差导致牛顿-拉夫逊迭代难以收敛^[31]。

本文提出一种适用于一般薄壁结构的波纹形干摩擦阻尼器，具有适用性强、正压力调节方便、易于安装等特点；并利用高保真有限元模型计算其频响特性, 展示其阻尼性能随安装螺栓压紧力的变化规律。在计算方法上，采用了加速动态拉格朗日法对强迫响应进行预测，并给出了解析形式的雅克比矩阵，使算法的精度和速度得以大幅提升。通过集中参数模型的算例说明了理论推导及程序编写的合理与正确性。利用一个四边固支的平板结构来说明波纹形摩擦片的阻尼性能。

1 波纹形摩擦阻尼片

本文所考虑的波纹形干摩擦阻尼片如图 1所示。阻尼片的2个接触面对称分布在安装面两侧，通过振动时接触面与底部承载结构之间的相对运动产生的摩擦来达到减振的目的。安装面利用螺栓与螺母进行固定。

接触面的正压力是干摩擦阻尼器设计时的关键参数，对干摩擦阻尼器的性能有着显著的影响。当正压力过小时，接触面产生的切向力较小，导致由摩擦损耗的能量较小；当正压力过大时，由于接触面之间的相对滑移量减小，使得减振性能下降；当正压力增大到使得接触面达到“完全阻滞”状态时，此时干摩擦阻尼器只有微小的调节固有频率的作用，而不具备阻尼作用。对于图 1(a)所示的阻尼器，可以通过改变螺栓的拧紧程度来调节接触面上的正压力。

在对波纹形阻尼器的减振特性进行分析时，采用了如图 1(b)所示的有限元模型。其中T₁、W₁分别代表阻尼片的厚度与宽度。摩擦片的轮廓线(在xOy平面的投影)关于中心(安装点)对称，共由3段曲线构成：中间段为长为L₁的直线，左右2段均为余弦曲线, 满足如下关系：

$ y = {H_1} \times \cos \left( {\frac{{\rm{ \mathit{ π} }}}{{{L_2}}}x} \right) $	（1）

式中：L₂为半波长; H₁为波的峰值。直线段分别与两边的余弦曲线段相切。工作过程中会通过拧紧安装面两侧的螺母来减小非摩擦界面处的相对运动，此时安装面近似于固支状态，因此在有限元分析中，螺栓与螺母结构可用图 1(b)中位于安装面区域内连接摩擦片与主体结构的实体单元来代替。接触节点位于阻尼片下侧的接触面上，它们与主体结构上对应的节点重合。

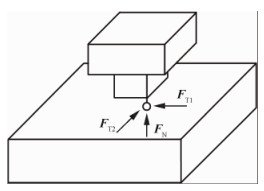
接触节点之间的相对运动相比于整体结构的振动幅值较小，因此可以采用点对点式的接触单元来描述微滑移运动，如图 2所示。该模型又被称为三维接触运动模型，其中F_N代表法向正压力，由接触对之间沿法向的相对位移决定，因此其能够考虑由于自身形变所导致正压力改变；F_T1与F_T2分别代表接触平面上2个正交方向的摩擦力，在计算中认为它们是互不影响的^[32]。该模型能够完备地描述三维空间中接触对之间的运动关系，在对高保真有限元模型研究时应用较为广泛^{[22-23, 26]}。

2 干摩擦结构响应的快速预测

为了展示波纹形干摩擦阻尼片的减振效果，用频响函数的峰值作为评价指标。为此，采用了基于时频转换(Alternating Frequency-Time domain, AFT)的速度型动态拉格朗日法^[26](Dynamic Lagrange Frequency-Time method，DLFT)。相比于以迟滞弹簧模型为基础的强迫响应预测算法^[27]，DLFT的主要优点为：①不需要确定切法向弹簧刚度的值，同时计算结果对引入的惩罚系数的值不敏感^[33]；②时域内不需要通过迭代来使得非线性力满足周期条件^[34]。在此基础上，引入了解析形式的雅克比矩阵使得算法的计算效率与收敛稳定性大幅提升。

2.1 高阶谐波平衡法求解非线性动力学方程

对于带有干摩擦阻尼的非线性系统，其离散形式的动力学方程可以写为

$ \mathit{\boldsymbol{M\ddot u}}\left( t \right) + \mathit{\boldsymbol{C\dot u}}\left( t \right) + \mathit{\boldsymbol{Ku}}\left( t \right) + {\mathit{\boldsymbol{q}}_{{\rm{nl}}}}\left( t \right) = {\mathit{\boldsymbol{q}}_{{\rm{ex}}}}\left( t \right) $	（2）

式中：M、C和K分别为质量、阻尼和刚度矩阵；q_ex(t)为外激振力向量，在本文中仅考虑其为时间的简谐形式；q_nl(t)代表作用于摩擦界面处的非线性干摩擦力，包括了切向与法向分量；u(t)为位移向量；上标(·)代表对时间的一次求导。直接在时域内求解式(2)这样的2阶非线性微分方程组将会耗费大量时间，尤其当自由度较多且求解的是稳态响应时，计算时间成本将迅速增加。故本文在频域内采用高阶谐波平衡法求解式(2)的稳态强迫响应。

高阶谐波平衡法的出发点是将位移、外激励和非线性力表示成傅里叶级数，并截取前N_h项。因此，位移项u(t)可写为

$ \mathit{\boldsymbol{u}}\left( t \right) = \Re \left\{ {\sum\limits_{n = 0}^{{N_{\rm{h}}}} {{{\mathit{\boldsymbol{\tilde u}}}^{\left( n \right)}}{{\rm{e}}^{{\rm{j}}n\omega t}}} } \right\} $	（3）

式中：${\mathit{\boldsymbol{\widetilde u}}^{\left( n \right)}}$为位移在频域内的第n次谐波分量；ω为角频率。同理，q_ex(t)可表示为

$ {\mathit{\boldsymbol{q}}_{{\rm{ex}}}}\left( t \right) = \Re \left\{ {\sum\limits_{n = 0}^{{N_{\rm{h}}}} {\mathit{\boldsymbol{\tilde q}}_{{\rm{ex}}}^{\left( n \right)}{{\rm{e}}^{{\rm{j}}n\omega t}}} } \right\} $	（4）

式中：$\mathit{\boldsymbol{\widetilde q}}_{{\rm{ex}}}^{\left( n \right)}$为激振力在频域内的第n次谐波分量。由于求解的是稳态响应，因此位移必然是时间周期的，非线性力q_nl(t)也是周期的，即可以写成傅里叶级数的形式：

$ {\mathit{\boldsymbol{q}}_{{\rm{nl}}}}\left( t \right) = \Re \left\{ {\sum\limits_{n = 0}^{{N_{\rm{h}}}} {\mathit{\boldsymbol{\tilde q}}_{{\rm{nl}}}^{\left( n \right)}{{\rm{e}}^{{\rm{j}}n\omega t}}} } \right\} $	（5）

式中：$\mathit{\boldsymbol{\widetilde q}}_{{\rm{nl}}}^{\left( n \right)}$是非线性力在频域内的第n次谐波分量。将式(3)~式(5)代入式(2)中，可得

$ \begin{array}{*{20}{l}} {\sum\limits_{n = 0}^{\mathit{N}{\rm{h}}} {\left( {\left[ { - {{\left( {n\omega } \right)}^2}\mathit{\boldsymbol{M}} + {\rm{j}}n\omega \mathit{\boldsymbol{C}} + \mathit{\boldsymbol{K}}} \right]{{\mathit{\boldsymbol{\tilde u}}}^{\left( n \right)}} + } \right.} }\\ {\;\;\;\;\;\left. {\mathit{\boldsymbol{\tilde q}}_{{\rm{nl}}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde q}}_{{\rm{ex}}}^{\left( n \right)}} \right){{\rm{e}}^{{\rm{j}}n\omega t}} = \mathit{\boldsymbol{0}}} \end{array} $

（6）

由于e^jnωt≠0，因此只能前面括号里的向量为零，从而获得一组非线性代数方程组：

$ {\mathit{\boldsymbol{H}}^{\left( n \right)}}{{\mathit{\boldsymbol{\tilde u}}}^{\left( n \right)}} + \mathit{\boldsymbol{\tilde q}}_{{\rm{nl}}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde q}}_{{\rm{ex}}}^{\left( n \right)} = \boldsymbol{0}\;\;\;\;n = 0,1, \cdots ,{N_{\rm{h}}} $	（7）

式中：H⁽ⁿ⁾为第n阶谐波的动刚度矩阵，即

$ {\mathit{\boldsymbol{H}}^{\left( n \right)}} = - {\left( {n\omega } \right)^2}\mathit{\boldsymbol{M}} + {\rm{j}}n\omega \mathit{\boldsymbol{C}} + \mathit{\boldsymbol{K}} $	（8）

在解该非线性代数方程组时，一般常用“牛顿-拉夫逊”迭代法以及其改进方法^[15]。然而随着方程自由度的提高，计算效率与稳定性都会明显下降。注意到相对于整个结构系统，接触面只占很小一部分，因此本文进行自由度凝缩，以减少迭代时方程的自由度。首先，将式(7)中的向量和矩阵分成线性自由度(下标l)与非线性自由度(下标nl)：

$ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}_{1,1}^{\left( n \right)}}&{\mathit{\boldsymbol{H}}_{1,{\rm{nl}}}^{\left( n \right)}}\\ {\mathit{\boldsymbol{H}}_{{\rm{nl}},1}^{\left( n \right)}}&{\mathit{\boldsymbol{H}}_{{\rm{nl}},{\rm{nl}}}^{\left( n \right)}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde u}}_1^{\left( n \right)}}\\ {\mathit{\boldsymbol{\tilde u}}_{{\rm{nl}}}^{\left( n \right)}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\bf{0}}\\ {\mathit{\boldsymbol{\tilde q}}_{{\rm{nl}}}^{\left( n \right)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde q}}_{{\rm{ex,1}}}^{\left( n \right)}}\\ {\mathit{\boldsymbol{\tilde q}}_{{\rm{ex}},{\rm{nl}}}^{\left( n \right)}} \end{array}} \right] $

（9）

再通过凝聚，仅保留非线性自由度：

$ {\mathit{\boldsymbol{D}}^{\left( n \right)}}\mathit{\boldsymbol{\tilde u}}_{{\rm{nl}}}^{\left( n \right)} + \mathit{\boldsymbol{\tilde q}}_{{\rm{nl}}}^{\left( n \right)} = \mathit{\boldsymbol{\tilde f}}_{{\rm{ex}}}^{\left( n \right)} $	（10）

式中：D⁽ⁿ⁾和$\mathit{\boldsymbol{\widetilde f}}_{{\rm{ex}}}^{\left( n \right)}$分别为凝缩后的动态刚度矩阵与外激励矢量，即

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{D}}^{\left( n \right)}} = \mathit{\boldsymbol{H}}_{{\rm{nl}},{\rm{nl}}}^{\left( n \right)} - \mathit{\boldsymbol{H}}_{{\rm{nl}},1}^{\left( n \right)}\mathit{\boldsymbol{H}}_{{\rm{l}},1}^{\left( n \right) - 1}\mathit{\boldsymbol{H}}_{1,{\rm{nl}}}^{\left( n \right)}\\ \mathit{\boldsymbol{\tilde f}}_{{\rm{ex}}}^{\left( n \right)} = \mathit{\boldsymbol{\tilde q}}_{{\rm{ex,nl}}}^{\left( n \right)} - \mathit{\boldsymbol{H}}_{{\rm{nl}},1}^{\left( n \right)}\mathit{\boldsymbol{H}}_{{\rm{l}},1}^{\left( n \right) - 1}\mathit{\boldsymbol{\tilde q}}_{{\rm{ex,l}}}^{\left( n \right)} \end{array} \right. $

（11）

这样，总自由度从(N_l+N_nl)×(N_h+1)变为N_nl×(N_h+1)，其中N_l和N_nl分别为线性自由度数与非线性自由度数。

一组接触点之间的非线性力大小相等方向相反，因此将非线性向量$\mathit{\boldsymbol{\widetilde u}}_{{\rm{nl}}}^{\left( n \right)}$分成2类：观察自由度$\mathit{\boldsymbol{\widetilde u}}_{{\rm{obs}}}^{\left( n \right)}$和参考自由度$\mathit{\boldsymbol{\widetilde u}}_{{\rm{ref}}}^{\left( n \right)}$，且接触的2个自由度在2组向量中的位置相同。将$\mathit{\boldsymbol{\widetilde u}}_{{\rm{obs}}}^{\left( n \right)}$所对应的非线性力$\mathit{\boldsymbol{\widetilde q}}_{{\rm{nl, obs}}}^{\left( n \right)}$用拉格朗日乘子${\mathit{\boldsymbol{\widetilde \lambda }}^{\left( n \right)}}$表示，则$\mathit{\boldsymbol{\widetilde q}}_{{\rm{nl, ref}}}^{\left( n \right)} = - {\mathit{\boldsymbol{\widetilde \lambda }}^{\left( n \right)}}$。由此，式(9)可以改写为

$ \mathit{\boldsymbol{\tilde u}}_{{\rm{nl}}}^{\left( n \right)} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde u}}_{{\rm{obs}}}^{\left( n \right)}}\\ {\mathit{\boldsymbol{\tilde u}}_{{\rm{ref}}}^{\left( n \right)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}_{{\rm{obs,obs}}}^{\left( n \right)}}&{\mathit{\boldsymbol{S}}_{{\rm{obs,ref}}}^{\left( n \right)}}\\ {\mathit{\boldsymbol{S}}_{{\rm{ref,obs}}}^{\left( n \right)}}&{\mathit{\boldsymbol{S}}_{{\rm{ref,ref}}}^{\left( n \right)}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde f}}_{{\rm{ex}},{\rm{obs}}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde \lambda }}}\\ {\mathit{\boldsymbol{\tilde f}}_{{\rm{ex}},{\rm{ref}}}^{\left( n \right)} + \mathit{\boldsymbol{\tilde \lambda }}} \end{array}} \right] $

（12）

式中：S⁽ⁿ⁾=[D⁽ⁿ⁾]^－1。对于任意一组接触点，引入相对位移：

$ \mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} = \mathit{\boldsymbol{\tilde u}}_{{\rm{obs}}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde u}}_{{\rm{ref}}}^{\left( n \right)} $	（13）

联立方程式(12)与式(13)，则动力学方程组可最终表示为相对位移的形式：

$ \mathit{\boldsymbol{D}}_{\rm{r}}^{\left( n \right)}\mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} + {{\mathit{\boldsymbol{\tilde \lambda }}}^{\left( n \right)}} = \mathit{\boldsymbol{\tilde f}}_{\rm{r}}^{\left( n \right)} $	（14）

其中：

$ \begin{array}{l} \mathit{\boldsymbol{D}}_{\rm{r}}^{\left( n \right)} = {\left( {\mathit{\boldsymbol{S}}_{{\rm{obs}},{\rm{obs}}}^{\left( n \right)} - \mathit{\boldsymbol{S}}_{{\rm{obs}},{\rm{ref}}}^{\left( n \right)} - \mathit{\boldsymbol{S}}_{{\rm{ref}},{\rm{obs}}}^{\left( n \right)} + \mathit{\boldsymbol{S}}_{{\rm{ref}},{\rm{ref}}}^{\left( n \right)}} \right)^{ - 1}}\\ \mathit{\boldsymbol{\tilde f}}_{\rm{r}}^{\left( n \right)} = \mathit{\boldsymbol{D}}_{{\rm{ref}}}^{\left( n \right)}\left( {\mathit{\boldsymbol{S}}_{{\rm{obs}},{\rm{obs}}}^{\left( n \right)} - \mathit{\boldsymbol{S}}_{{\rm{ref}},{\rm{obs}}}^{\left( n \right)}} \right)\mathit{\boldsymbol{\tilde f}}_{{\rm{ex}},{\rm{obs}}}^{\left( n \right)} + \\ \;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{D}}_{{\rm{ref}}}^{\left( n \right)}\left( {\mathit{\boldsymbol{S}}_{{\rm{obs}},{\rm{ref}}}^{\left( n \right)} - \mathit{\boldsymbol{S}}_{{\rm{ref}},{\rm{ref}}}^{\left( n \right)}} \right)\mathit{\boldsymbol{\tilde f}}_{{\rm{ex}},{\rm{ref}}}^{\left( n \right)} \end{array} $

（15）

由此，方程组的自由度数进一步降低到原来的一半，即N_nl×(N_h+1)/2。在对式(14)进行求解时，一般将其写为收敛残差的形式，即

$ {\mathit{\boldsymbol{R}}^{\left( n \right)}} = \mathit{\boldsymbol{D}}_{\rm{r}}^{\left( n \right)}\mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} + {{\mathit{\boldsymbol{\tilde \lambda }}}^{\left( n \right)}} - \mathit{\boldsymbol{\tilde f}}_{\rm{r}}^{\left( n \right)} $	（16）

当$\left\| {{\mathit{\boldsymbol{R}}^{\left( n \right)}}} \right\| \approx 0, n = 0, 1, \cdots , {N_{\rm{h}}}$时，方程收敛，同时得位移${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$和非线性力$\mathit{\boldsymbol{\widetilde \lambda }}$。将$\mathit{\boldsymbol{\widetilde q}}_{{\rm{nl, obs}}}^{\left( n \right)} = - \mathit{\boldsymbol{\widetilde q}}_{{\rm{nl, ref}}}^{\left( n \right)} = {\mathit{\boldsymbol{\widetilde \lambda }}^{\left( n \right)}}$代入式(9)中，即可求得完整的位移向量。

2.2 速度型动态拉格朗日法求解非线性力

在求解以${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$为未知量的非线性代数方程组式(16)时，采用牛顿-拉夫逊迭代法。虽然拉格朗日乘子(非线性力) $\mathit{\boldsymbol{\widetilde \lambda }}$由相对位移${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$决定，但当保留的谐波数N_h >3时，两者的解析关系难以在频域内给出^[15]。因此关键是如何通过每次迭代中的已知量——相对位移${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$计算未知量——非线性力$\mathit{\boldsymbol{\widetilde \lambda }}$。为此，首先用相对位移${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$计算相对速度${\mathit{\boldsymbol{\widetilde v}}_{\rm{r}}}$，即

$ \mathit{\boldsymbol{\tilde v}}_{\rm{r}}^{\left( n \right)} = {\rm{j}}n\omega \mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} $	（17）

并用如下关系计算非线性力：

$ \begin{array}{l} {{\mathit{\boldsymbol{\tilde \lambda }}}^{\left( n \right)}} = \mathit{\boldsymbol{\tilde f}}_{\rm{r}}^{\left( n \right)} - \mathit{\boldsymbol{D}}_{\rm{r}}^{\left( n \right)}\mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} + {\varepsilon _{\rm{T}}}\mathit{\boldsymbol{B}}_{\rm{T}}^{\rm{T}}\left( {{\mathit{\boldsymbol{B}}_{\rm{T}}}\mathit{\boldsymbol{\tilde v}}_{\rm{r}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde V}}_{\rm{T}}^{\left( n \right)}} \right) + \\ \;\;\;\;\;{\varepsilon _{\rm{N}}}\mathit{\boldsymbol{B}}_{\rm{N}}^{\rm{T}}\left( {{\mathit{\boldsymbol{B}}_{\rm{N}}}\mathit{\boldsymbol{\tilde u}}_{\rm{r}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde X}}_{\rm{N}}^{\left( n \right)}} \right) \end{array} $

（18）

式中：B_T和B_N是布尔矩阵，它们的作用是从相对位移向量中提出切向和法向分量，详见附录A；$\mathit{\boldsymbol{\widetilde V}}_{\rm{T}}^{\left( n \right)}$与$\mathit{\boldsymbol{\widetilde X}}_{\rm{N}}^{\left( n \right)}$分别为切向相对速度与法向相对位移的n次谐波分量的“修正值”，它们是通过后续的时频转换法得到的，作用是使得接触面间的相对运动在时域满足接触约束条件；ε_T和ε_N分别为切向和法向的惩罚系数。

式(17)可以看做是在式(14)的基础上，分别在切向(下标T)引入了一个关于相对速度的惩罚项以及在法向(下标N)引入了一个关于相对位移的惩罚项，其中ε为惩罚系数。

将式(18)中含$\mathit{\boldsymbol{\widetilde V}}_{\rm{T}}^{\left( n \right)}$和$\mathit{\boldsymbol{\widetilde X}}_{\rm{N}}^{\left( n \right)}$的项合并为$\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}^{\left( n \right)}$，其余项合并为$\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$，则式(18)可改写为

$ {{\mathit{\boldsymbol{\tilde \lambda }}}^{\left( n \right)}} = \mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)} - \mathit{\boldsymbol{\tilde \lambda }}_{\rm{x}}^{\left( n \right)} $	（19）

由于每次迭代过程都假设${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$已知，故${\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}}$的值可在频域内计算得到，因此求解$\mathit{\boldsymbol{\widetilde \lambda }}$的关键在于利用时频转换法求解$\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}^{\left( n \right)}$的大小。

利用傅里叶逆变换，将式(19)的每一项都变换到时域，此时每个自由度的运动都被离散至N_s个时间点上，其中任意第l个时间点下的拉格朗日乘子λ(l)可表示为

$ \mathit{\boldsymbol{\lambda }}\left( l \right) = {\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right) - {\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right) $	（20）

注意此时实际上已知的是λ_u，λ和λ_x暂时是未知的，采用下面的预测-修正方法求得。

对于任意接触点k，首先假设其在时间步l处为阻滞状态，即2个接触点之间没有相对运动，因此^kλ_x(l)=0，得到非线性力的预测值：

$ {}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{pre}}}}\left( l \right) = {}^k{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right) $	（21）

再利用库伦摩擦定律来判断该点的真实接触状态，并用^kλ_x(l)对非线性力进行修正，共有如下3种情况：

1) 分离：|^kλ_{pre, N}(l)|+|N₀|≤0，其中N₀代表施加在接触点上的初始正压力。此时接触对之间不存在接触力的作用，即^kλ(l)=0，此时：

$ {}^k{\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right) = {}^k{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right) $	（22）

2) 阻滞：|^kλ_{pre, N}(l)|+|N₀|>0，同时切向力|^kλ_{pre, T}(l)| < μ_f|^kλ_{pre, N}(l)+N₀|。其中μ_f代表接触面的摩擦系数。满足此条件时，说明当前的接触状态与预测结果相吻合，无需对非线性力进行修正，即

$ {}^k{\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right) = 0 $	（23）

3) 滑移：|^kλ_{pre, N}(l)|+|N₀|>0，同时切向力|^kλ_{pre, T}(l)| < μ_f|^kλ_{pre, N}(l)+N₀|。此时法向接触点之间相对位移的值为0；切向存在相对运动，且根据库伦摩擦定律，切向摩擦力的大小可表示为μ_f|^kλ_{pre, N}(l)+N₀ |，方向与相对速度的方向一致，因此可以得到滑移状态下的修正项：

$ \left\{ \begin{array}{l} {}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{x,N}}}}\left( l \right) = 0\\ {}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{x,T}}}}\left( l \right) = {}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{pre,T}}}}\left( l \right) - \\ \;\;\;\;\;\;\;{\mu _{\rm{f}}}\left| {{}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{pre,N}}}}\left( l \right) + {\mathit{\boldsymbol{N}}_0}} \right|{\rm{sign}}\left( {{}^k{\mathit{\boldsymbol{\lambda }}_{{\rm{pre,T}}}}\left( l \right)} \right) \end{array} \right. $

（24）

用式(20)~式(24)可得到非线性力在一个周期内的时间历程λ。利用傅里叶变换，就获得了非线性力在频域内的值$\mathit{\boldsymbol{\widetilde \lambda }}$。利用拉格朗日法求解非线性力的流程图如图 3所示。

需要注意的是，基于牛顿-拉夫逊法的迭代方法为局部收敛法，即当给的初值与方程的解较接近时，该方法具有较强的数值稳定性，反之方程容易不收敛。因此在求解频域内的强迫响应时，可以采用自适应步长的自然延拓法从小到大进行扫频计算，并以上一个频率点的迭代收敛解作为计算下一个频率点强迫响应的迭代初值。对于第一个频率点，一般将远离共振峰处系统不受非线性力作用下相对位移的频域值作为迭代初值。

2.3 用解析雅克比矩阵加速计算

在利用牛顿-拉夫逊法以及其改进方法进行迭代时，其中必要的一步则是用非线性代数方程组式(15)的雅克比矩阵来判断下一次迭代的值，在MATLAB中用fsolve函数解非线性方程组时，默认情况下该矩阵一般通过有限差分法给出。然而当方程中的非线性自由度数较大时，利用数值差分计算雅克比矩阵的时间成本较大，且精度也较低。如果能给出解析形式的雅克比矩阵，就能够有效地解决这一问题^[27]。因此，给出适用于速度型动态拉格朗日法的解析雅克比矩阵。

对于收敛残差形式的运动方程(16)，其雅克比矩阵可写为

$ \mathit{\boldsymbol{J}} = \frac{{\partial \mathit{\boldsymbol{R}}\left( {{{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}} \right)}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} = {\mathit{\boldsymbol{D}}_{\rm{r}}}\frac{{\partial \mathit{\boldsymbol{\tilde \lambda }}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} $	（25）

式中：D_r直接通过式(15)计算得到，因此计算J的关键就在于求解拉格朗日乘子对于相对位移矢量的偏导。利用求导的链式法则，式(25)的第2项写为

$ \frac{{\partial \mathit{\boldsymbol{\tilde \lambda }}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} = \left( {\mathit{\boldsymbol{I}} - \frac{{\partial {{\mathit{\boldsymbol{\tilde \lambda }}}_{\rm{x}}}}}{{\partial {{\mathit{\boldsymbol{\tilde \lambda }}}_{\rm{u}}}}}} \right)\frac{{\partial {{\mathit{\boldsymbol{\tilde \lambda }}}_{\rm{u}}}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} $

（26）

其中：

$ \frac{{\partial {{\mathit{\boldsymbol{\tilde \lambda }}}_{\rm{u}}}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} = - {\mathit{\boldsymbol{D}}_{\rm{r}}} + {\varepsilon _{\rm{T}}}\mathit{\boldsymbol{B}}_{\rm{T}}^{\rm{T}}{\mathit{\boldsymbol{B}}_{\rm{T}}}\frac{{\partial {{\mathit{\boldsymbol{\tilde v}}}_{\rm{r}}}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} + {\varepsilon _{\rm{N}}}\mathit{\boldsymbol{B}}_{\rm{N}}^{\rm{T}}{\mathit{\boldsymbol{B}}_{\rm{N}}}\frac{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}}{{\partial {{\mathit{\boldsymbol{\tilde u}}}_{\rm{r}}}}} $

（27）

需要注意的是，由于相对位移${\mathit{\boldsymbol{\widetilde u}}_{\rm{r}}}$为复数矢量，因此需要分别对实部与虚部求导。

基于傅里叶变换的线性特性，同样可以通过时频转换法来计算偏导矩阵$\partial {\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}}/\partial {\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}}$。以第m阶谐波分量下第k个接触点所受的非线性力关于第n阶谐波分量下第h个接触点所受的非线性力的偏导${\partial ^k}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}^{\left( m \right)}/{\partial ^h}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$为例，将$^k\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}^m$用时域内的^kλ_x来表示：

$ {}^k\mathit{\boldsymbol{\tilde \lambda }}_{\rm{x}}^{\left( m \right)} = \frac{1}{{{N_{\rm{s}}}}}\sum\limits_{l = 0}^{{N_{\rm{s}}} - 1} {{}^k{\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right){{\rm{e}}^{ - {\rm{j}}2ml{\rm{ \mathit{ π} }}/{N_{\rm{s}}}}}} $	（28）

再次利用链式法则，${\partial ^k}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{x}}^{\left( m \right)}/{\partial ^h}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$可表示为

$ \frac{{{\partial ^k}\mathit{\boldsymbol{\tilde \lambda }}_{\rm{x}}^{\left( m \right)}}}{{{\partial ^h}\mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)}}} = \frac{1}{{{N_{\rm{s}}}}}\sum\limits_{l = 0}^{{N_{\rm{s}}} - 1} {\frac{{{\partial ^k}{{\mathit{\boldsymbol{\lambda }}}_{\rm{x}}}\left( l \right)}}{{{\partial ^h}{{\mathit{\boldsymbol{\lambda }}}_{\rm{u}}}\left( l \right)}} \cdot \frac{{{\partial ^h}{{\mathit{\boldsymbol{\lambda }}}_{\rm{u}}}\left( l \right)}}{{{\partial ^h}\mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)}}}{{\rm{e}}^{ - {\rm{j}}2ml{\rm{ \mathit{ π} }}{N_{\rm{s}}}}}} $

（29）

由此，将计算拉格朗日乘子关于相对位移的偏导简化成为了计算$\;{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right)/\;{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)$和${\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)/{\partial ^h}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$的值。对于第1项，由于在时域内不同接触对之间的互相独立，因此当且仅当h=k时，${\partial ^k}{\mathit{\boldsymbol{\lambda }}_{\rm{x}}}\left( l \right)/\;{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)$的值不为0，且其大小与接触对的运动状态有关。其法向的修正项关于法向的预测项的偏导与运动状态的关系如下：

$ \frac{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x,N}}}}\left( l \right)}}{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{u,N}}}}\left( l \right)}} = \left\{ {\begin{array}{*{20}{c}} 1&{分离}\\ 0&{接触} \end{array}} \right. $	（30）

${\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x, N}}}}\left( l \right)/\;{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}_{, T}\left( l \right)$的值为0。另外2种情况则为切向的修正项关于切向的预测项的偏导${\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x, T}}}}\left( l \right)/\;{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}_{, T}\left( l \right)$：

$ \frac{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x,T}}}}\left( l \right)}}{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{u,T}}}}\left( l \right)}} = \left\{ {\begin{array}{*{20}{c}} 1&{分离}\\ 1&{滑移}\\ 0&{阻滞} \end{array}} \right. $	（31）

以及切向的修正项关于法向的预测项的偏导${\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x, T}}}}\left( l \right)/\;{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}_{, {\rm{N}}}\left( l \right)$：

$ \frac{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{x,T}}}}\left( l \right)}}{{{\partial ^k}{\mathit{\boldsymbol{\lambda }}_{{\rm{u,N}}}}\left( l \right)}} = \left\{ {\begin{array}{*{20}{c}} 0&{分离}\\ { - {\mu _{\rm{f}}}{\mathop{\rm sgn}} \left( {^k{\mathit{\boldsymbol{\lambda }}_{{\rm{u,N}}}}\left( l \right)} \right)}&{滑移}\\ 0&{阻滞} \end{array}} \right. $	（32）

对于式(29)中的第2项${\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)/{\partial ^h}\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$，将^hλ_u(l)写成傅里叶级数的形式，并保留前N_h阶谐波，可以得到

$ {}^k{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right) = \Re \left\{ {\sum\limits_{n = 0}^{{N_{\rm{h}}}} {{}^h\mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)}} {{\rm{e}}^{{\rm{j}}2nl{\rm{ \mathit{ π} }}/{N_{\rm{s}}}}}} \right\} $	（33）

式中：$^h\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}$包括实部$\Re \left\{ {^h\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}} \right\}$与虚部$\Im \left\{ {^h\mathit{\boldsymbol{\widetilde \lambda }}_{\rm{u}}^{\left( n \right)}} \right\}$，利用式(33)，不难得到

$ \left\{ \begin{array}{l} \frac{{{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)}}{{\partial \Re \left\{ {^h\mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)}} \right\}}} = \cos \left( {\frac{{2nl{\rm{ \mathit{ π} }}}}{{{N_{\rm{s}}}}}} \right)\\ \frac{{{\partial ^h}{\mathit{\boldsymbol{\lambda }}_{\rm{u}}}\left( l \right)}}{{\partial \Im \left\{ {^h\mathit{\boldsymbol{\tilde \lambda }}_{\rm{u}}^{\left( n \right)}} \right\}}} = - \sin \left( {\frac{{2nl{\rm{ \mathit{ π} }}}}{{{N_{\rm{s}}}}}} \right) \end{array} \right. $

（34）

通过式(25)~式(34)即可获得雅克比矩阵的解析表达式，从而提高利用DLFT法预测系统强迫响应的计算效率与数值稳定性。

2.4 计算流程简述

当线性自由度的数量较多时，式(11)中H_{l, l}⁽ⁿ⁾的求逆变得十分困难。一般采用模态综合法来降低动力学矩阵(M、C、K)维度^[35-36]。本文采用固定界面模态减缩，将绝大多数的线性自由度用模态坐标代替，仅保留非线性自由度以及少数用来施加激振力与用来观察响应的线性自由度。由于固定界面模态减缩属于成熟技术^[35]，因此限于篇幅本文不再赘述与此相关的技术细节。

图 4给出了针对具有摩擦片的有限元模型强迫响应预测算法的计算流程，概述如下：①利用标准有限元软件(本文使用ANSYS)对带有波纹形干摩擦阻尼片的结构的线性部分进行建模；②提取系统的刚度矩阵K、质量矩阵M与阻尼矩阵C；③对得到的K、M、C矩阵进行固定界面模态减缩，仅保留少量的主节点自由度。值得注意的是，该减缩仅在生成待求解代数方程组的过程中进行一次；④将方程的自由度凝聚到非线性自由度上，进一步减少计算规模；⑤利用图 3所示DFLT法求解非线性力的大小，在该步骤中采用时频转换技术，即先将频域获得的位移转化到时域，并在时域内对非线性力进行修正，再将修正的非线性力转回频域；⑥将非线性力代回运动方程式(10)，得到观察点的强迫响应计算结果。

2.5 程序正确性测试

对于2.4节计算流程，可以通过如图 5所示的具有2个摩擦面的集中参数模型，将计算结果与基于切/法向刚度的时频转换技术(Elastic Frequency-Time technique, EFT)的结果进行比较，从而说明程序的正确性。

图 5中的模型分为上下2个结构，不同结构的质量块之间存在接触。在验证模型中，每一个接触点包含1个切向与1个法向。在上结构中，每一个质量块受到大小为F的激振力激励。模型中各参数的取值如表 1所示。

利用切向/法刚度法验证速度型动态拉格朗日算法的正确性时，用如图 6所示的考虑接触刚度的迟滞库伦摩擦模型来描述接触面的力学特征。该模型认为在阻滞状态下，由于力的作用，接触点之间仍存在一定的弹性变形，并通过引入切/法向弹簧来描述这一特征。在验证模型中，切向弹簧与法向弹簧的刚度分别为k_t，k_n=1×10⁷ N/m。

分别利用速度型动态拉格朗日法与切/法向刚度法计算该模型在不同正压力下的强迫响应，其中观测点为质量块1沿着x方向的位移，同时上述2种方法都是基于解析雅克比矩阵的。两者的结果对比如图 7所示。

图 7中标注的离散点为利用基于切/法向迟滞弹簧模型的NewMark法直接在时域内求得的特定频率下的响应幅值。从图 7可以看出，利用切向/法向刚度法与速度型动态拉格朗日法的计算结果十分相近，其中存在的微小的差异是由于DLFT在时域上是利用不考虑迟滞弹簧的库伦模型去满足接触约束的。该计算结果与文献[33]中描述的现象相吻合。在计算时间上，以图 7为例，利用速度型动态拉格朗日法得到一条稳态响应曲线平均所用的CPU时间为145.3 s，而利用切/法向刚度法平均所用的CPU时间为638.7 s，可见在计算结果近似的情况下，前者的计算效率要明显高于后者。

3 波纹摩擦片的减振效果分析

本节将用上述数值工具研究波纹形摩擦阻尼片对于薄壁结构的减振效果。注意到，干摩擦阻尼器的减振效果与系统在全阻滞与全滑移状态下的共振频率差相关。一般来说较大的频率差对应着较好的减振性能^[37]。因此阻尼片应该布置在能够明显调整主体结构在目标频带内的固有频率的位置上。

平板结构为一种具有代表性的薄壁结构，本节通过在一块405 mm×405 mm，厚度为2 mm的板上布置波纹形干摩擦阻尼片，利用仿真模拟的手段研究阻尼片减振性能。板由钢构成，其材料参数为：弹性模量E=210 GPa，泊松比μ=0.3，密度ρ=7 800 kg/m³。边界条件为板的四边全部固支。

将第5阶模态作为目标模态，研究阻尼片对于由此模态所主导的振动的减振效果。其模态频率为400.47 Hz，模态振型如图 8所示。将4片阻尼片布置到如图 9所示的位置，每片阻尼片都对应平板四条边的中点，且其中一个接触面位于固定端3 mm处。阻尼片的材料参数为：弹性模量E=70 GPa，泊松比μ=0.3，密度ρ=2 700 kg/m³。阻尼片的几何尺寸如表 2所示。为激起该阶模态，在图 9中的施力点位置施加垂直于板方向的激振力，大小为F=15 N，同时相邻2点之间的激振力存在π/2的相位差。

在分析时，首先建立图 9中含有阻尼片的板结构的有限元模型(利用ANSYS)；再用固定界面模态减缩来降低模型的自由度，保留其中施力点与观测点的线性自由度，以及接触面上的所有非线性自由度。为保证计算精度，截取前50阶模态，由此得到的降阶模型前10阶的模态频率与原模型相比，误差小于0.5%，且模态振型相似性约等于1，故可以用此降阶模型的计算结果来替代原模型。

利用DLFT方法对上述模型进行计算，模型本身的阻尼比取ξ=0.002，文献[38]中表明摩擦系数的大小对干摩擦阻尼器的最优减振效果并不敏感，这里该参数的取值为μ_f=0.6。为保证计算精度，本文中保留的谐波数为N_h=5，计算得到如图 10所示的不同正压力下观测点的稳态强迫响应曲线。随着正压力的增大，共振频率向右偏移，完全自由状态下的共振频率为400.6 Hz，与纯平板结构下的固有频率变化不大，说明当阻尼片布置在该位置时，其附加质量对整体结构的动力学特性几乎没有影响。当接触面处于完全阻滞状态时，共振频率为408.4 Hz，频率偏移量为7.8 Hz。共振幅值随着正压力的增加先减小，后增大。当初始正压力为80 N时，阻尼片的减振性能最佳，共振幅值相对于完全分离状态下降了75.4%。同时，阻尼片的质量(考虑了安装所用的螺栓和螺母)占主体结构的0.6%。由此可见，该波纹形干摩擦阻尼器对于平板结构具有较为理想的减振性能。

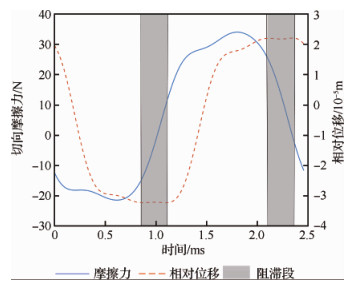
还可以对接触区域的局部动力学特性进行分析。以图 9中箭头所指的接触点为例，在初始正压力为80 N下达到共振峰时，该接触点在时域内的运动状态如图 11所示。其中实线代表接触点处所受的切向摩擦力，虚线代表接触对之间的切向相对位移。当接触状态为阻滞时(阴影部分)，接触对之间的相对位移保持不变；当接触状态为滑移时，由于切法向运动耦合的影响，导致切向的摩擦力并不是定值。

关于计算效率，以最优正压力下计算强迫响应为例，所用的时间与减缩过程中系统的自由度的变化如表 3所示。可见构造减缩模型所耗费的时间只占总分析时间的很小部分，却能有效地降低模型的自由度(降低了99.7%)，因此推荐在用DLFT分析较大规模的有限元模型时使用减缩技术。如果不采用解析雅克比矩阵而是用默认的数值差分近似，平均一个频率点所需的CPU时间为333.7 s；采用减缩方法后，计算706个频率点总共花了5 360.1 s，平均每1个频率点的CPU计算时间为7.6 s。可见如式(25)~式(34)所示的解析雅克比矩阵对速度型的动态拉格朗日法的计算效率至关重要，在计算自由度相对较多的结构时几乎是不可或缺的。

4 结论

本文提出了一种适用于薄壁结构的波纹形干摩擦阻尼器，其具有结构简单、附加质量小、易于安装与调节初始正压力的优点。利用仿真模拟的手段对阻尼片的减振性能进行了分析，在高阶谐波平衡法的基础上引入了速度型动态拉格朗日法，并通过提供解析形式的雅克比矩阵来提高迭代效率与计算稳定性，从而实现了对带有接触系统的频域强迫响应的快速预测，之后的仿真过程表明该算法具有较高的计算效率。

利用强迫响应预测算法对带有阻尼片的薄壁结构进行分析，可以看出，对于平板而言，通过合理布置阻尼片的位置，增大结构自由/阻滞时的频率差，从而获得较好的减振效果。以文中的平板结构为例，仅使用质量占整体结构0.6%的阻尼片就能使得共振峰值下降75.4%。

现有工作的一个展望是，针对干摩擦阻尼器在各频段下最优正压力不同的特点，还可以引入主动控制环节通过设计可控正压力提高干摩擦阻尼器在宽频内的减振性能^{[30, 39]}。这些后续工作仍然需要一种可以考虑干摩擦界面切-法向耦合的高效数值工具，本文提出的基于减缩模型和解析雅克比矩阵的速度型动态拉格朗日乘子方法仍适用。

附录A

布尔矩阵是元素只取0或1的矩阵，因此又被称为0-1矩阵。它的作用是提取含有m个元素的向量X中的某些特定项，并将提取的元素重新组成维度为n的向量Y。该过程所对应的布尔矩阵B的维度为n×m。

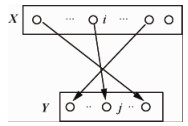
令X=[x₁ x₂…x_m]，Y=[y₁ y₂…y_n]，且Y∈X。2个向量中元素的对应关系如图A1所示。

记R为X和Y上的对应关系，则布尔矩阵中B的各元素满足：

$ \mathit{\boldsymbol{B}}\left[ {j,i} \right] = \left\{ {\begin{array}{*{20}{c}} {1\;\;\left( {{x_i},{y_i}} \right) \in {\rm{R}}}\\ {0\;\;\left( {{x_i},{y_i}} \right)\; \notin {\rm{R}}} \end{array}} \right. $	（A1）

其转置矩阵B^T则能将Y中的元素放回X中的对应位置。