2. 陆军工程大学 科研学术处, 南京 210000
2. Department of Scientific Research, Army Engineering University, Nanjing 210000, China
为增加战斗部的毁伤效能,有必要对导弹提出攻击角度约束的要求。由于滑模控制在滑动模态对干扰具有不变性,被广泛应用在制导律的设计中。通过选取包含弹目视线角速率和攻击角度约束项的滑模面,结合趋近律可设计出攻击角度约束的滑模制导律[1-2]。
传统滑模制导律采用线性滑模面,弹目视线角速率和攻击角度是渐进收敛的,收敛时间趋于无穷。但导弹攻击目标的时间是有限的,这就对制导律的设计提出了有限时间收敛的要求,而终端滑模控制采用非线性滑模面能够实现系统状态的有限时间收敛[3]。文献[4]设计了带攻击角度约束的终端滑模制导律。文献[5-6]在终端滑模面中加入线性项,进一步加快了收敛速度。但终端滑模制导律中含状态量的负指数项,会造成奇异问题。针对这个问题,目前主要有2种解决思路:积分滑模[7-8]和非奇异终端滑模[9-11]。积分滑模能保证系统状态的有限时间收敛,但不能确定其具体的收敛时间表达式。非奇异终端滑模与终端滑模结构类似,能使系统有限时间收敛。但其收敛时间与系统的初始状态相关,而系统初始状态一般是未知的,且不同的初始状态收敛时间也不同。为此,文献[12]提出了固定时间稳定性理论,能使系统收敛时间的上界不依赖于系统初始状态。文献[13-14]基于固定时间稳定性理论设计了非奇异终端滑模面,提出了固定时间收敛的终端滑模控制方法,其收敛时间上界仅与控制参数有关。
针对目标机动和系统扰动等干扰问题,目前大多数文献的处理方法为:利用滑模控制的鲁棒性抵抗干扰[15];设计自适应律估计干扰的上界[10];设计干扰观测器实时在线估计干扰[16]。前两种方法需要引入符号函数项,会使控制量不连续,引起抖振现象。大多数文献对符号项进行光滑处理来削弱抖振,但改变了滑模控制的固有结构,会降低控制精度。干扰观测器可实时估计干扰量前馈至控制律中,进而实现对干扰的抑制,且不需要引入符号函数项。近年来许多学者对干扰观测器进行了研究,以提高滑模控制的性能,如非线性干扰观测器[17]、自适应干扰观测器[18]、有限时间干扰观测器[19]、扩张状态观测器[20]等。这些观测器可以实现估计误差的有限时间收敛或者渐进收敛,但收敛时间的上界依赖于估计误差的初值。
在大气层内作战的导弹,由于受空气动力作用,以及导弹本身硬件设备的延迟特性,导致自动驾驶仪存在动态延迟。这对制导精度有很大的影响,尤其打击大机动目标时,会导致系统不稳定和较大脱靶量,因此在制导律的设计中需要加以考虑。目前,许多文献已对考虑驾驶仪动态特性的制导律进行了研究,所用方法主要为反步(Backstepping)递推设计或动态面控制[21]。文献[22]考虑自动驾驶仪一阶动态特性,采用终端滑模控制设计了有限时间收敛的制导律,但制导律中存在弹目视线角速率的高阶导数。实际上,自动驾驶仪一般具有高阶动态特性。若将其近似为高阶系统,能够很好地模拟驾驶仪的动态特性,但这会使制导律的形式过于复杂。将驾驶仪近似为二阶系统比较合理,既可以贴近驾驶仪实际动态特性,又能降低制导律的复杂程度。文献[23-24]基于动态面控制设计了考虑自动驾驶仪二阶动态特性的制导律,但不能保证有限时间收敛。因此,文献[25]采用滑模反步递推设计方法,提出了一种攻击角度约束的有限时间收敛制导律,但收敛时间的上界依赖于系统状态初值。
在上述讨论的启发下,本文提出了一种同时考虑攻击角度约束、自动驾驶动态特性和固定时间收敛的制导律。在三维空间内建立了考虑自动驾驶仪二阶动态特性的制导系统状态方程;针对目标机动等干扰问题,基于固定时间收敛和超螺旋算法,设计了一种滑模干扰观测器用于估计干扰;构造了一种包含弹目视线角速率和角度约束项的固定时间收敛非奇异终端滑模面,能使系统状态快速固定时间收敛;基于所提干扰观测器和滑模面,采用反步递推方法,对制导律进行设计。基于Lyapunov稳定性理论,证明了制导律的固定时间收敛特性,并给出了收敛时间的表达式;最后通过仿真分析,验证了所提制导律的有效性和优越性。
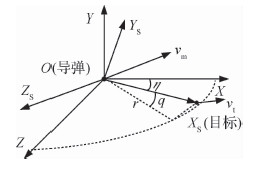
1 问题描述在三维惯性坐标系OXYZ上建立弹目相对运动关系如图 1所示。图中,OXSYSZS为弹目视线坐标系,r为弹目相对距离,q和η分别为弹目视线倾角和偏角。vm和vt分别为导弹和目标的速度,假定为恒速。
|
| 图 1 弹目相对运动关系 Fig. 1 Relationship of missile-to-target motion |
参考文献[26], 可得弹目相对运动的动力学方程为
| $ \left\{ \begin{array}{l} \ddot r - r{{\dot q}^2} - r{{\dot \eta }^2}{\cos ^2}q = {a_{{\rm{t}}r}} - {a_{{\rm{m}}r}}\\ r\ddot q + 2\dot r\dot q + r{{\dot \eta }^2}\cos q\sin q = {a_{{\rm{t}}q}} - {a_{{\rm{m}}q}}\\ - r\ddot \eta \cos q - 2r\dot \eta \cos q + 2r\dot q\dot \eta \sin q = {a_{{\rm{t}}\eta }} - {a_{{\rm{m}}\eta }} \end{array} \right. $ | (1) |
式中:atr、atq、atη和amr、amq、amη分别为目标和导弹的加速度在视线坐标系上的分量。
针对导弹的自动驾驶仪存在动态延迟的问题,这里将自动驾驶仪近似为二阶环节:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\ddot a}_{{\rm{m}}q}} = - 2\xi {\omega _{\rm{n}}}{{\dot a}_{{\rm{m}}q}} - \omega _{\rm{n}}^2{a_{{\rm{m}}q}} + \omega _{\rm{n}}^2{u_q}}\\ {{{\ddot a}_{{\rm{m}}\eta }} = - 2\xi {\omega _{\rm{n}}}{{\dot a}_{{\rm{m}}\eta }} - \omega _{\rm{n}}^2{a_{{\rm{m}}\eta }} + \omega _{\rm{n}}^2{u_\eta }} \end{array}} \right. $ | (2) |
式中:ξ为阻尼比;ωn为自动驾驶仪的自振频率;uq和uη为制导指令。
导弹攻击角度为制导末端导弹和目标速度矢量间的夹角,带攻击角度约束的制导问题可转化为终端视线角约束问题[1-4],即
| $ q\left( {{t_{\rm{f}}}} \right) = {q_{\rm{d}}},\eta \left( {{t_{\rm{f}}}} \right) = {\eta _{\rm{d}}} $ | (3) |
式中:tf为制导终端时刻; qd和ηd分别为期望终端视线倾角和偏角。
根据式(1)和式(2),在三维空间内建立考虑自动驾驶仪动态特性带攻击角度约束的制导系统方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2}}\\ {{{\mathit{\boldsymbol{\dot x}}}_2} = f\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right) + {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{x}}_3} - {\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{d}}}\\ {{{\mathit{\boldsymbol{\dot x}}}_3} = {\mathit{\boldsymbol{x}}_4}}\\ {{{\mathit{\boldsymbol{\dot x}}}_4} = a{\mathit{\boldsymbol{x}}_4} + {b_2}\mathit{\boldsymbol{u}} - {b_2}{\mathit{\boldsymbol{x}}_3}} \end{array}} \right. $ | (4) |
式中:
| $ \left\{ \begin{array}{l} f\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right) = \left[ {\begin{array}{*{20}{c}} { - \frac{{2\dot r}}{r}\dot q - {{\dot \eta }^2}\cos q\sin q}\\ { - \frac{{2\dot r}}{r}\dot \eta + 2\dot q\dot \eta \tan q} \end{array}} \right]\\ {\mathit{\boldsymbol{b}}_1} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{r}}&0\\ 0&{\frac{1}{{r\cos q}}} \end{array}} \right]\\ \mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{l}} {{d_1}}\\ {{d_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{a_{{\rm{t}}q}}}\\ {{a_{{\rm{t}}\eta }}} \end{array}} \right],a = - 2\xi {\omega _{\rm{n}}},{b_2} = \omega _{\rm{n}}^2 \end{array} \right. $ | (5) |
其中:x1=[x11, x12]T=[q-qd, η-ηd]T,x2=
在制导律设计之前,为理论推导和分析方便,给出如下相关的定义和引理。
定义1 为后文书写方便,作如下定义:sgnα(y)=|y|αsgn(y),|y|α=[|y1|α, |y2|α,…, |yn|α]T,其中,y=[y1, y2, …, yn]T,sgn(·)为符号函数,且sgn(0)=0。
针对如下非线性系统:
| $ \mathit{\boldsymbol{\dot x}}\left( t \right) = f(\mathit{\boldsymbol{x}}(t)),\mathit{\boldsymbol{x}}(0) = {\mathit{\boldsymbol{x}}_0} $ | (6) |
引理1[27] 假定存在Lyapunov函数V(x),满足a>0和0 < b < 1,
| $ {T_1} \le \frac{{{V^{1 - b}}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}}{{a(1 - b)}} $ | (7) |
引理2[28]假定存在Lyapunov函数V(x),满足
| $ {T_2} \le \frac{1}{{c(1 - b)}}\ln \left( {1 + \frac{{c{V^{1 - b}}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}}{a}} \right) $ | (8) |
注1 引理1和引理2为有限时间收敛特性分析中常用的两种引理,由式(7)和式(8)可以看出,收敛时间上界与参数和系统的初始状态有关,而系统的初始状态往往是未知的,因此不能准确估算收敛时间上界。为解决这个问题,文献[12]提出了固定时间稳定性的概念,相关定义及引理如下:
定义2 对于系统(6),若存在一个时刻Tmax>0,对任意x0∈R,t>Tmax,满足x(t)=0,则系统是固定时间稳定的。
引理3[29-30] 针对系统
| $ {T_3} < \frac{1}{{a(1 - \alpha )}} + \frac{1}{{b(\beta - 1)}} $ | (9) |
此外,若系统存在小的扰动,即
| $ {T_4} < \frac{1}{{a\left( {{2^a} - 1} \right)(1 - \alpha )}} + \frac{1}{{b(\beta - 1)}} $ | (10) |
引理4[31] 假定存在Lyapunov函数V(x)满足
| $ {T_5} < \frac{1}{{a(1 - \alpha )}} + \frac{1}{{b(\beta - 1)}} $ | (11) |
引理5[32] 对于任意实数xi(i=1, 2, …,n),存在实数0 < α < 1,使得式(12)成立:
| $ {\left( {\sum\limits_{i = 1}^n {\left| {{x_i}} \right|} } \right)^\alpha } \le \sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^\alpha }} $ | (12) |
引理6[33] 对于任意实数xi(i=1, 2, …,n),存在实数β>1,使得式(13)成立:
| $ {\left( {\sum\limits_{i = 1}^n {\left| {{x_i}} \right|} } \right)^\beta } \le {n^{\beta - 1}}\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^\beta }} $ | (13) |
根据引理5和引理6,有式(14)成立:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}^{\rm{T}}}\text{sgn}{^\alpha }(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^n {{{\left| {x_i^2} \right|}^{\frac{{\alpha + 1}}{2}}}} \ge {\left( {\sum\limits_{i = 1}^n {\left| {x_i^2} \right|} } \right)^{\frac{{\alpha + 1}}{2}}} = \\ \;\;\;\;\;\;\;{\left\| \mathit{\boldsymbol{x}} \right\|^{\alpha + 1}}\\ {\mathit{\boldsymbol{x}}^{\rm{T}}}\text{sgn}{^\beta }\left( \mathit{\boldsymbol{x}} \right) \ge {n^{1 - \frac{{\beta + 1}}{2}}}{\left( {\sum\limits_{i = 1}^n {\left| {x_i^2} \right|} } \right)^{\frac{{\beta + 1}}{2}}} = {n^{\frac{{1 - \beta }}{2}}}{\left\| \mathit{\boldsymbol{x}} \right\|^{\beta + 1}} \end{array} \right. $ | (14) |
在制导过程中,目标的加速度信息往往是无法进行测量的,因此在制导律设计前,需要对目标机动等干扰量进行估计。滑模干扰观测器是经常采用的一种估计系统不确定性及外部扰动的方法。它可以实现估计误差的渐进或有限时间收敛至零,但收敛时间取决于观测器参数和初始误差。若初始误差较大,其收敛时间也会相应增加,并且传统的滑模干扰观测器还存在抖振问题。针对这两个问题,借鉴固定有限时间收敛和超螺旋算法思想,设计了一种固定时间收敛的滑模干扰观测器。
定义y=[y1, y2]T=
| $ \mathit{\boldsymbol{\dot y}} = \left[ {\begin{array}{*{20}{c}} {{{\dot y}_1}}\\ {{{\dot y}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{f_1} + {d_1}}\\ {{f_2} + {d_2}} \end{array}} \right] $ | (15) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{f_1} = - \dot r\dot q - r{{\dot \eta }^2}\cos q\sin q - {a_{{\rm{m}}q}}}\\ {{f_2} = \dot r\dot \eta \cos q - r\dot q\dot \eta \sin q - {a_{{\rm{m}}\eta }}} \end{array}} \right. $ |
假设1 di是有界的,且其一阶导数
针对系统(15)设计滑模干扰观测器为
| $ \left\{ \begin{array}{l} {{\dot {\hat y}}_i} = {f_i} + {{\hat d}_i}\\ {{\hat d}_i} = {\lambda _{1i}}\text{sgn}{^{{\gamma _1}}}\left( {{{\tilde y}_i}} \right) + {\lambda _{2i}} \text{sgn}{ ^{{\gamma _2}}}\left( {{{\tilde y}_i}} \right) + \\ \;\;\;\;\;{\lambda _{3i}}\int_0^t \text{sgn} \left( {{{\tilde y}_i}(\tau )} \right){\rm{d}}\tau \end{array} \right. $ | (16) |
式中:
求
| $ {{\dot {\tilde y}}_i} = {{\dot y}_i} - {{\dot {\hat y}}_i} = {d_i} - {{\hat d}_i},i = 1,2 $ | (17) |
将式(16)代入式(17)可得
| $ \left\{ \begin{array}{l} {{\dot {\tilde y}}_i} = - {\lambda _1} \text{sgn}{ ^{{\gamma _1}}}\left( {{{\tilde y}_i}} \right) - {\lambda _2} \text{sgn}{ ^{{\gamma _2}}}\left( {{{\tilde y}_i}} \right) + {z_i}\\ {{\dot z}_i} = - {\lambda _3} \text{sgn} \left( {{{\tilde y}_i}} \right) + {{\dot d}_i}\;\;\;\;\;\;i = 1,2\\ {{\tilde y}_i}(0) = {y_i}(0) - {{\hat y}_i}(0),{z_i}(0) = 0 \end{array} \right. $ | (18) |
式中:zi为一个辅助变量。
定理1 针对系统(15),设计如式(16)所示的干扰观测器,若λ3i>Li,λ2i/h(λ2i)>λ3i+Li,h(λ2i)=1/λ2i+[2e/(λ3i-Li)λ2i]1/3,e为自然对数的底,则估计误差
| $ {t_{1i}} < \left( {1 + \frac{{{\lambda _{3i}} + {L_i}}}{{{\lambda _{3i}} - {L_i}}} \cdot \frac{1}{{1 - \left( {{\lambda _{3i}} + {L_i}} \right)h\left( {{\lambda _{2i}}} \right)/{\lambda _{2i}}}}} \right){{t'}_{1i}} $ | (19) |
式中:
证明:当
| $ {V_1} = \tilde y_i^2 $ | (20) |
微分得
| $ \begin{array}{l} {{\dot V}_1} = 2{{\tilde y}_i}{{\dot {\tilde y}}_i} = 2\left( { - {\lambda _{1i}}{{\left| {{{\tilde y}_i}} \right|}^{{\gamma _1} + 1}} - {\lambda _{2i}}{{\left| {{{\tilde y}_i}} \right|}^{{\gamma _2} + 1}} + } \right.\\ \left. {{{\tilde y}_i}{z_i}} \right) \le - 2{\lambda _{1i}}V_1^{\frac{{{\gamma _1} + 1}}{2}} - 2{\lambda _{2i}}V_1^{\frac{{{\gamma _2} + 1}}{2}} \end{array} $ | (21) |
由引理4可知
| $ {{t'}_{1i}} < \frac{1}{{{\lambda _{1i}}\left( {{\gamma _1} - 1} \right)}} + \frac{1}{{{\lambda _{2i}}\left( {1 - {\gamma _2}} \right)}} $ | (22) |
由式(18)可知,t′1i时刻时zi的值满足:
| $ \begin{array}{l} \left| {{z_i}\left( {{{t'}_{1i}}} \right)} \right| = \left| { - {\lambda _{3i}}}\text{sgn}{\left( {{{\tilde y}_i}} \right) + \dot d} \right|{{t'}_{1i}} \le \\ \;\;\;\;\left( {{\lambda _{3i}} + {L_i}} \right){{t'}_{1i}} \end{array} $ | (23) |
此时由于
| $ {{t'}_{2i}} \le \frac{{\sum_j {\left| {{{\dot {\tilde y}}_i}\left( {{T_j}} \right)} \right|} }}{{{\lambda _{3i}} - {L_i}}}\;\;\;\;j = 1,2, \cdots $ | (24) |
式中:Tj为
| $ t_{2i}^\prime \le \frac{{\left| {{{\dot {\tilde y}}_i}\left( {t_{1i}^\prime } \right)} \right|}}{{\left( {1 - {q_{1i}}} \right)\left( {{\lambda _{3i}} - {L_i}} \right)}} = \frac{{\left( {{\lambda _{3i}} + {L_i}} \right)t_{1i}^\prime }}{{\left( {1 - {q_{1i}}} \right)\left( {{\lambda _{3i}} - {L_i}} \right)}} $ | (25) |
结合式(22)和式(25)可得
注2 由观测器(16)的表达式可知,变结构项存在于积分项中,观测器的估计值是连续的,有效削弱了传统滑模干扰观测器的抖振问题。
注3 由观测器的收敛时间表达式(19)可以看出,收敛时间的上界由观测器的参数λ1i、λ2i、λ3i、γ1和γ2的取值决定,不依赖于系统的初始状态,估计误差是固定时间收敛的。
2.3 制导律设计针对系统,为使导弹以期望攻击角度精确打击目标,本文基于滑模控制,结合反步设计方法,对制导律进行设计。为使系统状态x1和x2固定时间收敛至零,基于引理3和分段滑模面思想,设计如下非奇异快速终端滑模面为
| $ {\mathit{\boldsymbol{s}}_1} = {\mathit{\boldsymbol{x}}_2} + {k_1}\text{sgn}{^{{\alpha _1}}}\left( {{\mathit{\boldsymbol{x}}_1}} \right) + {k_2}\varphi \left( {{\mathit{\boldsymbol{x}}_1}} \right) $ | (26) |
式中:φ(x1)=[φ(x11), φ(x12)]T,且
| $ \varphi \left( {{x_{1i}}} \right) = \left\{ {\begin{array}{*{20}{l}} {x_{1i}^{{a_2}}}&{\left| {{x_{1i}}} \right| \ge \delta }\\ {f\left( {{x_{1i}}} \right)}&{\left| {{x_{1i}}} \right| < \delta } \end{array}} \right. $ | (27) |
其中:α1>1,0 < α2=p1/p2 < 1,k1>0,k2>0,δ>0,p1、p2为正奇数。
对式(26)求一阶导数可得
| $ {{\mathit{\boldsymbol{\dot s}}}_1} = {{\mathit{\boldsymbol{\dot x}}}_2} + {k_1}{\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{{a_1} - 1}}{\mathit{\boldsymbol{x}}_2} + {k_2}{\varphi ^\prime }\left( {{\mathit{\boldsymbol{x}}_1}} \right){\mathit{\boldsymbol{x}}_2} $ | (28) |
式中:
| $ {\varphi ^\prime }\left( {{x_{1i}}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\alpha _2}{{\left| {{x_{1i}}} \right|}^{{a_2} - 1}}}&{\left| {{x_{1i}}} \right| \ge \delta }\\ {{f^\prime }\left( {{x_{1i}}} \right)}&{\left| {{x_{1i}}} \right| < \delta } \end{array}} \right. $ | (29) |
f(x1i)是关于x1i的函数,且满足如下条件:
1) f(x1i)在x1i∈(-δ, δ)上是光滑函数,且与x1i同号。
2) f(δ)=φ(δ)=-f(-δ)。
3) f′(δ)=f′(-δ)=φ′(δ),在x1i∈(-δ, δ)上,f′(x1i)>0。
注4 条件1)能够保证f′(x1i)为连续有界函数,消除奇异问题,且系统到达滑模面s1=0时,x1i与x2i始终是异号的,保证系统状态是可收敛的;条件2)保证了滑模面函数s1是连续的;条件3)保证了f(x1i)在x1i∈(-δ, δ)是有界的,且保证了φ′(x1i)是一个连续函数,从而保证s1是光滑的。
根据选取条件,选取一种f(x1i)函数为
| $ f\left( {{x_{1i}}} \right) = {\lambda _1}{x_{1i}} + {\lambda _2}x_{1i}^3 $ | (30) |
式中:
下面采用反步设计方法对制导律进行设计。
步骤1 x3的虚拟控制律设计
定义滑模误差面为
| $ {\mathit{\boldsymbol{s}}_2} = {\mathit{\boldsymbol{s}}_1} = {\mathit{\boldsymbol{x}}_2} + {k_1}\text{sgn}{^{{a_1}}}\left( {{\mathit{\boldsymbol{x}}_1}} \right) + {k_2}\varphi \left( {{\mathit{\boldsymbol{x}}_1}} \right) $ | (31) |
对式(31)微分并结合式(4)可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_2} = {{\mathit{\boldsymbol{\dot x}}}_2} + {k_1}{\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{{\alpha _1} - 1}}{\mathit{\boldsymbol{x}}_2} + {k_2}{\varphi ^\prime }\left( {{\mathit{\boldsymbol{x}}_1}} \right){\mathit{\boldsymbol{x}}_2} = \\ \;\;\;\;\;\;f\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right) + {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{x}}_3} - {\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{d}} + \left( {{k_1}{\alpha _1}{{\left| {{\mathit{\boldsymbol{x}}_1}} \right|}^{{\alpha _1} - 1}} + } \right.\\ \;\;\;\;\;\;\left. {{k_2}{\varphi ^\prime }\left( {{\mathit{\boldsymbol{x}}_1}} \right)} \right){\mathit{\boldsymbol{x}}_2} \end{array} $ | (32) |
设计虚拟控制律为
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_{3{\rm{c}}}} = - \mathit{\boldsymbol{b}}_1^{ - 1}\left[ {f\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right) - {\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{\hat d}} + {k_3}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right) + } \right.\\ \;\;\;\;\;\left. {{k_4}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right) + \left( {{k_1}{\alpha _1}{{\left| {{\mathit{\boldsymbol{x}}_1}} \right|}^{{a_1} - 1}} + {k_2}{\varphi ^\prime }\left( {{\mathit{\boldsymbol{x}}_1}} \right)} \right){\mathit{\boldsymbol{x}}_2}} \right] \end{array} $ | (33) |
式中:β1>1,0 < β2 < 1,
为避免对虚拟控制量的多次求导产生“微分膨胀”问题,借鉴动态面设计方法,引入一个新的虚拟控制律x3d,它由x3c经一阶低通滤波器得到。传统动态面设计方法采用一阶线性滤波器,不能保证系统有限/固定时间收敛。为保证固定时间收敛特性,基于引理3,设计一种一阶非线性滤波器为
| $ \left\{ {\begin{array}{*{20}{l}} {\tau {{\mathit{\boldsymbol{\dot x}}}_{3{\rm{d}}}} = \text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{x}}_{3{\rm{c}}}} - {\mathit{\boldsymbol{x}}_{3{\rm{d}}}}} \right) + \text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{x}}_{3{\rm{c}}}} - {\mathit{\boldsymbol{x}}_{3{\rm{d}}}}} \right)}\\ {{\mathit{\boldsymbol{x}}_{3{\rm{d}}}}(0) = {\mathit{\boldsymbol{x}}_{3{\rm{c}}}}(0)} \end{array}} \right. $ | (34) |
式中:τ>0。
注5 动态面控制所用的一阶线性滤波器为
步骤2 x4的虚拟控制律设计
定义滑模误差面为
| $ {\mathit{\boldsymbol{s}}_3} = {\mathit{\boldsymbol{x}}_3} - {\mathit{\boldsymbol{x}}_{3{\rm{d}}}} $ | (35) |
对式(35)微分并结合式(14)得
| $ {{\mathit{\boldsymbol{\dot s}}}_3} = {{\mathit{\boldsymbol{\dot x}}}_3} - {{\mathit{\boldsymbol{\dot x}}}_{3{\rm{d}}}} = {\mathit{\boldsymbol{x}}_4} - {{\mathit{\boldsymbol{\dot x}}}_{3{\rm{d}}}} $ | (36) |
设计虚拟控制律为
| $ {\mathit{\boldsymbol{x}}_{4{\rm{c}}}} = - {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_2} - {k_5}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right) - {k_6}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right) + {{\mathit{\boldsymbol{\dot x}}}_{3{\rm{d}}}} $ | (37) |
设计非线性滤波器为
| $ \left\{ {\begin{array}{*{20}{l}} {\tau {{\mathit{\boldsymbol{\dot x}}}_{4{\rm{d}}}} = \text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{x}}_{4{\rm{c}}}} - {\mathit{\boldsymbol{x}}_{4{\rm{d}}}}} \right) + \text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{x}}_{4{\rm{c}}}} - {\mathit{\boldsymbol{x}}_{4{\rm{d}}}}} \right)}\\ {{\mathit{\boldsymbol{x}}_{4{\rm{d}}}}(0) = {\mathit{\boldsymbol{x}}_{4{\rm{c}}}}(0)} \end{array}} \right. $ | (38) |
步骤3 实际制导律u的设计
定义滑模误差面为
| $ {\mathit{\boldsymbol{s}}_4} = {\mathit{\boldsymbol{x}}_4} - {\mathit{\boldsymbol{x}}_{4{\rm{d}}}} $ | (39) |
对式(39)微分并结合式(4)可得
| $ {{\mathit{\boldsymbol{\dot s}}}_4} = {{\mathit{\boldsymbol{\dot x}}}_4} - {{\mathit{\boldsymbol{\dot x}}}_{4{\rm{d}}}} = a{\mathit{\boldsymbol{x}}_4} + {b_2}\mathit{\boldsymbol{u}} - {b_2}{\mathit{\boldsymbol{x}}_3} - {{\mathit{\boldsymbol{\dot x}}}_{4{\rm{d}}}} $ | (40) |
设计实际制导律为
| $ \begin{array}{l} \mathit{\boldsymbol{u}} = - b_2^{ - 1}\left( {{a_2}{\mathit{\boldsymbol{x}}_4} - {b_2}{\mathit{\boldsymbol{x}}_3} + {\mathit{\boldsymbol{s}}_3} + {k_7}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right) + } \right.\\ \;\;\;\;\left. {{k_8}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right) - {{\mathit{\boldsymbol{\dot x}}}_{4{\rm{d}}}}} \right) \end{array} $ | (41) |
定理2 针对系统(4),在制导律(41)的作用下,系统状态x1和x2能够固定时间收敛至原点的一个较小邻域内。
证明
定义虚拟控制律误差
| $ {\mathit{\boldsymbol{y}}_i} = {\mathit{\boldsymbol{x}}_{i{\rm{d}}}} - {\mathit{\boldsymbol{x}}_{i{\rm{c}}}}\;\;\;\;i = 3,4 $ | (42) |
对式(42)求微分,并结合式(34)和式(38)可得
| $ {{\mathit{\boldsymbol{\dot y}}}_i} = {{\mathit{\boldsymbol{\dot x}}}_{i{\rm{d}}}} - {{\mathit{\boldsymbol{\dot x}}}_{i{\rm{c}}}} = - \frac{1}{\tau }\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{y}}_i}} \right) - \frac{1}{\tau }\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{y}}_i}} \right) - {{\mathit{\boldsymbol{\dot x}}}_{i{\rm{c}}}} $ | (43) |
| $ \mathit{\boldsymbol{y}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot y}}}_i} = - \frac{1}{\tau }\mathit{\boldsymbol{y}}_i^{\rm{T}}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{y}}_i}} \right) - \frac{1}{\tau }\mathit{\boldsymbol{y}}_i^{\rm{T}}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{y}}_i}} \right) - \mathit{\boldsymbol{y}}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_{i{\rm{c}}}} $ | (44) |
由文献[36]可知,存在正实数σi使得
| $ \begin{array}{l} \mathit{\boldsymbol{y}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot y}}}_i} \le - \frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_i}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_i}} \right\|^{{\beta _2} + 1}} + \\ \;\;\;\;\;\;\;\frac{{{{\left\| {{\mathit{\boldsymbol{y}}_i}} \right\|}^2} + \sigma _i^2}}{2} \end{array} $ | (45) |
结合式(32)、式(35)和式(42)可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_2} = f\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right) + {\mathit{\boldsymbol{b}}_1}\left( {{\mathit{\boldsymbol{s}}_3} + {\mathit{\boldsymbol{y}}_3} + {\mathit{\boldsymbol{x}}_{3{\rm{c}}}}} \right) - {\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{d}} + \\ \;\;\;\;\;\;{k_1}{\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{{\alpha _1} - 1}}{\mathit{\boldsymbol{x}}_2} + {k_2}{\varphi ^\prime }\left( {{\mathit{\boldsymbol{x}}_1}} \right){\mathit{\boldsymbol{x}}_2} = {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_3} + {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{y}}_3} - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{\widetilde d}} - {k_3}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right) - {k_4}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right) \end{array} $ | (46) |
式中:
结合式(36)、式(39)和式(42)可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_3} = {\mathit{\boldsymbol{s}}_4} + {\mathit{\boldsymbol{y}}_4} + {\mathit{\boldsymbol{x}}_{4{\rm{c}}}} - {\mathit{\boldsymbol{x}}_{3{\rm{d}}}} = {\mathit{\boldsymbol{s}}_4} + {\mathit{\boldsymbol{y}}_4} - {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_2} - \\ \;\;\;\;\;\;{k_5}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right) - {k_6}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right) \end{array} $ | (47) |
结合式(40)和式(41)可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_4} = a{\mathit{\boldsymbol{x}}_4} + {b_2}\mathit{\boldsymbol{u}} - {b_2}{\mathit{\boldsymbol{x}}_3} - {{\mathit{\boldsymbol{\dot x}}}_{4{\rm{d}}}} = - {\mathit{\boldsymbol{s}}_3} - {k_7}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right) - \\ \;\;\;\;\;{k_8}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right) \end{array} $ | (48) |
构造Lyapunov函数为
| $ V = \frac{1}{2}\sum\limits_{i = 2}^4 {\left( {\mathit{\boldsymbol{s}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_i}} \right)} + \frac{1}{2}\sum\limits_{i = 3}^4 {\left( {\mathit{\boldsymbol{y}}_i^{\rm{T}}{\mathit{\boldsymbol{y}}_i}} \right)} + \frac{1}{2}{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\mathit{\boldsymbol{\tilde d}} $ | (49) |
微分可得
| $ \begin{array}{l} \dot V = \sum\limits_{i = 2}^4 {\left( {\mathit{\boldsymbol{s}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_i}} \right)} + \sum\limits_{i = 3}^4 {\left( {\mathit{\boldsymbol{y}}_i^{\rm{T}}{{\mathop {\mathit{\boldsymbol{y}}}\limits^. }_i}} \right)} + {\mathit{\boldsymbol{\widetilde d}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\tilde d}}} \le {\mathit{\boldsymbol{s}}_2}\left( {{\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_3} + } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{y}}_3} - {\mathit{\boldsymbol{b}}_1}\mathit{\boldsymbol{\widetilde d}} - {k_3}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right) - {k_4}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_2}} \right)} \right) + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}_3}\left( {{\mathit{\boldsymbol{s}}_4} + {\mathit{\boldsymbol{y}}_4} - {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_2} - {k_5}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right) - {k_6}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_3}} \right)} \right) + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}_4}\left( { - {\mathit{\boldsymbol{s}}_3} - {k_7}\text{sgn}{^{{\beta _1}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right) - {k_8}\text{sgn}{^{{\beta _2}}}\left( {{\mathit{\boldsymbol{s}}_4}} \right)} \right) + {\mathit{\boldsymbol{\widetilde d}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\tilde d}}} - \\ \;\;\;\;\;\;\frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _2} + 1}} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|}^2}}}{2} + \frac{{\sigma _3^2}}{2} - \\ \;\;\;\;\;\;\frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _2} + 1}} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|}^2}}}{2} + \frac{{\sigma _4^2}}{2} = \\ \;\;\;\;\;\; - {2^{\frac{{1 - {\beta _1}}}{2}}}\left( {{k_3}\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|_1^{{\beta _1} + 1} + {k_5}{{\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|}^{{\beta _1} + 1}} + {k_7}{{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|}^{{\beta _1} + 1}}} \right)\\ \;\;\;\;\;\; - {k_4}{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^{{\beta _2} + 1}} - {k_6}{\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|^{{\beta _2} + 1}} - {k_8}{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|^{{\beta _2} + 1}} + {\mathit{\boldsymbol{\widetilde d}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\tilde d}}}\\ \;\;\;\;\;\; - \frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _2} + 1}} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|}^2}}}{2} + \frac{{\sigma _3^2}}{2}\\ \;\;\;\;\;\; - \frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|_{{\beta _1} + 1}^{{\beta _1} + 1} - \frac{1}{\tau }\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|_{{\beta _2} + 1}^{{\beta _2} + 1} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|}^2}}}{2} + \frac{{\sigma _4^2}}{2} + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{s}}_2}{\mathit{\boldsymbol{y}}_3} + {\mathit{\boldsymbol{s}}_3}{\mathit{\boldsymbol{y}}_4} \end{array} $ | (50) |
由定理1可知,当t>t1=max(t11, t12)时,
| $ \begin{array}{l} \dot V \le - {k_4}{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^{{\beta _2} + 1}} - {k_6}\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|_{{\beta _2} + 1}^{{\beta _2} + 1} - {k_8}{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|^{{\beta _2} + 1}} - \\ \;\;\;\;\;{2^{\frac{{1 - {\beta _1}}}{2}}}\left( {{k_3}\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|_1^{{\beta _1} + 1} + {k_5}{{\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|}^{{\beta _1} + 1}} + {k_7}{{\left\| {{{\bf{s}}_4}} \right\|}^{{\beta _1} + 1}}} \right) - \\ \;\;\;\;\;{k_4}{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^{{\beta _2} + 1}} - {k_6}{\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|^{{\beta _2} + 1}} - {k_8}{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|^{{\beta _2} + 1}} - \\ \;\;\;\;\;\frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _2} + 1}} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|}^2}}}{2} + \frac{{\sigma _3^2}}{2} - \\ \;\;\;\;\;\frac{1}{\tau }{2^{\frac{{1 - {\beta _1}}}{2}}}{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _1} + 1}} - \frac{1}{\tau }{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _2} + 1}} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|}^2}}}{2} + \frac{{\sigma _4^2}}{2} + \\ \;\;\;\;\frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2}{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^2} + \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2}{\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^2} + \frac{{{{\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|}^2}}}{2} \end{array} $ | (51) |
考虑不等式:
| $ p \le {p^{{m_1}}} + {p^{{m_2}}} $ | (52) |
式中:p≥0,m1>1,0 < m2 < 1。则式(53)成立
| $ \begin{array}{l} - {n_1}{p^{{m_1}}} - {n_2}{p^{{m_2}}} + {n_3}p \le - \left( {{n_1} - {n_3}} \right){p^{{m_1}}} - \left( {{n_2} - } \right.\\ \;\;\;\;\;\left. {{n_3}} \right){p^{{m_2}}} \end{array} $ | (53) |
式中:n1、n2、n3>0。
基于不等式(53),式(51)可写为
| $ \begin{array}{l} \dot V \le - \left( {{2^{\frac{{1 - {\beta _1}}}{2}}}{k_3} - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2}} \right){\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^{{\beta _1} + 1}} - \left( {2\frac{{1 - {\beta _1}}}{2}{k_5} - \frac{1}{2}} \right){\left\| {{\mathit{\boldsymbol{s}}_3}} \right\|^{{\beta _1} + 1}} - 2\frac{{1 - {\beta _1}}}{2}{k_7}{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|^{{\beta _1} + 1}} - \left( {\frac{{{2^{\frac{{1 - {\beta _1}}}{2}}}}}{\tau } - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\| + 1}}{2}} \right){\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _1} + 1}} - \\ \;\;\;\;\;\;\;\left( {\frac{{2\frac{{1 + n}}{2}}}{\tau } - 1} \right){\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _1} + 1}} - \left( {{k_4} - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2}} \right){\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|^{{\beta _2} + 1}} - \left( {{k_6} - \frac{1}{2}} \right){\left\| {{s_3}} \right\|^{{\beta _2} + 1}} - {k_8}{\left\| {{\mathit{\boldsymbol{s}}_4}} \right\|^{{\beta _2} + 1}} - \\ \;\;\;\;\;\;\;\left( {\frac{1}{\tau } - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\| + 1}}{2}} \right){\left\| {{\mathit{\boldsymbol{y}}_3}} \right\|^{{\beta _2} + 1}} - \left( {\frac{1}{\tau } - 1} \right){\left\| {{\mathit{\boldsymbol{y}}_4}} \right\|^{{\beta _2} + 1}} + \frac{{\sigma _3^2}}{2} + \frac{{\sigma _4^2}}{2} \le - M\left( {\sum\limits_{i = 2}^4 {{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{{\beta _1} + 1}}} + \sum\limits_{i = 3}^4 {{{\left\| {{\mathit{\boldsymbol{y}}_i}} \right\|}^{{\beta _1} + 1}}} } \right) - \\ \;\;\;\;\;\;\;N\left( {\sum\limits_{i = 2}^4 {{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{{\beta _2} + 1}}} + \sum\limits_{i = 3}^4 {{{\left\| {{\mathit{\boldsymbol{y}}_i}} \right\|}^{{\beta _2} + 1}}} } \right) + \sigma \end{array} $ | (54) |
式中:
| $ \left\{ \begin{array}{l} M = \min \left\{ {{2^{\frac{{1 - {\beta _1}}}{2}}}{k_3} - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2},{2^{\frac{{1 - {\beta _1}}}{2}}}{k_5} - \frac{1}{2},{2^{\frac{{1 - {\beta _1}}}{2}}}{k_7},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{2^{\frac{{1 - {\beta _1}}}{2}}}}}{\tau } - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\| + 1}}{2},\frac{{{2^{\frac{{1 - {\beta _1}}}{2}}}}}{\tau } - 1} \right\}\\ N = \min \left\{ {{k_4} - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\|}}{2},{k_6} - \frac{1}{2},{k_8},} \right.\\ \;\;\;\;\;\;\left. {\frac{1}{\tau } - \frac{{\left\| {{\mathit{\boldsymbol{b}}_1}} \right\| + 1}}{2},\frac{1}{\tau } - 1} \right\}\\ \sigma = \frac{{\sigma _3^2}}{2} + \frac{{\sigma _4^2}}{2} \end{array} \right. $ | (55) |
选取合适的制导参数使得M>0,N>0,根据引理5和引理6,可将式(54)重新整理为
| $ \begin{array}{l} \dot V \le - M{\left( {\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{s}}_3^{\rm{T}}{\mathit{\boldsymbol{s}}_3} + \mathit{\boldsymbol{s}}_4^{\rm{T}}{\mathit{\boldsymbol{s}}_4} + \mathit{\boldsymbol{y}}_3^{\rm{T}}{\mathit{\boldsymbol{y}}_3} + \mathit{\boldsymbol{y}}_4^{\rm{T}}{\mathit{\boldsymbol{y}}_4}} \right)^{\frac{{{\beta _1} + 1}}{2}}} - \\ \;\;\;\;\;\;\;{5^{\frac{{1 - {\beta _2}}}{2}}}N{\left( {\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{s}}_3^{\rm{T}}{\mathit{\boldsymbol{s}}_3} + \mathit{\boldsymbol{s}}_4^{\rm{T}}{\mathit{\boldsymbol{s}}_4} + \mathit{\boldsymbol{y}}_3^{\rm{T}}{\mathit{\boldsymbol{y}}_3} + \mathit{\boldsymbol{y}}_4^{\rm{T}}{\mathit{\boldsymbol{y}}_4}} \right)^{\frac{{{\beta _2} + 1}}{2}}} + \\ \;\;\;\;\;\;\;\sigma \le - {K_1}{V^{\frac{{{\beta _1} + 1}}{2}}} - {K_2}{V^{\frac{{{\beta _1} + 1}}{2}}} + \sigma \end{array} $ | (56) |
式中:
由于(β1+1)/2>1,1/2 < (β2+1)/2 < 1,根据引理3可知,系统可固定时间收敛至原点的一个较小邻域
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} = \left\{ {V \le 2{\vartheta _1}\left| {{K_1}\vartheta _1^{\frac{{{\beta _1} + 1}}{2}} + {K_2}\vartheta _1^{\frac{{{\beta _2} + 1}}{2}} = \sigma } \right.} \right\} $ | (57) |
收敛时间满足:
| $ {t_2} < \frac{1}{{{K_1}\left( {{\beta _1} - 1} \right)}} + \frac{1}{{{K_2}\left( {{2^{\frac{{{\beta _2} + 1}}{2}}} - 1} \right)\left( {1 - {\beta _2}} \right)}} $ | (58) |
由式(57)可知,V可固定时间收敛至原点的一个较小邻域内,此时,s2也是固定时间收敛的,通过合理的选取制导参数,可使
1) |x1i|≥δ,式(31)可写为
| $ {{\dot x}_{1i}} = - {k_1}\text{sgn}{^{{\alpha _1}}}\left( {{x_{1i}}} \right) - {k_2}\text{sgn}{^{{\alpha _2}}}\left( {{x_{1i}}} \right) + {\mu _i} $ | (59) |
由引理3可知,x1i能够有限时间收敛至区域
| $ \begin{array}{l} \left| {{x_{2i}}} \right| \le {k_1}{\left| {{x_{1i}}} \right|^{{\alpha _1}}} + {k_2}{\left| {{x_{1i}}} \right|^{{\alpha _2}}} + \left| {{\mu _i}} \right| \le \\ \;\;\;\;{k_1}{\left( {2{\vartheta _{2i}}} \right)^{{\alpha _1}}} + {k_2}{\left( {2{\vartheta _{2i}}} \right)^{{\alpha _2}}} + {\varepsilon _i} \end{array} $ | (60) |
收敛时间满足:
| $ {t_3} < \frac{1}{{{k_1}\left( {{\alpha _1} - 1} \right)}} + \frac{1}{{{k_2}\left( {{2^{{\alpha _2}}} - 1} \right)\left( {1 - {\alpha _2}} \right)}} $ | (61) |
2) |x1i| < δ,由式(31)可得
| $ \begin{array}{l} \left| {{x_{2i}}} \right| \le {k_1}{\left| {{x_{1i}}} \right|^{{\alpha _1}}} + {k_2}\left| {f\left( {{x_{1i}}} \right)} \right| + \left| {{\mu _i}} \right| < \\ \;\;\;\;\;{k_1}{\delta ^{{\alpha _1}}} + {k_2}{\delta ^{{\alpha _2}}} + {\varepsilon _i} \end{array} $ | (62) |
综合分析上述两种情况可得,x1i和x2i收敛至原点的邻域
| $ \left\{ \begin{array}{l} \left| {{x_{1i}}} \right| \le {\kappa _i} = \max \left\{ {2{\vartheta _{2i}},\delta } \right\},{k_1}\vartheta _{2i}^{{\alpha _1}} + \\ \;\;\;\;{k_2}\vartheta _{2i}^{{\alpha _2}} \le {\varepsilon _i}\\ \left| {{x_{2i}}} \right| \le {k_1}\kappa _i^{{a_1}} + {k_2}\kappa _i^{{a_2}} + {\varepsilon _i} \end{array} \right. $ | (63) |
制导系统总收敛时间满足T≤t1+t2+t3,即
| $ \begin{array}{l} T < {t_1} + \frac{1}{{{K_1}\left( {{\beta _1} - 1} \right)}} + \frac{1}{{{K_2}\left( {{2^{\frac{{{\beta _2} + 1}}{2}}} - 1} \right)\left( {1 - {\beta _2}} \right)}} + \\ \;\;\;\;\;\frac{1}{{{k_1}\left( {{\alpha _1} - 1} \right)}} + \frac{1}{{{k_2}\left( {{2^{{\alpha _2}}} - 1} \right)\left( {1 - {\alpha _2}} \right)}} \end{array} $ | (64) |
注6 本文基于反步设计方法和固定时间稳定理论,设计的制导律能够实现系统的固定时间有界性,保证系统状态有限时间收敛至原点的一个较小的邻域内,且收敛时间的上界与系统的初始状态无关。
注7 根据系统收敛时间和收敛域的表达式,可以确定制导参数的调整规则。对于干扰观测器而言,增大λ1、λ2、λ3、γ1,减小γ2可加快观测器的收敛速度,减小收敛时间,但过大的λ1、λ2、λ3、γ1,过小的γ2会导致过大的超调。对于制导律,增大ki(i=1, 2, …, 8)、α1和β1,减小τ、α2和β2能够有效加快收敛速度且提高控制精度,但较大ki(i=1, 2…, 8)、α1和β1,较小τ、α2和β2会产生较大的制导指令,需要导弹提供较大的过载,以满足制导需求。而导弹的可用过载是有限的,因此在参数选取时要折中考虑。
注8 为后文叙述方便,将本文所提考虑驾驶仪动态特性和攻击角度约束的固定时间收敛反步滑模制导律(Fixed-Time Convergent Backstepping Sliding Mode Guidance law, FTCBSMG)。
3 仿真分析本节基于弹道仿真对制导律性能进行仿真分析。设定导弹和目标的初始位置分别为(0 m, 0 m, 0 m)和(10 000 m, 5 000 m, 2 000 m),导弹的速度为vm=500 m/s,目标运动速度为vt=250 m/s。重力加速度g=9.8 m/s2,导弹的最大可用过载为20g。自动驾驶仪动态特性参数设置为:ξ=0.8,ωn=8 rad/s。FTCBSMG的制导参数设置为:k1=1,k2=2,k3=0.1,k4=0.2,α1=5/3,α2=3/5,k5=k6=k7=k8=10,β1=0.5,β2=2,δ=0.001,τ=0.1,λ11=λ12=20,λ21=λ22=50,λ31=λ32=150,L1=L2=50,γ1=0.5,γ2=1.5。仿真步长5 ms,采用4阶Runge-Kutta法对模型进行解算。根据式(64)可计算出制导系统的收敛时间上界为Tmax=13.76 s。
仿真中引入了文献[16]提出的非奇异二阶终端滑模制导律(SONTSMG)以及文献[24]提出的考虑自动驾驶仪动态特性的滑模制导律(ADSMG)进行仿真。SONTSMG的表达式为
| $ \begin{array}{l} u = - \frac{{2\dot r}}{r}{x_2} + \frac{{r\beta }}{\alpha }x_2^{2 - \alpha } + {z_1} + {k_1}{\left| s \right|^{1 - \frac{1}{\gamma }}}\text{sgn}(s) + \\ \;\;\;\;\;{k_2}\int_0^t {\frac{{x_2^{\alpha - 1}}}{r}} {\left| s \right|^{1 - \frac{2}{\gamma }}}\text{sgn}(s){\rm{d}}t \end{array} $ | (65) |
式中:z1为干扰观测器对系统干扰的估计值。参数设置为:k1=1 000,k2=50,α=5/3。β=1,γ=2.1。ADSMG的表达式为
| $ \begin{array}{l} u = \frac{1}{{\omega _n^2}}\left[ { - \frac{{{K_1}\left( {{K_2} + 1} \right){v_{\rm{m}}}\dot r}}{{{\tau _3}{\tau _4}r\cos \left( {q - {\theta _{\rm{m}}}} \right)}}{x_1} + \left( {2\xi {\omega _{\rm{n}}} - {K_4}} \right){x_4} + \frac{{{K_1}{v_{\rm{m}}} - \left( {2 + {K_2}} \right)\dot r}}{{{\tau _3}{\tau _4}\cos \left( {q - {\theta _{\rm{m}}}} \right)}}{x_2} + \left( {\omega _{\rm{n}}^2 - \frac{{{K_3}}}{{{\tau _4}}}} \right){x_3} + } \right.\\ \;\;\;\;\;\;\left. {\frac{{{\tau _3}{K_3} - 1}}{{{\tau _3}{\tau _4}}}{x_{3{\rm{d}}}} + \left( {{K_4} - \frac{1}{{{\tau _4}}}} \right){x_{4{\rm{d}}}} + \left( {\frac{\varepsilon }{{{\tau _3}{\tau _4}\cos \left( {q - {\theta _{\rm{m}}}} \right)}} + \omega _{\rm{n}}^2\rho } \right)\frac{{{x_2}}}{{\left| {{x_2}} \right| + \delta }}} \right] \end{array} $ | (66) |
制导参数设置为:K1=1,K2=K3=K4=10,ε=50,ρ=20,δ=0.001,τ3=τ4=0.1。
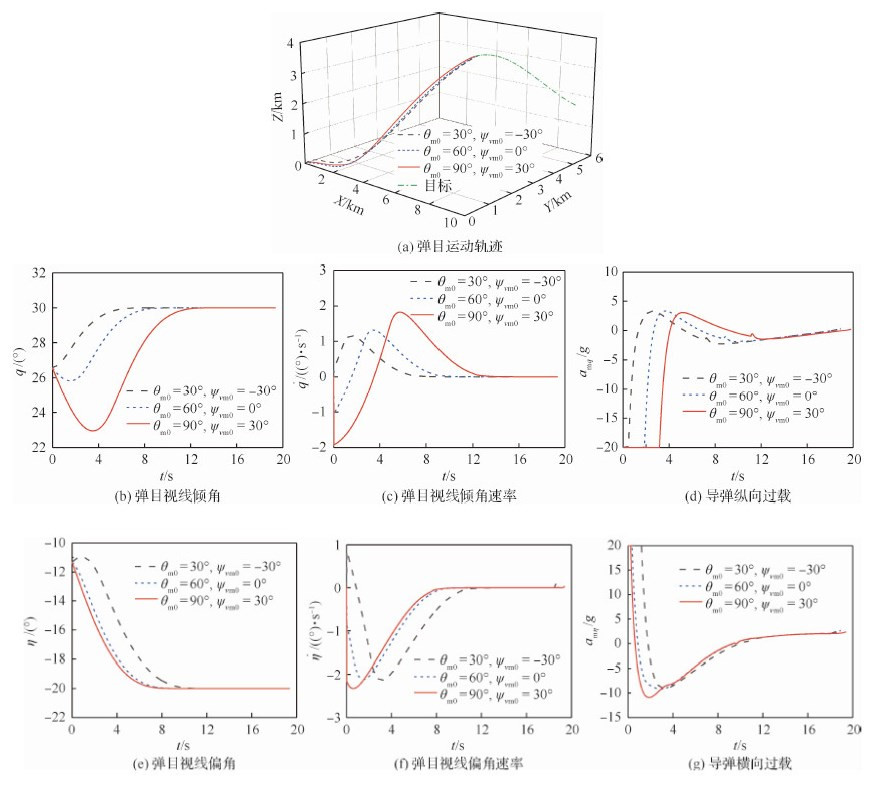
场景1 以不同导弹初始弹道倾角θm0和偏角ψvm0打击机动目标。设定θm0和ψvm0分别为30°和-30°;60°和0°;90°和30°。期望终端视线角qd=30°,ηd=-20°。目标常值机动,加速度为aty2 = atz2 = 20 m/s2,其中aty2和atz2表示目标在弹道坐标系下的纵向和横向加速度,目标初始航迹倾角和偏角分别为θt0 = 180°,ψvt0 = 10°。仿真结果如图 2所示。
|
| 图 2 场景1的仿真结果 Fig. 2 Simulation results of Situation 1 |
由图 2(a)可以看出,在不同初始弹道倾角和偏角下,FTCBSMG都能有效拦截目标,且弹道末段较平直,脱靶量分别为0.52 m、0.46 m和0.63 m。由图 2(b)、图 2(c)、图 2(e)和图 2(f)可知,在FTCBSMG的作用下,q、
场景2 不同的期望终端视线角约束下打击机动目标。设定qd和ηd分别为10°和-10°,20°和-20°、40°和-30°;θm0 = 60°,ψvm0 = 0°,θt0 = 180°,ψvt0 = 0°;目标余弦机动,加速度为aty2 = atz2 = 50cos(πt/5) m/s2。仿真结果如图 3所示。
从图 3(a)可看出,对于不同的qd和ηd,FTCBSMG都能使导弹有效跟踪和拦截目标,实现对目标的精确打击。由图 3(b)、图 3(c)、图 3(e)和图 3(f)可看出,在不同qd和ηd约束下,FTCBSMG都能使q和η在设定的收敛时间Tmax内稳定收敛至qd和ηd附近,

|
| 图 3 场景2的仿真结果 Fig. 3 Simulation results of Situation 2 |
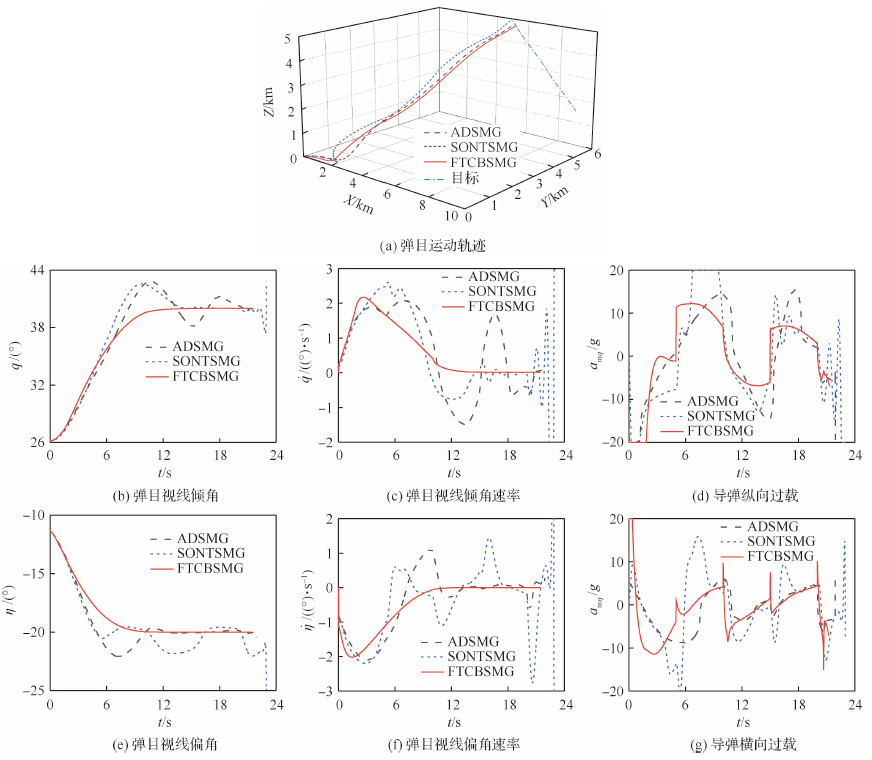
场景3 FTCBSMG和ADSMG、SONTS-MG的对比仿真。θm0 = 45°,ψvm0 = 0°,qd=40°,ηd=-20°,θt0 = 150°,ψvt0 = 10°。目标的机动考虑以下2种情况:
1) 正弦机动:aty2 = atz2 = 50sin(πt/5) m/s2。
2) 方波机动:aty2 = atz2 = 50sgn[sin(πt/5)] m/s2。
引入平均过载Nme(单位:g)来评估制导过程能量消耗,定义为
| $ {N_{{\rm{me}}}} = \frac{1}{K}\sum\limits_{i = 1}^K {\sqrt {a_{{\rm{m}}q}^2\left( i \right) + a_{{\rm{m}}\eta }^2\left( i \right)} } $ | (67) |
式中:K为总仿真步数。
仿真结果如图 4~图 6及表 1所示。由图 4(a)和图 5(a)可以看出,针对不同的目标机动,在3种制导律的作用下,导弹都能够跟踪和拦截目标;相比于ADSMG和SONTSMG,FTCBSMG的轨迹较为平缓,说明其攻击时间较短(由表 1可以验证)。图 4(b)、图 4(c)、图 4(e)、图 4(f)和图 5(b)、图 5(c)、图 5(e)、图 5(f)表明3种制导律都能使q、

|
| 图 4 目标正弦机动下的仿真结果 Fig. 4 Simulation results with target sinusoidal maneuver |
|
| 图 5 目标方波机动下的仿真结果 Fig. 5 Simulation results with target square wave maneuver |
|
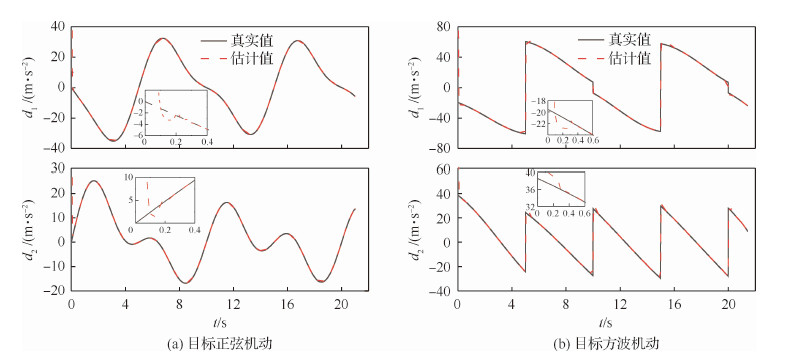
| 图 6 干扰观测器的估计结果 Fig. 6 Estimation results of disturbance observer |
| 目标机动方式 | 制导律 | 攻击时间/s | 脱靶量/m | 视线倾角误差/(°) | 视线偏角误差/(°) | Nme/ g |
| 正弦机动 | ADSMG | 21.90 | 1.06 | 0.26 | 0.15 | 8.6125 |
| SONTSMG | 20.99 | 2.51 | 7.94 | 4.71 | 9.4675 | |
| FTCBSMG | 21.57 | 0.36 | 0.04 | 0.05 | 7.8734 | |
| 方波机动 | ADSMG | 21.93 | 1.51 | 0.22 | 0.45 | 10.1614 |
| SONTSMG | 22.98 | 2.06 | 3.78 | 4.64 | 12.5603 | |
| FTCBSMG | 21.44 | 0.65 | 0.02 | 0.03 | 9.6465 |
图 6为本文所提固定时间收敛滑模干扰观测器对干扰d的估计结果,由式(19)可计算出设定的收敛时间上界为0.48 s,从图 6(a)和图 6(b)可以看出,无论目标正弦机动还是方波机动,所提干扰观测器的估计值都能在0.4 s左右快速收敛至d的真实值上,能够有效补偿干扰,保证制导系统整体的收敛性能。
表 1为在3种制导律作用下的攻击时间、脱靶量、终端视线角误差和平均过载的仿真结果,可以看出,相比ADSMG和SONTSMG,FTCBSMG的攻击时间、脱靶量、终端视线角误差和平均过载最小,说明FTCBSMG能以更短的时间、更高的制导精度和角度约束精度以及更少的能量消耗有效打击目标,验证了本文所提导引律的有效性和优越性。
4 结论本文基于终端滑模控制、固定时间稳定性理论和反步递推方法,设计了一种同时考虑攻击角度约束、自动驾驶仪动态特性和固定时间收敛的制导律。本文所做主要工作与得到的结论如下:
1) 为抵消干扰,设计了一种固定时间收敛滑模干扰观测器,能够实现对目标机动等干扰信息的有效估计,收敛时间上界与初始误差无关,只取决于观测器参数。
2) 针对攻击角度约束问题,设计了一种固定时间收敛的非奇异终端滑模面,能够使系统状态在固定时间内收敛至原点的一个较小邻域内,且邻域范围可控。
3) 针对自动驾驶仪存在动态延迟问题,基于滑模控制和反步设计方法,提出了一种固定时间收敛的反步滑模制导律,能够使弹目视线角和角速率固定时间快速收敛,且收敛时间的上界只取决于制导参数,与初始条件无关。
4) 仿真结果表明,针对不同的导弹初始航迹角和期望视线角,所提制导律都能使导弹以期望的弹目视线角精确打击目标,并且相比现有的制导律,所提制导律具有更高的制导精度和角度约束精度,且收敛时间更短,能量消耗更少。
| [1] | SONG J M, ZHANG T Q. Passive homing missile's variable structure proportional navigation with terminal angular constraint[J]. Chinese Journal of Aeronautics, 2001, 14(2): 83-87. |
| Click to display the text | |
| [2] | KUMAR S R, RAO S, GHOSE D. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J]. Journal of Guidance, Control and Dynamics, 2012, 35(4): 1230-1246. |
| Click to display the text | |
| [3] | ZHOU D, SUN S, TEO K L. Guidance law with finite time convergence[J]. Journal of Guidance, Control and Dynamics, 2009, 32(6): 1838-1846. |
| Click to display the text | |
| [4] | ZHANG Y X, SUN M W, CHEN Z Q. Finite-time convergent guidance law with impact angle constraint based on sliding-mode control[J]. Nonlinear Dynamic, 2012, 70(1): 619-625. |
| Click to display the text | |
| [5] | YU X H, MAN Z H. Fast terminal sliding-mode control design for nonlinear dynamical systems[J]. IEEE Transactions on Circuits and Systems:Fundamental Theory and Applications, 2002, 49(2): 261-264. |
| Click to display the text | |
| [6] | SONG J, SONG S, GUO Y, et al. Nonlinear disturbance observer based fast terminal sliding mode guidance with impact angle constraints[J]. International Journal of Innovative Computing, Information and Control, 2015, 11(3): 787-802. |
| Click to display the text | |
| [7] | ZONG Q, ZHAO Z S, ZHANG J. Higher order sliding mode control with self-tuning law based on integral sliding mode[J]. IET Control Theory and Application, 2008, 4(7): 1282-1289. |
| Click to display the text | |
| [8] | SONG J H, SONG S M. Three-dimensional guidance law based on adaptive integral sliding mode control[J]. Chinese Journal of Aeronautics, 2016, 29(1): 202-214. |
| Click to display the text | |
| [9] | FENG Y, YU X H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. |
| Click to display the text | |
| [10] | SONG J H, SONG S M, ZHOU H B. Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints[J]. International Journal of Control, Automation and Systems, 2016, 14(1): 99-114. |
| Click to display the text | |
| [11] | ZHANG X J, LIU M Y, LI Y. Nonsingular terminal sliding-mode-based guidance law design with impact angle constraints[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2019, 43(1): 47-54. |
| Click to display the text | |
| [12] | POLYAKOV A. Nonlinear feedback design for fixed-time stabilization of linear control systems[J]. IEEE Transactions on Automatic Control, 2012, 57(8): 2106-2110. |
| Click to display the text | |
| [13] | LI H, CAI Y. On SFTSM control with fixed-time convergence[J]. IET Control Theory & Applications, 2017, 11(6): 766-773. |
| Click to display the text | |
| [14] | ZHANG L, WEI C Z, WU R, et al. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle[J]. Aerospace Science and Technology, 2018, 82-83: 70-79. |
| Click to display the text | |
| [15] |
熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快速终端滑模制导律[J]. 控制理论与应用, 2014, 31(3): 269-278. XIONG S F, WANG W H, WANG S. Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J]. Control Theory & Applications, 2014, 31(3): 269-278. (in Chinese) |
| Cited By in Cnki (19) | Click to display the text | |
| [16] | HE S M, LIN D F, WANG J. Continuous second-order sliding mode based impact angle guidance law[J]. Aerospace Science and Technology, 2015, 41: 199-208. |
| Click to display the text | |
| [17] | ZHANG N, GAI W D, ZHONG M Y, et al. A fast finite-time convergent guidance law with nonlinear disturbance observer for unmanned aerial vehicles collision avoidance[J]. Aerospace Science and Technology, 2019, 86: 204-214. |
| Click to display the text | |
| [18] | ZHANG H, HAN J, LUO C, et al. Fault-tolerant control of a nonlinear system based on generalized fuzzy hyperbolic model and adaptive disturbance observer[J]. IEEE Transactions on Systems Man Cybernetics-Systems, 2017, 47(8): 2289-2300. |
| Click to display the text | |
| [19] | YANG Z J. Robust control of nonlinear semi-strict feedback systems using finite-time disturbance observers[J]. International Journal of Robust and Nonlinear Control, 2017, 27(17): 3582-3603. |
| Click to display the text | |
| [20] | GONZALEZ A, BALAGUER V, GARCIA P, et al. Gain-scheduled predictive extended state observer for time-varying delays systems with mismatched disturbance[J]. ISA Transactions, 2019, 84: 206-213. |
| Click to display the text | |
| [21] |
熊少锋, 王卫红, 刘晓东, 等. 考虑导弹自动驾驶仪动态特性的带攻击角度约束制导律[J]. 控制与决策, 2015, 30(4): 585-592. XIONG S F, WANG W H, LIU X D, et al. Impact angle guidance law considering missile's dynamics of autopilot[J]. Control and Decision, 2015, 30(4): 585-592. (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [22] | SUN S, ZHOU D, HOU W T. A guidance law with finite time convergence accounting for autopilot lag[J]. Aerospace Science and Technology, 2013, 25(1): 132-137. |
| Click to display the text | |
| [23] | ZHOU D, QU P P, SUN S. A guidance law with terminal impact angle constraint accounting for missile autopilot[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(5): 051009. |
| Click to display the text | |
| [24] | QU P P, ZHOU D. A dimension reduction observer-based guidance law accounting for dynamics of missile autopilot[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2013, 227(7): 1114-1121. |
| Click to display the text | |
| [25] | HE S M, LIN D F, WANG J. Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets[J]. Nonlinear Dynamics, 2015, 81(1-2): 881-892. |
| Click to display the text | |
| [26] | MEHDI G, IMAN M, AHMAD R V. Finite-time convergent guidance law based on integral backstepping control[J]. Aerospace Science and Technology, 2014, 39: 370-376. |
| Click to display the text | |
| [27] | ZHOU A M. Finite-time output feedback attitude tracking control for rigid spacecraft[[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 338-345. |
| Click to display the text | |
| [28] | LI B, HU Q L, YU Y B, et al. Observer-based fault-tolerant attitude control for rigid spacecraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2572-2582. |
| Click to display the text | |
| [29] | NI J K, LIU L, LIU C X, et al. Fixed-time dynamic surface high-order sliding mode control for chaotic oscillation in power system[J]. Nonlinear Dynamics, 2016, 86(1): 401-420. |
| Click to display the text | |
| [30] | WANG X, GUO J, TANG S J, et al. Fixed-time disturbance observer based fixed-time back-stepping control for an air-breathing hypersonic vehicle[J]. ISA Transactions, 2019, 88: 233-245. |
| Click to display the text | |
| [31] | JIANG B Y, HU Q L, FRISWELL M I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1892-1898. |
| Click to display the text | |
| [32] | BASIN M, PANATHULA C B, SHTESSEL Y. Multivariable continuous fixed-time second-order sliding mode control:design and convergence time estimation[J]. IET Control Theory & Applications, 2017, 11(8): 1104-1111. |
| Click to display the text | |
| [33] | HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance, Control and Dynamics, 2006, 29(6): 1315-1328. |
| Click to display the text | |
| [34] | SHTESSEL Y, EDWARDS C, FRIDMAN L, et al. Sliding mode control and observation[M]. New York: Springer, 2014: 155-158. |
| [35] | UTKIN V. On convergence time and disturbance rejection of super-twisting control[J]. IEEE Transactions on Automatic Control, 2013, 58(8): 2013-2017. |
| Click to display the text | |
| [36] | SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899. |
| Click to display the text |



