近年来,关于平动点任务的研究受到越来越多的关注。本文讨论的平动点属于三体问题范畴,是天体力学领域的基本问题之一。Euler和Lagrange分别在1765年和1772年研究限制性三体问题(Restricted Three Body Problem, RTBP)时,发现RTBP存在5个平衡点,称之为平动点或拉格朗日点[1],其中,位于两个主天体连线上的3个平动点称为共线平动点。由于平动点独特的动力学特性,将航天器部署到平动点上时,航天器在引力作用下,与主天体的相对位置保持不变。然而在真实空间环境下,平动点位置无法被精确确定,而相比于平动点,其附近的周期轨道更适用于航天任务。因此实际任务中通常将航天器部署在平动点附近的轨道上。
平动点的动力学内涵十分丰富[2],在其附近存在着丰富的轨道类型,包括周期轨道(如Lyapunov轨道、Halo轨道等)、拟周期轨道(如Lissajous轨道、拟Halo轨道等)以及不变流形等[3-5]。这些轨道为一些特殊的深空探测任务以及空间低能转移提供了可能。例如,日地L2点因其独特的空间位置和物理环境,为空间望远镜等深空观测卫星提供了良好的部署条件[6];日地L1点位于日地连线之间,是部署太阳活动监测卫星的绝佳地点[7];地月L2点位于地月连线上月球的背面,选择合适的轨道尺寸能够使部署在上面的航天器有效规避月掩,是为地球与月球背面提供中继通信的理想场所[8];此外,平动点在太阳系中广泛存在,这些平动点附近的不变流形相互连接,构成了一系列蜿蜒错综的管道,称为行星际高速公路(InterPlanetary Superhighway, IPS),利用IPS,可以实现行星际的低能转移[9]。
平动点轨道在实际任务中的应用起步相对较晚。1978年,美国航空航天局(NASA)成功发射ISEE-3探测器,是平动点轨道第1次在实际任务中得到应用。以ISEE-3的成功实践为起点,拉开了利用平动点进行深空探测的序幕[10]。在接下来的几十年里,以NASA和欧洲航天局(ESA)为代表的航天机构,先后成功实施了SOHO、ACE、MAP、Genesis、ARTEMIS等多次平动点任务[11],在太阳活动监测、深空观测等领域取得了丰硕的成果。中国先后进行了嫦娥二号、嫦娥五号T1以及“鹊桥”卫星3次平动点任务,其中于2018年成功发射的“鹊桥”通信中继卫星实现了人类历史上首次月背中继通信,为嫦娥四号进行人类首次月背软着陆探测提供了有力支撑。
虽然共线平动点附近存在着丰富的轨道类型,但由于其本身是不稳定的,运行在其附近轨道上的航天器若不施加控制,将会很快偏离标称轨道。因此,设计平动点任务时,进行平动点轨道维持研究十分必要。针对平动点轨道维持问题,许多学者进行了研究,并取得了一些成果。Simo等[12]利用Floquet模态理论针对拟Halo轨道和Halo轨道的维持问题进行了研究;Breakwell等[13]最早利用线性二次型调节器(LQR)方法实现了对Halo轨道的维持控制;Howell和Pernicka[14]提出了利用靶点法维持平动点轨道的策略,并在ARTEMIS任务中得到了应用;Lian等[15]利用离散时间滑模控制实现了对真实星历下地月系平动点轨道的维持控制;Nazari等[16]分别利用时变LQR、退步控制和反馈线性化实现了地月L1附近Halo轨道的维持控制,并对3种方法的仿真结果进行了对比分析;徐明和徐世杰[17]设计了一种线性周期控制策略实现了Halo轨道的维持控制。
基于特征模型的自适应控制方法是由吴宏鑫院士在20世纪80年代初提出的一种从实际应用角度出发的控制方法。经过30多年的发展,不仅在理论上取得了重要进展,同时还成功应用于神舟飞船再入返回控制、交会对接等重大工程中[18]。所谓特征模型,即结合对象动力学特征、环境特征和控制性能要求而不是仅以对象精确动力学分析所建立的模型,其具有以下特点[19]:①在同样控制作用下,对象特征模型和实际对象在输出上是等价的,在稳定情况下,输出是相等的;②特征模型的形式和阶次除考虑对象特征外,主要取决于控制性能要求;③特征模型建立的形式比原对象的动力学方程简单,易于控制器设计,工程实现容易、方便;④特征模型与高阶系统的降阶模型不同,它是把高阶模型有关信息都压缩到几个特征参量中,并不丢失信息,一般情况下用慢时变差分方程描述。
由于三体问题相对于二体问题更为复杂,而基于特征模型的控制方法具有将复杂问题简单化的优势,因此本文基于特征模型理论,研究了地月系L2点附近Halo轨道的维持控制问题。本文结构安排如下:第1节介绍两类动力学模型及标称轨道的获取;第2节介绍黄金分割控制器和PD控制器的设计过程;第3节介绍仿真结果及结果分析;第4节总结全文,给出结论。
1 动力学模型与标称轨道 1.1 圆型限制性三体模型圆型限制性三体问题(Circular Restricted Three Body Problem, CRTBP)是最简化形式的三体问题,其可以描述为:一个质量无穷小的天体在两个大质量天体的引力作用下的运动,其中两个大质量天体(又称为主天体)围绕其公共质心做圆形周期运动。在航天应用领域,常涉及的主天体主要是地球-月球或者太阳-地球/月球。
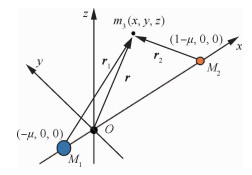
通常在如图 1所示的会合坐标系下对CRTBP进行研究。图中:m3为航天器; M1和M2为两个主天体(M1≥M2); 坐标原点O为它们的公共质心,Ox由M1指向M2,Oz指向M1和M2运动的角动量方向,xOy平面为M1和M2的运动平面,Oxyz构成右手坐标系;r、r1、r2分别为由O、M1和M2指向m3的矢径。为了方便计算,对各物理量进行无量纲化处理。归一化后的质量、长度、时间单位分别为
|
| 图 1 会合坐标系 Fig. 1 Syzygy frame |
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ M \right] = {M_1} + {M_2}}\\ {\left[ L \right] = {L_{12}}}\\ {\left[ T \right] = {{\left[ {\frac{{L_{12}^3}}{{G\left( {{M_1} + {M_2}} \right)}}} \right]}^{\frac{1}{2}}}} \end{array}} \right. $ | (1) |
式中:等式右边的各物理量均采用国际单位制,M1和M2分别为两个主天体的质量;L12为主天体之间的距离;G为万有引力常量,则可得到归一化后的主天体M1和M2的质量分别为1-μ和μ,μ为质量参数,形式为
| $ \mu = \frac{{{M_2}}}{{{M_1} + {M_2}}} $ | (2) |
主天体在会合坐标系中的坐标分别为(-μ, 0, 0)和(1-μ, 0, 0)。在地月系中,μ=0.012 150 585 61。
令[x y z]T为归一化条件下航天器的位置坐标,可以得到CRTBP中m3在会合坐标系中的动力学方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\ddot x - 2\dot y = \frac{{\partial \mathit{\Omega }}}{{\partial x}}}\\ {\ddot y + 2\dot x = \frac{{\partial \mathit{\Omega }}}{{\partial y}}}\\ {\ddot z = \frac{{\partial \mathit{\Omega }}}{{\partial z}}} \end{array}} \right. $ | (3) |
式中:Ω为有效势,其形式为
| $ \mathit{\Omega } = \frac{1}{2}\left( {{x^2} + {y^2}} \right) + \frac{{1 - \mu }}{{{r_1}}} + \frac{\mu }{{{r_2}}} $ | (4) |
其中:r1=||r1||和r2=||r2||分别为航天器与两个主天体之间的距离:
| $ \left\{ {\begin{array}{*{20}{l}} {{r_1} = {{\left[ {{{(x + \mu )}^2} + {y^2} + {z^2}} \right]}^{\frac{1}{2}}}}\\ {{r_2} = {{\left[ {{{(1 - x - \mu )}^2} + {y^2} + {z^2}} \right]}^{\frac{1}{2}}}} \end{array}} \right. $ | (5) |
CRTBP是最理想情况下的简化模型,在实际情况中,航天器在平动点轨道上的运动会受到第四体引力摄动、系统偏心率、太阳光压等摄动因素的影响。对于地月三体系统,太阳引力摄动是影响航天器运动的主要摄动源,因此在CRTBP基础上,引入太阳引力摄动,建立双圆限制性四体模型(BiCircular Restricted Four Body Model, BCRFBM)能够更加精确地模拟真实力学环境。
双圆限制性四体坐标系如图 2所示,在BCRFBM假设下,太阳在地月运动平面内绕系统质心做匀速圆周运动。图中:M4为太阳,坐标轴定义与会合坐标系相同;r、r1、r2、r4分别为由O、M1、M2和M4指向m3的矢径;d4为O指向太阳的矢径,θ4为d4与坐标系x轴的夹角。

|
| 图 2 双圆限制性四体坐标系 Fig. 2 Coordinate system of BCRFBM |
在BCRFBM假设下,航天器m3的动力学方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\ddot x - 2\dot y = \frac{{\partial {\mathit{\Omega }_4}}}{{\partial x}}}\\ {\ddot y + 2\dot x = \frac{{\partial {\mathit{\Omega }_1}}}{{\partial y}}}\\ {\ddot z = \frac{{\partial {\mathit{\Omega }_4}}}{{\partial z}}} \end{array}} \right. $ | (6) |
式中:
| $ \left\{ \begin{array}{l} {\mathit{\Omega }_4} = \frac{1}{2}\left( {{x^2} + {y^2}} \right) + \frac{{1 - \mu }}{{{r_1}}} + \frac{\mu }{{{r_2}}} + \frac{{{\mu _4}}}{{{r_4}}} - \\ \;\;\;\;\;\;\frac{{{\mu _4}}}{{d_4^2}}\left( {x\cos {\theta _4} + y\sin {\theta _4}} \right)\\ {r_4} = {\left[ {{{\left( {x - {d_4}\cos {\theta _4}} \right)}^2} + {{\left( {y - {d_4}\sin {\theta _4}} \right)}^2} + {z^2}} \right]^{\frac{1}{2}}}\\ {\theta _4} = {\omega _4}t + {\theta _{40}} \end{array} \right. $ | (7) |
其中:r4=||r4||; μ4=328 900.54为归一化单位下太阳的质量; ω4=0.925 2为太阳相对系统质心的角速度; θ40为初始时刻太阳相位角; d4=388.811 4为归一化单位下太阳与系统质心的平均距离,其他归一化单位下的参数与CRTBP下相同。
1.3 标称Halo轨道标称轨道是Halo轨道维持研究的基础。Halo轨道是共线平动点附近的一类周期轨道,是水平Lyapunov轨道分岔的结果。由于三体动力学系统具有强非线性特征,无法获得Halo轨道的精确解析解,因此标称轨道通常采用数值积分的方式求解。
数值积分的初值,通常通过修正由近似解析解提供的近似初值获得。Richardson[20]在1980年基于Lindstedt-Poincaré方法推导了Halo轨道的三阶近似解析解,其表达式为
| $ \left\{ \begin{array}{l} x = {a_{21}}A_x^2 + {a_{22}}A_z^2 - {A_x}\cos {\tau _1} + \left( {{a_{23}}A_x^2 - } \right.\\ \;\;\;\;\;\left. {{a_{24}}A_z^2} \right)\cos 2{\tau _1} + \left( {{a_{31}}A_x^3 - {a_{32}}{A_x}A_z^2} \right)\cos 3{\tau _1}\\ y = k{A_x}\sin {\tau _1} + \left( {{b_{21}}A_x^2 - {b_{22}}A_z^2} \right)\sin 2{\tau _1} + \\ \;\;\;\;\;\;\left( {{b_{31}}A_x^3 - {b_{32}}{A_x}A_z^2} \right)\sin 3{\tau _1}\\ z = {\delta _n}\left[ {{A_z}\cos {\tau _1} + {d_{21}}{A_x}{A_z}\left( {\cos 2{\tau _1} - 3} \right) + } \right.\\ \;\;\;\;\;\left. {\left( {{d_{32}}{A_z}A_x^2 - {d_{31}}A_z^3} \right)\cos 3{\tau _1}} \right] \end{array} \right. $ | (8) |
式中:τ1为Halo轨道的线性化相位角,τ1=τ0+ωt,τ0为初始相位角;Ax、Az分别为Halo轨道在平动点旋转坐标系中的线性化振幅,且Ax和Az之间存在限制性条件:
| $ {f_1}A_x^2 + {f_2}A_z^2 + \Delta = 0 $ | (9) |
式(8)和式(9)中的其他各参数定义见文献[20]。
利用式(8)获得的积分初值只是近似初值,直接利用此初值代入动力学方程式(3)中进行数值积分,结果将很快发散。因此,还需对近似初值进行修正,以获得满足精度要求的积分初值。
对近似初值的修正可以采用微分修正的方法进行。由于Halo轨道具有关于xOz平面对称的几何性质,因此选取Halo轨道与xOz平面的一个交点作为轨道初值,记为
| $ {\mathit{\boldsymbol{X}}_0} = {\left[ {\begin{array}{*{20}{l}} {{x_0}}&0&{{z_0}}&0&{{{\dot y}_0}}&0 \end{array}} \right]^{\rm{T}}} $ |
若初值为精确值,则积分半个轨道周期T/2时,轨道第一次穿越xOz平面,且有
| $ {\mathit{\boldsymbol{X}}_{\rm{d}}} = {\left[ {\begin{array}{*{20}{l}} {{x_{\rm{d}}}}&0&{{z_{\rm{d}}}}&0&{{{\dot y}_{\rm{d}}}}&0 \end{array}} \right]^{\rm{T}}} $ |
但由于初值不准确,导致实际Halo轨道穿越xOz平面时,Xd值会偏离精确值。通过调整初值x0、z0和
| $ {y_{\rm{d}}} = 0,{{\dot x}_{\rm{d}}} = 0,{{\dot z}_{\rm{d}}} = 0 $ |
可达到修正初值的效果。实际修正中,可固定z0,简化修正过程,则微分修正量可通过如下形式获得[21]:
| $ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {\delta {{\dot x}_{\text{d}}}} \\ {\delta {{\dot z}_{\text{d}}}} \end{array}} \right] = \left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\Phi }_{41}}}&{{\mathit{\Phi }_{45}}} \\ {{\mathit{\Phi }_{61}}}&{{\mathit{\Phi }_{65}}} \end{array}} \right] - } \right. \hfill \\ \frac{1}{{{{\dot y}_0}}}\left[ {\begin{array}{*{20}{c}} {{{\ddot x}_{\text{d}}}} \\ {{{\ddot z}_{\text{d}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\Phi }_{21}}}&{{\mathit{\Phi }_{25}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta }{x_0}} \\ {{\delta }{y_0}} \end{array}} \right] \hfill \\ \end{gathered} $ | (10) |
式中:
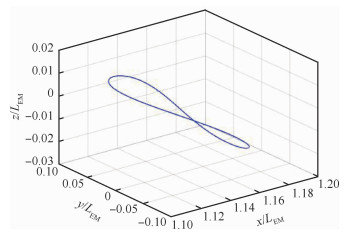
设置Halo轨道z向振幅为Az=0.016 6,依据微分修正方法获得了修正后的积分初值,然后将此初值代入动力学方程式(3),数值积分可得如图 3所示的Halo轨道,其轨道周期在归一化单位下为T=3.412 2,相当于约14.738 6天,图中LEM表示地球与月球之间的距离。
|
| 图 3 微分修正初值之后的Halo轨道 Fig. 3 Halo orbit with initial value obtained by differential correction |
值得注意的是,由于Halo轨道本身是不稳定的,经过微分修正初值后获得的Halo轨道也不是完全闭合的轨道,经过多圈积分之后仍会发散。考虑到实际任务需求,仅依靠微分修正后的Halo轨道作为标称轨道显然无法完成较长时间周期内的轨道维持,因此还需对微分修正后的轨道做进一步的修正,获得一条持续时间较长的标称轨道。
为获得满足需求的标称轨道,本文采用靶点法对Halo轨道进行了进一步的修正。靶点法的基本思想是通过最小化目标函数J,求解使轨道维持在标称轨道附近所需的最小速度脉冲,其中目标函数J是机动速度和靶点状态相对标称轨道偏差的加权和,具有以下形式:
| $ J = \Delta {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\Delta \mathit{\boldsymbol{v}} + \sum\limits_{k = 1}^n {\left( {\mathit{\boldsymbol{p}}_k^{\rm{T}}{\mathit{\boldsymbol{R}}_k}{\mathit{\boldsymbol{p}}_k} + \mathit{\boldsymbol{v}}_k^{\rm{T}}{\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{v}}_k}} \right)} $ | (11) |
式中:Q、Rk和Tk为权值矩阵;pk和vk为航天器在第k个靶点处相对标称轨道的位置和速度偏差,可利用状态转移矩阵Φ(tk, tc)获得
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_k}}\\ {{\mathit{\boldsymbol{v}}_k}} \end{array}} \right] = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{t_k},{t_c}} \right)\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{\rm{c}}}}\\ {{\mathit{\boldsymbol{v}}_{\rm{c}}} + \Delta \mathit{\boldsymbol{v}}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{\rm{c}}}}&{{\mathit{\boldsymbol{B}}_{\rm{c}}}}\\ {{\mathit{\boldsymbol{C}}_{\rm{c}}}}&{{\mathit{\boldsymbol{D}}_{\rm{c}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_{\rm{c}}}}\\ {{\mathit{\boldsymbol{v}}_{\rm{c}}} + \Delta \mathit{\boldsymbol{v}}} \end{array}} \right] \end{array} $ | (12) |
式中:pc和vc为当前时刻tc的位置和速度偏差。将pk和vk代入式(11)中,令
| $ \frac{{\partial J}}{{\partial \Delta \mathit{\boldsymbol{v}}}} = {\bf{0}} $ | (13) |
即可求得Δvmin。
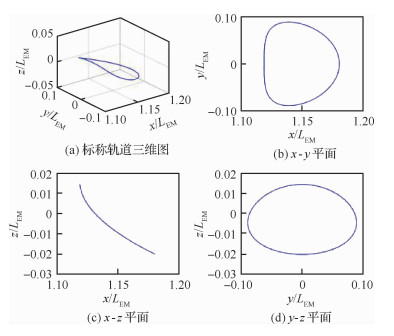
根据上述原理,以微分修正所获得的Halo轨道第一圈为基础,设计三靶点的修正策略,可以得到图 4所示的标称轨道。修正过程中,修正间隔为0.01 T,持续20个周期,图 5给出了速度修正量相对于速度的比例,可以看出除个别情况外,修正量均不超过速度的0.04%,因此可以认为标称轨道是连续的。
|
| 图 4 标称轨道(20周期) Fig. 4 Reference orbit (20 periods) |

|
| 图 5 修正量比例 Fig. 5 Ratio of correction |
令
| $ \mathit{\boldsymbol{\dot X}} = F\left( \mathit{\boldsymbol{X}} \right) + \mathit{\boldsymbol{Bu}} $ | (14) |
式中:
| $ F\left( \mathit{\boldsymbol{X}} \right) = \left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot z}\\ {2\dot y + \frac{{\partial \mathit{\Omega }}}{{\partial x}}}\\ { - 2\dot x + \frac{{\partial \mathit{\Omega }}}{{\partial y}}}\\ {\frac{{\partial \mathit{\Omega }}}{{\partial z}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{l}} {{u_1}}&{{u_2}}&{{u_3}} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]^{\rm{T}}} $ |
其中:u称为控制加速度。
2.1 速度跟踪的多变量黄金分割控制器根据文献[19],对多输入多输出系统建立特征模型,需输入输出同维。由于式(14)中控制量为3维,而为实现Halo轨道维持需要对全状态(6维)进行跟踪,因此无法对全状态建立特征模型,故考虑仅对速度跟踪特征建模。
在采样周期Δt满足一定条件下,速度跟踪的特征模型可用如下输出解耦型二阶差分方程组描述:
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}_1}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_1}\left( k \right){\mathit{\boldsymbol{X}}_1}\left( k \right) + {\mathit{\boldsymbol{F}}_2}\left( k \right){\mathit{\boldsymbol{X}}_1}\left( {k - 1} \right) + \\ {\mathit{\boldsymbol{G}}_0}\left( k \right){\mathit{\boldsymbol{U}}_1}\left( k \right) + {\mathit{\boldsymbol{G}}_1}\left( k \right){\mathit{\boldsymbol{U}}_1}\left( {k - 1} \right) \end{array} $ | (15) |
式中:
| $ {\mathit{\boldsymbol{X}}_1}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{x_1}\left( k \right)}&{{x_2}\left( k \right)}&{{x_3}\left( k \right)} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{U}}_1}\left( k \right) = {\left[ {\begin{array}{*{20}{l}} {{u_{11}}\left( k \right)}&{{u_{12}}\left( k \right)}&{{u_{13}}\left( k \right)} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{F}}_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{f_{11}}\left( k \right)}&0&0\\ 0&{{f_{12}}\left( k \right)}&0\\ 0&0&{{f_{13}}\left( k \right)} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{F}}_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{f_{21}}\left( k \right)}&0&0\\ 0&{{f_{22}}\left( k \right)}&0\\ 0&0&{{f_{23}}\left( k \right)} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{G}}_0}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{g_{0,11}}\left( k \right)}&{{g_{0,12}}\left( k \right)}&{{g_{0,13}}\left( k \right)}\\ {{g_{0,21}}\left( k \right)}&{{g_{0,22}}\left( k \right)}&{{g_{0,23}}\left( k \right)}\\ {{g_{0,31}}\left( k \right)}&{{g_{0,32}}\left( k \right)}&{{g_{0,33}}\left( k \right)} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{G}}_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{g_{1,11}}\left( k \right)}&{{g_{1,12}}\left( k \right)}&{{g_{1,13}}\left( k \right)}\\ {{g_{1,21}}\left( k \right)}&{{g_{1,22}}\left( k \right)}&{{g_{1,23}}\left( k \right)}\\ {{g_{1,31}}\left( k \right)}&{{g_{1,32}}\left( k \right)}&{{g_{1,33}}\left( k \right)} \end{array}} \right] $ |
且有当Δt→0时
| $ {f_{1j}}\left( k \right) \to 2\;\;\;j = 1,2,3 $ |
| $ {f_{2j}}\left( k \right) \to - 1\;\;\;\;j = 1,2,3 $ |
| $ {g_{0,jh}}\left( k \right) \to 0\;\;\;\;j,h = 1,2,3 $ |
| $ {g_{1,jh}}\left( k \right) \to 0\;\;\;\;j,h = 1,2,3 $ |
| $ \sum C = \sum\limits_{l = 1}^2 {{f_{ij}}} \left( k \right) + \sum\limits_{h = 1}^3 {\left[ {{g_{0,jh}}\left( k \right) + {g_{1,jh}}\left( k \right)} \right]} = 1 $ |
式(15)中的特征参量F1(k)、F2(k)、G0(k)和G1(k)由参数估计得到。尽管是多变量,对于式(15)的特征模型仍可按每路独立进行参数估计[19]。每一回路的特征方程可写为
| $ \begin{array}{l} {x_j}\left( k \right) = {f_{1j}}\left( k \right){x_j}(k - 1) + {f_{2j}}(k){x_j}(k - 2) + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{h = 1}^3 {{g_{0,jh}}} (k){u_{1h}}(k - 1) + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{h = 1}^3 {{g_{1,jh}}} (k){u_{1h}}(k - 2) = \phi _j^{\rm{T}}(k - 1){\mathit{\boldsymbol{\widehat \theta }}_j}(k) \end{array} $ | (16) |
式中:
| $ \begin{array}{l} {\phi _j}(k - 1) = \left[ {{x_j}(k - 1)\quad {x_j}(k - 2)\quad {u_{11}}(k - 1)} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{u_{12}}(k - 1)\quad {u_{13}}(k - 1)\quad {u_{11}}(k - 2)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {{u_{12}}(k - 2)\quad {u_{12}}(k - 2)} \right]^{\rm{T}}} \end{array} $ |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat \theta }}}_j}\left( k \right) = \left[ {{{\hat f}_{1j}}\left( k \right)\quad {{\hat f}_{2j}}\left( k \right)\quad {{\hat g}_{0,j1}}\left( k \right)\quad {{\hat g}_{0,j2}}\left( k \right)} \right.\\ \;\;\;\;\;\;\;{\left. {\begin{array}{*{20}{c}} {{{\hat g}_{0,j3}}\left( k \right)}&{{{\hat g}_{1,j1}}\left( k \right)}&{{{\hat g}_{1,j2}}\left( k \right)}&{{{\hat g}_{1,j3}}\left( k \right)} \end{array}} \right]^{\rm{T}}} \end{array} $ |
参数估计采用如下最小二乘递推算法:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{k}}_j}\left( k \right) = \frac{{{\mathit{\boldsymbol{p}}_j}\left( {k - 1} \right){\phi _j}\left( {k - 1} \right)}}{{\lambda + \phi _j^{\rm{T}}\left( {k - 1} \right){\mathit{\boldsymbol{p}}_j}\left( {k - 1} \right){\phi _j}\left( {k - 1} \right)}}\\ {{\mathit{\boldsymbol{\hat \theta }}}_j}\left( k \right) = {{\mathit{\boldsymbol{\hat \theta }}}_j}\left( {k - 1} \right) + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{k}}_j}\left( k \right)\left[ {{x_j}\left( k \right) - \phi _j^{\rm{T}}\left( {k - 1} \right){{\mathit{\boldsymbol{\hat \theta }}}_j}\left( {k - 1} \right)} \right]\\ {\mathit{\boldsymbol{p}}_j}\left( k \right) = \frac{1}{\lambda }\left[ {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{k}}_j}\left( k \right)\phi _j^{\rm{T}}\left( {k - 1} \right)} \right]{\mathit{\boldsymbol{p}}_j}\left( {k - 1} \right) \end{array} \right. $ | (17) |
为了实现速度跟踪,设期望输出为X1r(k),实际输出为X1(k),
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_1}\left( k \right) = - {\left[ {{{\mathit{\boldsymbol{\hat G}}}_0}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right]^{ - 1}}\left[ {{l_1}{{\mathit{\boldsymbol{\hat F}}}_1}\left( k \right){{\mathit{\boldsymbol{\tilde Y}}}_1}\left( k \right) + {l_2} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\mathit{\boldsymbol{\hat F}}}_2}\left( k \right){{\mathit{\boldsymbol{\tilde Y}}}_1}\left( {k - 1} \right) + {{\mathit{\boldsymbol{\hat G}}}_1}\left( k \right){\mathit{\boldsymbol{u}}_1}\left( {k - 1} \right)} \right] \end{array} $ | (18) |
式中:
为了实现Halo轨道的长期维持,除了跟踪速度量以外,还需要实现对位置量的跟踪。上述多变量黄金分割控制控制器设计中仅考虑的速度误差的反馈,因此还需设计控制器引入位置误差反馈。令X2r为期望输出,X2为实际输出,设计如下简单的PD控制器实现位置跟踪:
| $ {\mathit{\boldsymbol{u}}_2} = {\mathit{\boldsymbol{u}}_{\rm{p}}} + {\mathit{\boldsymbol{u}}_{\rm{d}}} $ | (19) |
式中:
| $ {\mathit{\boldsymbol{u}}_{\rm{p}}} = {\mathit{\boldsymbol{K}}_{\rm{p}}}{{\mathit{\boldsymbol{\tilde Y}}}_2}\left( k \right) $ | (20) |
其中:
为了便于调节,ud采用逻辑微分,其形式为
| $ \left\{ \begin{array}{l} {u_{{\rm{d}}j}} = {c_j}\left[ {{x_{2j}}(k) - {x_{2j}}(k - 1)} \right]\sqrt {\sum\limits_{i = 1}^{{N_j}} {\left\{ {{{\left[ {{{\tilde y}_{2j}}(k - i)} \right]}^2} + {{\left[ {{{\tilde y}_{2j}}(k - i) - {{\tilde y}_{2j}}(k - i - 1)} \right]}^2}} \right\}} } \\ {\mathit{\boldsymbol{u}}_{\rm{d}}} = {\rm diag} \left( {{u_{{\rm{d}}1}},{u_{{\rm{d}}2}},{u_{{\rm{d}}3}}} \right) \end{array} \right. $ | (21) |
式中:cj、Nj为常数。
至此,可以得到最终的控制器为
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_1} + {\mathit{\boldsymbol{u}}_2} $ | (22) |
由MIMO特征模型式(15)和黄金分割控制器式(18)组成的闭环系统的稳定性,一直是相关研究学者关注的问题,其中文献[22-23]均给出了闭环系统稳定的充分条件,但该充分条件仍有很大的局限性,因此基于MIMO特征模型的黄金分割控制器的稳定性证明仍有待进一步研究和完善。由于控制器(22)为离散形式,而原系统(14)为连续模型,因此由控制器(22)和原系统组成的闭环系统是一个典型的混杂系统,目前关于混杂系统稳定性证明尚无有效的工具,仍有待进一步研究。基于以上分析,本文中暂不涉及控制器稳定性的证明。
3 仿真结果为了验证第2节中设计的控制器的有效性,选取了地月L2点附近的Halo轨道进行了仿真,并与LQR方法下的仿真结果进行了对比。设置轨道z向振幅为Az=0.016 6,相当于约6 391.5 km;周期为T=3.412 2,相当于14.738 6天;仿真总时长为20个周期,约300天。
3.1 CRTBP模型下的仿真结果针对地月L2点附近的Halo轨道维持控制问题,利用第2节中设计的控制器,首先在CRTBP模型下进行了仿真。考虑到实际任务中,航天器进入Halo轨道时,不可避免地会产生入轨误差,导致实际轨道偏离标称轨道,因此,仿真时设置了初始位置误差和速度误差,其大小为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{X}}_0} = {\left[ {\begin{array}{*{20}{c}} {0.0001}&{0.0001}&{0.0001} \end{array}} \right]^{\rm{T}}}\\ \Delta {\mathit{\boldsymbol{V}}_0} = {\left[ {\begin{array}{*{20}{c}} {0.0001}&{0.0001}&{0.0001} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ |
约相当于国际单位制下的:
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{X}}_0} = {\left[ {\begin{array}{*{20}{c}} {38.44\;{\rm{km}}}&{38.44\;{\rm{km}}}&{38.44\;{\rm{km}}} \end{array}} \right]^{\rm{T}}}\\ \Delta {\mathit{\boldsymbol{V}}_0} = {\left[ {\begin{array}{*{20}{c}} {0.{\rm{1}}\;{\rm{m/s}}}&{0.{\rm{1}}\;{\rm{m/s}}}&{0.{\rm{1}}\;{\rm{m/s}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ |
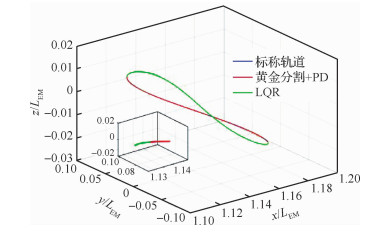
设置系统采样周期为Δt=0.001,仿真结果如图 6所示。
|
| 图 6 CRTBP模型下维持结果 Fig. 6 Station-keeping under CRTBP model |
位置误差曲线和速度误差曲线如图 7(a)和7(b)所示。由图 7(a)可以看出,采用黄金分割控制器和PD控制器的情况下,位置和速度误差均在很短时间内收敛到0;而采用LQR的情况下,速度误差虽然仍能很快收敛,但位置误差则表现出明显的震荡。

|
| 图 7 位置误差、速度误差和控制加速度(CRTBP) Fig. 7 Curves of position errors, velocity errors and control acceleration (CRTBP) |
稳态后采用两种控制器情况下的位置和速度误差均值如表 1所示。由表中数据可以看出,相比于LQR方法,采用本文设计的黄金分割控制器和PD控制器进行轨道维持,位置误差均值和速度误差均值均有显著下降,由此可以说明本文设计的控制器相比于LQR方法具有更高的控制精度。
| 误差 | 控制器 | x轴 | y轴 | z轴 |
| 位置误差均值/m | 黄金分割+PD | 10.345 9 | 7.423 4 | 0.826 9 |
| LQR | 11 007 | 26 557 | 1 124 | |
| 速度误差均值/(m·s-1) | 黄金分割+PD | 0.001 5 | 0.001 2 | 0.000 2 |
| LQR | 0.070 1 | 0.086 1 | 0.005 1 |
控制加速度曲线如图 7(c)所示。可以看出,采用黄金分割控制器和PD控制器情况下,控制加速度最大值出现在起始时刻,之后很快趋向于0;而采用LQR方法情况下,控制加速度则一直相对较小。对控制加速度进行时间积分可得到轨道维持过程中所需要的速度增量,如表 2所示。
| 项目 | 控制器 | 速度增量/(m·s-1) | |||
| x轴 | y轴 | z轴 | 总增量 | ||
| 20个周期 | 黄金分割+PD | 38.376 0 | 80.521 0 | 34.264 5 | 95.513 0 |
| LQR | 30.364 8 | 8.732 6 | 2.182 9 | 31.670 8 | |
| 第1周期 | 黄金分割+PD | 21.057 3 | 62.362 8 | 32.007 6 | 73.191 7 |
| LQR | 1.713 2 | 0.655 8 | 0.297 9 | 1.858 5 | |
| 稳态平均速度增量 | 黄金分割+PD | 0.906 2 | 0.955 7 | 0.118 8 | 1.322 4 |
| LQR | 1.508 0 | 0.425 1 | 0.099 2 | 1.569 9 | |
从表 2中数据可以看出,20个周期的仿真过程中,采用本文设计的控制器,所需要的总速度增量为95.513 0 m/s,采用LQR方法所需要的总速度增量为31.670 8 m/s。由于仿真初值加入了入轨误差,起始阶段为了克服初始误差,需要比较大的控制加速度,同时,由于参数辨识未收敛,也会导致初始控制量较大,采用本文设计的控制器时,第一个周期所需要的速度增量为73.191 7 m/s,相比于LQR方法下的1.858 5 m/s,控制消耗较大。而达到稳态后,采用本文设计的控制器时,每个周期所需要平均速度增量则仅为1.322 4 m/s,相比于第1周期有显著降低;而采用LQR方法,稳态后平均每个周期所需的速度增量为1.569 9 m/s,相比于第1周期也有所下降,但仍高于采用本文设计的控制器时的所需的速度增量。
由此可知,在CRTBP模型下,相比于LQR方法,利用第2节所设计的控制器进行轨道维持,可实现精度较高的控制效果,且进入稳态后,控制消耗较小。另外,提高入轨精度,减小入轨时的位置和速度误差,可以显著降低起始阶段的控制消耗。
3.2 BCRFBM模型下的仿真结果为验证控制器在太阳引力摄动影响下的有效性,本文基于BCRFBM模型,利用第2节设计的控制器以及LQR方法分别进行了仿真。仿真过程中,仍然考虑了入轨误差的影响,初始误差大小与式(23)相同,采样周期同3.1节,初始时刻太阳相位角取θ40=0。仿真结果如图 8所示。

|
| 图 8 BCRFBM模型下维持结果 Fig. 8 Station-keeping results under BCRFBM model |
位置误差曲线、速度误差曲线以及控制加速度曲线如图 9所示。可以看出,采用第2节设计的控制器时,位置和速度误差同CRTBP模型下的仿真结果一样,均能在很短时间内收敛到0;而采用LQR方法时,位置误差和速度误差均呈现明显的震荡,不能收敛。

|
| 图 9 位置误差、速度误差以及控制加速度曲线(BCRFBM) Fig. 9 Curves of position errors, velocity errors and control acceleration (BCRFBM) |
稳态后采用两种控制器情况下的位置和速度误差均值如表 3所示。由表中数据可以看出,采用第2节设计的黄金分割控制器和PD控制器进行轨道维持时,相比于初始误差,位置误差均值和速度误差均值仍能维持在较低的水平;而采用LQR方法时,位置和速度误差均值相比于初始误差均有较大幅度上升。由此可以再次说明本文设计的控制器在控制精度方面的优势。
| 误差 | 控制器 | x轴 | y轴 | z轴 |
| 位置误差/m | 黄金分割+PD | 71.862 3 | 73.483 2 | 1.365 1 |
| LQR | 120 330 | 423 470 | 43 300 | |
| 速度误差/(m·s-1) | 黄金分割+PD | 0.001 7 | 0.002 3 | 0.000 2 |
| LQR | 0.703 5 | 2.153 3 | 0.215 0 |
从控制加速度曲线图可以看出,与CRTBP模型下的仿真结果类似,采用第2节设计的控制器时,由于存在初始误差,且参数辨识尚未收敛,控制加速度在起始时刻较大,之后很快趋向于0;而采用LQR方法,控制加速度一直比较平稳。
对控制加速度进行时间积分可得到轨道维持过程中所需要的速度增量,如表 4所示。从表中数据可以看出,20个周期的仿真过程中,采用第2节设计的控制器时,所需要的总速度增量为745.024 6 m/s;由于仿真初值加入了入轨误差,起始阶段为了克服初始误差,同时由于参数辨识未收敛,需要比较大的控制加速度,第1周期所需要的速度增量为130.037 4 m/s;达到稳态后,每个周期所需要平均速度增量则仅为33.166 3 m/s,相比于第1周期有显著降低。而采用LQR方法时,所需的总速度增量、第1周期所需的速度增量以及稳态后每个周期所需要的平均速度增量,分别为610.551 6、30.294 2和30.544 7 m/s,相比于使用本文设计的控制器情况下均有所下降。
| 项目 | 控制器 | 速度增量/(m·s-1) | |||
| x轴 | y轴 | z轴 | 总增量 | ||
| 20个周期 | 黄金分割+PD | 482.211 7 | 567.592 6 | 19.292 3 | 745.024 6 |
| LQR | 479.282 1 | 377.499 4 | 23.581 8 | 610.551 6 | |
| 第1周期 | 黄金分割+PD | 35.683 9 | 124.328 3 | 13.373 7 | 130.037 4 |
| LQR | 25.119 8 | 16.877 3 | 1.374 9 | 30.294 2 | |
| 稳态平均速度增量 | 黄金分割+PD | 23.501 5 | 23.329 7 | 0.311 5 | 33.166 3 |
| LQR | 23.903 3 | 18.980 1 | 1.168 8 | 30.544 7 | |
与CRTBP模型下仿真结果对比可以看出,采用第2节设计的控制器时,在轨道维持过程中引入太阳引力摄动,所需要的速度增量提升了一个数量级;x轴和y轴的位置跟踪误差同样也提升了一个数量级,分析原因,主要在于太阳引力摄动主要作用于航天器x轴和y轴运动,对z轴运动则影响不大,但考虑到Halo轨道本身尺度较大,这样的位置误差仍是可以接受的;z轴的位置跟踪误差以及三轴的速度跟踪误差则与CRTBP下的仿真结果相差不大。同时,与CRTBP模型下的仿真结果类似,提高入轨精度,起始阶段的控制消耗有望进一步降低。而采用LQR方法时,虽然控制消耗有所下降,但其在消除跟踪误差方面表现很差,因此综合来看,在达到稳态后,本文设计的控制器仍具有优势。
从仿真位置和速度误差来看,本文所设计的控制方法是一种跟踪精度较高的策略。在Halo轨道的维持控制中,控制精度与控制消耗互相制约,更高的控制精度通常也意味着更高的控制消耗。此外,根据文献[24]中的研究结论,标称轨道的精确度与控制消耗密切相关。标称轨道越精确,维持控制所需要的控制消耗则越低。本文所采用的基准Halo轨道是在CRTBP模型下修正的结果,对于考虑太阳引力的BCRFBM模型下的维持控制来说,精确度不够。若能采用更精确的标称轨道,维持控制所需的总的速度增量有望进一步降低。
4 结论本文首先基于Richardson三阶近似解析解、微分修正及打靶法获得了CRTBP模型下的地月L2点附近的标称Halo轨道,然后设计了基于特征模型理论速度跟踪的黄金分割控制器以及位置跟踪的PD控制器,最后分别在CRTBP模型和BCRFBM下进行了地月L2点Halo轨道维持控制仿真,并与LQR方法下的仿真结果进行对比,验证了控制器的有效性。通过分析仿真结果,可以得到以下结论:
1) 在CRTBP模型下,仿真结果跟踪精度较高,控制消耗很小。
2) 在BCRFBM模型下,位置跟踪精度有所下降,但相比于Halo轨道的尺度,仍然可以接受;但由于太阳引力作用以及标称轨道精度影响,控制消耗显著增大。
3) 提高入轨精度,可以显著降低起始阶段的控制消耗。
| [1] |
徐明. 平动点轨道的动力学与控制研究综述[J]. 宇航学报, 2009, 30(4): 1299-1313. XU M. Overview of orbital dynamics and control for libration point orbits[J]. Journal of Astronautics, 2009, 30(4): 1299-1313. (in Chinese) |
| Cited By in Cnki (51) | Click to display the text | |
| [2] |
孟云鹤, 张跃东, 陈琪锋. 平动点航天器动力学与控制[M]. 北京: 科学出版社, 2016: 1-2. MENG Y H, ZHANG Y D, CHEN Q F. Dynamics and control of spacecraft near libration points[M]. Beijing: Science Press, 2016: 1-2. (in Chinese) |
| [3] |
雷汉伦.平动点, 不变流形及低能轨道[D].南京: 南京大学, 2015: 1-2. LEI H L. Equilibrium point, invariant manifold and low-energy trajectory[D]. Nanjing: Nanjing University, 2015: 1-2(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [4] |
钱霙婧.地月空间拟周期轨道上航天器自主导航与轨道保持研究[D].哈尔滨: 哈尔滨工业大学, 2013: 1-14. QIAN Y J. Research on autonomous navigation and station-keeping for quasi-periodic orbit in the Earth-Moon system[D]. Harbin: Harbin Institute of Technology, 2013: 1-14(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [5] |
侯锡云, 刘林. 共线平动点的动力学特征及在深空探测中的应用[J]. 宇航学报, 2008, 29(3): 736-747. HOU X Y, LIU L. The dynamics and applications of the collinear libration points in deep space exploration[J]. Journal of Astronautics, 2008, 29(3): 736-747. (in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [6] | XU M, LIANG Y, REN K. Survey on advances in orbital dynamics and control for libration point orbits[J]. Progress in Aerospace Sciences, 2016, 82: 24-35. |
| Click to display the text | |
| [7] |
周天帅, 李东, 陈新民, 等. 国外日-地动平衡点卫星应用及转移轨道实现方式[J]. 导弹与航天运载技术, 2004, 5: 30-34. ZHOU T S, LI D, CHEN X M, et al. Application of foreign spacecrafts of Sun-Earth libration points and manners of transfer trajectory[J]. Missiles and Space Vehicles, 2004, 5: 30-34. (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [8] | FARQUHAR R W. The control and use of libration-point satellites[R].Washington D.C.: NASA, 1970. |
| [9] | LO M W. The interplanetary superhighway and the orgins program[C]//Proceedings of IEEE Aerospace Conference. Piscataway, NJ: IEEE Press, 2002. |
| [10] |
李明涛.共线平动点任务节能轨道设计与优化[D].北京: 中国科学院, 2010: 2-3. LI M T. Low energy trajectory design and optimization for collinear libration points missions[D]. Beijing: Chinese Academy of Sciences, 2010: 2-3(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [11] | SHIROBOKOV M, TROFIMOV S, OVCHINNIKOV M. Survey of station-keeping techniques for libration point orbtis[J]. Journal of Guidance, Control and Dynamics, 2017, 40(5): 1085-1105. |
| Click to display the text | |
| [12] | SIMO C, GÓMEZ G, LLIBRE J, et al. Station keeping of a quasiperiodic halo orbit using invariant manifolds[C]//Proceedings of the Second International Symposium on Spacecraft Flight Dynamics. Darmstadt: ESA, 1986. |
| [13] | BREAKWELL J V, KAMEL A A, RATNER M J. Station-keeping for a translunar communication station[J]. Celestial Mechanics, 1974, 10: 357-373. |
| Click to display the text | |
| [14] | HOWELL K C, PERNICKA H J. Station-keeping method for libration point trajectories[J]. Journal of Guidance, Control and Dynamics, 1993, 16(1): 151-159. |
| Click to display the text | |
| [15] | LIAN Y, GOMEZ G, MASDEMONT J J, et al. Station-keeping of real Earth-Moon libration point orbits using discrete-time sliding mode control[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(10): 3792-3807. |
| Click to display the text | |
| [16] | NAZARI M, ANTHONY W, BUTCHER E A. Continuous thrust stationkeeping in Earth-Moon L1 halo orbits based on LQR control and Floquet theory[C]//AIAA/AAS Astrodynamics Specialist Conference. Reston, VA: AIAA, 2014. |
| [17] |
徐明, 徐世杰. Halo轨道维持的线性周期控制策略[J]. 航天控制, 2008, 26(3): 13-18. XU M, XU S J. Station-keeping strategy of halo orbit in linear periodic control[J]. Aerospace Control, 2008, 26(3): 13-18. (in Chinese) |
| Cited By in Cnki (18) | Click to display the text | |
| [18] |
孟斌. 基于特征模型的高超声速飞行器自适应控制研究进展[J]. 控制理论与应用, 2014, 31(12): 1640-1649. MENG B. Review of the characteristic model-based hypersonic flight vehicles adaptive control[J]. Control Theory & Applications, 2014, 31(12): 1640-1649. (in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [19] |
吴宏鑫, 胡军, 解永春. 基于特征模型的智能自适应控制[M]. 北京: 中国科学技术出版社, 2009: 1-2. WU H X, HU J, XIE Y C. Characteristic model-based intelligent adaptive control[M]. Beijing: China Science and Technology Press, 2009: 1-2. (in Chinese) |
| [20] | RICHARDSON D L. Analytic construction of periodic orbits about the collinear points[J]. Celestial Mechanics, 1980, 22: 241-253. |
| Click to display the text | |
| [21] | POPESCU M, CARDOS V. The domain of initial conditions for the class of three-dimensional halo periodic orbits[J]. Acta Astronautica, 1995, 36(4): 193-196. |
| Click to display the text | |
| [22] |
齐春子, 吴宏鑫, 吕振铎. 多变量全系数自适应控制系统稳定性的研究[J]. 控制理论与应用, 2000, 17(4): 489-494. QI C Z, WU H X, LV Z D. Study on the stability of multivariable all-coefficient adaptive control system[J]. Control Theory & Applications, 2000, 17(4): 489-494. (in Chinese) |
| Cited By in Cnki (40) | Click to display the text | |
| [23] | SUN D. Stability analysis of golden-section adaptive control systems based on the characteristic model[J]. Science China:Information Sciences, 2017, 60(9): 092205. |
| Click to display the text | |
| [24] | LI C, LIU G, HUANG J, et al. Station-keeping control for collinear libration point orbits using NMPC[C]//AAS/AIAA Astrodynamics Specialist Conference. Reston, VA: AIAA, 2015. |





